INTRODUCTION

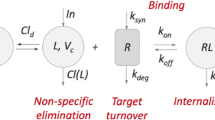
In recent years, target-mediated drug disposition has become an important topic in drug discovery and clinical development (cf. Sugiyama et al. (1), Levy (2), Mager and Jusko (3), Gibiansky et al. (4), Lowe et al. (5), Wagner (6), and also, historically developed for enzyme expression, Michaelis and Menten (7)). Since it combines such diverse processes as drug binding to a target and forming a complex, target turnover, non-specific drug clearance and drug-target complex internalisation, each with its own kinetic process, even the simplest, one-compartment model, such as shown in Fig. 1, displays a rich and complex scala of disposition patterns.

Fig. 1
figure 1

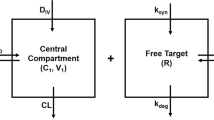
Schematic description of the one-compartment (left) and the two-compartment (right) model for target-mediated drug disposition involving ligand (L) binding target or receptor (R), yielding ligand-target complex (RL), target turnover, non-specific ligand elimination and ligand-complex internalisation. The right-hand model is described in Appendix A

Full size image

This complex disposition pattern in plasma is often captured after intravenous bolus dosing. In Fig. 2, we show schematically the different phases of a compartmental model involving a circulating target and complex (cf. (8)).

Fig. 2
figure 2

Typical pattern for a ligand versus time graph in target-mediated drug disposition after an iv bolus dose. The concentration of the ligand is displayed on a logarithmic scale. Note that linear first-order clearance prevails at high concentrations, when the target is saturated, and at low concentration, when both non-specific and target clearance are involved

Full size image

In the first phase (A), drug and target equilibrate (often rapidly). During the second phase (B), the target route is saturated and drug is mainly eliminated via a first-order non-specific clearance mechanism. During the third phase (C), the target is partly saturated and drug is eliminated via a mixed-order process, and in the final, fourth phase (D), the drug concentration is so low that elimination is a linear first-order process with non-specific as well as elimination through the drug-target complex.

The ubiquitousness of this model in practical situations (cf. (9–15)), as well as the elegance of its structure, has attracted attention from a practical as well as from a theoretical perspective. Important issues included (i) reduction of the model on the basis of the assumption that one or several of the processes have quickly reached equilibrium (cf. (4,16,17)) and (ii) parameter identification on the basis of characteristic features of ligand versus time data sets (cf. (8)) and, to a lesser extent, from ligand-receptor complex data sets.

Hitherto, the main focus has been on the analysis of data sets obtained after a rapid intravenous injection and the analysis of the different phases exhibited by the ligand versus time curves (cf. Peletier and Gabrielsson (8,18)). These disposition curves work well when high-resolution data are available at two or more doses showing phases (A) to (D) (cf. Fig. 2). However, the bioanalytical method may be a limiting factor if the limit of quantification falls above the terminal phase, and consequently reducing the disposition characteristics.

In this paper, we establish the relationships between target R and complex RL as a function of ligand L or input of ligand In. This allows us to directly assess the exposure of ligand (or input rate) that is required to suppress target to a certain extent or build up of target-ligand complex. As an alternative to iv bolus dosing, we also explore the potential use of constant-rate infusions.

METHODS

In the event of a constant-rate infusion protocol, graphs of steady-state values of ligand L ss, receptor R ss and ligand-receptor complex RL ss versus the infusion rate In display interesting characteristics. We present analytical expressions for typical properties of these graphs, such as the height and the slope of the different segments and sharp transitions. These explicit expressions provide an excellent diagnostic tool for studying the impact of the different parameters in the target-mediated drug disposition (TMDD) system.

Basic Model

We focus primarily on the basic, one-compartment version of the TMDD model shown in Fig. 1 (left). In mathematical terms, it is given by the system of differential equations.

$$ \left\{\begin{array}{ll}\frac{dL}{dt}\hfill & =\frac{In}{V}-{k}_{\mathrm{on}} L\cdot R+{k}_{\mathrm{off}} R L-\frac{C{ l}_{(L)}}{V} L\hfill \\ {}\frac{dR}{dt}\hfill & ={k}_{\mathrm{syn}}-{k}_{\deg } R-{k}_{\mathrm{on}} L\cdot R+{k}_{\mathrm{off}} R L\hfill \\ {}\frac{dR L}{dt}\hfill & ={k}_{\mathrm{on}} L\cdot R-\left({k}_{\mathrm{off}}+{k}_{e(RL)}\right) RL\hfill \end{array}\right. $$
(1)

where L, R and RL denote the concentrations of ligand (or drug), target (or receptor) and ligand-target complex, In denotes the infusion rate of ligand and V denotes the volume of the compartment. The rate constants k on and k off denote the second-order on and first-order off rate of ligand-receptor binding and Cl (L) the non-specific clearance of ligand from the central compartment. Through internalisation, ligand-target complex leaves the system according to a first-order process with a rate constant k e(RL). Finally, target synthesis and degradation are modelled by, respectively, zeroth- and first-order turnover rates k syn and k deg.

Analysing this model, it becomes clear that ligand infusion and target synthesis can be viewed as parallel processes, and so do non-specific ligand clearance and internalisation of ligand-target complex. Therefore, these processes are best described by quantities of equal dimension. Thus, we define the scaled ligand infusion rate k infus and non-specific elimination rate constant k e(L):

$$ {k}_{\mathrm{infus}}=\frac{In}{V}\kern2em \mathrm{and}\kern2em {k}_{e(L)}=\frac{C{ l}_{(L)}}{V} $$
(2)

In the presence of a constant-rate infusion of ligand In, the ligand- receptor- and ligand-receptor concentrations converge towards their steady-state concentrations L ss, R ss and RL ss. It turns out that the graphs of these steady-state concentrations versus the infusion rate In have a complex structure and reveal a great deal about the system and its different sub-processes.

Typically, these graphs are linear for high and low infusion rates and exhibit, an often sharp, transition between these regimes. We obtain analytical expressions for the height and the slope of these different segments and the infusion rate where the graphs show a transition. These explicit expressions provide an excellent diagnostic tool for studying the impact of the different parameters in the TMDD system (1).

An important determinant in assessing the dynamics of complex systems is the time it takes to reach, say 90 or 95% of the steady-state value of the concentration when prior to the initiation of the infusion, the system is at baseline, i.e. when

$$ L(0)=0,\kern2em R(0)={R}_0\overset{\mathrm{def}}{=}\frac{k_{\mathrm{syn}}}{k_{\deg }},\kern2em R L(0)=0 $$
(3)

Evidently, this time will depend on the steady-states concentrations L ss, R ss and RL ss, which in turn depend on the infusion rate In.

It is well known that conservation laws and balance equations, in this case of ligand and target, are useful in analysing the TMDD system ((3,4,8)). The total amount of ligand (L tot) and of receptor (R tot), given by

$$ {L}_{\mathrm{tot}}= L+ R L\kern2em \mathrm{and}\kern2em {R}_{\mathrm{tot}}= R+ R L $$
(4)

are seen to satisfy the following pair of equations:

$$ \left\{\begin{array}{ll}\frac{d{ L}_{\mathrm{tot}}}{ d t}\hfill & ={k}_{\mathrm{infus}}-{k}_{e(L)} L-{k}_{e(RL)} R L\hfill \\ {}\frac{d{ R}_{\mathrm{tot}}}{ d t}\hfill & ={k}_{\mathrm{syn}}-{k}_{\deg } R-{k}_{e(RL)} R L\hfill \end{array}\right. $$
(5)

in which, conveniently, the on and off rates of ligand-receptor binding, k on and k off, no longer appear. We recall from (8) that the total receptor concentration is limited, irrespective of the amount of ligand supplied. Specifically, it was shown that for all t ≥0,

$$ {R}_{\mathrm{tot}}(t)\le \max \left\{{R}_0,{R}_{\ast}\right\}\kern2em \mathrm{where}\kern2em {R}_{\ast}\overset{\mathrm{def}}{=}\frac{k_{\mathrm{syn}}}{k_{e(RL)}}=\frac{k_{\deg }}{k_{e(RL)}}{R}_0 $$
(6)

Thus, R * is the universal maximum of the total target concentration; it is a fundamental target concentration, such as the baseline target concentration R 0.

RESULTS

Equilibrium Relationships

We use the disposition parameters obtained from a bolus experiment (cf. (8)) in order to predict the equilibrium relationships between ligand, receptor, ligand-receptor complex and infusion rate. They are listed in Table I below.

Table I Parameter Values Used in Simulations
Full size table

In order to acquire an impression of the way these concentrations depend on the infusion rate, we show graphs of these equilibrium concentrations versus the infusion rate in Fig. 3 for the parameter values listed in Table I. In the left panel, the concentrations are given on a linear scale; in the right panel, they are given on a log-log scale.

Fig. 3
figure 3

The steady-state concentrations L ss, R ss and RL ss graphed versus the infusion rate k infus, on a linear scale (left) and on a log-log scale (right) for parameter values taken from Table I. (MatLab code: tmdd5infus1a.m)

Full size image

These graphs clearly reveal some of the intrinsic properties of the TMDD model: a two-phase ligand curve which displays a linear concentration versus infusion rate relationship at low and high infusion rates joined by an intermediate range of infusion rates in which the nonlinear contribution of the target route kicks in (compare with Fig. 2). When clearance through the target route becomes saturated, as k infus = In/V approaches k syn, the ligand concentration increases disproportionately with increasing infusion rate. At high infusion rates, disposition is linear again and there exist proportionality between ligand concentration and infusion rate (except for a shift). This behaviour is not intuitive by observing the ligand concentration-time course after a bolus dose.

As shown in Fig. 3, the steady-state ligand concentration increases monotonically with increasing infusion rate. Therefore, it is also possible to view R ss and RL ss as functions of the ligand concentration L ss. The graphs of these functions are shown in Fig. 4 with ligand concentration on a logarithmic scale and the concentrations of receptor and ligand-receptor complex on a linear scale. This is done for two data sets: on the left for data taken from Peletier and Gabrielsson (8) and Gabrielsson and Weiner (15) given in Table I, and on the right for data from (19), given in Table II:

Fig. 4
figure 4

RL ss and R ss versus L ss for the parameter values of Peletier and Gabrielsson (8) in Table I (left) and for those of Cao and Jusko (19) in Table II (right). The parameter L 50 is given by Eq. (20). It is a conglomerate of target turnover properties, binding properties and removal of complex

Full size image
Table II Parameter Values Cao and Jusko (2014) (19)
Full size table

In both graphs, the receptor concentration R ss approaches the baseline receptor concentration R 0 as the ligand concentration drops down to zero and vanishes when the ligand concentration becomes large. Similarly, the complex concentration RL ss first increases and then approaches a plateau when ligand concentrations become large. The ligand concentration L 50 at which half of the maximum value of receptor as well as of complex is attained appears to be close to 0.1 mg/L.

Note that in the two figures, the order of R * and R 0 is different. As we see from (6), the relative magnitude of R * and R 0 is determined by the two receptor elimination rate constants: k deg and k e(RL). In Table I, k deg > k e(RL) and hence R ∗ > R 0, and in Table II, it is the other way around.

Explanations of the Graphs in Figs. 3 and 4

In order to explain and quantify some of the properties of the curves for L ss, R ss and RL ss shown in Figs. 3 and 4, the equations for the total amount of ligand and receptor (4) offer a good starting point. The two equations of the system (5) yield the following relations between the steady-state concentrations:

$$ \left\{\begin{array}{ll}{L}_{\mathrm{ss}}\hfill & =\frac{1}{k_{e(L)}}\left({k}_{\mathrm{infus}}-{k}_{e(RL)} R{L}_{\mathrm{ss}}\right)\hfill \\ {}{R}_{\mathrm{ss}}\hfill & =\frac{1}{k_{\deg }}\left({k}_{\mathrm{syn}}-{k}_{e(RL)} R{L}_{\mathrm{ss}}\right)\hfill \end{array}\right. $$
(7)

We see that as the ligand-receptor concentration RL ss increases, the receptor concentration R ss decreases. However, at some point the receptor pool is exhausted. Since clearly R ss ≥ 0, the second equation of (7) implies that

$$ R{L}_{\mathrm{ss}}\le {R}_{\ast }=\frac{k_{\mathrm{syn}}}{k_{e(RL)}} $$
(8)

Therefore, when R ss has dropped to zero, no further rise in complex formation is seen and the concentration remains at a plateau RL ss ≈ R ∗ for larger infusion rates.

Thus, if the therapeutic (or pharmacodynamic) response depends on complex formation (complex exposure), increasing the ligand infusion rate much above the endogenous target synthesis k syn rate will no longer increase the complex concentration.

Because of their complex and non-trivial structure, the graphs shown in Figs. 3 and 4 can reveal a great deal of information about the processes involved in the TMDD model. Much of this information can be extracted from the explicit expressions that can be derived for L ss, R ss and RL ss. Evidently, thanks to the two relations in (7), it is sufficient to derive an expression for RL ss. This is done by equating each of the right hand sides of the equations in the system (1) to zero. Then, using (7) to eliminate the steady-state values of L and R, one obtains a quadratic equation in RL ss. Solving this equation yields the expression:

$$ R{L}_{\mathrm{ss}}=\frac{1}{2{k}_{e(RL)}}\left\{{k}_{\mathrm{infus}}+{k}_{\mathrm{syn}}\left(1+\theta \cdot {\kappa}_m\right)-\sqrt{{\left\{{k}_{\mathrm{infus}}+{k}_{\mathrm{syn}}\left(1+\theta \cdot {\kappa}_m\right)\right\}}^2-4{k}_{\mathrm{infus}}{k}_{\mathrm{syn}}}\right\}, $$
(9)

in which

$$ {k}_{\mathrm{infus}}=\frac{In}{V},\kern2em \theta =\frac{k_{e(L)}}{k_{e(RL)}},\kern2em {\kappa}_m=\frac{K_m}{R_0}\kern2em \mathrm{and}\kern2em {K}_m=\frac{k_{\mathrm{off}}+{k}_{e(RL)}}{k_{\mathrm{on}}} $$
(10)

A detailed derivation of this formula for RL ss can be found in Appendix B.

Expressions for Small and Large Infusion Rates

By an elementary computation we deduce from the expression given in (9), the following limiting behaviour for RL ss when k infus becomes large and when it becomes smallFootnote 1:

$$ \left\{\begin{array}{lll} R{L}_{\mathrm{ss}}\hfill & \to \frac{k_{\mathrm{syn}}}{k_{e(RL)}}={R}_{\ast}\hfill & \mathrm{as}\kern2em {k}_{\mathrm{infus}}\to \infty \hfill \\ {} R{L}_{\mathrm{ss}}\hfill & \sim \frac{1}{k_{e(RL)}}\frac{R_0}{R_0+\frac{k_{e(L)}}{k_{e(RL)}}{K}_m}\cdot {k}_{\mathrm{infus}}\hfill & \mathrm{as}\kern2em {k}_{\mathrm{infus}}\to 0\hfill \end{array}\right. $$
(11)

Clearly, as more ligand is supplied to the system, more of it binds to the receptor and eventually, the free receptor pool is consumed. According to (7), (8) and (11) this means that RL ss approaches R * from below as the ligand concentration L ss increases.

For small values of ligand, i.e. when k infus is small, ligand is eliminated directly through non-specific elimination (k e(L)) and through internalisation of the receptor (k e(RL)). Evidently, when the non-specific route dominates, i.e. k e(L) is large, there will be little ligand left to bind to the receptor and RL ss will be small. In the limits shown in (11), we see this trend confirmed and quantified. Conversely, when the non-specific route is limited, most of the elimination takes place through internalisation, with its associated rate constant (k e(RL)). Similarly, when k on is large and hence K m small, most of the ligand rapidly binds the receptor and will be eliminated through internalisation, as shown in Eq. (11).

For L ss, the first equation of (7), in combination with (11), yields:

$$ \left\{\begin{array}{lll}{L}_{\mathrm{ss}}\hfill & \sim \frac{1}{k_{e(L)}}\left({k}_{\mathrm{infus}}-{k}_{\mathrm{syn}}\right)\hfill & \mathrm{as}\kern2em {k}_{\mathrm{infus}}\to \infty \hfill \\ {}{L}_{\mathrm{ss}}\hfill & \sim \frac{1}{k_{e(L)}}\frac{\frac{k_{e(L)}}{k_{e(RL)}}{K}_m}{R_0+\frac{k_{e(L)}}{k_{e(RL)}}{K}_m}\cdot {k}_{\mathrm{infus}}\hfill & \mathrm{as}\kern2em {k}_{\mathrm{infus}}\to 0\hfill \end{array}\right. $$
(12)

and for R ss, the second equation of (7) and (11) yields:

$$ \left\{\begin{array}{lll}{R}_{\mathrm{ss}}\hfill & \to 0\hfill & \mathrm{as}\kern2em {k}_{\mathrm{infus}}\to \infty \hfill \\ {}{R}_{\mathrm{ss}}\hfill & \sim {R}_0\left(1-\frac{R_0}{R_0+\frac{k_{e(L)}}{k_{e(RL)}}{K}_m}\cdot {k}_{\mathrm{infus}}\right)\hfill & \mathrm{as}\kern2em {k}_{\mathrm{infus}}\to 0\hfill \end{array}\right. $$
(13)

In order to understand the ligand curves in the right hand panel of Fig. 3 where L ss and k infus are both plotted on a logarithmic scale, we translate the limits in (12) to the logarithmic coordinates. This yields the following limits:

$$ \left\{\begin{array}{lll} \ln \left({L}_{\mathrm{ss}}\right)\hfill & \sim \ln \left({k}_{\mathrm{infus}}\right)- \ln \left({k}_{e(L)}\right)\hfill & \mathrm{as}\kern2em {k}_{\mathrm{infus}}\to \infty \hfill \\ {} \ln \left({L}_{\mathrm{ss}}\right)\hfill & \sim \ln \left({k}_{\mathrm{infus}}\right)- \ln \left({k}_{e(L)}\right)- \ln\ \left(1+\frac{k_{e(RL)}}{k_{e(L)}}\frac{R_0}{K_m}\right)\hfill & \mathrm{as}\kern2em {k}_{\mathrm{infus}}\to 0\hfill \end{array}\right. $$
(14)

Thus, at the high and the low end, the logarithmic ligand graph of Fig. 3 approaches parallel straight lines L+ and L− − with slope +1: for small ligand, it is L− and for large ligand, it is L+. By (14), the line L− is seen to be lower than L− by an amount ∆ L given by

$$ {\Delta}_L= \ln\ \left(1+\frac{k_{e(RL)}}{k_{e(L)}}\frac{R_0}{K_m}\right) $$
(15)

The lines L+. and L− with slope +1 and the shift ∆ L between them are illustrated in Fig. 5.

Fig. 5
figure 5

Steady-state ligand concentration L ss versus the ligand infusion rate In on a log-log scale demonstrating the two parallel lines L+ and L− with slope +1 and the relative shift ∆ L

Full size image

Singular Behaviour at the Transition

An interesting feature of the three curves for L ss, R ss and RL ss in the left panel of Fig. 3 is that they are approximately piecewise-linear with a kink in each of them, close to the infusion rate where R ss vanishes.

The reason for this special shape is the fact that for the parameter values given in Table I, the dimensionless constant κ m  = K m /R 0 is very small, and the two elimination rates k e(L) and k e(RL) are comparable (κ m  = 0.0037 and k e(RL) = 2k e(L)). Expanding the expression for RL ss in (9) in terms of small values of κ m , we obtain

$$ R{L}_{\mathrm{ss}}\left({\kappa}_m\right)\to \left\{\begin{array}{ll}\frac{k_{i\mathrm{nfus}}}{k_{e(RL)}}\hfill & \mathrm{if}\kern2em {k}_{\mathrm{infus}}<{k}_{\mathrm{syn}}\hfill \\ {}\frac{k_{\mathrm{syn}}}{k_{e(RL)}}\hfill & \mathrm{if}\kern2em {k}_{\mathrm{infus}}>{k}_{\mathrm{syn}}\hfill \end{array}\right.\mathrm{a}\mathrm{s}\kern1em {\kappa}_m\to 0 $$
(16)

Details of the derivation of the two limits are given in Appendix B.

By the expressions (7) for L ss and R ss in terms of RL ss, this implies that as κ m  → 0,

$$ {L}_{\mathrm{ss}}\left({\kappa}_m\right)\to \left\{\begin{array}{ll}0\hfill & \mathrm{if}\kern2em {k}_{\mathrm{infus}}<{k}_{\mathrm{syn}}\hfill \\ {}\frac{1}{k_{e(L)}}\left({k}_{\mathrm{infus}}-{k}_{\mathrm{syn}}\right)\hfill & \mathrm{if}\kern2em {k}_{\mathrm{infus}}>{k}_{\mathrm{syn}}\hfill \end{array}\right. $$
(17)

and

$$ {R}_{\mathrm{ss}}\left({\kappa}_m\right)\to \left\{\begin{array}{ll}\frac{1}{k_{\deg }}\left({k}_{\mathrm{syn}}-{k}_{\mathrm{infus}}\right)\hfill & \mathrm{if}\kern2em {k}_{\mathrm{infus}}<{k}_{\mathrm{syn}}\hfill \\ {}0\hfill & \mathrm{if}\kern2em {k}_{\mathrm{infus}}>{k}_{\mathrm{syn}}\hfill \end{array}\right. $$
(18)

These expressions explain the singular character of the graphs shown in Fig. 3.

Relation Between Equilibrium Concentrations of RL and R, and L

Whereas in the previous formula’s RL ss, R ss and L ss were expressed as functions of k infus, it is also possible to express RL ss and R ss as functions of L ss. Since the ligand concentration L ss increases monotonically with the infusion rate k infus, the function L ss(k infus) may be inverted to yield a function of the form k infus(L ss). Substituting this function into (9), we obtain the desired relation between RL ss and L ss. Using (7), this also gives the relation between R ss and L ss. These relations are shown graphically in Fig. 4 for the parameter values of Tables I and II.

In fact, the resulting relations prove surprisingly simple, they are:

$$ R{L}_{\mathrm{ss}}={R}_{\ast}\frac{L_{\mathrm{ss}}}{L_{\mathrm{ss}}+{L}_{50}}\kern2em \mathrm{and}\kern2em {R}_{\mathrm{ss}}={R}_0\frac{L_{50}}{L_{\mathrm{ss}}+{L}_{50}} $$
(19)

in which

$$ {R}_{*}=\frac{k_{\mathrm{syn}}}{k_{e(RL)}}=\frac{k_{\deg }}{k_{e(RL)}}\cdot {R}_0\kern2em \mathrm{and}\kern2em {L}_{50}=\frac{k_{\deg }}{k_{e(RL)}}\cdot {K}_m $$
(20)

The details of this derivation are given in Appendix B. Thus, the L 50 parameter can be directly estimated from data obtained after iv bolus dosing (cf. Tables I and II).

Disposition from a Clearance Perspective

One may also approach the impact of the ligand infusion rate on the steady-state ligand concentration L ss through the notion of clearance, which is related to L ss by:

$$ {L}_{\mathrm{ss}}=\frac{In}{CL}=\frac{k_{\mathrm{infus}}\cdot V}{CL} $$
(21)

At low ligand exposure (Fig. 6 (left), at 1), the target route of elimination is not saturated and total clearance of ligand CL is the sum of two first-order processes, namely non-specific clearance Cl (L) and a first-order clearance via the target route Cl (RL), i.e.

$$ C L\to C{l}_{e(L)}+ C{l}_{e(RL)}\kern2em \mathrm{a}\mathrm{s}\kern2em In\to 0 $$
(22)
Fig. 6
figure 6

Left: Clearance of ligand CL as a function of ligand concentration L ss . Right: Ligand steady-state concentration L ss as a function of ligand infusion rate In. At low ligand concentrations L ss and infusion rates (1), the elimination of ligand is first-order and clearance is constant. When ligand concentrations increase the disposition of ligand becomes mixed-order (2), and at high ligand concentrations (3) only non-specific first-order elimination of ligand prevails

Full size image

Using the limiting behaviour of L ss as k infus tend to zero from Eq. (12) and the relation between Cl (L) and k e(L) from Eq. (2), we find that

$$ C{l}_{(RL)}={k}_{e(RL)}\frac{R_0}{K_m}\cdot V=\frac{k_{e(RL)}}{k_{\mathrm{off}}+{k}_{e(RL)}}{k}_{\mathrm{on}}{R}_0\cdot V $$
(23)

At high exposure (Fig. 6 (left), at 3), the target route is saturated and only first-order non-specific clearance remains, i.e.

$$ C L\to C{l}_{(L)}\kern2em \mathrm{a}\mathrm{s}\kern2em In\to \infty $$
(24)

Again, ligand disposition follows first-order kinetics. Between these two exposure ranges (Fig. 6 (left), at 2), a mixed-order elimination process dominates where the target route clearance is concentration-dependent.

One may compare this diagram with a diagram showing ligand concentration at steady state as a function of infusion rate of ligand (Fig. 6, right), as is done in the graphs shown in Fig. 3. The two phases show up here as different slopes: at low infusion rates and hence low ligand concentrations, CL is high and hence the slope is small, whilst for high infusion rates, the slope is large.

At intermediate concentrations, the system behaves as a nonlinear system. Slope is getting higher because clearance is getting lower and approaches eventually that of non-specific clearance.

Evidently, Cl (RL) increases with increasing internalisation rate k e(RL), although, clearly, Cl (RL) is bounded by the amount of target and the rate of the ligand binds to the target:

$$ C{l}_{(RL)}\to {k}_{\mathrm{on}}{R}_0\cdot V\kern2em \mathrm{a}\mathrm{s}\kern2em {k}_{e(RL)}\to \infty $$
(25)

Note that Cl (RL) depends linearly on the target expression level R 0 = k syn/k deg, i.e. the target baseline concentration. Therefore, the higher the target turnover the higher the clearance via the target route becomes. In two subjects with the same target level expression R 0, but with different turnover rates (and target half-lives), clearance via target will be highest when turnover of target is highest. It follows from the expression in (21) that the same limit for Cl (RL) holds if the dissociation rate K d  = k off/k on tends to zero.

For the parameter values of Table I, the limits in (22) and (25) are CL → 0.0015 L/h as In → ∞ and CL → 0.82 L/h as In → 0. These limits are confirmed by the simulated clearance versus infusion rate graphs shown in Fig. 7 below.

Fig. 7
figure 7

Clearance CL ss  = In/L ss graphed versus the infusion rate k infus, on a log-log scale for parameter values taken from Table I. Note the sharp transition at k infus  = k syn  = 0.11 (mg/L) h− 1

Full size image

The limiting expressions for CL shown in Eqs. (22) and (24) clearly reveal the relative importance of the two clearance mechanisms: non-specific clearance (Cl (L)) is present for all infusion rates (or ligand concentrations) while target mediated clearance (Cl (L) + Cl (RL)) becomes significant for smaller infusion rates (cf. Fig. 7).

We have highlighted different aspects of target-mediated drug disposition at different steady-state concentrations of ligand L ss, target R ss and complex RL ss. Thus, we have seen that equilibrium relationships reveal interesting (diagnostic) patterns.

While this manner of dosing may not be the primary regimen, we envision that certain experimental situations may benefit from it, particularly when studying the impact of a slow or fast target turnover process or when further knowledge about target turnover is sought, or when the limit of detection of ligand, target or complex is above the terminal phase.

Time to Steady-State

Whereas so far we have focussed on the steady-state concentrations of the compounds as they are impacted on by a constant ligand infusion rate In or k infus, we here discuss what determines the time to steady-state, e.g. the time it takes the ligand concentration L(t) to reach 90% of steady state when the infusion is switched on and to drop to 10% of the steady-state value when the infusion is switched off. For practical as well as diagnostic purposes, this is an important quantity. For instance, in questions involving disease progression, it is important to make long-term predictions on the basis of relatively short-term data sets.

In nonlinear models, one can often distinguish different phases in the concentration-time courses, such as a fast and a slow phase, associated with different sub-processes. Such a structure may offer a handle to acquire detailed quantitative information about the disposition. This, in turn, may then yield estimates for parameters involved in the system. In the absence of such a clear structure, one may have to rely on simulations as shown in Fig. 8 or merely on limiting situations, such as large or small infusion rates.

Fig. 8
figure 8

Ligand versus time graphs, scaled with respect to their limiting value L ss, for infusion rates that straddle the critical rate k infus  = k syn . In this example, k syn  = 0.11 h− 1 (cf. Table I)

Full size image

Simulations for Small and Large Rates of Infusion

In order to acquire a first impression about the manner in which the ligand concentration L(t) approaches its steady-state L ss, and in particular, how long it takes to do so, we show in Fig. 8 a series of ligand versus time graphs for different infusion rates k infus, where L is normalised with respect to its large time limit L ss. Thus, by construction, for each infusion rate, \( x(t)\overset{\mathrm{def}}{=} L(t)/{L}_{\mathrm{ss}}\to 1 \) as t → ∞.

Figure 8 displays a rich scala of different ligand versus time graphs, as the infusion rate k infus increases: on the left, the normalised ligand concentration x(t) and on the right, the difference between the scaled ligand concentration and its limit, 1−x(t), to assess the rate of convergence. We make the following observations:

  • For smaller infusion rates, specifically for k infus < k syn, the graphs show a clear two-phase structure: a very rapid upswing towards an intermediate value \( \overline{L} \), which we refer to as the plateau value, followed by a much more gradual rise towards the steady-state L ss. As the infusion rate increases, the plateau value is seen to decrease, and as k infus ≈ k syn, then \( \overline{L}\approx 0 \) and the two-phase structure is no longer in evidence.

  • For larger infusion rates, k infus > k syn, the right hand panel of Fig. 8 suggests that the scaled ligand concentration L(t)/L ss follows a mono-exponential graph for all time 0 < t < ∞. This graph does not appear to change much as the infusion rate increases further.

  • Note that for k infus ≈ k syn the ligand graphs in Fig. 8 show anomalous dependence on the infusion rate: for small values of k infus, the ligand curves drop as k infus increases, but this trend is reversed when k infus comes close to k syn.

  • The half-life of the ultimate convergence towards the steady state differs for small and for large infusion rates. For the parameter values of Table I, the half-life is shorter for small infusion rates than it is for large infusion rates.

Summarising, the nonlinearity of the TMDD system (1) is evident from Fig. 8; it shows how the disposition changes qualitatively as well as quantitatively as the infusion rate goes from small to large, in relation to the endogenous target synthesis rate k syn.

Analysis of the Structure of the Disposition

Because of the nonlinear dependence on the infusion rate we first focus on large and small values of k infus. Then, through a more detailed analysis of the structure of the ligand graphs, we gain insight into the disposition, and the time to steady-state, for intermediate infusion rates.

Large Infusion Rate

For values of k infus larger than the critical value k syn the amount of ligand in the system rapidly causes the target route to be saturated so that the ligand dynamics is well approximated by the equation

$$ \frac{dL}{dt}={k}_{\mathrm{infus}}-{k}_{e(L)} L-{k}_{\mathrm{syn}} $$
(26)

Hence, the terminal slope and the corresponding half-life are then given by

$$ {\lambda}_z={k}_{e(L)}\kern2em \mathrm{and}\kern2em {t}_{1/2}=\frac{ \ln (2)}{k_{e(L)}}=\frac{V}{C{ L}_{(L)}}\cdot \ln (2) $$
(27)

For the value of the elimination rate k e(L) given in Table I, this amounts to t 1/2 = 462 h, which agrees with the simulation shown in Fig. 8.

Small Infusion Rate

For small infusion rates the ligand versus time graphs in Fig. 8 exhibit a distinct two-phase structure: (i) A brief initial phase in which L(t) jumps to an intermediate value \( \overline{L} \), (ii) A subsequent long phase in which L(t) climbs from \( \overline{L} \) to its ultimate steady-state L ss. The reason is that for small infusion rates the receptor has a relatively large capacity and quickly absorbs the ligand pumped into the system.

As is well known, the disposition of nonlinear systems critically depends on the values of the parameters in the system. In the analysis below we make the following assumptions. They are the same as made in (8):

$$ \mathbf{A}:\varepsilon =\frac{K_d}{R_0}\ll 1.\kern3em \mathbf{B}:\frac{k_{e(L)}}{k_{\mathrm{off}}},\ \frac{k_{\deg }}{k_{\mathrm{off}}},\ \frac{k_{e(RL)}}{k_{\mathrm{off}}}< M $$
(28)

Here M is a constant that is not too large, i.e. ε⋅M ≪ 1. The parameter values of (8) (cf. Table I) and (19) (cf. Table II) are seen to agree with these conditions.

It can be shown that when the assumptions A and B are satisfied, then for a brief initial period the ligand equation can be well approximated by the simpler equation

$$ \frac{dL}{dt}={k}_{\mathrm{infus}}-{k}_{\mathrm{on}}{R}_0\cdot L. $$
(29)

Therefore, ligand is absorbed at the rate k on R 0, and hence during this first - absorption - phase

$$ L(t)\to \overline{L}\ \overset{\mathrm{def}}{=}\ \frac{k_{\mathrm{infus}}}{k_{\mathrm{on}}{R}_0}\kern2em \mathrm{and}\kern1em {t}_{1/2}=\frac{ \ln\ (2)}{k_{\mathrm{on}}{R}_0} $$
(30)

Note that in principle \( \overline{L}/{L}_{\mathrm{ss}} \) can be calculated explicitly from the expression for L ss obtained from (7) and (9) and (10). Hence, for the parameter values of Table I, the short-time half-life is 0.63 h. For details we refer to the short-time analysis given in Appendix D.

Using the limit of L ss(k infus) as k infus → 0, given by Eq. (12), we obtain the limit of the dimensionless plateau value of the ligand concentration \( \overline{L}/{L}_{\mathrm{ss}} \) as k infus → 0:

$$ \frac{\overline{L}\left({k}_{\mathrm{infus}}\right)}{L_{\mathrm{ss}}\left({k}_{\mathrm{infus}}\right)}\to \frac{1}{k_{\mathrm{on}}}\left(\frac{k_{e(L)}}{R_0}+\frac{k_{e(RL)}}{K_m}\right)\kern2em \mathrm{a}\mathrm{s}\kern2em {k}_{\mathrm{infus}}\to 0 $$
(31)

For the parameter values given in Table I the limit in (33) is \( \overline{L}/{L}_{\mathrm{ss}}\to 0.75 \).

In Fig. 9, we show a close-up of the short-time behaviour of the scaled ligand curves with time, as in Fig. 8 but for smaller infusion rates. The limiting values of the plateau value and the half-life, as k infus → 0, are seen to be close to the values derived in Eq. (31).

Fig. 9
figure 9

On the left: Ligand versus time graphs, scaled with respect to their limiting value L ss, for small values k infus, and On the right: \( \overline{\boldsymbol{L}}/{\boldsymbol{L}}_{\mathbf{ss}} \) versus k infus

Full size image

We see that the scaled plateau value \( \overline{L}/{L}_{\mathrm{ss}} \) decreases as the infusion rate increases. In order to understand this monotonicity property, we use the expression for the scaled plateau value of the ligand concentration obtained by a short-time analysis of the dynamics (cf. Appendix D). It yields the formula

$$ \frac{\overline{L}}{L_{\mathrm{ss}}}=\phi \left({k}_{\mathrm{infus}}\right)\overset{\mathrm{def}}{=}\frac{1}{k_{\mathrm{on}}{R}_0}\cdot \frac{k_{\mathrm{infus}}}{L_{\mathrm{ss}}\left({k}_{\mathrm{infus}}\right)} $$
(32)

Remembering from Fig. 3 that the graph of L ss versus k infus is convex, we conclude that \( \overline{L}/{L}_{\mathrm{ss}} \) is a decreasing function of k infus, as seen in the right panel of Fig. 9.

As the infusion rate becomes small, the steady states of ligand, receptor and ligand-receptor complex approach the trivial steady state: L = 0, R = R 0 and RL = 0, i.e.

$$ {L}_{\mathrm{ss}}\left({k}_{\mathrm{infus}}\right)\to 0,\kern2em {R}_{\mathrm{ss}}\left({k}_{\mathrm{infus}}\right)\to {R}_0,\kern2em R{L}_{\mathrm{ss}}\left({k}_{\mathrm{infus}}\right)\to 0\kern2em \mathrm{a}\mathrm{s}\kern2em {k}_{\mathrm{infus}}\to 0 $$
(33)

Accordingly, the terminal slope approaches that of the convergence to the trivial steady-state:

$$ {\lambda}_z\left({k}_{\mathrm{infus}}\right)\to {\lambda}_{z;0}\kern2em \mathrm{a}\mathrm{s}\kern2em {k}_{\mathrm{infus}}\to 0 $$
(34)

where λ z;0 denotes the terminal slope for convergence towards (L, R, RL) = (0, R 0, 0). Subject to the assumptions A and B given by (28), it can be shown that

$$ {\lambda}_{z;0}\approx {k}_{e(RL)}\kern2em \mathrm{and}\kern1em \mathrm{h}\mathrm{ence}\kern2em {t}_{1/2}\approx \frac{ln(2)}{k_{e(RL)}}=231\kern0.5em \mathrm{h} $$
(35)

Therefore, for the parameter values of Table I, for small infusion rates, the half-life is about half of what it is for large infusion rates. For the derivation, we refer again to Appendix C.

Thanks to the two-phase structure of the dynamics we deduce that for small infusion rates the time to steady state is considerably shorter than without such a structure, because the ligand concentration quickly jumps to a plateau value \( \overline{L} \) which may be quite close to the ultimate stationary ligand concentration L ss. For example, for the data of Table I, when k infus is small, L jumps about 75% of the way in a period of 2.5 h. Another half-life brings it up to ≈90% of the steady-state value L ss, much shorter than the usual 3–5 half-lives.

Washout Profiles

The practical value of washout profiles and steady-state conditions may be appreciated by looking at Figs. 3 and 10. Figure 10 combines both steady state and the washout profiles after multiple constant-rate infusion regimens. From a disposition point of view, the washout profiles after two or more intravenous (bolus or infusion) doses reveal at what concentrations the disposition deviates from linear first-order conditions. The washout profiles contain information about half-lives and other parameter values. They are typically used for regression of models after rapid iv injection doses. But nonlinear washout profiles are difficult to interpret and to convert to the steady-state situation which may be appreciated by Fig. 3.

Fig. 10
figure 10

Ligand versus time graphs with L on a logarithmic scale (above), and scaled with respect to their limiting value L ss (below), for infusion rates that straddle the critical rate k infus  = k syn (k infus  = 0.01, 0.05, 0.1 and 0.15 mg/L/h), as shown in Fig. 8, but in the presence of washout at t = 5,000 h

Full size image

In Fig. 10, we show simulations of a rise in plasma concentrations followed by washout at t = 5000 h. The disposition is seen to exhibit the same two-phase structure: a very rapid drop followed by a slower decline to zero. As expected, the ligand versus time graphs after washout are similar to those observed after an iv bolus administration, as is seen in the right hand figure in which the graph for k infus = 0.15 mg/L/h exhibits the characteristic TMDD profile shown in Fig. 2, without the initial phase (A).

DISCUSSION AND CONCLUSION

This communication focuses on the kinetics of target mediated disposition following constant-rate infusion of ligand followed by washout. To our knowledge, this regimen has not been considered from a mathematical/analytic approach previously. The major topics are (i) steady-state concentrations of L, R and RL as functions of the infusion rate In, (ii) clearance concepts, (iii) infusion and (iv) washout in experimental design. This study is aimed at supporting design, interpretation of data and communication across compounds and studies. The different topics are discussed in a series of subsections.

Steady States of L, R and RL as a Function of In

Analytical expressions are derived of ligand L, target R and complex RL at steady-state. They are accompanied in Fig. 3 by graphs of L ss, R ss and RL ss as functions of the ligand infusion rate (In or k infus). We take this further by deriving relationships of the target and complex concentration as functions of the ligand concentration at equilibrium (cf. Fig. 6). The graphs are given for the parameter values in Tables I and II. This new relationship between target R (or complex RL) and ligand L at steady state is derived and introduces the parameter L 50:

$$ {R}_{\mathrm{ss}}={R}_0\cdot \frac{L_{50}}{L_{\mathrm{ss}}+{L}_{50}}\kern2em \mathrm{where}\kern2em {R}_0=\frac{k_{\mathrm{syn}}}{k_{\deg }} $$
(36)

The parameter L 50, given by (20), is then the plasma concentration of ligand at which target and complex have their half-maximal values.

Surprisingly, when the internalisation of complex is much faster than the off rate, i.e. k e(RL) ≫ k off, then L 50 can be approximated by the ratio of k deg (degradation of target) and k on (binding on rate)

$$ {L}_{50}\approx \frac{k_{\deg }}{k_{\mathrm{on}}} $$
(37)

This suggests that when the on-rate k on is high and the fractional turnover rate of target is low, the system behaves more irreversibly and less ligand is required. If target turnover is increased (k deg increases and t 1/2;deg decreases), more frequent dosing or higher doses of ligand may be required.

Thus, if target R needs to be suppressed to a certain extent, say to less than 5% of its baseline value R 0, then Eq. (36) yields

$$ \frac{R_{\mathrm{ss}}}{R_0}=\frac{L_{50}}{L_{\mathrm{ss}}+{L}_{50}}<0.05\kern1em \mathrm{and}\kern0.75em \mathrm{hence}\kern1em {L}_{\mathrm{ss}}>19\times {L}_{50} $$
(38)

Again, this steady-state expression is simple and may serve as guidance for experimental design and dose selection.

The maximum value of the complex RL max will be R *, as seen in (6). Therefore,

$$ R{L}_{\max}\le \frac{k_{\mathrm{syn}}}{k_{e(RL)}}={R}_0\frac{k_{\deg }}{k_{e(RL)}} $$
(39)

Hence, the upper bound is a simple function of the target baseline R 0 and the ratio k deg to k e(RL). Again, understanding the turnover of target (k deg) yields pivotal information about the level of the complex. By (19), the ratio of the complex to target concentration at steady state becomes

$$ \frac{R{ L}_{\mathrm{ss}}}{R_{\mathrm{ss}}}=\frac{k_{\deg }}{k_{e(RL)}}\cdot \frac{L_{\mathrm{ss}}}{L_{50}} $$
(40)

Note that for the two data sets the ratio k deg/k e(RL) is very different:

$$ \frac{k_{\deg }}{k_{e(RL)}}=\left\{\begin{array}{l}3\kern2em \left(\mathrm{Table}1\right)\hfill \\ {}0.3\kern1.2em \left(\mathrm{Table}2\right)\hfill \end{array}\right. $$

Thus, interestingly, one can quite easily obtain the relative burden of complex to target by means of the expression (40). In other words, the slower target turnover (k deg low) relative to complex turnover (k e(RL) high), the smaller is the complex-to-target ratio.

Finally, we recall the characteristic—often piece-wise—shape of the graphs of the ligand, target and complex concentration versus the infusion rate, with a kink located at k infus ≈ k syn. The parameter that is responsible for this behaviour is the dimensionless parameter

$$ {\kappa}_m=\frac{K_m}{R_0} $$
(41)

which for both data sets, given in (8) and (19), is quite small.

Clearance Concepts

The clearance concept has since the early 1970s played a central role in pharmacokinetics (cf. Rowland, Benet and Graham (20,21) and Wilkinson and Shand (22)).

Clearance may, in the TMDD context be shown as a function of ligand concentration (Fig. 6, left) or as the inverse of the slope of ligand concentration when plotted versus the infusion rate In (Fig. 6, right). The TMDD model (Figs. 1 and 6) is operating between two boundaries of clearance. One that includes first-order elimination at low ligand concentration L via both specific TMDD and non-specific clearance routes. This is the upper boundary of clearance. The lower boundary is when the target route is saturated and the non-specific route Cl (L) is dominating. Clearly, target-dominated clearance Cl (RL) is bounded by target concentration and the second-order on rate when the internalisation route k e(RL) of complex is fast. We have derived analytical/mathematical expressions of clearance in parallel to simulations of its dependence on the infusion rate.

Again, the steady-state situation reveals properties of the system not easily obtained from bolus curves.

Infusion and Washout in Experimental Design

We also put the disposition of TMDD systems into a constant-rate infusion perspective. Even though extended constant-rate infusion protocols are seldom applied for antibodies, it is important to recognise its potential usefulness. For instance, in Peletier and de Winter (23), it served to warn against effects of drugs that have a dynamics that is slow compared to the usual time span over which clinical experiments are conducted.

From a disposition point of view, the washout profiles after two or more intravenous (bolus or infusion) doses reveal at what concentrations the disposition deviates from linear first-order conditions. They contain information about half-lives and other parameter values. Nonlinear washout profiles are difficult to interpret and to convert to the steady-state situation which may be appreciated by Fig. 3. The constant-rate iv infusion protocol, followed by the washout profiles is generally a more robust approach especially when nonlinear PK prevails. The primary reason for this is that with increasing infusion rates the time to steady state increases, the steady-state concentration increases disproportionately and the ability to identify parallel mixed-order elimination processes improves.

For a linear system, the rise of the ligand concentration during infusion offers the possibility to measure the impact of different infusion rates on the limiting steady-state concentrations, as well as the time to steady state which, as we have seen, may vary considerably for different infusion rates. Specifically, with increasing ligand infusion rates In, the time to steady state of L increases, the steady-state concentration increases disproportionately and the ability to identify parallel mixed-order elimination processes increases.

The rapid drop of the ligand concentration at the termination of the infusion yields concentration profiles which are akin to those obtained by iv bolus administration, except for the—usually brief—initial binding phase (cf. Fig. 10). Such profiles have been studied extensively, (see e.g. (4) and (8)) and they often also yield considerable insight into the different processes making up TMDD. Quite often though, the terminal phase involves very low ligand concentrations, sometimes too low to provide accurate data.

Conclusion

This paper highlights the impact of the nonlinear binding, linear non-specific elimination (clearance) and linear internalisation processes of the TMDD system with a circulating target. We derive useful equilibrium expressions for ligand L, target R and ligand-target complex RL. These expressions are based on iv bolus experiments.

Simulations of L ss, R ss and RL ss are then displayed as functions of varying constant-rate infusion regimens In. These simulations reveal, to our knowledge, new patterns of the primary variables (L, R, RL) which are of practical value for an understanding and experimental design point of view.