INTRODUCTION

Background

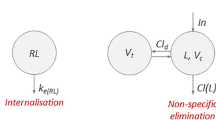
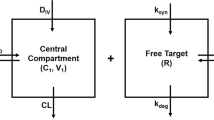
In this paper, we continue our study of in vivo potency of drug-target kinetics begun in Gabrielsson, Peletier et al. and Hjorth et al. (1,2) in the framework of Target-Mediated Drug Disposition (TMDD), an ubiquitous process in the action of drugs that has been extensively studied ever since the pioneering papers of Wagner (3), Sugiyama et al. (4) and Levy (5). We also refer to the seminal papers by Michaelis and Menten (6), Mager and Jusko (7), Mager and Krzyzansky (8), Gibiansky et al. (9) and Peletier and Gabrielsson (10). In Fig. 1, we show schematically the basic TMDD model: Ligand is supplied to the central compartment where it binds a receptor (the target) resulting in a ligand-receptor complex, which internalises to produce a pharmacologial response. In addition, ligand is cleared from the central compartment and exchanged with a peripheral compartment. Target is synthesised by a zeroth order process and degrades by a first-order process.

Fig. 1
figure 1

Schematic description of the model for Target Mediated Drug Disposition involving ligand in the central compartment (Lc) and in the peripheral compartment (Lp) binding a receptor (R) (the target), yielding ligand-target complexes (RL)

Full size image

In this paper, we extend the results for this TMDD model obtained in (1) to three generalisations of the TMDD model in which (i) the drug can bind two receptors (cf. 11), (ii) two drugs can bind one receptor (cf. 12) and (iii) the dug is supplied to the central compartment, but the receptor is located in the peripheral compartment (cf. 13).

Mathematically, the basic TMDD model, depicted in Fig. 1, can be formulated as a set of four differential equations, one for each compartment.

$$ \left\{\begin{array}{ll}\frac{d{L}_c}{dt}& =\frac{In}{V_c}-{k}_{\mathrm{on}}{L}_c\cdotp R+{k}_{\mathrm{off}} RL+\frac{C{l}_d}{V_c}\left({L}_p-{L}_c\right)-\frac{C{l}_{(L)}}{V_c}{L}_c\\ {}\frac{d{L}_p}{dt}& =\frac{C{l}_d}{V_p}\left({L}_c-{L}_p\right)\\ {}\frac{dR}{dt}& ={k}_{\mathrm{syn}}-{k}_{\mathrm{deg}}R-{k}_{\mathrm{on}}{L}_c\cdotp R+{k}_{\mathrm{off}} RL\\ {}\frac{dR L}{dt}& ={k}_{\mathrm{on}}{L}_c\cdotp R-\left({k}_{\mathrm{off}}+{k}_{e(RL)}\right) RL\end{array}\right. $$
(1)

Here, Lc and Lp denote the concentrations of ligand (or drug) in, respectively, the central and the peripheral compartment with volumes Vc and Vp. Concentrations of target and target-ligand complex in the central compartment are denoted by R and RL. Drug infusion takes place into the central compartment, with constant rate In where it binds to the target with rates kon and koff. Ligand is removed through non-specific clearance Cl(L) and exchanged with the peripheral compartment through inter-compartmental distribution Cld. By internalisation, ligand-target complex leaves the system according to a first-order process with a rate constant ke(RL). Finally, target synthesis and degradation are modelled by, respectively, zeroth- and first-order turnover with rates ksyn and kdeg.

We recall the analysis presented in (1) for the one-compartment TMDD-model shown in Fig. 1. There, relations between steady-state concentrations of target R, ligand L and complex RL were derived, and a new expression of the in vivo potency, denoted by L50, was established, particularly suited for Open Systems. Whereas the classical definition of potency is primarily based on the binding constants (cf. Black and Leff (14), Kenakin (15,16), Neubig et al. (17)) and target expression, in the definition of, in vivo potency drug and target kinetics, such as the degradation rate kdeg, are also incorporated. These concepts were further discussed from an open and closed system perspective in (2).

In this paper, we present three generalisations of the classical TMDD model: (i) a single ligand that can bind two receptors R1 and R2, (ii) two ligands, L1 and L2, that compete for a single receptor and (iii) a ligand that is supplied to the central compartment and distributed to the peripheral compartment where the target is located.

Steady States

In (1), it has been established how for the model shown in Fig. 1, the steady-state values of ligand (L), receptor (R) and ligand-receptor complex (RL), in the central compartment, are related to one another:

$$ RL={R}^{\ast}\cdotp \frac{L}{L+{L}_{50}}\kern1.5em \mathrm{and}\kern1.5em R={R}_0\cdotp \frac{L_{50}}{L+{L}_{50}} $$
(2)

where the baseline R0, the maximal impact R∗ and the in vivo potency EC50 (denoted by L50) are given by

$$ {R}_0=\frac{k_{syn}}{k_{deg}},\kern1.5em {R}^{\ast }=\frac{k_{syn}}{k_{e(RL)}}\kern1.5em \mathrm{and}\kern1.5em {L}_{50}=\frac{k_{deg}}{k_{e(RL)}}\cdotp {K}_m $$
(3)

and Km = (koff + ke(RL))/kon is called the Michaelis-Menten constant. Here, it is implicitly assumed that the constant rate infusion, In, is fixed at the appropriate value. In (1), the required infusion rate is also computed.

The definition of the in vivo potency, L50, expresses both the impact of rate processes of the target (kdeg, ke(RL)) and those of the binding dynamics (koff, kon), on the drug concentration (L) required to achieve the desired efficacy.

The resemblance of Eq. (2) with the Hill equation (below) is striking.

$$ E={E}_0\pm {E}_{\mathrm{max}}\frac{C^{n_H}}{E{C}_{50}^{n_H}+{C}^{n_H}}. $$

The Hill equation is often used in vivo and also contains a baseline parameter E0 in addition to the maximum drug induced effect Emax and the potency EC50. Equation (2) has intrinsically the baseline in terms of R0. The Emax parameter is equivalent to ∣RLmax − R0∣, and the potency parameter EC50 is expressed in Eq. (3) as L50.

The exponent nH of the Hill equation is interpreted as a fudge factor allowing the steepness of the Hill equation at the EC50 value to vary. In our experience nH is not necessarily an integer and varies typically within the range of 1–3. We have observed with high and variable plasma protein binding that nH will change depending on whether unbound or total plasma concentration (respectively Cu and Ctot) is used as drivers of the pharmacological effect.

Remark

It is interesting to note that Eq. (3) yields the following relation between the baseline target concentration, R0, the maximal ligand-target concentration, R∗, and the in vivo potency L50:

$$ {L}_{50}\cdotp {R}_0={K}_m\cdotp {R}^{\ast } $$
(4)

This means that if the baseline of target, the maximum ligand-target concentration and Km are obtained experimentally, then the in vivo potency L50 can be predicted. Thus, Km can be located either to the right or to the left of the in vivo potency, depending on the relative magnitude of R0 and R∗.

In Fig. 2, we show graphs for RL and R versus L for two parameter sets, one taken from Peletier and Gabrielsson (10) (left) and one from Cao and Jusko (18) (right) (cf. Appendix 2; Tables I and II).

Fig. 2
figure 2

RLss and Rssversus Lss for the parameter values of Peletier and Gabrielsson (10) (left) and Cao and Jusko (18) (right). The parameter values are given in Tables I and II in Appendix 2

Full size image
Table I Parameter Values of Peletier and Gabrielsson (10)
Full size table
Table II Parameter Values of Cao and Jusko (18)
Full size table

The values of R0, R∗ and L50 that appear in Eq. (2) are for these two references given by

$$ {\displaystyle \begin{array}{llll}& {R}_0=12,\kern0.5em & {R}^{\ast }=36\kern0.5em & {L}_{50}=0.13\kern1.25em \mathrm{Peletier}\ \mathrm{and}\ \mathrm{Gabrielsson}\ \left[10\right]\\ {}& {R}_0=10\kern0.5em & {R}^{\ast }=3.3\kern0.5em & {L}_{50}=0.10\kern1.25em \mathrm{Cao}\ \mathrm{and}\ \mathrm{Jusko}\ \left[18\right]\end{array}} $$
(5)

Thus, remembering that initially, R = R0 and RL = 0, it is evident that over time, the system settles into a steady state, in (10) where total target concentration exceeds R0 and in (18) where target concentration is less than target baseline.

It is interesting to note that despite similar in vivo potency’s (L50’s) of Cao and Jusko and Peletier and Gabrielsson, the target-to-complex ratios differ by one order of magnitude due to the comparable difference in ke(RL).

The proposed framework with a dynamic target protein may also be applicable to enzymatic reactions which may enhance the in vitro/in vivo extrapolation of metabolic data (cf Pang et al. 19,20).

Discussion and Conclusions

Eqs. (2) and (3) summarise what is needed to apply and explain target R, ligand-target RL and ligand L interactions when both ligand and target belongs to the central (plasma) compartment. Equation (3) clearly demonstrates that in vivo potency, a central parameter in pharmacology, is a conglomerate of target turnover, complex kinetics and ligand-target binding properties.

In the following three sections, we discuss generalisations of the basic TMDD model discussed in “INTRODUCTION” and derive generalisations of the functions RL = f(L) and R = g(L) applicable to these models.

TWO DIFFERENT RECEPTORS COMPETE FOR ONE LIGAND

Background

When one ligand, L, can bind two receptors, R1 and R2, two complexes are formed and internalised to form two different ligand-receptor complexes R1L and R2L; it is of great value to determine their relative impact on the pharmacological response, and it is important to determine how the responses of these two complexes are related. For instance, when one receptor mediates a beneficial effect of a drug and the other one mediates an adverse effect, one wishes to know the relative impact of the latter target and whether the two potencies EC50; 1 and EC50; 2 are sufficiently well separated so that a dose can be selected with minimally adverse effect. Figure 3 gives a schematic description of the model.

Fig. 3
figure 3

Schematic description of a model for the one-compartment two-target system in which ligand binds with two receptors R1 and R2, each forming a complex denoted by, respectively, R1L and R2L. The definition of parameters is the same as in Fig. 1

Full size image

Mathematically, the model shown in Fig. 3 can be described by the following system of ordinary differential equations:

$$ \left\{\begin{array}{ll}\frac{dL}{dt}& ={k}_{\mathrm{infus}}-{k}_{e(L)}L-{k}_{\mathrm{on};1}L\cdotp {R}_1+{k}_{\mathrm{off};1}{R}_1L-{k}_{\mathrm{on};2}L\cdotp {R}_2+{k}_{\mathrm{off};2}{R}_2L\\ {}\frac{d{R}_1}{dt}& ={k}_{\mathrm{syn};1}-{k}_{\deg; 1}{R}_1-{k}_{\mathrm{on};1}L\cdotp {R}_1+{k}_{\mathrm{off};1}{R}_1L\\ {}\frac{d{R}_1L}{dt}& ={k}_{\mathrm{on};1}L\cdotp {R}_1-\left({k}_{\mathrm{off};1}+{k}_{e\left({R}_1L\right)}\right){R}_1L\\ {}\frac{d{R}_2}{dt}& ={k}_{\mathrm{syn};2}-{k}_{\deg; 2}{R}_2-{k}_{\mathrm{on};2}L\cdotp {R}_2+{k}_{\mathrm{off};2}{R}_2L\\ {}\frac{d{R}_2L}{dt}& ={k}_{\mathrm{on};2}L\cdotp {R}_2-\left({k}_{\mathrm{off};2}+{k}_{e\left({R}_2L\right)}\right){R}_2L\end{array}\right. $$
(6)

in which the parameters are defined as in the system (1) and

$$ {k}_{\mathrm{infus}}=\frac{In}{V_c}\kern1.5em \mathrm{and}\kern1.5em {k}_{e(L)}=\frac{C{l}_{(L)}}{V_c} $$
(7)

For a related model, with a corresponding system of equations, we refer to (11). By adding the equations for free receptors R1 and R2 to the equations for the associated bound receptors R1L and R2L, we obtain two balance equations for, respectively, R1 and R2:

$$ \left\{\begin{array}{ll}\frac{d}{dt}\left({R}_1+{R}_1L\right)& ={k}_{\mathrm{syn};1}-{k}_{\deg; 1}{R}_1-{k}_{e\left({R}_1L\right)}{R}_1L\\ {}\frac{d}{dt}\left({R}_2+{R}_2L\right)& ={k}_{\mathrm{syn};2}-{k}_{\deg; 2}{R}_2-{k}_{e\left({R}_2L\right)}{R}_2L\end{array}\right. $$
(8)

For ligand, free or bound to one of the two receptors, we obtain the balance equation:

$$ \frac{d}{dt}\left(L+{R}_1L+{R}_2L\right)={k}_{\mathrm{inf}}-{k}_{e(L)}L-{k}_{e\left({R}_1L\right)}{R}_1L-{k}_{e\left({R}_2L\right)}{R}_2L $$
(9)

Steady States

As in the case of a single target, it is possible to obtain expressions for the concentrations of ligand-target complex and free target, i.e. for RiL and Ri (i = 1, 2) in terms of the ligand concentration L.

Following the steps taken in Gabrielsson and Peletier (1), it is possible to show that for the receptors individually, the expressions such as shown in (2) hold

$$ {R}_i={R}_{0.i}\cdotp \frac{L_{50;i}}{L+{L}_{50;i}}\kern1.25em \mathrm{and}\kern1.25em {R}_iL={R}_i^{\ast}\cdotp \frac{L}{L+{L}_{50;i}} $$
(10)

for i = 1 and i = 2.

The baseline receptor concentrations R0. i, the maximum values \( {R}_i^{\ast } \) of the receptor-ligand complexes and the in vivo potencies L50; i are given by

$$ {R}_{0,i}=\frac{k_{syn;i}}{k_{\mathit{\deg};i}},\kern1.25em {R}_i^{\ast }=\frac{k_{syn;i}}{k_{e\left({R}_iL\right)}},\kern1.25em {L}_{50;i}=\frac{k_{\mathit{\deg};i}}{k_{e\left({R}_iL\right)}}\cdotp {K}_{m;i} $$
(11)

for i = 1 and i = 2.

where \( {K}_{m;i}=\left({k}_{\mathrm{off};i}+{k}_{e\left({R}_iL\right)}\right)/{k}_{\mathrm{on};i} \). Details of the derivations of the formulas above are presented in Appendix 1.1.

Figure 4 shows the target suppression and complex formation of the two targets versus ligand concentration at equilibrium together with their respective L50 values. These graphs are useful in discriminating between two targets and deciding which target contributes most to complex formation at different ligand concentrations. The left figure shows the two target suppression curves R1 and R2versus ligand and the right figure the two ligand-target complexes R1L and R2L versus ligand L. The parameter values are chosen fictitiously in order to clearly highlight the differences (Table III, Appendix 2).

Fig. 4
figure 4

Target suppression (left) and ligand-target complex (right) versus ligand concentration for two receptors R1 and R2. The parameter values for the two receptors are given in Table II in Appendix 2. The dashed lines indicate the corresponding values for L50: L50;1 = 4.34 nM and L50;2 = 2.18 nM

Full size image
Table III Parameter Values for Fig. 4
Full size table

The model shown in Fig. 3 has been used as a two-state model to fit the data for the total free target concentration that were given in Gabrielsson and Weiner (PD2) p. 729 (21). The total free target concentration, i.e. R1 + R2, can be computed from Eq. (10) and (11) and is seen to be

$$ {R}_{\mathrm{free};\mathrm{tot}}={R}_1+{R}_2={R}_{0.1}\cdotp \frac{L_{50;1}}{L+{L}_{50;1}}+{R}_{0.2}\cdotp \frac{L_{50;2}}{L+{L}_{50;2}} $$
(12)

Evidently, in the absence of ligand, Rfree; tot = R0.1 + R0.2, while Rfree; tot → 0 as L → ∞.

In Fig. 5, we see how the model is fitted to data obtained from an experiment involving four total target concentrations (Rtot = 8050, 6510, 3540 and 1590 nM). As the ligand concentration increases, the first receptor kicks in at the lowest in vivo potency (0.025 nM), taking the free receptor concentration down to a lower intermediate plateau. Then, at the higher in vivo potency (37 nM), the free receptor concentration drops further and eventually converges to zero.

Fig. 5
figure 5

Total free target level Rtot;free = R1 + R2 and model predicted graphs (solid lines) of Rtot;freeversus L for four total receptor concentrations (Rtot = 8050, 6510, 3540 and 1590 nM) and R0,1 = Rtot · F and R0,2 = Rtot · (1 − F) with F = 0.6 Note the wide discrepancy between the two in vivo potencies L50;1 (denoted in the figure by IC50;1)(0.025 nM) and L50;2 (denoted in the figure by IC50;2) (37 nM). The high affinity drug is the target for therapeutic effect, and the low affinity drug is responsible for an adverse effect (cf. Gabrielsson and Weiner, PD2, page 729 21)

Full size image

Remark. The parameters kdeg, ke(RL), kon and koff are not given here since only equilibrium data from the experiments were available. Due to parameter unidentifiability, the model was parametrised with potencies L50; 1 and L50; 2 as parameters and not functions of their original determinants. One may also need other sources of information to fully appreciate the actual values of kdeg, ke(RL), kon and koff. In vitro binding experiments may yield kon and koff. In vivo time courses of circulating free ligand, target and ligand-target are necessary in order to estimate ke(RL). Information about the kdeg parameter may be found in the literature for commonly studied targets.

Discussion and Conclusion

Here, Eq. (10), (11) and (12) summarise what is needed to apply and explain target Ri, ligand-target RiL and ligand L interactions when ligand and both targets belong to the central (plasma) compartment. Equation (11) demonstrates again the complexity of in vivo potencies L50; i involving both turnover of the two targets, complex kinetics and ligand-target binding properties.

The explicit expressions for the ligand-receptor complexes RiL, the free receptor concentrations Ri and the in vivo potencies L50; i (cf. (12)), together with Figs. 4 and 5, provide valuable tools when assessing the individual contribution of each target and specifically the impact of target turnover and internalisation.

TWO DIFFERENT LIGANDS COMPETING FOR ONE RECEPTOR

Background

A common situation, for instance in combination therapy, is that not one but two ligands L1 and L2 bind a single receptor R. This results in two different complexes, RL1 and RL2, with different internalisation rates. For instance, one of the ligands is produced endogenously, and the other is a drug which is supplied in order to inhibit or stimulate the pharmacological effect caused by the endogenous ligand (cf. Benson et al. 22,23).

Recently, several authors have derived different drug-drug interaction models associated with TMDD with a different focus and often directed towards the situation when a constant target level prevails (cf. Koch et al. (24,25) and Gibiansky et al. (26)). In order to describe open, in vivo, processes, it is necessary to include target turnover, internalisation and drug clearance. This is done in the model shown in Fig. 6 in which two ligands, distinguished by subscripts i = 1 and 2, are supplied by constant-rate infusions Ini to the central compartment, each having its own volume of distribution Vci, nonspecific clearance \( C{l}_{\left({L}_i\right)} \), binding and dissociation rate kon; i and koff; i, and its own internalisation rate \( {k}_{e\left(R{L}_i\right)} \).

Fig. 6
figure 6

Schematic description of the competitive-interaction model in which a single target R binds two ligands L1 and L2, forming two complexes denoted by, respectively, RL1 and RL2

Full size image

Mathematically, the model shown in Fig. 6 can be described by the following system of differential equations for the two ligands, L1 and L2, the target R and the two ligand-target complexes RL1 and RL2 (see also (12)):

$$ \left\{\begin{array}{ll}\frac{d{L}_1}{dt}& ={k}_{\mathrm{infus};1}-{k}_{e\left({L}_1\right)}L-{k}_{\mathrm{on};1}{L}_1\cdotp R+{k}_{\mathrm{off};1}R{L}_1\\ {}\frac{d{L}_2}{dt}& ={k}_{\mathrm{infus};2}-{k}_{e\left({L}_2\right)}L-{k}_{\mathrm{on};2}{L}_2\cdotp R+{k}_{\mathrm{off};2}R{L}_2\\ {}\frac{dR}{dt}& ={k}_{\mathrm{syn}}-{k}_{\mathrm{deg}}R-{k}_{\mathrm{on};1}{L}_1\cdotp R+{k}_{\mathrm{off};1}R{L}_1-{k}_{\mathrm{on};2}{L}_2\cdotp R+{k}_{\mathrm{off};2}R{L}_2\\ {}\frac{dR{L}_1}{dt}& ={k}_{\mathrm{on};1}{L}_1\cdotp R-\left({k}_{\mathrm{off};1}+{k}_{e\left(R{L}_1\right)}\right)R{L}_1\\ {}\frac{dR{L}_2}{dt}& ={k}_{\mathrm{on};2}{L}_2\cdotp R-\left({k}_{\mathrm{off};2}+{k}_{e\left(R{L}_2\right)}\right)R{L}_2\end{array}\right. $$
(13)

where

$$ {k}_{\mathrm{infus},i}=\frac{I{n}_i}{V_c}\kern1.25em \mathrm{and}\kern1.25em {k}_{e\left({L}_i\right)}=\frac{C{l}_{\left({L}_i\right)}}{V_c},\kern1.25em \left(i=1,2\right) $$
(14)

Each of the ligands is present in free form (Li) and in bound form (RLi) (i = 1, 2). For the total amount of the two ligands, we then find two balance equations, one for L1 and one for L2:

$$ \left\{\begin{array}{ll}\frac{d}{dt}\left({L}_1+R{L}_1\right)& ={k}_{\mathrm{infus};1}-{k}_{e\left({L}_1\right)}{L}_1-{k}_{e\left(R{L}_1\right)}R{L}_1\\ {}\frac{d}{dt}\left({L}_2+R{L}_2\right)& ={k}_{\mathrm{infus};2}-{k}_{e\left({L}_2\right)}{L}_2-{k}_{e\left(R{L}_2\right)}R{L}_2\end{array}\right. $$
(15)

The receptor is present in free form (R) and in bound form (RLi). Adding the last three equations of the system (Eq. (13)), we obtain the following balance equation for the receptor:

$$ \frac{d}{dt}\left(R+R{L}_1+R{L}_2\right)={k}_{\mathrm{syn}}-{k}_{\mathrm{deg}}R-{k}_{e\left(R{L}_1\right)}R{L}_1-{k}_{e\left(R{L}_2\right)}R{L}_2 $$
(16)

These balance equations will be useful for analysing steady-state concentrations, when the left-hand sides vanish and we obtain three algebraic equations.

Steady States

We deduce from Eq. (16) that the steady-state concentrations R, RL1 and RL2 are related by the equation

$$ {k}_{\mathrm{syn}}-{k}_{\mathrm{deg}}R-{k}_{e\left(R{L}_1\right)}R{L}_1-{k}_{e\left(R{L}_2\right)}R{L}_2=0 $$
(17)

This allows us to express R in terms of the concentrations of the two complexes, RL1 and RL2:

$$ R=\frac{1}{k_{deg}}\left\{{k}_{\mathrm{syn}}-{k}_{e\left(R{L}_1\right)}R{L}_1-{k}_{e\left(R{L}_2\right)}R{L}_2\right\} $$
(18)

or

$$ R=\frac{1}{k_{deg}}\left({k}_{\mathrm{syn}}-{X}_1-{X}_2\right). $$
(19)

when we use the short-hand notation

$$ {X}_1={k}_{e\left(R{L}_1\right)}R{L}_1\kern1.25em \mathrm{and}\kern1.25em {X}_2={k}_{e\left(R{L}_2\right)}R{L}_2 $$
(20)

We substitute the expression for R in Eq. (19) into the right-hand side of each of the last two equations of Eq. (13) to obtain:

$$ \left\{\begin{array}{ll}& {L}_1\cdotp \frac{1}{k_{deg}}\left({k}_{\mathrm{syn}}-{X}_1-{X}_2\right)={K}_{m;1}\frac{X_1}{k_{e\left(R{L}_1\right)}}\\ {}& {L}_2\cdotp \frac{1}{k_{deg}}\left({k}_{\mathrm{syn}}-{X}_1-{X}_2\right)={K}_{m;2}\frac{X_2}{k_{e\left(R{L}_2\right)}}\end{array}\right. $$
(21)

where

$$ {K}_{m,i}=\frac{k_{off;i}+{k}_{e\left(R{L}_i\right)}}{k_{on;i}} $$

This is an algebraic system of two equations with two unknowns, X1 and X2, which can be solved. Translating these solutions back to the original variables, we obtain the following expressions for RL1 and RL2:

$$ \left\{\begin{array}{ll}R{L}_1& ={R}_1^{\ast}\frac{L_1}{L_1+\theta \cdotp {L}_2+{L}_{50;1}}\\ {}R{L}_2& ={R}_2^{\ast}\frac{L_2}{L_2+{\theta}^{-1}\cdotp {L}_1+{L}_{50;2}}\end{array}\right. $$
(22)

where L50; 1 and L50; 2 are given by

$$ {L}_{50;i}=\frac{k_{deg}}{k_{e\left(R{L}_i\right)}}\cdotp {K}_{m;i},\kern1.25em {R}_i^{\ast }=\frac{k_{deg}}{k_{e\left(R{L}_i\right)}}\kern1.25em \mathrm{and}\kern1.25em \theta =\frac{L_{50;1}}{L_{50;2}} $$
(23)

for i = 1 and i = 2.

The expressions for the complexes RL1 and RL2 can be used in Eq. (18) to derive an expression for R in terms of the two ligand concentrations:

$$ R={R}_0\left(1-\frac{L_1}{L_1+\theta \cdotp {L}_2+{L}_{50;1}}-\frac{L_2}{L_2+{\theta}^{-1}\cdotp {L}_1+{L}_{50;2}}\right) $$
(24)

where θ = L50; 1/L50; 2. Thus, the impact of the two ligand combined is seen to be additive.

Details of the derivations of the equations above are given in Appendix 1.2.

In the expressions for RL1 in Eq. (22), one can interpret the term (θ · L2 + L50; 1) in the numerator as a shift of potency L50; 1, and similarly in the expression for RL2, the term (θ−1 · L1 + L50; 2) can be viewed as a shift of potency L50; 2. Thus, the modifications of the potencies L50; 1 and L50; 2 (equivalent to EC50; 1 and EC50; 2) depend on the ligand concentrations in the following manner:

$$ E{C}_{50;1}\nearrow \kern1.25em \mathrm{when}\kern1.25em {L}_2\nearrow $$

i.e. EC50; 1increases when L2increases. Similarly, EC50;2 increases when L1 increases.

Note that by Eq. (22), when L2 is arbitrary but fixed, then

$$ R{L}_1\left({L}_1,{L}_2\right)\to \left\{\begin{array}{lll}& 0& \mathrm{as}\kern1.25em {L}_1\to 0\\ {}& R{L}_1\to {R}_1^{\ast }& \mathrm{as}\kern1.25em {L}_1\to \infty \end{array}\right. $$
(25)

In the context of an endogenous ligand (L1) and a drug (L2) which is administered to reduce the effect of the endogenous ligand, Eq. (22) is of practical value. Assuming that receptor occupancy RL1 is a measure for the effect of L1, it tells by how much the effect of L1 is reduced by a given concentration of L2.

Finally, we observe that

$$ \left\{\begin{array}{ll}R{L}_1\left({L}_1,{L}_2\right)& \to {R}_1^{\ast}\frac{L_1}{L_1+{L}_{50;1}}\kern1.25em \mathrm{as}\kern1.25em {L}_2\to 0\\ {}R{L}_2\left({L}_1,{L}_2\right)& \to {R}_2^{\ast}\frac{L_2}{L_2+{L}_{50;2}}\kern1.25em \mathrm{as}\kern1.25em {L}_1\to 0\end{array}\right. $$
(26)

These limits are consistent with the expression in Eq. (2) for a single receptor shown in “INTRODUCTION”. Plainly, RL1(L1, L2) = 0 when L1 = 0 and RL2(L1, L2) = 0 when L2 = 0.

It is illustrative to view the two complexes and the total free drug concentration as they depend on both ligand concentrations: L1 and L2. This is done in Fig. 7 where 3D graph of R versus L1 and L2 is shown as well as the corresponding Heat map. In both graphs, R0 = 100, L50; 1 = 50 and L50; 2 = 25 are taken so that θ = 2.

Fig. 7
figure 7

Graphs of R versus L1 and L2 according to Eq. (24). Here, R0 = 100, L50;1 = 50 and L50;2 = 25 so that θ = 2. Note that the level curves are straight lines with slope L1/L2 =  − 2

Full size image

As we see

$$ \left\{\begin{array}{llll}& R\left({L}_1,{L}_2\right)& \to {R}_0=100\kern0.5em & \mathrm{as}\kern1.25em \left({L}_1,{L}_2\right)\to \left(0,0\right)\\ {}& R\left({L}_1,{L}_2\right)& \to R{L}_1\left(0,{L}_2\right)=0\ & \mathrm{as}\kern1.25em {L}_1\to 0\end{array}.\right. $$
(27)

These limits are in agreement with the Eq. (22) for RL1 and Eq. (25) for R.

Discussion and Conclusion

Equations (22), (23) and (24) summarise what is needed to apply and explain target R, ligand-target complex RLi and ligand Li interactions when two ligands interact with one centrally located target. Equation (23) clearly demonstrates that in vivo potency is a conglomerate of target turnover, complex kinetics and ligand-target binding properties.

TARGET IN THE PERIPHERAL COMPARTMENT

Background

When ligand and target are located in the central compartment of the TMDD model, the steady-state relations of ligand, target and ligand-target complex have been derived in Gabrielsson and Peletier (1) and briefly summarised in the “Introduction” (cf Eqs. (2) and (3)). In this section, we generalise this situation to when ligand is supplied to the central compartment, but target is located in the peripheral compartment so that ligand has to be cleared from the central compartment into the peripheral compartment before it can bind the target.

We assume active transport between the two compartments, as may be caused by blood flow or transporters, and denote clearance from the central compartment by Cldα and from the peripheral compartment by Cldβ. These two processes allow concentration differences to build up across the membrane separating the two compartments..

The objective is here to derive expressions for the concentration of free receptor R and ligand-receptor complex RLp in the peripheral compartment and the ligand concentration Lc in the central compartment.

Figure 8 gives a schematic description of the model we study.

Fig. 8
figure 8

Schematic description of the model for Target Mediated Drug Disposition involving ligand in the central compartment (Lc) and in the peripheral compartment (Lp) binding a receptor (R) (the target), located in the peripheral compartment yielding ligand-target complexes (RLp)

Full size image

The system (1) now becomes

$$ \left\{\begin{array}{ll}\frac{d{L}_c}{d t}& =\frac{I{n}_i}{V_c}+\frac{1}{V_c}\left(C{l}_{d\beta}{L}_p-C{l}_{d\alpha}{L}_c\right)-\frac{C{l}_{(L)}}{V_c}{L}_c\\ {}\frac{d{L}_p}{d t}& =\frac{1}{V_p}\left(C{l}_{d\alpha}{L}_c-C{l}_{d\beta}{L}_p\right)-{k}_{\mathrm{on}}{L}_p\cdotp R+{k}_{\mathrm{off}}R{L}_p\\ {}\frac{d R}{d t}& ={k}_{\mathrm{syn}}-{k}_{\mathrm{deg}}R-{k}_{\mathrm{on}}{L}_p\cdotp R+{k}_{\mathrm{off}}R{L}_p\\ {}\frac{d R{L}_p}{d t}& ={k}_{\mathrm{on}}{L}_p\cdotp R-\left({k}_{\mathrm{off}}+{k}_{e\left(R{L}_p\right)}\right)R{L}_p\end{array}\right. $$
(28)

For convenience, we shall often write

$$ {k}_{\mathrm{infus}}=\frac{I{n}_i}{V_c}\kern1.25em {k}_{e(L)}=\frac{C{l}_{(L)}}{V_c},\kern1.25em {k}_{\mathrm{cp}}=\frac{C{l}_{d\alpha}}{V_c},\kern1.25em {k}_{\mathrm{pc}}=\frac{C{l}_{d\beta}}{V_p}. $$
(29)

The system (28) yields the following balance equations for the target and the ligand:

  • For the target, which involves free target R and bound target RLp: By adding the third and fourth equation of Eq. (28), we obtain

$$ \frac{d}{dt}\left(R+R{L}_p\right)={k}_{\mathrm{syn}}-{k}_{\mathrm{deg}}R-{k}_{e\left(R{L}_p\right)}R{L}_p $$
(30)

  • For the ligand, which involves Lc, Lp and RLp: By adding the first equation in Eq. (28) and the sum of the second and the fourth equation multiplied by μ = Vp/Vc, we obtain

$$ \frac{d}{dt}\left\{{L}_c+\mu\ \left({L}_p+R{L}_p\right)\right\}={k}_{\mathrm{infus}}-{k}_{\mathrm{deg}}\ R-\mu \cdotp {k}_{e\left(R{L}_p\right)}R{L}_p $$
(31)

Steady States

An expression for the concentration of ligand-target complex in terms of the ligand concentration in the peripheral compartment Lp can be derived in a manner which is analogous to the one employed before for the one-compartment model and yields the following equation:

$$ R{L}_p=\frac{k_{syn}}{k_{e\left(R{L}_p\right)}}\frac{L_p}{L_p+{L}_{p;50}},\kern1em \mathrm{where}\kern1em {L}_{p;50}=\frac{k_{deg}}{k_{e\left(R{L}_p\right)}}\cdotp {K}_m $$
(32)

Note that the expression for Lp; 50 is the same as the one defined for L50 in Eq. (3).

Next, we replace Lp in the expression for RLp by Lc. By adding the second and the fourth equation of the system (Eq. (28)), we express Lp in terms of Lc and RLp:

$$ {L}_p=\frac{1}{k_{pc}}\left\{{\mu}^{-1}\ {k}_{\mathrm{cp}}\ {L}_c-{k}_{e\left(R{L}_p\right)}R{L}_p\right\}. $$
(33)

When we use this equation in Eq. (32) to replace Lp by Lc, we arrive at an expression which only involves Lc and RLp. Specifically, putting \( X={k}_{e\left(R{L}_p\right)}R{L}_p \), we obtain

$$ {L}_c=f(X)\overset{\mathrm{def}}{=}\frac{\mu }{k_{cp}}\left(X+\frac{k_{\mathrm{p}c}{k}_{deg}}{k_{e\left(R{L}_p\right)}}\ {K}_m\cdotp \frac{X}{k_{syn}-X}\right) $$
(34)

Equation (34) provides an expression for Lc as a function of X, i.e. Lc = f(X). It is seen that the function f(X) is monotonically increasing so that it can be inverted to give an expression of X in terms of Lc and so yield the desired expression of RLp in terms of Lc.

In order to invert the function f(X), we multiply Eq. (34) by (ksyn − X) and so obtain a quadratic equation in X:

$$ {X}^2-\left({k}_{\mathrm{syn}}+a{L}_c+b\right)X+a{k}_{\mathrm{syn}}{L}_c=0 $$
(35)

in which

$$ a=\frac{k_{\mathrm{cp}}}{\mu }={k}_{pc}\kern0.5em \mathrm{and}\kern0.5em b=\frac{k_{\mathrm{pc}}{k}_{\mathrm{deg}}}{k_{e\;\left({RL}_p\right)}}\cdot \kern0.5em {k}_m $$
(36)

The roots of this equation are

$$ {X}_{\pm }=\frac{1}{2}\left\{\left({k}_{\mathrm{syn}}+a{L}_c+b\right)\pm \sqrt{{\left({k}_{\mathrm{syn}}+a{L}_c+b\right)}^2-4a\ {k}_{\mathrm{syn}}\ {L}_c}\right\} $$
(36)

Obviously, we need the root which vanishes when Lc = 0, i.e. we need X−. Therefore

$$ R{L}_p=\frac{1}{2\ {k}_{e\left(R{L}_p\right)}}\left\{\left({k}_{\mathrm{syn}}+a{L}_c+b\right)-\sqrt{{\left({k}_{\mathrm{syn}}+a{L}_c+b\right)}^2-4a\ {k}_{\mathrm{syn}}\ {L}_c}\right\} $$
(37)

The corresponding expression for target depression in terms of the ligand concentration in plasma (Lc) is found to be given by

$$ R=\frac{k_{syn}}{2}-\frac{1}{2}\left\{\left(a{L}_c+b\right)-\sqrt{{\left({k}_{\mathrm{syn}}+a{L}_c+b\right)}^2-4a\cdotp {k}_{\mathrm{syn}}\ {L}_c}\right\} $$
(38)

A more detailed derivation of these expressions for the concentration of ligand-receptor complex in terms of the ligand concentration in plasma can be found in the Appendix 1.1 (A.3 and A.4).

On the basis of the implicit expression (34) of X (i.e. RLp) in terms of Lc, it is also possible to define Lc; 50. Plainly, at Lc; 50, we have X = ksyn/2, i.e. RLp = R∗/2. When we substitute this value for X into Eq. (34), we obtain the following formula for Lc; 50:

$$ {L}_{c;50}=\frac{\mu }{k_{cp}}\left(\frac{k_{syn}}{2}+\frac{k_{pc}{k}_{deg}}{k_{e\left(R{L}_p\right)}}\ {K}_m\right) $$
(39)

or, when we replace the rates kcp and kpc by clearances again, we obtain

$$ {L}_{c;50}=\frac{1}{2}\frac{k_{syn}}{C{l}_{d\alpha}/{V}_p}+\frac{C{l}_{d\beta}}{C{l}_{d\alpha}}{L}_{p;50} $$
(40)

where we have used the definition of Lp; 50 in Eq. (32).

Passive Transport Between Central and Peripheral Compartment

If distribution between the two compartments is passive, i.e. Cldα = Cldβ = Cld, then the expression for Lc; 50 reduces to

$$ {L}_{c;50}=\frac{1}{2}\frac{k_{syn}}{C{l}_d/{V}_p}+{L}_{p;50} $$

Observation

Equation (40) immediately implies that

$$ C{l}_{d\beta}>C{l}_{d\alpha}\kern1em \Longrightarrow \kern1em {L}_{c;50}>{L}_{p;50} $$
(41)

If target-synthesis is small compared to in- and out-flow of ligand between the two compartments, the reverse inequalities are seen to hold as well.

It follows from this expression that Lc, 50increases when transport from the central towards the peripheral compartment becomes harder (Cldα↗) and vice versa, it decreases when it becomes easier (Cldβ↘).

If ksyn is small, more specifically, if

$$ \frac{k_{syn}}{2}\ll \frac{k_{deg}}{k_{e\left(R{L}_p\right)}}\frac{C{l}_{\beta }}{V_p}\ {K}_m $$
(42)

then, the expression (Eq. (40)) reduced to a particularly simple relation between Lc; 50 and Lp; 50:

$$ {L}_{c;50}\approx \frac{C{l}_{\beta }}{C{l}_{\alpha }}\ {L}_{p;50}. $$
(43)

in which the relative impact of the two clearances becomes very transparent.

The expression (Eq. (37)) for RLp in terms of Lc is fairly complex and not so easy to grasp. However, it is possible to derive a few properties of the dependence of RLp on Lc without going to the details of an explicit computation based on Eq. (37). Below we give a few examples.

  1. 1.

    It follows from Eq. (37) that 0 < X < ksyn. Therefore, remembering that \( X={k}_{e\left(R{L}_p\right)}R{L}_p \), it follows that

$$ R{L}_p<\frac{k_{syn}}{k_{e\left(R{L}_p\right)}}={R}^{\ast } $$
(44)

regardless of the ligand concentration Lc in the central compartment.

  1. 2.

    It is clear from Eq. (34) that Lc is an increasing function of X. Therefore, RLp is an increasing function of Lc:

$$ R{L}_p\left({L}_c\right)\nearrow {R}^{\ast}\kern1em \mathrm{as}\kern1em {L}_c\to \infty $$
(45)

Note that in Eqs. (44) and (45), the active transport between the central and the peripheral compartment (the parameters α and β) do not come into the upper bound and the limit for large Lc.

In Fig. 9, we show graphs of R and RLpversus Lc for three values of the clearance into the peripheral compartment Cldα (α = 0.001, α = 1 and α = 100), whilst reverse clearance, from the peripheral compartment into the central compartment is fixed. As predicted by Eq. (40), the potency Lc; 50decreases as α increases and hence when kcp decreases. Of course, this is understandable: When transport to the peripheral compartment becomes easier, drug reaches its target more easily, less of it is required to achieve the same effect and the in vivo potency increases.

Fig. 9
figure 9

Sensitivity graphs of R and RLpversus Lc, on a semi-logarithmic scale, with regard to the clearance rate from the central to the peripheral compartment αCld where α = 0.1,1,10 and the clearance rate from peripheral to central compartment βCd is fixed (β = 1). Other parameters are listed in Table I

Full size image
Fig. 10
figure 10

Left: Schematic illustrations of the consequences of two subjects with same the baseline target concentration (R0,A = R0,B), but different target turnover rates and losses. Right: Relationships between ligand concentration and normalised target occupancy when target baseline concentration is similar, but fractional turnover rates are different

Full size image

Comparing the graphs of the concentration of the ligand-target complex RLpversus the ligand concentration in the central compartment Lc in Figs. 2 and 9, the latter, when target is located peripherally, shows up to be (i) asymmetrical and (ii) to exhibit a shift between the central and peripheral concentrations.

Discussion and Conclusions

Equations (32), (37), (38) and (39) summarise what is needed to apply and explain target R, ligand-target complex RLp and ligand L (Lc and Lp) interactions when the target is peripherally located. The effect of the permeability of the membrane between central and peripheral compartment and the volumes of these compartments show up explicitly in the expression for the in vivo potency given in Eq. (39) in combination with target turnover and ligand-target binding properties. This explicit expressions make it possible to give quantitative estimates.

DISCUSSION AND CONCLUSIONS

In Vivo Potency—the Role of Target Dynamics

The new concept of potency discussed in this paper departs from the previous one, based on the assumption that the actual expression level of target rather than its turnover rate will determine the potency. Thus, looking at the data of two individuals with the same target expression level (concentration), one would assume that the two individuals would require the same drug exposure. In these papers, we have shown that in fact, this need not be true. Instead, according to the definition of L50, the subject with the higher target elimination rate (kdeg) will need more drug compared to a subject with a slow target turnover rate, whilst the subject with the higher internalisation rate (ke(RL)) will require less drug.

$$ {k}_{\deg; \mathrm{A}}<{k}_{\deg; \mathrm{B}}\Longrightarrow {L}_{50;\mathrm{A}}<{L}_{50;\mathrm{B}} $$

Expressed mathematically, we demonstrated how the potency L50 is given in open as opposed to closed systems by the definitions

$$ \left\{\begin{array}{lll}& {L}_{50}=\frac{k_{deg}}{k_{e(RL)}}\cdotp \frac{k_{off}+{k}_{e(RL)}}{k_{on}}& \mathrm{Open}\ \mathrm{systems}\\ {}& {L}_{50}=\frac{k_{off}}{k_{on}}& \mathrm{Closed}\ \mathrm{systems}\end{array}\right. $$
(46)

When target baseline levels are the same in two subjects, i.e. R0; A = R0; B, but one subject, say B as in Fig. 10 has a higher synthesis rate than A, i.e. ksyn; B > ksyn; A, the potency of drug in subject B will be numerically higher than in subject A, because kdeg; B > kdeg; A.

Non-symmetric Drug Distribution Between Central and Peripheral Compartment

We have seen that when target is located in the peripheral rather than the central compartment, the in vivo potency Lc; 50 will depend in the distributional rates between the two compartments, especially when they are not equal. Indeed, if Cldα denotes clearance out of the central compartment and Cldβ clearance into the central compartment, then, we have shown that if the synthesis rate of target ksyn is small, the in vivo potency with respect to the ligand concentration in the central compartment Lc; 50 and the in vivo potency with respect to the peripheral compartment Lp; 50 are related by the simple formula

$$ {L}_{c;50}=\frac{C{l}_{d\beta}}{C{l}_{d\alpha}}\cdotp {L}_{p;50}. $$
(47)

Thus, if Cldα > Cldβ relatively easily and high receptor occupancy will be reached for lower ligand concentrations in the central compartment, i.e. L50c will be relatively small.

On the other hand, when Cldα < Cldβ ligand has difficulty reaching the target and the potency, L50; c will now be larger.

We make two observations about the three graphs in Fig. 10.

  1. 1.

    The graphs appear to be translations of one another with a constant shift.

  2. 2.

    All three graphs have a larger radius of curvature for lower values of RLp and a smaller radius of curvature for higher values of RLp.

As regards the first observation, it follows from Eq. (47) that

$$ \log\ \left({L}_{c;50}\right)=\log\ \left(\frac{C{l}_{d\beta}}{C{l}_{d\alpha}}\right)+\log\ \left({L}_{p;50}\right), $$
(48)

so that the graph shifts by log (Cldβ/Cldα) as we move from one curve to the next in Fig. 10.

Overall Conclusions

This analysis has focused on the necessity of using an open systems approach for assessment of in vivo pharmacological data.

The major difference between potencies of closed and open systems is that the expression of the latter (L50 in Eq. (3)) shows that target turnover rate (kdeg) rather than target concentration (R0) will determine drug potency. The efficacy (typically denoted Emax/Imax) of a ligand is, on the other hand, dependent on both target concentration and target turnover rate. When target is located peripherally, the ratio of inter-compartmental distribution (CLdα/CLdβ) impacts the potency derived for a centrally located target.

Derived expressions are practically and conceptually applicable when interpreting data translation across individuals, species and studies are done, and also for communication of results to a biological audience.