Abstract
Because of its high-precision, low-cost and easy-operation, Precise Point Positioning (PPP) becomes a potential and attractive positioning technique that can be applied to self-driving cars and drones. However, the reliability and availability of PPP will be significantly degraded in the extremely difficult conditions where Global Navigation Satellite System (GNSS) signals are blocked frequently. Inertial Navigation System (INS) has been integrated with GNSS to ameliorate such situations in the last decades. Recently, the Visual-Inertial Navigation Systems (VINS) with favorable complementary characteristics is demonstrated to realize a more stable and accurate local position estimation than the INS-only. Nevertheless, the system still must rely on the global positions to eliminate the accumulated errors. In this contribution, we present a semi-tight coupling framework of multi-GNSS PPP and Stereo VINS (S-VINS), which achieves the bidirectional location transfer and sharing in two separate navigation systems. In our approach, the local positions, produced by S-VINS are integrated with multi-GNSS PPP through a graph-optimization based method. Furthermore, the accurate forecast positions with S-VINS are fed back to assist PPP in GNSS-challenged environments. The statistical analysis of a GNSS outage simulation test shows that the S-VINS mode can effectively suppress the degradation of positioning accuracy compared with the INS-only mode. We also carried out a vehicle-borne experiment collecting multi-sensor data in a GNSS-challenged environment. For the complex driving environment, the PPP positioning capability is significantly improved with the aiding of S-VINS. The 3D positioning accuracy is improved by 49.0% for Global Positioning System (GPS), 40.3% for GPS + GLOANSS (Global Navigation Satellite System), 45.6% for GPS + BDS (BeiDou navigation satellite System), and 51.2% for GPS + GLONASS + BDS. On this basis, the solution with the semi-tight coupling scheme of multi-GNSS PPP/S-VINS achieves the improvements of 41.8–60.6% in 3D positioning accuracy compared with the multi-GNSS PPP/INS solutions.
Similar content being viewed by others
Introduction
Precise Point Positioning (PPP) has been demonstrated as an effective tool in high-precision positioning and shows the advantages of efficiency and flexibility compared to the baseline network approach (Zumberge et al. 1997; Bisnath and Gao 2009). In recent years, the rapid development of Chinese BeiDou navigation satellite System (BDS) and European Galileo navigation satellite system (Galileo) brings new opportunities for PPP. A four-system PPP model was proposed by Li et al. (2015) to fully use the Global Positioning System (GPS), Global Navigation Satellite System (GLONASS), Galileo, and BDS observations. In their study, the multi-constellation Global Navigation Satellite System (GNSS) PPP presented faster solution convergence and higher positioning accuracy than single-system PPP. Recently, the investigation of multi-GNSS PPP data processing is not only about the dual-frequency models (Cai et al. 2015), but also focusing on the multi-frequency observations (Li et al. 2019b, 2020a, b). Briefly, the multi-frequency and multi-GNSS based PPP is becoming increasingly fashionable for precise positioning services (Alkan and Öcalan 2013; Guo et al. 2018), particularly in some new applications such as self-driving cars and unmanned aerial vehicles (Nie et al. 2019; Geng and Guo 2020).
However, PPP fails in the cases of observation outages or harsh signal environments (Zhang and Li 2012). Consequently, the Inertial Navigation System (INS) has been utilized to assist PPP in GNSS-challenged environments in the last decades (Roesler and Martell 2009; Gao et al. 2017). Shin and Scherzinger (2009) demonstrated that PPP/INS integration could realize a better accuracy and reliability of positioning in both open sky and GNSS blocked areas. Rabbou and El-Rabbany (2015) presented a tightly coupled multi-GNSS PPP/INS solution and achieved the positioning accuracy at decimeter to centimeter-level when the measurement updates from GNSS are available. Nevertheless, the performance of the GNSS/INS integration is degraded due to the rapid INS drift errors for the case of the long-term GNSS outages.
Favorable complementary properties of visual and inertial measurements make them suitable for fusion. Thus, extensive applications based on a visual-inertial integration were found in drones (Weiss et al. 2012) and self-driving vehicles (Li and Mourikis 2012). Generally, the existing visual-inertial fusion methods can be classified into the optimization-based (Yang and Shen 2017; Usenko et al. 2016) and the filter-based approaches (Bloesch et al. 2015; Tsotsos et al. 2015). A popular filter-based Visual-Inertial Odometry (VIO) algorithm was proposed by Mourikis and Roumeliotis (2007). In their approach, a versatile measurement model was presented to express the geometric constrains among multiple-camera poses with a common view. In practice, the optimization-based approaches can provide higher accuracy than the filter-based approaches given adequate computational resources (Delmerico and Scaramuzza 2018). The property of the re-linearization at each iteration contributes to the high accuracy of the optimization-based methods. Leutenegger et al. (2015) presented a keyframe-based Visual-Inertial Navigation System (VINS) and used Google’s Ceres solver to perform the nonlinear optimization (Agarwal et al. 2012). Besides, the sliding window strategy was adopted in their study to reduce the computation complexity of optimization. Qin et al. (2018) proposed a complete and versatile monocular VINS, which can realize the indoor positioning of drones with accuracy at a decimeter-level. Additionally, the translation error of the stereo VINS (S-VINS) is about 1% of the driving distance in an outdoor vehicular experiment (Qin et al. 2019). Although VINS can achieve a robust and accurate local pose estimation, the errors still accumulate over the time.
To eliminate the accumulated errors of VINS, many researchers integrate the GNSS and VINS for realizing a local accurate and global drift-free localization. Lynen et al. (2013) proposed a basic multi-sensor fusion framework to process delayed, relative, and absolute measurements from different sensors. Mascaro et al. (2018) proposed a decoupled optimization-based multi-sensor fusion method, which is demonstrated to be more accurate than other decoupled fusion strategies. Although some progress has been made with these methods in multi-sensor fusion navigation, they adopt the decoupled way to integrate the GPS and VINS. In addition, only the GPS derived positions are utilized in their framework rather than the GNSS raw observations with more available information. Vu et al. (2012) developed a multi-sensor fusion framework with differential GPS (DGPS), vision, and INS, which can provide a lane-level vehicle navigation in GNSS open-sky conditions. Moreover, Li et al. (2019a) proposed a tightly coupled fusion solution of multi-GNSS Real-Time Kinematic (RTK)/INS/vision, which can achieve centimeter-level positioning accuracy in GNSS degraded conditions. In the above two studies, the relative positioning methods were used to provide the global locations, which requires additional GNSS infrastructures such as reference stations and receivers in comparison to PPP. Zhu (2019) proposed a new structure named Semi-Tightly Coupled (STC) integration, which realized multi-sensor information fusion by the bidirectional location transfer and sharing in two separate navigation systems. The STC not only combines the advantages of the Loosely Coupled (LC) integration and Tightly Coupled (TC) integration, but also overcomes their main deficiencies.
In this contribution, we present a graph-optimization based and semi-tight coupling framework of multi-GNSS PPP and S-VINS for improving the PPP performance in a GNSS-challenged environment and realizing a stable and accurate global positioning outputs in a complex driving environment. In addition to a GNSS outage simulation test to verify the positioning capacity of S-VINS, the vehicle-borne experiment was also carried out in the campus of Wuhan University to assess the positioning performances of the S-VINS aided PPP solution and the multi-GNSS PPP/S-VINS solution. The contribution of the proposed method to precise positioning is presented and analyzed. In the following parts of this paper, we first describe the methods used in this study and then explain the algorithm implementation for the triple integrated system. Subsequently, the experimental situation is introduced, and the results are analyzed. Finally, the conclusions are summarized.
Methodology
In this section, we firstly introduce the PPP observation model. Then, a tightly coupled stereo VIO algorithm is described. Subsequently, the semi-tightly coupled multi-GNSS PPP/S-VINS fusion method is presented. Finally, the algorithm implementation of the developed multi-sensor fusion framework is explained.
PPP observation model
The GNSS observation equations for raw pseudorange and carrier phase are formulated as (Li et al. 2015):
where the symbols \(s\), \(r\), and \(j\) represent the satellite, receiver and carrier frequency, respectively; \(\rho\) is the geometric distance between the satellite and receiver; \(c\) is the speed of light in vacuum; \(t_{r}\) and \(t^{s}\) denote the receiver and satellite clock offsets, respectively; \(d_{r,j}\) and \(d_{j}^{s}\) are the code hardware delays for the receiver and the satellite, respectively; \(I_{r,1}^{s}\) is the ionospheric delay at the first carrier frequency, and \(\mu_{j} = {{f_{j}^{2} } \mathord{\left/ {\vphantom {{f_{j}^{2} } {f_{1}^{2} }}} \right. \kern-0pt} {f_{1}^{2} }}\) is the ionospheric coefficient associated to a frequency \(f_{j}\); \(T_{r}^{s}\) is the tropospheric delay; \(\lambda_{j}\) and \(N_{r,j}^{s}\) denote the wavelength and the integer ambiguity; \(b_{r,j}\) and \(b_{j}^{s}\) are the phase delays in receiver and satellite sides (Ge et al. 2008; Li et al. 2011); \(\Delta \rho\) denotes the other corrections which should be considered in the PPP model, such as phase wind-up effect, antenna Phase Center Offset (PCO) and Phase Center Variation (PCV), relativity effect, and earth rotation effect (Wu et al. 1993; Schmid et al. 2007); \(\varepsilon_{{P_{r,j}^{s} }}\) and \(\varepsilon_{{L_{r,j}^{s} }}\) represent the sum of measurement noises and multipath errors for code and phase, respectively.
The Ionospheric-Free (IF) combinations are usually applied to eliminate the ionospheric delay in the PPP model. The dual-frequency IF combinations can be written as:
where \(\gamma = {{f_{1}^{2} } \mathord{\left/ {\vphantom {{f_{1}^{2} } {(f_{1}^{2} - f_{2}^{2} }}} \right. \kern-0pt} {(f_{1}^{2} - f_{2}^{2} }})\), \(f_{1}\) and \(f_{2}\) are the frequencies of two carriers; \(\lambda_{\text{IF}} N_{\text{IF}} = \gamma (\lambda_{1} (N_{r,1}^{s} + b_{r,1} - b_{1}^{s} )) + (1 - \gamma )(\lambda_{2} (N_{r,2}^{s} + b_{r,2} - b_{2}^{s} ))\) is the IF ambiguity in meters. The measurements noises of IF pseudorange and phase can be denoted by \(\varepsilon_{{P_{\text{IF}} }} = \gamma \varepsilon_{{P_{r,1}^{s} }} + (1 - \gamma )\varepsilon_{{P_{r,2}^{s} }}\) and \(\varepsilon_{{L_{\text{IF}} }} = \gamma \varepsilon_{{L_{r,1}^{s} }} + (1 - \gamma )\varepsilon_{{L_{r,2}^{s} }}\). Additionally, \(d_{r,j}\) is absorbed in receiver clock offset, and \(d_{j}^{s}\) is corrected in the IF combinations when applying the precise clock products. The tropospheric delay \(T\) in Eqs. (1) and (2) is made up of the dry and wet components which can be expressed by the zenith delays (\(T_{\text{dry}} ,T_{\text{wet}}\)) and the corresponding mapping functions (\(m_{\text{dry}} ,m_{\text{wet}}\)). An empirical model can be used to correct the dry delay part (\(m_{\text{dry}} \cdot T_{\text{dry}}\)) (Saastamoinen 1972), while the wet component delay (\(m_{\text{wet}} \cdot T_{\text{wet}}\)) can be estimated from the observations.
When multi-GNSS observations are involved, the different signal structures and different hardware delays for each GNSS system will result in different code biases in one multi-GNSS receiver (Li et al. 2015). The differences between these biases are usually called Inter-System Biases (ISB) or Inter-Frequency Biases (IFB) for GLONASS satellites. ISB/IFB parameters must be introduced into the multi-GNSS estimator. The IF combinations of the multi-GNSS code and phase observations can be written as:
where \(t_{r}\) denotes the receiver clock offset of the reference GNSS system, namely GPS; \(ISB^{\text{sys}}\) represents the ISB of the non-reference GNSS system. As for GLONASS, the \(ISB^{\text{sys}}\) parameter will be set for each frequency. \(\rho_{T}\) represents the sum of the geometric distance and the dry tropospheric delay. The linearized equations of the IF combination can be expressed as:
where \(p_{\text{IF}}\) and \(l_{\text{IF}}\) signify observed-minus-computed pseudorange and phase IF measurement residuals; \(\varvec{u}\) represents the unit vector of the direction from the receiver to the satellite; \(\updelta\varvec{p}\) is the position correction vector. In this paper, the GNSS raw measurements are processed by the individual multi-GNSS PPP module of the multi-sensor fusion system. The detailed information on the multi-GNSS data processing in PPP is listed in Table 1.
Stereo visual-inertial odometry formulation
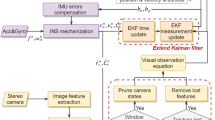
The visual front-end processes the stereo pairs from the stereo camera. For each new stereo pair, the Kanade–Lucas–Tomasi (KLT) sparse optical flow algorithm is applied to perform feature tracking of existing features (Lucas and Kanade 1981). In addition, the forward (previous frame to current frame) and backward (current frame to previous frame) feature tracking are both implemented to acquire high quality tracking results. Meanwhile, new corner features are detected to maintain a certain number of features (e.g., 100–300) in each image (Shi and Tomasi 1994). The stereo matches are also obtained by the KLT sparse optical flow algorithm between left and right images. As for the raw Inertial Measurement Unit (IMU) measurements, the IMU pre-integration technique is used to generate relative IMU measurements between two consecutive states in VIO sliding window (Lupton and Sukkarieh 2012). For the IMU state propagation in pre-integration, the mid-point integration is used for the discrete-time implementation. To propagate the uncertainty of the state, the covariance of the IMU state can be computed recursively, referring to Qin et al. (2018).
An initialization procedure is required for the stereo VIO. For each frame in the sliding window, we triangulate all features observed in the stereo pairs. Based on these triangulated features, a Perspective-n-Point (PnP) method is used to estimate the poses of all other frames in the window (Lepetit et al. 2009). Additionally, the pre-integration factor is constructed between each frame in the window. When the window size reaches 10, a visual-inertial bundle adjustment is performed to obtain the optimized states in the window.
After the initialization of estimator, a tightly coupled sliding window-based VIO is carried out to achieve accurate and robust state estimation, serving as local constraints in the global fusion. The definition of state vector in the sliding window can be written as (Qin et al. 2018):
where \(\varvec{\chi}_{{l_{\text{vio}} }}\) denotes the complete state vector including the IMU state vector \(\varvec{x}_{k}\), the extrinsic parameter \(\varvec{x}_{c}^{b}\) of IMU-camera, and the inverse depth \(\lambda_{l}\) of the \(l\)th feature from its first observation; \(c\) and \(b\) represent the camera frame and IMU frame, respectively. \(n\) and \(m\) are the quantities of keyframes and features in the sliding window, respectively; the \(\varvec{x}_{k}\) consists of the IMU states at the time when the \(k\) th image is captured; the position \(\varvec{p}_{{b_{k} }}^{{l_{\text{vio}} }}\), velocity \(\varvec{v}_{{b_{k} }}^{{l_{\text{vio}} }}\), and orientation \(\varvec{q}_{{b_{k} }}^{{l_{\text{vio}} }}\) of the IMU center is with respect to the local reference frame \(l_{\text{vio}}\) which is defined by the first IMU pose; \(\varvec{b}_{a}\) and \(\varvec{b}_{g}\) represent the accelerometer bias and gyroscope bias, respectively.
A maximum posteriori estimation of the VIO system states can be acquired by minimizing the sum of a priori and the Mahalanobis norm of all measurement residuals:
where \(\varvec{r}_{I} (\hat{\varvec{z}}_{{b_{k + 1} }}^{{b_{k} }} ,\varvec{\chi})\) and \(\varvec{r}_{C} (\hat{\varvec{z}}_{l}^{{c_{j} }} ,\varvec{\chi})\) denote the inertial and visual residuals, respectively; \(\left\{ {\varvec{r}_{p} - \varvec{H}_{p}\varvec{\chi}} \right\}\) represents the a priori information obtained by the process of marginalization in the sliding window; \(\rho ( \cdot )\) is the Huber function used for reducing the weight of the outliers in the least squares problems (Huber 1964). In addition, a strict outlier rejection mechanism is performed after each optimization by checking the average reprojection errors of (13), (14), and (15). When the window size is full, the oldest IMU state and corresponding features in the sliding window will be marginalized to bound the computational complexity of VIO.
There are two additional types of reprojection equations for the stereo VIO compared to the mono-VIO presented in Qin et al. (2018). Supposed that the \(l\)th feature is observed by the \(i\)th stereo images and the \(j\)th stereo images. Additionally, the first observation of the feature happens in the former. Three types of reprojection equations are used in our method, which can be expressed as:
where \([u_{l}^{{c_{i,1} }} ,v_{l}^{{c_{i,1} }} ]\) is the first observation of the lth feature, and \(c_{i,1}\) denotes the left image of the ith stereo images; \(\varvec{\pi}_{c}^{ - 1}\) is the back projection function which turns a pixel location into a unit vector using camera intrinsic parameters; \(\left( {\varvec{R}_{{c_{1} }}^{b} , \, \varvec{p}_{{c_{1} }}^{b} } \right)\) and \(\left( {\varvec{R}_{{c_{ 2} }}^{b} , \, \varvec{p}_{{c_{ 2} }}^{b} } \right)\) are the extrinsic parameters of left IMU-camera and right IMU-camera, respectively; \(\varvec{P}_{l}^{{c_{j,1} }}\) and \(\varvec{P}_{l}^{{c_{j,2} }}\) are the reprojection results from the observations in ith left image to the jth left image and right image, respectively; \(\varvec{P}_{l}^{{c_{i, 2} }}\) represents the reprojection results from the left image to the right image in the ith image pair. The visual measurement residuals can be obtained by the way of observed-minus-computed.
Multi-GNSS PPP/S-VINS fusion
The multi-sensor fusion problem is depicted by constructing a graph structure displayed in Fig. 1. The graph structure consists of a series of nodes and edges. Each node denotes the vehicle state in the global frame. The edge between two consecutive nodes is a local constraint formed by S-VINS. Another type of edge is the global constraint provided by the multi-GNSS PPP solution. Because of the low satellite availability in complex driving conditions, the positioning results from the PPP are selectively used as the global constraint. A Quality Number (QN) is adopted to indicate the accuracy of PPP solution, referring to (NovAtel Corporation 2018a). The quality of the positioning results from PPP solution are labeled with an integer 1–6 based on their covariances. In this paper, the QN within 4 will be maintained in the pose graph; the QN equal to 5 will be used only once and removed after the global optimization; and the QN more than 5 will be rejected. The growth rate of the node is dependent on the GNSS outputs.
The mathematical model of the fusion method can be expressed as a Maximum Likelihood Estimation (MLE) problem as described in Qin et al. (2019). For the completeness, we briefly introduce the theory. The state estimation of the global fusion can be converted to a nonlinear least squares problem, which can be written as:
where \(\varvec{\chi}{ = [}\varvec{x}_{0} , { }\varvec{x}_{1} , \, \ldots \varvec{x}_{n} ]\) is the state vector of all nodes in graph and \(\varvec{x}_{i} = [\varvec{p}_{i}^{G} , \, \varvec{q}_{i}^{G} ]\); \(\varvec{p}_{i}^{G}\) and \(\varvec{q}_{i}^{G}\) are the position and orientation of the node \(i\) with respect to the global reference frame \(G\); \(\varvec{S}\) is the set of measurements including the local poses (S-VINS) and global positions (multi-GNSS PPP), The Mahalanobis norm is \(\left\| \varvec{r} \right\|_{{{\varvec{\Omega}}_{t}^{k} }}^{2} = \varvec{r}^{\text{T}} {\varvec{\Omega}}^{ - 1} \varvec{r}\). Here \(\varvec{r}\) represents the vector of the measurement residual, and \({\varvec{\Omega}}\) is the corresponding covariance.
The error function \(\varvec{r} = \varvec{z}_{t}^{k} - h_{t}^{k} (\varvec{\chi})\) consists of two parts in the fusion model. Part one is the local measurement residual, which is formulated as:
the upper equation describes the relative pose error between time \(t - 1\) and \(t\). The first row denotes the relative position errors, and the second row denotes the relative rotation error. ⊖ is the minus operation on the error state of quaternion. The unified covariance is applied for all local measurements in our framework. Part two is the global measurement residual, which can be written as:
where \(\varvec{p}_{t}^{\text{ppp}}\) is the position measurement from the multi-GNSS PPP. The global location is directly used as the position constraint for every node. It should be noted that the local-level frame (ENU, East-North-Up) is adopted to represent the global reference frame \(G\), and the origin point is located at the first global location from the multi-GNSS PPP solution during the global fusion. Furthermore, the subsequent global positioning results are converted from the Earth-Centered Earth-Fixed (ECEF) frame to the ENU frame with respect to the first global location. The proposed triple integrated system can provide the covariances of the global locations, which contributes to a better use of the position information from the GNSS. In comparison, the original work in Qin et al. (2019) determines the covariance only by the number of the visible satellites.
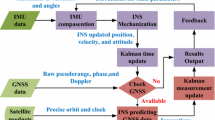
The nature of the fusion method is a rigid base frame alignment problem between a local reference frame and a global reference frame. The multi-sensor-fusion positioning in the global frame can be realized by carrying out this alignment process. The transformation between the local and the global reference frame will be updated after each global optimization. The subsequent positioning results from S-VINS can be converted from the local frame to the global frame by this transformation. Moreover, the predicted positions maintain a high accuracy in a short term, which can be utilized in the multi-GNSS PPP data processing. Thus, we transmit the global forecast position to the multi-GNSS PPP processor as the a priori information.
The a priori information is used for the following purposes in the multi-GNSS PPP processing. Firstly, the predicted position is used as an initial value for the PPP data processing to replace the Standard Point Positioning (SPP) result. On the one hand, SPP produces a position with low accuracy in GNSS-challenged conditions (Angrisano et al. 2013). On the other hand, the priori location has a comparable positioning accuracy with PPP in a short term, which is verified in the following experimental part. Secondly, when the number of available satellites is less than six, the forecast position will be used as the position constraint in the PPP processing. This criterion is used mainly to cope with the extremely poor observation conditions. The variance of the predicted position can be determined by:
where \(\sigma_{0} = \sqrt {\sigma_{{x_{0} }}^{2} + \sigma_{{y_{0} }}^{2} + \sigma_{{z_{0} }}^{2} }\) is the standard deviation of the global location used in last graph optimization; \((\sigma_{{x_{0} }}^{2} ,\sigma_{{y_{0} }}^{2} ,\sigma_{{z_{0} }}^{2} )\) is the variances of position in ECEF; \(D\) denotes the diving distance from the vehicle state of last graph optimization to current vehicle state in meters; 1% is the degradation rate of the local positioning accuracy (Qin et al. 2019). The unified variance \(\sigma^{2}\) is applied for different axes of the position vector \(\varvec{p} = [p_{x}^{e} ,p_{y}^{e} ,p_{z}^{e} ]\) in our algorithm for the degradation rate of the local positioning accuracy is hard to be decomposed to different axes. The position feedback mechanism in our solution is bootable when the number of the global locations maintained in the global fusion processor exceeds a certain threshold.
Implementation of multi-GNSS PPP/S-VINS algorithm
The architecture of the proposed semi-tightly coupled multi-GNSS PPP/S-VINS integration is shown in Fig. 2. A sliding window-based nonlinear optimization is operated for state updates after finishing the visual-inertial initialization. The newest local state is converted to the corresponding global state by the transformation between the local frame and the global frame. In addition, the transformation matrix is initially set to the identity matrix and gets updated after each global optimization. The IF combinations of GNSS raw pseudorange and phase measurements are applied to the PPP data processing. Once the feedback mechanism is activated, the predicted positions from S-VINS can be utilized in the PPP processing. When the PPP solution is completed, the global position with its uncertainty will be transferred to the global fusion processor. Nevertheless, only the positioning result that passes the quality check will be used in the global fusion. Practically, the measurements from the local (S-VINS) and global (PPP) processor have different sampling rates. If the timestamp of the newest local state is synchronized with the current GNSS epoch, the global optimization will proceed. Otherwise, only the forecast positions can be acquired. The Ceres Solver is used in the triple integrated system for state optimization (Agarwal et al. 2012). The optimal positioning results are obtained after carrying out the global graph optimization. Meanwhile, the transformation from the local frame to the global frame is updated.
Experimental description
The vehicular road test was carried out in the campus of Wuhan University where the trees with dense forest canopies are on both sides of the roads. Figure 3 displays the top view of the trajectory and the typical surroundings in the road. The total distance of the trajectory is about 2670 m, and it takes about 12 min in our experiment.
The equipment used for collecting the multi-sensor fusion data is displayed in Fig. 4. In our vehicular road test, only single GNSS antenna was used. As shown in the top panel of Fig. 4, a GNSS receiver and an IMU device are connected to the GNSS antenna through a signal power divider. Two cameras are tightly mounted on the front of the platform with a 505 mm baseline. The detailed information on the devices is listed in Table 2, and the specification of the IMU sensor is provided in Table 3. We achieved the time synchronization at the hardware level. More specifically, the Pulses Per Second (PPS) generated by the GNSS receiver is used to trigger the IMU to work and the stereo cameras to exposure at different frequencies. By this means, the time stamps of different sensors will synchronize to GPS time. The offset between GNSS antenna reference point and IMU center was measured precisely to compensate the lever-arm effect. The extrinsic parameters for stereo cameras and IMU-camera were calibrated offline (Furgale et al. 2013). Moreover, the extrinsic parameters of IMU-camera are also estimated in S-VINS based on the pre-calibrated values to compensate the small variations caused by the vehicle motion. We also calibrated the intrinsic parameters of the stereo cameras before and after the test.
Additionally, the multi-sensor fusion data were collected under the normal driving conditions including most common ground vehicle dynamics, such as acceleration, deceleration, and cornering. The bidirectional smoothed solution of tightly coupled multi-GNSS RTK/INS is used as the ground truth, which is calculated by the commercial software Inertial Explorer (IE) 8.7 (NovAtel Corporation 2018b).
Result analysis
In this part, the number of available GNSS satellites and the corresponding position Dilution of Precision (PDOP) are firstly presented. Then, a simulation test of complete GNSS outage is proceeded to validate the positioning capacity of S-VINS. Subsequently, the positioning capacity of the S-VINS aided multi-GNSS PPP solution is discussed. Finally, we assess the positioning performance of the multi-GNSS PPP/S-VINS solution.
Satellite availability
The top panel of Fig. 5 depicts the evolutions of the number of available satellites for GPS (G), GLONASS (R), BDS (C), and GPS + GLONASS + BDS (G + R+C) during the test at a cutoff elevation angle of \(7^{ \circ }\). The Galileo system is absent for only the single-frequency signals of Galileo can be received by our receiver during the test. The mean values of the number of visible satellites for different GNSS constellations are 4.8 (G), 3.2 (R), 4.1 (C), and 12.1 (G + R + C). There are frequent decreases in the satellite numbers as shown in Fig. 5, and the number of available GLONASS or BDS satellites sometimes becomes zero. The PDOP variations of different GNSS constellations are presented in the bottom of Fig. 5. The average PDOP values for different GNSS constellations are 3.1 (G), 4.7 (R),4.3 (C), and 1.2 (G + R + C). It is obvious that the value of the PDOP increases as the number of observed satellites decreases. On account of such GNSS partly blocked conditions, the number of observed satellites drops frequently, and the signal tracking is discontinued, which is a challenge to precise positioning.
S-VINS positioning performance during GNSS outage
In this section, we simulated the complete GNSS outage conditions to investigate the positioning performance of S-VINS compared with the INS-only solution. A complete dynamic trajectory (about 2670 m) in the real driving environment was divided into ten segments with the driving time of 100 s each. Meanwhile, the complete GNSS outage for 50 s was simulated in each segment. The average root mean square (RMS) values of the position drifts for the two solutions are shown in Fig. 6. During the GNSS outage time from 5 s to 50 s, the position RMS values of the INS mode are degraded from 0.05, 0.02, and 0.01 m to 3.12, 3.04, and 0.15 m in the east, north, and vertical directions, respectively. By contrast, the RMS values of S-VINS drop from 0.05, 0.06, and 0.01 m to 0.80, 1.16, and 0.12 m in east, north, and vertical directions, respectively. It can be seen that the S-VINS mode has a slower degradation in positioning accuracy than the INS-only mode. This indicates that redundant visual observation from the tracked features can help the S-VINS maintain an accurate local position.
As described above, the GNSS is in normal operation in the remaining 50 s of each segment. Thus, the accumulated positioning errors of S-VINS in the triple integrated system can be corrected after each global optimization. To have a comprehensive assessment of the positioning performance of S-VINS, the predicted position accuracy of S-VINS before each global optimization is calculated. The distribution of the predicted position differences is shown in Fig. 7. The results show that the percentage of position differences less than 5 cm is 71.9%, 63.8%, and 98.5% for east, north, and up components, respectively. The corresponding percentage is 22.6%, 33.2%, and 0.5% in the range of 5 cm to 10 cm. Given the above, it can be found that more than 90% of the predicted position differences are at centimeter level when GNSS is in normal operation, despite of the outliers caused by the visual instability resulting from the feature mismatches in the complex driving conditions.
Additionally, the S-VINS-only positioning performance is also evaluated in the same dynamic driving environment. We aligned the S-VINS trajectory (local coordinate) with the ground truth (ECEF coordinate) using a rigid body transformation (Horn 1987) and calculated the position differences of each matched positions. The RMS of position differences of S-VINS in the local coordinate system is given in Table 5.
Positioning capacity of the S-VINS aided multi-GNSS PPP solution
In our triple integrated system, the forecast position from S-VINS is used as an initial value or a position constraint to assist multi-GNSS PPP in GNSS-challenged conditions. The position differences of the IF PPP solution for the GPS, GPS + GLONASS, GPS + BDS, and GPS + BDS + GLONASS modes are shown in Fig. 8. The corresponding position differences for the S-VINS aided IF PPP solution are shown in Fig. 9. The results of both modes are listed in Table 4. For the PPP-only solutions, the positioning accuracy is seriously affected by the poor satellite visibility. The maximum values of positioning error are (4.99, − 24.68, − 55.14) m for GPS, (4.80, − 19.37, − 44.98) m for GPS + GLOBASS, (7.05, − 24.91, − 54.49) m for GPS + BDS, and (5.36, − 19.14, − 44.99) m for GPS + GLONASS + BDS in east, north, and vertical components, respectively. With the aiding of S-VINS, the positioning performance of the PPP-only solution is improved. The statistics indicates that the improvements of the positioning accuracy are (20.2%, 31.9%, 55.5%) for GPS, (24.0%, 22.6%, 44.4%) for GPS + GLOANSS, (19.8%, 43.3%, 47.8%) for GPS + BDS, and (0, 19.5%, 67.7%) for GPS + GLOANSS + BDS in east, north and up components, respectively. Simultaneously, the outliers are also effectively suppressed. Compared with the unaided PPP solution, the maximum values of positioning error are reduced to (2.58, − 3.88, − 4.81) m for GPS, (0.14, − 2.91, − 7.3) m for GPS + GLONASS, (2.17, − 3.28, − 6.12) m for GPS + BDS, and (2.00, − 2.78, − 3.13) m for GPS + GLONASS + BDS in east, north, and vertical directions, respectively. It can be seen that the positioning accuracy and availability of the IF PPP solution have a significant improvement with the aiding of S-VINS in such GNSS-challenged conditions. The main contribution of S-VINS is to provide a high-accuracy forecast position, which is immune to the unexpected sudden changes in the observation environment such as short-term GNSS signal losses. However, the absolute positioning accuracy of the S-VINS aided PPP solution still depends on the precision of PPP.
Positioning performance of the triple integrated system
The positioning performance of the triple integrated system is evaluated in this section. For comparison, the multi-GNSS PPP/INS solutions are calculated and analyzed. The combined mode of GPS + GLONASS + BDS is applied in the IF PPP processing. The position differences of the multi-GNSS PPP/S-VINS, LC multi-GNSS PPP/INS, and TC multi-GNSS PPP/INS are shown in Fig. 10, and the corresponding RMSs are listed in Table 5. As expected, the positioning accuracy of the multi-GNSS PPP/S-VINS solution is further improved by the S-VINS augmentation. The results show that the position RMS of the multi-GNSS PPP/S-VINS solution is 0.88, 1.47, and 0.96 m with an improvement of 7.4%, 6.4%, and 27.3% in east, north, and vertical directions, respectively, compared with the S-VINS aided PPP (G + R+C) solution. Additionally, the statistical analysis indicates that the improvements in 3D positioning accuracy with our method are 60.6% for the LC multi-GNSS PPP/INS solution and 41.8% for the TC multi-GNSS PPP/INS solution. More specifically, compared to the LC multi-GNSS PPP/INS solution, the positioning accuracy of the triple integrated solution is improved by 53.4%, and 71.4% in horizontal and vertical components, respectively. Besides, the maximum values of position differences are reduced from (21.11, 0.59, 0.89) m to (2.02, − 2.84, − 3.12) m. Compared to the TC multi-GNSS PPP/INS solution, the triple integrated solution achieves a significant improvement in the vertical component but less in the horizontal position. The main reason is that the overall positioning accuracy of the triple integrated system is still largely impacted by the PPP performance due to the location-based information fusion. In addition, the major improvement of PPP is in vertical component while the horizontal components obtain a modest improvement with the aiding of S-VINS. In conclusion, the multi-GNSS PPP/S-VINS solution achieves a higher positioning accuracy and availability compared with multi-GNSS/INS solutions in such GNSS-challenged environment.
Conclusion
To improve the positioning performance in GNSS-challenged environments, an optimization-based semi-tightly coupled multi-sensor fusion framework of multi-GNSS PPP/S-VINS was developed and validated in this study. Based on the GNSS outage simulation test and the vehicle-borne experiment, the positioning performances of the multi-GNSS PPP/S-VINS solution were comprehensively evaluated with respect to the stand-alone S-VINS positioning, the S-VINS aided multi-GNSS PPP positioning, and the triple integrated system positioning.
The GNSS outage simulation test demonstrates that the S-VINS can achieve a slower degradation in positioning accuracy than the INS-only. The statistical analysis of the complete GNSS outages for 50 s shows that the average RMS of position drifts for S-VINS is 0.80, 1.16, and 0.12 m with an improvement of 74.4%, 61.8%, 20.0% in north, east, and up components, respectively, compared with the INS-only mode. Furthermore, more than 90% of the predicted position differences is at centimeter level during one-second GNSS outages. According to the results of the vehicle-borne experiment, the accurate predicted positions from S-VINS can assist PPP to improve the overall positioning performance. The maximum position error of the stand-alone PPP (GPS + GLONASS + BDS) solution is reduced from (5.36, − 19.14, − 44.99) m to (2.00, − 2.78, − 3.13) m compared with the results of the aiding of S-VINS in east, north, and up components, respectively. Besides, the improvements of 3D positioning accuracy for the unaided PPP solution are 49.0% for GPS, 40.3% for GPS + GLONASS, 45.6% for GPS + BDS, and 51.2% for GPS + GLONASS + BDS. Due to the improvement in the positioning accuracy of the S-VINS aided PPP solution, better positioning results can participate in the graph optimization for global fusion. The statistics shows that that the RMSs of position errors of the multi-GNSS PPP/S-VINS solution are 0.88, 1.47, and 0.96 m with an improvement of 7.4%, 6.4%, and 27.3% in east, north, and up components, respectively, compared with the S-VINS aided PPP (GPS + GLONASS + BDS) solution. Moreover, the multi-GNSS PPP/S-VINS solution improves 3D positioning accuracy by 60.6% and 41.8% compared with the LC multi-GNSS PPP/INS solution and the TC multi-GNSS PPP/INS solution, respectively.
In conclusion, the positioning performance of the PPP solution can be significantly improved with the aiding of S-VINS. Meanwhile, the multi-GNSS PPP/S-VINS solution realizes a higher positioning accuracy and availability compared with the multi-GNSS PPP/INS solutions in GNSS-challenged environments, which shows a great potential of the multi-sensor fusion system for precise positioning.
Availability of data and materials
The datasets used and analysed in this study are available from the corresponding author on reasonable request.
References
Agarwal, S., Mierle, K., et al. (2012). Ceres solver. http://ceres-solver.org. Accessed 1 July 2020.
Alkan, R., & Öcalan, T. (2013). Usability of the GPS precise point positioning technique in marine applications. The Journal of Navigation, 66, 579–588.
Angrisano, A., Gaglione, S., & Gioia, C. (2013). Performance assessment of GPS/GLONASS single point positioning in an urban environment. Acta Geodaetica et Geophysica, 48(2), 149–161.
Bisnath, S., & Gao, Y. (2009). Current state of precise point positioning and future prospects and limitations. In Observing our changing earth (pp. 615–623). Springer.
Bloesch, M., Omari, S., Hutter, M., & Siegwart, R. (2015). Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (pp. 298–304).
Cai, C., Gao, Y., Pan, L., & Zhu, J. (2015). Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Advances in Space Research, 56(1), 133–143.
Dach, R., Schaer, S., Arnold, D., Prange, L., Sidorov, D., Susnik, A., et al. (2017). CODE final product series for the IGS. Astronomical Institute, University of Bern, Bern. http://www.aiub.unibe.ch/download/CODE.
Delmerico, J., & Scaramuzza, D. (2018). A benchmark comparison of monocular visual-inertial odometry algorithms for flying robots. In Proceedings of the IEEE international conference on robotics & automation (pp. 2502–2509).
FLIR Corporation. (2019). GS3-U3-28S5M-C Product specifications. https://www.flir.cn/products/grasshopper3-usb3/?model=GS3-U3-28S5M-C. Accessed 1 July 2020.
Furgale, P., Rehder, J., & Siegwart, R. (2013). Unified temporal and spatial calibration for multi-sensor systems. In Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (pp. 1280–1286).
Gao, Z., Zhang, H., Ge, M., Niu, X., Shen, W., Wickert, J., et al. (2017). Tightly coupled integration of multi-GNSS PPP and MEMS inertial measurement unit data. GPS Solutions, 21(2), 377–391.
Ge, M., Gendt, G., Rothacher, M., Shi, C., & Liu, J. (2008). Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. Journal of Geodesy, 82(7), 389–399.
Gendt, G., Dick, G., Reigber, C. H., Tomassini, M., Liu, Y., & Ramatschi, M. (2003). Demonstration of NRT GPS water vapor monitoring for numerical weather prediction in Germany. Journal of the Meteorological Society of Japan, 82(1B), 360–370.
Geng, J., & Guo, J. (2020). Beyond three frequencies: an extendable model for single-epoch decimeter-level point positioning by exploiting Galileo and BeiDou-3 signals. Journal of Geodesy, 94(1), 14.
Guo, J., Li, X., Li, Z., Hu, L., Yang, G., Zhao, C., et al. (2018). Multi-GNSS precise point positioning for precision agriculture. Precision Agriculture, 19, 895–911.
Horn, B. (1987). Closed-form solution of absolute orientation using unit quaternions. Journal of the Optical Society of America A, 4(4), 629–642.
Huber, P. (1964). Robust estimation of a location parameter. Annals of Mathematical Statistics, 35(2), 73–101.
Lepetit, V., Moreno-Noguer, F., & Fua, P. (2009). Epnp: an accurate o(n) solution to the pnp problem. International Journal of Computer Vision, 81(2), 155–166.
Leutenegger, S., Lynen, S., Bosse, M., Siegwart, R., & Furgale, P. (2015). Keyframe-based visual-inertial odometry using nonlinear optimization. The International Journal of Robotics Research, 34(3), 314–334.
Li, M. & Mourikis, A. I. (2012). Improving the accuracy of EKF-based visual-inertial odometry. In Proceedings of the IEEE international conference on robotics and automation (pp. 828–835).
Li, T., Zhang, H., Gao, Z., Niu, X., & El-Sheimy, N. (2019b). Tight fusion of a monocular camera, MEMS-IMU, and single-frequency multi-GNSS RTK for precise navigation in GNSS-challenged environments. Remote Sensing, 11(6), 610.
Li, X., Li, X., Liu, G., Feng, G., Yuan, Y., Zhang, K., et al. (2019a). Triple-frequency PPP ambiguity resolution with multi-constellation GNSS: BDS and Galileo. Jouranl of Geodesy, 93(8), 1105–1122.
Li, X., Li, X., Liu, G., Xie, W., & Feng, G. (2020a). The phase and code biases of Galileo and BDS-3 BOC signals: effect on ambiguity resolution and precise positioning. Journal of Geodesy, 94(1), 9.
Li, X., Liu, G., Li, X., Zhou, F., Feng, G., Yuan, Y., et al. (2020b). Galileo PPP rapid ambiguity resolution with five-frequency observations. GPS Solutions, 24(1), 24.
Li, X., Zhang, X., & Ge, M. (2011). Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. Journal of Geodesy, 85(3), 151–158.
Li, X., Zhang, X., Ren, X., Fritsche, M., Wickert, J., & Schuh, H. (2015). Precise positioning with current multi-constellation global navigation satellite systems: GPS, GLONASS: Galileo and BeiDou. Scientifc Reports, 5, 8328.
Lucas, B. D., & Kanade, T. (1981). An iterative image registration technique with an application to stereo vision. In Proceedings of the 7th international joint conference on Artificial intelligence (pp. 24–28).
Lupton, T., & Sukkarieh, S. (2012). Visual-inertial-aided navigation for highdynamic motion in built environments without initial conditions. IEEE Transactions on Robotics, 28(1), 61–76.
Lynen, S, Achtelik, M. W., Weiss, S., Chli, M., & Siegwart, R. (2013). A robust and modular multi-sensor fusion approach applied to MAV navigation. In Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (pp. 3923–3929).
Mascaro, R., Teixeira, L., Hinzmann, T., Siegwart, R., & Chli, M. (2018). GOMSF: graph-optimization based multi-sensor fusion for robust UAV pose estimation. In Proceedings of the IEEE international conference on robotics and automation (pp. 1421–1428).
Mourikis, A. I. & Roumeliotis, S. I. (2007). A multi-state constraint Kalman filter for vision-aided inertial navigation. In Proceedings of the IEEE international conference on robotics and automation (pp. 3565–3572).
Nie, Z., Liu, F., & Gao, Y. (2019). Real-time precise point positioning with a low-cost dual-frequency GNSS device. GPS Solutions, 24(1), 9.
NovAtel Corporation. (2015). IMU-FSAS product sheet. https://novatel.com/support/support-materials/product-sheet. Accessed 1 July 2020.
NovAtel Corporation. (2018a). GrafNav and GrafNet Software Version 8.70 user manual. https://novatel.com/support/support-materials/manual. Accessed 1 July 2020.
NovAtel Corporation. (2018b). Inertial Explorer 8.70 user manual. https://novatel.com/support/support-materials/manual. Accessed 1 July 2020.
Qin, T., Cao, S., Pan, J., & Shen, S. (2019). A general optimization-based framework for global pose estimation with multiple sensors. arXiv:1901.03642.
Qin, T., Li, P., & Shen, S. (2018). VINS-Mono: A robust and versatile monocular visual-inertial state estimator. IEEE Transactions on Robotics, 34(4), 1004–1020.
Rabbou, M. A., & El-Rabbany, A. (2015). Integration of multi-constellation GNSS precise point positioning and MEMS-based inertial systems using tightly coupled mechanization. Positioning, 6(4), 81.
Roesler, G., & Martell, H. (2009). Tightly coupled processing of precise point position (PPP) and INS data. In Proceedings of the ION GPS/GNSS 2009, Institute of Navigation (pp. 1898–1905).
Saastamoinen, J. (1972). Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. The Use of Artificial Satellites for Geodesy, 15, 247–251.
Schmid, R., Steigenberger, P., Gendt, G., Ge, M., & Rothacher, M. (2007). Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas. Jouranl of Geodesy, 81(12), 781–798.
Septentrio Corporation. (2019). PolaRx5 product datasheet. https://www.septentrio.com/en/products/gnss-receivers/reference-receivers/polarx-5. Accessed 1 July 2020.
Shi, J., & Tomasi, C. (1994). Good Features to Track. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition (pp. 593–600).
Shin, E., & Scherzinger, B. (2009). Inertially aided precise point positioning. In Proceedings of ION GNSS 2009 (pp. 1892–1897).
Tsotsos, K., Chiuso, A., & Soatto, S. (2015). Robust inference for visual-inertial sensor fusion. In Proceedings of the IEEE international conference on robotics and automation (pp. 5203–5210).
Usenko, V., Engel, J., Stückler, J., & D. Cremers. (2016). Direct visual-inertial odometry with stereo cameras. In Proceedings of the IEEE international conference on robotics and automation (pp. 1885–1892).
Vu, A., Ramanandan, A., Chen, A., Farrell, J. A., & Barth, M. (2012). Real-time computer vision/DGPS-aided inertial navigation system for lane-level vehicle navigation. IEEE Transactions on Intelligent Transportation Systems, 3(2), 899–913.
Weiss, S., Achtelik, M., Lynen, S., Chli, M. & Siegwart, R. (2012). Real-time onboard visual-inertial state estimation and self-calibration of MAVs in unknown environments. In Proceedings of the IEEE international conference on robotics and automation (pp. 957–964).
Wu, J. T., Wu, S. C., Hajj, G. A., Bertiger, W. I., & Lichten, S. M. (1993). Efects of antenna orientation on GPS carrier phase. Manuscripta Geodaetica, 18, 91–98.
Yang, Z., & Shen, S. (2017). Monocular visual–inertial state estimation with online initialization and camera–IMU extrinsic calibration. In Proceedings of the IEEE transactions on automation science and engineering (pp. 39–51).
Zhang, X., & Li, X. (2012). Instantaneous re-initialization in real-time kinematic PPP with cycle slip fixing. GPS Solutions, 16(3), 315–327.
Zhu, F. (2019). GNSS/SINS/vision multi-sensors integration for precise positioning and orientation determination. Ph.D. thesis, Wuhan University.
Zumberge, J. F., Heflin, M. B., Jefferson, D. C., Watkins, M. M., & Webb, F. H. (1997). Precise point positioning for the efficient and robust analysis of GPS data from large networks. Journal of Geophysical Research: Solid Earth, 102(B3), 5005–5017.
Acknowledgements
The numerical calculations in this paper was done on the supercomputing system in the Supercomputing Center of Wuhan University.
Funding
This study is financially supported by the National Natural Science Foundation of China (Grant No. 41774030, Grant 41974027), the Hubei Province Natural Science Foundation of China (Grant No. 2018CFA081), the National Youth Thousand Talents Program, the frontier project of basic application from Wuhan science and technology bureau (Grant No. 2019010701011395), and the Sino-German mobility programme (Grant No. M-0054).
Author information
Authors and Affiliations
Contributions
XL conceived the idea and revised the paper; XW analyzed the data and wrote the paper; JL and SL assisted in data acquisition and article revision; XL and HL helped with the writing. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, X., Wang, X., Liao, J. et al. Semi-tightly coupled integration of multi-GNSS PPP and S-VINS for precise positioning in GNSS-challenged environments. Satell Navig 2, 1 (2021). https://doi.org/10.1186/s43020-020-00033-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43020-020-00033-9