Abstract
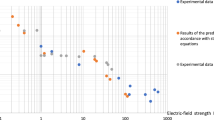
The theory of stochastic equations and the theory of equivalence of measures previously applied to flows in the boundary layer and in the pipe are considered to calculate the velocity profile of the flat jet. This theory previously made it possible to determine the critical Reynolds number and the critical point for the flow of the plane jet. Here based on these results the analytical dependence for the index of the velocity profile is derived. Velocity profiles are calculated for a laminar-turbulent transition in the jet. This formula reliably reflects an increase of the energy transferred from a deterministic state to a random one with an increase of the index of the velocity profile. Results show satisfactory agreement with the known experimental data for the velocity profile of the flat jet. Using obtained results it is possible to determine the location of technical devices for laminarization of the flow in the jet. This is important both for reducing friction in the flow around aerodynamic vehicles and for maintaining the jet profile if it is necessary to ensure the stability of the flow characteristics. Also the obtained relations can be useful for researching of the processes in combustion chambers, in the case of welding and in other technical devices.
Similar content being viewed by others
1 Introduction
The ideas of the theory of the onset of turbulence [1,2,3,4,5,6,7,8,9,10,11,12,13] both theoretical and numerical [14,15,16,17,18,19,20,21,22,23], including also the statistic and DNS modeling [2, 24,25,26,27,28,29,30,31,32], provide the necessity for determination of the stochastic equations and the regularity of equivalence of measures. Investigations of the onset of turbulence based on the theories of stochastic equations and the equivalence of measures between deterministic and random motion were carried out mainly for flows in shear flows in a circular tube [33,34,35,36,37,38,39,40,41,42,43], on a flat smooth plate [44,45,46,47,48,49,50,51,52,53,54,55], as well as for motion near a rotating disk [56] and for motion between rotating coaxial cylinders [57]. The last research was done for laminar–turbulent transition on a flat plate [58, 59]. All of these publications refer to shear flows in the presence of a solid surface (wall). An article related to forced shear flow in the absence of a wall determined the critical Reynolds number and the critical point for a plane jet flow [60]. In this regard, it seems important to present a procedure for deriving the velocity profile parameters for a plane jet flow during the transition from laminar to turbulent motion. The problem of the transition of laminar flow in a jet to turbulent is discussed in articles [60,61,62,63,64,65,66,67,68]. Note that in accordance to the opinions of works [61, 64], the problem of the transition to turbulence in the jet does not cause such a keen interest because the transition has already happened when critical Reynolds numbers equal to 30. In this case, the Reynolds number is made up of the entire width of a flat slit. In the case where the Reynolds number is made up using half the width of a flat slit, it equals 5–10. In this article, the procedure of calculation of parameters velocity profile of flat jet is considered on the basis of the theory of stochastic equations and the theory of equivalence of measures. The analytical dependence for the index of the velocity profile has the right and the left sides. The right side of the equation includes turbulent Reynolds numbers. The left side of the equation, which includes the desired profile index, is determined by the parameters of the averaged motion values and Reynolds number. As a result, having calculated the left side of the formula from the averaged values of the motion at a fixed velocity profile index, we obtain the result and compare it with the right side of the equation, which is determined by the experimental turbulent Reynolds number. If both parts of the equation agree satisfactorily, we compare the given speed profile index with its values from the known experimental range.
2 Conservation stochastic equations
Conservation stochastic equations were derived in [33,34,35,36,37,38,39,40,41,42,43]:
the equation of continuity
the momentum equation
and the energy equation
Here, \(E,\rho, \overrightarrow{U},{u}_i,{u}_j,{u}_l,\mu, \tau, {\tau}_{i,j}\) are the energy, the density; the velocity vector; the velocity components in directions xi, xj, xl (i, j, l = 1, 2, 3); the dynamic viscosity; the time; and the stress tensor τi,j = P + σi,j, \({\sigma}_{ij}=\mu \left(\frac{\partial {u}_i}{\partial {x}_j}+\frac{\partial {u}_j}{\partial {x}_i}\right)-{\delta}_{ij}\left(\xi -\frac{2}{3}\mu \right)\frac{\partial {u}_l}{\partial {x}_l}\), \({{\tau}_{cor}=\frac{L}{{\left({\left({E}_{st}\right)}_{U,P}/\rho \right)}^{1/2}}}\), δij = 1 if i = j, δij = 0 for i ≠ j. Р is the pressure of liquid or gas; λ is the thermal conductivity; cp and cv are the specific heat at constant pressure and volume, respectively; F is the external force. Further, L = LU, P = LU is the scale of turbulence. Indexes (U, P) and (U) refer to the velocity field. Ly on x2 = y, or Lx, x1 = x. Here, x1 and x2 are coordinates along and normal to the axis of the jet. Index “colst” refers to components, which are actually the deterministic. Index “st” refers to component, which are actually the stochastic. Then for the non-isothermal motion of the medium, using the definition of equivalency measures between deterministic and random process in the critical point, the sets of stochastic equations of energy, momentum, and mass are defined for the next space-time areas: 1) the beginning of the generation (index 1,0 or 1); 2) generation (index 1,1); 3) diffusion (1,1,1) and 4) the dissipation of the turbulent fields. These results provide an opportunity to introduce the concept of the correlator, which is defined for the potential physical quantities and combinations (N, M). This correlator, in its structure, will determine the possible range of motion in space depending on the different combinations of (M, N) and the corresponding values that determine the correlation interval of space-time. According to [2, 32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50], the correlator in space-time is
Subscript j denotes the parameters mcj (j = 3 means mass, momentum, and energy). For the case of the binary intersections, it was written that X = Y + Z + W. Here subscripts cr or c refer to critical point r(xcr, τcr) or rc: the space-time point of the beginning of the interaction between the deterministic field and random field that leads to turbulence. In addition, subsets Y, Z, W are сalled extended in X. For the transfer of the substantial quantity Φ (mass (density ρ), momentum (ρU), energy (E)) of the deterministic (laminar) motion into a random (turbulent) one, for domain 1 of the start of turbulence generation, pair (N, M) = (1, 0), with the equivalence of measures being written as (\({d\Phi}_{col_{st}}\))1,0 = − R1,0(Φst) and \({\left(\frac{d{\left(\Phi \right)}_{{col}_{st}}}{d\tau}\right)}_{1,0}=-{R}_{1,0}\left(\frac{\Phi_{st}}{\tau_{cor}}\right)\). Applying correlation DN,M(rc; mci; τc) = D1,1(rc; mci, τc) derived in [2, 32,33,34,35,36,37,38,39,40,41,42], the equivalence relation for pair (N, M) = (1, 1) was defined as (\({d\Phi}_{col_{st}}\))1,1 = − R1,1(dΦst), \({\left(\frac{d{\left(\Phi \right)}_{col_{st}}}{d\tau}\right)}_{1,1}=-{R}_{1,1}\left(\frac{d{\Phi}_{st}}{d\tau}\right)\), where R1,0 and R1,1 are fractal coefficients, \(\Phi_{col_{st}}\) is the part of the field of Φ, notably, its deterministic component (subscript colst) is the stochastic component of the measure, which is zero; Φst is the part of Φ, notably, the proper stochastic component (subscript st).
3 Critical Reynolds number and critical point
In article [58] it was shown that the critical Reynolds number and critical point for the plane jet were determined using the set of stochastic Eqs. (1)–(3) for the area 1), which, referring the pair (N, M) = (1, 0) is:
So, the formula for critical Reynolds number was written as
and in according with data [52,53,54,55,56,57], the theoretical value for critical Reynolds number is
Um is the average velocity on the jet axis, h the width of the initial section of the jet. The definition of the value of the critical point is found from the equation \(\int\limits_{-\Delta V\left|2\right.}^{+\Delta V\left|2\right.}d{\left({{E}}_{col_{st}}\right)}_{1,0}=\underset{X}{\int }{dE}_{st}\). Here Est is the stochastic energy component in the space X with the measure m(Est) < ∞ and \({E}_{st}={E}_{st}\left(\overrightarrow{x_i},{\tau}_i,{m}_i\right)<\infty\). According to the main results of the ergodic theory we have \(\underset{X}{\int }{dE}_{st}=\frac{1}{\Delta V}\underset{V}{\int }{E}_{st}\delta \left({\left(\Delta V\right)}_{critic}-\Delta V\right) d V=\frac{1}{\tau_{cor}^0}\underset{\tau }\int {E}_{st}\delta \left({\tau}_{cor}^0-\tau \right) d\tau ={\left({E}_{st}\right)}_{critic}\). (Est)critic is the stochastic energy at the critical point. Then it is possible to write as \(\underset{X}{\int }{dE}_{st}=\frac{1}{L}\underset{L}{\int }{E}_{st}\delta \left({\left({{x}}_i\right)}_{critic}-{{x}}_i\right) d L=\frac{1}{\tau_{cor}^0}\underset{\tau }{\int }{E}_{st}\delta \left({\tau}_{cor}^0-\tau \right) d\tau ={\left({E}_{st}\right)}_{critic}\), here L is the scale of disturbance. So using these formulas, the equation for the critical point in the plane jet was determined [58]:
and in according with data [52,53,54,55,56,57,58], the theoretical value for critical point \({\left(\frac{{x}_2}{{x}_1}\right)}_{cr}\) is
4 The velocity profile characteristics of the flat jet
The set of stochastic Eqs. (1)–(3) for the area 2), referring the pair (N,M) = (1,1) is:
Then, taking into account the definition of the velocity u1 of laminar motion in a plane jet [61, 64].
Taking into account that
and introducing the relation
the derivative \(\frac{du_1}{dx_1}\) is
In case of small values of ξ for laminar flow we have next formulas:
So finally we have
For the flow region of the beginning of turbulence initiation, we assume the same dependence, but with a different degree “n”. As is known, if the velocity u1 in laminar motion is ~ (x1)-1/3, then for a developed turbulent region u1 ~ (x1)-1/n and “n = 2”. Thus, for the transition region the values of degree “n” are in the interval 2 ≤ n ≤ 3. Next, we write down the relation determined earlier from the equivalence of measures for the region (1, 1) - the generation of turbulence [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]:
As it was shown in the papers [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58], the Eq. (23) determines the relative increase of the energy transferred from the deterministic state to the random one. Subscript “lamin” refers to the laminar flow, and subscript “stoch” refers to the non-laminar flow. Taking into account that for transition regime formula (22) may be written as \(\mu {\left(\frac{du_1}{dx_1}\right)}^2=\rho \nu \left[\frac{1}{n^2}{0.4543}^2{\left(\frac{U_m}{x_1}\right)}^2{\left(\frac{h}{x_1}\right)}^{2/n}{\left({Re}\right)}^{2/n}\right]\). Then in accordance with [44,45,46,47,48,49, 60], the Eq. (23) is
Easy to see that for laminar flow n = 3, the right side of Eq. (24) is equal to 1. Let us determine the value of the left side of the Eq. (23) (or the right side of Eq. 24) for various values of the indicator “n” and then compare with the calculated value of the right side of the Eq. (23). For the left side of the equation, if n = 2.5, we have \({K}_{\tau }=\frac{\Delta {\tau}_{stoch}}{\Delta {\tau}_l}\approx 0.8\div 1.2\) [56,57,58] and in accordance with [61,62,63,64,65,66], \(\left(\frac{h}{L_2}\right)\cdot \left(\frac{L_2}{x_1}\right)=\left(2.5\div 14.5\right)\cdot \left(0.01\div 0.0157\right)=0.025\div 0.22765\). As can be seen, the experimental spread of values refers to the magnitude of the turbulence scale \(\left(\frac{h}{L_2}\right)\). Therefore, the main attention will be focused on the correspondence of the calculated values of the right side of Eq. (24) to the left side of this equation. Then it can be written that
So for n = 2.5, the left side of the equation is
Then for n = 2.0 and the same initial data for the critical Reynolds number (Re)cr ~ 7.25 ÷ 25, \({K}_{\tau }=\frac{\Delta {\tau}_{stoch}}{\Delta {\tau}_l}\approx 0.8\div 1.2\) [54,55,56,57,58] and \(\left(\frac{h}{L_2}\right)\cdot \left(\frac{L_2}{x_1}\right)=\left(2.5\div 14.5\right)\cdot \left(0.01\div 0.0157\right)=0.025\div 0.22765\) [61,62,63,64,65,66,67], the next equation can be written as
Substituting the numerical values, it is possible to find that
So for n = 2.0, the left side of the equation is
Then determine the right side of Eq. (23). Within the framework of the available data in the case of the origin of turbulence, experimental values of turbulent Reynolds number are Rest ~ 0.4÷0.5 [61,62,63,64,65,66,67]. In the case of the developed turbulence, according to [2], experimental values of turbulent Reynolds number are Rest ~ 2÷4. So the right side of Eq. (23) for n = 3.0 ÷ 2.5 has value
and for n = 2.0 the value is
Thus, the estimate of the profile index is satisfactorily determined by the obtained relation n = 2.0, corresponding to the turbulent flow value of index ‘n’ in empirical formula u1 ~ (x1)-1/2 [61, 64]. It should be noted that the main last studies [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119] do not contain information on analytical solutions for the jet profile in the laminar-turbulent transition regime.
5 Conclusions
On the basis of the theory of stochastic equations and the theory of equivalence of measures, the velocity profile of a plane jet is considered. In accordance with these theories, the analytical dependence of the velocity profile of flat jet is derived for the transition flow from the laminar flow to turbulent motion. It should be noted that the calculated values obtained from the formulas for the transition from laminar movement to turbulent flow in a plane jet are different to the calculated values for the velocity profile in the boundary layer on the flat plate and in the pipe, in the case of a smooth wall [33,34,35,36,37,38,39,40,41,42,43, 49,50,51,52]. This fact agrees with the well-known data [61, 64]. It is also seen that the analytical formulas (27) and (30) reliably reflect an increase of the transferred energy from a deterministic state to a random one with an increase of the index (1/n). It is shown that the new equation reflects the experimental fact of changing the dependence for the longitudinal velocity u1 during laminar motion from the coordinate along the axis of the jet u1 ~ (x1)-1/3 (n = 3) into a dependence for the developed turbulent region u1 ~ (x1)-1/2 (n = 2). The calculations carried out using new formulas (24)–(31) showed satisfactory agreement with the known experimental values for parameters of the velocity profile of flat jet.
The practical significance of the theoretical determination of velocity profiles in a jet at a laminar-turbulent transition from the values of the Reynolds number and vice versa is essential for a number of processes taking place, in particular, in combustion chambers [30] and in the case of welding [43, 120]. Also, knowing the initial parameters of the disturbance, it is possible, depending on the distance x1, to determine the amount of energy transferred into random motion. This makes it possible to determine the location of technical devices for reducing friction [58, 59] in the flow around aerodynamic vehicles and for maintaining the jet profile if it is necessary to ensure the stability of the flow characteristics.
Availability of data and materials
The datasets analyzed and used during the current study are available from the corresponding author as mentioned in references.
References
Landau LD (1944) On the problem of turbulence. Dokl Akad Nauk SSSR 44:339–343. (in Russian)
Landau LD, Lifshitz EM (1959) Fluid mechanics. Pergamon Press, Oxford
Lorenz EN (1963) Deterministic nonperiodic flow. J Atmos Sci 20:130–141. https://doi.org/10.1175/1520-0469
Feigenbaum MJ (1980) The transition to aperiodic behavior in turbulent systems. Commun Math Phys 77:65–86
Ruelle D, Takens F (1971) On the nature of turbulence. Commun Math Phys 20:167–192. https://doi.org/10.1007/bf01646553
Kolmogorov AN (1941) Dissipation of energy in locally isotropic turbulence. Dokl Akad Nauk SSSR 32(1):16–18
Kolmogorov AN (1958) A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. Dokl Akad Nauk SSSR 119(5):861–864
Kolmogorov AN (1959) Entropy per unit time as a metric invariant of automorphisms. Dokl Akad Nauk SSSR 124(4):754–755
Kolmogorov AN (2004) Mathematical models of turbulent motion of an incompressible viscous fluid. Usp Mat Nauk 59(1):5–10
Struminskii VV (1989) The onset of turbulence. Dokl Akad Nauk SSSR 307(3):564–567
Klimontovich YL (1989) Problems in the statistical theory of open systems: Criteria for the relative degree of order in self-organization processes. Sov Phys Usp 32(5):416–433. https://doi.org/10.1070/PU1989v032n05ABEH002717
Samarskii AA, Mazhukin VI, Matus PP et al (1997) L2-conservative schemes for Korteweg-de Vries equation. Dokl Akad Nauk 357(4):458–461
Haller G (1999) Chaos near resonance. Springer, New York. https://doi.org/10.1007/978-1-4612-1508-0
Orszag SA, Kells LC (1980) Transition to turbulence in plane Poiseuille and plane Couette flow. J Fluid Mech 96(1):159–205. https://doi.org/10.1017/s0022112080002066/
Ladyzhenskaya OA (1975) A dynamical system generated by the Navier-Stokes equations. J Sov Math 3:458–479
Vishik MI, Komech AI (1983) Kolmogorov equations corresponding to a two-dimensional stochastic Navier-Stokes system. Tr Mosk Mat Obs 46:3–43
Packard NH, Crutchfield JP, Farmer JD, Shaw RS (1980) Geometry from a time series. Phys Rev Lett 45(9):712–716
Malraison B, Atten P, Berge P et al (1983) Dimension of strange attractors: an experimental determination for the chaotic regime of two convective systems. J Phys Lett 44(22):897–902. https://doi.org/10.1051/jphyslet:019830044022089700
Dmitrenko AV (2002) Calculation of the boundary layer of a two-phase medium. High Temp 40(5):706–715. https://doi.org/10.1023/A:1020436720213
Dmitrenko AV (2000) Heat and mass transfer and friction in injection to a supersonic region of the Laval nozzle. Heat Trans Res 31(6–8):338–399. https://doi.org/10.1615/HeatTransRes.v31.i6-8.30
Grassberger P, Procaccia I (1984) Dimensions and entropies of strange attractors from a fluctuating dynamics approach. Phys D Nonlinear Phenom 13(1–2):34–54. https://doi.org/10.1016/0167-2789(84)90269-0
Kozlov VV, Rabinovich MI, Ramazanov MP et al (1987) Correlation dimension of the flow and spatial development of dynamical chaos in a boundary layer. Phys Lett A 128(9):479–482
Brandstäter A, Swift J, Swinney HL et al (1983) Low-dimensional chaos in hydrodynamic system. Phys Rev Lett 51(16):1442–1446
Sreenivasan KR (1991) Fractals and multifractals in fluid turbulence. Annu Rev Fluid Mech 23:539–604
Priymak VG (2013) Splitting dynamics of coherent structures in a transitional round-pipe flow. Dokl Phys 58(10):457–465
Newton PK (2016) The fate of random initial vorticity distributions for two-dimensional Euler equations on a sphere. J Fluid Mech 786:1–4
Dmitrenko AV (2008) Fundamentals of heat and mass transfer and hydrodynamic of single-phase and two-phase media. Criterion, integral, statistical and DNS methods, vol 398. Galleya Print, Moscow
Dmitrenko AV (1997) Film cooling in nozzles with the large geometric expansion using method of integral relations and second moment closure model for turbulence. Paper presented at the 33rd joint propulsion conference and exhibit, Seattle, 6-9 July 1997. https://doi.org/10.2514/6.1997-2911
Dmitrenko AV (2017) Estimation of the critical Rayleigh number as a function of the initial turbulence of the boundary layer at a vertical heated plate. Heat Trans Res 48(13):1195–1202. https://doi.org/10.1615/HeatTransRes.2017018750
Dmitrenko AV (1998) Heat and mass transfer in combustion chamber using a second-moment turbulence closure including an influence coefficient of the density fluctuation in film cooling conditions. Paper presented at the 34th AIAA/ASME/SAE/ASEE joint propulsion conference and exhibit, Cleveland, 13-15 July 1998. https://doi.org/10.2514/6.1998-3444
Dmitrenko AV (1993) Nonselfsimilarity of a boundary-layer flow of a high-temperature gas in a Laval nozzle. Aviats Tekh 1:39–42
Dmitrenko AV (1986) Computational investigations of a turbulent thermal boundary layer in the presence of external flow pulsations. In: Proceedings of the 11th conference on young scientists, Moscow, Physicotechnical Institute, part 2, p 48–52. Deposited at VINITI 08.08.86, no. 5698-B8
Dmitrenko AV (2007) Calculation of pressure pulsations for a turbulent heterogeneous medium. Dokl Phys 52(7):384–387. https://doi.org/10.1134/s1028335807120166
Dmitrenko AV (2013) Equivalence of measures and stochastic equations for turbulent flows. Dokl Phys 58(6):228–235. https://doi.org/10.1134/s1028335813060098
Dmitrenko AV (2014) Some analytical results of the theory of equivalence measures and stochastic theory of turbulence for non-isothermal flows. Adv Stud Theor Phys 8(25):1101–1111. https://doi.org/10.12988/astp.2014.49131
Dmitrenko AV (2016) Determination of critical Reynolds numbers for nonisothermal flows by using the stochastic theories of turbulence and equivalent measures. Heat Trans Res 47(1):41–48. https://doi.org/10.1615/HeatTransRes.2015014191
Dmitrenko AV (2016) The theory of equivalence measures and stochastic theory of turbulence for non-isothermal flow on the flat plate. Int J Fluid Mech Res 43(2):182–187. https://doi.org/10.1615/InterJFluidMechRes.v43.i2.60
Dmitrenko AV (2015) Analytical estimation of velocity and temperature fields in a circular pipe on the basis of stochastic equations and equivalence of measures. J Eng Phys Thermophy 88(6):1569–1576. https://doi.org/10.1007/s10891-015-1344-x
Dmitrenko AV (2016) An estimation of turbulent vector fields, spectral and correlation functions depending on initial turbulence based on stochastic equations. The Landau fractal equation. Int J Fluid Mech Res 43(3):271–280. https://doi.org/10.1615/InterJFluidMechRes.v43.i3.60
Dmitrenko AV (2017) Stochastic equations for continuum and determination of hydraulic drag coefficients for smooth flat plate and smooth round tube with taking into account intensity and scale of turbulent flow. Continuum Mech Thermodyn 29(1):1–9. https://doi.org/10.1007/s00161-016-0514-1
Dmitrenko AV (2017) Analytical determination of the heat transfer coefficient for gas, liquid and liquid metal flows in the tube based on stochastic equations and equivalence of measures for continuum. Continuum Mech Thermodyn 29(6):1197–1205. https://doi.org/10.1007/s00161-017-0566-x
Dmitrenko AV (2017) Determination of the coefficients of heat transfer and friction in supercritical-pressure nuclear reactors with account of the intensity and scale of flow turbulence on the basis of the theory of stochastic equations and equivalence of measures. J Eng Phys Thermophy 90(6):1288–1294. https://doi.org/10.1007/s10891-017-1685-8
Dmitrenko AV (2018) Results of investigations of non-isothermal turbulent flows based on stochastic equations of the continuum and equivalence of measures. J Phys Conf Ser 1009:012017. https://doi.org/10.1088/1742-6596/1009/1/012017
Dmitrenko AV (2018) The stochastic theory of the turbulence. IOP Conf Ser Mater Sci Eng 468:012021. https://doi.org/10.1088/1757-899X/468/1/01202
Dmitrenko AV (2019) Determination of the correlation dimension of an attractor in a pipe based on the theory of stochastic equations and equivalence of measures. J Phys Conf Ser 1250:012001. https://doi.org/10.1088/1742-6596/1250/1/012001
Dmitrenko AV (2019) The construction of the portrait of the correlation dimension of an attractor in the boundary layer of Earth’s atmosphere. J Phys Conf Ser 1301:012006. https://doi.org/10.1088/1742-6596/1301/1/012006
Dmitrenko AV (2019) The theoretical solution for the Reynolds analogy based on the stochastic theory of turbulence. JP J Heat and Mass Transf 18(2):463–476. https://doi.org/10.17654/HM018020463
Dmitrenko AV (2020) The correlation dimension of an attractor determined on the base of the theory of equivalence of measures and stochastic equations for continuum. Continuum Mech Thermodyn 32(2):63–74. https://doi.org/10.1007/s00161-019-00784-0
Dmitrenko AV (2020) The possibility of using low-potential heat based on the organic Rankine cycle and determination of hydraulic characteristics of industrial units based on the theory of stochastic equations and equivalence of measures. JP J Heat Mass Transf 21(1):125–132. https://doi.org/10.17654/HM021010125
Dmitrenko AV (2020) Some aspects of the formation of the spectrum of atmospheric turbulence. JP J Heat Mass Transf 19(1):201–208
Dmitrenko AV (2020) The uncertainty relation in the turbulent continuous medium. Continuum Mech Thermodyn 32(1):161–171. https://doi.org/10.1007/s00161-019-00792-0
Dmitrenko AV (2020) Formation of a turbulence spectrum in the inertial interval on the basis of the theory of stochastic equations and equivalence of measures. J Eng Phys Thermophy 93(1):122–127. https://doi.org/10.1007/s10891-020-02098-4
Dmitrenko AV (2020) The spectrum of the turbulence based on theory of stochastic equations and equivalence of measures. J Phys Conf Ser 1705:012021. https://doi.org/10.1088/1742-6596/1705/1/012021
Dmitrenko AV (2021) Reynolds analogy based on the theory of stochastic equations and equivalence of measures. J Eng Phys Thermophy 94:186–193. https://doi.org/10.1007/s10891-021-02296-8
Dmitrenko AV (2021) Theoretical solutions for spectral function of the turbulent medium based on the stochastic equations and equivalence of measures. Continuum Mech Thermodyn 33:603–610. https://doi.org/10.1007/s00161-020-00890-4
Dmitrenko AV (2021) Determination of critical Reynolds number for the flow near a rotating disk on the basis of the theory of stochastic equations and equivalence of measures. Fluids 6(1):5. https://doi.org/10.3390/fluids6010005
Dmitrenko AV (2021) Analytical estimates of critical Taylor number for motion between rotating coaxial cylinders based on theory of stochastic equations and equivalence of measures. Fluids 6(9):306. https://doi.org/10.3390/fluids6090306
Dmitrenko AV (2022) Prediction of laminar–turbulent transition on flat plate on the basis of stochastic theory of turbulence and equivalence of measures. Continuum Mech Thermodyn 34:601–615. https://doi.org/10.1007/s00161-021-01078-0
Dmitrenko AV (2022) Theoretical calculation of laminar–turbulent transition in the round tube on the basis of stochastic theory of turbulence and equivalence of measures. Continuum Mech Thermodyn 34:1375–1392. https://doi.org/10.1007/s00161-022-01125-4
Dmitrenko AV (2020) Determination of critical Reynolds number in the jet based on the theory of stochastic equations and equivalence of measures. J Phys Conf Ser 1705:012015. https://doi.org/10.1088/1742-6596/1705/1/012015
Davidson PA (2004) Turbulence: an introduction for scientists and engineers, 1st edn. Oxford University Press, New York, p 678
Schlichting H (1968) Boundary-layer theory, 6th edn. McGraw-Hill Book Co., Inc., New York, p 747
Hinze JO (1975) Turbulence. McGraw-Hill Book Co., Inc., New York, p 790
Abramovich GN (1963) The theory of turbulent jets. MIT Press, Cambridge, p 671
Corrsin S (1943) Investigation of flow in an axially symmetrical heated jet of air. NACA Wartime Rep NACA-ACR-3L23
Corrsin S, Uberoi MS (1949) Further experiments on the flow and heat transfer in a heated turbulent air jet. NACA Tech Note NACA-TN-1865
Wygnanski IJ, Champagne FH (1973) On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J Fluid Mech 59(2):281–335
Wygnanski I, Sokolov M, Friedman D (1975) On transition in a pipe. Part 2. The equilibrium puff. J Fluid Mech 69(2):283–304
Risso F, Fabre J (1997) Diffusive turbulence in a confined jet experiment. J Fluid Mech 337:233–261
Karimipanah T (1996) Turbulent jets in confined spaces. Dissertation, Royal Institute of Technology, Sweden
Arndt REA, Long DF, Glauser MN (1997) The proper orthogonal decomposition of pressure fluctuations surrounding a turbulent jet. J Fluid Mech 340:1–33
Citriniti JH, George WK (2000) Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J Fluid Mech 418:137–166
Tam CKW, Auriault L (1999) Jet mixing noise from fine-scale turbulence. AIAA J 37(2):145–153
Mataoui A, Schiestel R, Salem A (2001) Flow regimes of a turbulent plane jet into a rectangular cavity: experimental approach and numerical modeling. Flow Turbul Combust 67:267–304
Mataoui A, Schiestel R, Salem A (2002) Oscillatory phenomena of a turbulent plane jet flowing inside a rectangular cavity. In: Rahman M, Verhoeven R, Brebbia CA (eds) Advances in fluid mechanics IV. WIT Press, Southampton, p 151–162
Mataoui A, Schiestel R, Salem A (2003) Study of the oscillatory regime of a turbulent plane jet impinging in a rectangular cavity. Appl Math Model 27(2):89–114
Saiyed NH, Mikkelsen KL, Bridges JE (2003) Acoustics and thrust of quiet separate-flow high-bypass-ratio nozzles. AIAA J 41(3):372–378
Alkislar MB, Krothapalli A, Choutapalli I et al (2005) Structure of supersonic twin jets. AIAA J 43(11):2309–2318
Kompenhans J, Arnott A, Agos A et al (2002) Application of PIV for the investigation of high speed flow fields. In: West East High Speed Flow Field. Artes Gráficas Torres S.A., Barcelona, p 39–52
Knob M, Safarik P, Uruba V et al (2005) The effect of the side walls on a two-dimensional impinging jet. Paper presented at the 16th international symposium on transport phenomena, Prague, 2005. http://fluids.fs.cvut.cz/akce/konference/istp_2005/full/168.pdf
Suzuki T, Colonius T (2006) Instability waves in a subsonic round jet detected using a near-field phased microphone array. J Fluid Mech 565:197–226
Kopiev V, Zaitsev MY, Chernyshev SA et al (2007) Vortex ring input in subsonic jet noise. Int J Aeroacoust 6(4):375–405
Jordan P, Gervais Y (2008) Subsonic jet aeroacoustics: associating experiment, modelling and simulation. Exp Fluids 44:1–21
Tam CKW, Viswanathan K, Ahuja KK et al (2008) The sources of jet noise: experimental evidence. J Fluid Mech 615:253–292
Guadalfajara M (2009) Interference between supply jet and room surfaces in ventilated room - a model study. Thesis, University of Gävle, Sweden
Gudmundsson K (2010) Instability wave models of turbulent jets from round and serrated nozzles. Dissertation, California Institute of Technology
Yarygin V, Gerasimov Y, Krylov A et al (2011) Experimental study of the International Space Station contamination by its orientation thrusters jets. Microgravity Sci Technol 23(Suppl 1):15–23
Shimshi E, Ben-Dor G, Levy A (2011) Viscous simulation of shock reflection hysteresis in ideal and tapered overexpanded planar nozzles. Shock Waves 21(3):205–214. https://doi.org/10.1007/s00193-011-0325-z
van Hooff T, Blocken B, Defraeye T et al (2012) PIV measurements of plane wall jet in a confined space at transitional slot Reynolds numbers. Exp Fluids 53:499–517
Gvozdeva LG, Gavrenkov SA (2013) Influence of the adiabatic index on switching between different types of shock wave reflection in a steady supersonic gas flow. Tech Phys 58(8):1238–1241. https://doi.org/10.1134/S1063784213080148
Gvozdeva LG, Gavrenkov SA (2012) Formation of triple shock configurations with negative reflection angle in steady flows. Tech Phys Lett 38(4):372–374. https://doi.org/10.1134/S1063785012040232
Cavalieri AVG, Rodríguez D, Jordan P et al (2013) Wavepackets in the velocity field of turbulent jets. J Fluid Mech 730:559–592
Jordan P, Colonius T (2013) Wave packets and turbulent jet noise. Annu Rev Fluid Mech 45:173–195
Gvozdeva LG, Gavrenkov SA (2015) A new configuration of irregular reflection of shock waves. Prog Flight Phys 7:437–452. https://doi.org/10.1051/eucass/201507437
Hadjadj A, Perrot Y, Verma S (2015) Numerical study of shock/boundary layer interaction in supersonic overexpanded nozzles. Aerosp Sci Technol 42:158–168. https://doi.org/10.1016/j.ast.2015.01.010
Benderskii LA, Krasheninnikov SY (2016) Investigation of noise generation by turbulent jets on the basis of numerical simulation of unsteady flow in mixing layers. Fluid Dyn 51(4):568–580
Kopiev VF, Chernyshev SA (2012) New correlation model for the cascade of turbulent pulsations as a noise source in jets. Acoust Phys 58(4):442–456
Lyu B, Dowling AP, Naqavi I (2017) Prediction of installed jet noise. J Fluid Mech 811:234–268
Bychkov OP, Faranosov GA (2018) An experimental study and theoretical simulation of jet-wing interaction noise. Acoust Phys 64(4):437–452
Belyaev IV, Bychkov OP, Zaitsev MY et al (2018) Development of the strategy of active control of instability waves in unexcited turbulent jets. Fluid Dyn 53(3):347–360
Krasheninnikov SY, Mironov AK, Benderskii LA (2018) Analysis of noise generation by turbulent jets from consideration of their near acoustical field. Acoust Phys 64(6):718–730
Xu HY, Xing SL, Ye ZY (2015) Numerical study of the S809 airfoil aerodynamic performance using a co-flow jet active control concept. J Renew Sustain Ener 7(2):023131
Xu HY, Qiao CL, Ye ZY (2016) Dynamic stall control on the wind turbine airfoil via a co-flow jet. Energies 9(6):429
Yang YC, Zha GC (2018) Super lift coefficient of co-flow jet circular cylinder. Paper presented at the 2018 AIAA aerospace sciences meeting, Kissimmee, 8-12 January 2018
Zhang JH, Xu KW, Yang YC et al (2018) Aircraft control surfaces using co-flow jet active flow control airfoil. Paper presented at the 2018 applied aerodynamics conference, Atlanta, 25-29 June 2018
Yang XD, Jiang WR, Zhang SL (2019) Analysis of co-flow jet effect on dynamic stall characteristics applying to rotor airfoils. IOP Conf Ser Mater Sci Eng 491:012010
Bychkov O, Faranosov G, Kopiev V et al (2019) The modelling of jet-plate interaction noise in the presence of co-flow. Paper presented at the 25th AIAA/CEAS aeroacoustics conference, Delft, 20-23 May 2019
Xu KW, Zhang JH, Zha GC (2019) Drag minimization of co-flow jet control surfaces at cruise conditions. Paper presented at the AIAA Scitech 2019 forum, San Diego, 7-11 January 2019
Yang YC, Fernandez M, Zha GC (2018) Improved delayed detached eddy simulation of super-lift coefficient of subsonic co-flow jet flow control airfoil. Paper presented at the 2018 AIAA aerospace sciences meeting, Kissimmee, 8-12 January 2018
Lemanov V, Lukashov V, Sharov K et al (2019) Turbulent spots in the flame of a diffusion torch. J Phys Conf Ser 1382:012058. https://doi.org/10.1088/1742-6596/1382/1/012058
Dubnishchev YN, Arbuzov VA, Lukashov VV et al (2019) Optical Hilbert diagnostics of hydrogen jet burning. Optoelectron Instrum Data Process 55(1):16–19. https://doi.org/10.3103/S8756699019010035
Soares LFM, Cavalieri AVG, Kopiev V et al (2020) Flight effects on turbulent-jet wave packets. AIAA J 58(9):3877–3888
Baykov ND, Petrov AG (2020) Collapse of capillary-gravitational waves and the generation of cumulative jets. Fluid Dyn 55:953–964
Lemanov VV, Lukashov VV, Sharov KA (2020) Transition to turbulence through intermittence in inert and reacting jets. Fluid Dyn 55:768–777
Alekseenko SV, Bilsky AV, Dulin VM et al (2007) Experimental study of an impinging jet with different swirl rates. Int J Heat Fluid Flow 28(6):1340–1359. https://doi.org/10.1016/j.ijheatfluidflow.2007.05.011
Ball CG, Fellouah H, Pollard A (2012) The flow field in turbulent round free jets. Prog Aerosp Sci 50:1–26. https://doi.org/10.1016/j.paerosci.2011.10.002
Zaiko YS, Reshmin AI, Teplovodskii SK et al (2018) Investigation of submerged jets with an extended initial laminar region. Fluid Dyn 53(1):95–104. https://doi.org/10.1134/S0015462818010184
Bychkov OP, Faranosov GA (2021) On the relationship between velocity and pressure fluctuations at the axis of a turbulent jet and in its near field. Fluid Dyn 56:481–491
Zhang YZ, Xu HY, Chu YW et al (2021) Two-dimensional numerical study of the pulsed co-flow jet. Fluid Dyn 56(3):361–370
Dudoladov SO, Larionov NV (2021) The condition for application of the Crocco integral in the mathematical description of a laser welding plasma plume. St Petersburg Polytechnic Univ J Phys Math 14(3):60–75
Acknowledgements
Not applicable.
Funding
This work was supported by the program “PRIORITET-2030”.
Author information
Authors and Affiliations
Contributions
Dmitrenko A.V. realized the derivation of formulas, calculations, formulation of conclusions. Selivanov A.S. conducted a search for experimental data and participated in the calculations and drawing conclusions. The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declared no potential conflicts of interest with respect to the research, authorship and publication of this article.
Additional information
This article is dedicated to the memory of Academician N. A. Anfimov.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dmitrenko, A.V., Selivanov, A.S. An estimation of the velocity profile for the laminar-turbulent transition in the plane jet on the basis of the theory of stochastic equations and equivalence of measures. Adv. Aerodyn. 4, 40 (2022). https://doi.org/10.1186/s42774-022-00130-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s42774-022-00130-0