1 Introduction

Throughout this paper, we assume that H is a real Hilbert space whose inner product and norm are denoted by \(\langle\cdot,\cdot \rangle\) and \(\|\cdot\|\), respectively. We also assume that \(T : H \to H\) is a nonexpansive operator, that is, \(\| Tx - Ty \| \leq\| x-y \|\) for all \(x,y \in H\). The fixed point set of T is denoted by \(F(T)\), that is, \(F(T) = \{ x \in H : Tx = x \}\). It is well known that \(F(T)\) is closed and convex (see [1]).

Let C be a nonempty closed convex subset of H and \(S : C \to H\) be a nonexpansive mapping. The hierarchical fixed point problem (in short, HFPP) is to find \(x\in F(T)\) such that

$$ \langle x-Sx, y-x \rangle\geq0, \quad \forall y\in F(T). $$
(1.1)

It is linked with some monotone variational inequalities and convex programming problems. Various methods have been proposed to solve (1.1); see, for example, [2–18] and the references therein.

Yao et al. [2] introduced the following iterative algorithm to solve HFPP (1.1):

$$ \begin{aligned} &y_{n} = \beta_{n}Sx_{n}+(1- \beta_{n})x_{n}, \\ &x_{n+1} = P_{C}\bigl[\alpha_{n} f(x_{n})+(1-\alpha_{n})Ty_{n}\bigr],\quad \forall n \geq 0, \end{aligned} $$
(1.2)

where \(f: C\to H\) is a contraction mapping and \(\{\alpha_{n}\}\) and \(\{ \beta_{n}\}\) are sequences in \((0,1)\). Under some restrictions on parameters, they proved that the sequence \(\{ x_{n}\}\) generated by (1.2) converges strongly to a point \(z\in F(T)\) which is also a unique solution of the following variational inequality problem (VIP): Find \(z \in F(T)\) such that

$$ \bigl\langle (I-f)z,y-z\bigr\rangle \geq0,\quad \forall y\in F(T). $$
(1.3)

In 2011, Ceng et al. [19] investigated the following iterative method:

$$ x_{n+1}=P_{C}\bigl[\alpha_{n} \rho U(x_{n})+(I-\alpha_{n}\mu F) \bigl(T(x_{n})\bigr) \bigr],\quad \forall n\geq0, $$
(1.4)

where U is a Lipschitzian mapping and F is a Lipschitzian and strongly monotone mapping. They proved that under some approximate assumptions on the operators and parameters, the sequence \(\{x_{n}\}\) generated by (1.4) converges strongly to a unique solution of the following variational inequality problem (VIP): Find \(z \in F(T)\) such that

$$ \bigl\langle \rho U(z)-\mu F(z), y-z\bigr\rangle \geq0, \quad \forall y\in F(T). $$
(1.5)

Simultaneously, the hierarchical fixed point problem is considered for a family of finite nonexpansive mappings. By using a \(W_{n}\)-mapping [20], Yao [21] introduced the following iterative method:

$$ x_{n+1}=\alpha_{n}\gamma f(x_{n})+ \beta x_{n}+\bigl((1-\beta)I-\alpha _{n}A\bigr)W_{n}x_{n}, \quad \forall n\geq0, $$
(1.6)

where A is a strongly positive linear bounded operator, that is, there exists \(\alpha>0\) such that \(\langle Ax ,x \rangle\ge\alpha\|x\|^{2}\), \(f: C\to H\) is a contraction mapping and \(\{\alpha_{n}\}\) and \(\{\beta _{n}\}\) are sequences in \((0,1)\). Under some restrictions on parameters, he proved that the sequence \(\{ x_{n}\}\) generated by (1.6) converges strongly to a unique solution of the following variational inequality problem defined on the set of common fixed points of nonexpansive mappings \(T_{i} : H \to H\), \(i =1,2, \ldots,N\): Find \(z \in\bigcap_{i=1}^{N} F(T_{i})\) such that

$$ \bigl\langle (A-\gamma f)z,y-z\bigr\rangle \geq0,\quad \forall y\in \bigcap_{i=1}^{N} F(T_{i}). $$
(1.7)

By combining Korpelevich’s extragradient method and the viscosity approximation method, Ceng et al. [22] introduced and analyzed implicit and explicit iterative schemes for computing a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of a variational inequality problem for an α-inverse-strongly monotone mapping defined on a real Hilbert space. Under suitable assumptions, they established the strong convergence of the sequences generated by the proposed schemes.

By combining Krasnoselskii-Mann type algorithm and the steepest-descent method, Buong and Duong [23] introduced the following explicit iterative algorithm:

$$ x_{k+1}=\bigl(1-\beta_{k}^{0} \bigr)x_{k}+\beta_{k}^{0}T_{0}^{k}T_{N}^{k} \cdots T_{1}^{k}x_{k}, $$
(1.8)

where \(T_{i}^{k}=(1-\beta_{k}^{i})x_{k}+\beta_{k}^{i}T_{i}\) for \(1\leq i\leq N\), \(\{T_{i}\}^{N}_{i=1}\) are N nonexpansive mappings on a real Hilbert space H, \(T_{0}^{k}=I-\lambda_{k}\mu F\), and F is an L-Lipschitz continuous and η-strongly monotone mapping. They proved that the sequence \(\{x_{k}\}\) generated by (1.8) converges strongly to a unique solution of the following variational inequality problem: Find \(z \in\bigcap_{i=1}^{N} F(T_{i})\) such that

$$ \langle Fz,y-z\rangle\ge0,\quad \forall y\in\bigcap _{i=1}^{N} F(T_{i}). $$
(1.9)

Recently, Zhang and Yang [24] considered the following explicit iterative algorithm:

$$ x_{k+1}=\alpha_{k}\gamma V(x_{k})+(I- \mu\alpha_{k}F)T_{N}^{k}T_{N-1}^{k} \cdots T_{1}^{k}x_{k}, $$
(1.10)

where V is an α-Lipschitzian on a real Hilbert space H, F is an L-Lipschitz continuous and η-strongly monotone mapping and \(T_{i}^{k}=(1-\beta_{k}^{i})x_{k}+\beta_{k}^{i}T_{i}\) for \(1\leq i\leq N\). Under suitable assumptions, they proved that the sequence \(\{x_{k}\}\) generated by the iterative algorithm (1.10) converges strongly to a unique solution of the variational inequality problem of finding \(z \in\bigcap_{i=1}^{N} F(T_{i})\) such that

$$ \bigl\langle (\mu F-\gamma V)z,y-z\bigr\rangle \ge0,\quad \forall y \in\bigcap_{i=1}^{N} F(T_{i}). $$
(1.11)

In this paper, motivated by the above works and related literature, we introduce an iterative algorithm for hierarchical fixed point problems of a finite family of nonexpansive mappings in the setting of real Hilbert spaces. We establish a strong convergence theorem for the sequence generated by the proposed method. In order to verify the theoretical assertions, some numerical examples are given. The algorithm and results presented in this paper improve and extend some recent corresponding algorithms and results; see, for example, Yao et al. [2], Suzuki [14], Tian [15], Xu [16], Ceng et al. [19], Buong and Duong [23], Zhang and Yang [24], and the references therein.

2 Preliminaries

In this section, we present some known definitions and results which will be used in the sequel.

Definition 2.1

A mapping \(T:C\to H\) is said to be α-inverse strongly monotone if there exists \(\alpha>0\) such that

$$ \langle Tx-Ty,x-y\rangle\geq\alpha\|Tx-Ty\|^{2},\quad \forall x,y\in C. $$

Lemma 2.1

[19]

Let \(U:C \to H\) be a τ-Lipschitzian mapping, and let \(F:C\to H \) be a k-Lipschitzian and η-strongly monotone mapping, then for \(0\leq\rho\tau<\mu\eta\), \(\mu F-\rho U\) is \(\mu\eta -\rho\tau\)-strongly monotone, i.e.,

$$\bigl\langle (\mu F-\rho U)x-(\mu F-\rho U)y,x-y\bigr\rangle \ge(\mu\eta-\rho \tau)\|x-y\|^{2},\quad \forall x,y\in C. $$

Definition 2.2

[21]

A mapping \(T: H \to H\) is said to be an averaged mapping if there exists \(\alpha\in(0,1)\) such that

$$ T=(1-\alpha)I+\alpha R, $$
(2.1)

where \(I: H\to H\) is the identity mapping and \(R: H \to H\) is a nonexpansive mapping. More precisely, when (2.1) holds, we say that T is α-averaged.

It is easy to see that the averaged mapping T is also nonexpansive and \(F(T ) = F(R)\).

Lemma 2.2

[25, 26]

If the mappings \(\{T_{i}\}^{N}_{i=1}\) defined on a real Hilbert space H are averaged and have a common fixed point, then

$$\bigcap_{i=1}^{N} F(T_{i})=F(T_{1} T_{2} \cdots T_{N}). $$

Lemma 2.3

[1]

Let C be a nonempty closed convex subset of a real Hilbert space H. If \(T : C \rightarrow C\) is a nonexpansive mapping with \(F(T)\neq \emptyset\), then the mapping \(I -T\) is demiclosed at 0, i.e., if \(\{x_{n}\}\) is a sequence in C weakly converging to x, and if \(\{(I -T )x_{n}\}\) converges strongly to 0, then \((I -T )x = 0\).

Definition 2.3

A mapping \(T : C \to H\) is said to be a k-strict pseudo-contraction if there exists a constant \(k \in[0, 1)\) such that

$$\| Tx - Ty \|^{2} \leq\| x-y \|^{2} + k \bigl\Vert (I-T)x - (I-T) y\bigr\Vert ^{2},\quad \forall x,y \in C. $$

Lemma 2.4

[27]

Let C be a nonempty closed convex subset of a real Hilbert space H and \(S: C \to H\) be a k-strict pseudo-contraction mapping. Define \(B: C \to H\) by \(Bx=\lambda Sx+(1-\lambda)x\) for all \(x\in C\). Then, as \(\lambda\in[k,1)\), B is a nonexpansive mapping such that \(F(B)=F(S)\).

Lemma 2.5

[28]

Let \(T:C\to H\) be a k-Lipschitzian and η-strongly monotone operator. Let \(0<\mu<\frac{2\eta}{k^{2}}\), \(W=I-\lambda\mu T\) and \(\mu(\eta -\frac{\mu k^{2}}{2})=\tau\). Then, for \(0 < \lambda< \min\{1,\frac{1}{\tau}\}\), W is a contraction mapping with constant \(1-\lambda\tau\), that is,

$$\|W x- W y\|\leq(1-\lambda\tau)\|x-y\|, \quad \forall x,y\in C. $$

Lemma 2.6

[29]

Let \(\{x_{n}\}\) and \(\{y_{n}\}\) be bounded sequences in a Banach space E and \(\{\beta_{n}\}\) be a sequence in \([0,1]\) with \(0 < \liminf_{n\to\infty} \beta_{n} \leq\limsup_{n\to\infty} \beta_{n} < 1\). Suppose \(x_{n+1}=\beta_{n}x_{n}+(1-\beta_{n})y_{n}\), \(\forall n\geq0\) and \(\limsup_{n\to\infty}(\|y_{n+1}-y_{n}\|-\|x_{n+1}-x_{n}\|) \leq0\). Then \(\lim_{n\to\infty}\|y_{n}-x_{n}\|=0\).

We close this section by presenting the following lemma on the sequences of real numbers.

Lemma 2.7

[30]

Let \(\{a_{n}\}\) be a sequence of nonnegative real numbers such that

$$a_{n+1}\leq(1-\upsilon_{n}) a_{n}+ \delta_{n}, $$

where \(\{\upsilon_{n}\}\) is a sequence in \((0,1)\) and \(\delta_{n}\) is a sequence such that

  1. (i)

    \(\sum_{n=1}^{\infty}\upsilon_{n}=\infty\);

  2. (ii)

    \(\limsup_{n\to\infty} \frac{\delta_{n}}{\upsilon_{n}} \leq0\) or \(\sum_{n=1}^{\infty}|\delta_{n}|<\infty\).

Then \(\lim_{n\to\infty}a_{n}=0\).

3 An iterative method and strong convergence results

Let C be a nonempty closed convex subset of a real Hilbert space H and \(\{T_{i}\}^{N}_{i=1}\) be N nonexpansive mappings on C such that \(\Omega=\bigcap_{i=1}^{N} F(T_{i})\neq\emptyset\). Let \(T: C \to C\) be a k-Lipschitzian mapping and η-strongly monotone, and \(f: C \to C\) be a contraction mapping with a constant τ. We consider the following hierarchical fixed point problem (in short, HFPP) of finding \(z \in\Omega\) such that

$$ \bigl\langle \rho f(z)-\mu T(z), y-z\bigr\rangle \leq0,\quad \forall y \in\Omega =\bigcap_{i=1}^{N} F(T_{i}). $$
(3.1)

Now we suggest the following algorithm for finding a solution of HFPP (3.1).

Algorithm 3.1

For a given arbitrarily point \(x_{0}\in C\), let the iterative sequences \(\{x_{n}\}\) and \(\{y_{n}\}\) be generated by

$$ \left \{ \textstyle\begin{array}{l} y_{n} = \beta_{n} x_{n} + (1-\beta_{n}) T_{N}^{n} T_{N-1}^{n} \cdots T_{1}^{n} x_{n}; \\ x_{n+1} = \alpha_{n} \rho f(y_{n})+\gamma_{n}x_{n}+((1-\gamma_{n})I-\alpha _{n}\mu T)(y_{n}),\quad \forall n \geq0, \end{array}\displaystyle \right . $$
(3.2)

where \(T_{i}^{n}=(1-\delta_{n}^{i})I+\delta_{n}^{i}T_{i}\) and \(\delta_{n}^{i}\in (0,1)\) for \(i=1,2,\ldots,N\). Suppose the parameters satisfy \(0<\mu<\frac{2\eta}{k^{2}}\) and \(0\leq \rho< \frac{\nu}{\tau}\), where \(\nu= \mu ( \eta-\frac{\mu k^{2}}{2} )\). Also \(\{\gamma_{n}\}\), \(\{\alpha_{n}\}\) and \(\{\beta_{n}\}\) are sequences in \((0,1)\) satisfying the following conditions:

  1. (a)

    \(0 < \liminf_{n\to\infty} \gamma_{n} \leq\limsup_{n\to \infty}\gamma_{n} < 1\),

  2. (b)

    \(\lim_{n\to\infty}\alpha_{n}=0\) and \(\sum_{n=1}^{\infty }\alpha_{n}=\infty\),

  3. (c)

    \(\{\beta_{n}\}\subset[\sigma,1)\) and \(\lim_{n\to\infty }\beta_{n}=\beta<1\),

  4. (d)

    \(\lim_{n\to\infty}|\delta_{n-1}^{i}-\delta_{n}^{i}|=0\) for \(i=1,2,\ldots,N\).

Remark 3.1

Algorithm 3.1 can be viewed as an extension and improvement of some well-known results.

  1. (a)

    If \(\beta_{n}=0\), \(\gamma_{n}=\beta\), \(\mu=1\), \(\rho =\gamma\) and \(f(y_{n})=f(x_{n})\), then Algorithm 3.1 reduces to the one studied in [21].

  2. (b)

    If \(\beta_{n}=0\), \(N=1\), \(\gamma_{n}=0\), \(\rho=1\) and \(f(y_{n})=f(x_{n})\), then Algorithm 3.1 can be seen as an extension of an algorithm considered in [2].

  3. (c)

    If \(\beta_{n}=0\), \(N=1\), \(\delta_{n}^{1}=1\), \(\gamma_{n}=0\) and \(f(y_{n})=U(x_{n})\), then Algorithm 3.1 reduces to that considered and studied in [19].

  4. (d)

    If \(\beta_{n}=0\), \(\gamma_{n}=1-\beta_{n}^{0}\), \(\rho=0\), then Algorithm 3.1 reduces to following algorithm:

    $$ x_{n+1}=\bigl(1-\beta_{n}^{0} \bigr)x_{n}+\beta_{n}^{0}(I-\lambda_{n}\mu T)T_{N}^{n} \cdots T_{1}^{n} x_{n}, $$
    (3.3)

    where \(\lambda_{n}=\frac{\alpha_{n}}{\beta_{n}^{0}}\). We can see that (3.3) coincides with the algorithm proposed in [23].

  5. (e)

    If \(\beta_{n}=0\), \(\gamma_{n}=0\) and \(f(y_{n})=V(x_{n})\), then Algorithm 3.1 reduces to the one considered in [24].

This shows that Algorithm 3.1 is quite general and unified one. We expect the wide applicability of Algorithm 3.1.

Lemma 3.1

The sequences \(\{x_{n}\}\) and \(\{y_{n}\}\) are bounded.

Proof

Let \(x^{*} \in\Omega\). We have

$$\begin{aligned} \bigl\Vert y_{n}-x^{*}\bigr\Vert =&\bigl\Vert (1- \beta_{n}) \bigl(T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n} x_{n} -x^{*}\bigr)+ \beta_{n}\bigl(x_{n}-x^{*}\bigr)\bigr\Vert \\ \leq&(1-\beta_{n})\bigl\Vert x_{n}-x^{*}\bigr\Vert + \beta_{n}\bigl\Vert x_{n}-x^{*}\bigr\Vert =\bigl\Vert x_{n}-x^{*}\bigr\Vert . \end{aligned}$$
(3.4)

Since \(\lim_{n\to\infty}\alpha_{n}=0\), without loss of generality, we may assume that \(\alpha_{n} \leq\min\{\epsilon,\frac{\epsilon}{\tau}\}\) for all \(n\geq1\), where \(0 < \epsilon< 1 - \limsup_{n\to\infty}\gamma_{n}\). From (3.2) and (3.4), we obtain

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*}\bigr\Vert =&\bigl\Vert \alpha_{n}\rho f(y_{n})+\gamma_{n}x_{n}+ \bigl((1-\gamma _{n})I-\alpha_{n}\mu T\bigr) (y_{n})-x^{*}\bigr\Vert \\ =&\bigl\Vert \alpha_{n}\bigl(\rho f(y_{n})-\mu T\bigl(x^{*} \bigr)\bigr)+\gamma_{n}\bigl(x_{n}-x^{*}\bigr)+\bigl((1-\gamma _{n})I-\alpha_{n}\mu T\bigr) (y_{n}) \\ &{}-\bigl((1-\gamma_{n})I-\alpha_{n}\mu T\bigr) \bigl(x^{*} \bigr) \bigr\Vert \\ \leq&\alpha_{n}\rho\tau\bigl\Vert y_{n}-x^{*}\bigr\Vert + \alpha_{n}\bigl\Vert (\rho f-\mu T)x^{*}\bigr\Vert + \gamma_{n}\bigl\Vert x_{n}-x^{*}\bigr\Vert \\ &{}+\bigl\Vert \bigl((1-\gamma_{n})I-\alpha_{n}\mu T \bigr) (y_{n}) -\bigl((1-\gamma_{n})I-\alpha_{n}\mu T\bigr) \bigl(x^{*}\bigr) \bigr\Vert \\ =&\alpha_{n}\rho\tau\bigl\Vert y_{n}-x^{*}\bigr\Vert + \alpha_{n}\bigl\Vert (\rho f-\mu T)x^{*}\bigr\Vert +\gamma _{n}\bigl\Vert x_{n}-x^{*}\bigr\Vert \\ &{}+(1-\gamma_{n}) \biggl\Vert \biggl( I-\frac{\alpha_{n}\mu}{(1-\gamma _{n})} T \biggr) (y_{n}) - \biggl( I-\frac{\alpha_{n}\mu}{(1-\gamma_{n})} T \biggr) \bigl(x^{*}\bigr) \biggr\Vert \\ \leq& \alpha_{n} \rho\tau\bigl\Vert y_{n}-x^{*}\bigr\Vert + \alpha_{n}\bigl\Vert (\rho f-\mu T)x^{*}\bigr\Vert \\ &{}+\gamma_{n}\bigl\Vert x_{n}-x^{*}\bigr\Vert +(1- \gamma_{n}-\alpha_{n}\nu)\bigl\Vert y_{n}-x^{*}\bigr\Vert \\ \leq&\alpha_{n}\rho\tau\bigl\Vert x_{n}-x^{*}\bigr\Vert + \alpha_{n}\bigl\Vert (\rho f-\mu T)x^{*}\bigr\Vert + \gamma_{n}\bigl\Vert x_{n}-x^{*}\bigr\Vert \\ &{}+(1-\gamma_{n}-\alpha_{n}\nu)\bigl\Vert x_{n} -x^{*}\bigr\Vert \\ =&\alpha_{n}\rho\tau\bigl\Vert x_{n}-x^{*}\bigr\Vert + \alpha_{n}\bigl\Vert (\rho f-\mu T)x^{*}\bigr\Vert +(1- \alpha_{n}\nu)\bigl\Vert x_{n} -x^{*}\bigr\Vert \\ =&\bigl(1-\alpha_{n}(\nu-\rho\tau)\bigr)\bigl\Vert x_{n}-x^{*}\bigr\Vert +\alpha_{n}\bigl\Vert (\rho f-\mu T)x^{*}\bigr\Vert \\ \leq& \max\biggl\{ \bigl\Vert x_{n}-x^{*}\bigr\Vert , \frac{1}{\nu-\rho\tau}\bigl(\bigl\Vert (\rho f-\mu T)x^{*}\bigr\Vert \bigr) \biggr\} , \end{aligned}$$

where the second inequality follows from Lemma 2.5 and the third inequality follows from (3.4). By induction on n, we obtain

$$\bigl\Vert x_{n}-x^{*}\bigr\Vert \leq\max\biggl\{ \bigl\Vert x_{n}-x^{*}\bigr\Vert ,\frac{1}{\nu-\rho\tau}\bigl(\bigl\Vert (\rho f-\mu T)x^{*}\bigr\Vert \bigr)\biggr\} ,\quad \forall n\geq0 \mbox{ and } x_{0}\in C. $$

Hence, \(\{x_{n}\}\) is bounded, and consequently, we deduce that \(\{y_{n}\} \), \(\{Ty_{n}\}\), \(\{T_{1}x_{n+1}\}\), \(\|T_{1}^{n}x_{n+1}\|, \|T_{2}T_{1}^{n}x_{n+1}\|, \ldots , \|T_{N-1}^{n} \cdots T_{1}^{n}x_{n+1}\|, \|T_{N}T_{N-1}^{n} \cdots T_{1}^{n}x_{n+1}\|\) and \(\{f(y_{n})\}\) are bounded. □

Lemma 3.2

Let \(\{x_{n}\}\) be a sequence generated by Algorithm 3.1. Then:

  1. (a)

    \(\lim_{n\to\infty}\|x_{n+1}-x_{n}\|=0\).

  2. (b)

    The weak w-limit set \(w_{w}(x_{n}) \subset\Omega\) (\(w_{w}(x_{n})=\{x: x_{n_{i}}\rightharpoonup x\}\)).

Proof

We estimate

$$\begin{aligned}& \Vert y_{n}-y_{n-1}\Vert \\& \quad = \bigl\Vert (1-\beta_{n})T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n} + \beta_{n} x_{n}-\bigl[(1-\beta_{n-1})T_{N}^{n-1}T_{N-1}^{n-1} \cdots T_{1}^{n-1}x_{n-1}+\beta_{n-1}x_{n-1} \bigr]\bigr\Vert \\& \quad = \bigl\Vert (1-\beta_{n}) \bigl(T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n}-T_{N}^{n-1}T_{N-1}^{n-1} \cdots T_{1}^{n-1}x_{n-1}\bigr) \\& \qquad {} -(\beta_{n}-\beta_{n-1})T_{N}^{n-1}T_{N-1}^{n-1} \cdots T_{1}^{n-1}x_{n-1}+\beta_{n}(x_{n}-x_{n-1})-( \beta_{n-1}-\beta _{n})x_{n-1}\bigr\Vert \\& \quad \leq \Vert x_{n-1}-x_{n}\Vert +(1- \beta_{n})\bigl\Vert T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n}-T_{N}^{n-1}T_{N-1}^{n-1} \cdots T_{1}^{n-1}x_{n-1}\bigr\Vert \\& \qquad {} +|\beta_{n}-\beta_{n-1}|\bigl\Vert T_{N}^{n-1}T_{N-1}^{n-1} \cdots T_{1}^{n-1}x_{n-1}-x_{n-1}\bigr\Vert . \end{aligned}$$
(3.5)

It follows from the definition of \(T_{i}^{n+1}\) that

$$\begin{aligned}& \bigl\Vert T_{2}^{n+1}T_{1}^{n+1}x_{n+1}-T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert \\& \quad \leq \bigl\Vert T_{2}^{n+1}T_{1}^{n+1}x_{n+1}-T_{2}^{n+1}T_{1}^{n}x_{n+1} \bigr\Vert +\bigl\Vert T_{2}^{n+1}T_{1}^{n}x_{n+1}-T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert \\& \quad \leq \bigl\Vert T_{1}^{n+1}x_{n+1}-T_{1}^{n}x_{n+1} \bigr\Vert +\bigl\Vert T_{2}^{n+1}T_{1}^{n}x_{n+1}-T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert \\& \quad = \bigl\Vert \bigl(1-\delta_{n+1}^{1} \bigr)x_{n+1}+\delta_{n+1}^{1}T_{1}x_{n+1}- \bigl(1-\delta _{n}^{1}\bigr)x_{n+1}- \delta_{n}^{1}T_{1}x_{n+1}\bigr\Vert \\& \qquad {}+\bigl\Vert \bigl(1-\delta_{n+1}^{2} \bigr)T_{1}^{n}x_{n+1}+\delta _{n+1}^{2}T_{2}T_{1}^{n}x_{n+1}- \bigl(1-\delta_{n}^{2}\bigr)T_{1}^{n}x_{n+1} -\delta_{n}^{2}T_{2}T_{1}^{n}x_{n+1} \bigr\Vert \\& \quad \leq \bigl\vert \delta_{n+1}^{1}- \delta_{n}^{1}\bigr\vert \bigl(\Vert x_{n+1} \Vert +\Vert T_{1}x_{n+1}\Vert \bigr) +\bigl\vert \delta_{n+1}^{2}-\delta_{n}^{2} \bigr\vert \bigl(\bigl\Vert T_{1}^{n}x_{n+1} \bigr\Vert +\bigl\Vert T_{2}T_{1}^{n}x_{n+1} \bigr\Vert \bigr), \end{aligned}$$
(3.6)

and from (3.6) we have

$$\begin{aligned}& \bigl\Vert T_{3}^{n+1}T_{2}^{n+1}T_{1}^{n+1}x_{n+1}-T_{3}^{n}T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert \\& \quad \leq \bigl\Vert T_{3}^{n+1}T_{2}^{n+1}T_{1}^{n+1}x_{n+1}-T_{3}^{n+1}T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert \\& \qquad {} +\bigl\Vert T_{3}^{n+1}T_{2}^{n}T_{1}^{n}x_{n+1}-T_{3}^{n}T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert \\& \quad \leq \bigl\Vert T_{2}^{n+1}T_{1}^{n+1}x_{n+1}-T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert +\bigl\Vert \bigl(1-\delta_{n+1}^{3} \bigr)T_{2}^{n}T_{1}^{n}x_{n+1} \\& \qquad {} +\delta_{n+1}^{3}T_{3}T_{2}^{n}T_{1}^{n}x_{n+1}- \bigl(1-\delta _{n}^{3}\bigr)T_{2}^{n}T_{1}^{n}x_{n+1} -\delta_{n}^{3}T_{3}T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert \\& \quad \leq \bigl\vert \delta_{n+1}^{1}- \delta_{n}^{1}\bigr\vert \bigl(\Vert x_{n+1} \Vert +\Vert T_{1}x_{n+1}\Vert \bigr) +\bigl\vert \delta_{n+1}^{2}-\delta_{n}^{2}\bigr\vert \bigl(\bigl\Vert T_{1}^{n}x_{n+1}\bigr\Vert \\& \qquad {} +\bigl\Vert T_{2}T_{1}^{n}x_{n+1} \bigr\Vert \bigr) + \bigl\vert \delta_{n+1}^{3}- \delta_{n}^{3}\bigr\vert \bigl(\bigl\Vert T_{2}^{n}T_{1}^{n}x_{n+1}\bigr\Vert +\bigl\Vert T_{3}T_{2}^{n}T_{1}^{n}x_{n+1} \bigr\Vert \bigr). \end{aligned}$$

By induction on N, we have

$$\begin{aligned}& \bigl\Vert T_{N}^{n+1}T_{N-1}^{n+1} \cdots T_{1}^{n+1}x_{n+1}-T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n+1}\bigr\Vert \\& \quad \leq \bigl\vert \delta_{n+1}^{1}- \delta_{n}^{1}\bigr\vert \bigl(\Vert x_{n+1} \Vert +\Vert T_{1}x_{n+1}\Vert \bigr) +\bigl\vert \delta_{n+1}^{2}-\delta_{n}^{2}\bigr\vert \bigl(\bigl\Vert T_{1}^{n}x_{n+1}\bigr\Vert +\bigl\Vert T_{2}T_{1}^{n}x_{n+1} \bigr\Vert \bigr) \\& \qquad {} +\cdots+\bigl\vert \delta_{n+1}^{N}- \delta_{n}^{N}\bigr\vert \bigl(\bigl\Vert T_{N-1}^{n}\cdots T_{1}^{n}x_{n+1} \bigr\Vert +\bigl\Vert T_{N}T_{N-1}^{n}\cdots T_{1}^{n}x_{n+1}\bigr\Vert \bigr). \end{aligned}$$

Since \(\lim_{n\to\infty}|\delta_{n+1}^{i}-\delta_{n}^{i}|=0\) for \(i=1,2,\ldots,N\), and \(\|x_{n+1}\|, \|T_{1}x_{n+1}\|, \|T_{1}^{n}x_{n+1}\|, \|T_{2}T_{1}^{n}x_{n+1}\|, \ldots, \|T_{N-1}^{n} \cdots T_{1}^{n}x_{n+1}\|, \|T_{N}T_{N-1}^{n} \cdots T_{1}^{n}x_{n+1}\|\) are bounded, we obtain

$$\lim_{n\to\infty}\bigl\Vert T_{N}^{n+1}T_{N-1}^{n+1} \cdots T_{1}^{n+1}x_{n+1}-T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n+1}\bigr\Vert =0. $$

Define \(w_{n}=\frac{x_{n+1}-\gamma_{n}x_{n}}{1-\gamma_{n}}\). Then \(x_{n+1}=(1-\gamma_{n})w_{n}+\gamma_{n}x_{n}\), and therefore, from (3.5), we have

$$\begin{aligned}& \Vert w_{n+1}-w_{n}\Vert \\& \quad \leq \frac{\alpha_{n+1}}{1-\gamma_{n+1}}\bigl\Vert \rho f(y_{n+1})-\mu T(y_{n+1})\bigr\Vert +\frac{\alpha_{n}}{1-\gamma_{n}}\bigl\Vert \rho f(y_{n})-\mu T(y_{n})\bigr\Vert +\Vert y_{n+1}-y_{n}\Vert \\& \quad \leq \frac{\alpha_{n+1}}{1-\gamma_{n+1}}\bigl\Vert \rho f(y_{n+1})-\mu T(y_{n+1})\bigr\Vert \\& \qquad {} +\frac{\alpha_{n}}{1-\gamma_{n}}\bigl\Vert \rho f(y_{n})-\mu T(y_{n})\bigr\Vert +\Vert x_{n+1}-x_{n}\Vert \\& \qquad {} +(1-\beta_{n+1})\bigl\Vert T_{N}^{n+1}T_{N-1}^{n+1} \cdots T_{1}^{n+1}x_{n+1}-T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n+1}\bigr\Vert \\& \qquad {} +\vert \beta_{n+1}-\beta_{n}\vert \bigl\Vert T_{N}^{n}T_{N-1}^{n}\cdots T_{1}^{n}x_{n}-x_{n}\bigr\Vert . \end{aligned}$$

Since \(\lim_{n\to\infty}\alpha_{n}=0\), \(\lim_{n\to\infty}\beta _{n}=\beta\), \(\liminf_{n\to\infty}\gamma_{n} < \limsup_{n\to\infty}\gamma_{n}<1\) and

$$\lim_{n\to\infty}\bigl\Vert T_{N}^{n+1}T_{N-1}^{n+1} \cdots T_{1}^{n+1}x_{n+1}-T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n+1}\bigr\Vert =0, $$

we get

$$\limsup_{n\to\infty}\bigl(\Vert w_{n+1}-w_{n} \Vert -\|x_{n+1}-x_{n}\|\bigr)\leq0. $$

By Lemma 2.6, we have \(\lim_{n\to\infty}\|w_{n}-x_{n}\|=0\). Since \(\|x_{n+1}-x_{n}\|=(1-\gamma_{n})\|w_{n}-x_{n}\|\), we obtain

$$\lim_{n\to\infty}\|x_{n+1}-x_{n}\|=0. $$

We next estimate

$$\begin{aligned} \|x_{n}-y_{n}\| \leq&\|x_{n+1}-x_{n}\|+ \|x_{n+1}-y_{n}\| \\ \leq&\|x_{n+1}-x_{n}\|+\|x_{n+1}-y_{n}\| \\ \leq&\|x_{n+1}-x_{n}\|+\alpha_{n}\bigl\Vert \rho f(y_{n})-\mu T(y_{n})\bigr\Vert +\gamma_{n}\| x_{n}-y_{n}\| , \end{aligned}$$

which implies that

$$(1-\gamma_{n})\|x_{n}-y_{n}\|\leq \|x_{n+1}-x_{n}\|+\alpha_{n}\bigl\Vert \rho f(y_{n})-\mu T(y_{n})\bigr\Vert . $$

Since \(\lim_{n\to\infty}\alpha_{n}=0\) and \(\liminf_{n\to\infty}\gamma_{n} < \limsup_{n\to\infty}\gamma _{n}<1\), we have

$$ \lim_{n\to\infty}\|x_{n}-y_{n}\|=0. $$
(3.7)

Define a mapping \(W: C\to H\) by

$$Wx=\beta x+(1-\beta)T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x, $$

with \(\sigma\leq\beta<1\). It follows from Lemma 2.4 that W is a nonexpansive mapping and \(F(W)=\Omega\). Note that

$$\begin{aligned} \|Wx_{n}-x_{n}\| \leq&\|Wx_{n}-y_{n}\|+ \|x_{n}-y_{n}\| \\ \leq&|\beta_{n}-\beta|\bigl\Vert T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n}-x_{n}\bigr\Vert + \|x_{n}-y_{n}\|. \end{aligned}$$

Since \(\lim_{n\to\infty}\beta_{n}=\beta\) and \(\lim_{n\to\infty}\| x_{n}-y_{n}\|=0\), we obtain

$$\lim_{n\to\infty}\|Wx_{n}-x_{n}\|=0. $$

Since \(\{x_{n}\}\) is bounded, without loss of generality we may assume that \(x_{n}\rightharpoonup x^{*}\in C\). It follows from Lemma 2.3 that \(x^{*}\in F(W)=\Omega\). Therefore, \(w_{w}(x_{n}) \subset\Omega\). □

Theorem 3.1

The sequence \(\{x_{n}\}\) generated by Algorithm 3.1 converges strongly to \(z \in\Omega=\bigcap_{i=1}^{N} F(T_{i})\) such that it is also a unique solution of HFPP (3.1).

Proof

Since \(\{x_{n}\}\) is bounded and \(x_{n} \rightharpoonup w\), from Lemma 3.2 we have \(w \in\Omega\). Since \(0 \leq\rho\tau< \mu\eta\), from Lemma 2.1 it can be easily seen that the operator \(\mu T-\rho f\) is \(\mu\eta -\rho\tau\) strongly monotone, and we get the uniqueness of the solution of HFPP (3.1). Let us denote this unique solution of HFPP (3.1) by \(z\in\Omega\).

Since \(\{x_{n}\}\) is bounded, there exists a subsequence \(\{x_{n_{k}}\}\) of \(\{x_{n}\}\) such that

$$\begin{aligned} \limsup_{n\to\infty} \bigl\langle \rho f(z)-\mu T(z),x_{n}-z \bigr\rangle = & \limsup_{k\to\infty}\bigl\langle \rho f(z)-\mu T(z),x_{n_{k}}-z\bigr\rangle \\ = & \bigl\langle \rho f(z)-\mu T(z),w-z\bigr\rangle \leq0. \end{aligned}$$

Next, we show that \(x_{n}\rightarrow z\). We have

$$\begin{aligned}& \|x_{n+1}-z\|^{2} \\& \quad = \bigl\langle \alpha_{n}\rho f(y_{n})+ \gamma_{n}x_{n}+\bigl((1-\gamma_{n})I-\alpha _{n}\mu T\bigr) (y_{n})-z,x_{n+1}-z\bigr\rangle \\& \quad = \alpha_{n}\bigl\langle \rho f(y_{n})-\mu T(z),x_{n+1}-z\bigr\rangle +\gamma _{n}\langle x_{n}-z,x_{n+1}-z\rangle \\& \qquad {} +\bigl\langle \bigl((1-\gamma_{n})I-\alpha_{n}\mu T \bigr) (y_{n})-\bigl((1-\gamma_{n})I-\alpha _{n}\mu T\bigr) (z),x_{n+1}-z\bigr\rangle \\& \quad \leq \alpha_{n}\bigl\langle \rho\bigl(f(y_{n})-f(z) \bigr),x_{n+1}-z\bigr\rangle +\alpha _{n}\bigl\langle \rho f(z) - \mu T(z),x_{n+1}-z\bigr\rangle \\& \qquad {} +\gamma_{n}\| x_{n}-z\|\|x_{n+1}-z\|+(1- \gamma_{n}-\alpha_{n}\nu)\|y_{n}-z\| \|x_{n+1}-z\| \\& \quad \leq \alpha_{n}\rho\tau\|x_{n}-z\|\|x_{n+1}-z \|+\alpha_{n}\bigl\langle \rho f(z)-\mu T(z),x_{n+1}-z\bigr\rangle \\& \qquad {} +\gamma_{n}\| x_{n}-z\|\|x_{n+1}-z\|+(1- \gamma_{n}-\alpha_{n}\nu)\|x_{n}-z\| \|x_{n+1}-z\| \\& \quad = \bigl(1-\alpha_{n}(\nu- \rho\tau)\bigr)\|x_{n}-z\| \|x_{n+1}-z\|+\alpha _{n}\bigl\langle \rho f(z)-\mu T(z),x_{n+1}-z\bigr\rangle \\& \quad \leq \frac{1-\alpha_{n}(\nu- \rho\tau)}{2}\bigl(\|x_{n}-z\|^{2}+\| x_{n+1}-z\|^{2}\bigr)+\alpha_{n}\bigl\langle \rho f(z) -\mu T(z),x_{n+1}-z\bigr\rangle \\& \quad \leq \frac{1-\alpha_{n}(\nu- \rho\tau)}{2}\|x_{n}-z\|^{2}+ \frac {1}{2}\|x_{n+1}-z\|^{2}+\alpha_{n}\bigl\langle \rho f(z) -\mu T(z),x_{n+1}-z\bigr\rangle , \end{aligned}$$

which implies that

$$\|x_{n+1}-z\|^{2}\leq\bigl(1-\alpha_{n}(\nu- \rho \tau)\bigr)\|x_{n}-z\|^{2}+2\alpha _{n}\bigl\langle \rho f(z) -\mu T(z),x_{n+1}-z\bigr\rangle . $$

Let \(\upsilon_{n}=\alpha_{n}(\nu- \rho\tau)\) and \(\delta_{n}=2\alpha_{n}\langle\rho f(z)-\mu T(z),x_{n+1}-z\rangle\). Then we have

$$\sum_{n=1}^{\infty}\alpha_{n}=\infty \quad \mbox{and}\quad \limsup_{n\to\infty} \biggl\{ \frac{1}{\nu- \rho\tau} \bigl\langle \rho f(z)-\mu T(z),x_{n+1}-z\bigr\rangle \biggr\} \leq0. $$

It follows that

$$\sum_{n=1}^{\infty}\upsilon_{n}= \infty \quad \mbox{and}\quad \limsup_{n\to\infty}\frac{\delta_{n}}{\upsilon_{n}} \leq0. $$

Thus, all the conditions of Lemma 2.7 are satisfied. Hence we deduce that \(x_{n}\to z\). This completes the proof. □

4 Examples

To illustrate Algorithm 3.1 and the convergence result, we consider the following examples.

Example 4.1

Let \(\alpha_{n}=\frac{1}{2(n+1)}\), \(\beta_{n}=\frac{1}{n^{3}}\) and \(\gamma_{n}=\frac{1}{4}\). It is easy to show that the sequences \(\{\alpha_{n}\}\), \(\{\beta_{n}\}\) and \(\{\gamma_{n}\}\) satisfy conditions (a), (b) and (c). Let \(\delta_{n}^{i}=\frac{n+i}{n+i+1}\) for \(i=1,2\). Then

$$\begin{aligned} \lim_{n\to\infty}\bigl\vert \delta_{n-1}^{i}- \delta_{n}^{i}\bigr\vert =&\lim_{n\to\infty } \biggl\vert \frac{n-1+i}{n+i}-\frac{n+i}{n+i+1}\biggr\vert \\ =&\lim_{n\to\infty}\biggl\vert \frac{1}{(n+i)(n+1+i)}\biggr\vert \\ =&0. \end{aligned}$$

This implies that the sequence \(\{\delta_{n}^{i}\}\) satisfies condition (d).

Let \(T_{1}, T_{2} : \mathbb{R} \to\mathbb{R}\) be defined by

$$T_{1}(x) = \sin(x) \quad \mbox{and}\quad T_{2}(x)= \frac{x}{3}, \quad \forall x \in \mathbb{R}, $$

and let the mapping \(f: \mathbb{R}\to\mathbb{R}\) be defined by

$$f(x)=\frac{x}{14}, \quad \forall x\in\mathbb{R}. $$

It is easy to see that \(T_{1}\) and \(T_{2}\) are nonexpansive, and f is a contraction mapping with constant \(\frac{1}{7}\). Clearly,

$$\Omega=\bigcap_{i=1}^{2}F(T_{i})= \{0\}. $$

Let \(T: \mathbb{R}\to\mathbb{R}\) be defined by

$$T(x)=\frac{2x+3}{7}, \quad \forall x\in\mathbb{R}. $$

Then T is 1-Lipschitzian and \(\frac{1}{7}\)-strongly monotone.

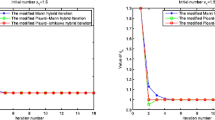
In all tests we take \(\rho=\frac{1}{30}\) and \(\mu=\frac{1}{7}\). In this example, \(\eta=\frac{1}{7}\), \(k=1\) and \(\tau=\frac{1}{7}\). It is easy to see that the parameters satisfy \(0<\mu<\frac{2\eta }{k^{2}}\) and \(0\leq\rho\tau<\nu\), where \(\nu=\mu ( \eta-\frac{\mu k^{2}}{2} )\). All codes were written in Matlab, the values of \(\{y_{n}\}\) and \(\{x_{n}\}\) with different n are reported in Table 1.

Table 1 The values of \(\pmb{\{y_{n}\}}\) and \(\pmb{\{x_{n}\}}\) with initial values \(\pmb{x_{1} = -10}\) and \(\pmb{x_{1} = 20}\)
Full size table

Remark 4.1

Table 1 and Figure 1 show that the sequences \(\{y_{n}\}\) and \(\{x_{n}\}\) converge to 0. Also, \(\{0\}=\Omega\).

Figure 1
figure 1

The convergence of \(\pmb{\{u_{n}\}}\) , \(\pmb{\{y_{n}\}}\) and \(\pmb{\{ x_{n}\}}\) with initial values \(\pmb{x_{1} = -10}\) and \(\pmb{x_{1} = 20}\) .

Full size image

Example 4.2

All the mappings and parameters are the same as in Example 4.1 except \(T_{1}\), \(T_{2}\) and f. Let \(T_{1}, T_{2}, T_{3} : \mathbb{R}\to\mathbb{R}\) be defined by

$$T_{1}(x) = \cos(1-x), \qquad T_{2}(x) = \sin(x-1)+1, \qquad T_{3}(x) = \frac{-2x+5}{3},\quad \forall x \in\mathbb{R}, $$

and let \(f: \mathbb{R}\to\mathbb{R}\) be defined by

$$f(x)=\frac{2x+14}{7}, \quad \forall x\in\mathbb{R}. $$

Then \(T_{1}\), \(T_{2}\) and \(T_{3}\) are nonexpansive mappings, and f is a contraction mapping with constant \(\frac{2}{7}\). Clearly,

$$\Omega=\bigcap_{i=1}^{3}F(T_{i})= \{1\}. $$

Let \(\delta_{n}^{i}=\frac{n+i}{n+i+1}\) for \(i=1,2,3\).

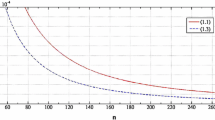
All codes were written in Matlab, the values of \(\{y_{n}\}\) and \(\{x_{n}\}\) with different n are reported in Table 2.

Table 2 The values of \(\pmb{\{y_{n}\}}\) and \(\pmb{\{x_{n}\}}\) with initial values \(\pmb{x_{1} = -20}\) and \(\pmb{x_{1} = 30}\)
Full size table

Remark 4.2

Table 2 and Figure 2 show that the sequences \(\{y_{n}\}\) and \(\{x_{n}\}\) converge to 1. Also, \(\{1\}=\Omega\).

Figure 2
figure 2

The convergence of \(\pmb{\{u_{n}\}}\) , \(\pmb{\{y_{n}\}}\) and \(\pmb{\{ x_{n}\}}\) with initial values \(\pmb{x_{1} = -20}\) and \(\pmb{x_{1} = 30}\) .

Full size image