Abstract
The purpose of this paper is to investigate the problem of finding an approximate point of the common set of solutions of an equilibrium problem and a hierarchical fixed point problem in the setting of real Hilbert spaces. We establish the strong convergence of the proposed method under some mild conditions. Several special cases are also discussed. Numerical examples are presented to illustrate the proposed method and convergence result. The results presented in this paper extend and improve some well-known results in the literature.
MSC:49J30, 47H09, 47J20, 49J40.
Similar content being viewed by others
1 Introduction
Let H be a real Hilbert space whose inner product and norm are denoted by and , respectively. Let C be a nonempty closed convex subset of H and be a bifunction. The equilibrium problem (in short, EP) is to find such that
The solution set of EP (1.1) is denoted by .
The equilibrium problem provides a unified, natural, innovative and general framework to study a wide class of problems arising in finance, economics, network analysis, transportation, elasticity and optimization. The theory of equilibrium problems has witnessed an explosive growth in theoretical advances and applications across all disciplines of pure and applied sciences; see [1–10] and the references therein.
If , where is a nonlinear operator, then EP (1.1) is equivalent to find a vector such that
It is a well-known classical variational inequality problem. We now have a variety of techniques to suggest and analyze various iterative algorithms for solving variational inequalities and the related optimization problems; see [1–27] and the references therein.
The fixed point problem for the mapping is to find such that
We denote by the set of solutions of (1.3). It is well known that is closed and convex, and is well defined.
Let be a nonexpansive mapping, that is, for all . The hierarchical fixed point problem (in short, HFPP) is to find such that
It is linked with some monotone variational inequalities and convex programming problems; see [12]. Various methods have been proposed to solve HFPP (1.4); see, for example, [13–17] and the references therein. In 2010, Yao et al. [12] studied the following iterative algorithm to solve HFPP (1.4):
where is a contraction mapping and and are sequences in . Under certain restrictions on the parameters, They proved that the sequence generated by (1.5) converges strongly to , which is also a unique solution of the following variational inequality:
In 2011, Ceng et al. [18] investigated the following iterative method:
where U is a Lipschitzian mapping, and F is a Lipschitzian and strongly monotone mapping. They proved that under some approximate assumptions on the operators and parameters, the sequence generated by (1.7) converges strongly to a unique solution of the variational inequality:
In this paper, motivated by the work of Ceng et al. [18, 20], Yao et al. [12], Bnouhachem [19] and others, we propose an iterative method for finding an approximate element of the common set of solutions of EP (1.1) and HFPP (1.4) in the setting of real Hilbert spaces. We establish a strong convergence theorem for the sequence generated by the proposed method. The proposed method is quite general and flexible and includes several known methods for solving of variational inequality problems, equilibrium problems, and hierarchical fixed point problems; see, for example, [12, 13, 15, 18, 19, 21] and the references therein.
2 Preliminaries
We present some definitions which will be used in the sequel.
Definition 2.1 A mapping is said to be k-Lipschitz continuous if there exists a constant such that
-
If , then T is called nonexpansive.
-
If , then T is called contraction.
Definition 2.2 A mapping is said to be
-
(a)
monotone if
-
(b)
strongly monotone if there exists an such that
-
(c)
α-inverse strongly monotone if there exists an such that
It is easy to observe that every α-inverse strongly monotone mapping is monotone and Lipschitz continuous. Also, for every nonexpansive mapping , we have
for all . Therefore, for all , we have
The following lemma provides some basic properties of the projection onto C.
Lemma 2.1 Let denote the projection of H onto C. Then we have the following inequalities:
-
(a)
, , ;
-
(b)
, ;
-
(c)
, ;
-
(d)
, , .
Assumption 2.1 [1]
Let be a bifunction satisfying the following assumptions:
(A1) , ;
(A2) is monotone, that is, , ;
(A3) For each , ;
(A4) For each , is convex and lower semicontinuous.
Lemma 2.2 [2]
Let C be a nonempty closed convex subset of a real Hilbert space H and satisfy conditions (A1)-(A4). For and , define a mapping as
Then the following statements hold:
-
(i)
is nonempty single-valued;
-
(ii)
is firmly nonexpansive, that is,
-
(iii)
;
-
(iv)
is closed and convex.
Lemma 2.3 [22]
Let C be a nonempty closed convex subset of a real Hilbert space H. If is a nonexpansive mapping with , then the mapping is demiclosed at 0, that is, if is a sequence in C converges weakly to x and converges strongly to 0, then .
Lemma 2.4 [18]
Let be a τ-Lipschitzian mapping and be a k-Lipschitzian and η-strongly monotone mapping. Then, for , is -strongly monotone, that is,
Lemma 2.5 [23]
Let , , and be an k-Lipschitzian and η-strongly monotone operator. In association with a nonexpansive mapping , define a mapping by
Then is a contraction provided , that is,
where .
Lemma 2.6 [25]
Let C be a closed convex subset of a real Hilbert space H and be a bounded sequence in H. Assume that
-
(i)
the weak w-limit set , where
-
(ii)
for each , exists.
Then the sequence is weakly convergent to a point in C.
Lemma 2.7 [24]
Let be a sequence of nonnegative real numbers such that
where is a sequence in and is a sequence such that
-
(i)
;
-
(ii)
or .
Then .
3 An iterative method and strong convergence results
In this section, we propose and analyze an iterative method for finding the common solutions of EP (1.1) and HFPP (1.4).
Let C be a nonempty closed convex subset of a real Hilbert space H. Let be a bifunction that satisfy conditions (A1)-(A4), and let be nonexpansive mappings such that . Let be a k-Lipschitzian mapping and η-strongly monotone, and let be a τ-Lipschitzian mapping.
Algorithm 3.1 For any given , let the iterative sequences , , and be generated by
Suppose that the parameters satisfy and , where . Also, , , , and are sequences in satisfying the following conditions:
-
(a)
, ,
-
(b)
and ,
-
(c)
,
-
(d)
, and ,
-
(e)
and .
Remark 3.1 Algorithm 3.1 can be viewed as an extension and improvement for some well-known methods.
-
If , then the proposed method is an extension and improvement of a method studied in [19, 26].
-
If , , , and , then we obtain an extension and improvement of a method considered in [12].
-
The contractive mapping f with a coefficient in other papers [12, 21, 23] is extended to the cases of the Lipschitzian mapping U with a coefficient constant .
Lemma 3.1 Let . Then , , and are bounded.
Proof It follows from Lemma 2.2 that . Let , then . Define .
We prove that the sequence is bounded. Without loss of generality, we can assume that for all . From (3.1), we have
where the third inequality follows from Lemma 2.5. By induction on n, we obtain
for and . Hence, is bounded, and consequently, we deduce that , , , , , and are bounded. □
Lemma 3.2 Let and be a sequence generated by Algorithm 3.1. Then the following statements hold.
-
(a)
.
-
(b)
The weak w-limit set .
Proof From the definition of the sequence in Algorithm 3.1, we have
Since and , we have
and
Take in (3.3) and in (3.4), we get
and
Adding (3.5) and (3.6), and using the monotonicity of , we obtain
which implies that
and then
Without loss of generality, assume that there exists a real number χ such that for all positive integers n. Then we get
It follows from (3.2) and (3.7) that
Next, we estimate that
where the second inequality follows from Lemma 2.5. From (3.8) and (3.9), we have
where
It follows from conditions (b), (d), (e) of Algorithm 3.1, and Lemma 2.7 that
Next, we show that . Since is firmly nonexpansive, we have
Hence, we get
From above inequality, we have
which implies that
Hence,
Since , , , we have
Since , we have
Since , , , , and and are bounded, and , we obtain
Since is bounded, without loss of generality, we can assume that . It follows from Lemma 2.3 that . Therefore, . □
Theorem 3.1 The sequence generated by Algorithm 3.1 converges strongly to , which is also a unique solution of the variational inequality:
Proof From Lemma 3.2, we have since is bounded and . We show that . Since , we have
It follows from the monotonicity of that
and
Since and , it is easy to observe that . For any and , let . Then we have , and from (3.14) we obtain
Since , it follows from (3.15) that
Since satisfies (A1)-(A4), it follows from (3.16) that
which implies that . Letting , we have
which implies that . Thus, we have
Observe that the constants satisfy and
therefore, from Lemma 2.4, the operator is strongly monotone, and we get the uniqueness of the solution of variational inequality (3.13), and denote it by .
Next, we claim that . Since is bounded, there exists a subsequence of such that
Next, we show that . We have
which implies that
Let and
We have and
It follows that
Thus, all the conditions of Lemma 2.7 are satisfied. Hence, we deduce that . This completes the proof. □
Putting in Algorithm 3.1, we obtain the following result, which can be viewed as an extension and improvement of the method studied in [26].
Corollary 3.1 Let C be a nonempty closed convex subset of a real Hilbert space H. Let be a bifunction that satisfies (A1)-(A4) and be nonexpansive mappings such that . Let be a k-Lipschitzian mapping and η-strongly monotone, and let be a τ-Lipschitzian mapping. For a given , let the iterative sequences , and be generated by
where , . Suppose that the parameters satisfy , , where . Also, , , and are sequences satisfying conditions (b)-(e) of Algorithm 3.1. Then the sequence converges strongly to some element , which is also a unique solution of the variational inequality:
Putting , , , and , we obtain an extension and improvement of the method considered in [12].
Corollary 3.2 Let C be a nonempty closed convex subset of a real Hilbert space H. Let be a bifunction that satisfies (A1)-(A4) and be nonexpansive mappings such that . Let be a τ-Lipschitzian mapping. For a given , let the iterative sequences , , and be generated by
where , , are sequences in which satisfy conditions (b)-(e) of Algorithm 3.1. Then the sequence converges strongly to some element which is also a unique solution of the variational inequality:
4 Examples
To illustrate Algorithm 3.1 and the convergence result, we consider the following examples.
Example 4.1 Let , , and . Then we have ,
and
The sequences and satisfy conditions (a) and (b). Since
condition (c) is satisfied. We compute
It is easy to show . Similarly, we can show and . The sequences , , and satisfy condition (d). We have
and
Then the sequence satisfies condition (e).
Let the mappings be defined as
and let the mapping be defined by
It is easy to show that T and S are nonexpansive mappings, F is 1-Lipschitzian and -strongly monotone and U is -Lipschitzian. It is clear that
From the definition of , we have
Then
Let . Then is a quadratic function of y with coefficient , , . We determine the discriminant Δ of B as follows:
We have , . If it has at most one solution in ℝ, then , and we obtain
For every , from (4.1), we rewrite (3.1) as follows:
In all the tests we take , , and for Algorithm 3.1. In this example , , . It is easy to show that the parameters satisfy , , where .
The values of , , and with different n are reported in Tables 1 and 2. All codes were written in Matlab.
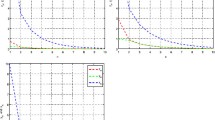
Remark 4.1 Table 1 and Figure 1 show that the sequences , , and converge to 0, where .
Example 4.2 In this example we take the same mappings and parameters as in Example 4.1 except T and .
Let be defined by
and be defined by
It is clear to see that
By the definition of , we have
Then
Let . Then is a quadratic function of y with coefficient , , . We determine the discriminant Δ of A as follows:
We have , . If it has at most one solution in ℝ, then , we obtain
For every , from (4.2), we rewrite (3.1) as follows:
Remark 4.2 Table 2 and Figure 2 show that the sequences , , and converge to 1, where .
5 Conclusions
In this paper, we suggested and analyzed an iterative method for finding an element of the common set of solutions of (1.1) and (1.4) in real Hilbert spaces. This method can be viewed as a refinement and improvement of some existing methods for solving variational inequality problem, equilibrium problem and a hierarchical fixed point problem. Some existing methods, for example, [12, 13, 15, 18, 19, 21], can be viewed as special cases of Algorithm 3.1. Therefore, Algorithm 3.1 is expected to be widely applicable. In the hierarchical fixed point problem (1.4), if , then we can get the variational inequality (3.13). In (3.13), if then we get the variational inequality , , which just is a variational inequality studied by Suzuki [23].
Misc
Equal contributors
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63: 123–145.
Combettes PL, Hirstoaga SA: Equilibrium programming using proximal like algorithms. Math. Program. 1997, 78: 29–41.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert space. J. Nonlinear Convex Anal. 2005, 6: 117–136.
Ceng LC, Yao JC: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. J. Comput. Appl. Math. 2008, 214: 186–201. 10.1016/j.cam.2007.02.022
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Anal. 2008, 69: 1025–1033. 10.1016/j.na.2008.02.042
Reich S, Sabach S: Three strong convergence theorems regarding iterative methods for solving equilibrium problems in reflexive Banach spaces. Contemp. Math. 568. Optimization Theory and Related Topics 2012, 225–240.
Kassay G, Reich S, Sabach S: Iterative methods for solving systems of variational inequalities in reflexive Banach spaces. SIAM J. Optim. 2011, 21: 1319–1344. 10.1137/110820002
Chang SS, Joseph Lee HW, Chan CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Anal. 2009, 70: 3307–3319. 10.1016/j.na.2008.04.035
Latif A, Ceng LC, Ansari QH: Multi-step hybrid viscosity method for systems of variational inequalities defined over sets of solutions of equilibrium problem and fixed point problems. Fixed Point Theory Appl. 2012., 2012: Article ID 186
Marino C, Muglia L, Yao Y: Viscosity methods for common solutions of equilibrium and variational inequality problems via multi-step iterative algorithms and common fixed points. Nonlinear Anal. 2012, 75: 1787–1798. 10.1016/j.na.2011.09.019
Suwannaut S, Kangtunyakarn A: The combination of the set of solutions of equilibrium problem for convergence theorem of the set of fixed points of strictly pseudo-contractive mappings and variational inequalities problem. Fixed Point Theory Appl. 2013., 2013: Article ID 291
Yao Y, Cho YJ, Liou YC: Iterative algorithms for hierarchical fixed points problems and variational inequalities. Math. Comput. Model. 2010, 52(9–10):1697–1705. 10.1016/j.mcm.2010.06.038
Mainge PE, Moudafi A: Strong convergence of an iterative method for hierarchical fixed-point problems. Pac. J. Optim. 2007, 3(3):529–538.
Moudafi A: Krasnoselski-Mann iteration for hierarchical fixed-point problems. Inverse Probl. 2007, 23(4):1635–1640. 10.1088/0266-5611/23/4/015
Cianciaruso F, Marino G, Muglia L, Yao Y: On a two-steps algorithm for hierarchical fixed point problems and variational inequalities. J. Inequal. Appl. 2009., 2009: Article ID 208692
Marino G, Xu HK: Explicit hierarchical fixed point approach to variational inequalities. J. Optim. Theory Appl. 2011, 149(1):61–78. 10.1007/s10957-010-9775-1
Crombez G: A hierarchical presentation of operators with fixed points on Hilbert spaces. Numer. Funct. Anal. Optim. 2006, 27: 259–277. 10.1080/01630560600569957
Ceng LC, Anasri QH, Yao JC: Some iterative methods for finding fixed points and for solving constrained convex minimization problems. Nonlinear Anal. 2011, 74: 5286–5302. 10.1016/j.na.2011.05.005
Bnouhachem A: A modified projection method for a common solution of a system of variational inequalities, a split equilibrium problem and a hierarchical fixed-point problem. Fixed Point Theory Appl. 2014., 2014: Article ID 22
Ceng LC, Anasri QH, Yao JC: Iterative methods for triple hierarchical variational inequalities in Hilbert spaces. J. Optim. Theory Appl. 2011, 151: 489–512. 10.1007/s10957-011-9882-7
Tian M: A general iterative algorithm for nonexpansive mappings in Hilbert spaces. Nonlinear Anal. 2010, 73: 689–694. 10.1016/j.na.2010.03.058
Geobel K, Kirk WA Stud. Adv. Math. 28. In Topics in Metric Fixed Point Theory. Cambridge University Press, Cambridge; 1990.
Suzuki N: Moudafi’s viscosity approximations with Meir-Keeler contractions. J. Math. Anal. Appl. 2007, 325: 342–352. 10.1016/j.jmaa.2006.01.080
Xu HK: Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 2002, 66: 240–256. 10.1112/S0024610702003332
Acedo GL, Xu HK: Iterative methods for strictly pseudo-contractions in Hilbert space. Nonlinear Anal. 2007, 67: 2258–2271. 10.1016/j.na.2006.08.036
Wang Y, Xu W: Strong convergence of a modified iterative algorithm for hierarchical fixed point problems and variational inequalities. Fixed Point Theory Appl. 2013., 2013: Article ID 121
Cianciaruso F, Marino G, Muglia L, Yao Y: A hybrid projection algorithm for finding solutions of mixed equilibrium problem and variational inequality problem. Fixed Point Theory Appl. 2010., 2010: Article ID 383740
Acknowledgements
In this research, the second and third author were financially supported by King Fahd University of Petroleum & Minerals (KFUPM), Dhahran, Saudi Arabia. It was partially done during the visit of third author to KFUPM, Dhahran, Saudi Arabia.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bnouhachem, A., Al-Homidan, S. & Ansari, Q.H. An iterative method for common solutions of equilibrium problems and hierarchical fixed point problems. Fixed Point Theory Appl 2014, 194 (2014). https://doi.org/10.1186/1687-1812-2014-194
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2014-194