An iterative algorithm for system of generalized equilibrium problems and fixed point problem

Abstract

In this paper, we propose an iterative algorithm for finding a common solution of a system of generalized equilibrium problems and a fixed point problem of strictly pseudo-contractive mapping in the setting of real Hilbert spaces. We prove the strong convergence of the sequence generated by the proposed method to a common solution of a system of generalized equilibrium problems and a hierarchical fixed point problem. Preliminary numerical experiments are included to verify the theoretical assertions of the proposed method. The iterative algorithm and results presented in this paper generalize, unify, and improve the previously known results of this area.

MSC:49J30, 47H09, 47J20.

1 Introduction

Let H be a real Hilbert space, whose inner product and norm are denoted by $〈\cdot ,\cdot 〉$ and $\parallel \cdot \parallel$. Let C be a nonempty closed convex subset of H. Recently, Ceng and Yao [1] considered the following system of generalized equilibrium problems, which involves finding $(x^{\ast },y^{\ast })\in C\times C$:

$$\{\begin{array}{l}{F}_1(x^{\ast },x)+〈B_1{y}^{\ast },x-x^{\ast }〉+\frac{1}{{\mu }_1}〈x^{\ast }-y^{\ast },x-x^{\ast }〉\ge 0;\mathrm{\forall }x\in C\text{ and }{\mu }_1>0,\\ F_2(y^{\ast },y)+〈B_2{x}^{\ast },y-y^{\ast }〉+\frac{1}{{\mu }_2}〈y^{\ast }-x^{\ast },y-y^{\ast }〉\ge 0;\mathrm{\forall }y\in C\text{ and }{\mu }_2>0,\end{array}$$

(1.1)

where $F_i:C\times C\to H$ is two bifunctions and $B_i:C\to H$ is a nonlinear mapping for each $i=1,2$. The solution set of (1.1) is denoted by Ω.

If $F_1=F_2=F$, $B_1=B_2=B$, and $x^{\ast }=y^{\ast }$, then problem (1.1) becomes the following generalized equilibrium problem: Finding $x\in C$ such that

$$F(x,y)+〈Bx,y-x〉\ge 0,\mathrm{\forall }y\in C,$$

(1.2)

which was studied by Takahashi and Takahashi [2]. Inspired by the work of Takahashi and Takahashi [2], and Ceng et al. [3], Ceng et al. [4] introduced and analyzed an iterative scheme for finding the approximate solutions of the generalized equilibrium problem (1.2), a system of general generalized equilibrium problems (1.1) and a fixed point problem of a nonexpansive mapping in a Hilbert space. Under appropriate conditions, they proved that the sequence converges strongly to a common solution of these three problems. Recently, Ansari [5] studied the existence of solutions of equilibrium problems in the setting of metric spaces. Inspired by the method in [6], Latif et al. [7] introduced and analyzed an iterative algorithm by the hybrid iterative method for finding a solution of the system of generalized equilibrium problems with constraints of several problems: a generalized mixed equilibrium problem, finitely many variational inclusions, and the common fixed point problem of an asymptotically strict pseudo-contractive mapping in the intermediate sense and infinitely many nonexpansive mappings in a real Hilbert space. Under mild conditions, they proved the weak convergence of this iterative algorithm.

If $F_1=F_2=0$, then problem (1.1) reduces to the following general system of variational inequalities, which involves finding $(x^{\ast },y^{\ast })\in C\times C$:

$$\{\begin{array}{l}〈{\mu }_1{B}_1{y}^{\ast }+x^{\ast }-y^{\ast },x-x^{\ast }〉\ge 0;\mathrm{\forall }x\in C\text{ and }{\mu }_1>0,\\ 〈{\mu }_2{B}_2{x}^{\ast }+y^{\ast }-x^{\ast },x-y^{\ast }〉\ge 0;\mathrm{\forall }x\in C\text{ and }{\mu }_2>0,\end{array}$$

(1.3)

this problem was considered and investigated by Ceng et al. [3]. As pointed out in [8] that the system of variational inequalities is used as a tool to study the Nash equilibrium problem; see, for example, [9–11] and the references therein.

If $F_1=F_2=0$, and $B_1=B_2=B$, then problem (1.1) reduces to finding $(x^{\ast },y^{\ast })\in C\times C$ such that

$$\{\begin{array}{l}〈{\mu }_{1}B{y}^{\ast }+x^{\ast }-y^{\ast },x-x^{\ast }〉\ge 0;\mathrm{\forall }x\in C\text{ and }{\mu }_1>0,\\ 〈{\mu }_{2}B{x}^{\ast }+y^{\ast }-x^{\ast },x-y^{\ast }〉\ge 0;\mathrm{\forall }x\in C\text{ and }{\mu }_2>0,\end{array}$$

(1.4)

which has been introduced and studied by Verma [12, 13].

If $x^{\ast }=y^{\ast }$ and ${\mu }_1={\mu }_2$, then problem (1.4) collapses to the classical variational inequality, finding $x^{\ast }\in C$ such that

$$〈B{x}^{\ast },x-x^{\ast }〉\ge 0,\mathrm{\forall }x\in C.$$

The theory of variational inequalities emerged as a rapidly growing area of research because of its applications in nonlinear analysis, optimization, economics, game theory; see for example [14–17]. For recent applications, numerical techniques, and physical formulation, see [1–50].

The fixed point problem for the mapping T is to find $x\in C$ such that

$$Tx=x.$$

(1.5)

We denote by $F(T)$ the set of solutions of (1.5). It is well known that $F(T)$ is closed and convex, and $P_F(T)$ is well defined (see [19]).

Let $S:C\to H$ be a nonexpansive mapping, that is, $\parallel Sx-Sy\parallel \le \parallel x-y\parallel$ for all $x,y\in C$. The hierarchical fixed point problem is to find $x\in F(T)$ such that

$$〈x-Sx,y-x〉\ge 0,\mathrm{\forall }y\in F(T).$$

(1.6)

It is linked with some monotone variational inequalities and convex programming problems; see [20]. Various methods have been proposed to solve (1.6); see, for example, [21–35]. By combining Korpelevich’s extragradient method and the viscosity approximation method, Ceng et al. [36] introduced and analyzed implicit and explicit iterative schemes for computing a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality for an α-inverse strongly monotone mapping in a Hilbert space. Under suitable assumptions, they proved the strong convergence of the sequences generated by the proposed schemes. In 2010, Yao et al. [20] introduced the following strong convergence iterative algorithm to solve problem (1.6):

$$\begin{array}{r}{y}_n={\beta }_{n}S{x}_n+(1-{\beta }_n)x_n,\\ x_{n+1}=P_C[{\alpha }_{n}f(x_n)+(1-{\alpha }_n)T{y}_n],\mathrm{\forall }n\ge 0,\end{array}$$

(1.7)

where $f:C\to H$ is a contraction mapping and $\{{\alpha }_n\}$ and $\{{\beta }_n\}$ are two sequences in $(0,1)$. Under some certain restrictions on parameters, Yao et al. proved that the sequence $\{x_n\}$ generated by (1.7) converges strongly to $z\in F(T)$, which is the unique solution of the following variational inequality:

$$〈(I-f)z,y-z〉\ge 0,\mathrm{\forall }y\in F(T).$$

(1.8)

In 2011, Ceng et al. [37] investigated the following iterative method:

$$x_{n+1}=P_C[{\alpha }_n\rho U(x_n)+(I-{\alpha }_n\mu F)(T(y_n))],\mathrm{\forall }n\ge 0,$$

(1.9)

where U is a Lipschitzian mapping, and F is a Lipschitzian and strongly monotone mapping. They proved that under some approximate assumptions on the operators and parameters, the sequence $\{x_n\}$ generated by (1.9) converges strongly to the unique solution of the variational inequality

$$〈\rho U(z)-\mu F(z),x-z〉\ge 0,\mathrm{\forall }x\in Fix(T).$$

(1.10)

Very recently, Wang and Xu [38] investigated an iterative method for a hierarchical fixed point problem by

$$\begin{array}{r}{y}_n={\beta }_{n}S{x}_n+(1-{\beta }_n)x_n,\\ x_{n+1}=P_C[{\alpha }_n\rho U(x_n)+(I-{\alpha }_n\mu F)(T(y_n))],\mathrm{\forall }n\ge 0,\end{array}$$

(1.11)

where $S:C\to C$ is a nonexpansive mapping. They proved that under some approximate assumptions on the operators and parameters, the sequence $\{x_n\}$ generated by (1.11) converges strongly to the unique solution of the variational inequality (1.10). In 2014, Ansari et al. [39] presented a hybrid iterative algorithm for computing a fixed point of a pseudo-contractive mapping and for finding a solution of triple hierarchical variational inequality in the setting of real Hilbert space. Under very appropriate conditions, they proved that the sequence generated by the proposed algorithm converges strongly to a fixed point which is also a solution of this triple hierarchical variational inequality.

In this paper, motivated by the work of Ceng et al. [4], Yao et al. [20], Bnouhachem [33, 34] and by the recent work going in this direction, we give an iterative method for finding the approximate element of the common set of solutions of (1.1) and (1.6) in real Hilbert space. We establish a strong convergence theorem based on this method. In order to verify the theoretical assertions and to compare the numerical results between the system of generalized equilibrium problems and the generalized equilibrium problems, an example is given. Our results can be viewed as significant extensions of the previously known results.

2 Preliminaries

We present some definitions which will be used in the sequel.

Definition 2.1 A mapping $T:C\to H$ is said to be k-Lipschitz continuous if there exists a constant $k>0$ such that

$$\parallel Tx-Ty\parallel \le k\parallel x-y\parallel ,\mathrm{\forall }x,y\in C.$$

• If $k=1$, then T is called nonexpansive.

• If $k\in (0,1)$, then T is called a contraction.

Definition 2.2 A mapping $T:C\to H$ is said to be

• (a) strongly monotone if there exists an $\alpha >0$ such that

  $$〈Tx-Ty,x-y〉\ge \alpha {\parallel x-y\parallel }^2,\mathrm{\forall }x,y\in C;$$

• (b) α-inverse strongly monotone if there exists an $\alpha >0$ such that

  $$〈Tx-Ty,x-y〉\ge \alpha {\parallel Tx-Ty\parallel }^2,\mathrm{\forall }x,y\in C;$$

• (c) a k-strict pseudo-contraction, if there exists a constant $0\le k<1$ such that

  $${\parallel Tx-Ty\parallel }^2\le {\parallel x-y\parallel }^2+k{\parallel (I-T)x-(I-T)y\parallel }^2,\mathrm{\forall }x,y\in C.$$

Assumption 2.1 [42]

Let $F:C\times C\to \mathbb{R}$ be a bifunction satisfying the following assumptions:

(A₁) $F(x,x)=0$, $\mathrm{\forall }x\in C$;

(A₂) F is monotone, i.e., $F(x,y)+F(y,x)\le 0$, $\mathrm{\forall }x,y\in C$;

(A₃) for each $x,y,z\in C$, ${lim}_{t\to 0}F(tz+(1-t)x,y)\le F(x,y)$;

(A₄) for each $x\in C$, $y\to F(x,y)$ is convex and lower semicontinuous.

We list some fundamental lemmas that are useful in the consequent analysis.

Lemma 2.1 [43]

Let C be a nonempty closed convex subset of H. Let $F:C\times C\to \mathbb{R}$ satisfies (A₁)-(A₄). Assume that for $r>0$ and $\mathrm{\forall }x\in H$, define a mapping $T_r:H\to C$ as follows:

$$T_r(x)=\{z\in C:F(z,y)+\frac{1}{r}〈y-z,z-x〉\ge 0,\mathrm{\forall }y\in C\}.$$

Then the following hold:

• (i) $T_r$ is nonempty and single-valued;

• (ii) $T_r$ is firmly nonexpansive, i.e.,

  $${\parallel T_r(x)-T_r(y)\parallel }^2\le 〈T_r(x)-T_r(y),x-y〉,\mathrm{\forall }x,y\in H;$$

• (iii) $F(T_r)=EP(F)$;

• (iv) $EP(F)$ is closed and convex.

Lemma 2.2 [4]

Let $F_1,F_2:C\times C\to \mathbb{R}$ be two bifunctions satisfying (A₁)-(A₄). For any $(x^{\ast },y^{\ast })\in C\times C,(x^{\ast },y^{\ast })$ is a solution of (1.1) if and only if $x^{\ast }$ is a fixed point of the mapping $Q:C\to C$ defined by

$$Q(x)=T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]],\mathrm{\forall }x\in C,$$

(2.1)

where $y^{\ast }=T_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]$, ${\mu }_i\in (0,2{\theta }_i)$, and $B_i:C\to C$ is a ${\theta }_i$-inverse strongly monotone mapping for each $i=1,2$.

Lemma 2.3 [44]

Let C be a nonempty closed convex subset of a real Hilbert space H.

If $T:C\to C$ is a nonexpansive mapping with $Fix(T)\ne \mathrm{\varnothing }$, then the mapping $I-T$ is demiclosed at 0, i.e., if $\{x_n\}$ is a sequence in C that weakly converges to x, and if $\{(I-T)x_n\}$ converges strongly to 0, then $(I-T)x=0$.

Lemma 2.4 [37]

Let $U:C\to H$ be a τ-Lipschitzian mapping, and let $F:C\to H$ be a k-Lipschitzian and η-strongly monotone mapping, then for $0\le \rho \tau <\mu \eta$, $\mu F-\rho U$ is μη-ρτ-strongly monotone, i.e.,

$$〈(\mu F-\rho U)x-(\mu F-\rho U)y,x-y〉\ge (\mu \eta -\rho \tau ){\parallel x-y\parallel }^2,\mathrm{\forall }x,y\in C.$$

Lemma 2.5 [45]

Let C be a nonempty closed convex subset of a real Hilbert space H, and $S:C\to H$ be a k-strict pseudo-contraction mapping. Define $B:C\to H$ by $Bx=\lambda Sx+(1-\lambda )x$ for all $x\in C$. Then as $\lambda \in [k,1)$, B is a nonexpansive mapping such that $F(B)=F(S)$.

Lemma 2.6 [46]

Let H be a real Hilbert space, $T:C\to H$ be a k-Lipschitzian and η-strongly monotone operator. Let $0<\mu <\frac{2\eta }{k^2}$, let $W=I-\lambda \mu T$ and $\mu (\eta -\frac{\mu k^2}{2})=\tau$, then for $0<\lambda <min\{1,\frac{1}{\tau }\}$, W is a contraction with a constant $1-\lambda \tau$, that is,

$$\parallel Wx-Wy\parallel \le (1-\lambda \tau )\parallel x-y\parallel ,\mathrm{\forall }x,y\in C.$$

Lemma 2.7 [47]

Let $\{x_n\}$, $\{y_n\}$ be bounded sequences in a Banach space E and $\{{\beta }_n\}$ be a sequence in $[0,1]$ with $0<{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\beta }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\beta }_n<1$.

Suppose $x_{n+1}={\beta }_n{x}_n+(1-{\beta }_n)y_n$, $\mathrm{\forall }n\ge 0$ and ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}(\parallel y_{n+1}-y_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0$. Then ${lim}_{n\to \mathrm{\infty }}\parallel y_n-x_n\parallel =0$.

Lemma 2.8 [48]

Assume $\{a_n\}$ is a sequence of nonnegative real numbers such that

$$a_{n+1}\le (1-{\upsilon }_n)a_n+{\delta }_n,$$

where $\{{\upsilon }_n\}$ is a sequence in $(0,1)$ and ${\delta }_n$ is a sequence such that

• (1) ${\sum }_{n=1}^{\mathrm{\infty }}{\upsilon }_n=\mathrm{\infty }$;

• (2) ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\delta }_n/{\upsilon }_n\le 0$ or ${\sum }_{n=1}^{\mathrm{\infty }}|{\delta }_n|<\mathrm{\infty }$.

Then ${lim}_{n\to \mathrm{\infty }}{a}_n=0$.

Lemma 2.9 [49]

Let C be a closed convex subset of H. Let $\{x_n\}$ be a bounded sequence in H. Assume that

• (i) the weak w-limit set $w_w(x_n)\subset C$ where $w_w(x_n)=\{x:x_{n_i}\rightharpoonup x\}$;

• (ii) for each $z\in C$, ${lim}_{n\to \mathrm{\infty }}\parallel x_n-z\parallel$ exists.

Then $\{x_n\}$ is weakly convergent to a point in C.

Lemma 2.10 [50]

Let H be a real Hilbert space. Then the following inequality holds:

$${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2〈y,x+y〉,\mathrm{\forall }x,y\in H.$$

3 The proposed method and some properties

In this section, we suggest and analyze our method for finding the common solutions of the system of the generalized equilibrium problem (1.1) and the hierarchical fixed point problem (1.6). Let C be a nonempty closed convex subset of a real Hilbert space H. Let $F_1,F_2:C\times C\to \mathbb{R}$ be two bifunctions satisfying (A₁)-(A₄). Let $B_i:C\to H$ be a ${\theta }_i$-inverse strongly monotone mapping for each $i=1,2$, and let $S:C\to H$ be a σ-strict pseudo-contraction mapping such that $\mathrm{\Omega }\cap F(S)\ne \mathrm{\varnothing }$. Let $T:C\to C$ be a k-Lipschitzian mapping and be η-strongly monotone, and let $f:C\to C$ be a τ-Lipschitzian mapping.

Algorithm 3.1 For an arbitrarily given $x_0\in C$, let the iterative sequences $\{x_n\}$, $\{y_n\}$, and $\{z_n\}$ be generated by

$$\{\begin{array}{l}{z}_n=T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]];\\ y_n={\beta }_{n}S{z}_n+(1-{\beta }_n)z_n;\\ x_{n+1}={\alpha }_n\rho f(x_n)+{\gamma }_n{x}_n+((1-{\gamma }_n)I-{\alpha }_n\mu T)(y_n),\mathrm{\forall }n\ge 0,\end{array}$$

(3.1)

where ${\mu }_i\in (0,2{\theta }_i)$ for each $i=1,2$. Suppose the parameters satisfy $0<\mu <\frac{2\eta }{k^2}$, $0\le \rho <\nu /\tau$, where $\nu =\mu (\eta -\frac{\mu k^2}{2})$. Also $\{{\gamma }_n\}$, $\{{\alpha }_n\}$, and $\{{\beta }_n\}$ are sequences in $(0,1)$ satisfying the following conditions:

• (a) $0<{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\gamma }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\gamma }_n<1$;

• (b) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and ${\sum }_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

• (c) $\{{\beta }_n\}\subset [\sigma ,1)$ and ${lim}_{n\to \mathrm{\infty }}{\beta }_n=\beta <1$.

If $F_1=F_2=F$, $B_1=B_2=B$, and ${\mu }_1={\mu }_2=r$, then Algorithm 3.1 reduces to Algorithm 3.2 for finding the common solutions of the generalized equilibrium problem (1.2) and the hierarchical fixed point problem (1.6).

Algorithm 3.2 For an arbitrarily given $x_0\in C$ arbitrarily, let the iterative sequences $\{u_n\}$, $\{x_n\}$, $\{y_n\}$, and $\{z_n\}$ be generated by

$$\{\begin{array}{l}F(z_n,y)+〈B{x}_n,y-z_n〉+\frac{1}{r}〈y-z_n,z_n-x_n〉\ge 0,\mathrm{\forall }y\in C;\\ y_n={\beta }_{n}S{z}_n+(1-{\beta }_n)z_n;\\ x_{n+1}={\alpha }_n\rho f(x_n)+{\gamma }_n{x}_n+((1-{\gamma }_n)I-{\alpha }_n\mu T)(y_n),\mathrm{\forall }n\ge 0.\end{array}$$

Suppose that the parameters satisfy $0<\mu <\frac{2\eta }{k^2}$, $0\le \rho \tau <\nu$, where $\nu =1-\sqrt{1-\mu (2\eta -\mu k^2)}$. Also $\{{\gamma }_n\}$, $\{{\alpha }_n\}$, and $\{{\beta }_n\}$ are sequences in $(0,1)$ satisfying the following conditions:

• (a) $0<{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\gamma }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\gamma }_n<1$;

• (b) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and ${\sum }_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

• (c) $\{{\beta }_n\}\subset [\sigma ,1)$ and ${lim}_{n\to \mathrm{\infty }}{\beta }_n=\beta <1$.

Remark 3.1 If $\rho =\mu =1$, ${\gamma }_n=0$, and $S{z}_n=S{x}_n$, we obtain an extension and improvement of the method of Yao et al. [20] and Wang and Xu [38] for finding the approximate element of the common set of solutions of a system of generalized equilibrium problem and a hierarchical fixed point problem in a real Hilbert space.

Lemma 3.1 Let $x^{\ast }\in \mathrm{\Omega }\cap F(S)$. Then $\{x_n\}$, $\{z_n\}$, and $\{y_n\}$ are bounded.

Proof Let $x^{\ast }\in \mathrm{\Omega }\cap F(S)$, we have

$$x^{\ast }=T_{{\mu }_1}^{F_1}[y^{\ast }-{\mu }_1{B}_1{y}^{\ast }],$$

where

$$y^{\ast }=T_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }].$$

We set $v_n=T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]$. Since $B_2$ is a ${\theta }_2$-inverse strongly monotone mapping, it follows that

$$\begin{array}{rcl}{\parallel v_n-y^{\ast }\parallel }^2& =& {\parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-T_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]\parallel }^2\\ \le & {\parallel x_n-x^{\ast }-{\mu }_2(B_2{x}_n-B_2{x}^{\ast })\parallel }^2\\ \le & {\parallel x_n-x^{\ast }\parallel }^2-{\mu }_2(2{\theta }_2-{\mu }_2){\parallel B_2{x}_n-B_2{x}^{\ast }\parallel }^2\\ \le & {\parallel x_n-x^{\ast }\parallel }^2.\end{array}$$

(3.2)

Since $B_i$ is a ${\theta }_i$-inverse strongly monotone mapping for each $i=1,2$, we get

$$\begin{array}{rcl}{\parallel z_n-x^{\ast }\parallel }^2& =& \parallel T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]]\\ {-T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]]\parallel }^2\\ \le & \parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]\\ {-(T_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }])\parallel }^2\\ =& \parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-T_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]\\ {-{\mu }_1(B_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-B_1{T}_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }])\parallel }^2\\ \le & {\parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-T_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]\parallel }^2\\ -{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-B_1{T}_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]\parallel }^2\\ \le & {\parallel (x_n-{\mu }_2{B}_2{x}_n)-(x^{\ast }-{\mu }_2{B}_2{x}^{\ast })\parallel }^2\\ -{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-B_1{T}_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]\parallel }^2\\ \le & {\parallel x_n-x^{\ast }\parallel }^2-{\mu }_2(2{\theta }_2-{\mu }_2){\parallel B_2{x}_n-B_2{x}^{\ast }\parallel }^2\\ -{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{v}_n-B_1{y}^{\ast }\parallel }^2\\ \le & {\parallel x_n-x^{\ast }\parallel }^2.\end{array}$$

(3.3)

By Lemma 2.5 and the inequality above, it is easy to show that

$$\parallel y_n-x^{\ast }\parallel \le \parallel z_n-x^{\ast }\parallel \le \parallel x_n-x^{\ast }\parallel .$$

(3.4)

Next, we prove that the sequence $\{x_n\}$ is bounded. Since ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, without loss of generality we can assume that ${\alpha }_n\le min\{ϵ,\frac{ϵ}{\tau }\}$ for all $n\ge 1$, where $0<ϵ<1-{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\gamma }_n$. From (3.1) and (3.4), we have

$$\begin{array}{rcl}\parallel x_{n+1}-x^{\ast }\parallel & \le & \parallel {\alpha }_n\rho f(x_n)+{\gamma }_n{x}_n+((1-{\gamma }_n)I-{\alpha }_n\mu T)(y_n)-x^{\ast }\parallel \\ =& \parallel {\alpha }_n(\rho f(x_n)-\mu T\left(x^{\ast }\right))+{\gamma }_n(x_n-x^{\ast })+((1-{\gamma }_n)I-{\alpha }_n\mu T)(y_n)\\ -((1-{\gamma }_n)I-{\alpha }_n\mu T)\left(x^{\ast }\right)\parallel \\ \le & {\alpha }_n\rho \tau \parallel x_n-x^{\ast }\parallel +{\alpha }_n\parallel (\rho f-\mu T)x^{\ast }\parallel +{\gamma }_n\parallel x_n-x^{\ast }\parallel \\ +\parallel ((1-{\gamma }_n)I-{\alpha }_n\mu T)(y_n)-((1-{\gamma }_n)I-{\alpha }_n\mu T)\left(x^{\ast }\right)\parallel \\ =& {\alpha }_n\rho \tau \parallel x_n-x^{\ast }\parallel +{\alpha }_n\parallel (\rho f-\mu T)x^{\ast }\parallel +{\gamma }_n\parallel x_n-x^{\ast }\parallel \\ +(1-{\gamma }_n)\parallel (I-\frac{{\alpha }_n\mu }{(1-{\gamma }_n)}T)(y_n)-(I-\frac{{\alpha }_n\mu }{(1-{\gamma }_n)}T)\left(x^{\ast }\right)\parallel \\ \le & {\alpha }_n\rho \tau \parallel x_n-x^{\ast }\parallel +{\alpha }_n\parallel (\rho f-\mu T)x^{\ast }\parallel +{\gamma }_n\parallel x_n-x^{\ast }\parallel \\ +(1-{\gamma }_n-{\alpha }_n\nu )\parallel y_n-x^{\ast }\parallel \\ \le & {\alpha }_n\rho \tau \parallel x_n-x^{\ast }\parallel +{\alpha }_n\parallel (\rho f-\mu T)x^{\ast }\parallel +{\gamma }_n\parallel x_n-x^{\ast }\parallel \\ +(1-{\gamma }_n-{\alpha }_n\nu )\parallel x_n-x^{\ast }\parallel \\ =& {\alpha }_n\rho \tau \parallel x_n-x^{\ast }\parallel +{\alpha }_n\parallel (\rho f-\mu T)x^{\ast }\parallel +(1-{\alpha }_n\nu )\parallel x_n-x^{\ast }\parallel \\ =& (1-{\alpha }_n(\nu -\rho \tau ))\parallel x_n-x^{\ast }\parallel +{\alpha }_n\parallel (\rho f-\mu T)x^{\ast }\parallel \\ \le & max\{\parallel x_n-x^{\ast }\parallel ,\frac{1}{\nu -\rho \tau }\left(\parallel (\rho f-\mu T)x^{\ast }\parallel \right)\},\end{array}$$

where the third inequality follows from Lemma 2.6 and the fourth inequality follows from (3.4). By induction on n, we obtain $\parallel x_n-x^{\ast }\parallel \le max\{\parallel x_n-x^{\ast }\parallel ,\frac{1}{\nu -\rho \tau }(\parallel (\rho f-\mu T)x^{\ast }\parallel )\}$, for $n\ge 0$ and $x_0\in C$. Hence $\{x_n\}$ is bounded, and consequently we deduce that $\{z_n\}$, $\{v_n\}$, $\{y_n\}$, $\{S(z_n)\}$, $\{T(y_n)\}$, and $\{f(x_n)\}$ are bounded. □

Lemma 3.2 Let $x^{\ast }\in \mathrm{\Omega }\cap F(S)$ and $\{x_n\}$ be the sequence generated by Algorithm 3.1. Then we have:

• (a) ${lim}_{n\to \mathrm{\infty }}\parallel x_{n+1}-x_n\parallel =0$.

• (b) The weak w-limit set $w_w(x_n)\subset F(S)$ ($w_w(x_n)=\{x:x_{n_i}\rightharpoonup x\}$).

Proof Next, we estimate

$$\begin{array}{rcl}{\parallel z_n-z_{n-1}\parallel }^2& =& \parallel T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]]\\ {-T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}]]\parallel }^2\\ \le & \parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]\\ {-(T_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}])\parallel }^2\\ =& \parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-T_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}]\\ {-{\mu }_1(B_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-B_1{T}_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}])\parallel }^2\\ \le & {\parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-T_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}]\parallel }^2\\ -{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-B_1{T}_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}]\parallel }^2\\ \le & {\parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-T_{{\mu }_2}^{F_2}[x_{n-1}-{\mu }_2{B}_2{x}_{n-1}]\parallel }^2\\ \le & {\parallel (x_n-x_{n-1})-{\mu }_2(B_2{x}_n-B_2{x}_{n-1})\parallel }^2\\ \le & {\parallel x_n-x_{n-1}\parallel }^2-{\mu }_2(2{\theta }_2-{\mu }_2){\parallel B_2{x}_n-B_2{x}_{n-1}\parallel }^2\\ \le & {\parallel x_n-x_{n-1}\parallel }^2.\end{array}$$

(3.5)

From (3.1) and (3.5), we have

$$\begin{array}{rcl}\parallel y_n-y_{n-1}\parallel & \le & \parallel {\beta }_{n}S{z}_n+(1-{\beta }_n)z_n-({\beta }_{n-1}S{z}_{n-1}+(1-{\beta }_{n-1})z_{n-1})\parallel \\ =& \parallel {\beta }_n(S{z}_n-S{z}_{n-1})+({\beta }_n-{\beta }_{n-1})S{z}_{n-1}\\ +(1-{\beta }_n)(z_n-z_{n-1})+({\beta }_{n-1}-{\beta }_n)z_{n-1}\parallel \\ \le & \parallel z_n-z_{n-1}\parallel +|{\beta }_n-{\beta }_{n-1}|\parallel S{z}_{n-1}-z_{n-1}\parallel \\ \le & \parallel x_{n-1}-x_n\parallel +|{\beta }_n-{\beta }_{n-1}|\parallel S{z}_{n-1}-z_{n-1}\parallel .\end{array}$$

(3.6)

We define $w_n=\frac{x_{n+1}-{\gamma }_n{x}_n}{1-{\gamma }_n}$, which implies that $x_{n+1}=(1-{\gamma }_n)w_n+{\gamma }_n{x}_n$. It follows from (3.6) that

$$\begin{array}{rcl}\parallel w_{n+1}-w_n\parallel & \le & \frac{{\alpha }_{n+1}}{1-{\gamma }_{n+1}}\parallel \rho f(x_{n+1})-\mu T(y_{n+1})\parallel \\ +\frac{{\alpha }_n}{1-{\gamma }_n}\parallel \rho f(x_n)-\mu T(y_n)\parallel +\parallel y_{n+1}-y_n\parallel \\ \le & \frac{{\alpha }_{n+1}}{1-{\gamma }_{n+1}}\parallel \rho f(x_{n+1})-\mu T(y_{n+1})\parallel \\ +\frac{{\alpha }_n}{1-{\gamma }_n}\parallel \rho f(x_n)-\mu T(y_n)\parallel +\parallel x_{n+1}-x_n\parallel \\ +|{\beta }_{n+1}-{\beta }_n|\parallel S{z}_n-z_n\parallel .\end{array}$$

(3.7)

Since ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${lim}_{n\to \mathrm{\infty }}{\beta }_n=\beta$, and ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\gamma }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\gamma }_n<1$, we get

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}(\parallel w_{n+1}-w_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0.$$

By Lemma 2.7, we have ${lim}_{n\to \mathrm{\infty }}\parallel w_n-x_n\parallel =0$. Since $\parallel x_{n+1}-x_n\parallel =(1-{\gamma }_n)\parallel w_n-x_n\parallel$, we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-x_n\parallel =0.$$

Next, we estimate

$$\begin{array}{rcl}\parallel x_n-y_n\parallel & \le & \parallel x_{n+1}-x_n\parallel +\parallel x_{n+1}-y_n\parallel \\ \le & \parallel x_{n+1}-x_n\parallel +\parallel x_{n+1}-y_n\parallel \\ \le & \parallel x_{n+1}-x_n\parallel +{\alpha }_n\parallel \rho f(x_n)-\mu T(y_n)\parallel +{\gamma }_n\parallel x_n-y_n\parallel ,\end{array}$$

which implies

$$(1-{\gamma }_n)\parallel x_n-y_n\parallel \le \parallel x_{n+1}-x_n\parallel +{\alpha }_n\parallel \rho f(x_n)-\mu T(y_n)\parallel .$$

Since ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\gamma }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\gamma }_n<1$, we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-y_n\parallel =0.$$

(3.8)

Next, we show that ${lim}_{n\to \mathrm{\infty }}\parallel z_n-x_n\parallel =0$. Since $x^{\ast }\in \mathrm{\Omega }\cap F(S)$ by using Lemma 2.10, (3.4), and (3.3), we obtain

$$\begin{array}{rcl}{\parallel x_{n+1}-x^{\ast }\parallel }^2& =& {\parallel {\gamma }_n(x_n-x^{\ast })+(1-{\gamma }_n)(y_n-x^{\ast })+{\alpha }_n(\rho f(x_n)-\mu T(y_n))\parallel }^2\\ \le & {\parallel {\gamma }_n(x_n-x^{\ast })+(1-{\gamma }_n)(y_n-x^{\ast })\parallel }^2+2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}-x^{\ast }〉\\ \le & {\gamma }_n{\parallel x_n-x^{\ast }\parallel }^2+(1-{\gamma }_n){\parallel y_n-x^{\ast }\parallel }^2+2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}-x^{\ast }〉\\ \le & {\gamma }_n{\parallel x_n-x^{\ast }\parallel }^2+(1-{\gamma }_n){\parallel z_n-x^{\ast }\parallel }^2+2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}-x^{\ast }〉\\ \le & {\gamma }_n{\parallel x_n-x^{\ast }\parallel }^2+(1-{\gamma }_n)\{{\parallel x_n-x^{\ast }\parallel }^2-{\mu }_2(2{\theta }_2-{\mu }_2){\parallel B_2{x}_n-B_2{x}^{\ast }\parallel }^2\\ -{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{v}_n-B_1{y}^{\ast }\parallel }^2\}+2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}-x^{\ast }〉\\ =& {\parallel x_n-x^{\ast }\parallel }^2-(1-{\gamma }_n)\{{\mu }_2(2{\theta }_2-{\mu }_2){\parallel B_2{x}_n-B_2{x}^{\ast }\parallel }^2\\ +{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{v}_n-B_1{y}^{\ast }\parallel }^2\}\\ +2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}-x^{\ast }〉,\end{array}$$

(3.9)

which implies that

$$\begin{array}{c}(1-{\gamma }_n)\{{\mu }_2(2{\theta }_2-{\mu }_2){\parallel B_2{x}_n-B_2{x}^{\ast }\parallel }^2+{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{v}_n-B_1{y}^{\ast }\parallel }^2\}\hfill \\ \le {\parallel x_n-x^{\ast }\parallel }^2-{\parallel x_{n+1}-x^{\ast }\parallel }^2+2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}-x^{\ast }〉\hfill \\ \le (\parallel x_n-x^{\ast }\parallel +\parallel x_{n+1}-x^{\ast }\parallel )\parallel x_{n+1}-x_n\parallel +2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}-x^{\ast }〉.\hfill \end{array}$$

Since ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\gamma }_n<1$, $2{\theta }_1-{\mu }_1>0$, $2{\theta }_2-{\mu }_2>0$, ${lim}_{n\to \mathrm{\infty }}\parallel x_{n+1}-x_n\parallel =0$ and ${\alpha }_n\to 0$, we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel B_2{x}_n-B_2{x}^{\ast }\parallel =0$$

and

$$\underset{n\to \mathrm{\infty }}{lim}\parallel B_1{v}_n-B_1{y}^{\ast }\parallel =0.$$

Since $T_{{\mu }_2}^{F_2}$ is firmly nonexpansive, we have

$$\begin{array}{rcl}{\parallel v_n-y^{\ast }\parallel }^2& =& {\parallel T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-T_{{\mu }_2}^{F_2}[x^{\ast }-{\mu }_2{B}_2{x}^{\ast }]\parallel }^2\\ \le & 〈v_n-y^{\ast },(x_n-{\mu }_2{B}_2{x}_n)-(x^{\ast }-{\mu }_2{B}_2{x}^{\ast })〉\\ =& \frac{1}{2}\{{\parallel v_n-y^{\ast }\parallel }^2+{\parallel x_n-x^{\ast }-{\mu }_2(B_2{x}_n-B_2{x}^{\ast })\parallel }^2\\ -{\parallel x_n-x^{\ast }-{\mu }_2(B_2{x}_n-B_2{x}^{\ast })-(v_n-y^{\ast })\parallel }^2\}\\ \le & \frac{1}{2}\{{\parallel v_n-y^{\ast }\parallel }^2+{\parallel x_n-x^{\ast }\parallel }^2-{\mu }_2(2{\theta }_2-{\mu }_2){\parallel B_2{x}_n-B_2{x}^{\ast }\parallel }^2\\ -{\parallel x_n-x^{\ast }-{\mu }_2(B_2{x}_n-B_2{x}^{\ast })-(v_n-y^{\ast })\parallel }^2\}\\ \le & \frac{1}{2}\{{\parallel v_n-y^{\ast }\parallel }^2+{\parallel x_n-x^{\ast }\parallel }^2\\ -{\parallel x_n-v_n-{\mu }_2(B_2{x}_n-B_2{x}^{\ast })-(x^{\ast }-y^{\ast })\parallel }^2\}\\ =& \frac{1}{2}\{{\parallel v_n-y^{\ast }\parallel }^2+{\parallel x_n-x^{\ast }\parallel }^2-{\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_2〈x_n-v_n-(x^{\ast }-y^{\ast }),B_2{x}_n-B_2{x}^{\ast }〉-{\mu }_2^2{\parallel B_2{x}_n-B_2{x}^{\ast }\parallel }^2\}\\ \le & \frac{1}{2}\{{\parallel v_n-y^{\ast }\parallel }^2+{\parallel x_n-x^{\ast }\parallel }^2-{\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_2\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel \parallel B_2{x}_n-B_2{x}^{\ast }\parallel \}.\end{array}$$

Hence, we get

$$\begin{array}{rcl}{\parallel v_n-y^{\ast }\parallel }^2& \le & {\parallel x_n-x^{\ast }\parallel }^2-{\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_2\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel \parallel B_2{x}_n-B_2{x}^{\ast }\parallel .\end{array}$$

(3.10)

On the other hand, from (3.1) and Lemma 2.1(ii), we obtain

$$\begin{array}{rcl}{\parallel z_n-x^{\ast }\parallel }^2& =& {\parallel T_{{\mu }_1}^{F_1}[v_n-{\mu }_1{B}_1{v}_n]-T_{{\mu }_1}^{F_1}[y^{\ast }-{\mu }_1{B}_1{y}^{\ast }]\parallel }^2\\ \le & 〈z_n-x^{\ast },(v_n-{\mu }_1{B}_1{v}_n)-(y^{\ast }-{\mu }_1{B}_1{y}^{\ast })〉\\ =& \frac{1}{2}\{{\parallel z_n-x^{\ast }\parallel }^2+{\parallel v_n-y^{\ast }-{\mu }_1(B_1{v}_n-B_1{y}^{\ast })\parallel }^2\\ -{\parallel v_n-y^{\ast }-{\mu }_1(B_1{v}_n-B_1{y}^{\ast })-(z_n-x^{\ast })\parallel }^2\}\\ =& \frac{1}{2}\{{\parallel z_n-x^{\ast }\parallel }^2+{\parallel v_n-y^{\ast }\parallel }^2-2{\mu }_1〈v_n-y^{\ast },B_1{v}_n-B_1{y}^{\ast }〉\\ +{\mu }_1^2{\parallel B_1{v}_n-B_1{y}^{\ast }\parallel }^2-{\parallel v_n-y^{\ast }-{\mu }_1(B_1{v}_n-B_1{y}^{\ast })-(z_n-x^{\ast })\parallel }^2\}\\ \le & \frac{1}{2}\{{\parallel z_n-x^{\ast }\parallel }^2+{\parallel v_n-y^{\ast }\parallel }^2-{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{v}_n-B_1{y}^{\ast }\parallel }^2\\ -{\parallel v_n-y^{\ast }-{\mu }_1(B_1{v}_n-B_1{y}^{\ast })-(z_n-x^{\ast })\parallel }^2\}\\ \le & \frac{1}{2}\{{\parallel z_n-x^{\ast }\parallel }^2+{\parallel v_n-y^{\ast }\parallel }^2\\ -{\parallel v_n-z_n-{\mu }_1(B_1{v}_n-B_1{y}^{\ast })+(x^{\ast }-y^{\ast })\parallel }^2\}\\ \le & \frac{1}{2}\{{\parallel z_n-x^{\ast }\parallel }^2+{\parallel v_n-y^{\ast }\parallel }^2-{\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_1〈v_n-z_n+(x^{\ast }-y^{\ast }),B_1{v}_n-B_1{y}^{\ast }〉\}\\ \le & \frac{1}{2}\{{\parallel z_n-x^{\ast }\parallel }^2+{\parallel v_n-y^{\ast }\parallel }^2-{\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_1\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel \parallel B_1{v}_n-B_1{y}^{\ast }\parallel \},\end{array}$$

which implies that

$$\begin{array}{rcl}{\parallel z_n-x^{\ast }\parallel }^2& \le & {\parallel v_n-y^{\ast }\parallel }^2-{\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_1\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel \parallel B_1{v}_n-B_1{y}^{\ast }\parallel \\ \le & {\parallel x_n-x^{\ast }\parallel }^2-{\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_2\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel \parallel B_2{x}_n-B_2{x}^{\ast }\parallel \\ -{\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel }^2+2{\mu }_1\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel \parallel B_1{v}_n-B_1{y}^{\ast }\parallel ,\end{array}$$

where the last inequality follows from (3.10). From (3.9) and the above inequality, we have

$$\begin{array}{rcl}{\parallel x_{n+1}-x^{\ast }\parallel }^2& \le & {\gamma }_n{\parallel x_n-x^{\ast }\parallel }^2+(1-{\gamma }_n){\parallel z_n-x^{\ast }\parallel }^2+2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}〉\\ \le & {\gamma }_n{\parallel x_n-x^{\ast }\parallel }^2+2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}〉+(1-{\gamma }_n){\parallel x_n-x^{\ast }\parallel }^2\\ +(1-{\gamma }_n)(-{\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_2\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel \parallel B_2{x}_n-B_2{x}^{\ast }\parallel )\\ +(1-{\gamma }_n)(-{\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_1\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel \parallel B_1{v}_n-B_1{y}^{\ast }\parallel )\\ =& {\parallel x_n-x^{\ast }\parallel }^2+2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}〉\\ +(1-{\gamma }_n)(-{\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_2\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel \parallel B_2{x}_n-B_2{x}^{\ast }\parallel )\\ +(1-{\gamma }_n)(-{\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel }^2\\ +2{\mu }_1\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel \parallel B_1{v}_n-B_1{y}^{\ast }\parallel ),\end{array}$$

which implies that

$$\begin{array}{c}(1-{\gamma }_n)({\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel }^2+{\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel }^2)\hfill \\ \le 2{\alpha }_n〈\rho f(x_n)-\mu T(y_n),x_{n+1}〉+(\parallel x_n-x^{\ast }\parallel +\parallel x_{n+1}-x^{\ast }\parallel )\parallel x_{n+1}-x_n\parallel \hfill \\ +2(1-{\gamma }_n){\mu }_2\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel \parallel B_2{x}_n-B_2{x}^{\ast }\parallel \hfill \\ +2(1-{\gamma }_n){\mu }_1\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel \parallel B_1{v}_n-B_1{y}^{\ast }\parallel .\hfill \end{array}$$

Since ${lim}_{n\to \mathrm{\infty }}\parallel x_{n+1}-x_n\parallel =0$, ${lim}_{n\to \mathrm{\infty }}{\alpha }_n\to 0$, $0<lim\hspace{0.17em}inf{\gamma }_n<lim\hspace{0.17em}sup{\gamma }_n<1$, ${lim}_{n\to \mathrm{\infty }}\parallel B_2{x}_n-B_2{x}^{\ast }\parallel =0$, ${lim}_{n\to \mathrm{\infty }}\parallel B_1{v}_n-B_1{y}^{\ast }\parallel =0$, we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel =0\text{and}\underset{n\to \mathrm{\infty }}{lim}\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel =0.$$

Since

$$\parallel x_n-z_n\parallel \le \parallel x_n-v_n-(x^{\ast }-y^{\ast })\parallel +\parallel v_n-z_n+(x^{\ast }-y^{\ast })\parallel ,$$

we get

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-z_n\parallel =0.$$

(3.11)

It follows from (3.8) and (3.11) that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel y_n-z_n\parallel =0.$$

(3.12)

We define a mapping $W:C\to H$ by $Wx=\beta Sx+(1-\beta )x$ with $\sigma \le \beta <1$. It follows from Lemma 2.5 that W is a nonexpansive mapping and $F(W)=F(S)$. Note that

$$\begin{array}{rcl}\parallel W{z}_n-z_n\parallel & \le & \parallel W{z}_n-y_n\parallel +\parallel z_n-y_n\parallel \\ \le & |{\beta }_n-\beta |\parallel S{z}_n-z_n\parallel +\parallel z_n-y_n\parallel .\end{array}$$

Since ${lim}_{n\to \mathrm{\infty }}{\beta }_n=\beta$ and ${lim}_{n\to \mathrm{\infty }}\parallel y_n-z_n\parallel =0$, we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel W{z}_n-z_n\parallel =0.$$

Since $\{x_n\}$ is bounded and without loss of generality we can assume that $x_n\rightharpoonup x^{\ast }\in C$, from (3.11), it is easy to observe that $z_n\rightharpoonup x^{\ast }$. It follows from Lemma 2.3 that $x^{\ast }\in F(W)=F(S)$. Therefore $w_w(x_n)\subset F(S)$. □

Theorem 3.1 The sequence $\{x_n\}$ generated by Algorithm  3.1 converges strongly to z, which is the unique solution of the variational inequality

$$〈\rho f(z)-\mu T(z),x-z〉\le 0,\mathrm{\forall }x\in \mathrm{\Omega }\cap F(S).$$

(3.13)

Proof Since $\{x_n\}$ is bounded $x_n\rightharpoonup w$ and from Lemma 3.2, we have $w\in F(S)$. Next, we show that $w\in \mathrm{\Omega }$. Since ${lim}_{n\to \mathrm{\infty }}\parallel x_n-z_n\parallel =0$ and there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that $x_{n_k}\to w$, it is easy to observe that $z_{n_k}\to w$. For any $x,y\in C$, using (2.1), we have

$$\begin{array}{rcl}{\parallel Q(x)-Q(y)\parallel }^2& =& \parallel T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]]\\ {-T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[y-{\mu }_2{B}_{2}y]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[y-{\mu }_2{B}_{2}y]]\parallel }^2\\ \le & \parallel (T_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]-T_{{\mu }_2}^{F_2}[y-{\mu }_2{B}_{2}y])\\ {-{\mu }_1(B_1{T}_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]-B_1{T}_{{\mu }_2}^{F_2}[y-{\mu }_2{B}_{2}y])\parallel }^2\\ \le & {\parallel T_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]-T_{{\mu }_2}^{F_2}[y-{\mu }_2{B}_{2}y]\parallel }^2\\ -{\mu }_1(2{\theta }_1-{\mu }_1){\parallel B_1{T}_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]-B_1{T}_{{\mu }_2}^{F_2}[y-{\mu }_2{B}_{2}y]\parallel }^2\\ \le & {\parallel T_{{\mu }_2}^{F_2}[x-{\mu }_2{B}_{2}x]-T_{{\mu }_2}^{F_2}[y-{\mu }_2{B}_{2}y]\parallel }^2\\ \le & {\parallel (x-{\mu }_2{B}_{2}x)-(y-{\mu }_2{B}_{2}y)\parallel }^2\\ \le & {\parallel x-y\parallel }^2-{\mu }_2(2{\theta }_2-{\mu }_2){\parallel B_{2}x-B_{2}y\parallel }^2\\ \le & {\parallel x-y\parallel }^2.\end{array}$$

This implies that $Q:C\to C$ is nonexpansive. On the other hand

$$\begin{array}{rcl}{\parallel z_n-Q(z_n)\parallel }^2& =& {\parallel T_{{\mu }_1}^{F_1}[T_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]-{\mu }_1{B}_1{T}_{{\mu }_2}^{F_2}[x_n-{\mu }_2{B}_2{x}_n]]-Q(z_n)\parallel }^2\\ =& {\parallel Q(x_n)-Q(z_n)\parallel }^2\\ \le & {\parallel x_n-z_n\parallel }^2.\end{array}$$

Since ${lim}_{n\to \mathrm{\infty }}\parallel x_n-z_n\parallel =0$ (see (3.11)), we have ${lim}_{n\to \mathrm{\infty }}\parallel z_n-Q(z_n)\parallel =0$. It follows from Lemma 2.3 that $w=Q(w)$, which implies from Lemma 2.2 that $w\in \mathrm{\Omega }$. Thus we have

$$w\in \mathrm{\Omega }\cap F(S).$$

Since $0\le \rho \tau <\mu \eta$, from Lemma 2.4, the operator $\mu T-\rho f$ is μη-ρτ-strongly monotone, and we get the uniqueness of the solution of the variational inequality (3.13) and denote it by $z\in \mathrm{\Omega }\cap F(S)$.

Next, we claim that ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}〈\rho f(z)-\mu T(z),x_n-z〉\le 0$. Since $\{x_n\}$ is bounded, there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that

$$\begin{array}{c}\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈\rho f(z)-\mu T(z),x_n-z〉\hfill \\ =\underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈\rho f(z)-\mu T(z),x_{n_k}-z〉\hfill \\ =〈\rho f(z)-\mu T(z),w-z〉\le 0.\hfill \end{array}$$

Next, we show that $x_n\to z$. We have

$$\begin{array}{rcl}{\parallel x_{n+1}-z\parallel }^2& =& 〈{\alpha }_n\rho f(x_n)+{\gamma }_n{x}_n+((1-{\gamma }_n)I-{\alpha }_n\mu T)(y_n)-z,x_{n+1}-z〉\\ =& {\alpha }_n〈\rho f(x_n)-\mu T(z),x_{n+1}-z〉+{\gamma }_n〈x_n-z,x_{n+1}-z〉\\ +〈((1-{\gamma }_n)I-{\alpha }_n\mu T)(y_n)-((1-{\gamma }_n)I-{\alpha }_n\mu T)(z),x_{n+1}-z〉\\ \le & {\alpha }_n〈\rho (f(x_n)-f(z)),x_{n+1}-z〉+{\alpha }_n〈\rho f(z)-\mu T(z),x_{n+1}-z〉\\ +{\gamma }_n\parallel x_n-z\parallel \parallel x_{n+1}-z\parallel +(1-{\gamma }_n-{\alpha }_n\nu )\parallel y_n-z\parallel \parallel x_{n+1}-z\parallel \\ \le & {\alpha }_n\rho \tau \parallel x_n-z\parallel \parallel x_{n+1}-z\parallel +{\alpha }_n〈\rho f(z)-\mu T(z),x_{n+1}-z〉\\ +{\gamma }_n\parallel x_n-z\parallel \parallel x_{n+1}-z\parallel +(1-{\gamma }_n-{\alpha }_n\nu )\parallel x_n-z\parallel \parallel x_{n+1}-z\parallel \\ =& (1-{\alpha }_n(\nu -\rho \tau ))\parallel x_n-z\parallel \parallel x_{n+1}-z\parallel +{\alpha }_n〈\rho f(z)-\mu T(z),x_{n+1}-z〉\\ \le & \frac{1-{\alpha }_n(\nu -\rho \tau )}{2}({\parallel x_n-z\parallel }^2+{\parallel x_{n+1}-z\parallel }^2)\\ +{\alpha }_n〈\rho f(z)-\mu T(z),x_{n+1}-z〉\\ \le & \frac{1-{\alpha }_n(\nu -\rho \tau )}{2}{\parallel x_n-z\parallel }^2+\frac{1}{2}{\parallel x_{n+1}-z\parallel }^2\\ +{\alpha }_n〈\rho f(z)-\mu T(z),x_{n+1}-z〉,\end{array}$$

(3.14)

which implies that

$${\parallel x_{n+1}-z\parallel }^2\le (1-{\alpha }_n(\nu -\rho \tau )){\parallel x_n-z\parallel }^2+2{\alpha }_n〈\rho f(z)-\mu T(z),x_{n+1}-z〉.$$

Let ${\upsilon }_n={\alpha }_n(\nu -\rho \tau )$ and ${\delta }_n=2{\alpha }_n〈\rho f(z)-\mu T(z),x_{n+1}-z〉$.

We have

$$\sum _{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$$

and

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\left\{\frac{1}{\nu -\rho \tau }〈\rho f(z)-\mu T(z),x_{n+1}-z〉\right\}\le 0.$$

It follows that

$$\sum _{n=1}^{\mathrm{\infty }}{\upsilon }_n=\mathrm{\infty }\text{and}\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{{\delta }_n}{{\upsilon }_n}\le 0.$$

Thus all the conditions of Lemma 2.8 are satisfied. Hence we deduce that $x_n\to z$. This completes the proof. □

4 Applications

To verify the theoretical assertions, we consider the following example.

Example 4.1 Let ${\alpha }_n=\frac{1}{3n}$, ${\beta }_n=\frac{1}{n^3}$, and ${\gamma }_n=\frac{2n-1}{3n}$.

It is easy to show that the sequence $\{{\gamma }_n\}$ satisfies condition (a).

We have

$$\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n=\frac{1}{3}\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}=0$$

and

$$\sum _{n=1}^{\mathrm{\infty }}{\alpha }_n=\frac{1}{3}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}=\mathrm{\infty }.$$

The sequence $\{{\alpha }_n\}$ satisfies condition (b).

Let ℝ be the set of real numbers, $B_1=B_2=0$, and let the mapping $T:\mathbb{R}\to \mathbb{R}$ be defined by

$$T(x)=\frac{2x+5}{7},\mathrm{\forall }x\in \mathbb{R},$$

let the mapping $S:\mathbb{R}\to \mathbb{R}$ be defined by

$$S(x)=\frac{x}{3},\mathrm{\forall }x\in \mathbb{R},$$

let the mapping $f:\mathbb{R}\to \mathbb{R}$ be defined by

$$f(x)=\frac{x}{14},\mathrm{\forall }x\in \mathbb{R}.$$

It is easy to show that T is a 1-Lipschitzian mapping and $\frac{1}{7}$-strongly monotone, S is a 0-strict pseudo-contraction mapping and f is $\frac{1}{7}$-Lipschitzian. Let the mapping $F_2:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ be defined by

$$F_2(x,y)=-5x^2+xy+4y^2,\mathrm{\forall }(x,y)\in \mathbb{R}\times \mathbb{R}.$$

By the definition of $F_2$, we have

$$\begin{array}{rcl}0& \le & F_2(u_n,y)+\frac{1}{{\mu }_2}〈y-u_n,u_n-x_n〉\\ =& -5u_n^2+u_{n}y+4y^2+\frac{1}{{\mu }_2}(y-u_n)(u_n-x_n).\end{array}$$

Then

$$\begin{array}{rcl}0& \le & {\mu }_2(-5u_n^2+u_{n}y+4y^2)+(y{u}_n-y{x}_n-u_n^2+u_n{x}_n)\\ =& 4{\mu }_2{y}^2+({\mu }_2{u}_n+u_n-x_n)y-5{\mu }_2{u}_n^2-u_n^2+u_n{x}_n.\end{array}$$

Let $A(y)=4{\mu }_2{y}^2+({\mu }_2{u}_n+u_n-x_n)y-5{\mu }_2{u}_n^2-u_n^2+u_n{x}_n$. $A(y)$ is a quadratic function of y with coefficients $a=4{\mu }_2$, $b={\mu }_2{u}_n+u_n-x_n$, $c=-5{\mu }_2{u}_n^2-u_n^2+u_n{x}_n$. We determine the discriminant Δ of A as follows:

$$\begin{array}{rcl}\mathrm{\Delta }& =& b^2-4ac\\ =& {({\mu }_2{u}_n+u_n-x_n)}^2-16{\mu }_2(-5{\mu }_2{u}_n^2-u_n^2+u_n{x}_n)\\ =& 81{\mu }_2^2{u}_n^2+18{\mu }_2{u}_n^2+u_n^2-18{\mu }_2{u}_n{x}_n-2u_n{x}_n+x_n^2\\ =& x_n^2+(81{\mu }_2^2+18{\mu }_2+1)u_n^2-2x_n{u}_n(9{\mu }_2+1)\\ =& {(x_n-u_n(9{\mu }_2+1))}^2.\end{array}$$

We have $A(y)\ge 0$, $\mathrm{\forall }y\in \mathbb{R}$. If it has at most one solution in ℝ, then $\mathrm{\Delta }=0$, we obtain

$$u_n=\frac{x_n}{1+9{\mu }_2}.$$

(4.1)

Let the mapping $F_1:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ be defined by

$$F_1(x,y)=-3x^2+xy+2y^2,\mathrm{\forall }(x,y)\in \mathbb{R}\times \mathbb{R}.$$

By the definition of $F_1$, we have

$$\begin{array}{rl}0& \le F_1(u_n,y)+\frac{1}{{\mu }_1}〈y-u_n,u_n-x_n〉\\ =-3u_n^2+u_{n}y+2y^2+\frac{1}{{\mu }_1}(y-u_n)(u_n-x_n).\end{array}$$

Then

$$\begin{array}{rcl}0& \le & {\mu }_1(-3u_n^2+u_{n}y+2y^2)+(y{u}_n-y{x}_n-u_n^2+u_n{x}_n)\\ =& 2{\mu }_1{y}^2+({\mu }_1{u}_n+u_n-x_n)y-3{\mu }_1{u}_n^2-u_n^2+u_n{x}_n.\end{array}$$

Let $B(y)=2{\mu }_1{y}^2+({\mu }_1{u}_n+u_n-x_n)y-3{\mu }_1{u}_n^2-u_n^2+u_n{x}_n$. $B(y)$ is a quadratic function of y with coefficients $a=2{\mu }_1$, $b={\mu }_1{u}_n+u_n-x_n$, $c=-3{\mu }_1{u}_n^2-u_n^2+u_n{x}_n$. We determine the discriminant Δ of B as follows:

$$\begin{array}{rcl}\mathrm{\Delta }& =& b^2-4ac\\ =& {({\mu }_1{u}_n+u_n-x_n)}^2-8{\mu }_1(-3{\mu }_1{u}_n^2-u_n^2+u_n{x}_n)\\ =& u_n^2+10{\mu }_1{u}_n^2+25u_n^2{\mu }_1^2-2x_n{u}_n-10x_n{u}_n{\mu }_1+x_n^2\\ =& {(u_n+5u_n{\mu }_1)}^2-2x_n(u_n+5u_n{\mu }_1)+x_n^2\\ =& {(u_n+5u_n{\mu }_1-x_n)}^2.\end{array}$$

We have $B(y)\ge 0$, $\mathrm{\forall }y\in \mathbb{R}$. If it has at most one solution in ℝ, then $\mathrm{\Delta }=0$, we obtain

$$u_n=\frac{x_n}{1+5{\mu }_1}.$$

(4.2)

For every $n\ge 1$, from (4.1) and (4.2), we rewrite (3.1) as follows:

$$\{\begin{array}{l}{z}_n=\frac{x_n}{(1+5{\mu }_1)(1+9{\mu }_2)};\\ y_n=\frac{z_n}{3n^3}+(1-\frac{1}{n^3})z_n;\\ x_{n+1}=(\frac{\rho }{42n}+\frac{2n-1}{3n})x_n+\frac{(n+1)y_n}{3n}-\mu \frac{2y_n+5}{21n}.\end{array}$$

In all tests we take $\rho =\frac{1}{15}$ and $\mu =\frac{1}{7}$. In our example $\eta =\frac{1}{7}$, $k=1$, $\tau =\frac{1}{7}$. It is easy to show that the parameters satisfy $0<\mu <\frac{2\eta }{k^2}$, $0\le \rho \tau <\nu$, where $\nu =\mu (\eta -\frac{\mu k^2}{2})$. All codes were written in Matlab, the values of $\{z_n\}$, $\{y_n\}$, and $\{x_n\}$ with different n are reported in Tables 1 and 2.

Table 1 The values of $\mathbf{\{}{\mathit{z}}_{\mathit{n}}\mathbf{\}}$ , $\mathbf{\{}{\mathit{y}}_{\mathit{n}}\mathbf{\}}$ , and $\mathbf{\{}{\mathit{x}}_{\mathit{n}}\mathbf{\}}$ with initial value ${\mathit{x}}_{\mathbf{1}}\mathbf{=}\mathbf{10}$

Table 2 The values of $\mathbf{\{}{\mathit{z}}_{\mathit{n}}\mathbf{\}}$ , $\mathbf{\{}{\mathit{y}}_{\mathit{n}}\mathbf{\}}$ , and $\mathbf{\{}{\mathit{x}}_{\mathit{n}}\mathbf{\}}$ with initial value ${\mathit{x}}_{\mathbf{1}}\mathbf{=}\mathbf{-}\mathbf{10}$

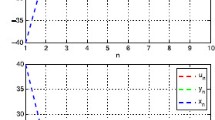
Remark 4.1 Tables 1 and 2, and Figures 1 and 2 show that the sequences $\{z_n\}$, $\{y_n\}$, and $\{x_n\}$ converge to 0, where $\{0\}=\mathrm{\Omega }\cap F(S)$. Also Tables 1 and 2 show that the convergence of Algorithm 3.1 is faster than Algorithm 3.2.

Figure 1

The convergence of $\mathbf{\{}{\mathit{z}}_{\mathit{n}}\mathbf{\}}$ , $\mathbf{\{}{\mathit{y}}_{\mathit{n}}\mathbf{\}}$ , and $\mathbf{\{}{\mathit{x}}_{\mathit{n}}\mathbf{\}}$ with initial value ${\mathit{x}}_{\mathbf{1}}\mathbf{=}\mathbf{10}$ for Algorithm  3.1 and Algorithm  3.2 with $\mathit{F}\mathbf{=}{\mathit{F}}_{\mathbf{1}}$ and with $\mathit{F}\mathbf{=}{\mathit{F}}_{\mathbf{2}}$ .

Figure 2

The convergence of $\mathbf{\{}{\mathit{z}}_{\mathit{n}}\mathbf{\}}$ , $\mathbf{\{}{\mathit{y}}_{\mathit{n}}\mathbf{\}}$ , and $\mathbf{\{}{\mathit{x}}_{\mathit{n}}\mathbf{\}}$ with initial value ${\mathit{x}}_{\mathbf{1}}\mathbf{=}\mathbf{-}\mathbf{10}$ for Algorithm  3.1 and Algorithm  3.2 with $\mathit{F}\mathbf{=}{\mathit{F}}_{\mathbf{1}}$ and with $\mathit{F}\mathbf{=}{\mathit{F}}_{\mathbf{2}}$ .

5 Conclusions

In this paper, we suggest and analyze an iterative method for finding the approximate element of the common set of solutions of (1.1) and (1.6) in real Hilbert space, which can be viewed as a refinement and improvement of some existing methods for solving equilibrium problem, and a hierarchical fixed point problem. Strong convergence of the proposed method is proved under mild assumptions. Furthermore, some preliminary numerical results are reported to verify the theoretical assertions of the proposed method and show that our algorithm for the system of generalized equilibrium problems is more attractive in practice than our algorithm for the generalized equilibrium problems.