1 Introduction

To analyse or describe numbers of urbane dynamical systems in sciences, social sciences, engineering and health sciences, neutral and stochastic differential equations, with or without delay or randomness, cannot be disregarded or unnoticed. In general, applications of functional differential equations are found in viscoelasticity, pre-predator and control problems, aeroautoelasticity, Brownian particles found in a limitless environment (or medium), motion of a rigid body under control, stretching of a polymer filament, dynamics of oscillator in a vacuum tube, energy source and their interaction in physics, motion of auto-generators with delay, general theory of relativity [10, 13, 14, 22–24, 26]. These amazing practical utilisations of functional differential equations in solving real-life phenomena have recently geared up or accelerated research in these directions, see for example the survey books of Arnold [10], Burton [13, 14], Driver [19], Hale [22–24], Kolmanovskii and Myshkis [26], Yoshizawa [50], to mention but a few, where theories and applications of functional differential equations are discussed.

Furthermore, a considerable number of strategies such as the direct method of Lyapunov, the continuous-time Markov chains, linear matrix inequality, fixed point approach, the technique of stochastic analysis, theory of semigroup, Euler–Maruyama, Rosenblatt process and so on, have been developed by authors to study criteria for stability, boundedness, existence and uniqueness, periodicity, exponential stability for system of neutral stochastic functional differential equations. We can mention the papers of Annamalai1 et al. [9], Chen et al. [17, 18], El Hassan [20], Fernándeza [21], Huang and Mao [25], Lien et al. [27], Liu and Raffoul [28], Liu [29], Liu et al. [30], Luo et al. [31], Mahmoud [33], Mao et al. [34], Mao [35–39] and the cited references therein.

In addition, outstanding papers on properties of solutions of nonlinear second and third order neutral and stochastic differential equations, using various techniques, have been discussed by researchers, see for example the works of Abou-El-Ela et al. [1–3], Ademola [4], Ademola et al. [5–7], Adesina et al. [8], Bohner et al. [11], Bouakkaz et al. [12], Cahlon and Schmidt [15], Chen et al. [16], Mahmoud and Tunç [32], Oudjedi et al. [42], Panigrahi and Basu [43], Philos and Purnaras [44], Tripathy et al. [47], Yeniçerioğlu and Demir [49] and the references cited therein.

Abou-El-Ela et al. [1], by employing Lyapunov direct method, addressed the problem of stochastic asymptotic stability and the uniform stochastic boundedness of nonzero solutions for the third order differential equation

$$w^{\prime \prime \prime }(t)+a_{1}w^{\prime \prime }(t)+ b_{1}w^{\prime }(t)+c_{1}w(t)+ \sigma _{1} w(t)\rho ^{\prime }(t)=e_{1} \bigl(t,x(t), w^{\prime }(t),w^{ \prime \prime }(t) \bigr), $$

where \(a_{1}\), \(b_{1}\), \(c_{1}\) and \(\sigma _{1}\) are positive constants \(\rho (t)\in \mathbb{R}\) is the standard Brownian motion defined on the probability space. Ademola [4], using the second method of Lyapunov, discussed the problem of stability, boundedness, existence and uniqueness of solution of the third order nonlinear stochastic differential equation with delay, namely

$$ w^{\prime \prime \prime }(t)+a_{2}w^{\prime \prime }(t)+ b_{2}w^{\prime }(t)+h \bigl(w(t- \tau ) \bigr)+\sigma _{2} w(t)\rho ^{\prime }(t)=e_{2} \bigl(t,w(t), w^{\prime }(t),w^{ \prime \prime }(t) \bigr),$$

where \(a_{2}>0\), \(b_{2}>0\), \(\sigma _{2}>0\) are constants, h, \(e_{2}\) are nonlinear continuous functions depending on the displayed arguments, \(h(0)=0\), \(\tau >0\) is a constant delay and \(\rho (t)\in \mathbb{R}\) is defined above.

By introducing more nonlinear functions into the existing equations, Mahmoud and Tunç [32] constructed a suitable Lyapunov functional and applied it to give criteria for the asymptotic stability of the zero solution to nonlinear third order stochastic differential equations with variable and constant delays defined as

$$ w^{\prime \prime \prime }(t)+a_{3}w^{\prime \prime }(t)+\phi \bigl(w^{\prime } \bigl(t-r(t) \bigr) \bigr)+ \psi \bigl(w \bigl(t-r(t) \bigr) \bigr) +\sigma _{3} w(t-h)\rho ^{\prime }(t)=0,$$

where \(a_{3}>0\), \(\sigma _{3}>0\), \(h>0\) are constants, \(r(t)\) is a continuously differentiable function with \(0\leq r(t)\leq \gamma _{1}\), \(\gamma _{1}>0\) is a constant, ϕ, ψ are continuously differentiable functions defined on \(\mathbb{R}\) such that \(\phi (0)=0=\psi (0)\), and \(\rho (t)\in \mathbb{R}^{m}\) is defined above.

Many papers have been published on the stability and boundedness of solutions of neutral differential equations, Oudjedi et al. [42] established conditions for integrability, boundedness and convergence of solutions to the third order neutral delay differential equations

$$ \bigl[w(t)+\beta w(t-\tau ) \bigr]^{\prime \prime \prime }+\phi (t)w^{\prime \prime }(t)+ \varphi (t) w^{\prime }(t)+ \chi (t)f \bigl(w(t-r) \bigr)=e_{3}(t),$$

where β and τ are constants with \(0\leq \beta \leq 1\) and \(\tau \geq 0\), \(e_{3}(t)\) and \(f(w)\) continuous functions depending only on the arguments shown and \(f^{\prime }(w)\) exists and is continuous for all w. By replacing the linear differentiable function \(w^{\prime }(t)\) with a nonlinear delay differentiable function, Ademola et al. [5] itemized criteria for uniform asymptotic stability and boundedness of solutions to the nonlinear third order neutral functional differential equation with delay defined as

$$ \bigl[w(t)+\phi w(t-\tau ) \bigr]^{\prime \prime \prime }+\varphi (t)w^{\prime \prime }(t) +\chi (t)g \bigl(w^{\prime }(t-\tau ) \bigr)+\psi (t)h \bigl(w(t-\tau ) \bigr)=e_{4}(t),$$

where \(\tau >0\) is a constant delay, ϕ is a constant satisfying \(0\leq \phi \leq 1\), the functions \(\varphi (t)\), \(\chi (t)\), \(\psi (t)\), \(g(y)\), \(h(w)\) are continuous in their respective arguments on \(\mathbb{R}^{+}\), \(\mathbb{R}^{+}\), \(\mathbb{R}^{+}\), \(\mathbb{R}\), \(\mathbb{R}\) respectively. Besides, it is supposed that the derivatives \(g^{\prime }(y)\) and \(h^{\prime }(w)\) exist and are continuous for all w, y and \(h(0)=0\).

The objective of this paper is to obtain sufficient conditions for the stability and boundedness of solutions of the following neutral stochastic differential equation with delay of third order:

$$\begin{aligned}& \bigl[x^{\prime \prime }(t)+\phi x^{\prime \prime } \bigl(t-\tau (t) \bigr) \bigr]^{\prime }+ax^{ \prime \prime }(t)+bx^{\prime } \bigl(t- \tau (t) \bigr)+\psi (t)h \bigl(x \bigl(t-\tau (t) \bigr) \bigr) \\& \quad {}+ \sigma x(t)\omega ^{\prime }(t)=p(\cdot ), \end{aligned}$$
(1.1)

where \(p(\cdot )=p(t,x(t),x(t-\tau (t)),x^{\prime }(t)))\), ϕ is a constant satisfying \(0\leq \phi \leq \frac{1}{2}\), the continuous functions \(\psi (t)\), \(h(x)\) and \(p(\cdot )\) depending only on the arguments shown and \(h^{\prime }(x)\) exist and are continuous for all x; the constants σ, a, b and β are positive with \(0\leq \tau (t)\leq \beta \), which will be determined later, \(\omega (t)\in \mathbb{R}\) is the standard Brownian motion.

Setting \(x^{\prime }(t)=y(t)\), \(x^{\prime \prime }(t)=z(t)\) and \(Y(t)=x^{\prime }(t)+\phi x^{\prime }(t-\tau (t))\), then (1.1) is equivalent to the system of first order differential equations

$$ \begin{gathered} x^{\prime }(t)=y(t), \\ y^{\prime }(t)=z(t), \\ \begin{aligned} Z^{\prime }(t)={}&p(\cdot )-az-by-\psi (t)h(x)-\sigma x(t) \omega ^{ \prime }(t)+b \int ^{t}_{t-\tau (t)}z(s)\,ds \\ &{} +\psi (t) \int ^{t}_{t-\tau (t)}h^{\prime } \bigl(x(s) \bigr)y(s)\,ds. \end{aligned} \end{gathered} $$
(1.2)

By a solution of (1.1) or (1.2), we have a continuous function \(x:[t_{x},\infty )\rightarrow \mathbb{R}\) such that \(Z(t)=z(t)+\phi z(t-\tau (t))\in C^{1}([t_{x},\infty ),\mathbb{R})\), which satisfies (1.1) on \([t_{x},\infty )\).

Then from (1.2) we get

$$ \begin{aligned}[b] Y^{\prime }(t)&=y^{\prime }(t)+ \phi y^{\prime } \bigl(t-\tau (t) \bigr) \bigl(1-\tau ^{ \prime }(t) \bigr) \\ &=z(t)+\phi z \bigl(t-\tau (t) \bigr) \bigl(1-\tau ^{\prime }(t) \bigr) \\ &=Z(t)-\phi \tau ^{\prime }(t)z \bigl(t-\tau (t) \bigr).\end{aligned} $$
(1.3)

We observed that the stochastic differential equations discussed in [1–4, 6–8, 32] exempt neutral term similar to [5, 11, 12, 15, 16, 42–44, 47] where neutral differential equations are considered and the stochastic term is exempted. Equation (1.1) is therefore an extension of these results and the references listed therein as both terms (neutral and stochastic which formed the major contribution of this paper) are included in equation (1.1).

It is noteworthy to mention at this junction that the inclusion of both neutral and stochastic terms to equation (1.1) make the authentication or confirmation of Lyapunov functional more difficult to obtain than before. Thus the Lyapunov functional employed in this study includes and generalises the existing functionals employed in [1–4, 6–8, 32] and [5, 11, 12, 15, 16, 42–44, 47] where qualitative behaviour of solution of stochastic differential equations and neutral functional differential equations are respectively considered. In addition, equation (1.1) is a special case of the systems of neutral stochastic differential equations discussed in [9, 10, 20–22, 34–39, 45, 46].

For more information on stability and boundedness to a kind of stochastic delay differential equations, see Ademola et al. [6], Arnold [10], Mao [40, 41] and Tunç and Tunç [48].

Consider a non-autonomous n-dimensional stochastic delay differential equation

$$ dx(t)=f \bigl(t, x(t), x(t-r) \bigr)\,dt+g \bigl(t, x(t), x(t-r) \bigr)\,dB(t) $$
(1.4)

for \(t>0\) with the initial data \(\{x(\vartheta ):-r\leq \vartheta \leq 0\}\), \(x_{0}\in \mathcal{C}([-r,0];\mathbb{R}^{n})\). Here \(f: \mathbb{R}^{+}\times \mathbb{R}^{2n}\rightarrow \mathbb{R}^{n}\) and \(g: \mathbb{R}^{+}\times \mathbb{R}^{2n}\rightarrow \mathbb{R}^{n \times m}\) are measurable functions and satisfy the local Lipschitz condition. Let \(B(t)=(B_{1}(t), B_{2}(t),\ldots , B_{m}(t))^{T}\) be an m-dimensional Brownian motion defined on the probability space. Hence, the stochastic delay differential equation admits trivial solution \(x(t,0)\equiv 0\) for any given initial value \(x_{0}\in \mathcal{C}([-r,0];\mathbb{R}^{n})\).

Definition 1.1

The trivial solution of the stochastic differential equation (1.4) is said to be stochastically stable if, for every pair \(\varepsilon \in (0,1)\) and \(\kappa >0\), there exists \(\delta _{0}=\delta _{0}(\varepsilon , \kappa )>0\) such that

$$ \Pr \bigl\{ \bigl\vert x(t;x_{0}) \bigr\vert < \kappa \text{ for all } t\geq 0 \bigr\} \geq 1- \varepsilon \quad \text{whenever } \vert x_{0} \vert < \delta _{0}.$$

Otherwise, it is said to be stochastically unstable.

Definition 1.2

The trivial solution of the stochastic differential equation (1.4) is said to be stochastically asymptotically stable if it is stochastically stable and, in addition, if for every \(\varepsilon \in (0,1)\) and \(\kappa >0\) there exists \(\delta =\delta (\varepsilon )>0\) such that

$$ \Pr \Bigl\{ \lim_{t\rightarrow \infty }x(t;x_{0})=0 \Bigr\} \geq 1- \varepsilon \quad \text{whenever}\ \vert x_{0} \vert < \delta .$$

Definition 1.3

A solution \(x(t_{0};x_{0})\) of the stochastic differential equation (1.4) is said to be stochastically bounded if it satisfies

$$ E^{x_{0}} \bigl\Vert x(t,x_{0}) \bigr\Vert \leq \mathcal{C} \bigl(t_{0}, \Vert x_{0} \Vert \bigr)\quad \text{for all}\ t\geq t_{0}, $$
(1.5)

where \(\mathcal{C}:\mathbb{R}^{+}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{+}\) is a constant function depending on \(t_{0}\) and \(x_{0}\), \(E^{x_{0}}\) denotes the expectation operator with respect to the probability low associated with \(x_{0}\).

Definition 1.4

The solution \(x(t_{0};x_{0})\) of the stochastic differential equation (1.4) is said to be uniformly stochastically bounded if \(\mathcal{C}\) in (1.5) is independent of \(t_{0}\).

Section 2 considers the stability of the trivial solution, ultimate boundedness of solution is discussed in Sect. 3, and finally illustrative examples are presented in the last section.

2 Stability of the trivial solution

Now, we shall state here the stability result of (1.1) with \(p(\cdot )\equiv 0\).

Theorem 2.1

In addition to the assumptions imposed on the functions that appeared in (1.1), suppose that there are positive constants \(\psi _{0}\), \(h_{0}\), \(h_{1}\) and α such that the following conditions are satisfied:

\((H_{1})\):

\(\psi _{0}\leq \psi (t)\leq b\) and \(\psi ^{\prime }(t)\leq 0\) for all \(t\geq 0\);

\((H_{2})\):

\(h(0)=0\), \(h_{0}\leq \frac{h(x)}{x}\leq h_{1}\) for all \(x\neq 0\) and \(h^{\prime }(x)\leq |h^{\prime }(x)|\leq \alpha < a\) for all x;

\((H_{3})\):

for some \(\beta \geq 0\), \(0<\beta _{1},\beta _{2}<1\), such that \(0\leq \tau (t)\leq \beta \) and \(\beta _{1}\leq \tau ^{\prime }(t)\leq \beta _{2}\);

\((H_{4})\):

\(\max \{\alpha , a\phi \}<\mu <\frac{a}{2}\);

\((H_{5})\):

\(\sigma ^{2}<2\psi _{0}h_{0}-bh_{0}\beta _{1}\phi -a-b-2\);

\((H_{6})\):

\([2b(\mu -\alpha )-b-3-\phi -b\phi (1+\alpha +\beta _{1}) ](1- \beta _{2})-b\phi (1+\alpha )-b\phi ^{2}(1-\beta _{1})=A_{1}>0\); and

\((H_{7})\):

\([a-2\mu -1-\phi (\mu +b+a) ](1-\beta _{2})-b\phi \beta _{1}(1+h_{0})- \phi (\mu +b+1)-b\phi ^{2}(1-\beta _{1})=A_{2}>0\).

Then the trivial solution of (1.1) is uniformly stochastically asymptotically stable, provided that

$$ \begin{aligned} \beta < {}&\min \biggl\{ \frac{2\psi _{0}h_{0}-bh_{0}\beta _{1}\phi -a-b-2-\sigma ^{2}}{b(1+\alpha )}, \frac{A_{1}}{2\alpha b(\mu +2)+2\mu b(1+\alpha )(1-\beta _{2})}, \\ &{} \frac{A_{2}}{2b(\mu +2)+2b\phi (1+\alpha )+2b(1+\alpha )(1-\beta _{2})} \biggr\} . \end{aligned} $$

Remark 2.1

If \(p(t,x(t),x(t-\tau (t)),x^{\prime }(t))=0\) in equation (1.1), we have the following observations:

  1. (i)

    In the case \(h(x(t-\tau (t)))=cx\) and \(\sigma x\omega ^{\prime }=p(t,x,x^{\prime },x^{\prime \prime })= 0\), equation (1.1) specialises to the linear first order homogeneous ordinary differential equation

    $$ x^{\prime \prime \prime }+ax^{\prime \prime }+bx^{\prime }+cx=0,$$
    (2.1)

    and assumptions (\(H_{1}\)) to (\(H_{7}\)) of Theorem 2.1 reduce to Routh Hurwitz criteria \(a > 0\), \(b > 0\), \(c > 0\), \(ab > c\) for asymptotic stability of the trivial solution of equation (2.1);

  2. (ii)

    Whenever \(\phi =0\), \(bx^{\prime }(t-\tau (t))=b_{2}\omega ^{\prime }(t)\), \(\psi (t)=1\) and \(\tau (t)=\tau >0\) a constant delay, equation (1.1) is cut down to that discussed in [4]. The assumptions of Theorem 2.1 include and extend the stability results in [4] Theorems 3.3 and 3.4;

  3. (iii)

    Suppose that \(\phi =0\) and \(\psi (t)=c_{1}\), then equation (1.1) is weakened to that discussed in [1] and some of our assumptions are similar. Thus the uniform stability result obtained in Theorem 2.1 include and extend the stochastic stability result (Theorem 2.3) discussed in [1];

  4. (iv)

    If \(\tau (t)=\tau >0\) is a constant delay and \(\sigma =0\), then equation (1.1) specialises to that considered in [5] and [42], our assumptions in Theorem 2.1 include Theorem 2.1, Corollary 2.2 in [5] and the asymptotic stability Theorem 2.1 in [42] provided that \(a(t)=b(t)=\) constant;

  5. (v)

    To crown it all, Theorem 2.1 includes and extends the stochastic stability results considered in [1, 4, 5, 42] and the references cited therein.

Proof of Theorem 2.1. Let \((x_{t},y_{t},z_{t})\) be any solution of (1.1) or (1.2) with \(p(\cdot )\equiv 0\), we define a Lyapunov continuously differentiable functional \(V=V(x_{t},y_{t},z_{t},t)\) employed in this work as follows:

$$ \begin{aligned}[b] V={}&V_{0}+V_{1}+ \lambda _{1} \int ^{0}_{-\tau (t)} \int ^{t}_{t+s}y^{2}( \vartheta )\,d \vartheta \,ds+\lambda _{2} \int ^{0}_{-\tau (t)} \int ^{t}_{t+s}z^{2}( \vartheta )\,d \vartheta \,ds \\ &{}+\eta _{1} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds+\eta _{2} \int ^{t}_{t- \tau (t)}z^{2}(s)\,ds, \end{aligned} $$
(2.2)

where

$$\begin{aligned}& V_{0}=\mu \psi (t) \int ^{x}_{0}h(\xi )\,d\xi +\psi (t)h(x)Y+ \frac{b}{2}Y^{2},\\& V_{1}=\frac{1}{2}\mu a y^{2}+\mu y Z+ \frac{1}{2}Z^{2}+x^{2}+xZ \end{aligned}$$

with \(\lambda _{1}\), \(\lambda _{2}\), \(\eta _{1}\) and \(\eta _{2}\) being positive constants which will be specified later.

From conditions \((H_{1})\) and \((H_{2})\), we have

$$ \begin{aligned} V_{0}&=\mu \psi (t) \int ^{x}_{0}h(\xi )\,d\xi +\frac{b}{2} \biggl(Y+ \frac{\psi (t)h(x)}{b} \biggr)^{2} -\frac{\psi (t)^{2} h^{2}(x)}{2b} \\ &\geq \mu \psi (t) \int ^{x}_{0}h(\xi )\,d\xi - \frac{\psi (t)^{2} h^{2}(x)}{2b} \\ &=\mu \psi (t) \int ^{x}_{0} \biggl(1-\frac{\psi (t)}{\mu b}h^{\prime }( \xi ) \biggr)h(\xi )\,d\xi \\ &\geq \mu \psi (t) \int ^{x}_{0} \biggl(1-\frac{\alpha }{\mu } \biggr)h(\xi )\,d\xi \\ &\geq \Delta \int ^{x}_{0}h(\xi )\,d\xi \geq \frac{\Delta h_{0}}{2}x^{2}, \end{aligned} $$

where

$$ \Delta =\mu \psi _{0} \biggl(1-\frac{\alpha }{\mu } \biggr)>\mu \psi _{0} \biggl(1-\frac{\mu }{\mu } \biggr)=0, \quad \text{since } \alpha < \mu . $$

Furthermore, from the definition of \(V_{1}\), we get

$$ \begin{aligned} V_{1}&=\frac{1}{2}\mu a y^{2}+\mu y Z+\frac{1}{4}Z^{2}+ \biggl(x+ \frac{Z}{2} \biggr)^{2} \\ &=\frac{1}{4}(Z+2\mu y)^{2} +\frac{1}{2}\mu (a-2\mu )y^{2}+ \biggl(x+ \frac{Z}{2} \biggr)^{2}. \end{aligned} $$

In the same way, it follows that

$$ V_{1}=\frac{\mu a}{2} \biggl(y+\frac{Z}{a} \biggr)^{2}+\frac{1}{4} \biggl( \frac{a-2\mu }{a} \biggr)Z^{2}+ \biggl(x+\frac{Z}{2} \biggr)^{2}. $$

Then

$$ \begin{aligned} V_{1}&=\frac{1}{8}(Z+2\mu y)^{2}+\frac{\mu a}{4} \biggl(y+\frac{Z}{a} \biggr)^{2}+ \biggl(x+\frac{Z}{2} \biggr)^{2}+ \frac{1}{4}\mu (a-2\mu )y^{2}+ \frac{1}{8} \biggl(\frac{a-2\mu }{a} \biggr)Z^{2} \\ & \geq \frac{1}{4}\mu (a-2\mu )y^{2}+ \frac{1}{8} \biggl( \frac{a-2\mu }{a} \biggr)Z^{2}. \end{aligned} $$

From this inequality and \((H_{4})\), we can deduce a positive constant \(K_{0}\) such that

$$ V_{1}\geq K_{0} \bigl(y^{2}+Z^{2} \bigr), $$

where

$$ K_{0}=\min \biggl\{ \frac{\mu }{4}(a-2\mu ), \frac{1}{8a}(a-2\mu ) \biggr\} .$$

Since

$$\begin{aligned}& \lambda _{1} \int ^{0}_{-\tau (t)} \int ^{t}_{t+s}y^{2}(\vartheta )\,d \vartheta \,ds+\lambda _{2} \int ^{0}_{-\tau (t)} \int ^{t}_{t+s}z^{2}( \vartheta )\,d \vartheta \,ds+\eta _{1} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds\\& \quad {}+ \eta _{2} \int ^{t}_{t-\tau (t)}z^{2}(s) \,ds>0, \end{aligned}$$

which implies that

$$ V\geq K_{1} \bigl(x^{2}+y^{2}+Z^{2} \bigr), $$
(2.3)

where

$$ K_{1}=\min \biggl\{ \frac{\Delta h_{0}}{2},K_{0} \biggr\} .$$

Since \(\frac{h(x)}{x}\leq h_{1}\) and \(\psi (t)\leq b\), then we get

$$ \begin{aligned} V\leq {}&\mu b \int ^{x}_{0}h_{1} \xi \,d\xi +bh_{1}xY+\frac{b}{2}Y^{2}+ \frac{1}{2}\mu a y^{2}+\mu y Z+\frac{1}{2}Z^{2}+x^{2}+xZ \\ &{}+\lambda _{1} \int ^{t}_{t-\tau (t)} \bigl\{ \vartheta -t+\tau (t) \bigr\} y^{2}( \vartheta )\,d \vartheta +\lambda _{2} \int ^{t}_{t-\tau (t)} \bigl\{ \vartheta -t+ \tau (t) \bigr\} z^{2}(\vartheta )\,d \vartheta \\ &{}+\eta _{1} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds+\eta _{2} \int ^{t}_{t- \tau (t)}z^{2}(s)\,ds. \end{aligned} $$

Using the fact \(2|uv|\leq u^{2}+v^{2}\), we obtain

$$ \begin{aligned} V\leq{} &\frac{1}{2}\mu bh_{1} x^{2}+\frac{1}{2}bh_{1} \bigl(x^{2}+Y^{2} \bigr)+ \frac{b}{2}Y^{2}+\frac{1}{2}\mu a y^{2}+\frac{\mu }{2} \bigl(y^{2}+ Z^{2} \bigr)+ \frac{1}{2}Z^{2}+x^{2} \\ &{}+ \frac{1}{2} \bigl(x^{2}+Z^{2} \bigr)+\frac{1}{2}\lambda _{1}\tau ^{2}(t) \Vert y \Vert ^{2} +\frac{1}{2}\lambda _{2} \tau ^{2}(t) \Vert z \Vert ^{2}++ \eta _{1} \tau (t) \Vert y \Vert ^{2}+\eta _{2}\tau (t) \Vert z \Vert ^{2}. \end{aligned} $$

Since \(\tau (t)\leq \beta \), \(Y(t)=y(t)+\phi y(t-\tau (t))\) and \(Z(t)=z(t)+\phi z(t-\tau (t))\), it follows that

$$\begin{aligned} V \leq &\frac{1}{2} \bigl\{ bh_{1}(\mu +1)+3 \bigr\} \Vert x \Vert ^{2}+ \frac{1}{2} \bigl\{ \mu (a+1)+\lambda _{1}\beta ^{2}+\eta _{1} \beta +b(1+h_{1}) (1+ \phi )^{2} \bigr\} \Vert y \Vert ^{2} \\ &{}+\frac{1}{2} \bigl\{ \lambda _{2}\beta ^{2}+ \eta _{2}\beta +(\mu +2) (1+ \phi )^{2} \bigr\} \Vert z \Vert ^{2}. \end{aligned}$$
(2.4)

Then there exists a positive constant \(K_{2}\) such that

$$ V\leq K_{2} \bigl(x^{2}+y^{2}+z^{2} \bigr). $$
(2.5)

Therefore, from (2.3) and (2.5), we note that the Lyapunov functional V satisfies the inequalities

$$ \nu _{1} \bigl( \vert x \vert \bigr)\leq V(t,x)\leq \nu _{2} \bigl( \vert x \vert \bigr).$$

By using Itô’s formula, the derivative of the Lyapunov functional V is given by

$$\begin{aligned} \mathcal{L}V =&\mu \psi ^{\prime }(t) \int ^{x}_{0}h(\xi )\,d\xi +\psi ^{ \prime }(t)h(x)Y+\mu \psi (t)h(x)y+\psi (t)h^{\prime }(x)yY\\ &{}+ \bigl( \psi (t)h(x)+bY \bigr)Y^{\prime } +\mu ayz+\mu zZ+(x+\mu y+Z)Z^{\prime }+2xy+yZ+\frac{1}{2}\sigma ^{2}x^{2} \\ &{}+\lambda _{1}\tau (t)y^{2}-\lambda _{1} \bigl(1-\tau ^{\prime }(t) \bigr) \int ^{t}_{t- \tau (t)}y^{2}(s)\,ds +\lambda _{2}\tau (t)z^{2}-\lambda _{2} \bigl(1- \tau ^{ \prime }(t) \bigr) \int ^{t}_{t-\tau (t)}z^{2}(s)\,ds \\ &{}+\eta _{1}y^{2}-\eta _{1}y^{2} \bigl(t-\tau (t) \bigr) \bigl(1-\tau ^{\prime }(t) \bigr) + \eta _{2}z^{2}-\eta _{2}z^{2} \bigl(t-\tau (t) \bigr) \bigl(1-\tau ^{\prime }(t) \bigr). \end{aligned}$$

From system (1.2) and (1.3), with conditions \((H_{1})-(H_{3})\), it follows that

$$\begin{aligned} \mathcal{L}V \leq & (\mu -a+\lambda _{2} \beta +\eta _{2} )z^{2}+ (b\alpha -\mu b+\lambda _{1}\beta +\eta _{1} )y^{2}+ \frac{1}{2}\sigma ^{2}x^{2}-axz-bxy-\psi _{0}h(x)x \\ &{}+2xy+yz+b\alpha \phi yy \bigl(t-\tau (t) \bigr)-bh_{0}\beta _{1}\phi xz \bigl(t-\tau (t) \bigr)-b \beta _{1}\phi yz \bigl(t-\tau (t) \bigr) \\ &{}+b\phi zy \bigl(t-\tau (t) \bigr)+b\phi ^{2}y \bigl(t-\tau (t) \bigr)z \bigl(t-\tau (t) \bigr) (1- \beta _{1})+\mu \phi zz \bigl(t- \tau (t) \bigr)\\ &{}-a\phi zz \bigl(t- \tau (t) \bigr)+\phi yz \bigl(t-\tau (t) \bigr) \\ &{} +(x+\mu y+Z) \biggl(b \int ^{t}_{t-\tau (t)}z(s)\,ds+b\alpha \int ^{t}_{t- \tau (t)}y(s)\,ds \biggr) \\ &{} -\lambda _{1}(1-\beta _{2}) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds- \lambda _{2}(1-\beta _{2}) \int ^{t}_{t-\tau (t)}z^{2}(s)\,ds \\ &{} -\eta _{1}(1-\beta _{2})y^{2} \bigl(t- \tau (t) \bigr) -\eta _{2}(1-\beta _{2})z^{2} \bigl(t- \tau (t) \bigr). \end{aligned}$$

Applying the estimate \(|uv|\leq \frac{1}{2}(u^{2}+v^{2})\), we obtain

$$\begin{aligned} \mathcal{L}V \leq &- \frac{1}{2} \bigl\{ 2\psi _{0}h_{0}-bh_{0} \beta _{1} \phi -a-b-2-\sigma ^{2}-b(1+\alpha )\beta \bigr\} x^{2} \\ &{} -\frac{1}{2} \bigl\{ 2b(\mu -\alpha )-b-3-\phi -b\phi (1+\alpha + \beta _{1})-\mu b\beta (1+\alpha )-2\eta _{1}-2\lambda _{1}\beta \bigr\} y^{2} \\ &{} -\frac{1}{2} \bigl\{ a-2\mu -1-\phi (\mu +a+b)-b\beta (1+\alpha )-2 \eta _{2}-2\lambda _{2}\beta \bigr\} z^{2} \\ &{} +\frac{1}{2} \bigl\{ b\phi (1+\alpha )+b\phi ^{2}(1- \beta _{1})-2 \eta _{1}(1-\beta _{2}) \bigr\} y^{2} \bigl(t-\tau (t) \bigr) \\ &{}+\frac{1}{2} \bigl\{ b\beta _{1}\phi (1+h_{0})+ \phi (\mu +b+1)+b\beta \phi (1+\alpha ) \\ &{}+b\phi ^{2}(1-\beta _{1})-2\eta _{2}(1-\beta _{2}) \bigr\} z^{2} \bigl(t-\tau (t) \bigr) \\ &{}+\frac{1}{2} \bigl\{ b\alpha (\mu +2)-2\lambda _{1}(1- \beta _{2}) \bigr\} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds \\ &{}+ \frac{1}{2} \bigl\{ b(\mu +2)-2 \lambda _{2}(1-\beta _{2}) \bigr\} \int ^{t}_{t-\tau (t)}z^{2}(s)\,ds. \end{aligned}$$
(2.6)

If we let

$$\begin{aligned}& \lambda _{1}=\frac{b\alpha (\mu +2)}{2(1-\beta _{2})}>0,\qquad \lambda _{2}=\frac{b(\mu +2)}{2(1-\beta _{2})}>0,\qquad \eta _{1}= \frac{b\phi (1+\alpha )+b\phi ^{2}(1-\beta _{1})}{2(1-\beta _{2})}>0 \end{aligned}$$

and

$$\begin{aligned}& \eta _{2}= \frac{b\beta _{1}\phi (1+h_{0})+\phi (\mu +b+1)+b\beta \phi (1+\alpha )+b\phi ^{2}(1-\beta _{1})}{2(1-\beta _{2})}>0. \end{aligned}$$

It follows that

$$\begin{aligned} \mathcal{L}V \leq &-\frac{1}{2} \bigl\{ 2\psi _{0}h_{0}-bh_{0}\beta _{1} \phi -a-b-2-\sigma ^{2}-b(1+\alpha )\beta \bigr\} x^{2} \\ &{} -\frac{1}{2} \biggl\{ 2b(\mu -\alpha )-b-3-\phi -b\phi (1+\alpha + \beta _{1})- \frac{b\phi (1+\alpha )+b\phi ^{2}(1-\beta _{1})}{(1-\beta _{2})} \\ &{} -\mu b\beta (1+\alpha )- \frac{b\alpha \beta (\mu +2)}{(1-\beta _{2})} \biggr\} y^{2} \\ &{} -\frac{1}{2} \biggl\{ a-2\mu -1-\phi (\mu +a+b)-b\beta (1+\alpha )- \frac{b\beta \phi (1+\alpha )}{(1-\beta _{2})}- \frac{b\beta (\mu +2)}{(1-\beta _{2})} \\ &{} - \frac{b\beta _{1}\phi (1+h_{0})+\phi (\mu +b+1)+b\phi ^{2}(1-\beta _{1})}{(1-\beta _{2})} \biggr\} z^{2}. \end{aligned}$$

From conditions \((H_{6})\) and \((H7)\), the last inequality becomes

$$\begin{aligned} \mathcal{L}V \leq &-\frac{1}{2} \bigl\{ 2\psi _{0}h_{0}-bh_{0}\beta _{1} \phi -a-b-2-\sigma ^{2}-b(1+\alpha )\beta \bigr\} x^{2} \\ &{} -\frac{1}{2} \biggl\{ \frac{A_{1}}{1-\beta _{2}}- \frac{\mu b(1+\alpha )(1-\beta _{2})+b\alpha (\mu +2)}{1-\beta _{2}} \beta \biggr\} y^{2} \\ &{} -\frac{1}{2} \biggl\{ \frac{A_{2}}{1-\beta _{2}}- \frac{b(1+\alpha )(1-\beta _{2})+b\phi (1+\alpha )+b(\mu +2)}{1-\beta _{2}} \beta \biggr\} z^{2}. \end{aligned}$$

Therefore, there exists a positive constant \(K_{3}\) such that

$$ \mathcal{L}V\leq -K_{3} \bigl(x^{2}+y^{2}+z^{2} \bigr), $$
(2.7)

provided that

$$ \begin{aligned} \beta < {}& \min \biggl\{ \frac{2\psi _{0}h_{0}-bh_{0}\beta _{1}\phi -a-b-2-\sigma ^{2}}{b(1+\alpha )}, \frac{A_{1}}{2\alpha b(\mu +2)+2\mu b(1+\alpha )(1-\beta _{2})}, \\ &{} \frac{A_{2}}{2b(\mu +2)+2b\phi (1+\alpha )+2b(1+\alpha )(1-\beta _{2})} \biggr\} . \end{aligned} $$

Thus, from (2.7) the inequality

$$ \mathcal{L}V(t,x)\leq -\nu _{3} \bigl( \vert x \vert \bigr) \quad \text{for all}\ (t,x)\in \mathbb{R}^{+}\times \mathbb{R}^{3}$$

is satisfied, then the trivial solution of (1.1) with \(p(\cdot )\equiv 0\) is uniformly stochastically asymptotically stable.

This completes the proof of Theorem 2.1.

3 Ultimate boundedness of solutions

Our main theorem in this section with respect to (1.1) is as follows.

Theorem 3.1

Assume that all the conditions of Theorem 2.1hold and there exist positive constants m, γ, \(M_{1}\) and \(M_{2}\) such that the following conditions are satisfied:

\((H_{8})\):

\(ab-\gamma >0\).

\((H_{9})\):

\(\|p(\cdot )\|\leq m\).

\((H_{10})\):

\(\sigma ^{2}< \frac{2\psi _{0}h_{0}(1+\gamma )-bh_{0}\beta _{1}(1+a)\phi -a-b-2}{1+a}\).

\((H_{11})\):

\(M_{1}=A_{1}+ [2a(ab-\gamma )-ab\beta _{1}\phi -(ab\alpha +\gamma )(1+ \phi ) ](1-\beta _{2})-ab\phi (1+\alpha )-ab\phi ^{2}(1-\beta _{1})\).

\((H_{12})\):

\(M_{2}=A_{2}+ [-\gamma -ab\phi ](1-\beta _{2})-ab\beta _{1} \phi (1+h_{0})-\gamma \phi -ab\phi ^{2}(1-\beta _{1})\),

provided that

$$ \begin{aligned} \beta < {}&\min \biggl\{ \frac{2\psi _{0}h_{0}(1+\gamma )-bh_{0}\beta _{1}(1+a)\phi -a-b-2-\sigma ^{2}(1+a)}{2b(1+\alpha )(1+\gamma )}, \\ &{} \frac{M_{1}}{2\alpha b(\mu +a+a^{2}+2)+2ab\gamma +2b(1+\alpha )(\mu +a^{2})(1-\beta _{2})}, \\ &{}\frac{M_{2}}{2b(\mu +a+a^{2}+2)+2b\phi (1+\alpha )(1+a)+2b\gamma +2b(1+\alpha )(1+a)(1-\beta _{2})} \biggr\} . \end{aligned} $$

Then

  1. (1)

    All solutions of (1.1) are uniformly stochastically bounded.

  2. (2)

    The zero solution of (1.1) is ω-uniformly exponentially asymptotically stable in probability.

Remark 3.1

When \(p(\cdot )\neq 0\) in (1.1), we have the following comparisons:

  1. (i)

    Whenever \(\phi =0\) and \(\psi (t)=c_{1}\) in (1.1), assumptions (\(H_{8}\)) to (\(H_{12}\)) of Theorem 3.1 specialise to assumptions (i) to (iii) of Theorem 3.6 in [1] and our conclusions coincide. Thus, Theorem 3.1 includes and generalises the boundedness results discussed in [1];

  2. (ii)

    If \(\phi =0\), \(bx^{\prime }(t-\tau (t))=b_{2}\omega ^{\prime }(t)\) and \(\psi (t)=1\) in (1.1), some of our assumptions of Theorem 3.1 coincide with the assumptions of ultimate boundedness results discussed in Theorems 3.1 and 3.2 in [4] and our conclusion on uniformly stochastically boundedness falls together with that in [4]. We have similar cases in [5, 6] and [8];

  3. (iii)

    Suppose that \(a=\varphi (t)\), \(b=\chi (t)\), \(p(\cdot )=e_{4}(t)\) and \(\sigma =0\), then (1.1) and boundedness Theorem 3.1 come down to neutral differential equation (1.2) and Theorems 3.1, 3.3 and Corollary 3.2 in [5]; and finally

  4. (iv)

    Theorem 3.1 is a general case of the results discussed in [1, 4–6, 8] and the references cited therein.

Proof of Theorem 3.1. Consider the Lyapunov functional \(U(x_{t},y_{t},z_{t},t)\) as follows:

$$ U(x_{t},y_{t},z_{t},t)=V(x_{t},y_{t},z_{t},t)+W(x_{t},y_{t},z_{t},t), $$
(3.1)

where V is defined as (2.2) and W is defined as follows:

$$\begin{aligned} W =&a^{2}\psi (t) \int ^{x}_{0}h(\xi )\,d\xi +a\psi (t)h(x)Y+ \frac{a \psi (t)}{2}Y^{2} \\ &{}+\frac{b\gamma }{2}x^{2} + \gamma x(Z+ay)+ \frac{a}{2}(Z+ay)^{2}. \end{aligned}$$
(3.2)

Now, we shall prove that

$$ \Vert x \Vert ^{p_{1}}\leq V(t,x)\leq \Vert x \Vert ^{p_{2}}$$

is satisfied for (1.1) where \(p_{1}\) and \(p_{2}\) are positive constants, \(p_{1}\geq 1\). It suffices to show it for W, since it was already proved for V in Sect. 2. We shall use the same techniques, which have already been demonstrated in the proof of Theorem 2.1. Thus from (3.2) we get

$$\begin{aligned} W =&a\psi (t) \int ^{x}_{0} \bigl\{ a-h^{\prime }(\xi ) \bigr\} h(\xi )\,d\xi + \frac{1}{2}a\psi (t) \bigl\{ h(x)+Y \bigr\} ^{2}\\ &{}+\frac{a}{2} \biggl\{ (Z+ay)+ \frac{\gamma }{a}x \biggr\} ^{2}+\frac{(ab-\gamma )\gamma }{2a}x^{2}. \end{aligned}$$

Therefore, from \((H_{2})\) and \((H_{8})\), we obtain

$$ W\geq L \bigl(x^{2}+y^{2}+Z^{2} \bigr) \quad \text{for some } L>0. $$
(3.3)

Thus, by gathering (2.3) and (3.3), there exists a positive constant \(D_{1}\) such that

$$ U(x_{t},y_{t},z_{t},t) \geq D_{1} \bigl(x^{2}+y^{2}+Z^{2} \bigr), $$
(3.4)

where \(D_{1}=\min \{K_{1}, L\}\).

Now, by using conditions \((H_{1})\) and \((H_{2})\) of Theorem 2.1, we can rewrite (3.2) as the following form:

$$ W\leq a^{2}b \int ^{x}_{0}h_{1} \xi \,d\xi +ab h_{1} \vert xY \vert +\frac{a b}{2}Y^{2}+ \frac{b\gamma }{2}x^{2} +\gamma \bigl\vert x(Z+ay) \bigr\vert +\frac{a}{2}(Z+ay)^{2}. $$

Since \(|uv|\leq \frac{1}{2}(u^{2}+v^{2})\), then we get

$$\begin{aligned} W \leq & \frac{1}{2} \bigl\{ bh_{1} \bigl(a+a^{2} \bigr)+\gamma (a+b+1) \bigr\} \Vert x \Vert ^{2} \\ &{} + \frac{1}{2} \bigl\{ ab(1+h_{1}) (1+\phi )^{2}+a \bigl(\gamma +a+a^{2} \bigr) \bigr\} \Vert y \Vert ^{2} \\ &{} +\frac{1}{2} \bigl\{ \bigl(\gamma +a+a^{2} \bigr) (1+ \phi )^{2} \bigr\} \Vert z \Vert ^{2}. \end{aligned}$$
(3.5)

Combining the foregoing inequalities (2.4), (3.1) and (3.5), we have

$$ \begin{aligned} U\leq {}& \frac{1}{2} \bigl\{ bh_{1} \bigl(\mu +a+a^{2}+1 \bigr)+\gamma (a+b+1)+3 \bigr\} \Vert x \Vert ^{2} \\ &{}+\frac{1}{2} \bigl\{ \mu (a+1)+a \bigl(\gamma +a+a^{2} \bigr)+\lambda _{1}\beta ^{2}+ \eta _{1} \beta +b(1+a) (1+h_{1}) (1+\phi )^{2} \bigr\} \Vert y \Vert ^{2} \\ &{} +\frac{1}{2} \bigl\{ \lambda _{2}\beta ^{2}+\eta _{2}\beta + \bigl(\mu + \gamma +a+a^{2}+2 \bigr) (1+\phi )^{2} \bigr\} \Vert z \Vert ^{2}. \end{aligned} $$

Then we can find a positive constant \(D_{2}\) such that the last inequality gives

$$ U(x_{t},y_{t},z_{t},t) \leq D_{2} \bigl(x^{2}+y^{2}+z^{2} \bigr). $$
(3.6)

Now from the results (3.4) and (3.6), we can find the Lyapunov functional U which satisfies the inequalities

$$ \Vert x \Vert ^{p_{1}}\leq V(t,x)\leq \Vert x \Vert ^{p_{2}}.$$

Also we can check that

$$ V(t,x)-V^{n/{p_{2}}}(t,x)\leq \Gamma $$

is satisfied since \(p_{1}=p_{2}=2\) and \(\Gamma =0\).

From (3.2), (1.2), (1.3) and the definitions of \(Y(t)\) and \(Z(t)\), we get

$$\begin{aligned} \mathcal{L}W =&W_{1}+a\psi (t)h^{\prime }(x)y^{2}+a\psi (t)\phi h^{ \prime }(x) yy \bigl(t-\tau (t) \bigr)-a\psi (t)\phi \tau ^{\prime }(t)h(x)z \bigl(t- \tau (t) \bigr)\\ &{}+a\psi (t)yz + a\psi (t)\phi yz \bigl(t-\tau (t) \bigr) \bigl(1-\tau ^{\prime }(t) \bigr)+a\psi (t)\phi zy \bigl(t- \tau (t) \bigr)-abyz\\ &{}-\gamma \psi (t)h(x)x+\gamma yz+\gamma ay^{2} +a\psi (t)\phi ^{2} y \bigl(t-\tau (t) \bigr)z \bigl(t-\tau (t) \bigr) \bigl(1-\tau ^{\prime }(t) \bigr)\\ &{}+ \gamma \phi yz \bigl(t-\tau (t) \bigr)-a^{2}by^{2}-ab\phi yz \bigl(t-\tau (t) \bigr) \\ &{} + \bigl(\gamma x +a^{2}y+aZ \bigr) \biggl(b \int ^{t}_{t-\tau (t)}z(s)\,ds+ \psi (t) \int ^{t}_{t-\tau (t)}h^{\prime } \bigl(x(s) \bigr)y(s)\,ds+p(\cdot ) \biggr), \end{aligned}$$

where

$$ W_{1}=a^{2}\psi ^{\prime }(t) \int ^{x}_{0}h(\xi )\,d\xi +a\psi ^{\prime }(t)h(x)Y+ \frac{a\psi ^{\prime }(t)}{2}Y^{2}. $$

First, we show that \(W_{1}\) is a negative definite function, we can rewrite \(W_{1}\) as the following form:

$$ \begin{aligned} W_{1}&=a\psi ^{\prime }(t) \int ^{x}_{0} \bigl\{ a-h^{\prime }(\xi ) \bigr\} h(\xi )\,d\xi +\frac{a\psi ^{\prime }(t)}{2}h^{2}(x)+a\psi ^{\prime }(t)h(x)Y+ \frac{a\psi ^{\prime }(t)}{2}Y^{2} \\ & =a\psi ^{\prime }(t) \int ^{x}_{0} \bigl\{ a-h^{\prime }(\xi ) \bigr\} h(\xi )\,d\xi + \frac{1}{2}a\psi ^{\prime }(t) \bigl(h(x)+Y \bigr)^{2}. \end{aligned} $$

From the assumptions \(\psi ^{\prime }(t)\leq 0\) and \(h^{\prime }(x)\leq a\), we get \(W_{1}\leq 0\).

Then from the assumptions of Theorem 3.1 and by using \(|uv|\leq \frac{1}{2}(u^{2}+v^{2})\), we can rewrite the above equation \(\mathcal{L}W\) as follows:

$$\begin{aligned} \mathcal{L}W \leq &- \frac{1}{2} \bigl\{ 2\psi _{0}h_{0}\gamma -abh_{0} \beta _{1}\phi -a\sigma ^{2}-b \gamma (1+\alpha )\beta \bigr\} x^{2} \\ &{} -\frac{1}{2} \bigl\{ 2a(ab-\gamma )-ab\beta _{1}\phi -(ab\alpha + \gamma ) (1+\phi )-a^{2}b\beta (1+\alpha ) \bigr\} y^{2} \\ &{} -\frac{1}{2} \bigl\{ \gamma +ab\phi +ab\beta (1+\alpha ) \bigr\} z^{2} + \frac{1}{2} \bigl\{ ab\phi (1+\alpha )+ab\phi ^{2}(1-\beta _{1}) \bigr\} y^{2} \bigl(t- \tau (t) \bigr) \\ &{} +\frac{1}{2} \bigl\{ ab\beta _{1}\phi (1+h_{0})+ab\phi ^{2}(1-\beta _{1})+ab \beta \phi (1+\alpha )+\gamma \phi \bigr\} z^{2} \bigl(t-\tau (t) \bigr) \\ &{}+\frac{1}{2} \bigl\{ b\alpha \gamma +a^{2}b\alpha +ab \alpha \bigr\} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds \\ &{}+\frac{1}{2} \bigl\{ b\gamma +a^{2}b+ab \bigr\} \int ^{t}_{t-\tau (t)}z^{2}(s)\,ds \\ &{}+\gamma m \vert x \vert +a^{2}m \vert y \vert +am(1+\phi ) \vert z \vert . \end{aligned}$$
(3.7)

From (2.2) and (1.2) and condition \((H_{9})\) of Theorem 3.1 with (2.6), we find

$$\begin{aligned} \mathcal{L}V \leq &- \frac{1}{2} \bigl\{ 2\psi _{0}h_{0}-bh_{0} \beta _{1} \phi -a-b-2-\sigma ^{2}-b(1+\alpha )\beta \bigr\} x^{2} \\ &{} -\frac{1}{2} \bigl\{ 2b(\mu -\alpha )-b-3-\phi -b\phi (1+\alpha + \beta _{1})-\mu b\beta (1+\alpha )-2\eta _{1}-2\lambda _{1}\beta \bigr\} y^{2} \\ &{} -\frac{1}{2} \bigl\{ a-2\mu -1-\phi (\mu +a+b)-b\beta (1+\alpha )-2 \eta _{2}-2\lambda _{2}\beta \bigr\} z^{2} \\ &{} +\frac{1}{2} \bigl\{ b\phi (1+\alpha )+b\phi ^{2}(1- \beta _{1})-2 \eta _{1}(1-\beta _{2}) \bigr\} y^{2} \bigl(t-\tau (t) \bigr) \\ &{}+\frac{1}{2} \bigl\{ b\beta _{1}\phi (1+h_{0})+ \phi (\mu +b+1)+b\beta \phi (1+\alpha ) \\ &{}+b\phi ^{2}(1-\beta _{1})-2\eta _{2}(1-\beta _{2}) \bigr\} z^{2} \bigl(t-\tau (t) \bigr) \\ &{}+\frac{1}{2} \bigl\{ b\alpha (\mu +2)-2\lambda _{1}(1- \beta _{2}) \bigr\} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds \\ &{}+\frac{1}{2} \bigl\{ b(\mu +2)-2\lambda _{2}(1-\beta _{2}) \bigr\} \int ^{t}_{t- \tau (t)}z^{2}(s)\,ds \\ &{}+m \vert x \vert +\mu m \vert y \vert +m(1+\phi ) \vert z \vert . \end{aligned}$$
(3.8)

Therefore, by combining inequalities (3.7) and (3.8), we obtain

$$\begin{aligned} \mathcal{L}U \leq &-\frac{1}{2} \bigl\{ 2\psi _{0}h_{0}(1+\gamma )-bh_{0} \beta _{1}\phi (1+a)-a-b-2-\sigma ^{2}(1+a)-b(1+\alpha ) (1+ \gamma ) \beta \bigr\} x^{2} \\ &{} -\frac{1}{2} \bigl\{ 2b(\mu -\alpha )+2a(ab-\gamma )-b\phi (1+\alpha + \beta _{1}+a\beta _{1})-b-3-\phi \\ &{}-(ab\alpha +\gamma ) (1+\phi ) - \bigl(\mu +a^{2} \bigr) b\beta (1+\alpha )-2\eta _{1}-2\lambda _{1} \beta \bigr\} y^{2} \\ &{} -\frac{1}{2} \bigl\{ a-2\mu -\gamma -1-(\mu +a+b+ab)\phi -b\beta (1+a) (1+ \alpha )-2\eta _{2}-2\lambda _{2}\beta \bigr\} z^{2} \\ &{} +\frac{1}{2} \bigl\{ b\phi (1+\alpha ) (1+a)+b\phi ^{2}(1+a) (1-\beta _{1})-2 \eta _{1}(1- \beta _{2}) \bigr\} y^{2} \bigl(t-\tau (t) \bigr) \\ &{}+\frac{1}{2} \bigl\{ b\beta _{1}\phi (1+a) (1+h_{0})+(\mu +b+1+\gamma ) \phi +b\beta \phi (1+\alpha ) (1+a) \\ &{}+b\phi ^{2}(1+a) (1-\beta _{1})-2\eta _{2}(1-\beta _{2}) \bigr\} z^{2} \bigl(t- \tau (t) \bigr) \\ &{} +\frac{1}{2} \bigl\{ b\alpha \bigl(\mu +a+a^{2}+2 \bigr)-ab\gamma -2\lambda _{1}(1- \beta _{2}) \bigr\} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds \\ &{} +\frac{1}{2} \bigl\{ b \bigl(\mu +a+a^{2}+2 \bigr)+b \gamma -2\lambda _{2}(1- \beta _{2}) \bigr\} \int ^{t}_{t-\tau (t)}z^{2}(s)\,ds \\ &{}+m(\gamma +1) \vert x \vert + \bigl(\mu +a^{2} \bigr) m \vert y \vert +m(1+a) (1+\phi ) \vert z \vert . \end{aligned}$$

Now, if we choose

$$\begin{aligned}& \lambda _{1}= \frac{b\alpha (\mu +a+a^{2}+2)+ab\gamma }{2(1-\beta _{2})}>0,\qquad \lambda _{2}=\frac{b(\mu +a+a^{2}+2)+b\gamma }{2(1-\beta _{2})}>0,\\& \eta _{1}= \frac{b\phi (1+\alpha )(1+a)+b\phi ^{2}(1+a)(1-\beta _{1})}{2(1-\beta _{2})}>0 \quad \text{and}\\& \begin{aligned} \eta _{2}&= \frac{b\beta _{1}\phi (1+a)(1+h_{0})+\phi (\mu +b+1+\gamma )+b\beta \phi (1+a)(1+\alpha )+b\phi ^{2}(1+a)(1-\beta _{1})}{2(1-\beta _{2})}\\ &>0. \end{aligned} \end{aligned}$$

It follows that

$$\begin{aligned} \mathcal{L}U \leq &- \frac{1}{2} \bigl\{ 2\psi _{0}h_{0}(1+\gamma )-bh_{0} \beta _{1}\phi (1+a)-a-b-2-\sigma ^{2}(1+a) \\ &{} -b(1+\alpha ) (1+\gamma ) \beta \bigr\} x^{2}-\frac{1}{2} \biggl\{ \frac{M_{1}}{1-\beta _{2}}- \frac{b\alpha (\mu +a+a^{2}+2)+ab\gamma }{1-\beta _{2}} \beta \\ &{} -b(1+ \alpha ) \bigl(\mu +a^{2} \bigr)\beta \biggr\} y^{2}-\frac{1}{2} \biggl\{ \frac{M_{2}}{1-\beta _{2}}- \frac{b\phi (1+\alpha )(1+a)}{1-\beta _{2}} \beta \\ &{}- \frac{b(\mu +a+a^{2}+2)+b\gamma }{1-\beta _{2}}\beta -b(1+\alpha ) (1+a) \beta \biggr\} z^{2}+m(\gamma +1) \vert x \vert \\ &{} + \bigl(\mu +a^{2} \bigr) m \vert y \vert +m(1+a) (1+\phi ) \vert z \vert . \end{aligned}$$
(3.9)

Provided that

$$ \begin{aligned} \beta < {}&\min \biggl\{ \frac{2\psi _{0}h_{0}(1+\gamma )-bh_{0}\beta _{1}(1+a)\phi -a-b-2-\sigma ^{2}(1+a)}{2b(1+\alpha )(1+\gamma )}, \\ &{} \frac{M_{1}}{2\alpha b(\mu +a+a^{2}+2)+2ab\gamma +2b(1+\alpha )(\mu +a^{2})(1-\beta _{2})}, \\ &{} \frac{M_{2}}{2b(\mu +a+a^{2}+2)+2b\phi (1+\alpha )(1+a)+2b\gamma +2b(1+\alpha )(1+a)(1-\beta _{2})} \biggr\} . \end{aligned} $$

Then one can conclude for some positive constants K and ω that

$$ \begin{aligned} \mathcal{L}U&\leq -\omega \bigl(x^{2}+y^{2}+z^{2} \bigr)+K\omega \bigl( \vert x \vert + \vert y \vert + \vert z \vert \bigr) \\ &=-\frac{\omega }{2} \bigl(x^{2}+y^{2}+z^{2} \bigr)-\frac{\omega }{2} \bigl\{ \bigl( \vert x \vert -K \bigr)^{2}+ \bigl( \vert y \vert -K \bigr)^{2}+ \bigl( \vert z \vert -K \bigr)^{2} \bigr\} +\frac{3\omega }{2}K^{2} \\ & \leq -\frac{\omega }{2} \bigl(x^{2}+y^{2}+z^{2} \bigr)+\frac{3\omega }{2}K^{2}, \end{aligned} $$

where

$$ K=\max \bigl\{ \gamma +1, \mu +a^{2}, (1+a) (1+\phi ) \bigr\} .$$

Then we find

$$\begin{aligned}& \delta _{1}(t)=\frac{\omega }{2},\qquad \delta _{2}(t)= \frac{3\omega }{2}K^{2},\qquad n=2,\qquad p_{1}=p_{2}=2,\qquad \Gamma =0, \quad \text{it follows that}\\& \begin{aligned} \int ^{t}_{t_{0}} \bigl\{ \Gamma \delta _{1}(u)+\delta _{2}(u) \bigr\} e^{-\int ^{t}_{u} \delta _{1}(s)\,ds}\,du&= \frac{3\omega }{2}K^{2} \int ^{t}_{t_{0}}e^{-\int ^{t}_{u} \frac{\omega }{2}\,ds}\,du \\ & =\frac{3\omega }{2}K^{2} \int ^{t}_{t_{0}}e^{-\frac{\omega }{2}(t-u)}\,du \\ &\leq 3K^{2}\quad \text{for all } t\geq t_{0}\geq 0, \end{aligned} \end{aligned}$$

Thus, satisfying the inequality

$$ \int ^{t}_{t_{0}} \bigl\{ \Gamma \delta _{1}(u)+\delta _{2}(u) \bigr\} e^{- \int ^{t}_{u}\delta _{1}(s)\,ds}\,du \leq \mathcal{M}\quad \text{for all } t \geq t_{0}\geq 0, $$
(3.10)

for some positive constant \(\mathcal{M}\). Now, we have the following:

$$\begin{aligned} &g^{T}= \begin{pmatrix}0 &0& -\sigma x(t) \end{pmatrix}, \\ & \begin{aligned} U_{x}={}&(V)_{x}+(W)_{x}\\ ={}&\mu \psi (t)h(x)+ \psi (t)h'(x) (1+\phi )y+(1+ \phi )z+2x+a^{2}\psi (t)h(x)+a\psi (t)h'(x) (1+\phi )y \\ & {}+\gamma bx+\gamma (1+\phi )z+ \gamma ay, \end{aligned} \\ & \begin{aligned} U_{y}={}&(V)_{y}+(W)_{y} \\ ={}&\psi (t)h(x) (1+ \phi )+b(1+\phi )^{2}y+G(y)+ \mu ay+\mu (1+\phi )z+a\psi (t)h(x) (1+ \phi ) \\ &{} +a\psi (t) (1+\phi )^{2}y+a \gamma x+a^{2}(1+ \phi )z+a^{3}y, \end{aligned} \\ &U_{z}=(V)_{z}+(W)_{z}=\mu (1+\phi ) y+(1+\phi )^{2}z+(1+\phi )x+ \gamma (1+\phi )x+a(1+\phi )^{2}z. \end{aligned}$$

It follows that

$$\begin{aligned} \bigl\vert V_{x_{i}}(t,x_{t})g_{ik}(t,x) \bigr\vert \leq{} &\sigma \biggl[\frac{1}{2} \bigl\{ \mu (1+\phi )+(1+a) (1+\phi )^{2}+2(1+\gamma ) (1+\phi ) \bigr\} x^{2}\\ &{} + \frac{\mu (1+\phi )}{2}y^{2} +\frac{(1+a)(1+\phi )^{2}}{2} z^{2} \biggr]:=\chi (t). \end{aligned}$$

Hence, all solutions of (1.1) are uniformly stochastically bounded. Therefore, the proof of Theorem 3.1 is completed. Next

$$ \begin{aligned} \int ^{t}_{t_{0}} \bigl\{ \Gamma \delta _{1}(u)+\delta _{2}(u) \bigr\} e^{\int ^{u}_{t_{0}} \delta _{1}(u)\,ds}\,du&= \frac{3\omega }{2}K^{2} \int ^{t}_{t_{0}}e^{ \frac{\omega }{2}\int ^{u}_{t_{0}}\,ds}\,du \\ &=3K^{2} \bigl(e^{\frac{\omega }{2}(t-t_{0})}-1 \bigr) \leq \mathcal{M} \end{aligned} $$

for all \(t\geq t_{0}\geq 0\), where \(\mathcal{M}\) is a positive constant. Thus, we find that the trivial solution of (1.1) is ω-uniformly exponentially asymptotically stable with \(N=\frac{1}{2}\).

Corollary 3.1

If assumptions (H1), (H2) and (H9) on functions \(\psi (t)\), \(h(x) \) and \(p(\cdot )\) hold and in addition \(0 \leq \phi \leq \frac{1}{2}\), then system (1.1) satisfies the global Lipschitz continuous and the linear growth conditions.

Proof

See (2.4)–(2.6) on page 202 in [38]. □

Remark 3.2

It is noteworthy to mention here that some of our assumptions, and the result of Corollary 3.1 in particular, complement some existing results on the system of neutral stochastic differential equations with delay in literature.

4 Examples and discussion

In this section two examples are given to illustrate the correctness of the obtained results of the stability and boundedness in Sects. 2 and 3.

Example 4.1

Consider the following third order non-autonomous neutral stochastic differential equation with delay:

$$\begin{aligned}& \bigl[x^{\prime \prime }(t)+\phi x^{\prime \prime } \bigl(t-\tau (t) \bigr) \bigr]^{\prime }+36x^{ \prime \prime }(t)+6.1x^{\prime } \bigl(t-\tau (t) \bigr) \\& \quad{} + \biggl(6+\frac{1}{10+t^{2}} \biggr) \biggl(4x \bigl(t-\tau (t) \bigr)+ \frac{x(t-\tau (t))}{1+x^{2}(t-\tau (t))} \biggr) +x(t)\omega ^{\prime }(t)=0. \end{aligned}$$
(4.1)

The above equation is equivalent to a system of first order differential equations as the following:

$$ \begin{gathered} x^{\prime }(t)=y(t), \\ y^{\prime }(t)=z(t), \\ \begin{aligned} Z^{\prime }(t)={}&{-}36z-6.1y- \biggl(6+ \frac{1}{10+t^{2}} \biggr) \biggl(4x+ \frac{x}{1+x^{2}} \biggr)- x(t)\omega ^{\prime }(t)\\ &{}+6.1 \int ^{t}_{t- \tau (t)}z(s)\,ds + \biggl(6+\frac{1}{10+t^{2}} \biggr) \int ^{t}_{t-\tau (t)} \biggl(4+\frac{1-x^{2}}{(1+x^{2})^{2}} \biggr)y(s)\,ds. \end{aligned} \end{gathered} $$
(4.2)

Comparing equations (1.2) and (4.2), we find \(a=36\), \(b=6.1\), \(\sigma =1\), and the following functions:

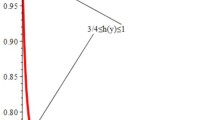
$$ 6=\psi _{0}\leq \psi (t)=6+\frac{1}{10+t^{2}}\leq 6.1=b,\quad \text{it follows that}\quad \psi ^{\prime }(t)= \frac{-2t}{(10+t^{2})^{2}}\leq 0.$$

Figures 1 and 2 depict the function \(\psi (t)\), its bounds on the interval \(-20\leq t\leq 20\) and the derivative \(\psi ^{\prime }(t)\) also on \(0\leq t\leq 20\) respectively. The function \(h(x)=4x+\frac{x}{1+x^{2}}\) fulfills \(h(0)=0\) and

$$ 4=h_{0}\leq \frac{h(x)}{x}=4+\frac{1}{1+x^{2}}\leq 5=h_{1} \quad \text{with } x\neq 0. $$

The function \(\frac{h(x)}{x}\) and its bounds are shown in Fig. 3. The derivative of \(h(x)\) is defined as

$$ h^{\prime }(x)=4+\frac{1-x^{2}}{(1+x^{2})^{2}}, \qquad \bigl\vert h^{\prime }(x) \bigr\vert \leq 5=\alpha .$$

The coinciding paths of \(h^{\prime }(x)\) and \(|h^{\prime }(x)|\) are presented in Fig. 4. If we let \(\beta _{1}=0.1\), \(\beta _{2}=0.3\) and\(\phi =0.02\), then from condition \((H_{4})\) we can take \(\mu =8\). Also, from conditions \((H_{6})\) and \((H_{7})\), we have

$$ A_{1}=17.98064>0 \quad \text{and}\quad A_{2}=12.172404>0,$$

provided that

$$ \beta < \min \{0.07790, 0.01763, 0.06967\}=0.01763,$$

If we take \(\beta =0.017\), then we find

$$ \lambda _{1}\cong 217.86>0, \qquad \lambda _{2}\cong 43.57>0,\qquad \eta _{1}\cong 0.5244>0\quad \text{and}\quad \eta _{2} \cong 0.3133>0.$$

Then all the conditions of Theorem 2.1 are contented with. Hence the trivial solution of (4.1) is stochastically asymptotically stable.

Figure 1
figure 1

Bounds on the function \(\psi (t)\) for \(t\in [-20,20]\)

Full size image
Figure 2
figure 2

Path of \(\psi ^{\prime }(t)\) for \(t\in [0,20]\)

Full size image
Figure 3
figure 3

The function \(\frac{h(x)}{x}\) and its bounds for \(x\in [-20,20]\)

Full size image
Figure 4
figure 4

The behaviour of functions \(h^{\prime }(x)\) and \(|h^{\prime }(x)|\) for \(t\in [-4,4]\)

Full size image

Example 4.2

As an application of Theorem 3.1, we consider the third order neutral stochastic delay differential equation such that

$$ \begin{aligned}[b] & \bigl[x^{\prime \prime }(t)+\phi x^{\prime \prime } \bigl(t-\tau (t) \bigr) \bigr]^{\prime }+36x^{ \prime \prime }(t)+6.1x^{\prime } \bigl(t-\tau (t) \bigr) \\ &\qquad {} + \biggl(6+\frac{1}{10+t^{2}} \biggr) \biggl(4x \bigl(t-\tau (t) \bigr)+ \frac{x(t-\tau (t))}{1+x^{2}(t-\tau (t))} \biggr) +x(t)\omega ^{\prime }(t)\\ &\quad =p \bigl(t, x(t),x \bigl(t-\tau (t) \bigr),x^{\prime }(t) \bigr). \end{aligned} $$
(4.3)

Its equivalent system is given by

$$ \begin{aligned} &x^{\prime }(t)=y(t), \\ & y^{\prime }(t)=z(t), \\ & \begin{aligned} Z^{\prime }(t)={}&{-}36z-6.1y- \biggl(6+ \frac{1}{10+t^{2}} \biggr) \biggl(4x+ \frac{x}{1+x^{2}} \biggr)- x(t)\omega ^{\prime }(t)\\ &{} +6.1 \int ^{t}_{t- \tau (t)}z(s)\,ds + \biggl(6+\frac{1}{10+t^{2}} \biggr) \int ^{t}_{t-\tau (t)} \biggl(4+\frac{1-x^{2}}{(1+x^{2})^{2}} \biggr)y(s)\,ds\\ &{} +p \bigl(t, x(t),x \bigl(t-\tau (t) \bigr),y(t) \bigr). \end{aligned} \end{aligned} $$
(4.4)

By using the estimates in Example 4.1, we have

$$\begin{aligned}& a=36,\qquad b=6.1,\qquad \sigma =1, \qquad \psi _{0}=6,\qquad h_{0}=4, \qquad h_{1}=5,\\& \alpha =5, \qquad \beta _{1}=0.1, \qquad \beta _{2}=0.3,\qquad\mu =8,\\& A_{1}=17.98064>0 \quad \text{and}\quad A_{2}=12.172404>0. \end{aligned}$$

If we let \(\gamma =2\), then we obtain \(ab-\gamma =217.6>0\).

Also it is obvious that

$$\begin{aligned}& \frac{2\psi _{0}h_{0}(1+\gamma )-bh_{0}\beta _{1}(1+a)\phi -a-b-2}{1+a} \cong 2.65>1=\sigma ^{2},\\& M_{1}=10172.88237, \qquad M_{2}=5.382948, \end{aligned}$$

provided that

$$ \beta < \min \{0.278, 0.068, 0.000293\}=0.000293.$$

If we choose \(\beta =0.0002\), we obtain

$$ \lambda _{1}\cong 29550>0, \qquad \lambda _{2}\cong 5856>0,\qquad \eta _{1}\cong 19.4>0\quad \text{and}\quad \eta _{2} \cong 1.92>0.$$

Let \(m=0.01\), therefore (3.9) takes the following form:

$$ \mathcal{L}U\leq -30.53 x^{2}-7252.45 y^{2}-2.53 z^{2}+0.03 \vert x \vert +13.04 \vert y \vert +0.3774 \vert z \vert . $$

If we take \(\omega =2.53\), \(K\cong 13.04\), \(\delta _{1}(t)=1.265\), \(\delta _{2}(t)=645.31\), \(n=2\), with \(p_{1}=p_{2}=2\) and \(\Gamma =0\), it follows that

$$ \int ^{t}_{t_{0}} \bigl\{ \Gamma \delta _{1}(u)+\delta _{2}(u) \bigr\} e^{-\int ^{t}_{u} \delta _{1}(s)\,ds}\,du \leq 510,\quad \text{for all } t\geq t_{0}\geq 0. $$

Therefore condition (3.10) holds. Now since

$$ \bigl\vert V_{x_{i}}(t,x_{t})g_{ik}(t,x) \bigr\vert \leq 26.3874 x^{2}+4.08 y^{2}+19.2474 z^{2}:=\chi (t). $$

Hence, it is evident that all the solutions of (4.3) with \(|P|\leq 0.01\) are (USB) and satisfy

$$ E^{x_{0}} \bigl\Vert x(t, t_{0}, x_{0}) \bigr\Vert \leq \bigl\{ x^{2}_{0}+510 \bigr\} ^{\frac{1}{2}}\quad \text{for all } t\geq t_{0}\geq 0. $$

Next

$$ \begin{aligned} \int ^{t}_{t_{0}} \bigl\{ \Gamma \delta _{1}(u)+\delta _{2}(u) \bigr\} e^{\int ^{t}_{u} \delta _{1}(s)\,ds}\,du \leq 510 \bigl(e^{1.265(t-t_{0})}-1 \bigr) \leq \mathcal{M} \end{aligned} $$

for all \(t\geq t_{0}\geq 0\), where \(\mathcal{M}\) is a positive constant.

Hence we find that the trivial solution of (4.3) is ω-uniformly exponentially asymptotically stable in probability with \(N=\frac{1}{2}\).

5 Conclusion

In this paper a third order neutral stochastic differential equation is discussed using the second technique of Lyapunov. A standard Lyapunov functional is derived and used to obtain suitable conditions which guarantee the stability of the zero solution and ultimate boundedness of the nonzero solutions. Our results are new and extend many outstanding existing findings in the literature. Only some behaviour of solutions of this novel equation is discussed here, existence and uniqueness, asymptotic behaviour as \(t\rightarrow \infty \), oscillatory and nonoscillatory, integrability properties of solutions are still open for further consideration.