1 Introduction

Distributed-order fractional derivatives indicate fractional derivatives that are integrated over the order of the differentiation within a given range [55]. In recent decades, distributed-order fractional differential equations (DOFDEs) have been used to model more phenomena in various fields such as visco-elastic [4, 6], dielectrics [10], diffusions [11, 24, 26, 28, 40, 42, 49, 52], signal processing [29], biosciences [17, 30], finance [16, 32], electrochemistry [44], and optimal control [54, 56]. The motivation of DOFDEs is the generalization of single-order and multi-term fractional differential equations [27].

In [5], Atanacković et al. studied the existence and uniqueness of solutions for DOFDEs of the form

$$\begin{aligned} & {D^{2}}f(t) = \lambda \int _{0}^{2} {p(q)_{0}^{C}D_{t}^{q}f(t) \,dq} = G \bigl( {t,f(t)} \bigr),\quad t > 0, \\ & {f^{(i)}}(0) = f_{0}^{(i)},\quad i = 0,1, \end{aligned}$$

in \(L_{\mathrm{loc}}^{1}(\mathbb{R}) \cap {C^{1}}([0,\infty )) \). Such equations arise in distributed derivative models of system identification theory and visco-elasticity.

In this research study, we consider general nonlinear DOFDEs in the time domain \(\Omega =[0,{t_{f}}] \) as follows:

$$\begin{aligned} \int _{\alpha }^{\beta }{{G_{1}} \bigl(q,{{}_{0}^{C}D{}_{t}^{q}}f(t) \bigr)\,dq} + {G_{2}} \bigl(t,f(t ),{{}_{0}^{C}D{}_{t}^{{\alpha _{1}}}}f(t ), \ldots,{{}_{0}^{C}D{}_{t}^{{\alpha _{r}}}}f(t) \bigr) = g(t), \end{aligned}$$
(1)

with the initial conditions

$$\begin{aligned} {f^{(k)}}(0) = f_{0}^{(k)},\quad k = 0, 1, \ldots, \max \bigl\{ \lceil {{\alpha _{r}}} \rceil, \lceil \beta \rceil \bigr\} - 1. \end{aligned}$$
(2)

Here, \({G_{1}}(\cdot) \) is a linear or nonlinear function,

$$\begin{aligned} {G_{2}} \bigl( {t,f(t),_{0}^{C}D_{t}^{{\alpha _{1}}}f(t), \ldots,_{0}^{C}D_{t}^{{ \alpha _{r}}}f(t)} \bigr) = {\kappa _{0}}f(t) + \sum_{i = 1}^{r} {{\kappa _{i}} {}_{0}^{C}D_{t}^{{\alpha _{i}}}f(t)}, \end{aligned}$$

where \({\kappa _{i}} \in \mathbb{R} \); and α, β, \({\alpha _{i}} ({\alpha _{1}}<\cdots <{\alpha _{r}}) \) for \({i = 0,1, \ldots,r} \) are positive real numbers. Also, \(\lceil \beta \rceil \) denotes the ceiling function and is the smallest integer greater than or equal to β.

Note that Eq. (1) is the general form of DOFDEs in the time domain which for the case \({G_{1}} (q,{{}_{0}^{C}D{}_{t}^{q}}f(t) ) = \Gamma (q){{}_{0}^{C}D{}_{t}^{q}}f(t)\), \(g(t)=0\), \({\kappa _{j}} =0\), \(j = 1, \ldots,r\), leads to the distributed-order fractional relaxation equation [31]. When \({G_{1}} (q,{{}_{0}^{C}D{}_{t}^{q}}f(t) ) = b \Gamma (q){{}_{0}^{C}D{}_{t}^{q}}f(t)\) with a constant b, \({\alpha _{1}} =2\), \({\kappa _{j}} =0\), \(j = 2, \ldots,r\), Eq. (1) is the Bagley–Torvik equation [7, 8]. Also, for the case \(\int _{0}^{1} {{a^{q}} {{}_{0}^{C}D{}_{t}^{q}}\sigma (t)\,dq} = \gamma \int _{0}^{1} {{b^{q}} {{}_{0}^{C}D{}_{t}^{q}}f(t)\,dq}\), \({\alpha _{1}} =2\), \({\kappa _{0}} =\omega ^{2}\), \({\kappa _{1}} =1\), \({\kappa _{j}} =0\), \(j = 2, \ldots,r\), we have the model that describes the motion of the oscillator [20], where \(\gamma, a, b \) are constants; ω is the eigen frequency of the undamped system; \(g(t) \) is the external forcing function; and \(f(t) \), \(\sigma (t) \) are the displacement and the dissipation force.

As the realm of DOFDEs describing the real-life response of physical systems grows, the demand for numerical solutions to analyze the behavior of these equations becomes more pronounced in order to overcome the mathematical complexity of analytical solutions. Therefore, the development of effective and easy-to-use numerical schemes for solving such equations acquires an increasing interest. While several numerical techniques have been proposed to solve many different problems (see, for instance, [1–3, 13, 15, 25, 33–35, 43, 45, 48] and the references therein), there have been few research studies that developed numerical methods to solve general DOFDEs (see [19, 21, 36, 38, 47, 50, 53]). The development, however, for efficient numerical methods to solve DOFDEs is still an important issue [21].

The aim of this paper is to provide sufficient conditions for the existence and uniqueness of solutions for Eqs. (1) and (2). Also, we are going to approximate solutions for the mentioned equations with high precision. To do this, in Sect. 2, we present a review of fractional calculus, an introduction of the second kind Chebyshev wavelets (SKCWs), shifted fractional-order Jacobi polynomials (SFOJPs), function approximations, and operational matrices for the Riemann–Liouville fractional integral operator. In Sect. 3, we provide sufficient conditions for the existence and uniqueness of solutions for general DOFDEs. In Sect. 4, by using operational matrices, mentioned in Sect. 2, we approximate the solution of Eqs. (1) and (2). In Sect. 5, we obtain the error bounds for the approximations. In Sect. 6, we solve two test problems and some famous distributed-order models, such as the model that describes the motion of the oscillator, the distributed-order fractional relaxation equation, and the Bagley–Torvik equation, to show that our approaches will increase the accuracy of the methods used for such operational matrices. Finally, a conclusion is given in Sect. 7.

2 Preliminaries

2.1 Fractional calculus

Definition 2.1

([41])

The Riemann–Liouville integral of fractional order \(\iota >0 \) is defined as follows:

$$\begin{aligned} {{}_{0}^{R}I{}_{t}^{\iota }}f(t)= \textstyle\begin{cases} {\frac{1}{\Gamma (\iota )}\int _{0}^{t} {{{(t - \tau )}^{\iota - 1}}f( \tau ) \,d\tau }} = {\frac{1}{\Gamma (\iota )} {t ^{\iota - 1}}*f(t),} & { \lceil \iota \rceil -1< \iota \leq \lceil \iota \rceil,} \\ f(t), & {\iota = 0}, \end{cases}\displaystyle \end{aligned}$$

where ∗ and \(\Gamma (\cdot) \) are the convolution product and gamma function, respectively.

Definition 2.2

([41])

The Caputo derivative of fractional order \(\iota >0 \) is defined as follows:

$$\begin{aligned} {{}_{0}^{C}D{}_{t}^{\iota }}f(t) = \textstyle\begin{cases} {\frac{1}{\Gamma ( \lceil \iota \rceil -\iota )}\int _{0}^{t} {{{(t - \tau )}^{ \lceil \iota \rceil - 1 - \iota }}{f^{( \lceil \iota \rceil )}}(\tau ) \,d\tau },} & { \lceil \iota \rceil -1< \iota < \lceil \iota \rceil,} \\ { f^{( \lceil \iota \rceil )}}(t), & {\iota = \lceil \iota \rceil }, \end{cases}\displaystyle \end{aligned}$$

with the following properties:

$$\begin{aligned} &{{{}_{0}^{C}D{}_{t}^{\iota }} {{}_{0}^{R}I{}_{t}^{\iota }}f(t) = f(t),} \\ &{{}_{0}^{R}I{}_{t}^{\iota }} {{}_{0}^{C}D{}_{t}^{\iota }}f(t) = f(t) - \sum_{j = 0}^{ \lceil \iota \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}} {{t ^{j}}}}, \end{aligned}$$
(3)
$$\begin{aligned} &{{}_{0}^{C}D{}_{t}^{\iota }}f(t ) = {{}_{0}^{R}I{}_{t}^{ \lceil \iota \rceil - \iota }} {{}_{0}^{C}D{}_{t}^{ \lceil \iota \rceil }}f(t ), \\ &{{}_{0}^{C}D{}_{t}^{\mu }} {{}_{0}^{R}I{}_{t}^{\iota }}f(t ) = {{}_{0}^{R}I{}_{t}^{ \iota - \mu }}f(t ), \quad\iota \ge \mu, \\ &{{{}_{0}^{C}D{}_{t}^{\mu }}c = 0 \quad \text{for constant }c, } \end{aligned}$$
(4)
$$\begin{aligned} & {{}_{0}^{C}D{}_{t}^{\iota }} {t^{k}} = \frac{\Gamma (k+1)}{\Gamma (k+1 - \iota )} t^{k - \iota }, \quad{k \geq \lceil \iota \rceil }. \end{aligned}$$
(5)

Definition 2.3

([18])

The distributed-order fractional derivative is defined as follows:

$$\begin{aligned} {{}_{0}^{C}D_{t}^{p(\upsilon )}}f(t ) = \int _{{\upsilon _{1}}}^{{ \upsilon _{2}}} {p(\upsilon ) {{}_{0}^{C}D{}_{t}^{\upsilon }}f(t )\,d \upsilon }, \end{aligned}$$

where \({\upsilon _{1}} \), \({\upsilon _{2}}\in \mathbb{R}^{+} \), and \(p(\upsilon ) \) is distribution of order \(\upsilon \in [{\upsilon _{1}},{\upsilon _{2}}] \).

2.2 SKCWs and function approximation

SKCWs are as follows:

$$\begin{aligned} {{\psi } _{i,j}}(t )= \textstyle\begin{cases} {\sqrt{\frac{2^{{k+3}}}{{t_{f}}{\pi }}} {T_{j}^{*}} ( \frac{2^{k}}{{t_{f}}}t - i + 1 ),} & { \frac{{i - 1}}{{{2^{k}}}}{{t_{f}}} \le t < \frac{i}{{{2^{k}}}} {{t_{f}}},} \\ 0, & \mathrm{otherwise}, \end{cases}\displaystyle \end{aligned}$$

where \(i=1,2,\dots,{2^{k}}, j=0,1,\dots,M-1\). Here, \({T_{j}^{*}}(t) \) is the shifted Chebyshev polynomial of the second kind of degree \(j\geq 0 \), defined on the interval \([0,1] \) by

$$\begin{aligned} {T_{j}^{*}}(t ) = \sum_{k = 0}^{j} {{c_{k,j}} {t^{j-k}}}, \end{aligned}$$

where

$$\begin{aligned} {c_{k,j}} = \frac{{(-1)^{k}}{2^{2j-2k}}\Gamma (2j-k+2)}{\Gamma (k+1)\Gamma (2j-2k+2)} . \end{aligned}$$

Let \(w(t) = \sqrt{t-{t^{2}}} \) be the weight function. A function \(f(t)\in {L_{\omega }^{2}}([0,{{t_{f}}}))\) can be expanded by SKCWs as follows:

$$\begin{aligned} f(t)=\sum_{i=1}^{\infty }\sum _{j=0}^{\infty } {\hat{f}}_{i,j} {\psi }_{i,j}(t), \end{aligned}$$
(6)

where

$$\begin{aligned} {{\hat{f}}_{i,j}} = \int _{0}^{{t_{f}}} {f(t){\psi _{i,j}}(t) \omega (t){ \,{{d}}}t}. \end{aligned}$$

and \(\omega (t) = w ( {\frac{{{2^{k}}}}{{{t_{f}}}}t - i + 1} ) \). We truncate the infinite series given in Eq. (6), and then we approximate a function \(f(t)\) in the following form:

$$\begin{aligned} f(t)\simeq f_{{2^{k}},M-1}(t)=\sum _{i=1}^{{2^{k}}}\sum_{j=0}^{M-1} { \hat{f}}_{i,j} {\psi }_{i,j}(t)={\hat{F}}^{T}{ \Psi }(t), \end{aligned}$$
(7)

where

$$\begin{aligned} &{\hat{F}}= [{\hat{f}}_{1,0},\dots,{\hat{f}}_{1,M-1},\ldots,{ \hat{f}}_{{2^{k}},0},\dots,{\hat{f}}_{{2^{k}},M-1} ]^{T}, \\ &{\Psi }(t)= \bigl[{\psi }_{1,0}(t),\dots,{\psi }_{1,M-1}(t), \dots,{ \psi }_{{2^{k}},0}(t),\dots,{\psi }_{{2^{k}},M-1}(t) \bigr]^{T}, \end{aligned}$$

are \({2^{k}}M \times 1 \) vectors.

2.3 SFOJPs and function approximation

SFOJPs of order i are defined on the interval \([0,{t_{f}}] \) by the following formula [22]:

$$\begin{aligned} {\mathcal{J}}_{{t_{f}},i}^{(\lambda,\theta,\vartheta )}(t) = \sum _{k = 0}^{i} {{{( - 1)}^{i - k}} \frac{{\Gamma (i + \vartheta + 1)\Gamma (i + k + \theta + \vartheta + 1)}}{{\Gamma (k + \vartheta + 1)\Gamma (i + \theta + \vartheta + 1)(i - k)!k!{t_{f}^{{k}{\lambda }}}}}{t^{{k}{ \lambda }}}}, \end{aligned}$$

where \(\theta,\vartheta \in \mathbb{R} \) and \(0<\lambda <1 \).

The orthogonality property of \({\mathcal{J}}_{{t_{f}},i}^{(\lambda,\theta,\vartheta )}(t) \) is as follows:

$$\begin{aligned} \int _{0}^{t_{f}} {{\mathcal{J}}_{{t_{f}},i}^{(\lambda,\theta, \vartheta )}(t){ \mathcal{J}}_{{t_{f}},i'}^{(\lambda,\theta, \vartheta )}(t)w_{t_{f}}^{(\lambda,\theta,\vartheta )}(t) \,{d}t} = h_{{t_{f}},i}^{(\lambda,\theta,\vartheta )}{\delta _{ii'}}, \end{aligned}$$

where \({\delta _{ii'}}\) and \(w_{t_{f}}^{(\lambda,\theta,\vartheta )}(t) = {\lambda }{t^{{ \lambda }\vartheta +{\lambda }-1} }{({{t_{f}^{\lambda }}} - t^{\lambda })^{\theta }} \) are Kronecker delta and weight functions, respectively. Also,

$$\begin{aligned} {h_{{t_{f}},i}^{(\lambda,\theta,\vartheta )}} = \frac{{{{{t_{f}^{(\theta + \vartheta + 1)\lambda }}}}\Gamma (i + \theta + 1)\Gamma (i + \vartheta + 1)}}{{(2i + \theta + \vartheta + 1)i!\Gamma (i + \theta + \vartheta + 1)}}. \end{aligned}$$

By using SFOJPs, a function \(f(t)\in {L_{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}^{2}}([0,{t_{f}}])\) can be approximated as follows:

$$\begin{aligned} f(t)\simeq f_{N}(t)=\sum_{i=0}^{N} {\tilde{f}}_{i} {\phi }_{i}(t)={ \tilde{F}}^{T}{ \Phi }(t), \end{aligned}$$
(8)

where

$$\begin{aligned} {{\tilde{f}}_{i}} = \frac{1}{h_{{t_{f}},i}^{(\lambda,\theta,\vartheta )}} \int _{0}^{{t_{f}}} {f(t){\phi _{i}}(t){w_{t_{f}}^{(\lambda,\theta,\vartheta )}(t)} \,{{{d}}}t} . \end{aligned}$$

Also, F̃ and \({\Phi }(t) \) are \((N+1) \times 1 \) vectors given by

$$\begin{aligned} &{\tilde{F}} = [{\tilde{f}}_{0},{\tilde{f}}_{1},\dots,{ \tilde{f}}_{N} ]^{T}, \\ &{\Phi }(t)= \bigl[ {{\mathcal{J}}_{t_{f},0}^{(\lambda,\theta,\vartheta )}(t)},{{ \mathcal{J}}_{t_{f},1}^{(\lambda,\theta,\vartheta )}(t)}, \ldots,{{ \mathcal{J}}_{t_{f},N}^{(\lambda,\theta,\vartheta )}(t)} \bigr]^{T}. \end{aligned}$$

2.4 Operational matrices of the Riemann–Liouville fractional integral operator

Following [23, 51], we can obtain the operational matrix of the Riemann–Liouville fractional integral operator based on SKCWs for \(t \in [0, {t_{f}}) \) in the following theorem.

Theorem 2.1

Let \(\Psi (t) \) be the vector of SKCWs. Then

$$\begin{aligned} {{}_{0}^{R}I{}_{t}^{q}} {\Psi }(t ) \simeq {\mathbf{I}^{q}} {\Psi }(t ) = \widehat{\Psi }(t,q), \end{aligned}$$
(9)

where

$$\begin{aligned} {\mathbf{I}^{q}} = {\Lambda } {\mathbf{P}^{q}} {\Lambda ^{ - 1}}. \end{aligned}$$

Also,

$$\begin{aligned} \Lambda \triangleq \biggl[ {\Psi \biggl( { \frac{{t_{f}}}{{{{2^{k+1}}M}}}} \biggr), \Psi \biggl( { \frac{3{t_{f}}}{{{{2^{k+1}}M}}}} \biggr), \ldots, \Psi \biggl( { \frac{({{{2^{k+1}}M} - 1}){t_{f}}}{{{{2^{k+1}}M}}}} \biggr)} \biggr] \end{aligned}$$

is a \({{2^{k}}M}\times {{2^{k}}M} \) matrix and

P q = ( t f 2 k M ) q 1 Γ ( q + 2 ) [ 1 η 1 η 2 … η 2 k M − 1 0 1 η 1 … η 2 k M − 2 0 0 1 … η 2 k M − 3 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 … 1 ]

is the operational matrix of fractional integral operator for the block-pulse functions, where

$$\begin{aligned} {\eta _{{l}}} = {(l + 1)^{q + 1}} - 2{l^{q + 1}} + {(l - 1)^{q+ 1}},\quad l=1,2,\ldots,{{2^{k}}M}-1 . \end{aligned}$$

According to our previous work [37], we have the following theorem.

Theorem 2.2

Let \(\Phi (t) \) be the vector of SFOJPs. Then

$$\begin{aligned} {{}_{0}^{R}I{}_{t}^{q}} \Phi (t) \simeq {\mathbf{I}^{{t_{f}},{q}}} \Phi (t) = \widehat{\Phi }(t,q), \end{aligned}$$

where \({\mathbf{I}^{{t_{f}},{q}}} \) is the operational matrix of the Riemann–Liouville integral operator of fractional order q with entries

$$\begin{aligned} {\mathbf{{I}}}_{kl}^{t_{f},q } = {}& \sum _{j = 0}^{k} { \Biggl( {{{( - 1)}^{k - j}} \frac{{\Gamma (k + \vartheta + 1)\Gamma (k + j + \theta + \vartheta + 1)\Gamma (j\lambda + 1)}}{{\Gamma (j + \vartheta + 1)\Gamma (k + \theta + \vartheta + 1)(k - j)!j!\Gamma (q + j\lambda + 1)}}} } \\ & {}{ \times \sum_{i = 0}^{l} {{{( - 1)}^{l - i}} \frac{{(2l + \theta + \vartheta + 1)l!\Gamma (l + i + \theta + \vartheta + 1){t_{f} ^{q }}B ( {\theta + 1,i + j + \vartheta + 1 + \frac{q }{\lambda }} )}}{{\Gamma (l + \theta + 1)\Gamma (i + \vartheta + 1)(l - i)!i!}}} } \Biggr). \end{aligned}$$

Here, \(B(.,.) \) is a beta function and \(k,l=0,1,\ldots, N\).

3 Existence and uniqueness of solutions

In the following theorem, by using Schauder’s fixed point theorem [57], we prove the local existence of solutions for general DOFDEs in a Banach space.

Theorem 3.1

Let \({G_{1}} \) be Lipschitz with the constant ς. Suppose that

  1. (C1)

    \(G_{1} \in C(\Omega \times {\mathbb{R}}^{n},{\mathbb{R}}^{n}) \) and \({g}, {g_{1}}, {f}, {v} \in C(\Omega,{\mathbb{R}}^{n}) \);

  2. (C2)

    \(\vert {{g}(t) - {g_{1}}(t)} \vert < \frac{ \vert \kappa _{0} \vert \varepsilon }{3} \);

  3. (C3)

    \(\vert {{G_{1}} ( {q,_{0}^{C}D_{t}^{q}f(t)} ) - {G_{1}} ( {q,_{0}^{C}D_{t}^{q}v(t)} )} \vert < \frac{{ \vert \kappa _{0} \vert } \varepsilon }{{3(\beta - \alpha )}} \);

  4. (C4)

    \(\vert {{}_{0}^{C}D_{t}^{{\alpha _{i}}}f(t) - {}_{0}^{C}D_{t}^{{ \alpha _{i}}}v(t)} \vert \le {\zeta _{i}} \).

Also, suppose that \(\sum_{i = 1}^{r} { \vert \frac{\kappa _{i}}{\kappa _{0}} \vert {\zeta _{i}}} \le \frac{\varepsilon }{3} \). Then general DOFDEs have at least one solution on Ω.

Proof

Consider \(D =\{ (t,f): t\in \Omega, |f(t)| \leq b \} \). Suppose that \(|{g}(t)|\leq \frac{{{ \vert \kappa _{0} \vert }b}}{3} \), \(\vert {{G_{1}} ( {q,_{0}^{C}D_{t}^{q}f(t)} )} \vert \le \xi \), \(\vert {{}_{0}^{C}D_{t}^{{\alpha _{i}}}f(t)} \vert \le {\eta _{i}} \) on D. Choose \(\frac{{(\beta - \alpha )\xi }}{{{ \vert \kappa _{0} \vert }}} \le \frac{b}{3} \), \(\sum_{i = 1}^{r} { \vert \frac{\kappa _{i}}{\kappa _{0}} \vert {\eta _{i}}} \le \frac{b}{3} \), and let \({\Pi _{0}}=\{f: f\in C({\Omega _{0}},{\mathbb{R}}^{n}), \Vert f \Vert \leq b\} \), where \(\Vert f \Vert = \mathop{\max }_{t \in {\Omega _{0}}} |f(t)| \) and \({\Omega _{0}}=[0,{\tau _{f}}] \). It is clear that the set \({\Pi _{0}} \) is convex, closed, and bounded.

Define the operator

$$\begin{aligned} Tf(t) = \frac{1}{\kappa _{0}}g(t) - \frac{1}{{{\kappa _{0}}}} \int _{\alpha }^{\beta }{{G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f(t)} \bigr)\,dq} - \sum_{i = 1}^{r} {\frac{{{\kappa _{i}}}}{{{\kappa _{0}}}}{}_{0}^{C}D_{t}^{{ \alpha _{i}}}f(t)},\quad t \in {\Omega _{0}}, \end{aligned}$$

for any \(f \in {\Pi _{0}}\). Clearly, we have

$$\begin{aligned} \bigl\vert {Tf(t)} \bigr\vert \le \frac{1}{{{ \vert \kappa _{0} \vert }}} \bigl\vert {g(t)} \bigr\vert + \frac{1}{{{ \vert \kappa _{0} \vert }}} \int _{\alpha }^{\beta }{ \bigl\vert {{G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f(t)} \bigr)} \bigr\vert \,dq} + \sum_{i = 1}^{r} { \biggl\vert \frac{{{\kappa _{i}}}}{{{\kappa _{0}}}} \biggr\vert \bigl\vert {{}_{0}^{C}D_{t}^{{ \alpha _{i}}}f(t)} \bigr\vert } \le b. \end{aligned}$$

Therefore, \(\Vert {Tf} \Vert \le b \), and we can deduce \(T({\Pi _{0}}) \subset {\Pi _{0}} \). Furthermore, for any \({t_{1}}, {t_{2}} \in \Omega _{0} \) such that \({t_{2}}>{t_{1}} \), we have

$$\begin{aligned} Tf({t_{2}}) - Tf({t_{1}}) ={} & \frac{1}{\kappa _{0}} \bigl(g({t_{2}}) - g({t_{1}})\bigr) - \frac{1}{\kappa _{0}} \int _{\alpha }^{\beta }{ \bigl( {{G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f({t_{2}})} \bigr) - {G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f({t_{1}})} \bigr)} \bigr)\,dq} \\ & {}- \sum_{i = 1}^{r} {\frac{\kappa _{i}}{\kappa _{0}} \bigl( {{}_{0}^{C}D_{t}^{{\alpha _{i}}}f({t_{2}}) - {}_{0}^{C}D_{t}^{{ \alpha _{i}}}f({t_{1}})} \bigr)}. \end{aligned}$$

Since \({G_{1}} \) is Lipschitz with the constant ς, we get

$$\begin{aligned} \bigl\vert {{G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f({t_{2}})} \bigr) - {G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f({t_{1}})} \bigr)} \bigr\vert \le \varsigma \bigl\vert {{}_{0}^{C}D_{t}^{q}f({t_{2}}) - _{0}^{C}D_{t}^{q}f({t_{1}})} \bigr\vert . \end{aligned}$$

Now we can write

$$\begin{aligned} & \bigl\vert {Tf({t_{2}}) - Tf({t_{1}})} \bigr\vert \\ &\quad \le \frac{1}{ \vert \kappa _{0} \vert } \bigl\vert {g({t_{2}}) - g({t_{1}})} \bigr\vert + \frac{1}{ \vert \kappa _{0} \vert } \int _{\alpha }^{\beta }{ \bigl\vert {{G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f({t_{2}})} \bigr) - {G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f({t_{1}})} \bigr)} \bigr\vert \,dq} \\ &\qquad{} + \sum_{i = 1}^{r} { \biggl\vert \frac{\kappa _{i}}{\kappa _{0}} \biggr\vert \bigl\vert {{}_{0}^{C}D_{t}^{{ \alpha _{i}}}f({t_{2}}) - {}_{0}^{C}D_{t}^{{\alpha _{i}}}f({t_{1}})} \bigr\vert } \\ &\quad\le \frac{1}{ \vert \kappa _{0} \vert } \bigl\vert {g({t_{2}}) - g({t_{1}})} \bigr\vert + \frac{{\varsigma (\beta - \alpha )}}{ \vert \kappa _{0} \vert } \bigl\vert {{}_{0}^{C}D_{t}^{q}f({t_{2}}) - _{0}^{C}D_{t}^{q}f({t_{1}})} \bigr\vert \\ &\qquad{} + \sum_{i = 1}^{r} { \biggl\vert \frac{\kappa _{i}}{\kappa _{0}} \biggr\vert \bigl\vert {{}_{0}^{C}D_{t}^{{ \alpha _{i}}}f({t_{2}}) - {}_{0}^{C}D_{t}^{{\alpha _{i}}}f({t_{1}})} \bigr\vert }. \end{aligned}$$
(10)

Note that if \({t_{2}}\to {t_{1}} \), then the right-hand side of (10) tends to zero. Therefore, \(T: {\Pi _{0}} \to {\Pi _{0}} \) is equicontinuous, and consequently, from the Arzela–Ascoli theorem [12], the closure of \(T({\Pi _{0}}) \) is compact.

Let

$$\begin{aligned} Tv(t) = \frac{1}{{{\kappa _{0}}}}{g_{1}}(t) - \frac{1}{{{\kappa _{0}}}} \int _{\alpha }^{\beta }{{G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}v(t)} \bigr)\,dq} - \sum_{i = 1}^{r} { \frac{{{\kappa _{i}}}}{{{\kappa _{0}}}}{}_{0}^{C}D_{t}^{{\alpha _{i}}}v(t)} , \end{aligned}$$

where \(v \in {\Pi _{0}} \). We need to show that T is continuous. Clearly, we have

$$\begin{aligned} \bigl\vert {Tf(t) - Tv(t)} \bigr\vert \le {}& \frac{1}{ \vert \kappa _{0} \vert } \bigl\vert {g(t) - {g_{1}}(t)} \bigr\vert + \frac{1}{ \vert \kappa _{0} \vert } \int _{\alpha }^{\beta }{ \bigl\vert {{G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}f(t)} \bigr) - {G_{1}} \bigl( {q,_{0}^{C}D_{t}^{q}v(t)} \bigr)} \bigr\vert \,dq} \\ & {}+ \sum_{i = 1}^{r} { \biggl\vert \frac{\kappa _{i}}{\kappa _{0}} \biggr\vert \bigl\vert {{}_{0}^{C}D_{t}^{{ \alpha _{i}}}f(t) - {}_{0}^{C}D_{t}^{{\alpha _{i}}}v(t)} \bigr\vert }. \end{aligned}$$

Suppose that, for any \(\varepsilon > 0 \), there exists \(\delta > 0 \) such that \(| f(t)-v(t) |<\delta \). Assume that assumptions \((\mathrm{C1})\)–\((\mathrm{C4}) \) hold, therefore

$$\begin{aligned} \bigl\vert {Tf(t) - Tv(t)} \bigr\vert \leq \varepsilon, \end{aligned}$$

and the proof is completed. □

Now, by using Tychonoff’s fixed point theorem [57], we are going to discuss a global existence result for general DOFDEs.

Theorem 3.2

Assume that

  1. (D1)

    \({G_{1}} \in C({{\mathbb{R}}_{+}} \times {\mathbb{R}}^{n},{ \mathbb{R}}^{n}) \) and \(K \in C({\mathbb{R}_{+}^{2}},{\mathbb{R}}^{n}) \);

  2. (D2)

    \(K ( {q,_{0}^{C}D_{t}^{q} u({t})} ) \) is monotone nondecreasing in u for each \(t\in {\mathbb{R}}_{+} \);

  3. (D3)

    \(\vert {G_{1}} ( {q,_{0}^{C}D_{t}^{q} f} ) \vert \le K ( {q, \vert _{0}^{C}D_{t}^{q} f \vert } ) \) for \(( {q,_{0}^{C}D_{t}^{q} f} ) \in {{\mathbb{R}}_{+}} \times {{\mathbb{R}}^{n}} \);

  4. (D4)

    \(\vert _{0}^{C}D_{t}^{q} f(t) \vert \leq {{}_{0}^{C}D_{t}^{q} u(t)} \) and \(\vert {{}_{0}^{C}D_{t}^{{\alpha _{i}}}f(t)} \vert \le {}_{0}^{C}D_{t}^{{ \alpha _{i}}}u(t) \) for \(i=1,2,\ldots,r \).

Then the following DOFDE

$$\begin{aligned} u(t) = \frac{1}{{{\kappa '_{0}}}}x(t) + \frac{1}{{{\kappa _{0}}}} \int _{\alpha }^{\beta }{K \bigl( {q,_{0}^{C}D_{t}^{q}u(t)} \bigr)\,dq} + \sum_{i = 1}^{r} { \frac{{{\kappa '_{i}}}}{{{\kappa '_{0}}}}{}_{0}^{C}D_{t}^{{ \alpha _{i}}}u(t)}, \end{aligned}$$
(11)

has a solution \(u(t) \) which exists for every \(t\geq 0 \), where \({\kappa '_{0}}\leq \vert {{\kappa }_{0}} \vert \) and \(\vert {{\kappa }_{i}} \vert \leq {\kappa '_{i}} \) for \(i=1,2,\ldots,r \). Also, then for every \(x(t)\in {{\mathbb{R}}_{+}} \) such that \(\vert g(t) \vert \leq x(t) \), there exists a solution \(f(t) \) for Eq. (1) which satisfies \(\vert f(t) \vert \leq u(t) \).

Proof

Let \(\mathcal{V} \) be a real space of all continuous functions from \((0,\infty ) \) into \({\mathbb{R}}^{n} \). The topology on \(\mathcal{V} \) being that induced by the family of pseudo-norms \(\{ {\mathcal{V}_{m}}(f)\} _{{m} = 1}^{\infty }\), where \({\mathcal{V}_{m}}(f) = \mathop{\sup }_{0 \le t \le m} \vert {f(t)} \vert \), for \(f \in \mathcal{V} \). Let \(\{{\mathcal{S}_{m}}\} _{m = 1}^{\infty }\) be a set of neighborhoods, where \({\mathcal{S}_{m}} = \{ f \in \mathcal{V}: {\mathcal{V}_{m}}(f) \le 1\} \). Under this topology, \(\mathcal{V} \) is a linear space, locally convex and complete.

Now consider

$$\begin{aligned} {\mathcal{V}_{0}} = \bigl\{ f \in \mathcal{V}: \bigl\vert {f(t)} \bigr\vert \le u(t), t \ge 0 \bigr\} \subseteq \mathcal{V}, \end{aligned}$$

where \(u(t) \) is a solution of (11). Clearly, in the topology of \(\mathcal{V} \), \(\mathcal{V}_{0} \) is bounded, convex, and closed.

Consider (11) whose fixed point corresponds to a solution of (1). Evidently, in the topology of \(\mathcal{V} \), the map T is compact. Hence, in view of the boundedness of \({\mathcal{V}_{0}} \), the closure of \(T({\mathcal{V}_{0}}) \) is compact.

Considering assumptions \((\mathrm{D1})\)–\((\mathrm{D4}) \) yields

$$\begin{aligned} \bigl\vert {Tf(t)} \bigr\vert & \le \frac{1}{ \vert \kappa _{0} \vert } \bigl\vert {g(t)} \bigr\vert + \frac{1}{ \vert \kappa _{0} \vert } \int _{\alpha }^{\beta }{ \bigl\vert {{G_{1}} \bigl( {q,{{}_{0}^{C}D_{t}^{q}f(t)}} \bigr)} \bigr\vert \,dq} + \sum_{i = 1}^{r} { \biggl\vert \frac{\kappa _{i}}{\kappa _{0}} \biggr\vert \bigl\vert {{}_{0}^{C}D_{t}^{{ \alpha _{i}}}f(t)} \bigr\vert } \\ & \le \frac{1}{ \vert \kappa _{0} \vert } \bigl\vert {g(t)} \bigr\vert + \frac{1}{ \vert \kappa _{0} \vert } \int _{\alpha }^{\beta }{K \bigl( {q, \bigl\vert {{}_{0}^{C}D_{t}^{q}f(t)} \bigr\vert } \bigr)\,dq} + \sum_{i = 1}^{r} { \biggl\vert \frac{{\kappa } _{i}}{{\kappa } _{0}} \biggr\vert \bigl\vert {{}_{0}^{C}D_{t}^{{ \alpha _{i}}}f(t)} \bigr\vert } \\ & \le \frac{1}{\kappa '_{0}}x(t) + \frac{1}{{{\kappa '_{0}}}} \int _{\alpha }^{\beta }{K \bigl( {q,{{}_{0}^{C}D_{t}^{q}u(t)}} \bigr)\,dq} + \sum_{i = 1}^{r} { \frac{\kappa '_{i}}{\kappa '_{0}}{{}_{0}^{C}D_{t}^{{ \alpha _{i}}}u(t)}} = u(t). \end{aligned}$$

Since \(u(t) \) is a solution of (11), using the definition of \(\mathcal{V}_{0}\) gives \(\vert {Tf(t)} \vert \le u(t) \). Thus, \(T({\mathcal{V}_{0}}) \subset {\mathcal{V}_{0}}\), and from Tychonoff’s fixed point theorem [57], T has a fixed point in \({\mathcal{V}_{0}} \). Therefore, the proof of this theorem is completed. □

Now we are going to prove the uniqueness of the solution for general DOFDEs.

Theorem 3.3

Let \({G_{1}} \in C(\mathbb{R} \times {\mathbb{R}}^{n},{\mathbb{R}}^{n}) \), \(f \in C(\Omega,{\mathbb{R}}^{n}) \). Assume that there exists \(0 < L_{j} < 1 \) \((j=0,1,\ldots,r) \) such that

$$\begin{aligned} & \bigl\vert {{G_{1}} \bigl( {q,{{}_{0}^{C}D_{t}^{q}f(t)}} \bigr) - {G_{1}} \bigl( {q,{{}_{0}^{C}D_{t}^{q}{f_{1}}(t)}} \bigr)} \bigr\vert \le {L_{0}} \bigl\vert {f(t) - {f_{1}}(t)} \bigr\vert , \\ & \bigl\vert {{{}_{0}^{C}D_{t}^{{\alpha _{i}}}f(t)} - {{}_{0}^{C}D_{t}^{{ \alpha _{i}}}{f_{1}}(t)}} \bigr\vert \le {L_{i}} \bigl\vert {f(t) - {f_{1}}(t)} \bigr\vert . \end{aligned}$$

If \(( \frac{{L_{0}}{(\beta - \alpha )}}{ \vert \kappa _{0} \vert } + \sum_{i = 1}^{r} { \vert \frac{\kappa _{i}}{\kappa _{0}} \vert {L_{i}}} ) < 1 \), then the general DOFDE has a unique solution.

Proof

Let

$$\begin{aligned} T{f_{1}}(t) = \frac{1}{\kappa _{0}}g(t) - \frac{1}{{{\kappa _{0}}}} \int _{\alpha }^{\beta }{{G_{1}} \bigl( {q,{{}_{0}^{C}D_{t}^{q}{f_{1}}(t)}} \bigr)\,dq} - \sum_{i = 1}^{r} { \frac{{{\kappa _{i}}}}{{{\kappa _{0}}}}{{}_{0}^{C}D_{t}^{{\alpha _{i}}}{f_{1}}(t)}},\quad t \in \Omega. \end{aligned}$$

Then we have

$$\begin{aligned} \bigl\vert {Tf(t) - T{f_{1}}(t)} \bigr\vert \le {}& \frac{1}{ \vert \kappa _{0} \vert } \int _{\alpha }^{\beta }{ \bigl\vert {{G_{1}} \bigl( {q,{{}_{0}^{C}D_{t}^{q}f(t)}} \bigr) - {G_{1}} \bigl( {q,{{}_{0}^{C}D_{t}^{q}{f_{1}}(t)}} \bigr)} \bigr\vert \,dq} \\ &{} + \sum_{i = 1}^{r} { \biggl\vert \frac{\kappa _{i}}{\kappa _{0}} \biggr\vert \bigl\vert {{{}_{0}^{C}D_{t}^{{ \alpha _{i}}}f(t)} - {{}_{0}^{C}D_{t}^{{\alpha _{i}}}{f_{1}}(t)}} \bigr\vert } \\ \le {}& \frac{{{L_{0}}(\beta - \alpha )}}{ \vert \kappa _{0} \vert } \bigl\vert {f(t) - {f_{1}}(t)} \bigr\vert + \sum_{i = 1}^{r} { \biggl\vert \frac{\kappa _{i}}{\kappa _{0}} \biggr\vert {L_{i}} \bigl\vert {f(t) - {f_{1}}(t)} \bigr\vert } \\ < {} & \Biggl( \frac{{L_{0}}{(\beta - \alpha )}}{ \vert \kappa _{0} \vert } + \sum_{i = 1}^{r} { \biggl\vert \frac{\kappa _{i}}{\kappa _{0}} \biggr\vert {L_{i}}} \Biggr) \bigl\vert {f(t) - {f_{1}}(t)} \bigr\vert \end{aligned}$$

for any \(t \in \Omega \) and \({f}, {f_{1}} \in C(\Omega,{\mathbb{R}}^{n}) \). Therefore,

$$\begin{aligned} \bigl\Vert {Tf(t) - T{f_{1}}(t)} \bigr\Vert \leq \Biggl( \frac{{L_{0}}{(\beta - \alpha )}}{ \vert \kappa _{0} \vert } + \sum_{i = 1}^{r} { \biggl\vert \frac{\kappa _{i}}{\kappa _{0}} \biggr\vert {L_{i}}} \Biggr) \Vert {f - {f_{1}}} \Vert . \end{aligned}$$

Since \(( \frac{{L_{0}}{(\beta - \alpha )}}{ \vert \kappa _{0} \vert } + \sum_{i = 1}^{r} { \vert \frac{\kappa _{i}}{\kappa _{0}} \vert {L_{i}}} ) <1 \), then T is a contraction map in \(C(\Omega,{\mathbb{R}}^{n}) \). Consequently, it has a unique fixed point, and therefore the general DOFDE has a unique solution \({f} \in C(\Omega,{\mathbb{R}}^{n}) \). □

4 The methods of solution

4.1 Explanation of the SKCWs method

In this section, without loss of generality we suppose that \(\beta \geq \alpha _{r} \). Now we approximate \({{}_{0}^{C}D{}_{t}^{\beta }}f(t ) \) by the SKCWs as follows:

$$\begin{aligned} {{}_{0}^{C}D{}_{t}^{\beta }}f(t ) \simeq {{\hat{F}}^{T}} \Psi (t ). \end{aligned}$$

By applying Eqs. (3) and (9), one can obtain

$$\begin{aligned} f(t ) \simeq {{\hat{F}}^{T}}\widehat{\Psi }(t,\beta ) + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}}{t ^{j}}}. \end{aligned}$$
(12)

Now we take the operator \({{}_{0}^{C}D{}_{t}^{q}} \) of Eq. (12). So, we have

$$\begin{aligned} {{}_{0}^{C}D{}_{t}^{q}}f(t ) \simeq {{\hat{F}}^{T}}\widehat{\Psi }(t, \beta - q) + \sum _{j = 0}^{ \lceil \beta \rceil - 1} {\frac{{f_{0}^{(j)}}}{{j!}} {{}_{0}^{C}D{}_{t}^{q}} \bigl({t ^{j}}\bigr)}. \end{aligned}$$

Note that from properties (4) and (5), \({{}_{0}^{C}D{}_{t}^{q}}({t ^{j}}) \) can be determined.

Also, we take the operator \({{}_{0}^{C}D{}_{t}^{\alpha _{i}}}, i=1,2,\ldots, r \), of Eq. (12). Using the obtained results in (1) gives

$$\begin{aligned} & \int _{\alpha }^{\beta }{{G_{1}} \Biggl( {q,{{ \hat{F}}^{T}}\widehat{\Psi }(t ,\beta - q) + \sum _{j = 0}^{ \lceil \beta \rceil - 1} {\frac{{f_{0}^{(j)}}}{{j!}} {{}_{0}^{C}D{}_{t}^{q}} \bigl({t ^{j}}\bigr)} } \Biggr)\,dq} + {G_{2}} \Biggl( {t,{{ \hat{F}}^{T}}\widehat{\Psi }(t, \beta )} \\ &\quad{} + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}}{t ^{j}}}, {{\hat{F}}^{T}}\widehat{\Psi }(t, \beta - {\alpha _{1}}) + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}} {{}_{0}^{C}D{}_{t}^{{ \alpha _{1}}}} \bigl({t ^{j}}\bigr)}, \ldots,{{\hat{F}}^{T}}\widehat{\Psi }(t, \beta - {\alpha _{r}}) \\ &\quad{} + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}} {{}_{0}^{C}D{}_{t}^{{\alpha _{r}}}} \bigl({t ^{j}}\bigr)} \Biggr) \simeq g(t ). \end{aligned}$$

Using the Gauss–Legendre formula and collocating the obtained equation at

$$\begin{aligned} {t _{m}}= \frac{(m-0.5) {t_{f}}}{{2^{k}}M},\quad m=1,2,\ldots, {2^{k}}M, \end{aligned}$$

leads to

$$\begin{aligned} &\sum_{n = 1}^{N'} {\frac{{\beta - \alpha }}{2}{w_{n}} {G_{1}} \Biggl( {\frac{{\beta + \alpha }}{2} + \frac{{\beta - \alpha }}{2}{ \tau _{n}},{{\hat{F}}^{T}}\widehat{\Psi } \biggl( {{t _{m}},\beta - \biggl( {\frac{{\beta + \alpha }}{2} + \frac{{\beta - \alpha }}{2}{ \tau _{n}}} \biggr)} \biggr)} } \\ &\quad{} + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}} \bigl({{}_{0}^{C}D{}_{t}^{ ( { \frac{{\beta + \alpha }}{2} + \frac{{\beta - \alpha }}{2}{\tau _{n}}} )}} \bigl(t^{j}\bigr) \bigr)_{t={t _{m}}} } \Biggr) + {G_{2}} \Biggl( {{t _{m}},{{\hat{F}}^{T}} \widehat{\Psi }({t _{m}},\beta ) } \\ &\quad{} + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}}t _{m}^{j}},{{\hat{F}}^{T}}\widehat{\Psi }({t _{m}},\beta - {\alpha _{1}}) + \sum _{j = 0}^{ \lceil \beta \rceil - 1} {\frac{{f_{0}^{(j)}}}{{j!}} \bigl({{}_{0}^{C}D{}_{t}^{{ \alpha _{1}}}} \bigl(t^{j}\bigr) \bigr)_{t={t _{m}}}}, \ldots,{{ \hat{F}}^{T}} \widehat{\Psi }({t _{m}},\beta - {\alpha _{r}}) \\ & \quad{} + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}} \bigl({{}_{0}^{C}D{}_{t}^{{\alpha _{r}}}} \bigl(t^{j}\bigr) \bigr)_{t={t _{m}}}} \Biggr) \simeq g({t _{m}}), \end{aligned}$$

where \({w_{n}} \) and \({\tau _{n}} \) are weights and nods of Gauss–Legendre quadrature rule [9], respectively. By using the “fsolve” command of Maple 2018, we solve the arising system, and then we determine F̂. Finally, from Eq. (7), an approximate solution for Eqs. (1) and (2) can be obtained.

4.2 Explanation of the SFOJPs method

Now similar to Sect. 4.1, by using SFOJPs, we convert Eqs. (1) and (2) to a system of equations as follows:

$$\begin{aligned} &\sum_{n' = 1}^{N''} {\frac{{\beta - \alpha }}{2}{w_{n'}} {G_{1}} \Biggl( {\frac{{\beta + \alpha }}{2} + \frac{{\beta - \alpha }}{2}{ \tau _{n'}},{{\tilde{F}}^{T}}\widehat{\Phi } \biggl( {{t _{m'}},\beta - \biggl( {\frac{{\beta + \alpha }}{2} + \frac{{\beta - \alpha }}{2}{ \tau _{n'}}} \biggr)} \biggr)} } \\ &\quad{} + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}} \bigl({{}_{0}^{C}D{}_{t}^{ ( { \frac{{\beta + \alpha }}{2} + \frac{{\beta - \alpha }}{2}{\tau _{n'}}} )}} \bigl(t^{j}\bigr) \bigr)_{t={t _{m'}}} } \Biggr) + {G_{2}} \Biggl( {{t _{m'}},{{\tilde{F}}^{T}} \widehat{\Phi }({t _{m'}},\beta ) } \\ &\quad{} + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}}t _{m'}^{j}}, {{\tilde{F}}^{T}} \widehat{\Phi }({t _{m'}},\beta - {\alpha _{1}}) + \sum _{j = 0}^{ \lceil \beta \rceil - 1} {\frac{{f_{0}^{(j)}}}{{j!}} \bigl({{}_{0}^{C}D{}_{t}^{{\alpha _{1}}}} \bigl(t^{j}\bigr) \bigr)_{t={t _{m'}}}} , \ldots,{{ \tilde{F}}^{T}}\widehat{\Phi }({t _{m'}},\beta - {\alpha _{r}}) \\ &\quad{} + \sum_{j = 0}^{ \lceil \beta \rceil - 1} { \frac{{f_{0}^{(j)}}}{{j!}} \bigl({{}_{0}^{C}D{}_{t}^{{\alpha _{r}}}} \bigl(t^{j}\bigr) \bigr)_{t={t _{m'}}}} \Biggr) \simeq g({t _{m'}}), \end{aligned}$$

where \({t _{m'}} \), \({m'}=0,1,\ldots,N \), are roots of SFOJPs. Also, \({w_{n'}} \) and \({\tau _{n'}} \) are weights and nods of Gauss–Legendre quadrature rule [9], respectively. By the “fsolve” command of Maple 2018, we solve the above system, and then the unknown vector F̃ can be determined. Finally, from Eq. (8), we obtain an approximate solution for Eqs. (1) and (2).

5 Error bounds

5.1 Error bounds for the SKCWs method

In this subsection, we present error bounds for the SKCWs method. To do this, we define

$$\begin{aligned} &{{ \langle u,v \rangle }_{\omega }} = \int _{0}^{t_{f}} {u(t)v(t){ \omega }(t) \,{d}t},\quad \forall u,v \in L_{\omega }^{2} \bigl([0,{t_{f}} )\bigr), \\ &{ \Vert u \Vert _{\omega }} = { \biggl( \int _{0}^{t_{f}} {{u^{2}}(t){ \omega }(t) \,{d}t } \biggr)^{\frac{1}{2}}}, \quad\forall u \in L_{\omega }^{2} \bigl([0,{t_{f}})\bigr), \end{aligned}$$

which are inner product and norm on the space \(L_{\omega }^{2} ([0,{t_{f}})) \), respectively.

Now we recall the following theorems from our previous work [47].

Theorem 5.1

Let \(f(t)\in L_{\omega }^{2} ([0,{t_{f}}))\) with \(\vert {f''(t)} \vert \le \mathfrak{L}\). The Eq. (7) converges uniformly to \(f(t)\) and the coefficients in (6) explicitly satisfy

$$\begin{aligned} \vert {\hat{f}}_{i,j} \vert < 4\sqrt{2{t_{f}}\pi } \mathfrak{L}\frac{1}{i^{\frac{5}{2}}{(j + 1)}^{2}}, \quad i \ge 1,~ j \ge 0. \end{aligned}$$

Theorem 5.2

Let \(f(t)\in L_{\omega }^{2} ([0,{t_{f}})) \). Then we have

$$\begin{aligned} { \Vert {f - {f_{{2^{k}},M - 1}}} \Vert _{\omega}} < 4 \sqrt{2{t_{f}} \pi } {\mathfrak{L}} { \Biggl( {\sum _{i = 0}^{\infty }{\sum_{j = M}^{\infty }{ \frac{1}{{{{i}^{5}}{{(j + 1)}^{4}}}}} } } + { \sum_{i = {2^{k}} + 1}^{\infty }{ \sum_{j = 0}^{\infty }{ \frac{1}{{{{i}^{5}}{{(j + 1)}^{4}}}}} } } \Biggr)^{\frac{1}{2}}}. \end{aligned}$$

Theorem 5.3

Let \({}_{0}^{C}D_{t}^{\alpha _{l}} f(t) \in L_{\omega }^{2} ([0,{t_{f}})) \) and \(\vert {}_{0}^{C}D_{t}^{\alpha _{l} +2} f(t) \vert \leq \mathfrak{L}_{l}\) for \(l=1,2,\ldots, r \). Then we have

$$\begin{aligned} \bigl\Vert {{}_{0}^{C}D_{t}^{\alpha _{l}} f - {{ \bigl( {{}_{0}^{C}D_{t}^{ \alpha _{l}} f} \bigr)}_{{2^{k}},M - 1}}} \bigr\Vert _{\omega } < 4 \sqrt{2{t_{f}} \pi } {\mathfrak{L}_{l}} \Biggl( \sum_{i = 0}^{\infty }{ \sum_{j = M}^{\infty }{ \frac{1}{{{i^{5}}{{(j + 1)}^{4}}}}} } + \sum_{i = {2^{k}} + 1}^{\infty }{\sum _{j = 0}^{\infty }{ \frac{1}{{{i^{5}}{{(j + 1)}^{4}}}}} } \Biggr)^{\frac{1}{2}}. \end{aligned}$$

5.2 Error bounds for the SFOJPs method

Here, we discuss error bounds for the SFOJPs method. To do this, first, we define the following inner product and norm on the weighted space \(L_{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}^{2} ([0,{t_{f}}]) \):

$$\begin{aligned} &{{ \langle u,v \rangle }_{{w_{t_{f}}^{(\lambda,\theta, \vartheta )}}}} = \int _{0}^{t_{f}} {u(t)v(t){w_{t_{f}}^{(\lambda, \theta,\vartheta )}}(t) \,{d}t},\quad \forall u,v \in L_{w_{t_{f}}^{( \lambda,\theta,\vartheta )}}^{2} \bigl([0,{t_{f}}]\bigr), \\ &{ \Vert u \Vert _{{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}}} = { \biggl( \int _{0}^{t_{f}} {{u^{2}}(t){w_{t_{f}}^{(\lambda,\theta, \vartheta )}}(t) \,{d}t } \biggr)^{\frac{1}{2}}},\quad \forall u \in L_{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}^{2} \bigl([0,{t_{f}}]\bigr). \end{aligned}$$

Let

$$\begin{aligned} {{\Lambda }_{N}} = \operatorname{span} \bigl\{ {{ \mathcal{J}}_{i}^{(\lambda,\theta, \vartheta )}(t),~ 0\leq i\leq N } \bigr\} , \end{aligned}$$
(13)

be the fractional-polynomial space of finite dimension.

Theorem 5.4

Let \({}_{0}^{C}D_{t}^{j \lambda } f(t) \in C([0,{t_{f}}])\), for \(j=0,1,\ldots,N\). If \({f_{N}}(t)\) is the best approximation to \(f(t)\) from \({{\Lambda }_{N}}\), then

$$\begin{aligned} { \Vert {f - {f_{N}}} \Vert _{{w_{t_{f}}^{(\lambda,\theta, \vartheta )}}}} \le \frac{{\mathcal{L}}}{{\Gamma ((N + 1)\lambda + 1)}}\sqrt{ \frac{{t_{f}^{(2N + 3 + \vartheta + \theta )\lambda }\Gamma (1 + \theta )\Gamma (2N + 3 + \vartheta )}}{{\Gamma (4 + 2N + \theta + \vartheta )}}} , \end{aligned}$$
(14)

where \(\mathcal{L} \ge \vert {{}_{0}^{C}D_{t}^{(N + 1)\lambda }f(t)} \vert \), for \(t \in [0,{t_{f}}]\).

Proof

Since \({f_{N}}(t)\) is the best approximation to \(f(t)\) from \({{\Lambda }_{N}}\), defined in (13), we have

$$\begin{aligned} { \Vert {f - {f_{N}}} \Vert _{{w_{t_{f}}^{(\lambda,\theta, \vartheta )}}}} \le { \Vert {f - u} \Vert _{{w_{t_{f}}^{( \lambda,\theta,\vartheta )}}}}, \quad\forall u(t) \in {\Lambda _{N}}. \end{aligned}$$

Considering the generalized Taylors formula \(u(t) = \sum_{j = 0}^{N} { \frac{{{t^{j\lambda }}}}{{\Gamma (j\lambda + 1)}} ( {}_{0}^{C}D_{t}^{j \lambda }u ) ({0^{+} })}\) yields

$$\begin{aligned} \bigl\vert {f(t) - u(t)} \bigr\vert = \Biggl\vert {f(t) - \sum_{j = 0}^{N} {\frac{{{t^{j\lambda }}}}{{\Gamma (j\lambda + 1)}} \bigl( {}_{0}^{C}D_{t}^{j \lambda }u \bigr) \bigl({0^{+} }\bigr)} } \Biggr\vert \le \mathcal{L} \frac{{{t^{(N + 1)\lambda }}}}{{\Gamma ((N + 1)\lambda + 1)}}. \end{aligned}$$
(15)

Taking \({L_{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}^{2}}\)-norm in both sides of inequality (15) leads to

$$\begin{aligned} \Vert {f - u} \Vert _{{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}}^{2} & \le \frac{{\mathcal{L}^{2}}}{{{{(\Gamma ((N + 1)\lambda + 1))}^{2}}}} \int _{0}^{{t_{f}}} {{t^{2(N + 1)\lambda }} {w_{t_{f}}^{(\lambda, \theta,\vartheta )}}\,{d}t} \\ &=\frac{{\mathcal{L}^{2}}}{{{{(\Gamma ((N + 1)\lambda + 1))}^{2}}}} \lambda \int _{0}^{{t_{f}}} {{t^{\lambda (2N + 3 + \vartheta ) - 1}} {{ \bigl(t_{f}^{\lambda }- {t^{\lambda }}\bigr)}^{\theta }} \,{d}t}. \end{aligned}$$
(16)

Let \(z = t_{f}^{\lambda }- {t^{\lambda }} \). Then we obtain

$$\begin{aligned} \lambda \int _{0}^{{t_{f}}} {{t^{\lambda (2N + 3 + \vartheta ) - 1}} {{ \bigl(t_{f}^{\lambda }- {t^{\lambda }}\bigr)}^{\theta }} \,{d}t} = \int _{0}^{t_{f}^{\lambda }} {{{ \bigl( {t_{f}^{\lambda }- z} \bigr)}^{2N + 2 + \vartheta }} {z^{\theta }}\,dz}. \end{aligned}$$
(17)

Now setting \(s = \frac{z}{{t_{f}^{\lambda }}} \) gives

$$\begin{aligned} \int _{0}^{t_{f}^{\lambda }} {{{ \bigl( {t_{f}^{\lambda }- z} \bigr)}^{2N + 2 + \vartheta }} {z^{\theta }}\,dz} & = t_{f}^{(2N + 3 + \vartheta + \theta )\lambda } \int _{0}^{1} {{{ ( {1 - s} )}^{2N + 2 + \vartheta }} {s^{\theta }}\,ds} \\ & = t_{f}^{(2N + 3 + \vartheta + \theta )\lambda } \frac{{\Gamma (1 + \theta )\Gamma (2N + 3 + \vartheta )}}{{\Gamma (4 + 2N + \theta + \vartheta )}}. \end{aligned}$$
(18)

By substituting the above relation into (17) and from (16), we can write

$$\begin{aligned} \Vert {f - u} \Vert _{{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}}^{2} \le \frac{{\mathcal{L}^{2}}}{{{{(\Gamma ((N + 1)\lambda + 1))}^{2}}}}t_{f}^{(2N + 3 + \vartheta + \theta )\lambda } \frac{{\Gamma (1 + \theta )\Gamma (2N + 3 + \vartheta )}}{{\Gamma (4 + 2N + \theta + \vartheta )}}. \end{aligned}$$
(19)

By taking the square root of (19), we obtain inequality (14). □

Theorem 5.5

Let \(_{0}^{C}D_{t}^{j \lambda + \alpha _{l}} f(t) \in C([0,{t_{f}}])\). If \({ ( {{}_{0}^{C}D_{t}^{\alpha _{l}} f} )}_{N} (t)\) is the best approximation to \({{}_{0}^{C}D_{t}^{\alpha _{l}} f}(t)\) from \({{\Lambda }_{N}}\), then

$$\begin{aligned} & \bigl\Vert {{}_{0}^{C}D_{t}^{\alpha _{l}} f - {{ \bigl( {{}_{0}^{C}D_{t}^{ \alpha _{l}} f} \bigr)}_{N}}} \bigr\Vert _{{w_{t_{f}}^{(\lambda, \theta,\vartheta )}}} \\ &\quad \leq \frac{{{\mathcal{L}_{l} }}}{{\Gamma ((N + 1)\lambda + 1)}} \sqrt{ \frac{{t_{f}^{(2N + 3 + \vartheta + \theta )\lambda }\Gamma (1 + \theta )\Gamma (2N + 3 + \vartheta )}}{{\Gamma (4 + 2N + \theta + \vartheta )}}} , \end{aligned}$$
(20)

where \({\mathcal{L}_{l} } \ge \vert {{}_{0}^{C}D_{t}^{(N + 1)\lambda + { \alpha _{l}} }f(t)} \vert \), for \(l=1,2,\ldots,r\) and \(t \in [0,{t_{f}}]\).

Proof

Since \({{ ( {{}_{0}^{C}D_{t}^{{\alpha _{l}}}f} )}_{N}}(t)\) is the best approximation to \({{{{}_{0}^{C}D_{t}^{{\alpha _{l}}}} }}f(t)\) from \({{\Lambda }_{N}}\), we have

$$\begin{aligned} { \bigl\Vert {{}_{0}^{C}D_{t}^{{\alpha _{l}}}f - {{ \bigl( {{}_{0}^{C}D_{t}^{{ \alpha _{l}}}f} \bigr)}_{N}}} \bigr\Vert _{{w_{t_{f}}^{(\lambda, \theta,\vartheta )}}}} \le { \bigl\Vert {{}_{0}^{C}D_{t}^{{\alpha _{l}}}f - _{0}^{C}D_{t}^{{\alpha _{l}}}u} \bigr\Vert _{{w_{t_{f}}^{(\lambda, \theta,\vartheta )}}}},\quad \forall u(t) \in {\Lambda _{N}}. \end{aligned}$$

Considering the generalized Taylor formula \({}_{0}^{C}D_{t}^{{\alpha _{l}}}u(t) = \sum_{j = 0}^{N} { \frac{{{t^{j\lambda }}}}{{\Gamma (j\lambda + 1)}} ( {}_{0}^{C}D_{t}^{j \lambda + {\alpha _{l}}}u ) ({0^{+} })}\) yields

$$\begin{aligned} \bigl\vert {{}_{0}^{C}D_{t}^{{\alpha _{l}}}f(t) - _{0}^{C}D_{t}^{{\alpha _{l}}}u(t)} \bigr\vert & = \Biggl\vert {{}_{0}^{C}D_{t}^{{\alpha _{l}}}f(t) - \sum_{j = 0}^{N} { \frac{{{t^{j\lambda }}}}{{\Gamma (j\lambda + 1)}} \bigl( {}_{0}^{C}D_{t}^{j \lambda + {\alpha _{l}}}u \bigr) \bigl({0^{+} }\bigr)} } \Biggr\vert \\ & \le {\mathcal{L}_{l}} \frac{{{t^{(N + 1)\lambda }}}}{{\Gamma ((N + 1)\lambda + 1)}}. \end{aligned}$$
(21)

Taking \({L_{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}^{2}}\)-norm in both sides of inequality (21) leads to

$$\begin{aligned} \bigl\Vert {{}_{0}^{C}D_{t}^{{\alpha _{l}}}f - _{0}^{C}D_{t}^{{\alpha _{l}}}u} \bigr\Vert _{{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}}^{2} & \le \frac{{\mathcal{L}_{l}^{2}}}{{{{(\Gamma ((N + 1)\lambda + 1))}^{2}}}} \int _{0}^{{t_{f}}} {{t^{2(N + 1)\lambda }} {w_{t_{f}}^{(\lambda, \theta,\vartheta )}}\,{d}t} \\ &= \frac{{\mathcal{L}_{l}^{2}}}{{{{(\Gamma ((N + 1)\lambda + 1))}^{2}}}} \lambda \int _{0}^{{t_{f}}} {{t^{\lambda (2N + 3 + \vartheta ) - 1}} {{ \bigl(t_{f}^{\lambda }- {t^{\lambda }}\bigr)}^{\theta }} \,{d}t}. \end{aligned}$$
(22)

From (17), (18), and (22), we can write

$$\begin{aligned} \bigl\Vert {{}_{0}^{C}D_{t}^{{\alpha _{l}}}f - _{0}^{C}D_{t}^{{\alpha _{l}}}u} \bigr\Vert _{{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}}^{2} & \le \frac{{\mathcal{L}_{l}^{2}}}{{{{(\Gamma ((N + 1)\lambda + 1))}^{2}}}} \int _{0}^{{t_{f}}} {{t^{2(N + 1)\lambda }} {w_{t_{f}}^{(\lambda, \theta,\vartheta )}}\,{d}t} \\ & = \frac{{\mathcal{L}_{l}^{2} t_{f}^{(2N + 3 + \vartheta + \theta )\lambda }\Gamma (1 + \theta )\Gamma (2N + 3 + \vartheta )}}{{{{(\Gamma ((N + 1)\lambda + 1))}^{2}}\Gamma (4 + 2N + \theta + \vartheta )}}. \end{aligned}$$
(23)

Now we take the square root of both sides of (23), and therefore inequality (20) can be obtained. □

Theorem 5.6

Let \({}_{0}^{C}D_{t}^{j \lambda } f(t)\), \({}_{0}^{C}D_{t}^{j \lambda + q} f(t)\), \({}_{0}^{C}D_{t}^{j \lambda + \alpha _{l}} f(t) \in C([0,{t_{f}}]) \). Suppose that \(\vert {}_{0}^{C}D_{t}^{j \lambda } f(t) \vert \leq \mathcal{L}\), \(\vert {}_{0}^{C}D_{t}^{j \lambda + q} f(t) \vert \leq \mathcal{L}_{q}\), \(\vert {}_{0}^{C}D_{t}^{j \lambda + \alpha _{l} } f(t) \vert \leq \mathcal{L}_{l}\), for \(l=1,2,\ldots,r\). In Eq. (1), let \(G_{1} \) be Lipschitz with the constant μ. Therefore, the error bound of the SFOJPs method for the modified equation is

$$\begin{aligned} { \bigl\Vert {E_{{k}}^{M}} \bigr\Vert _{{w_{t_{f}}^{(\lambda,\theta, \vartheta )}}}} \leq \frac{ ( {\mu } (\beta - \alpha ) + (r+1){\kappa } )\rho }{\Gamma ((N + 1)\lambda + 1)} \sqrt{ \frac{{t_{f}^{(2N + 3 + \vartheta + \theta )\lambda }\Gamma (1 + \theta )\Gamma (2N + 3 + \vartheta )}}{{\Gamma (4 + 2N + \theta + \vartheta )}}} , \end{aligned}$$

where \(\kappa = \mathop{\max }_{j = 0, \ldots,r} \{ { \kappa _{j}} \} \) and \(\rho = \mathop{\max }_{l = 1, \ldots,r} \{ \mathcal{L},{\mathcal{L}_{q}},{\mathcal{L}_{l}} \} \).

Proof

Since \(G_{1} \) is Lipschitz with the constant μ, we can write

$$\begin{aligned} { \vert {E_{N}} \vert } ={}& \biggl\vert { \int _{\alpha }^{\beta }{{G_{1}} \bigl(q,{{ \bigl( {{}_{0}^{C}D_{t}^{q} f} \bigr)}_{N}}(t) \bigr)\,dq}} \\ &{} + {G_{2}} \bigl(t,{f_{N}}(t),{{ \bigl( {{}_{0}^{C}D_{t}^{ \alpha _{1}} f} \bigr)}_{N}}(t), \ldots,{{ \bigl( {{}_{0}^{C}D_{t}^{ \alpha _{r}} f} \bigr)}_{N}}(t) \bigr) - g(t) \biggr\vert \\ ={}& \biggl\vert \int _{\alpha }^{\beta }{{G_{1}} \bigl(q,{{ \bigl( {{}_{0}^{C}D_{t}^{q} f} \bigr)}_{N}}(t) \bigr)\,dq} + {G_{2}} \bigl(t,{f_{N}}(t),{{ \bigl( {{}_{0}^{C}D_{t}^{\alpha _{1}} f} \bigr)}_{N}}(t), \ldots, {{ \bigl( {{}_{0}^{C}D_{t}^{\alpha _{r}} f} \bigr)}_{N}}(t) \bigr) \\ &{} - \int _{\alpha }^{\beta }{{G_{1}} \bigl(q,{{}_{0}^{C}D{}_{t}^{q}}f(t) \bigr)\,dq} - {G_{2}} \bigl(t,f(t),{{}_{0}^{C}D{}_{t}^{{\alpha _{1}}}}f(t), \ldots,{{}_{0}^{C}D{}_{t}^{{\alpha _{r}}}}f(t) \bigr) \biggr\vert \\ \le{} & {\mu } \int _{\alpha }^{\beta }{{{ \bigl\vert {{{}_{0}^{C}D{}_{t}^{q}}f(t) - {{ \bigl( {{}_{0}^{C}D_{t}^{q} f} \bigr)}_{N}}(t)} \bigr\vert }}\,dq} + { \kappa } { \bigl\vert {f(t) - {f_{N}}(t)} \bigr\vert } \\ &{}+ {\kappa } { \bigl\vert {{{}_{0}^{C}D{}_{t}^{{\alpha _{1}}}}f(t) - {{ \bigl( {{}_{0}^{C}D_{t}^{\alpha _{1}} f} \bigr)}_{N}}(t)} \bigr\vert } + \cdots + {\kappa } { \bigl\vert {{{}_{0}^{C}D{}_{t}^{{\alpha _{r}}}}f(t) - {{ \bigl( {{}_{0}^{C}D_{t}^{\alpha _{r}} f} \bigr)}_{N}}(t)} \bigr\vert } \\ \le {}& {\mu } \int _{\alpha }^{\beta }{{{ \bigl\Vert {{{}_{0}^{C}D{}_{t}^{q}}f - {{ \bigl( {{}_{0}^{C}D_{t}^{q} f} \bigr)}_{N}}} \bigr\Vert }_{w_{t_{f}}^{( \lambda,\theta,\vartheta )}}}\,dq} + {\kappa } { \Vert {f - {f_{N}}} \Vert _{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}} \\ &{}+ {\kappa } { \bigl\Vert {{{}_{0}^{C}D{}_{t}^{{\alpha _{1}}}}f - {{ \bigl( {{}_{0}^{C}D_{t}^{\alpha _{1}} f} \bigr)}_{N}}} \bigr\Vert _{w_{t_{f}}^{( \lambda,\theta,\vartheta )}}} + \cdots + {\kappa } { \bigl\Vert {{{}_{0}^{C}D{}_{t}^{{ \alpha _{r}}}}f - {{ \bigl( {{}_{0}^{C}D_{t}^{\alpha _{r}} f} \bigr)}_{N}}} \bigr\Vert _{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}}. \end{aligned}$$

By using Theorems 5.4 and 5.5, we obtain

$$\begin{aligned} { \Vert {E_{N}} \Vert _{{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}}} \leq \frac{{\mu } (\beta - \alpha ) {\mathcal{L}_{q}} + {\kappa } ( {\mathcal{L}} + {\mathcal{L}_{1}} + \cdots + {\mathcal{L}_{r}} )}{{\Gamma ((N + 1)\lambda + 1)}} \sqrt{ \frac{{t_{f}^{(2N + 3 + \vartheta + \theta )\lambda }\Gamma (1 + \theta )\Gamma (2N + 3 + \vartheta )}}{{\Gamma (4 + 2N + \theta + \vartheta )}}} . \end{aligned}$$

Let

$$\begin{aligned} \rho = \mathop{\max } _{l = 1, \ldots,r} \{ \mathcal{L},{\mathcal{L}_{q}},{ \mathcal{L}_{l}} \}. \end{aligned}$$

Therefore, we get

$$\begin{aligned} { \Vert {E_{N}} \Vert _{{w_{t_{f}}^{(\lambda,\theta,\vartheta )}}}} \leq \frac{ ( {\mu } (\beta - \alpha ) + (r+1){\kappa } )\rho }{\Gamma ((N + 1)\lambda + 1)} \sqrt{ \frac{{t_{f}^{(2N + 3 + \vartheta + \theta )\lambda }\Gamma (1 + \theta )\Gamma (2N + 3 + \vartheta )}}{{\Gamma (4 + 2N + \theta + \vartheta )}}} . \end{aligned}$$

 □

6 Illustrative examples

In this section, we present five problems which are tested by Maple 2018. Also, we obtain the absolute errors by

$$\begin{aligned} \bigl\vert {f(t) - f_{k,M}(t)} \bigr\vert \quad \mbox{and} \quad \bigl\vert {f(t) - f_{N}(t)} \bigr\vert , \quad t\in [0,{t_{f}}),~ k,M,N\in \mathbb{N}. \end{aligned}$$

Note that, in all tables, m̂ denotes the numbers of bases.

Example 6.1

Consider the following nonlinear DOFDE:

$$\begin{aligned} & \int _{0}^{3} {{{ \biggl( { \frac{{\Gamma ( {4.5 - q} )}}{{105\sqrt{\pi }}} {{}_{0}^{C}D{}_{t}^{q}}f(t)} \biggr)}^{\frac{1}{2}}}\,dq} = \frac{{\sqrt[4]{t}(t\sqrt{t} - 1)}}{{2\ln (t)}}, \\ & f(0) = f'(0) = f''(0) = 0, \end{aligned}$$

with the exact solution \(f(t) = {t^{3}}\sqrt{t} \).

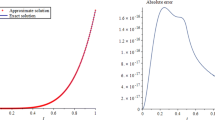
In the above problem, the distributed-order term is discretized with the seven-point Gauss–Legendre quadrature rule. The numerical results at the interval \([0,1)\), obtained by the SKCWs method, are reported in Table 1 by selecting \({\hat{m}} = {2^{k}}M =6,12\). Graphs of the exact and approximate solutions and also absolute errors, obtained by the mentioned method with \(k=2 \), \(M=3 \), are plotted in Fig. 1. This figure and Table 1 illustrate the efficiency and accuracy of the method.

Figure 1
figure 1

Graphs of the obtained results at the interval \([0,1) \) by the SKCWs method with \(k=2 \), \(M=3 \), for Example 6.1

Full size image
Table 1 Absolute errors at the interval \([0,1) \) with \(M = 3 \), for Example 6.1
Full size table

Example 6.2

Consider the DOFDE in the following form [14, 19, 21, 39]:

$$\begin{aligned} & \int _{0}^{2} {\frac{\Gamma (6 - q)}{120} {{}_{0}^{C}D{}_{t}^{q}}f(t)\,dq} = \frac{{{t^{5}} - {t^{3}}}}{{\ln t}}, \\ & f(0) = f'(0) = 0, \end{aligned}$$

with the exact solution \(f(t) = {t^{5}} \).

In the above problem, we discretize the distributed-order term with the eight-point Gauss–Legendre quadrature rule. In Table 2, we report the absolute errors at the interval \([0,1)\) for the SKCWs method by selecting \({\hat{m}} = N+1 = 9,12 \) with \(\lambda =\frac{1}{2}\), \(\theta =\frac{3}{2} \), \(\vartheta =3\); for the SFOJPs method by selecting \({\hat{m}} = {2^{k}}M = 16,20 \); for the hybrid of Legendre polynomials and block-pulse functions (HLBP) method [39] by selecting \({\hat{m}} = NM = 24 \); and for the block-pulse functions (BPFs) method [39] by selecting \({\hat{m}} =N= 32 \). Graphs of the exact and approximate solutions and also absolute errors, obtained by the SKCWs and SFOJPs methods with \(k=1\), \(M=10\), \(N=11\), \(\lambda =\frac{1}{2}\), \(\theta =\frac{3}{2} \), \(\vartheta =3\), are plotted in Fig. 2. This figure and Table 2 show the efficiency and accuracy of the new methods in comparison with the other methods reported in [39].

Figure 2
figure 2

Graphs of the obtained results at the interval \([0,1) \) by the SKCWs and SFOJPs methods with \(k=1\), \(M=10\), \(N=11\), \(\lambda =\frac{1}{2}\), \(\theta =\frac{3}{2} \), \(\vartheta =3\), for Example 6.2

Full size image
Table 2 Absolute errors at the interval \([0,1) \), for Example 6.2
Full size table

Example 6.3

Consider the DOFDE in the following form [19–21, 38, 50, 53]:

$$\begin{aligned} & {f''}(t) + \omega ^{2} f(t) + \sigma (t) = g(t),\qquad f(0) = f'(0) = 0, \\ & \int _{0}^{1} {{a^{q}} {{}_{0}^{C}D{}_{t}^{q}}\sigma (t)\,dq} = \gamma \int _{0}^{1} {{b^{q}} {{}_{0}^{C}D{}_{t}^{q}}f(t)\,dq}. \end{aligned}$$

The above equations describe the motion of the oscillator, where \(\gamma, a, b \) are constants; ω is the eigen frequency of the undamped system; \(g(t) \) is the external forcing function; \(f(t) \) and \(\sigma (t) \) are the displacement and the dissipation force, respectively. In this problem, the forced vibrations of the distributed-order oscillator subjected to the harmonic excitation \(g(t) = {g_{0}} \sin (\Omega t) \) are studied. The solution of this problem is obtained with \(g_{0} = 1 \), \(\Omega = 1.2\omega \), \(\omega = 3 \), and \(\gamma = 1 \). If \(a = b \), the solution is identical to the elastic with \(\omega _{el} = \sqrt{1+\omega ^{2}} = \sqrt{10} \), and the exact solution is

$$\begin{aligned} f(t) = \frac{{{g_{0}}}}{{\omega _{el}^{2} - {\Omega ^{2}}}} \biggl( { \sin \Omega t - \frac{\Omega }{{{\omega _{el}}}}\sin { \omega _{el}}t} \biggr). \end{aligned}$$

In Table 3, we report the absolute errors at the interval \([0,10)\) for the SFOJPs method by selecting \({\hat{m}} = N+1 =39,49 \) with \(\lambda =\frac{1}{2}\), \(\theta =\vartheta =0\); for the second kind Chebyshev wavelets (SKCWs) method [47] by selecting \({\hat{m}} = N({M} + 1) = 52 \); and for the Müntz–Legendre wavelets (MLWs) method [36] by selecting \({\hat{m}} = N({M} + 1) = 60 \). We emphasize that the results reported in [36, 47] have been compared with the results reported in [19, 38, 39, 53], and it was concluded that the methods in [36, 47] are more accurate than the other methods. Therefore, here, we just compare our method with the methods of [36, 47]. Graphs of the exact and approximate solutions and also absolute errors, obtained by the SKCWs and SFOJPs with \(k=4 \), \(M=5 \), \(N=49 \), \(\lambda =\frac{1}{2}\), \(\theta =\vartheta =0\), are plotted in Fig. 3. This figure and Table 3 show the efficiency and accuracy of the SFOJPs method in comparison with the methods reported in [36, 47].

Figure 3
figure 3

Graphs of the obtained results at the interval \([0,10) \) by the SKCWs and SFOJPs methods with \(k=4 \), \(M=5 \), \(N=49 \), \(\lambda =\frac{1}{2}\), \(\theta =\vartheta =0\), for Example 6.3

Full size image
Table 3 Absolute errors at the interval \([0,10) \), for Example 6.3
Full size table

Example 6.4

Consider the following distributed-order fractional relaxation equation [18, 31, 50]:

$$\begin{aligned} & {{}_{0}^{C}D{}_{t}^{p(q)}}f(t) + 0.1 f(t) = 0,\qquad p(q) = 6q(1 - q),\quad 0 \le q \le 1, \\ & f(0) = 1, \end{aligned}$$

with the exact solution [31]

$$\begin{aligned} F(s) = {\mathscr{L}}\bigl\{ f(t)\bigr\} = \frac{\Theta (s)/s}{0.1+\Theta (s)}, \end{aligned}$$

in the Laplace domain, where

$$\begin{aligned} \Theta (s)=\frac{\ln (s) (6s+6)-12s+12}{(\ln (s))^{3}}. \end{aligned}$$

In the above problem, we discretize the distributed-order term with the three-point Gauss–Legendre quadrature rule. In Table 4, we report the absolute errors at the interval \([0,10) \) for the SFOJPs method by selecting \({\hat{m}} = N+1 = 4,9 \) with \(\lambda =\frac{1}{2}\), \(\theta =\frac{3}{2} \), \(\vartheta =3\); and for the Müntz–Legendre wavelets (MLWs) method [36] with \({\hat{m}} = {2^{k-1}}M = 16,32 \). Figure 4 shows that by using 8 number of SFOJPs the obtained results are better than the results of [50] that obtained by using 1000 BPFs for solving this problem.

Figure 4
figure 4

Graphs of the obtained results at the interval \([0,10) \) by the SFOJPs method with \(N=8 \), \(\lambda =\frac{1}{2}\), \(\theta =\frac{3}{2} \), \(\vartheta =3\), for Example 6.4

Full size image
Table 4 Absolute errors at the interval \([0,10) \), for Example 6.4
Full size table

Example 6.5

Consider the following Bagley–Torvik equation [7, 8], where the damping term is expressed in terms of distributed-order derivatives [46]:

$$\begin{aligned} & a {f''}(t) + b {{}_{0}^{C}D{}_{t}^{p(q)}}f(t) + c f(t) = \textstyle\begin{cases} 8, & 0\leq t \leq 1, \\ 0, & t>1, \end{cases}\displaystyle \qquad p(q) = 6q(1 - q),~ 0 \le q \le 1, \\ & f(0) = 0,~ f'(0) = 0. \end{aligned}$$

This equation is called fractional oscillator equation, when the order of damping term is constant.

In the above problem, the distributed-order term is discretized with the three-point Gauss–Legendre quadrature rule. The graph of the approximate solution at the interval \([0,30) \) is plotted in Fig. 5 by using the SKCWs method with \(k=5 \), \(M=3 \), \(a=b=c=1 \). This figure has a good agreement with Fig. 8, reported in [46].

Figure 5
figure 5

The approximate solution at the interval \([0,30) \) by the SKCWs method with \(k=5 \), \(M=3 \), for Example 6.5

Full size image

7 Conclusion

In this research paper, based on Schauder’s and Tychonoff’s fixed point theorems, sufficient conditions for the local and global existence of solutions were provided for general DOFDEs. Also, sufficient conditions were provided for the uniqueness of the solutions. Furthermore, we proposed new methods to solve DOFDEs of the general form in the time domain. By using these methods, the mentioned equations were reduced to systems of algebraic equations. We solved these systems by using the “fsolve” command of Maple 2018. The error bounds of the methods have been discussed. In addition, the presented methods were implemented for two test problems and some famous distributed-order models, such as the model that describes the motion of the oscillator, the distributed-order fractional relaxation equation, and the Bagley–Torvik equation. It showed that by applying the SKCWs and SFOJPs methods, the obtained results are better than the other existing methods. We deduce that the proposed methods are efficient numerical tools for solving DOFDEs.