Abstract
In this paper, we study the rubella disease model with the Caputo–Fabrizio fractional derivative. The mathematical solution of the liver model is presented by a three-step Adams–Bashforth scheme. The existence and uniqueness of the solution are discussed by employing fixed point theory. Finally some numerical simulations are showed to underpin the effectiveness of the used derivative.
Similar content being viewed by others
1 Introduction
Rubella was first described in the mid-eighteenth century. Friedrich Hoffmann made the first clinical description of rubella in 1740, which was confirmed by de Bergen in 1752 and Orlow in 1758 [1]. Rubella, also known as German measles or three-day measles, is an infection caused by the rubella virus and has symptoms that are similar to those of flu. However, the primary symptom of rubella virus infection is the appearance of a rash (exanthem) on the face which spreads to the trunk and limbs and usually fades after three days [2]. It usually spreads through the air via coughs of people who are infected. People are infectious during the week before and after the appearance of the rash [3]. This disease is often mild with half of people not realizing that they are infected [4]. Rubella is a common infection in many areas of the world, and each year about 100,000 cases of congenital rubella syndrome occur [5].
The mathematical model of measles and rubella has been studied by a number of mathematicians (see, for example, [6–10]). It has been demonstrated by many scientists and mathematicians that fractional extensions of mathematical models of integer order represent the natural fact in a very systematic way such as in the approach of Caputo [11], Podlubny [12], Baleanu et al. [13], Haq et al. [14], Atangana et al. [15], Erturk et al. [16], Kilbas et al. [17], Zafar et al. [18–22]. In a very recent attempt, Caputo and Fabrizio [11] propounded a novel fractional derivative having exponential kernel; in addition, Losada and Nieto [23] analyzed the properties of a newly presented fractional derivative. The classical fractional derivatives, especially the Caputo and Riemann derivatives, have their own limitation because their kernel is singular. Since the kernel is employed to describe the memory effect of the physical system, it is obvious that due to this weakness, both derivatives cannot precisely describe the full effect of the memory. Recently, many works related to the fractional equations and applications have been published (see, for example, [24–39]).
Therefore, we use the novel Caputo–Fabrizio (CF) fractional derivative to study the rubella disease model and explain this problem in a better and more efficient manner. We recall some fundamental notions. The Caputo fractional derivative of order α for a continuous function f is defined by
Our second notion is a fractional derivative without singular kernel introduced by Caputo and Fabrizio [11, 34]. Let \(b>0\), \(u\in H^{1}(a,b)\), and \(\alpha \in (0,1)\). The Caputo–Fabrizio derivative of order α for a function f is defined by
where \(t>0\) and \(M(\alpha )\) is a normalization constant depending on α such that \(M(0)=M(1)=1\). It is well known that the Laplace transform plays an important role in the study of ordinary differential equations [23]. Let \(\alpha \in (0,1)\) and \(n\geq 1\). The Laplace transform of CFD is defined by
and \(L[{}^{\mathrm{CF}}D^{(\alpha )}u(t)](s)=\frac{sL[u(t)]-u(0)}{s+\alpha (1-s)}\) (for \(n=0\)),
(for \(n=1\)). The Riemann–Liouville fractional integral of order \(0<\alpha <1\) is defined by [12]
whenever the integral exists. Also, the fractional integral of Caputo–Fabrizio is defined by [23]
Losada and Nieto gave an explicit formula for \(M(\alpha )\) as \(M(\alpha )=\frac{2}{2-\alpha }\) (for \(0<\alpha <1\)). Thus, the fractional Caputo–Fabrizio derivative of order \(0<\alpha <1\) for a function u is given by \({}^{\mathrm{CF}}D^{\alpha } u(t)=\frac{1}{1-\alpha }\int _{0}^{t} \exp (\frac{-\alpha }{1-\alpha }(t-s))u'(s)\,ds\). For \(n\geq 1\) and \(\alpha \in (0,1)\), the fractional derivatives \({}^{\mathrm{CF}}D^{\alpha +n}\) of order \({n+\alpha }\) are defined by \({}^{\mathrm{CF}}D^{\alpha +n} u(t):={{}^{\mathrm{CF}}D^{\alpha }(D^{n} u(t))}\) [26].
2 Mathematical model for the spread of rubella disease
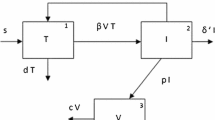
In this section, we investigate the rubella disease model discussed by Koca [8]. He considered the model of rubella disease by employing the Atangana–Baleanu fractional derivative as follows:
where \(S(t)\), \(E(t)\), \(I(t)\), \(R(t)\), \(V(t)\) are susceptible, latent, infectious, recovered, and vaccinated parameters respectively. \(P(a)\) is a parameter for which immunized by vaccination and \(\lambda (a,t)\) is the force of infection of age a at time t and σ is the latent rate and β is the infection rate [40]. In this section, we moderate the system by substituting the time-derivative by the newly introduced Caputo–Fabrizio derivative [11] for \(\alpha \in (0,1)\) given by
with initial conditions
In system (2), the right-hand sides of the equations have dimension \((\mathit{time})^{-1}\). When we change the order of the equations to α, the dimension of the left-hand side would be \((\mathit{time})^{(-\alpha )}\). In order to have the dimensions match, we should change the dimensions of the parameters σ, β, and the system we obtain eventually is
The system state is made up with S, E, I, R, V.
3 Existence and uniqueness of a system of solutions of rubella model
We examine the existence of the system of solutions by applying the fixed point theorem. Employing the fractional integral operator due to Nieto and Losada [23] on equation (3), we obtain
By using the notation presented by Nieto and Losada [23], we get
For clarity, we write
Theorem 1
The kernel\(P_{1}\)satisfies the Lipschitz condition and contraction if the following inequality holds:
Proof
Let S and \(S_{1}\) be two functions, then we assess the following:
Taking \(\gamma _{1}=\lambda (a,t)+P(a)+\mu (a)\) are bounded functions, we get
Hence the Lipschitz condition is satisfied for \(P_{1}\). If additionally
then it is also a contraction for \(P_{1}\). □
Similarly, the kernels \(P_{2}\), \(P_{2}\), \(P_{3}\), \(P_{4}\), \(P_{5}\) satisfy the Lipschitz condition given as follows:
On consideration of the aforesaid kernels, equation (5) becomes
Now, we present the following recursive formula on consideration of the aforesaid kernels, equation (5) becomes
The initial conditions are given as follows:
Now we present the difference between the successive terms in the following manner:
It is worth noticing that
On the other hand,
By using the triangular inequality, we get
Since the kernel satisfies the Lipschitz condition, we have
then we get
Similarly, we get the following results:
By taking the above results, we can present the following theorem.
Theorem 2
Fractional rubella model (3) has a system of solutions under the conditions that we can find\(t_{0}\)such that
Proof
We have considered that the functions \(S(t)\), \(E(t)\), \(I(t)\), \(R(t)\), \(V(t)\) are bounded. Additionally, we have proven that the kernels satisfy the Lipschitz condition, hence by taking the results of equations (19) and (20) and by employing the recursive method, we derive the succeeding relation as follows:
Therefore, the system of functions (15) exists and is smooth. To show that the above functions are a system of solutions of the system of equation (3), we assume
Therefore, we get
By using this process recursively, it yields
Now, taking the limit on equation (25) as n tends to infinity, we get
Similarly, we have
This completes the proof. □
To prove the uniqueness of a system of solutions of equation (3), we present the following theorem.
Theorem 3
The system of equations (3) has a unique system of solutions if the following condition holds:
Proof
Let there exist another system of solutions of (3)
then
Applying the norm on equation (29), we get
By employing the Lipschitz conditions of the kernel, we get
It gives
On the other hand, (28) holds, then
We conclude from (31) and (32) that
Then we get \(S(t)=S_{1}(t)\). Similarly, we have
This completes the proof. □
4 Equilibrium points of the model and asymptotic stability
To determine the equilibrium points of fractional order system (3), we set the right-hand side of the equations to zero
By solving the algebraic equations, we obtain the equilibrium point \(E^{*}=(S^{*},E^{*},I^{*},R^{*},V^{*})\) such that
To investigate the stability of equilibrium point, first consider the fractional-order linear system as follows:
where \(u(t)\in R^{n}\), \(T\in R^{n\times n}\), \(0<\alpha <1\).
Definition 4
([41])
For system (37) with Caputo–Fabrizio fractional derivative, the characteristic equation is given by
Theorem 5
([41])
If\((I-(1-\alpha )T)\)is invertible, then system (37) is asymptotically stable if and only if the roots to the characteristic equation of system (37) have negative real parts.
The Jacobian matrix associated with system (3) is given as follows:
Thus the characteristic equation of system (3) is
Theorem 6
The equilibrium point\(E^{*}\)of model (3) is asymptotically stable if and only if real parts of the roots of the characteristic equation (39) are negative.
Proof
According to the above Jacobian matrix, we have \(J=J(E^{*})\). Therefore, it is sufficient that we compute the roots of equation (39). We have
By solving this algebraic equation, we get
Since \(\alpha \in (0,1)\), then \(s_{1}\), \(s_{2}\), \(s_{3}\), \(s_{4}\) are negative. Hence by using Theorem 5, the equilibrium point \(E^{*}\) of model (3) is asymptotically stable. □
4.1 Numerical method and simulations
In this section, using the Adams–Bashforth scheme, we present a numerical solution for the rubella model (3). Owolabi and Atangana introduced the three-step Adams–Bashforth scheme with the Caputo–Fabrizio fractional derivative [42]. We use this method to find three step Adams–Bashforth scheme for fractional order system (3).
Consider the fractional differential equation with Caputo–Fabrizio derivative
Applying the Caputo–Fabrizio fractional integral on both sides of equation (40), we have
By discretizing the time interval \([0,t]\) in steps of h, we obtain the sequence \(t_{0}=0\), \(t_{j+1}=t_{j}+h\), \(j=0,1,2,\ldots,n-1\), \(t_{j}=t\). By replacing \(t=t_{j+1}\) and \(t=t_{j}\) in equation (41) and computing the difference of the resulting equations, we obtain
By approximating the integral \(\int _{t_{j}}^{t_{j+1}} f(\tau ,x(\tau ))\,d\tau \) with the approximation of \(\int _{t_{j}}^{t_{j+1}} Q_{2}(\tau )\,d\tau \), where \(Q_{2}(\tau )\) is the Lagrange interpolating polynomial of degree two passing through the points \((t_{j-2}, f (t_{j-2},x(t_{j-2})))\), \((t_{j-1}, f (t_{j-1},x(t_{j-1})))\), and \((t_{j}, f (t_{j},x(t_{j})))\). That is,
where \(L_{i}(\tau )\) are the Lagrange basis polynomials on the points \(t_{j-2}\), \(t_{j-1}\), \(t_{j}\). Let \(x_{j}=x(t_{j})\), using the change of variable \(s=\frac{t_{j+1}-\tau }{h}\), substituting for the Lagrange basis polynomials and integrating, we obtain
Then
In this method, the error is
In the following, we obtain the numerical simulations of model (3) using the three-step Adams–Bashforth scheme for Caputo–Fabrizio fractional derivative in equation (44). Consider the vectors \({\mathbf{x}}(t)=(S(t),E(t),I(t),R(t),V(t))\) and \({\mathbf{f}}(t,{\mathbf{x}}(t))=(f_{1}(t,{\mathbf{x}}(t)),f_{2}(t,{\mathbf{x}}(t)), f_{3}(t, {\mathbf{x}}(t)),f_{4}(t,{\mathbf{x}}(t)),f_{5}(t,{\mathbf{x}}(t)))\), where \(f_{i}(t,{\mathbf{x}}(t))\), \(i=1,2,3,4\), are scalar functions that are defined from system (3) as follows:
We write system (3) in the vector form as follows:
Using equation (44), we obtain the solution of system (3) as the following iterative formula:
Assume \({\mathbf{x}}_{0}={\mathbf{x}}(t_{0})=[S(t_{0}), E(t_{0}), I(t_{0}), R(t_{0}), V(t_{0})]^{T}\), \({\mathbf{x}}_{j-2}={\mathbf{x}}(t_{j-2})\), \({\mathbf{x}}_{j-1}={\mathbf{x}}(t_{j-1})\), \({\mathbf{x}}_{j}={\mathbf{x}}(t_{j})\), \({\mathbf{x}}_{j+1}={\mathbf{x}}(t_{j+1})\), then
Thus, we obtain the iterative formulas
For numerical simulations, we utilize the values of the parameters \(B=100\), \(P=0.3\), \(\lambda =0.4\), \(\mu =0.4\), \(\sigma =0.3\), \(\beta =0.4\), \(D=0.2\), and the initial conditions are given by \(S_{0}=300\), \(E_{0}=0\), \(I_{0}=0\), \(R_{0}=0\), \(V_{0}=0\).
The equilibrium point is \(E^{*}=(S^{*}, E^{*}, I^{*}, R^{*}, V^{*})=(90.9, 49.24, 19.87, 21.78, 45.454)\). Fig. (1) shows the plots of the solutions of model (3) for \(\alpha =0.9\). As can be seen, the system is stable at equilibrium point. Figures 2–4 show plots for \(S(t)\), \(E(t)\), \(I(t)\), \(R(t)\), \(V(t)\) in model (3) for the fractional orders \(\alpha =0.9, 0.8, 0.7, 0.6\), respectively. We can observe from these plots that the curves of each variable have the same trend when α is changed. However, their values are slightly different. We can observe from Fig. 2 that the curves of \(S(t)\) are decreasing, and they finally converge to the equilibrium point \(S^{*} =90.9\). Figure 2 shows that all the graphs of \(E(t)\) increase with time and tend to the equilibrium point \(E^{*}=49.24\). Figures 3 and 4 show that all graphs of \(I(t)\), \(R(t)\), and \(V(t)\) increase with time and then converge to the equilibrium points \(I^{*}=19.87\), \(R^{*}=21.78\), and \(V^{*}=45.454\), respectively.
Plots of all variables in model (3) with \(\alpha =0.9\)
Tables 1–5 present the comparative study between the standard derivative, Caputo derivatives, and the Caputo–Fabrizio derivative. It can easily be observed from Tables 1–5 that the Caputo–Fabrizio fractional derivative shows the new nature compared to the standard derivative and Caputo fractional derivative. The graphical representation shows that the model depends notably on the fractional order. Figures 2–4 and Tables 1–5 show the clear difference at different values of α.
5 Conclusion
In this paper, we have investigated a Caputo–Fabrizio fractional differential equation model for the spread of rubella disease. Using fixed point theory, we have demonstrated the existence of a unique solution. Also, we have determined the equilibrium point of the model and investigated its stability. We have used a three-step fractional Adams–Bashforth scheme to obtain numerical results of the fractional system of rubella model. Eventually, we have presented the numerical simulations for different values of the fractional-order \(\alpha =0.9, 0.8, 0.7, 0.6\) and have compared the numerical results of the standard derivative with two fractional derivatives of rubella model for \(\alpha =0.95\).
References
Wesselhoeft, C.: Rubella and congenital deformities. N. Engl. J. Med. 240(7), 258–261 (1949)
Edlich, R.F., Winters, K.L., Long, W.B., Gubler, K.D.: Rubella and congenital rubella (German measles). J. Long-Term Eff. Med. Implants 15(3), 319–328 (2005)
Trmal, J., Limberkova, R.: Report on a measles epidemic in the Usti nad Labem Region. Epidemiol. Mikrobiol. Imunol. 64(3), 139–145 (2015)
Neighbors, M., Tannehill-Jones, R.: Childhood diseases and disorders. In: Human Diseases, pp. 457–479. Clifton Park, New York (2010)
Ackerknecht, E.H.: A Short History of Medicine. Johns Hopkins University Press, Baltimore (1982)
Edmunds, W.J., Heijden, O.G., Eerola, M., Gay, N.J.: Modelling rubella in Europe. Epidemiol. Infect. 125(3), 617–634 (2000)
Fred, M.O., Sigey, J.K., Okello, J.A., Okwoyo, J.M., Kangethe, G.J.: Mathematical modeling on the control of measles by vaccination: case study of KISII county, Kenya. SIJ Trans. Comput. Sci. Eng. Appl. (CSEA) 2(3), 61–69 (2014)
Koca, I.: Analysis of rubella disease model with non-local and non-singular fractional derivatives. Int. J. Optim. Control 8(1), 17–25 (2018)
Mac Intyre, C.R., Gay, N.J., Gidding, H.F., Hull, B.I., Gilbert, G.L., McIntyre, I.B.: A mathematical model to measure the impact of the Measles Control Campaign on the potential for measles transmission in Australia. J. Infect. Dis. 6(4), 277–282 (2002)
Ochoche, J.M., Gweryina, R.I.: A mathematical model of measles with vaccination and two phases of infectiousness. IOSR J. Math. 10(1), 95–105 (2014)
Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1(2), 73–85 (2015)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Baleanu, D., Guvenc, Z.B., Machado, J.A.T.: New Trends in Nano Technology and Fractional Calculus Applications. Springer, Dordrecht (2010). https://doi.org/10.1007/978-90-481-3293-5
Haq, F., Shah, K., Rahman, G., Shahzad, M.: Numerical analysis of fractional order model of HIV-1 infection of CD4+ T-cells. Comput. Methods Differ. Equ. 5(1), 1–11 (2017)
Atangana, A., Alkahtani, B.S.T.: Analysis of the Keller–Segel model with a fractional derivative without singular kernel. Entropy 17(6), 4439–4453 (2015)
Erturk, V.S., Zaman, G., Momani, S.: A numeric analytic method for approximating a giving up smoking model containing fractional derivatives. Comput. Math. Appl. 65(10), 3068–3074 (2012)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, New York (2006)
Khalid, M., Sultana, M., Zaidi, F., Arshad, U.: Application of Elzaki transform method on some fractional differential equations. Math. Theory Model. 5(1), 89–96 (2015)
Zafar, Z.U.A., Rehan, K., Mushtaq, M.: Fractional-order scheme for bovine babesiosis disease and tick populations. Adv. Differ. Equ. 2017, 86 (2017)
Zafar, Z.U.A., Rehan, K., Mushtaq, M.: HIV/AIDS epidemic fractional-order model. J. Differ. Equ. Appl. 23(7), 1298–1315 (2017)
Zafar, Z.U.A., Mushtaq, M., Rehan, K.: A non-integer order dengue internal transmission model. Adv. Differ. Equ. 2018, 23 (2018)
Zafar, Z.U.A.: Fractional order Lengyel–Epstein chemical reaction model. Comput. Appl. Math. 2019, 131 (2019)
Losada, J., Nieto, J.J.: Properties of the new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1(2), 87–92 (2015)
Akbari Kojabad, E., Rezapour, Sh.: Approximate solutions of a sum-type fractional integro-differential equation by using Chebyshev and Legendre polynomials. Adv. Differ. Equ. 2017, 351 (2017)
Alizadeh, Sh., Baleanu, D., Rezapour, Sh.: Analyzing transient response of the parallel RCL circuit by using the Caputo–Fabrizio fractional derivative. Adv. Differ. Equ. 2020, 55 (2020)
Aydogan, M.S., Baleanu, D., Mousalou, A., Rezapour, Sh.: On high order fractional integro-differential equations including the Caputo–Fabrizio derivative. Bound. Value Probl. 2018, 90 (2018)
Aydogan, S.M., Baleanu, D., Mousalou, A., Rezapour, Sh.: On approximate solutions for two higher-order Caputo–Fabrizio fractional integro-differential equations. Adv. Differ. Equ. 2017, 221 (2017)
Baleanu, D., Ghafarnezhad, Kh., Rezapour, Sh., Shabibi, M.: On the existence of solutions of a three steps crisis integro-differential equation. Adv. Differ. Equ. 2018, 135 (2018)
Baleanu, D., Ghafarnezhad, Kh., Rezapour, Sh.: On a three steps crisis integro-differential equation. Adv. Differ. Equ. 2019, 153 (2019)
Baleanu, D., Jajarmi, A., Mohammadi, H., Mozyrska, D.: Analysis of the human liver model with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 134, 109705, 7 pages (2020)
Baleanu, D., Mohammadi, H., Rezapour, Sh.: Analysis of the model of HIV-1 infection of CD4+ T-cell with a new approach of fractional derivative. Adv. Differ. Equ. 2020, 71 (2020)
Baleanu, D., Mohammadi, H., Rezapour, Sh.: On a nonlinear fractional differential equation on partially ordered metric spaces. Adv. Differ. Equ. 2013, 83 (2013)
Baleanu, D., Rezapour, Sh., Mohammadi, H.: Some existence results on nonlinear fractional differential equations. Philos. Trans. - Royal Soc., Math. Phys. Eng. Sci. 371, 20120144 (2013). https://doi.org/10.1098/rsta.2012.0144
Baleanu, D., Mohammadi, H., Rezapour, Sh.: The existence of solutions for a nonlinear mixed problem of singular fractional differential equations. Adv. Differ. Equ. 2013, 359 (2013)
Baleanu, D., Mousalou, A., Rezapour, Sh.: A new method for investigating approximate solutions of some fractional integro-differential equations involving the Caputo–Fabrizio derivative. Adv. Differ. Equ. 2017, 51 (2017)
Baleanu, D., Mousalou, A., Rezapour, Sh.: The extended fractional Caputo–Fabrizio derivative of order \(0 \leq \sigma <1\) on \(C_{\mathbb{R} } [0,1]\) and the existence of solutions for two higher-order series-type differential equations. Adv. Differ. Equ. 2018, 255 (2018)
Baleanu, D., Mousalou, A., Rezapour, Sh.: On the existence of solutions for some infinite coefficient-symmetric Caputo–Fabrizio fractional integro-differential equations. Bound. Value Probl. 2017, 145 (2017)
Baleanu, D., Hedayati, V., Rezapour, Sh., Al-Qurashi, M.M.: On two fractional differential inclusions. SpringerPlus 5, 882 (2016)
Baleanu, D., Rezapour, Sh., Saberpour, Z.: On fractional integro-differential inclusions via the extended fractional Caputo–Fabrizio derivation. Bound. Value Probl. 2019, 79 (2019)
Gay, N., Pelletier, L., Duclos, P.: Modelling the incidence of measles in Canada: An assessment of the options for vaccination policy. Vaccine 16(8), 794–801 (1998)
Li, H., Cheng, J., Li, H.B., Zhong, S.M.: Stability analysis of a fractional-order linear system described by the Caputo–Fabrizio derivative. Mathematics 7(2), 200 (2019)
Owolabi, K.M., Atangana, A.: Analysis and application of new fractional Adams–Bashforth scheme with Caputo–Fabrizio derivative. Chaos Solitons Fractals 105, 111–119 (2017)
Acknowledgements
Research of the third author was supported by Azarbaijan Shahid Madani University. Research of the second author was supported by Miandoab Branch of Islamic Azad University. The authors thank dear referees for the valuable comments which improved basically the final version of this work.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Funding
Not available.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Baleanu, D., Mohammadi, H. & Rezapour, S. A mathematical theoretical study of a particular system of Caputo–Fabrizio fractional differential equations for the Rubella disease model. Adv Differ Equ 2020, 184 (2020). https://doi.org/10.1186/s13662-020-02614-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02614-z