Abstract
In this work, the exponential stability problem of impulsive recurrent neural networks is investigated; discrete time delay, continuously distributed delay and stochastic noise are simultaneously taken into consideration. In order to guarantee the exponential stability of our considered recurrent neural networks, two distinct types of sufficient conditions are derived on the basis of the Lyapunov functional and coefficient of our given system and also to construct a Lyapunov function for a large scale system a novel graph-theoretic approach is considered, which is derived by utilizing the Lyapunov functional as well as graph theory. In this approach a global Lyapunov functional is constructed which is more related to the topological structure of the given system. We present a numerical example and simulation figures to show the effectiveness of our proposed work.
Similar content being viewed by others
1 Introduction
The differential dynamics model is one of the basic tools in the characterization of natural and engineering processes [7, 14, 19, 22, 40, 41], and it is also a basic block of the complicated neural network [18, 65]. A simplified mathematical description of natural neural networks is known as the artificial neural networks (ANNs) model. Since 1940, due to its application, network modeling has been used in the area of pattern recognition, optimization, classification, parallel computation, signal and image processing, associative memory, system identification and control, sequence recognition, medical diagnosis, data mining, and visualization [2, 13, 17, 21, 23, 30, 35, 46, 47, 60, 61]. Over the past few years, several types of neural networks (NNs) have been applied in many areas, while in 1984 Hopfield proposed the following differential equations model [10]:
Here \(z_{i}(t)\) denotes the state vector at time t, for \(t\geq 0\), \(i,j=1,2,3,\ldots,n\); \(\eta _{i}(t)\) represents the initial value; \(d_{i}>0\); \(\alpha _{ij}\) is a positive constants; the activation function is denoted by \(f_{j}\) and the external input is \(I_{i}(t)\). At the same time, the dynamical nature of bifurcation, attractors, oscillation, chaotic, almost periodic solution, periodic solution, stability, synchronisation and instability of various types of differential equations models is focused by lots of researchers [4, 12, 15, 49, 52,53,54, 58, 64].
Till now, the time delay of dynamics systems also has received interest from many researchers [5, 6, 8, 11, 15, 16, 20, 24,25,26,27,28, 42, 51, 55, 56, 63]. From the practical perspective, it is familiar that the natural NNs as well as ANNs due to the information processing, delay appears. Frequently, it may originate in the network system and leads to instability, oscillation and chaos. Because of the finite switching speed of amplifiers, the delay occurs in the transmission and responses of the neuron, more particularly in the electronic application of analog NNs. In recent days, the dynamical behavior of RNNs with discrete time-varying delays has been extensively studied [3, 34, 38].
Huang, Cao and Wang [28] investigate the following RNN with constant time delays:
For \(i=1,2,3,\ldots,n\); and \(t\geq 0\), \(z_{i}(t)\) indicates the state vector, \(d_{i}, \alpha _{ij},\beta _{ij}>0\); the activation functions are represented by \(f_{j}\), \(g_{j}\), the constant delay is \(\tau _{i}>0\) and the external input is \(I_{i}(t)\).
In addition, NNs are of a spatial nature because of its parallel pathways having various sizes and lengths of axons, which entails that the signal propagation no longer is instantaneous but distributed during a certain period of time. Even though it is observed that in the propagation of signals distributed over certain duration of time which can be modeled as distributed time delays, it may also be instantaneous in some moment so that the distributed delay should be incorporated. It is necessary to introduce the infinite distributed delay during a certain period of time in such a manner that the current behavior of the state is in contrast to the distant past, which has less influence. Several research works are related to the stability of mixed delay, for instance, see [1, 8, 34, 37, 39, 43, 49, 58, 62] for the case of continuously distributed delay. In 2009 Xiang and Cao [58] discussed the RNN with continuously distributed delays,
Here, for \(i=1,2,3,\ldots,n\); and \(t\geq 0\), \(d_{i}\), \(\alpha _{ij}\), \(\beta _{ij}\), \(\gamma _{ij}\) are all positive constants; the state response is denoted by \(z_{i}(t)\), the activation functions are represented by \(f_{j}\), \(g_{j}\), \(h_{j}\), \(\tau _{i}(t)>0\) denotes the time-varying delays and \(\kappa _{ij}\) indicates the delay kernels.
Furthermore, the release of neurotransmitters and other probability causes in the synapsis transmission is a noisy process induced by the random fluctuation. In the literature [45] Mao demonstrated the stabilization and destabilization of NN systems with stochastic input. In this work, the NN models with external random perturbations are viewed as nonlinear dynamical systems with white noise (perturbation of Brownian motion). In 2007, Sun and Cao [51] investigate the following stochastic recurrent neural networks (SRNNs) with discrete and distributed time-varying delays:
where \(d_{i}>0\); \(\alpha _{ij}\), \(\beta _{ij}\) are all positive constants; the activation functions are represented by \(f_{j}\), \(g_{j}\), the discrete time-varying transmission delays \(\tau _{i}(t)\), stochastic noise \(\omega _{j}\) and the external input is \(I_{i}(t)\).
Moreover, the transformation process of the state of neurons changes instantaneously or abruptly at particular instants of time. These effects of the dynamical system are known as impulsive effects. Owing to its application in the fields like electronics, biology, economics, medicine, and telecommunication, impulsive effects of NNs receive more attention [1, 29, 31, 59]. In 2016, Tang and Wu studied the following impulsive RNNs:
Here, for \(i,j=1,2,3,\ldots,n\); the state vector is denoted by \(z_{i}(t)\); \(d_{i}>0\) and positive constants \(\alpha _{ij}\), \(\beta _{ij}\), \(\gamma _{ij}\). The activation functions are denoted by \(f_{j}\), \(g_{j}\), \(h _{j}\). The instantaneous change of the state at the impulsive moment \(t_{k}\), \(k=1,2,3,\ldots,n\) is represented by the impulsive function \(P_{ik}(z_{i}(t_{k}))\).
In recent years, exponential stability analysis of neural networks with time-varying delays, stochastic, impulsive effects was investigated by many researchers. Among them there exist various approaches to showing the stability of neural networks. For instance, [29, 45] Raja et al. investigate the exponential stability of neural networks by using Lyapunov and linear matrix inequality; in [59] Congcong et al. study the exponential stability by using the Lyapunov and impulsive delay differentiable inequality techniques, Li et al. [31] investigate exponential stability by using Razumikhin techniques and the Lyapunov functional approach as well as stochastic analysis. In [1] one studies the fixed point theorem, the generalized Gronwall–Bellman inequality and differential inequalities and in [36] Li et al. investigate the exponential neural networks system by utilizing the \(\mathcal{L}\)-operator delay differential inequality with impulses and using the stochastic analysis technique. Moreover, the stability of neural networks has been applied in various areas [44] like image encryption [57] and character recognition, forecasting, marketing, retails and sales, banking and finance, and medicine.
It is well known that in stability theory the Lyapunov method plays a major role, but the construction of a suitable Lyapunov function for large scale systems is quite harder, so in order to overcome this problem a novel technique was explored on the basis of Kirchhoff’s matrix tree theorem and the Lyapunov function, which is originated by Li et al. [33]. More specifically, a mathematical representation of the NNs is viewed as a directed graph with a vertex system as a single neuron, and interaction or interconnection among neurons in the synaptic connections as directed arcs. The main advantage of this work is to construct a global Lyapunov function to the large scale system that is more related to the topological structure of the framework. The benefit of this approach is to avoid constructing a particular Lyapunov function for a particular system directly. Utilizing the achievements of the pioneering works, few researchers have initiated their work and applied this approach. For instance, in [48], exponential synchronization of stochastic reaction–diffusion Cohen–Grossberg neural networks with time-varying delays was studied by using graph theory and the Lyapunov functional method; in [9], global exponential stability for multi-group neutral delayed systems was studied based on Razumikhin method and graph theory, in [50] exponential stability of BAM neural networks with delays and reaction–diffusion was studied with the help of a graph-theoretic approach. In this novel approach, to the best of the authors’ knowledge, researchers have not correlated them with NNs; there are one or two of them that are used in NNs. However, this novel approach was frequently used.
Compared with the outcome of some existing research work, in this work we concentrated on the pth moment’s exponential stability issues of ISRNNs with continuous time delay through the novel graph-theoretic approach. We proceed by applying some inequality techniques and also constructing a systematic method of a global Lyapunov function for ISRNNs by using the combination of graph theory and the Lyapunov function. The main contribution of this proposed work is as follows:
To the best of the authors’ knowledge, the problem of exponential stability of RNNs with continuously distributed delay and impulsive effects in the sense of a graph-theoretic approach is still open. Hence we desire to solve this complicated problem.
In this considered RNNs model impulse, discrete time delay, continuously distributed delay and white noise are simultaneously taken into consideration to show the pth moment’s exponential stability.
By using the results in graph theory, we construct a suitable Lyapunov function for the vertex system to avoid the complication in construction of the Lyapunov function straightly.
Using the combination of graph theory and the Lyapunov function as well as some inequality techniques, novel sufficient conditions are provided in terms of Lyapunov and coefficient-type theorems, respectively.
To illustrate the exactness of our proposed work, we provide a numerical example and some simulations.
The remainder of this work is summarized as follows: In the upcoming section, we present the mathematical description of the impulsive stochastic recurrent neural networks with mixed delays (ISRNNMDs), preliminaries which correspond to the given work, some assumptions and basic notations are given. The main results of this work is presented in the third section, which yields the sufficient condition to ensure the exponential stability of the given system. Finally, an example and numerical simulations are given to illustrate the effectiveness of our present study.
2 Mathematical model of impulsive stochastic recurrent neural networks
Inspired by the above analysis, we consider the system of RNNs with mixed time-varying delays, stochastic and impulsive effects described as follows:
for \(i,j=1,2,3,\ldots,n\), in which \(n\geq 2\) indicates the number of components in the NNs, at time \(t>0\) the state vector of the ith component is denoted by \(z_{i}(t)\in \mathbb{R}\). We have the positive constant \(d_{i}>0\); the positive weight matrices \(A=(\alpha _{ij})_{n \times n}\), \(B=(\beta _{ij})_{n\times n}\), \(C=(\gamma _{ij})_{n\times n}\) denotes the connection strength and delayed connection strength of the jth neuron to ith neuron separately. Neuronal activation functions of the jth neurons are represented by \(f_{j}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}\), \(g_{j}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}\), \(h_{j}: \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}\). The time-varying transmission delays \(\tau _{i}>0\) with the condition \(0<\tau _{i}(t)<\tau \) and the non-negative continuous real-valued delay kernel function \(\kappa _{ij}(\cdot)>0\) is defined on \([0,\infty )\). Moreover, a Borel measure function \(\sigma _{ij}:\mathbb{R}\times \mathbb{R}^{n}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{m\times n}\) indicates the diffusion coefficient of the stochastic effects; the \(\omega _{j}(t)\) identify Brownian motion on a complete probability space \((\varOmega , \mathfrak{f},\mathbb{P})\) with natural filtration \(\mathfrak{f}_{t \geq 0}\). In addition the second part is the discrete part of (1), where \(P_{ik}(z_{i}(t_{k}))\) represents the impulsive perturbation of the sudden change of the state \(z_{i}\) at the impulsive moment \(t_{k}\), the discrete set of impulsive moments satisfy \(0=t_{0}< t_{1}< t_{2}<\cdots<t_{k}<\cdots\) and \(\lim_{k\rightarrow \infty }t _{k}=\infty \). The left and right hand side limits at the moment \(t_{k}\) are represented individually by \(z_{i}(t_{k}^{-})\) and \(z_{i}(t_{k}^{+})\). For the system (1) the initial conditions are given in the form
Remark 2.1
Assume that if \(g_{j}=h_{j}=\sigma _{ij}=0\) (\(i,j=1,2,3,\ldots,n\)) (1) is simplified to
Hence, the outcome of our study generalizes the one in [39] strictly.
3 Preliminaries
In this work, we investigate the exponential stability analysis of ISRNNMD, for the whole of this work we consider the following: In this article we consider \(\mathbb{D}=\{1,2,\ldots,n\}\), \(\mathbb{R}=(-\infty ,+\infty )\) to represent the set of real numbers, \(\mathbb{R}^{+}=(0,+ \infty )\), \(\mathbb{N}\) indicates the set of natural numbers, the n-dimensional Euclidean space is \(\mathbb{R}^{n}\) and the set of all \(n\times m\) real matrices is \(\mathbb{R}^{n\times m}\). We represent the mathematical expectation \(\mathbb{E}(\cdot)\) with respect to the probability measure \(\mathbb{P}\), the Euclidean norm for any vector z and the trace norm for any matrix A are denoted \(|z|\) and \(\sqrt{ \operatorname{trace}(A^{T}A)}\), respectively. Denote the n-dimensional Brownian motion as \(\omega (t)=(\omega _{1}(t),\omega _{2}(t),\ldots,\omega _{n}(t))^{T}\) for \(t\geq 0\), which is defined on the complete probability space \((\varOmega ,\mathfrak{f},\mathbb{E},\mathbb{P})\) with the natural filtration \(\{\mathfrak{f}_{t}\} for t\geq 0\).
Graph theory
A non-empty directed graph \(\mathcal{G}=(\mathcal{V},\mathcal{E})\) consists of vertices or nodes \(\mathcal{V}=\{1,2,\ldots,n\}\) and the set of all edges or links \(\mathcal{E}\) consist of the arcs \((i,j)\) from the nodes i to the node j.
If we allocate a positive weight \(w_{ij}\) for every arc \((i,j)\) then the digraph is said to be weighted digraph. The product of the weights on all of its arcs in subgraphs \(\mathcal{H}\) is denoted by \(\mathcal{W}( \mathcal{H})\).
A dipath \(\mathcal{P}=(\mathcal{I},\mathcal{X})\) is a subgraph of \(\mathcal{G}\) which connects the sequence of nodes \((h_{i},h_{i+1}), \forall i\in \mathcal{D}\) where all \(h_{i}\) are distinct and all the arcs are oriented in the same direction. Moreover, the directed path \(\mathcal{P}\) is said to be dicycle \(\mathfrak{C}\) if the initial and terminal nodes are similar, that is, \(h_{1}=h_{n}\).
A subgraph \(\mathfrak{T}\) of \(\mathcal{G}\) is said to be a tree if \(\mathfrak{T}\) is a connected digraph without directed cycle. The node i is called the root of the rooted tree of \(\mathcal{T}\), if for any arc, i is not an end vertex of exactly one arc. A subgraph \(\mathfrak{U}\) of \(\mathcal{G}\) is unicyclic if it is a disjoint union of rooted trees whose roots form a directed cyclic.
The Laplacian matrix of \(\mathcal{G}\) is defined as
$$ L_{p}= \textstyle\begin{cases} -w_{ij}, & \mbox{if }i\neq j, \\ \sum_{h\neq j}w_{ih}, & i=j. \end{cases} $$A directed \(\mathcal{G}\) is called strongly connected if for any two distinct pair of nodes \((i,j)\) there exist directed paths from i to j and vice versa.
For the Lyapunov function \(v_{i}(t,z_{i})\in \mathbf{C}^{1,2}( \mathbb{R}^{+}\times \mathbb{R}^{n};\mathbb{R}^{+})\), \(i\in \mathbb{D}\), which is differentiable and continuous at t and twice differentiable at \(z_{i}\) we define the differential operator \(\mathfrak{L}v_{i}(t,z _{i})\) conjoined with the ith vertex of (1) by
Here
4 Basic definition and lemmas in graph theory
Definition 4.1
([26])
I f for any given \(\epsilon >0\), there exist a positive constant δ and \(a>0\) such that
for all \(t\geq 0\), then the given system (1) is as regards the pth moment exponentially stable. If \(p=2\) the given system is exponentially stable in the mean square sense.
Definition 4.2
The function \(v_{i}(t,z_{i}(t))\in \mathbf{C}^{1,2}(\mathbb{R}^{+} \times \mathbb{R}^{n};\mathbb{R}^{+})\), \(i\in \mathbb{D,}\) is said to be a vertex-Lyapunov function for system (1) if the following conditions are satisfied:
- \((D_{1})\):
Let us assume that \(a_{i}\), \(b_{i}\) be the positive constants such that
$$ a_{i} \vert z_{i} \vert ^{p}\leq v_{i}\bigl(z_{i}(t),t\bigr)\leq b_{i} \vert z_{i} \vert ^{p}. $$(5)- \((D_{2})\):
If there exist positive scalars \(\sigma _{i}\), \(\lambda _{i} and \eta _{i}\), \((a_{ij})_{n\times n}\) is a matrix, for \(a_{ij}>0\) and an arbitrary function \(F_{ij}(z_{i}(t),z_{j}(t),t)\) for every i, j, then
$$\begin{aligned} \mathfrak{L}v_{i}\bigl(z_{i}(t),t\bigr)\leq {}&{-}\sigma _{i}v_{i}\bigl(z_{i}(t),t\bigr)+ \lambda _{i}v_{i}\bigl(z_{i}\bigl(t-\tau _{i}(t)\bigr),t\bigr)+\sum_{j=1}^{n}a_{ij}F_{ij} \bigl(z _{i}(t),z_{j}(t),t\bigr) \\ &{}+\eta _{i} \int _{-\infty }^{t}\mathcal{K}_{ij}(t-s)v_{i} \bigl(s,z _{i}(s)\bigr)\,ds,\quad \mbox{for }t\neq t_{k}. \end{aligned}$$(6)- \((D_{3})\):
Along the directed cycle \(\mathfrak{C}\) of the directed graph \((\mathcal{G}, \mathcal{A})\)
$$ \sum_{(k,h)\in \mathcal{E}(\mathfrak{C})}F_{kh}\bigl(z_{k}(t),z_{h}(t),t \bigr) \leq 0. $$(7)
Lemma 4.3
(Young’s inequality)
Let \(s,t\geq 0\), \(m\geq n\geq 0\). Then
Lemma 4.4
([32])
Let the number of vertices be \(n \geq 2\)and the weighted digraph \((\mathcal{G},\mathcal{A})\)with \(\mathcal{A}=(a_{ij})_{n \times n}\). Let the set of all spanning unicyclic graphs of \((\mathcal{G},\mathcal{A})\)be \(\mathfrak{U}\)and theith diagonal element of cofactor of the \(L_{p}\)be denoted as \(c_{k}\), then the following identity holds:
Here, for \(k,h\in \mathbb{D}\), an arbitrary function \(F_{kh}(t,z_{k}(t),z _{h}(t))\), the set of all spanning unicyclic graph \(\mathfrak{U}\), \(\mathcal{W}(\mathcal{U})\)and \(\mathcal{U}\), \(\mathfrak{C}_{ \mathcal{U}}\)denotes, respectively, the weight and dicycle of \(\mathcal{U}\). Additionally, \(c_{i}>0\)if \((\mathcal{G},\mathcal{A})\)is strongly connected for \(i=1,2,\ldots,n\).
5 Main results
Throughout this work, to get our main results for the given ISRNNMD (1), we suggest the following standard postulations:
- \((P_{1})\):
For every \(j\in \mathbb{D}\) the functions \(f_{j}(\cdot)\), \(g _{j}(\cdot)\) and \(h_{j}(\cdot)\) are Lipschitz continuous with Lipschitz constants \(L_{j}(\cdot)\), \(M_{j}(\cdot)\) and \(N_{j}(\cdot)\) individually.
- \((P_{2})\):
For any positive constant ν such that \(V(t_{k},z+P_{ik}(z))\leq \nu _{i}V(t_{k}^{-},z)\) for \(t=t_{k}\).
- \((P_{3})\):
There exist non-negative constants \(\mu _{i}\), \(\phi _{i}\), \(\psi _{i} (i\in \mathbb{D})\), such that
$$ \operatorname{tr} \bigl(\sigma _{ij}^{T}(t,u_{j},v_{j},w_{j}) \sigma _{ij}(t,u_{j},v_{j},w _{j}) \bigr) \leq \mu _{i} \vert u_{j} \vert ^{2}+\phi _{i} \vert v_{j} \vert ^{2}+\psi _{i} \vert w_{j} \vert ^{2}. $$- \((P_{4})\):
There exist a delay kernel function \(\kappa _{ij}\) and a non-negative constant \(\chi _{ij}\) and \(\mathfrak{K}_{ij}\) such that
$$ \bigl\vert \kappa _{ij}(t) \bigr\vert \leq \chi _{ij},\quad t\in [0,\infty )\ (i,j\in \mathbb{D}). $$- \((P_{5})\):
-
$$ \int _{0}^{\infty }\kappa _{ij}(t)\,dt=1 \quad \mbox{and}\quad \int _{0}^{\infty }e^{rt}\kappa _{ij}(t)\,dt=\mathfrak{K}_{ij}< \infty . $$
- \((P_{6})\):
\(f_{j}(0)=g_{j}(0)=h_{j}(0)=0\) and \(\sigma _{ij}(0,0,0)=0\).
- \((P_{7})\):
For every \(k\in \mathbb{L}\) there exist scalars \(\upsilon _{i}\) such that
$$ \bigl\vert P_{ik}\bigl(z_{i}\bigl(t_{k}^{-} \bigr)\bigr) \bigr\vert \leq \upsilon _{i} \bigl\vert z_{i}\bigl(t_{k}^{-}\bigr) \bigr\vert . $$
Theorem 5.1
Let \(\zeta =\inf_{k\in \mathbb{N}}\{t_{k}-t_{k-1}\}\)be finite and let \((\mathcal{G},\mathcal{A})\)be strongly connected, there exist constantsσ, λ, ν, η, \(1<\nu <e^{(\sigma -\lambda \nu )\zeta }\)and suppose that the system (1) allows the vertex-Lyapunov function \(v_{i}(t,z_{i}(t))\)and the assumption \((P_{2})\)holds, then the trivial solution of the system (1) is exponentially stable in thepth moment.
Proof
There exists a positive constant \(\delta (\varepsilon )>0\), for any \(\varepsilon >0\) such that \(b_{i}\delta <\nu _{i}a_{i}\varepsilon \). We assign \(z(t)=z(t,t_{0},\xi )\) to be the solution of (1) by means of \((t_{0},\xi )\), for some \(t_{0}\geq 0\) and \(z(t_{0})=z_{t_{0}}= \xi \) which is in \(PC_{\mathcal{F}_{0}(\delta )}^{b}\). We will show that
Let us consider the global Lyapunov function
Here \(c_{i}\) indicates the cofactor element of \(L_{p}\) of the digraph \((\mathcal{G},\mathcal{A})\), since the digraph is strongly connected, by Lemma 4.4 we have \(c_{i}>0\) for any \(i\in \mathbb{D}\). Choose an arbitrary constant θ and we set
When \(t\neq t_{k}\), we use Itô’s formula,
where \(t\in [t_{k-1},t_{k})\), \(k\in \mathbb{N}\). By integrating the above expression from \(t_{k}\) to \(t+\Delta t\) for small enough \(\Delta t>0\) and taking the mathematical expectation, we obtain, for \(t\geq 0\), \(t+ \Delta t\in [t_{k},t_{k+1})\),
which implies that
Here, \(D^{+}W(t,z(t))\) denotes the upper-right Dini derivative of \(W(t,z(t))\) defined by
Also
and we can choose \(\delta >0\) for any given \(\varepsilon > 0\), such that \(b_{i}\delta <\nu _{i}a_{i}\varepsilon \). Currently, we assign \(\mathbb{E}\|\xi \|^{p}<\delta \). By (3) we obtain
We mainly prove that
Suppose, on the contrary, that we have \(s\in (t_{0},t_{1})\) such that
Set
In such a way it is obvious for \(t\in [s_{2},s_{1}]\), for \(z_{i}(t- \tau _{i}(t))= (z_{1}(t-\tau _{1}(t)),z_{2}(t-\tau _{2}(t)),\ldots,z_{n}(t- \tau _{n}(t)) )\), where \(\tau =\max_{1\leq j\leq n}\{\tau _{j}\}\), for \(t\in [s_{2},s_{1}]\) that
Hence,
Therefore from (6), \(t\in [s_{2},s_{1}]\), we induce that
Integrating the above inequality, for \(t\in [s_{1},s_{2}]\), we get
Hence,
which is a contradiction with
Next, we consider, for \(m=1,2,3,\ldots,k\) and \(k\in \mathbb{N}\),
We want to prove that
On the contrary, there exist some \(t\in [t_{k},t_{k+1})\) such that
By using assumption \((P_{2})\) and (9), we obtain
Now, set
Let
For \(t\in (s_{2},s_{1})\), we get
Hence,
Similarly, we can derive \(\mathbb{E}W(s_{2},z(s_{2}))< a_{i}\varepsilon \) which is a contradiction to \(\mathbb{E}W(t,z(t))\leq a_{i}\varepsilon \) for \(t\epsilon [t_{k},t_{k+1})\). Hence the proof of the theorem is completed.
By mathematical induction \(\mathbb{E}W(t,z(t))\leq a_{i} \varepsilon \) for \(t\geq t_{0}\). Hence,
□
Remark 5.2
In the study of the stability of ISNNMD, to construct a Lyapunov function is a formidable task. However, Theorem 5.1 offers a technique to construct systematically a Lyapunov function for (1) by using the Lyapunov function \(v_{i}(t,z_{i}(t))=v_{i1}(t,z_{i}(t))+v_{i2}(t,z_{i}(t))+v_{i3}(t,z_{i}(t))\) of each vertex system, which avoids the difficulty of finding a Lyapunov function directly for ISNNMD. In the final section, an example is presented to show the validity of the technique.
Remark 5.3
It should be noticed that Theorem 5.1 holds if \(c_{i}>0\), that is, the graph \((\mathcal{G},\mathcal{A})\) is strongly connected, which means that exponential stability of RNNs has a close relationship with the topology property of the network. Therefore, we can get some better results in the following.
Theorem 5.4
Assume that the assumptions \((P_{1})\)–\((P_{7})\)hold; then the considered system (1) is exponentially stable.
Proof
Let us define the subsequent Lyapunov–Krasovskii functional for (1) as follows:
Now, we can calculate the Lie derivative of \(v_{i}(t,z_{1}(t))\) for \(t\neq t_{k}\). By using Itô’s formula along the trajectories of the model (1), we obtain
where
By using Lemma 4.3, we obtain
Similarly,
and
We use the assumption and the well-known Cauchy–Schwartz inequality
Substituting (13)–(17) in (12) we get
Next,
And
Substituting (18)–(20) in (11) we get
On the other hand, for \(t=t_{k}\),
Now, we define \(v_{i}(t,z_{i}(t))=e^{rt}|z_{i}(t)|^{p}\) and the suitable constants \(T_{i1}\), \(T_{i2}\), \(T_{i3}\) such that the condition (4) is satisfied, then by using Theorem 5.1 we ensure the pth moment’s exponential stability of (1). Here
□
6 Example
To show the efficiency of our work we provide an example and some numerical simulations in this section.
Example 6.1
Consider the following two-dimensional RNNs with impulse effects, stochastic and mixed delays of two neurons:
where the state vector is \(z_{i}=(z_{1},z_{2})\), \((d_{1},d_{2})=(2.5,0.2)\), and
Here
\(\kappa _{ij}(t)=e^{-t}\) for \(i,j=1,2\) and
The impulsive function is
Then we check that the Lipschitz constants \(L_{j}=M_{j}=N_{j}=1\) and all the given assumptions \((P_{1})\)–\((P_{7})\) are verified. Let us consider \(v_{i}(t,z_{i}(t))=|z_{i}(t)|^{2}\). It is easy to check that the condition \((D_{1})\) is true with the values \(\alpha _{1}=0.25\), \(\alpha _{2}=0.1\), \(\beta _{1}=2.5\), \(\beta _{2}=4\). Let us calculate the \(\mathfrak{L}v_{i}(t,z_{i}(t))\) as follows:
If \(\max (-2D+2|A|+|B|+|C|)<0\), then we have
Here
and
Hence the conditions \((D_{1})\)–\((D_{3})\) satisfied. Therefore by Theorem 5.1 the given system (1) is exponentially stable.
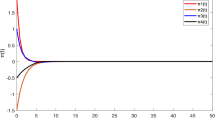
For the initial condition \(\eta _{1}(t)=0.3\), \(\eta _{2}=0.5\), the trajectory of \(z_{1}(t)\) in (20) with infinite delay, stochastic and impulsive effects
For the initial condition \(\eta _{1}(t)=0.3\), \(\eta _{2}=0.5\), the trajectory of \(z_{2}(t)\) in (20) with infinite delay, stochastic and impulsive effects
Trajectory of the second moment of (20)
7 Conclusions
This paper mainly focuses on exploring a graph theory-based approach investigating the pth moment’s exponential stability for a RNNs with impulse, discrete and continuously distributed time-varying delays and stochastic disruptions. Here we successfully obtain two new principles which guarantee the pth moment’s exponential stability of the RNNs. Further it is pointed out that the method and techniques presented here are more precise variations of the previous methods and techniques such as using the linear matrix inequality and the method of variation of parameters. As far as it is concerned, the graph-theoretic approach could be extended to many kinds of neural networks, such as complex neural networks, competitive neural networks, bidirectional memory neural networks, with Markovian jumping, impulses, infinite delay, which are either in continuous or discrete time neural networks. Such a kind of problems which occurred in the real-world applications described by using this new approach could be discussed in the near future.
References
Aouiti, C., Mhamdi, M.S., Chrif, F., Alimi, A.M.: Impulsive generalized high-order recurrent neural networks with mixed delays: stability and periodicity. Neurocomputing 321, 296–307 (2018)
Cai, Z., Huang, J., Huang, L.: Periodic orbit analysis for the delayed Filippov system. Proc. Am. Math. Soc. 146(11), 4667–4682 (2018)
Chen, G., Gaans, O., Lunel, S.V.: Fixed points and pth moment exponential stability of stochastic delayed recurrent neural networks with impulses. Appl. Math. Lett. 27, 36–42 (2014)
Chen, T., Huang, L., Yu, P., Huang, W.: Bifurcation of limit cycles at infinity in piecewise polynomial systems. Nonlinear Anal., Real World Appl. 41, 82–106 (2018)
Chen, W., Zheng, W.: A new method for complete stability stability analysis of cellular neural networks with time delay. IEEE Trans. Neural Netw. 21(7), 1126–1137 (2010)
Duan, L., Fang, X., Huang, C.: Global exponential convergence in a delayed almost periodic Nicholson’s blowflies model with discontinuous harvesting. Math. Methods Appl. Sci. 41(5), 1954–1965 (2018)
Duan, L., Huang, C.: Existence and global attractivity of almost periodic solutions for a delayed differential neoclassical growth model. Math. Methods Appl. Sci. 40(3), 814–822 (2017)
Gao, H.J., Chen, T.W.: New results on stability of discrete-time systems with time-varying state delay. IEEE Trans. Autom. Control 52, 328–334 (2007)
Guo, Y., Wang, Y., Ding, X.: Global exponential stability for multi-group neutral delayed systems based on Razumikhin method and graph theory. J. Franklin Inst. 355, 3122–3144 (2018)
Hopfield, J.: Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 81(10), 3088–3092 (1984)
Hu, H., Liu, L., Mao, J.: Multiple nonlinear oscillations in a \(D_{3} \times D_{3}\)-symmetrical coupled system of identical cells with delays. Abstr. Appl. Anal. 2013, Article ID 417678 (2013). https://doi.org/10.1155/2013/417678
Hu, H., Yi, T., Zou, X.: On spatial-temporal dynamics of Fisher–KPP equation with a shifting environment. Proc. Am. Math. Soc. (2019). https://doi.org/10.1090/proc/14659
Hu, H., Yuan, X., Huang, L., Huang, C.: Global dynamics of an SIRS model with demographics and transfer from infectious to susceptible on heterogeneous networks. Math. Biosci. Eng. 16(5), 5729–5749 (2019)
Hu, H., Zou, X.: Existence of an extinction wave in the Fisher equation with a shifting habitat. Proc. Am. Math. Soc. 145(11), 4763–4771 (2017)
Huang, C., Cao, J., Cao, J.: Stability analysis of switched cellular neural networks: a mode-dependent average dwell time approach. Neural Netw. 82, 84–99 (2016)
Huang, C., Cao, J., Wen, F., Yang, X.: Stability analysis of SIR model with distributed delay on complex networks. PLoS ONE 11(8) e0158813 (2016)
Huang, C., Liu, B.: New studies on dynamic analysis of inertial neural networks involving non-reduced order method. Neurocomputing 325, 283–287 (2019)
Huang, C., Liu, B., Tian, X., Yang, L., Zhang, X.: Global convergence on asymptotically almost periodic SICNNs with nonlinear decay functions. Neural Process. Lett. 49(2), 625–641 (2019)
Huang, C., Long, X., Huang, L., Fu, S.: Stability of almost periodic Nicholson’s blowflies model involving patch structure and mortality terms. Can. Math. Bull. (2019). https://doi.org/10.4153/S0008439519000511
Huang, C., Qiao, Y., Huang, L., Agarwal, R.: Dynamical behaviors of a food-chain model with stage structure and time delays. Adv. Differ. Equ. 2018, 186 (2018). https://doi.org/10.1186/s13662-018-1589-8
Huang, C., Su, R., Cao, J., Xiao, S.: Asymptotically stable high-order neutral cellular neural networks with proportional delays and D operators. Math. Comput. Simul. (2019). https://doi.org/10.1016/j.matcom.2019.06.001
Huang, C., Yang, Z., Yi, T., Zou, X.: On the basins of attraction for a class of delay differential equations with non-monotone bistable nonlinearities. J. Differ. Equ. 256(7), 2101–2114 (2014)
Huang, C., Zhang, H.: Periodicity of non-autonomous inertial neural networks involving proportional delays and non-reduced order method. Int. J. Biomath. 12(2), 1950016 (2019)
Huang, C., Zhang, H., Cao, J., Hu, H.: Stability and Hopf bifurcation of a delayed prey–predator model with disease in the predator. Int. J. Bifurc. Chaos 29(7), 1950091 (2019)
Huang, C., Zhang, H., Huang, L.: Almost periodicity analysis for a delayed Nicholson’s blowflies model with nonlinear density-dependent mortality term. Commun. Pure Appl. Anal. 18(6), 3337–3349 (2019)
Huang, C.D., Cao, J.D.: Impact of leakage delay on bifurcation in high-order fractional BAM neural networks. Neural Netw. 98, 223–235 (2018)
Huang, C.D., Li, H., Li, T.X., Chen, S.J.: Stability and bifurcation control in a fractional predator–prey model via extended delay feedback. Int. J. Bifurc. Chaos 29, 1950150 (2019). https://doi.org/10.1142/S0218127419501505
Huang, H., Cao, J., Wang, J.: Global exponential stability and periodic solution of recurrent neural networks with delays. Phys. Lett. A 298, 393–404 (2002)
Karthik Raja, U., Raja, R., Samidurai, R., Leelamani, A.: Exponential stability for stochastic delayed recurrent neural networks with mixed time-varying delays and impulses: the continuous-time case. Phys. Scr. 87, 055802 (2013)
Kumari, S., Chugh, R., Cao, J., Huang, C.: Multi fractals of generalized multivalued iterated function systems in b-metric spaces with applications. Mathematics 7, 967 (2019). https://doi.org/10.3390/math7100967
Li, D., Cheng, P., Hua, M., Yao, F.: Robust exponential stability of uncertain impulsive stochastic neural networks with delayed impulses. J. Franklin Inst. 355(17), 8597–8618 (2018)
Li, M.Y., Shuai, Z.: Global-stability problem for coupled systems of differential equations on networks. J. Differ. Equ. 248, 1–20 (2010)
Li, M.Y., Shuai, Z.: Global-stability problem for coupled systems of differential equations on networks. J. Differ. Equ. 248, 1–20 (2010)
Li, T., Fei, S.M.: Stability analysis of Cohen–Grossberg neural networks with time-varying and distributed delays. Neurocomputing 71, 1069–1081 (2008)
Li, T., Liu, X., Wu, J., Wan, C., Guan, Z.H., Wang, Y.: An epidemic spreading model on adaptive scale-free networks with feedback mechanism. Phys. A, Stat. Mech. Appl. 450, 649–656 (2016)
Li, X.: Existence and global exponential stability of periodic solution for delayed neural networks with impulsive and stochastic effects. Neurocomputing 73(4–6), 749–758 (2010)
Li, X., Ding, D., Feng, J., Hu, S.: Existence and exponential stability of anti-periodic solutions for interval general bidirectional associative memory neural networks with multiple delays. Adv. Differ. Equ. 2016, 190 (2016)
Lin, W., He, Y., Zhang, C., Wu, M., Ji, M.: Stability analysis of recurrent neural networks with interval time-varying delay via free-matrix-based integral inequality. Neurocomputing 205(12), 490–497 (2016)
Liu, Y., Wang, Z., Liu, X.: Global exponential stability of generalized recurrent neural networks with discrete and distributed delays. Neural Netw. 19, 667–675 (2006)
Liu, Y., Wu, J.: Fixed point theorems in piecewise continuous function spaces and applications to some nonlinear problems. Math. Methods Appl. Sci. 37(4), 508–517 (2014)
Long, X., Gong, S.: New results on stability of Nicholson’s blowflies equation with multiple pairs of time-varying delays. Appl. Math. Lett. (2019). https://doi.org/10.1016/j.aml.2019.106027
Maharajan, C., Raja, R., Cao, J., Rajchakit, G.: Fractional delay segments method on time-delayed recurrent neural networks with impulsive and stochastic effects: an exponential stability approach. Neurocomputing 323, 277–298 (2019)
Maharajan, C., Raja, R., Cao, J., Rajchakit, G., Alsaedi, A.: Impulsive Cohen–Grossberg BAM neural networks with mixed time-delays: an exponential stability analysis issue. Neurocomputing 275, 2588–2602 (2018)
Manivannan, R., Samidurai, R., Cao, J., Alsaedi, A.: New delay-interval-dependent stability criteria for switched Hopfield neural networks of neutral type with successive time-varying delay components. Cogn. Neurodyn. 10, 543–562 (2016). https://doi.org/10.1007/s11571-016-9396-y
Mao, X.: Stochastic Differential Equations and Application, 2nd edn. Horwood, Chichester (2007)
Rajchakit, G., Pratap, A., Raja, R., Cao, J., Alzabut, J., Huang, C.: Hybrid control scheme for projective lag synchronization of Riemann–Liouville sense fractional order memristive BAM neural networks with mixed delays. Mathematics 7(8), 759 (2019). https://doi.org/10.3390/math7080759
Song, C., Fei, S., Cao, J., Huang, C.: Robust synchronization of fractional-order uncertain chaotic systems based on output feedback sliding mode control. Mathematics 7(7), 599 (2019). https://doi.org/10.3390/math7070599
Song, H., Chen, D., Li, W., Qua, Y.: Graph-theoretic approach to exponential synchronization of stochastic reaction–diffusion Cohen–Grossberg neural networks with time-varying delays. Neurocomputing (2016). https://doi.org/10.1016/j.neucom.2015.11.036
Song, Y.Y., Han, Y., Peng, Y.: Stability and Hopf bifurcation in an unidirectional ring of n neurons with distributed delays. Neurocomputing 121, 442–452 (2013)
Su, H., He, Z., Zhao, Y., Ding, X.: A graph-theoretic approach to exponential stability of BAM neural networks with delays and reaction–diffusion. Appl. Anal. 94(10), 2037–2056 (2015). https://doi.org/10.1080/00036811.2014.964690
Sun, Y., Cao, J.: pth moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Anal., Real World Appl. 8, 1171–1185 (2007)
Wang, J., Chen, X., Huang, L.: The number and stability of limit cycles for planar piecewise linear systems of node-saddle type. J. Math. Anal. Appl. 469(1), 405–427 (2019)
Wang, J., Huang, C., Huang, L.: Discontinuity-induced limit cycles in a general planar piecewise linear system of saddle-focus type. Nonlinear Anal. Hybrid Syst. 33, 162–178 (2019)
Wang, L., Zhang, G., Zhang, K.: Existence and stability of stationary solution to compressible Navier Stokes Poisson equations in half line. Nonlinear Anal. 145, 97–117 (2016)
Wang, P., Hu, H., Zheng, J., Tan, Y., Liu, L.: Delay-dependent dynamics of switched Cohen–Grossberg neural networks with mixed delays. Abstr. Appl. Anal. 2013, Article ID 826426 (2013). https://doi.org/10.1155/2013/826426
Wang, Y., Zheng, C., Feng, E.: Stability analysis of mixed recurrent neural networks with time delay in the leakage term under impulsive perturbations. Neurocomputing 119, 454–461 (2013)
Wei, T., Lin, P., Wang, P.: Stability of stochastic impulsive reaction–diffusion neural networks with S-type distributed delays and its application to image encryption. Neural Netw. (2019). https://doi.org/10.1016/j.neunet.2019.03.016
Xiang, H., Cao, H.: Almost periodic solutions of recurrent neural networks with continuously distributed delays. Nonlinear Anal. 71, 6097–6108 (2009)
Xu, C.C.: Exponential stability of impulsive stochastic recurrent neural networks with time-varying delays and Markovian jumping. Wuhan Uiv. J. Nat. Sci. 19(1), 71–78 (2014)
Yang, C., Huang, L., Li, F.: Exponential synchronization control of discontinuous nonautonomous networks and autonomous coupled networks. Complexity 2018, Article ID 6164786 (2018)
Yang, X., Wen, S., Liu, Z., Li, C., Huang, C.: Dynamic properties of foreign exchange complex network. Mathematics 7(9), 832 (2019). https://doi.org/10.3390/math7090832
Zhang, B.Y., Xu, S.Y., Zou, Y.: Improved delay-dependent exponential stability criteria for discrete-time recurrent neural networks with time-varying delays. Neurocomputing 72, 321–330 (2008)
Zhang, Z., Liu, X., Chen, J., Guo, R., Zhou, S.: Further stability analysis for delayed complex-valued recurrent neural networks. Neurocomputing 251, 81–89 (2017)
Zhu, K., Xie, Y., Zhou, F.: Pullback attractors for a damped semilinear wave equation with delays. Acta Math. Sin. Engl. Ser. 34(7), 1131–1150 (2018)
Zuo, Y., Wang, Y., Liu, X.: Adaptive robust control strategy for rhombus-type lunar exploration wheeled mobile robot using wavelet transform and probabilistic neural network. Comput. Appl. Math. 37, 314–337 (2018)
Funding
The work is partially supported by the National Natural Science Foundation of China (Nos. 11971076, 51839002), RUSA-Phase 2.0 Grant No. F 24-51/2014-U, Policy (TN Multi-Gen), Dept. of Edn. Govt. of India, UGC-SAP (DRS-I) Grant No. F.510/8/DRS-I/2016(SAP-I), DST (FIST - level I) 657876570 Grant No. SR/FIST/MS-I/2018/17, Prince Sultan University for funding this work through research group Nonlinear Analysis Methods in Applied Mathematics (NAMAM) group number RG-DES-2017-01-17 and Thailand Research Grant Fund RSA6280004.
Author information
Authors and Affiliations
Contributions
Each of the authors contributed to each part of this study equally and read and approved the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iswarya, M., Raja, R., Rajchakit, G. et al. A perspective on graph theory-based stability analysis of impulsive stochastic recurrent neural networks with time-varying delays. Adv Differ Equ 2019, 502 (2019). https://doi.org/10.1186/s13662-019-2443-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2443-3