1 Introduction

As is well known, neural networks have been effectively applied in numerous disciplines such as pattern recognition, classification, associative memory, optimization, signal and image processing, parallel computation, nonlinear optimization problems, and so on (see [1–8]). Thus there is a lot of work focusing on the dynamical nature of various neural networks, such as stability, periodic solution, almost periodic solution, bifurcation, and chaos. A great deal of interesting findings of neural networks have been reported (see [9–19]). In 2006, Ding and Huang [20] investigated the following interval general bidirectional associative memory (BAM) neural networks with multiple delays:

$$ \left \{ \textstyle\begin{array}{l} \frac{x_{i}(t)}{dt}=-a_{i}x_{i}(t)+\sum_{j=1}^{m}s_{ji}f_{j}[x_{j}(t),y_{j}(t-\tau _{ji})]+c_{i}, \\ \frac{y_{j}(t)}{dt}=-b_{j}y_{j}(t)+\sum_{i=1}^{m}t_{ij}g_{i}[x_{i}(t-\delta _{ij}),y_{i}(t)]+d_{j}, \end{array}\displaystyle \right . $$
(1.1)

where \(i,j=1,2,\ldots,m\), \(x_{i}\) and \(y_{j}\) stand for the activations of the ith and jth neurons, respectively; \(f_{j}(\cdot, \cdot)\) and \(g_{i}(\cdot, \cdot)\) denote the activation functions of the jth and ith units, respectively; \(a_{i}\) and \(b_{j}\) are constants; the time delays \(\tau_{ji}\) and \(\delta_{ij}\) are nonnegative constants; \(s_{ji}\) and \(t_{ij}\) denote the connection weights, which stand for the strengths of connectivity between cells j and i; and \(c_{i}\) and \(d_{j}\) denote the ith and jth components of an external input source introduced from outside the network to cell i and cell j, respectively. Using fixed point theory, the authors discussed the existence and uniqueness of the equilibrium point for (1.1). By constructing a suitable Lyapunov functions, the authors got some sufficient conditions to ensure the global robust exponential stability of (1.1). In many situations, the coefficients of neural networks often fluctuate in time and it is cockamamie to analyze the existence and stability of periodic solutions for continuous systems and discrete systems, respectively, Zhang and Liu [21] investigated the following interval general bidirectional associative memory (BAM) neural networks with multiple delays on time scales:

$$ \left \{ \textstyle\begin{array}{l} {x_{i}^{\Delta}(t)}=-a_{i}(t)x_{i}(t)+\sum_{j=1}^{m}s_{ji}(t)f_{j}[x_{j}(t),y_{j}(t-\tau_{ji})]+c_{i}(t), \\ {y_{j}^{\Delta}(t)}=-b_{j}(t)y_{j}(t)+\sum_{i=1}^{m}(t)t_{ij}g_{i}[x_{i}(t-\delta _{ij}),y_{i}(t)]+d_{j}(t). \end{array}\displaystyle \right . $$
(1.2)

With the help of the continuation theorem of coincidence degree theory and constructing some suitable Lyapunov functionals, the authors discussed the existence and global exponential stability of periodic solutions for system (1.2).

Lots of researchers think that anti-periodic solutions can describe the dynamical nature of nonlinear differential systems effectively [22–27], for example, the signal transmission process of neural networks can be described as an anti-periodic phenomenon. Then the discussion of the anti-periodic solutions of neural networks has important theoretical value and tremendous potential for applications. Therefore it is meaningful to discuss the existence and stability of anti-periodic solutions of neural networks. In recent decades, there have been many articles that deal with this content. For instance, Li et al. [28] discussed the anti-periodic solution of generalized neural networks with impulses and delays on time scales, Abdurahman and Jiang [29] established some sufficient conditions on the existence and stability of the anti-periodic solution for delayed Cohen-Grossberg neural networks with impulses, Ou [30] considered the anti-periodic solutions for high-order Hopfield neural networks, Peng and Huang [31] made a detailed analysis on the anti-periodic solutions of shunting inhibitory cellular neural networks with distributed delays. For details, see [32–45]. Inspired by the idea and work above, we will investigate the anti-periodic solutions of the following interval general bidirectional associative memory (BAM) neural networks with multiple delays:

$$ \left \{ \textstyle\begin{array}{l} \frac{x_{i}(t)}{dt}=-a_{i}x_{i}(t)+\sum_{j=1}^{m}s_{ji}(t)f_{j}[x_{j}(t),y_{j}(t-\tau _{ji})]+c_{i}(t), \\ \frac{y_{j}(t)}{dt}=-b_{j}y_{j}(t)+\sum_{i=1}^{m}t_{ij}(t)g_{i}[x_{i}(t-\delta _{ij}),y_{i}(t)]+d_{j}(t), \end{array}\displaystyle \right . $$
(1.3)

where \(i,j=1,2,\ldots,m\). The main object of this article is to discuss the existence and exponential stability of anti-periodic solution for system (1.3). By applying the fundamental solution matrix, the Lyapunov function, and constructing fundamental function sequences based on the solution of networks, we obtain a set of sufficient criteria which ensure the existence and global exponential stability of anti-periodic solutions of system (1.3). The obtained results complement the work of [22–45].

The rest of this paper is organized as follows. In Section 2, we introduce necessary notations and results. In Section 3, we obtain some sufficient criteria on the existence and global exponential stability of anti-periodic solution of the networks. In Section 4, the theoretical predictions are verified by an example and computer simulations. The paper ends with a brief conclusion in Section 5.

2 Preliminary results

In this section, we first introduce some notations and lemmas. Denote

$$\bar{s}_{ji}=\sup_{t\in R}\bigl\vert s_{ji}(t)\bigr\vert ,\qquad \bar{t}_{ij}=\sup _{t\in R}\bigl\vert t_{ij}(t)\bigr\vert ,\qquad \bar{c}_{i}=\sup_{t\in R}\bigl\vert c_{i}(t)\bigr\vert ,\qquad \bar{d}_{j}=\sup _{t\in R}\bigl\vert d_{j}(t)\bigr\vert . $$

For any vector \(U=(u_{1},u_{2},\ldots,u_{m})^{T}\) and matrix \(M=(m_{ij})_{m\times{m}}\), define the following norm:

$$\|U\|= \Biggl(\sum_{i=1}^{m}u_{i}^{2} \Biggr)^{\frac{1}{2}},\qquad \|M\|= \Biggl(\sum_{i,j=1}^{m}m_{ij}^{2} \Biggr)^{\frac{1}{2}}. $$

Let

$$\begin{aligned}& \varphi(s)=\bigl(\varphi_{1}(s),\varphi_{2}(s), \ldots, \varphi_{m}(s)\bigr)^{T},\quad \varphi_{i}(s)\in{C} \bigl([-\delta,0],R\bigr),i=1,2, \ldots,m, \\& \psi(s)=\bigl(\psi_{1}(s),\psi_{2}(s), \ldots, \psi_{m}(s)\bigr)^{T},\quad \psi_{i}(s)\in{C} \bigl([-\tau,0],R\bigr),i=1,2, \ldots,m, \end{aligned}$$

where \(\tau=\max_{1\leq{i,j}\leq{m}}\{\tau_{ij}\}\), \(\delta=\max_{1\leq{i,j}\leq {m}}\{\delta_{ji}\}\). Define

$$\|\varphi\|=\sup_{-\delta\leq{s}\leq0} \Biggl(\sum _{i=1}^{m}\bigl\vert \varphi _{i}(s)\bigr\vert ^{2} \Biggr)^{\frac{1}{2}},\qquad \|\psi\|=\sup _{-\tau\leq{s}\leq0} \Biggl(\sum_{i=1}^{m} \bigl\vert \psi_{i}(s)\bigr\vert ^{2} \Biggr)^{\frac{1}{2}}. $$

The initial conditions of (1.3) are given by

$$ \left \{ \textstyle\begin{array}{l} x_{i0}(s)=\varphi_{i}(s),\quad -\sigma\leq s\leq0, \\ y_{i0}(s)=\psi_{i}(s),\quad -\tau\leq s\leq0. \end{array}\displaystyle \right . $$
(2.1)

Let \(x(t)=(x_{1}(t),x_{2}(t), \ldots,x_{m}(t))^{T}\), \(y(t)=(y_{1}(t),y_{2}(t), \ldots,y_{m}(t))^{T} \) be the solution of system (1.3) with initial conditions (2.1). We say the solution \(x(t)=(x_{1}(t),x_{2}(t), \ldots,x_{m}(t))^{T}\) is T-anti-periodic on \(R^{m}\) if \(x_{i}(t+T)=-x_{i}(t)\) (\(i=1,2, \ldots,m\)) for all \(t\in{R}\), where T is a positive constant.

Throughout this paper, we assume that the following conditions hold.

  1. (H1)

    \(f_{i}, g_{i}\in C(R^{2},R)\), \(i,j=1,2,\ldots,m\), there exist constants \(\alpha_{if}>0\), \(\alpha_{ig}>0\), \(\beta_{if}>0\), and \(\beta_{ig}>0\) such that

    $$\left \{ \textstyle\begin{array}{lc} |f_{i}(u_{i}, u_{j} )-f_{i}(\bar{u}_{i}, \bar{u}_{j})| \leq\alpha_{if}|u_{i} -\bar {u}_{i}|+\beta_{if}|u_{j} -\bar{u}_{j}|, \qquad |f_{i}(u,v)|\leq F_{i}, \quad i\neq j, \\ |g_{i}(u_{i}, u_{j} )-g_{i}(\bar{u}_{i}, \bar{u}_{j})| \leq\alpha_{ig}|u_{i} -\bar {u}_{i}|+\beta_{ig}|u_{j} -\bar{u}_{j}|,\qquad |g_{i}(u,v)|\leq G_{i},\quad i\neq j \end{array}\displaystyle \right . $$

    for all \(u_{i}, u_{j}, \bar{u}_{i}, \bar{u}_{j}, u, v \in{R} \).

  2. (H2)

    For all \(t,u,v\in{R}\),

    $$\left \{ \textstyle\begin{array}{l} s_{ji}(t+T)f_{j}(u,v)=-s_{ji}(t)f_{j}(-u,-v), \\ t_{ij}(t+T)g_{i}(u,v)=-t_{ij}(t)g_{i}(-u,-v), \\ c_{i}(t+T)=-c_{i}(t),\qquad d_{j}(t+T)=-d_{j}(t), \end{array}\displaystyle \right . $$

    where \(i,j=1,2,\ldots,m \) and T is a positive constant.

Definition 2.1

The solution \((x^{*}(t),y^{*}(t))^{T}\) of model (1.3) is said to globally exponentially stable if there exist constants \(\beta>0\) and \(M>1\) such that

$$\sum_{i=1}^{m}\bigl\vert x_{i}(t)-x_{i}^{*}(t)\bigr\vert ^{2}+\sum _{j=1}^{m}\bigl\vert y_{j}(t)-y_{j}^{*}(t) \bigr\vert ^{2}\leq {M}e^{-\beta t}\bigl\Vert \varphi-\varphi^{*} \bigr\Vert ^{2} $$

for each solution \((x(t),y(t))^{T}\) of model (1.3).

Lemma 2.1

Let

$$A=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} -a_{i} & 0 \\ 0 & -b_{j} \end{array}\displaystyle \right ),\qquad \alpha=\min _{1\leq i,j\leq m}\{a_{i},b_{i}\}, $$

then

$$\|\exp A t\|\leq\sqrt{2}e^{-\alpha t}, \quad \forall t\geq0. $$

Proof

Note that

$$A=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} -a_{i} & 0 \\ 0 & -b_{j} \end{array}\displaystyle \right ), $$

then

$$\exp A t=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} e^{-a_{i}t} & 0 \\ 0 & e^{-b_{j}t} \end{array}\displaystyle \right ), $$

in view of the definition of matrix norm, we have

$$\|\exp A t\|= \bigl(e^{ -2a_{1}t}+e^{ -2a_{2}t} \bigr)^{\frac{1}{2}}\leq \sqrt {2}e^{-\alpha t}. $$

 □

Lemma 2.2

Suppose that

$$({\mathrm{H}3})\quad \left \{ \textstyle\begin{array}{l} -2a_{i}+\sum_{j=1}^{m}\bar{s}_{ji} (\alpha_{jf}^{2\epsilon_{j}}+\alpha _{jf}^{2(1-\epsilon_{j})}+\beta_{jf}^{2\varepsilon_{j}} ) + \sum_{j=1}^{m}\bar{t}_{ij}\alpha_{ig}^{2(1-\xi_{i})}< 0, \\ -2b_{j}+\sum_{i=1}^{m}\bar{t}_{ij} (\alpha_{ig}^{2\xi_{i}}+\beta _{ig}^{2\varsigma_{i}}+\beta_{ig}^{2(1-\varsigma_{i})} ) +\sum_{i=1}^{m}\bar{s}_{ji}\beta_{jf}^{2(1-\varepsilon_{j})}< 0, \end{array}\displaystyle \right . $$

where \(0\leq\epsilon_{j},\varepsilon_{j}, \xi_{i}, \varsigma_{i}<1\) (\(i,j=1,2,\ldots,m\)) are any constants. Then there exists \(\beta>0\) such that

$$\begin{aligned}& \beta-2a_{i}+\sum_{j=1}^{m} \bar{s}_{ji} \bigl(\alpha_{jf}^{2\epsilon _{j}}+ \alpha_{jf}^{2(1-\epsilon_{j})}+\beta_{jf}^{2\varepsilon_{j}} \bigr) + \sum_{j=1}^{m}\bar{t}_{ij} \alpha_{ig}^{2(1-\xi_{i})}e^{\beta\delta _{ij}}\leq0, \\& \beta-2b_{j}+\sum_{i=1}^{m} \bar{t}_{ij} \bigl(\alpha_{ig}^{2\xi_{i}}+\beta _{ig}^{2\varsigma_{i}}+\beta_{ig}^{2(1-\varsigma_{i})} \bigr) +\sum _{i=1}^{m}\bar{s}_{ji} \beta_{jf}^{2(1-\varepsilon_{j})}e^{\beta\tau _{ji}}\leq0. \end{aligned}$$

Proof

Let

$$\begin{aligned}& \varrho_{1i}(\beta) = \beta-2a_{i}+\sum _{j=1}^{m}\bar {s}_{ji} \bigl( \alpha_{jf}^{2\epsilon_{j}}+\alpha_{jf}^{2(1-\epsilon _{j})}+ \beta_{jf}^{2\varepsilon_{j}} \bigr) + \sum_{j=1}^{m} \bar{t}_{ij}\alpha_{ig}^{2(1-\xi_{i})}e^{\beta\delta _{ij}}, \\& \varrho_{2j}(\beta) = \beta-2b_{j}+\sum _{i=1}^{m}\bar{t}_{ij} \bigl(\alpha _{ig}^{2\xi_{i}}+\beta_{ig}^{2\varsigma_{i}}+ \beta_{ig}^{2(1-\varsigma _{i})} \bigr) +\sum_{i=1}^{m} \bar{s}_{ji}\beta_{jf}^{2(1-\varepsilon_{j})}e^{\beta\tau_{ji}}. \end{aligned}$$

Clearly, \(\varrho_{1i}(\beta)\), \(\varrho_{2j}(\beta)\) (\(i,j=1,2,\ldots,m\)) are continuously differential functions. One has

$$\left \{ \textstyle\begin{array}{l} \frac{d\varrho_{1i}(\beta)}{d\beta}=1+\sum_{j=1}^{m}\bar{t}_{ij}\alpha _{ig}^{2(1-\xi_{i})}\delta_{ij} e^{\beta\delta_{ij}}>0,\qquad \lim_{\beta\rightarrow{+\infty}}\varrho_{1i}(\beta)=+\infty,\qquad \varrho _{1i}(0)< 0, \\ \frac{d\varrho_{2j}(\beta)}{d\beta}=1+\sum_{i=1}^{m}\bar{s}_{ji}\beta _{jf}^{2(1-\varepsilon_{j})}\tau_{ji}e^{\beta\tau_{ji}}>0,\qquad \lim_{\beta\rightarrow{+\infty}}\varrho_{2j}(\beta)=+\infty,\qquad \varrho_{2j}(0)< 0. \end{array}\displaystyle \right . $$

According to the intermediate value theorem, we can conclude that there exist constants \(\beta_{i}^{*}>0\), \(\beta_{j}^{*}>0\) such that

$$\varrho_{1i}\bigl(\beta_{i}^{*}\bigr)=0,\qquad \varrho_{2j}\bigl(\beta_{j}^{*}\bigr)=0,\quad i,j=1,2,\ldots,m. $$

Let \(\beta_{0}=\min\{\beta_{1},\beta_{2},\ldots, \beta_{m}, \beta_{1}^{*},\beta_{2}^{*}, \ldots,\beta_{m}^{*}\}\), then it follows that \(\beta_{0}>0\) and

$$\varrho_{1i}(\beta_{0})\leq0,\qquad \varrho_{2j}( \beta_{0})\leq0, \quad i, j=1,2,\ldots,m. $$

The proof of Lemma 2.2 is complete. □

Lemma 2.3

Suppose that (H1) holds true. Then for any solution \((x(t),y(t))^{T}\) of model (1.3), there exists a constant

$$\gamma=\sqrt{2}\bigl(\|\varphi\|^{2}+\|\psi\|^{2}\bigr)+ \frac{\sqrt{2}}{\alpha} \Biggl[\sum_{j=1}^{m}( \bar{s}_{ji}F_{j}+\bar{c}_{i})+\sum _{i=1}^{m}(\bar {t}_{ij}G_{i}+ \bar{d}_{j}) \Biggr] $$

such that

$$\bigl\vert x_{i}(t)\bigr\vert \leq{\gamma},\qquad \bigl\vert y_{j}(t)\bigr\vert \leq{\gamma}, \quad i,j=1,2,\ldots,n, \forall t>0. $$

Proof

Let

$$\begin{aligned}& z_{ij}(t)=\left ( \textstyle\begin{array}{@{}c@{}} x_{i}(t)\\ y_{j}(t) \end{array}\displaystyle \right ), \\& A=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} -a_{i} & 0 \\ 0 & -b_{j} \end{array}\displaystyle \right ),\qquad B_{ij}(t)= \left ( \textstyle\begin{array}{@{}c@{}} c_{i}(t) \\ d_{j}(t) \end{array}\displaystyle \right ), \\& F_{ij}\bigl(x_{i}(t),y_{j}(t)\bigr)=\left ( \textstyle\begin{array}{@{}c@{}} \sum_{j=1}^{m}s_{ji}(t)f_{j}[x_{j}(t),y_{j}(t-\tau_{ji})] \\ \sum_{i=1}^{m}t_{ij}(t)g_{i}[x_{i}(t-\delta_{ij}),y_{i}(t)] \end{array}\displaystyle \right ), \end{aligned}$$

then the model (1.3) takes the following form:

$$ z_{ij}'(t)\leq{A}z_{ij}(t)+F_{ij} \bigl(x_{i}(t),y_{j}(t)\bigr)+B_{ij}(t). $$
(2.2)

By (2.2), we get

$$z_{ij}(t)\leq{e^{At}}z_{ij}(0)+ \int _{0}^{t}e^{A(t-s)}\bigl[F_{ij} \bigl(x_{i}(s),y_{j}(s)\bigr)+B_{ij}(s)\bigr]\, ds. $$

In view of Lemma 2.1, we have

$$\begin{aligned} \begin{aligned}[b] \bigl\Vert z_{ij}(t)\bigr\Vert &\leq \sqrt{2}e^{-\alpha t}\bigl\Vert z_{ij}(0)\bigr\Vert +\sqrt{2} \int_{0}^{t}e^{\alpha (t-s)}\bigl[\bigl\Vert F_{ij}\bigl(x_{i}(s),y_{j}(s)\bigr)\bigr\Vert + \bigl\vert B_{ij}(s)\bigr\vert \bigr]\, ds \\ &\leq\sqrt{2}\bigl(\Vert \varphi \Vert ^{2}+\Vert \psi \Vert ^{2}\bigr)+\frac{\sqrt{2}}{\alpha} \bigl(1-e^{-\alpha t} \bigr) \Biggl[\sum _{j=1}^{m}(\bar{s}_{ji}F_{j}+ \bar{c}_{i})+\sum_{i=1}^{m}(\bar {t}_{ij}G_{i}+\bar{d}_{j}) \Biggr] \\ &\leq\sqrt{2}\bigl(\Vert \varphi \Vert ^{2}+\Vert \psi \Vert ^{2}\bigr)+\frac{\sqrt{2}}{\alpha} \Biggl[\sum_{j=1}^{m}( \bar{s}_{ji}F_{j}+\bar{c}_{i})+\sum _{i=1}^{m}(\bar {t}_{ij}G_{i}+ \bar{d}_{j}) \Biggr]. \end{aligned} \end{aligned}$$

Let

$$ \gamma=\sqrt{2}\bigl(\|\varphi\|^{2}+\|\psi \|^{2}\bigr)+\frac{\sqrt{2}}{\alpha} \Biggl[\sum_{j=1}^{m}( \bar{s}_{ji}F_{j}+\bar{c}_{i})+\sum _{i=1}^{m}(\bar {t}_{ij}G_{i}+ \bar{d}_{j}) \Biggr]. $$
(2.3)

Then it follows that \(|x_{i}(t)|\leq\gamma\), \(|y_{j}(t)|\leq\gamma\) for all \(t>0\). This completes the proof of Lemma 2.3. □

3 Main results

In this section, we state our main findings for model (1.3).

Theorem 3.1

Suppose that (H1)-(H3) are satisfied. Then any solution \((x^{*}(t),y^{*}(t))^{T}\) of model (1.3) is globally exponentially stable.

Proof

Let \(u_{i}(t)=x_{i}(t)-x_{i}^{*}(t)\), \(v_{j}(t)=y_{j}(t)-y_{j}^{*}(t)\), \(i,j=1,2,\ldots,m\). By model (1.3), we have

$$ \left \{ \textstyle\begin{array}{l} \frac{u_{i}(t)}{dt}=-a_{i}u_{i}(t)+\sum_{j=1}^{m}s_{ji}(t)[f_{j}(x_{j}(t),y_{j}(t-\tau_{ji}))-f_{j}(x_{j}^{*}(t),y_{j}^{*}(t-\tau _{ji}))], \\ \frac{v_{j}(t)}{dt}=-b_{j}v_{j}(t)+\sum_{i=1}^{m}t_{ij}(t)[g_{i}(x_{i}(t-\delta _{ij}),y_{i}(t))-g_{i}(x_{i}^{*}(t-\delta_{ij}),y_{i}^{*}(t))], \end{array}\displaystyle \right . $$
(3.1)

which leads to

$$ \left \{ \textstyle\begin{array}{l} \frac{1}{2}\frac{du_{i}^{2}(t)}{dt}=-a_{i}u_{i}^{2}(t)+u_{i}(t)\sum_{j=1}^{m}s_{ji}(t)[f_{j}(x_{j}(t),y_{j}(t-\tau_{ji}))-f_{j}(x_{j}^{*}(t),y_{j}^{*}(t-\tau _{ji}))], \\ \frac{1}{2}\frac{dv_{j}^{2}(t)}{dt}=-b_{j}v_{j}^{2}(t)+v_{j}(t)\sum_{i=1}^{m}t_{ij}(t)[g_{i}(x_{i}(t-\delta_{ij}),y_{i}(t))-g_{i}(x_{i}^{*}(t-\delta _{ij}),y_{i}^{*}(t))]. \end{array}\displaystyle \right . $$
(3.2)

Then

$$ \left \{ \textstyle\begin{array}{l} \frac{du_{i}^{2}(t)}{dt}\leq-2a_{i}u_{1}^{2}(t)+\sum_{j=1}^{m}\bar{s}_{ji} [\alpha_{jf}^{2\epsilon_{j}}u_{i}^{2}(t)+\alpha_{jf}^{2(1-\epsilon _{j})}u_{j}^{2}(t) ] \\ \hphantom{\frac{du_{i}^{2}(t)}{dt}\leq{}}{}+\sum_{j=1}^{m}\bar{s}_{ji} [\beta_{jf}^{2\varepsilon_{j}} u_{i}^{2}(t)+\beta_{jf}^{2(1-\varepsilon_{j})}v_{j}^{2}(t-\tau_{ji}) ], \\ \frac{dv_{j}^{2}(t)}{dt}\leq-2b_{j}v_{j}^{2}(t) +\sum_{i=1}^{m}\bar{t}_{ij} [\alpha_{ig}^{2\xi_{i}}v_{j}^{2}(t)+\alpha _{ig}^{2(1-\xi_{i})}u_{i}^{2}(t-\delta_{ij}) ] \\ \hphantom{\frac{dv_{j}^{2}(t)}{dt}\leq{}}{}+\sum_{i=1}^{m}\bar{t}_{ij} [\beta_{ig}^{2\varsigma_{i}}v_{j}^{2}(t)+\beta_{ig}^{2(1-\varsigma _{i})}v_{i}^{2}(t) ], \end{array}\displaystyle \right . $$
(3.3)

where \(0\leq\epsilon_{j},\varepsilon_{j}, \xi_{i}, \varsigma_{i}<1\), \(i,j=1,2,\ldots,m\). Now we define a Lyapunov function as follows:

$$\begin{aligned} \begin{aligned}[b] V(t)={}&e^{\beta t} \Biggl[\sum_{i=1}^{m}u_{i}^{2}(t)+ \sum_{j=1}^{m}v_{j}^{2}(t) \Biggr] +\sum_{i=1}^{m}\sum _{j=1}^{m} \bar{s}_{ji}\beta_{jf}^{2(1-\varepsilon _{j})} \int_{t-\tau_{ji}}^{t}e^{\beta(s+\tau_{ji})}v_{j}^{2}(s) \, ds \\ &{}+\sum_{j=1}^{m}\sum _{i=1}^{m} \bar{t}_{ij}\alpha_{ig}^{2(1-\xi_{i})} \int_{t-\delta_{ji}}^{t}e^{\beta (s+\delta_{ij})}u_{i}^{2}(s) \, ds, \end{aligned} \end{aligned}$$
(3.4)

where β is defined by Lemma 2.2. Differentiating \(V(t)\) along solutions to model (1.3), together with (3.3), we have

$$\begin{aligned} \frac{dV(t)}{dt} \leq&\beta{e^{\beta t}} \Biggl[\sum _{i=1}^{m}u_{i}^{2}(t)+ \sum_{j=1}^{m}v_{j}^{2}(t) \Biggr] \\ &{}+e^{\beta t}\sum_{i=1}^{m} \Biggl\{ -2a_{i}u_{1}^{2}(t)+\sum _{j=1}^{m}\bar {s}_{ji} \bigl[ \alpha_{jf}^{2\epsilon_{j}}u_{i}^{2}(t)+\alpha _{jf}^{2(1-\epsilon_{j})}u_{j}^{2}(t) \bigr] \\ &{}+\sum_{j=1}^{m}\bar{s}_{ji} \bigl[\beta_{jf}^{2\varepsilon _{j}}u_{i}^{2}(t)+ \beta_{jf}^{2(1-\varepsilon_{j})}v_{j}^{2}(t- \tau_{ji}) \bigr] \Biggr\} \\ &{}+e^{\beta t}\sum_{j=1}^{m} \Biggl\{ -2b_{j}v_{j}^{2}(t) +\sum _{i=1}^{m}\bar{t}_{ij} \bigl[ \alpha_{ig}^{2\xi_{i}}v_{j}^{2}(t)+\alpha _{ig}^{2(1-\xi_{i})}u_{i}^{2}(t- \delta_{ij}) \bigr] \\ &{}+\sum_{i=1}^{m}\bar{t}_{ij} \bigl[\beta_{ig}^{2\varsigma _{i}}v_{j}^{2}(t)+ \beta_{ig}^{2(1-\varsigma_{i})}v_{i}^{2}(t) \bigr] \Biggr\} \\ &{}+\sum_{i=1}^{m}\sum _{j=1}^{m} \bar{s}_{ji}\beta_{jf}^{2(1-\varepsilon_{j})} \bigl[e^{\beta(t+\tau _{ji})}v_{j}^{2}(t)-e^{\beta t}v_{j}^{2}(t- \tau_{ji}) \bigr] \\ &{}+\sum_{j=1}^{m}\sum _{i=1}^{m} \bar{t}_{ij}\alpha_{ig}^{2(1-\xi_{i})} \bigl[e^{\beta(t+\delta _{ij})}u_{i}^{2}(t)-e^{\beta t}u_{i}^{2}(t- \delta_{ij}) \bigr] \\ \leq&e^{\beta t}\sum_{i=1}^{m} \Biggl[\beta-2a_{i}+\sum_{j=1}^{m} \bar{s}_{ji} \bigl(\alpha _{jf}^{2\epsilon_{j}}+ \alpha_{jf}^{2(1\epsilon_{j})}+\beta _{jf}^{2\varepsilon_{j}} \bigr) + \sum_{j=1}^{m}\bar{t}_{ij} \alpha_{ig}^{2(1-\xi_{i})}e^{\beta\delta _{ij}} \Biggr]u_{i}^{2}(t) \\ &{}+e^{\beta t}\sum_{j=1}^{m} \Biggl[\beta-2b_{j}+\sum_{i=1}^{m} \bar{t}_{ij} \bigl(\alpha _{ig}^{2\xi_{i}}+ \beta_{ig}^{2-\varsigma_{i})}+\beta_{ig}^{2(1-\varsigma _{i})} \bigr) + \sum_{i=1}^{m}\bar{s}_{ji} \beta_{jf}^{2(1-\varepsilon_{j})}e^{\beta\tau _{ji}} \Biggr] \\ &{}\times v_{j}^{2}(t). \end{aligned}$$
(3.5)

In view of Lemma 2.2, we have \(\frac{dV(t)}{dt}\leq0\), which implies that \(V(t)\leq{V(0)}\) for all \(t>0\). Thus

$$\begin{aligned} e^{\beta t} \Biggl[\sum_{i=1}^{m}u_{i}^{2}(t)+ \sum_{j=1}^{m}v_{j}^{2}(t) \Biggr] \leq& \sum_{i=1}^{m}u_{i}^{2}(0)+ \sum_{j=1}^{m}v_{j}^{2}(0) \\ &{}+\sum_{i=1}^{m}\sum _{j=1}^{m} \bar{s}_{ji}\beta_{jf}^{2(1-\varepsilon _{j})} \int_{-\tau}^{0}e^{\beta(s+\tau)}v_{j}^{2}(s)\,ds \\ &{}+\sum_{j=1}^{m}\sum _{i=1}^{m} \bar{t}_{ij}\alpha_{ig}^{2(1-\xi_{i})} \int_{-\delta}^{0}e^{\beta(s+\delta )}u_{i}^{2}(s)\,ds \\ \leq&\bigl\Vert \varphi-\varphi^{*}\bigr\Vert ^{2}+\bigl\Vert \psi-\psi^{*}\bigr\Vert ^{2} \\ &{}+\sum_{i=1}^{m}\max _{1\leq j\leq m} \bigl(\bar{s}_{ji}\beta _{jf}^{2(1-\varepsilon_{j})} \bigr)\frac{1}{\beta}e^{\beta\tau}\bigl\Vert \psi-\psi ^{*}\bigr\Vert ^{2} \\ &{}+\sum_{j=1}^{m}\max _{1\leq i\leq m} \bigl(\bar{t}_{ij}\alpha_{ig}^{2(1-\xi_{i})} \bigr) \frac{1}{\beta }e^{\beta\delta}\bigl\Vert \varphi-\varphi^{*}\bigr\Vert ^{2} \\ =& \Biggl[1+\sum_{j=1}^{m}\max _{1\leq i\leq m} \bigl(\bar{t}_{ij}\alpha_{ig}^{2(1-\xi_{i})} \bigr) \frac{1}{\beta}e^{\beta\delta} \Biggr]\bigl\Vert \varphi-\varphi^{*} \bigr\Vert ^{2} \\ &{}+ \Biggl[1+\sum_{i=1}^{m}\max _{1\leq j\leq m} \bigl(\bar{s}_{ji}\beta_{jf}^{2(1-\varepsilon_{j})} \bigr)\frac{1}{\beta }e^{\beta\tau} \Biggr]\bigl\Vert \psi-\psi^{*}\bigr\Vert ^{2}. \end{aligned}$$
(3.6)

Let

$$ M=\max \Biggl\{ 1+\sum_{j=1}^{m} \max_{1\leq i\leq m} \bigl(\bar{t}_{ij}\alpha_{ig}^{2(1-\xi_{i})} \bigr) \frac{1}{\beta}e^{\beta\delta},1+\sum_{i=1}^{m} \max_{1\leq j\leq m} \bigl(\bar{s}_{ji}\beta_{jf}^{2(1-\varepsilon_{j})} \bigr)\frac{1}{\beta }e^{\beta\tau} \Biggr\} >1. $$
(3.7)

By (3.6), one has

$$\sum_{i=1}^{m}u_{i}^{2}(t)+ \sum_{j=1}^{m}v_{j}^{2}(t) \leq{M}e^{-\beta t} \bigl(\bigl\Vert \varphi-\varphi^{*}\bigr\Vert ^{2}+\bigl\Vert \psi-\psi^{*}\bigr\Vert ^{2} \bigr) $$

for all \(t>0\). Then

$$\sum_{i=1}^{m}\bigl\vert x_{i}(t)-x_{i}^{*}(t)\bigr\vert ^{2}+\sum _{j=1}^{m}\bigl\vert y_{j}(t)-y_{j}^{*}(t) \bigr\vert ^{2}\leq {M}e^{-\beta t}\bigl\Vert \varphi-\varphi^{*} \bigr\Vert ^{2} $$

for all \(t>0\). Thus the solution \((x^{*}(t),y^{*}(t))^{T}\) of model (1.3) is globally exponentially stable. □

Theorem 3.2

Suppose that (H1)-(H3) hold. Then model (1.3) has exactly one T-anti-periodic solution which is globally stable.

Proof

By model (1.3) and (H2), for each \(k\in{N}\), we get

$$\begin{aligned}& \frac{d}{dt} \bigl[(-1)^{k+1}x_{i} \bigl(t+(k+1)T\bigr) \bigr] \\& \quad =(-1)^{k+1} \Biggl[a_{i}x_{i}\bigl(t+(k+1)T \bigr)+\sum_{j=1}^{m}s_{ji} \bigl(t+(k+1)T\bigr) \\& \qquad {}\times f_{j}\bigl[x_{j}\bigl(t+(k+1)T \bigr),y_{j}\bigl(t+(k+1)T-\tau_{ji}\bigr) \bigr]+c_{i}\bigl(t+(k+1)T\bigr) \Biggr] \\& \quad = a_{i}(-1)^{k+1}x_{i}\bigl(t+(k+1)T\bigr)+ \sum_{j=1}^{m}s_{ji}(t)f_{j} \bigl[(-1)^{k+1}x_{j}\bigl(t+(k+1)T\bigr), \\& \qquad (-1)^{k+1}y_{j}\bigl(t+(k+1)T-\tau_{ji} \bigr)\bigr]+c_{i}(t). \end{aligned}$$
(3.8)

In a similar way, we have

$$\begin{aligned} \begin{aligned}[b] &\frac{d}{dt} \bigl[(-1)^{k+1}y_{j} \bigl(t+(k+1)T\bigr) \bigr] \\ &\quad =-b_{j}(-1)^{k+1}y_{j}\bigl(+(k+1)T\bigr)+ \sum_{i=1}^{m}t_{ij}(t)g_{i} \bigl[(-1)^{k+1}x_{i}\bigl(t+(k+1)T-\delta_{ij} \bigr), \\ &\qquad (-1)^{k+1}y_{i}\bigl(t+(k+1)T\bigr) \bigr]+d_{j}(t).\end{aligned} \end{aligned}$$
(3.9)

Let

$$\begin{aligned}& \bar{x}(t)=\bigl((-1)^{k+1}x_{1}\bigl(t+(k+1)T \bigr),(-1)^{k+1}x_{2}\bigl(t+(k+1)T\bigr),\ldots, (-1)^{k+1}x_{m}\bigl(t+(k+1)T\bigr)\bigr)^{T}, \\& \bar{y}(t)=\bigl((-1)^{k+1}y_{1}\bigl(t+(k+1)T \bigr),(-1)^{k+1}y_{2}\bigl(t+(k+1)T\bigr),\ldots, (-1)^{k+1}y_{m}\bigl(t+(k+1)T\bigr)\bigr)^{T}. \end{aligned}$$

Clearly, for any \(k\in{N}\), \((\bar{x}^{T}(t),\bar{y}^{T}(t))^{T}\) is also the solution of model (1.3). If the initial functions \(\varphi_{i}(s)\), \(\psi_{j}(s)\) (\(i,j=1,2,\ldots,m\)) are bounded, it follows from Theorem 3.1 that there exists a constant \(\gamma>1\) such that

$$\begin{aligned}& \bigl\vert (-1)^{k+1}x_{i}\bigl(t+(k+1)T \bigr)-(-1)^{k}x_{i}(t+kT)\bigr\vert \\& \quad \leq{M}e^{-\beta(t+kT)}\sup_{-\delta\leq{s}\leq0}\sum _{i=1}^{m}\bigl\vert x_{i}(t+T)+x_{i}(s) \bigr\vert ^{2} \\& \quad \leq\gamma e^{-\beta(t+kT)}, \end{aligned}$$
(3.10)

where \(t+kT>0\), \(i=1,2,\ldots,m\). For any \(k\in{N}\) we have

$$ (-1)^{k+1} x_{i} \bigl(t + (k+1)T\bigr) = x_{i} (t ) +\sum_{j=0}^{k} \bigl[(-1)^{j+1} x _{i}\bigl(t + (j+1)T\bigr)-(-1)^{j} x_{i} (t + jT)\bigr]. $$
(3.11)

Then

$$ (-1)^{k+1} x_{i} \bigl(t + (k+1)T\bigr) \leq \bigl\vert x_{i} (t )\bigr\vert +\sum_{j=0}^{k} \bigl\vert (-1)^{j+1} x_{i}\bigl(t + (j+1)T \bigr)-(-1)^{j} x_{i} (t + jT)\bigr\vert . $$
(3.12)

In view of Lemma 2.3, we know that the solutions of system (1.3) are bounded. In view of (3.10) and (3.12), we can easily see that \(\{(-1)^{k+1} x_{i}(t + (k+1)T)\}\) uniformly converges to a continuous function \(x^{*}(t)=(x^{*}_{1}(t),x^{*}_{2}(t), \ldots,x^{*}_{m}(t) )^{T}\) on any compact set of R. In a similar way, we can easily prove that \(\{(-1)^{k+1} y_{j}(t + (k+1)T)\}\) uniformly converges to a continuous function \(y^{*}(t)=(y^{*}_{1}(t),y^{*}_{2}(t), \ldots,y^{*}_{m}(t) )^{T}\) on any compact set of R. Now we will show that \((x^{*}(t), y^{*}(t))^{T}\) is a T-anti-periodic solution of (1.3). Since

$$\begin{aligned} x^{*}(t+T) =&\lim_{k\to\infty}(-1)^{k }x(t +T+ kT) \\ =&-\lim_{(k+1)\to\infty}(-1)^{k+1 } x\bigl(t +(k +1)T \bigr)=-x^{*}(t ). \end{aligned}$$
(3.13)

Thus \(x^{*}(t)\) is the T-anti-periodic solution. Similarly, \(y^{*}(t)\) is also the T-anti-periodic solution. Thus we know that \((x^{(}t),y^{*}(t))^{T}\) is the solution of model (1.3). In fact, together with the continuity of the right side of model (1.3), letting \(k\to\infty\), we can easily get

$$ \left \{ \textstyle\begin{array}{l} \frac{x_{i}^{*}(t)}{dt}=-a_{i}x_{i}^{*}(t)+\sum_{j=1}^{m}s_{ji}(t)f_{j}[x_{j}^{*}(t),y_{j}^{*}(t-\tau_{ji})]+c_{i}(t), \\ \frac{y_{j}^{*}(t)}{dt}=-b_{j}y_{j}^{*}(t)+\sum_{i=1}^{m}t_{ij}(t)g_{i}[x_{i}^{*}(t-\delta_{ij}),y_{i}^{*}(t)]+d_{j}(t). \end{array}\displaystyle \right . $$
(3.14)

Therefore, \((x^{*}(t),y^{*}(t))^{T}\) is the T-periodic solution of (1.3). Finally, by applying Theorem 3.1, it is easy to check that \((x^{*}(t),y^{*}(t))^{T}\) is globally exponentially stable. The proof of Theorem 3.2 is completed. □

Remark 3.1

In [22, 24–45], the authors investigated the existence and exponential stability of anti-periodic solutions for some neural networks by applying the differential inequality techniques, the continuation theorem of coincidence degree theory, the contraction mapping principle, and the Lyapunov functional method, respectively. All the results in [22, 24–45] cannot applicable to model (1.3) to obtain the existence and exponential stability of the anti-periodic solutions. In [23], the authors studied the existence and exponential stability of anti-periodic solutions of neural networks by the fundamental solution matrix of coefficients, the inequality technique, and the Lyapunov method. But the activation functions of neural networks are single variable functions. In this paper, the activation functions of neural networks model (1.3) are two-variable functions. All the results in [23] cannot applicable to model (1.3) to obtain the existence and exponential stability of the anti-periodic solutions. This implies that the results of this paper are essentially new and complement previously known results in [22–45].

4 An example

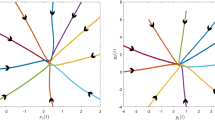
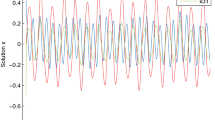
In this section, to illustrate the feasibility of our theoretical findings obtained in previous sections, we give an example. Consider the following interval general bidirectional associative memory (BAM) neural networks with multiple delays:

$$ \left \{ \textstyle\begin{array}{l} \frac{x_{1}(t)}{dt}=-a_{1}x_{1}(t)+\sum_{j=1}^{2}s_{j1}(t)f_{j}[x_{j}(t),y_{j}(t-\tau _{j1})]+c_{1}(t), \\ \frac{x_{2}(t)}{dt}=-a_{2}x_{2}(t)+\sum_{j=1}^{2}s_{j2}(t)f_{j}[x_{j}(t),y_{j}(t-\tau _{j2})]+c_{2}(t), \\ \frac{y_{1}(t)}{dt}=-b_{1}y_{1}(t)+\sum_{i=1}^{2}t_{i1}(t)g_{i}[x_{i}(t-\delta _{i1}),y_{i}(t)]+d_{1}(t), \\ \frac{y_{2}(t)}{dt}=-b_{2}y_{2}(t)+\sum_{i=1}^{2}t_{i2}(t)g_{i}[x_{i}(t-\delta _{i2}),y_{i}(t)]+d_{2}(t), \end{array}\displaystyle \right . $$
(4.1)

where \(a_{1}=2\), \(a_{2}=2\), \(b_{1}=2\), \(b_{2}=2.5\), \(s_{11}(t)=0.2+0.2\sin t\), \(s_{21}(t)=0.2+0.1\cos t\), \(s_{12}(t)=0.3+0.2\sin t\), \(s_{22}(t)=0.3+0.1\cos t\), \(t_{11}(t)=0.3+0.1\sin t\), \(t_{21}(t)=0.4+0.1\cos t\), \(t_{12}(t)=0.3+0.2\cos t\), \(t_{22}(t)=0.4+0.1\cos t\), \(c_{1}(t)=0.5+0.1\cos t\), \(c_{2}(t)=0.2+0.1\cos t\), \(d_{1}(t)=0.3+0.1\sin t\), \(d_{2}(t)=0.4+0.1\sin t\), \(\tau_{11}=0.5\), \(\tau_{21}=0.2\), \(\tau_{12}=0.3\), \(\tau_{22}=0.4\), \(\delta_{11}=0.4\), \(\delta_{21}=0.3\), \(\delta_{12}=0.2\), \(\delta_{22}=0.1\). Set \(f_{j}(x_{j},y_{j})=|x_{j}(t)|+|y_{j}(t-\tau_{ji}(t))|\), \(g_{i}(x_{i},y_{i})=|x_{i}(t-\delta_{ij}(t))|+|y_{i}(t)|\), \(i,j=1,2\). Then \(\alpha_{1f}=\alpha_{2f}=\beta_{1f}=\beta_{2f}=\alpha_{1g}=\alpha _{2g}=\beta_{1g}=\beta_{2g}=1\), \(\bar{s}_{11}=0.4\), \(\bar{s}_{21}=0.3\), \(\bar{s}_{12}=0.5\), \(\bar{s}_{22}=0.4\), \(\bar{t}_{11}=0.4\), \(\bar{t}_{21}=0.5\), \(\bar{t}_{12}=0.5\), \(\bar{t}_{22}=0.5\). It is easy to verify that

$$ \left \{ \textstyle\begin{array}{l} -2a_{1}+\sum_{j=1}^{2}\bar{s}_{j1} (\alpha_{jf}^{2\epsilon_{j}}+\alpha _{jf}^{2(1-\epsilon_{j})}+\beta_{jf}^{2\varepsilon_{j}} ) + \sum_{j=1}^{2}\bar{t}_{1j}\alpha_{ig}^{2(1-\xi_{1})}=-1< 0, \\ -2a_{2}+\sum_{j=1}^{2}\bar{s}_{j2} (\alpha_{jf}^{2\epsilon_{j}}+\alpha _{jf}^{2(1-\epsilon_{j})}+\beta_{jf}^{2\varepsilon_{j}} ) + \sum_{j=1}^{2}\bar{t}_{2j}\alpha_{2g}^{2(1-\xi_{2})}=-0.3< 0, \\ -2b_{1}+\sum_{i=1}^{2}\bar{t}_{i1} (\alpha_{ig}^{2\xi_{i}}+\beta _{ig}^{2\varsigma_{i}}+\beta_{ig}^{2(1-\varsigma_{i})} ) +\sum_{i=1}^{2}\bar{s}_{1i}\beta_{1f}^{2(1-\varepsilon _{1})}=-0.6< 0, \\ -2b_{2}+\sum_{i=1}^{2}\bar{t}_{i2} (\alpha_{ig}^{2\xi_{i}}+\beta _{ig}^{2\varsigma_{i}}+\beta_{ig}^{2(1-\varsigma_{i})} ) +\sum_{i=1}^{2}\bar{s}_{2i}\beta_{2f}^{2(1-\varepsilon_{2})}=-1.1< 0. \end{array}\displaystyle \right . $$
(4.2)

Then all the conditions (H1)-(H3) hold. Thus model (4.1) has exactly one π-anti-periodic solution which is globally exponentially stable.

5 Conclusions

In this article, a class of interval general bidirectional associative memory (BAM) neural networks with multiple delays have been dealt with. Applying the matrix theory and the inequality technique, a series of sufficient criteria to guarantee the existence and global exponential stability of anti-periodic solutions for the interval general bidirectional associative memory (BAM) neural networks with multiple delays have been established. The derived criteria are easily to check in practice. Finally, an example with its numerical simulations is carried out to illustrative the effectiveness of our findings. The obtained results in this article complement the studies of [22–45].