1 Introduction

It is well known that predation activities are ubiquitous in nature [1]. Modeling of predator-prey interaction has become an important topic in mathematical biology. Song and Yuan [2] studied bifurcation analysis in a predator-prey system with time delay. Ruan and Xiao [3] provided a global analysis in a predator-prey system with a nonmonotonic functional response, and they proved the existence of two limit cycles. Huang and Xiao [4] considered a bifurcation analysis and stability for a predator-prey system with Holling-IV functional response. Xiao and Ruan [5] and Xue and Duan [6] considered time-delay effects to a predator-prey model with Holling-IV type functional response, where stability and bifurcation of periodic solutions were investigated. For the non-autonomous case, Chen [7] proved the existence of two periodic solutions for a model with Holling-IV functional response, and Xia et al. [8] obtained some sufficient conditions for the existence of two periodic solutions in a stage-structured predator-prey model. Li et al. [9] established the existence of multiple periodic solutions for a stage-structured model with harvesting terms. Wang et al. [10] studied the existence of multiple periodic solutions for an impulsive model with a Holling IV type functional response. A two-species model (the so-called LG model) was proposed by Leslie and Gower [11] in 1960. Korobeinikov [12] proved the existence of the limit cycle in such a model. For autonomous predator-prey models with Holling II or III type functional response, the existence of a limit cycle was proved and for the non-autonomous case, the existence of periodic solutions was established. Yu [13] reported some important research for a modified Leslie–Gower model. The Leslie–Gower type predator-prey model with Holling type IV functional response is described by

$$ \textstyle\begin{cases} \frac{du}{dt} = [r(1-\frac{u}{K})- \frac{mv}{\frac{u^{2}}{i}+u+a} ]u, \\ \frac{dv}{dt} = s(1-\frac{nv}{u})v, \end{cases} $$
(1.1)

where \(u\equiv u(t)\) and \(v\equiv v(t)\) are the prey and predator population density, respectively, r and s are intrinsic growth rates of the prey and predator, respectively. K is the carrying capacity of prey population; here m and i denote the maximum per capita predation rate and a measure of the predator’s immunity from or tolerance of the prey, respectively, and a and n are the half saturation constant and the number of prey required to support one predator at equilibrium, respectively. Upadhyay et al. [14] studied that interaction between prey and predator with a Holling type IV functional response. We know that there are three main types of harvesting in the biomodel article: (1) constant rate of harvesting, (2) proportional harvesting \(H(x)=qEx\), and (3) nonlinear harvesting \(H(u)=\frac{qEu}{m_{1}E+m_{2}u}\), where \(m_{1}\), \(m_{2}\) are suitable constants, E is the effort applied to harvest individuals and q is the catchability coefficient. Zhang et al. [15] introduced the nonlinear harvesting \(H(u)=\frac{qEu}{m_{1}E+m_{2}u}\) into model (1.1), and it can be described by

$$ \textstyle\begin{cases} \frac{du}{dt} = [r(1-\frac{u}{K})- \frac{mv}{\frac{u^{2}}{i}+u+a}-\frac{qE}{m_{1}E+m_{2}u} ]u, \\ \frac{dv}{dt} = s(1-\frac{nv}{u})v. \end{cases} $$
(1.2)

Taking

$$\begin{aligned} &u=Kx,\qquad t=rT,\qquad h=\frac{qE}{rm_{2}K},\qquad c=\frac{m_{1}E}{m_{2}K},\qquad v= \frac{rKy}{m},\qquad \alpha =\frac{i}{k},\\ & \beta =\frac{nr}{m},\qquad \gamma = \frac{a}{K},\qquad \delta =\frac{s}{r}, \end{aligned}$$

then system (1.2) becomes

$$ \textstyle\begin{cases} \frac{dx}{dt} = x(1-x)-\frac{xy}{\frac{x^{2}}{\alpha }+x+\gamma }-\frac{hx}{x+c}, \\ \frac{dy}{dt} = {\delta }y(1-\beta \frac{y}{x}). \end{cases} $$
(1.3)

In spite of a lot of works focused on the global dynamics and bifurcation analysis of the ecological systems (e.g., [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]), in realistic environment, ecological systems are usually affected by the seasonable perturbations or other unpredictable disturbances (e.g., see [24,25,26,27,28,29,30,31,32,33,34,35,36]). Thus the time-varying parameters are more reasonable when we try to consider the periodic environment. In this paper, we consider the following non-autonomous model:

$$ \textstyle\begin{cases} \frac{dx}{dt} = x(1-x)-\frac{xy}{\frac{x^{2}}{\alpha (t)}+x+\gamma (t)}- \frac{h(t)x}{x+c(t)}, \\ \frac{dy}{dt} = {\delta (t)}y(1-\beta (t)\frac{y}{x}). \end{cases} $$
(1.4)

The rest of this paper is organized as follows. In Sect. 2, we discuss the permanence for the general nonautonomous case. Section 3 is to obtain some sufficient conditions for the existence of periodic solution of system (1.4). Finally, we use numerical simulation to fully demonstrate the existence of our periodic solution.

2 Permanence

In this section, we assume that \(\alpha (t), \gamma (t), h(t), c(t), \delta (t)\), and \(\beta (t)\) are all continuous and bounded above and below by positive constants. Let \(\mathbb{R}_{+}^{2}:=\) \(\{(x,y) \in \mathbb{R}^{2}\mid x\geq 0, y\geq 0 \}\). For a continuous bounded function \(f(t)\) on \(\mathbb{R}\), denote

$$ f^{u}:= \operatorname{sup}_{t\in \mathbb{R}} f(t),\qquad f^{l}:= \operatorname{inf}_{t \in \mathbb{R}} f(t). $$

From a biological viewpoint, we assume that the initial conditions satisfy

$$ x(t_{0})=x_{0}>0,\qquad y(t_{0})=y_{0}>0. $$

Definition 2.1

If a positive solution \((x(t), y(t))\) of system (1.4) satisfies

$$ \min { \Bigl\{ \lim_{t\rightarrow \infty }\inf x(t), \lim_{t\rightarrow \infty } \inf y(t) \Bigr\} }=0, $$

then system (1.4) is non-persistent.

Definition 2.2

If there exist two positive constants ϕ and \(\varphi (0< \phi < \varphi )\) with

$$\begin{aligned} &\min { \Bigl\{ \lim_{t\rightarrow \infty }\inf x(t), \lim_{t\rightarrow \infty } \inf y(t) \Bigr\} }\geq \phi, \\ &\max { \Bigl\{ \lim_{t\rightarrow \infty }\sup x(t), \lim_{t\rightarrow \infty } \sup y(t) \Bigr\} }\leq \varphi, \end{aligned}$$

then system (1.4) is permanent.

Define the collections:

$$\begin{aligned} &S_{1}= \bigl\{ \bigl(c^{u}, c^{l}, h^{u}, \gamma ^{l}, \alpha ^{u}\bigr)\mid c^{u}>1, c ^{l}>h^{u}, 4\gamma ^{l}< \alpha ^{u} \bigr\} ; \\ &S_{2}= \bigl\{ \bigl(c^{u}, c^{l}, h^{u}, h^{l}, \gamma ^{l}, \alpha ^{u}, \beta ^{l}\bigr)\mid c^{u}>1, c^{l}>h^{u}, 4 \gamma ^{l}>\alpha ^{u},\\ &\phantom{S_{2}=} \beta ^{l}\bigl(c ^{u}-1\bigr) \bigl(c^{l}-h^{u}\bigr) \bigl(4\gamma ^{l}-\alpha ^{u}\bigr)>4c^{l}\bigl(c^{u}-h^{l} \bigr) \bigr\} ; \\ &S_{3}= \biggl\{ \bigl(c^{u}, c^{l}, h^{u}, h^{l}, \gamma ^{l}, \alpha ^{u}, \beta ^{l}\bigr)\mid c^{u}>h^{l}, c^{u}>1, c^{l}< h^{u}, 4\gamma ^{l}< \alpha ^{u},\\ &\phantom{S_{3}=}\frac{4c ^{l}(c^{u}-h^{l})}{(4\gamma ^{l}-\alpha ^{u})}>\beta ^{l}\bigl(c^{u}-1\bigr) \bigl(c^{l}-h ^{u}\bigr) \biggr\} ; \\ &S_{4}= \bigl\{ \bigl(c^{u}, c^{l}, h^{u}, h^{l}, \gamma ^{l}, \alpha ^{u}, \beta ^{l}\bigr)\mid c^{u}< h^{l}, c^{u}< 1, 4\gamma ^{l}< \alpha ^{u},\\ &\phantom{S_{4}= } 4c^{l} \bigl(c^{u}-h ^{l}\bigr)>\beta ^{l} \bigl(c^{u}-1\bigr) \bigl(c^{l}-h^{u}\bigr) \bigl(4 \gamma ^{l}-\alpha ^{u}\bigr) \bigr\} . \end{aligned}$$

The set Γ is defined by

$$ \varGamma = \bigl\{ (x, y)\in \mathbb{R}^{2} \mid 0< g_{1}\leq x \leq G_{1}, 0< g _{2}\leq y \leq G_{2} \bigr\} , $$
(2.1)

where

$$\begin{aligned} &G_{1}=\frac{c^{u}-h^{l}}{c^{u}-1},\qquad g_{1}= \frac{\beta ^{l} (c^{u}-1)(c ^{l}-h^{u})(4\gamma ^{l}-\alpha ^{u})-4c^{l}(c^{u}-h^{l})}{\beta ^{l}c ^{l}(c^{u}-1)(4\gamma ^{l}-\alpha ^{u})}, \end{aligned}$$
(2.2)
$$\begin{aligned} &G_{2}=\frac{c^{u}-h^{l}}{\beta ^{l}(c^{u}-1)}, \qquad g_{2}=\frac{\beta ^{l}(c ^{u}-1)(c^{l}-h^{u})(4\gamma ^{l}-\alpha ^{u})-4c^{l}(c^{u}-h^{l})}{ \beta ^{u}\beta ^{l}c^{l}(c^{u}-1)(4\gamma ^{l}-\alpha ^{u})}. \end{aligned}$$
(2.3)

Theorem 2.3

If \(S_{1}\cup S_{2}\cup S_{3}\cup S_{4}\neq \emptyset \), then the set Γ is a positively invariant and bounded region with respect to system (1.4).

Proof

Let \((x(t), y(t))\) be any solution of system (1.4) satisfying the initial values \((x(t_{0}), y(t_{0}))=(x_{0}, y_{0}) \in \varGamma \). It suffices to show that all the solutions starting from the point in Γ keep inside Γ. From the first equation of system (1.4), we get

$$\begin{aligned} \dot{x}(t) &\leq x(t) \biggl(1-x(t)-\frac{h^{l}}{x(t)+c^{u}}\biggr) \\ &=\frac{x(t)}{x(t)+c^{u}} \bigl\{ x(t)-x^{2}(t)+c^{u}-c^{u}x(t)-h^{l} \bigr\} \\ &\leq \frac{x(t)}{x(t)+c^{u}} \bigl\{ c^{u}-h^{l}- \bigl(c^{u}-1\bigr)x(t) \bigr\} \\ &\leq \frac{x(t)(c^{u}-1)}{x(t)+c^{u}} \biggl\{ \frac{c^{u}-h^{l}}{c ^{u}-1}-x(t) \biggr\} \\ &=\frac{x(t)(c^{u}-1)}{x(t)+c^{u}} \bigl\{ G_{1}-x(t) \bigr\} , \end{aligned}$$

which implies

$$ 0\leq x(t_{0})\leq G_{1}\Rightarrow x(t)\leq G_{1}, \quad t\geq t_{0}. $$

From the second equation of system (1.4), we obtain

$$\begin{aligned} \dot{y}(t) &\leq \delta ^{u}y(t) \biggl[1-\frac{\beta ^{l}y(t)}{G_{1}} \biggr] \\ &= \frac{\delta ^{u}\beta ^{l}(c^{u}-1)y(t)}{c^{u}-h^{l}} \biggl[\frac{c ^{u}-h^{l}}{\beta ^{l}(c^{u}-1)}-y(t) \biggr] \\ &= \frac{\delta ^{u}\beta ^{l}(c^{u}-1)y(t)}{c^{u}-h^{l}} \bigl[G_{2}-y(t) \bigr], \end{aligned}$$

which implies

$$ 0\leq y(t_{0})\leq G_{2}\Rightarrow y(t)\leq G_{2},\quad t\geq t_{0}. $$

Similarly, we have

$$\begin{aligned} \dot{x}(t) &\geq x(t) \biggl[1-x(t)-\frac{h^{u}}{c^{l}}-\frac{G_{2} \alpha ^{u}}{x(t)^{2}+\alpha ^{u}x(t)+\alpha ^{u}\gamma ^{l}} \biggr] \\ &\geq x(t) \biggl[1-x(t)-\frac{h^{u}}{c^{l}}-\frac{4G_{2}\alpha ^{u}}{4 \alpha ^{u}\gamma ^{l}-(\alpha ^{u})^{2}} \biggr] \\ &= x(t) \biggl[\frac{\beta ^{l}(c^{u}-1)(c^{l}-h^{u})(4\gamma ^{l}-\alpha ^{u})-4c^{l}(c^{u}-h^{l})}{\beta ^{l}c^{l}(c^{u}-1)(4\gamma ^{l}-\alpha ^{u})}-x(t) \biggr] \\ &= x(t) \bigl[g_{1}-x(t) \bigr], \end{aligned}$$

which leads to

$$ x(t_{0})\geq g_{1}\Rightarrow x(t)\geq g_{1},\quad t \geq t_{0}. $$

Moreover, it follows from the predator equation that

$$\begin{aligned} \dot{y}(t) &\geq \delta ^{l}y(t) \biggl[1-\frac{\beta ^{u}y}{g_{1}} \biggr] \\ &=\frac{\beta ^{u}\delta ^{l}y(t)}{g_{1}} \biggl[\frac{\beta ^{l}(c^{u}-1)(c ^{l}-h^{u})(4\gamma ^{l}-\alpha ^{u})-4c^{l}(c^{u}-h^{l})}{\beta ^{u} \beta ^{l}c^{l}(c^{u}-1)(4\gamma ^{l}-\alpha ^{u})}-y \biggr] \\ &=\frac{\beta ^{u}\delta ^{l}y(t)}{g_{1}} [g_{2}-y ], \end{aligned}$$

and hence,

$$ y(t_{0})\geq g_{2}\Rightarrow y(t)\geq g_{1}, \quad t \geq t_{0}. $$

This completes the proof of Theorem 2.3. □

Theorem 2.4

Assume that the condition in Theorem 2.3 is satisfied. Then the set Γ is the ultimately bounded region of system (1.4).

3 Periodic case

This section is to obtain some sufficient conditions for the existence of a periodic solution of system (1.4). When we study the non-autonomous periodic system, we focus on obtaining the existence of positive periodic solutions. Therefore, we assume that all the parameters of system (1.4) are periodic in t of period \(\omega > 0\). It is easy to follow from Brouwer’s fixed point theorem that

Theorem 3.1

In addition to the conditions of Theorem 2.3, system (1.4) has at least one positive periodic solution of period ω, say \((x^{*}(t),y^{*}(t))\), which lies in Γ, i.e., \(g _{1}\leq x^{*}(t)\leq G_{2}, g_{2}\leq y^{*}(t)\leq g_{2}(t)\), where \(g_{i}, G_{i}, i=1, 2\), are defined in (2.2).

Alternatively, we can employ another method (coincidence degree theory) to investigate periodic solutions of system (1.4). We adopt the notations and lemmas from [24, 27, 37,38,39]. We denote \(\bar{f}:=\frac{1}{\omega }\int ^{\omega }_{0}f(t)\,dt\) when \(f(t)\) is a periodic and continuous function with period ω (see [31]). Let

$$\begin{aligned} &H_{1}:= \ln {\biggl\{ 1+\frac{\bar{h}}{\bar{c}}\biggr\} }+2 \omega,\qquad H_{2}:= \ln {\biggl\{ \frac{\exp {\{H_{1}\}}}{\bar{\beta }}\biggr\} }+2\bar{\delta } \omega, \\ &H_{3}:=\ln { \biggl\{ \frac{(\bar{c}-\bar{h})(4\gamma ^{l}-\alpha ^{u})-4 \exp {\{H_{2}\}}\bar{c}}{\bar{c}(4\gamma ^{l}-\alpha ^{u})} \biggr\} }-2 \omega,\qquad H_{4}:=\ln {\biggl\{ \frac{\exp {\{H_{3}\}}}{\bar{\beta }}\biggr\} }-2\bar{\delta }\omega, \end{aligned}$$

and define the collections

$$\begin{aligned} &\bar{S}_{1}= \bigl\{ \bigl(\bar{c}, \bar{h},\gamma ^{l}, \alpha ^{u}\bigr)\mid 4\gamma ^{l}< \alpha ^{u}, \bar{c}>\bar{h} \bigr\} ; \\ &\bar{S}_{2}= \bigl\{ \bigl(\bar{c}, \bar{h},\gamma ^{l}, \alpha ^{u}, H_{2}\bigr)\mid 4\gamma ^{l}>\alpha ^{u}, \bar{c}>\bar{h}, (\bar{c}-\bar{h}) \bigl(4\gamma ^{l}- \alpha ^{u}\bigr)>4\exp {\{H_{2}\}}\bar{c} \bigr\} ; \\ &\bar{S}_{3}= \bigl\{ \bigl(\bar{c}, \bar{h},\gamma ^{l}, \alpha ^{u}, H_{2}\bigr)\mid 4\gamma ^{l}< \alpha ^{u}, \bar{c}< \bar{h}, (\bar{c}-\bar{h}) \bigl(4\gamma ^{l}- \alpha ^{u}\bigr)< 4\exp {\{H_{2}\}}\bar{c} \bigr\} . \end{aligned}$$

Theorem 3.2

If \((S_{1}\cup S_{2}\cup S_{3}\cup S_{4})\cap ( \bar{S}_{1}\cup \bar{S}_{2}\cup \bar{S}_{3})\neq \emptyset \), then system (1.4) has at least one positive ω periodic solution, namely \((x^{*}(t), y^{*}(t))\).

Proof

We make the change of variables:

$$ x(t)=\exp {\bigl\{ \tilde{x}(t)\bigr\} },\qquad y(t)=\exp {\bigl\{ \tilde{y}(t)\bigr\} }. $$

Then system (1.4) becomes

$$ \textstyle\begin{cases} \tilde{x}'(t)=1-\exp {\{\tilde{x}(t)\}}-\frac{\alpha (t)\exp {\{\tilde{y}(t)\}}}{( \exp {\{\tilde{x}(t)\}})^{2}+\alpha (t)\exp {\{\tilde{x}(t)\}}+\alpha (t)\gamma (t)} -\frac{h(t)}{\exp {\{\tilde{x}(t)\}}+c(t)}, \\ \tilde{y}'(t)=\delta (t) (1-\beta (t)\frac{\exp {\{\tilde{y}(t)\}}}{\exp {\{\tilde{x}(t)\}}} ). \end{cases} $$
(3.1)

We denote

$$\begin{aligned} &\mathcal{X}=\mathcal{Y}= \bigl\{ (\tilde{x}, \tilde{y}) \in C\bigl( \mathbb{R}, \mathbb{R}^{2}\bigr) | \tilde{x}(t+\omega )=\tilde{x}, \tilde{y}(t+ \omega )=\tilde{y} \bigr\} , \\ &\bigl\Vert (\tilde{x}, \tilde{y}) \bigr\Vert =\max_{t\in [0, \omega ]} \bigl( \bigl\vert \tilde{x}(t) \bigr\vert + \bigl\vert \tilde{y}(t) \bigr\vert \bigr),\quad (\tilde{x}, \tilde{y})\in \mathcal{X}\ (\text{or } \mathcal{Y}). \end{aligned}$$

Clearly, \(\mathcal{X}\) and \(\mathcal{Y}\) are Banach spaces. Let

$$\begin{aligned} &N \begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix}= \begin{bmatrix} 1-\exp {\{\tilde{x}(t)\}}-\frac{\alpha (t)\exp {\{\tilde{y}(t)\}}}{( \exp {\{\tilde{x}(t)\}})^{2}+\alpha (t)\exp {\{\tilde{x}(t)\}}+\alpha (t)\gamma (t)} -\frac{h(t)}{\exp {\{\tilde{x}(t)\}}+c(t)} \\ \delta (t) (1-\beta (t)\frac{\exp {\{\tilde{y}(t)\}}}{\exp {\{\tilde{x}(t)\}}} ) \end{bmatrix}, \\ &L \begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix}= \begin{bmatrix} \tilde{x}' \\ \tilde{y}' \end{bmatrix},\qquad P \begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix}=Q \begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix}= \begin{bmatrix} \frac{1}{\omega }\int _{0}^{\omega }\tilde{x}(t) \,dt \\ \frac{1}{\omega }\int _{0}^{\omega }\tilde{y}(t) \,dt \end{bmatrix}. \end{aligned}$$

We easily see that the inverse \(Kp: \operatorname{Im}L\rightarrow \operatorname{Dom}L\cap \operatorname{ker}P\) exists, and a simple computation leads to

$$ QN \begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix}= \begin{bmatrix} \frac{1}{\omega }\int _{0}^{\omega } [1-\exp {\{\tilde{x}(t)\}}-\frac{\alpha (t)\exp {\{\tilde{y}(t)\}}}{( \exp {\{\tilde{x}(t)\}})^{2}+\alpha (t)\exp {\{\tilde{x}(t)\}}+\alpha (t)\gamma (t)} -\frac{h(t)}{\exp {\{\tilde{x}(t)\}}+c(t)} ]\,dt \\ \frac{1}{\omega }\int _{0}^{\omega } [\delta (t) (1-\beta (t)\frac{\exp {\{\tilde{y}(t)\}}}{\exp {\{\tilde{x}(t)\}}} ) ]\,dt \end{bmatrix} $$

and

$$ Kp(I-Q)N \begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix}= \begin{bmatrix} \int _{0}^{t}N_{1}(s)\,ds-\frac{1}{\omega }\int _{0}^{\omega }\int _{0} ^{t}N_{1}(s)\,ds\,dt-(\frac{t}{\omega }-\frac{1}{2})\int _{0}^{\omega }N _{1}(s)\,ds \\ \int _{0}^{t}N_{2}(s)\,ds-\frac{1}{\omega }\int _{0}^{\omega }\int _{0} ^{t}N_{2}(s)\,ds\,dt-(\frac{t}{\omega }-\frac{1}{2})\int _{0}^{\omega }N _{2}(s)\,ds \end{bmatrix}. $$

Also, it is easy to prove that N is L-compact on Ω̅ with any open bounded set \(\varOmega \subset X\). Now we find an appropriate open bounded subset Ω for the application of the continuation theorem of [24, 37]. According to the equation \(Lx=\lambda Nx, \lambda \in (0, 1)\), we get

$$ \textstyle\begin{cases} \tilde{x}'(t)=\lambda [1-\exp {\{\tilde{x}(t)\}}-\frac{\alpha (t)\exp {\{\tilde{y}(t)\}}}{( \exp {\{\tilde{x}(t)\}})^{2}+\alpha (t)\exp {\{\tilde{x}(t)\}}+\alpha (t)\gamma (t)} -\frac{h(t)}{\exp {\{\tilde{x}(t)\}}+c(t)} ], \\ \tilde{y}'(t)=\lambda [\delta (t) (1-\beta (t)\frac{\exp {\{\tilde{y}(t)\}}}{\exp {\{\tilde{x}(t)\}}} ) ]. \end{cases} $$
(3.2)

Assume that \((\tilde{x}(t), \tilde{y}(t))\) is an arbitrary solution of system (3.1) with certain \(\lambda \in (0, 1)\). Integration on both sides of system (3.2) over the interval \([0, \omega ]\) leads to

$$ \textstyle\begin{cases} \omega =\int _{0}^{\omega } [\exp {\{\tilde{x}(t)\}}+\frac{\alpha (t)\exp {\{\tilde{y}(t)\}}}{( \exp {\{\tilde{x}(t)\}})^{2}+\alpha (t)\exp {\{\tilde{x}(t)\}}+\alpha (t)\gamma (t)} +\frac{h(t)}{\exp {\{\tilde{x}(t)\}}+c(t)} ]\,dt, \\ \bar{\delta }\omega =\int _{0}^{\omega } [\delta (t)\beta (t)\frac{\exp {\{\tilde{y}(t)\}}}{\exp {\{ \tilde{x}(t)\}}} ]\,dt. \end{cases} $$
(3.3)

According to system (3.2) and (3.3), we get

$$ \textstyle\begin{cases} \int _{0}^{\omega } \vert \tilde{x}'(t) \vert \,dt\\ \quad\leq \lambda [\int _{0}^{ \omega }1\,dt +\int _{0}^{\omega }\exp {\{\tilde{x}(t)\}}\,dt+\int _{0}^{\omega }\frac{\alpha (t)\exp {\{\tilde{y}(t)\}}}{( \exp {\{\tilde{x}(t)\}})^{2}+\alpha (t)\exp {\{\tilde{x}(t)\}}+\alpha (t)\gamma (t)}\,dt \\ \qquad{}+\int _{0}^{\omega }\frac{h(t)}{\exp {\{\tilde{x}(t)\}}+c(t)}\,dt ] \\ \quad < 2\omega, \\ \int _{0}^{\omega } \vert \tilde{y}'(t) \vert \,dt\\ \quad\leq \lambda [\int _{0}^{ \omega }\delta (t)\,dt+ \int _{0}^{\omega }\delta (t)\beta (t)\frac{\exp {\{\tilde{y}(t)\}}}{\exp {\{ \tilde{x}(t)\}}}\,dt ] \\ \quad< 2\bar{\delta }\omega. \end{cases} $$
(3.4)

Since \((\tilde{x}(t), \tilde{y}(t))\in \mathcal{X}\), we know that there exist \(\xi _{i}\) and \(\eta _{i}\in [0, \omega ], i=1,2\), such that

$$\begin{aligned} \begin{aligned}& \tilde{x}(\xi _{1})=\min _{t\in [0,\omega ]}\tilde{x}(t),\qquad \tilde{x}(\eta _{1})=\max _{t\in [0,\omega ]}\tilde{x}(t), \\ &\tilde{y}(\xi _{2})=\min_{t\in [0,\omega ]}\tilde{y}(t),\qquad \tilde{y}(\eta _{2})=\max_{t\in [0,\omega ]}\tilde{y}(t). \end{aligned} \end{aligned}$$
(3.5)

According to the first equation of system (3.3), we have

$$\begin{aligned} &\omega \geq \int _{0}^{\omega }\exp {\bigl\{ \tilde{x}(\xi _{1})\bigr\} }\,dt- \int _{0}^{\omega } \frac{h(t)}{c(t)}\,dt=\exp {\bigl\{ \tilde{x}(\xi _{1})\bigr\} }\omega -\frac{\bar{h}}{\bar{c}}\omega , \\ &\tilde{x}(\xi _{1})\leq \ln {\biggl\{ 1+\frac{\bar{h}}{\bar{c}}\biggr\} }. \end{aligned}$$

From systems (3.4) and (3.5), we obtain

$$ \tilde{x}(t)\leq \tilde{x}(\xi _{1})+ \int _{0}^{\omega } \bigl\vert \tilde{x}'(t) \bigr\vert \,dt< \ln {\biggl\{ 1+\frac{\bar{h}}{\bar{c}}\biggr\} }+2 \omega:=H_{1}. $$
(3.6)

According to system (3.5) and the second equation of system (3.3), we have

$$\begin{aligned} &\bar{\delta }\omega \geq \int _{0}^{\omega }\beta (t)\delta (t)\frac{\exp {\{\tilde{y}(\xi _{2})\}}}{\exp {\{H _{1}\}}} \,dt=\bar{\beta }\bar{\delta }\frac{\exp {\{\tilde{y}(\xi _{2})\}}}{ \exp {\{H_{1}\}}}\omega, \\ &\tilde{y}(\xi _{2})\leq \ln {\biggl\{ \frac{\exp {\{H_{1}\}}}{\bar{\beta }}\biggr\} }, \end{aligned}$$

and hence,

$$\begin{aligned} \tilde{y}(t)\leq \tilde{y}(\xi _{2})+ \int _{0}^{\omega } \bigl\vert \tilde{y}'(t) \bigr\vert \,dt< \ln {\biggl\{ \frac{\exp {\{H_{1}\}}}{\bar{\beta }}\biggr\} }+2\bar{\delta }\omega :=H_{2}. \end{aligned}$$
(3.7)

From the first equation of system (3.3), we also obtain

$$\begin{aligned} \omega &\leq \int _{0}^{\omega } \biggl[\exp {\bigl\{ \tilde{x}(\eta _{1})\bigr\} }+ \frac{4\alpha (t)\exp {\{H_{2}\}}}{4 \alpha (t)\gamma (t)-\{\alpha (t)\}^{2}}+ \frac{h(t)}{c(t)} \biggr]\,dt \\ &=\exp {\bigl\{ \tilde{x}(\eta _{1})\bigr\} }\omega +\frac{4\exp {\{H_{2}\}}}{4 \gamma ^{l}-\alpha ^{u}} \omega +\frac{\bar{h}}{\bar{c}}\omega, \end{aligned}$$

and therefore,

$$\begin{aligned} \exp {\bigl\{ \tilde{x}(\eta _{1})\bigr\} }&\geq 1-\frac{4\exp {\{H_{2}\}}}{4 \gamma ^{l}-\alpha ^{u}}- \frac{\bar{h}}{\bar{c}} \\ &=\frac{4\gamma ^{l}\bar{c}-\alpha ^{u}\bar{c}-4\exp {\{H_{2}\}}\bar{c}- \bar{h}(4\gamma ^{l}-\alpha ^{u})}{\bar{c}(4\gamma ^{l}-\alpha ^{u})} \\ &=\frac{(\bar{c}-\bar{h})(4\gamma ^{l}-\alpha ^{u})-4\exp {\{H_{2}\}} \bar{c}}{\bar{c}(4\gamma ^{l}-\alpha ^{u})}, \end{aligned}$$

which implies

$$ \tilde{x}(\eta _{1})\geq \ln { \biggl\{ \frac{(\bar{c}-\bar{h})(4\gamma ^{l}-\alpha ^{u})-4\exp {\{H_{2}\}}\bar{c}}{\bar{c}(4\gamma ^{l}-\alpha ^{u})} \biggr\} }. $$

Thus,

$$ \tilde{x}(t)\geq \tilde{x}(\eta _{1})- \int _{0}^{\omega } \bigl\vert \tilde{x}'(t) \bigr\vert \,dt>\ln { \biggl\{ \frac{(\bar{c}-\bar{h})(4\gamma ^{l}-\alpha ^{u})-4 \exp {\{H_{2}\}}\bar{c}}{\bar{c}(4\gamma ^{l}-\alpha ^{u})} \biggr\} }-2 \omega :=H_{3}. $$
(3.8)

The second equation of system (3.3) also produces

$$\begin{aligned} &\bar{\delta }\omega \leq \int _{0}^{\omega }\beta (t)\delta (t)\frac{\exp {\{\tilde{y}(\eta _{2})\}}}{\exp {\{H_{3}\}}} \,dt=\beta \delta \frac{\exp {\{\tilde{y}(\xi _{2})\}}}{\exp {\{H_{3}\}}}\omega, \\ &\tilde{y}(\eta _{2})\geq \ln {\biggl\{ \frac{\exp {\{H_{3}\}}}{\bar{\beta }} \biggr\} }; \end{aligned}$$

and consequently,

$$ \tilde{y}(t)\geq \tilde{y}(\eta _{2})- \int _{0}^{\omega } \bigl\vert \tilde{y}'(t) \bigr\vert \,dt >\ln {\biggl\{ \frac{\exp {\{H_{3}\}}}{\bar{\beta }}\biggr\} }-2\bar{\delta }\omega :=H_{4}. $$
(3.9)

It follows from (3.6)–(3.9) that

$$ \textstyle\begin{cases} \max_{t\in [0,\omega ]} \vert \tilde{x}(t) \vert \leq \max \{ \vert H_{1} \vert , \vert H _{3} \vert \}:=C_{1}, \\ \max_{t\in [0,\omega ]} \vert \tilde{y}(t) \vert \leq \max \{ \vert H_{2} \vert , \vert H _{4} \vert \}:=C_{2}. \end{cases} $$
(3.10)

We choose \(C>0\) such that \(C>C_{1}+C_{2}\). Let \(\varOmega =\{(\tilde{x}, \tilde{y})\in X\mid \Vert (\tilde{x}, \tilde{y}) \Vert < C\}\). Then it is easy to verify that requirement \((1)\) in the continuation theorem of [24, 37] is satisfied. Also,

$$ QN \begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix}= \begin{bmatrix} 1-\frac{1}{\omega }\int _{0}^{\omega }\exp {\{\tilde{x}(t)\}}\,dt-\frac{1}{ \omega }\int _{0}^{\omega }\frac{\alpha (t)\exp {\{\tilde{y}(t)\}}}{( \exp {\{\tilde{x}(t)\}})^{2}+\alpha (t)\exp {\{\tilde{x}(t)\}}+\alpha (t)\gamma (t)}\,dt \\ -\frac{1}{\omega }\int _{0}^{\omega }\frac{h(t)}{\exp {\{\tilde{x}(t) \}}+c(t)}\,dt, \\ \frac{1}{\omega }\int _{0}^{\omega }\delta (t)\,dt-\frac{1}{\omega }\int _{0}^{\omega }\delta (t)\beta (t)\frac{\exp {\{\tilde{y}(t)\}}}{\exp {\{ \tilde{x}(t)\}}}\,dt \end{bmatrix} \neq \begin{bmatrix} 0 \\ 0 \end{bmatrix}. $$

In addition, we have \(\operatorname{deg}\{JQN, \varOmega \cap \operatorname{Ker}L,0\}\neq 0\). Thus all the conditions in the continuation theorem are satisfied (see, e.g., [24, 37]). Hence, system (3.1) has at least one ω periodic solution \((\tilde{x}^{*}(t), \tilde{y}^{*}(t))\). It is easy to see that \(x^{*}(t)=\exp {\{\tilde{x}^{*}(t)\}}, y^{*}(t)=\exp {\{\tilde{y} ^{*}(t)\}}\), and then \((x^{*}(t), y^{*}(t))\) is an ω periodic solution of system (1.4). The proof of Theorem 3.2 is complete. □

4 Numerical simulations

To support the previous theoretical analysis, in this section, we present two numerical simulation results for the different coefficients of system (1.4).

Example 1

Consider the following model:

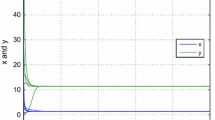
$$ \textstyle\begin{cases} \frac{dx}{dt}= x(1-x)-\frac{xy}{\frac{x^{2}}{[2+\sin (0.1\pi t)]}+x+[101+ \sin (0.1\pi t)]}-\frac{[2+\sin (0.1\pi t)]x}{x+[3+\sin (0.1\pi t)]}, \\ \frac{dy}{dt} = {[3+\sin (0.1\pi t)]}y(1-[2+\sin (0.1\pi t)]\frac{y}{x}). \end{cases} $$
(4.1)

It is easy to verify that the coefficients of system (1.4) satisfy the conditions in Theorem 3.2. Thus, system (1.4) has a 20-periodic solution. Figure 1 shows the validity of our results.

Figure 1
figure 1

20-periodic solution

Full size image

Example 2

Consider the following model:

$$ \textstyle\begin{cases} \frac{dx}{dt} = x(1-x)-\frac{xy}{\frac{x^{2}}{[100+\sin (0.01\pi t)]}+x+[3+ \sin (0.01\pi t)]}- \frac{[2+\sin (0.01\pi t)]x}{x+[5+\sin (0.01\pi t)]}, \\ \frac{dy}{dt} = {[3+\sin (0.01\pi t)]} y(1-[2+\sin (0.01\pi t)]\frac{y}{x}). \end{cases} $$
(4.2)

It is easy to verify that the coefficients of system (1.4) satisfy the conditions in Theorem 3.2. Thus, system (1.4) has a 200-periodic solution. Figure 2 shows the validity of our results.

Figure 2
figure 2

200-periodic solution

Full size image

5 Conclusions

This paper considers a non-autonomous modified Leslie–Gower model with Holling type IV functional response and nonlinear prey harvesting. We study the permanence of the model. Sufficient conditions are obtained for the existence of a periodic solution by Brouwer fixed point theorem and coincidence degree theory, respectively. Also, we give examples and simulations to verify our theoretical analysis.