Abstract
In this paper, we study a stage-structured predator–prey model incorporating refuge for prey and additional food for predator. By analyzing the corresponding characteristic equations, we investigate the local stability of equilibria and the existence of Hopf bifurcation at the positive equilibrium taking the time delay as a bifurcation parameter. Furthermore, we obtain the direction of the Hopf bifurcation and the stability of bifurcating periodic solutions applying the center manifold theorem and normal form theory. Numerical simulations are illustrated to verify our main results.
Similar content being viewed by others
1 Introduction
Since the first mathematical model for predator–prey was developed independently by Lotka [1] and Volterra [2], the predator–prey models in ecology have received great attention [3,4,5,6,7]. Researchers studied the predator–prey models by analyzing their life history. In the natural world, species can be divided into two stages: immaturity and maturity. Therefore, the predator–prey models with stage structure are more reasonable than the ones without stage structure. With the prey species as immature individual organisms, we suppose that they are not attacked by predators, but as mature individuals, in order to reduce their rate of encounter with predators, prey refuges play an important role in affording the prey some degree of protection from predation. Kuang [4] showed that a time delay could destroy the stability of the positive equilibrium and cause a Hopf bifurcation. The delayed predator–prey models with stage structure or refuge have been studied by many authors, see [8,9,10,11,12]. Especially, Wei and Fu [13] investigated Hopf bifurcation and stability of a delayed predator–prey model with stage structure for prey incorporating prey refuge,
where \(x_{1}(t)\), \(x_{2}(t)\) and \(y(t)\) denote the densities of immature prey, mature prey and predator at time t, respectively. m is a refuge parameter with \(m\in[0,1)\), \(\tau\geq0\) is the time delay due to the gestation of the predator.
Prey refuge can protect the prey from the attack of predators in some degree. What will happen if the predators cannot eat the prey? Now, additional food is very important for the predators. In fact, additional food is an important component of most predators. Recently, the effects of the additional food to predator in prey–predator models were investigated [14,15,16,17,18,19]. Srinivasu et al. [14] reported the dynamics of prey–predator system in the presence of additional food for predator and discussed the effect of quality and quantity of the additional food. Ghosh et al. [18] considered a predator–prey model with logistic growth rate and prey refuge in presence of additional food for predator
where \(N(t)\) and \(P(t)\) represent the densities of the prey and predator at time t, respectively. The parameters \(c'\) is a refuge parameter with \(c'\in[0,1)\).
Motivated by the above work, we propose a delayed predator–prey model with stage structure for prey incorporating refuge and providing additional food to the predator,
where \(x_{1}(t)\), \(x_{2}(t)\) and \(y(t)\) denote the densities of immature prey species, mature prey species and predator species at time t, respectively. a is the intrinsic growth rate of the immature prey species. b, c and r denote the death rates of immature prey, mature prey and predator, respectively. α is the transformation rate from immature prey to mature prey. d is intra species competition rate of mature prey. m is a refuge parameter with \(m\in[0,1)\), \(k_{1}(1-m)\) is the capturing rate of the predator. \(k_{2}\) is the conversion rate of nutrients into the production of predator species. \(\tau\geq0\) is the time delay due to the gestation of the predator. \(h_{1}\) and \(e_{1}\), respectively represent the handling time of the predator per unit quantity of mature prey, ability of the predator to detect the mature prey. \(h_{2}\) and \(e_{2}\), respectively, represent the handling time of the predator per unit quantity of additional food, the ability of the predator to identify the additional food. \(A'\) represents the biomass of the additional food. All the parameters are nonnegative constants.
Define \(k_{1}:=\frac{k_{1}}{h_{1}}\), \(k_{2}:=\frac {k_{2}}{h_{1}}\), \(a_{1}:=\frac{a_{1}}{e_{1}h_{1}}\), \(\beta=\frac {h_{2}}{h_{1}}\), \(\eta=\frac{e_{2}}{e_{1}}\). The model (1.3) can be written as
By denoting \(u_{1}(t)=\frac{x_{1}(t)}{a_{1}}\), \(u_{2}(t)=\frac {x_{2}(t)}{a_{1}}\), \(v(t)=\frac{k_{1}y(t)}{a_{1}}\), \(d_{1}=a_{1}d\), \(\xi =\frac{\eta A'}{a_{1}}\), the model (1.4) reduces to the following form:
where the term β and ξ are the parameters which characterize the “quality” and “quantity” of additional food, respectively. The initial conditions for model (1.5) take the form
where \((\varphi_{1}(\theta),\varphi_{2}(\theta),\varphi_{3}(\theta))\in C \{[-\tau,0],R^{3}_{+}\}\), \(R^{3}_{+}=\{(u_{1},u_{2},v):u_{1}\geq 0,u_{2}\geq0,v\geq0\}\).
From the fundamental theory of functional differential equations [20], the model (1.5) has a unique solution \((u_{1}(t),u_{2}(t),v(t))\) satisfying the initial conditions (1.6). It is easy to show that all solutions of (1.5) with initial conditions (1.6) are defined on \([0,+\infty)\) and remain positive for all \(t\geq0\).
The main contributions of the present paper are: (1) A stage-structured predator–prey model incorporating refuge for prey and additional food for predator is formulated. (2) The existence and local stability of equilibria and the existence of Hopf bifurcation of the model are given. (3) The direction of the Hopf bifurcation and the stability of bifurcating periodic solutions are obtained by applying the center manifold theorem and the normal form theory. (4) Numerical simulations are illustrated to show our main results.
In this paper, we assume the following conditions hold.
where \(u^{\ast}_{2}\), A can be found in Sect. 2 and Sect. 3, respectively.
Now we give the biological interpretation of the conditions (\(\mathrm{H}_{1}\))–(\(\mathrm{H}_{10}\)).
From (\(\mathrm{H}_{1}\)), we have \(a\alpha>(b+\alpha)c\), which means that the prey species keeps a linear net growth without the predator species. The condition (\(\mathrm{H}_{3}\)) can be rewritten in the form \(r>\frac{k_{2}\xi}{1+\beta\xi}\). It means that additional food cannot ensure the survival of the predator species without the prey species. The condition (\(\mathrm{H}_{5}\)) is explained that prey species can ensure the survival of predator species without additional food even if the prey species have refuge. It is clear that the conditions (\(\mathrm{H}_{2}\)), (\(\mathrm{H}_{4}\)), (\(\mathrm{H}_{6}\)) have opposite interpretation with (\(\mathrm{H}_{1}\)), (\(\mathrm{H}_{3}\)), (\(\mathrm{H}_{5}\)), respectively. The term \(\frac{a\alpha-(b+\alpha)c}{d_{1}(b+\alpha)}\) in condition (\(\mathrm{H}_{7}\)) is the ratio of net growth with their own retarded growth of prey species. This ratio is a critical value for \(u^{\ast}_{2}\). The condition (\(\mathrm{H}_{8}\)) can be simplified as \(0< a\alpha-(b+\alpha)c<(b+\alpha )(2d_{1}u^{\ast}_{2}+A)\). It implies that on the one hand the prey species keep linear net growth and on the other hand this growth is limited by some value. Obviously, if (\(\mathrm{H}_{9}\)) holds, then (\(\mathrm{H}_{8}\)) holds. The condition (\(\mathrm{H}_{10}\)) shows that the linear net growth of the prey species is higher than the limit value.
2 Equilibria of the model (1.5)
In order to obtain the equilibria of the model (1.5), we consider the prey nullcline and predator nullcline of this model, which are given by
Obviously, the model (1.5) always has a trivial equilibrium \(E_{0}(0,0,0)\).
If the condition (\(\mathrm{H}_{1}\)) holds, then the model (1.5) has a predator-extinction equilibrium \(E_{1}(\bar{u}_{1},\bar{u}_{2},0)\), where \(\bar{u}_{1}=\frac{a[a\alpha-(b+\alpha)c]}{(b+\alpha)^{2}d_{1}}\), \(\bar{u}_{2}=\frac{a\alpha-(b+\alpha)c}{(b+\alpha)d_{1}}\).
If the conditions (\(\mathrm{H}_{1}\)), (\(\mathrm{H}_{3}\)), (\(\mathrm{H}_{5}\)) and (\(\mathrm{H}_{7}\)) hold, which imply
then there exists a unique coexisting equilibrium \(E_{2}(u^{\ast }_{1},u^{\ast}_{2},v^{\ast})\) of the model (1.5), where
3 Local stability of the equilibria
Let \(E(u_{1},u_{2},v)\) be any arbitrary equilibrium, then Jacobian matrix at E is given by
(a) Trivial equilibrium point: At the trivial equilibrium point \(E_{0}(0,0,0)\), the Jacobian matrix is given by
and the characteristic equation at \(E_{0}\) becomes
then the equation
has two roots, and we have \(\lambda_{1}+\lambda_{2}=-(b+\alpha+c)<0\), \(\lambda_{1}\lambda_{2}=c(b+\alpha)-a\alpha\).
If (\(\mathrm{H}_{1}\)) holds, then \(\lambda_{1}\lambda_{2}<0\), that is, \(E_{0}\) is an unstable saddle; If (\(\mathrm{H}_{2}\)) holds, then \(\lambda _{1}\lambda_{2}>0\), that is, \(\operatorname{Re}(\lambda_{i})<0\), \(i=1,2\). Another root of (3.1) is determined by the equation
Denote
If (\(\mathrm{H}_{2}\)) and (\(\mathrm{H}_{3}\)) hold, we claim that \(E_{0}\) is locally asymptotically stable. Otherwise, there is a root λ satisfying \(\operatorname{Re}(\lambda)\geq0\), it follows from (3.2) that
which is contradiction. Hence the equilibrium \(E_{0}\) is locally asymptotically stable.
If (\(\mathrm{H}_{4}\)) holds, it is easy to show that, for real λ, \(f_{1}(0)=r-\frac{k_{2}\xi}{1+\beta\xi}<0\), and
Hence, \(f_{1}(\lambda)=0\) has a positive real root.
From the above discussions, we can get the following theorem.
Theorem 3.1
For the model (1.5):
-
(i)
If (\(\mathrm{H}_{1}\)) or (\(\mathrm{H}_{4}\)) holds, then the trivial equilibrium \(E_{0}(0,0,0)\) is unstable.
-
(ii)
If (\(\mathrm{H}_{2}\)) and (\(\mathrm{H}_{3}\)) hold, then the trivial equilibrium \(E_{0}(0,0,0)\) is locally asymptotically stable.
Remark 3.1
It is easy to understand Theorem 3.1 from the biological meaning of (\(\mathrm{H}_{1}\))–(\(\mathrm{H}_{4}\)).
(b) Predator-extinction equilibrium point: At equilibrium point \(E_{1}(\bar{u}_{1},\bar{u}_{2},0)\), the Jacobian matrix is given by
and the characteristic equation at \(E_{1}\) becomes
then the equation
has two roots, and
If (\(\mathrm{H}_{1}\)) holds, then \(\lambda_{1}\lambda_{2}>0\), that is \(\operatorname{Re}\lambda_{i}<0\), \(i=1,2\). Another root of (3.3) is determined by
Denote
If (\(\mathrm{H}_{4}\)) and (\(\mathrm{H}_{5}\)) hold, it is easy to show that, for real λ,
and \(\lim_{\lambda\rightarrow+\infty}f_{2}(\lambda)=+\infty\). Hence, \(f_{2}(\lambda)=0\) has a positive real root.
If (\(\mathrm{H}_{3}\)) and (\(\mathrm{H}_{6}\)) hold, we have \(f_{2}(0)>0\). We claim that \(E_{1}\) is locally asymptotically stable. Otherwise, there is a root λ satisfying \(\operatorname{Re}\lambda\geq0\). It follows from (3.4) that
which is a contradiction. Hence, when (\(\mathrm{H}_{3}\)) and (\(\mathrm{H}_{6}\)) hold, then \(\operatorname{Re}\lambda<0\).
Based on the above discussions, the following theorem can be obtained.
Theorem 3.2
Suppose that (\(\mathrm{H}_{1}\)) holds. For the model (1.5), we have:
-
(i)
If (\(\mathrm{H}_{4}\)) and (\(\mathrm{H}_{5}\)) hold, then the predator-extinction equilibrium \(E_{1}(\bar{u}_{1},\bar{u}_{2},0)\) is unstable.
-
(ii)
If (\(\mathrm{H}_{3}\)) and (\(\mathrm{H}_{6}\)) hold, then the predator-extinction equilibrium \(E_{1}(\bar{u}_{1},\bar{u}_{2},0)\) is locally asymptotically stable.
Remark 3.2
It is easy to understand Theorem 3.2 from the biological meaning of (\(\mathrm{H}_{3}\))–(\(\mathrm{H}_{6}\)).
(c) Co-existing equilibrium point: At the coexisting equilibrium point \(E_{2}(u^{\ast}_{1},u^{\ast}_{2},v^{\ast})\), the Jacobian matrix is given by
and the characteristic equation at \(E_{2}\) becomes
where \(A=\frac{(1-m)(1+\beta\xi)}{(1+\beta\xi+u^{\ast}_{2})^{2}}v^{\ast }>0\), \(B=\frac{k_{2}[(1-m)u^{\ast}_{2}+\xi]}{1+\beta\xi+u^{\ast }_{2}}=r>0\), and \(C=A-\frac{\xi v^{\ast}}{(1+\beta\xi+u^{\ast }_{2})^{2}}>0\), when \(m<1-\frac{\xi}{1+\beta\xi}\).
One can rewrite (3.5) so that it has the following form:
Let
Equation (3.6) can be written as
Case 3.1. \(\tau=0\).
Equation (3.7) turns to
then
If the condition (\(\mathrm{H}_{8}\)) holds, then \((P_{1}-r)(P_{2}+P_{4})-(P_{3}+P_{5})>0\). By the Routh–Hurwitz criterion, we see that the coexisting equilibrium point \(E_{2}\) is locally asymptotically stable.
Case 3.2. \(\tau> 0\).
Let \(\lambda=i\omega\) (\(\omega>0\)) be a root of (3.7), then
Separating real part and imaginary part of (3.9), we have
that is,
Taking the square on both sides of (3.10) implies that
Suppose \(\nu=\omega^{2}\). Then (3.11) becomes
where
Denoting \(m_{1}=b+\alpha\), \(m_{2}=c+2d_{1}u^{\ast}_{2}+A\), \(m_{3}=\frac {k_{2}C(1-m)u^{\ast}_{2}}{1+\beta\xi+u^{\ast}_{2}}\), we have
If (\(\mathrm{H}_{9}\)) holds, then we have \(a\alpha<(b+\alpha )(c+2d_{1}u^{\ast}_{2}+A)\). Obviously, if (\(\mathrm{H}_{9}\)) holds, it implies that \(P_{3}^{2}-P_{5}^{2}>0\), and \((P_{1}-r)(P_{2}+P_{4})-(P_{3}+P_{5})>0\), then (3.11) has no positive real roots. Therefore, by Theorem 3.4.1 in [10], all roots of (3.11) have negative real parts for all \(\tau\geq0\), which implies that the positive equilibrium \(E_{2}(u^{\ast}_{1},u^{\ast }_{2},v^{\ast})\) is locally asymptotically stable for all \(\tau\geq0\).
If (\(\mathrm{H}_{10}\)) \(a\alpha>(b+\alpha)(c+2d_{1}u^{\ast}_{2}+A)\) holds, which implies that
then \(P_{3}^{2}-P_{5}^{2}<0\). Hence, there exists a unique positive root \(\omega_{0}\) satisfying (3.11). From (3.10), we get
Denote
Taking \(\tau_{0}=\min\{\tau_{n}: n=0,1,2,\ldots\}\), we see that \(\pm i\omega_{0}\) is a pair of purely imaginary roots of (3.7) with \(\tau =\tau_{n}\). Differentiating the two sides of (3.7) with respect to τ, it follows that
then
where
Since
we have
By simple computation, we derive that
Therefore, the transversal condition holds and a Hopf bifurcation occurs at \(\omega=\omega_{0}\), \(\tau=\tau_{0}\). In conclusion, we have the following results.
Theorem 3.3
Assume that (\(\mathrm{H}_{1}\)), (\(\mathrm{H}_{3}\)), (\(\mathrm{H}_{5}\)), (\(\mathrm{H}_{7}\)) hold and \(m<1-\frac{\xi}{1+\beta\xi}\). For the model (1.5), we have:
-
(i)
If (\(\mathrm{H}_{9}\)) holds, then the coexisting equilibrium \(E_{2}(u^{\ast}_{1},u^{\ast}_{2},v^{\ast})\) is locally asymptotically stable for all \(\tau\geq0\).
-
(ii)
If (\(\mathrm{H}_{10}\)) holds, then there exists a positive number \(\tau_{0}\), such that \(E_{2}(u^{\ast}_{1},u^{\ast}_{2},v^{\ast})\) is locally asymptotically stable for \(0\leq\tau<\tau_{0}\) and unstable for \(\tau>\tau_{0}\). Furthermore, the model (1.5) undergoes a Hopf bifurcation at \(E_{2}\) when \(\tau=\tau_{0}\).
4 Stability of bifurcated periodic solutions
In this section, we will establish the direction and stability of periodic solutions bifurcating from the positive equilibrium \(E_{2}\), and we shall derive explicit formulae for determining the properties of the Hopf bifurcation at \(\tau_{0}\) by using the normal form theory and the center manifold theorem introduced by Hassard et al. [21].
For the model (1.5), expanding the nonlinear part by Taylor expansion, we rewrite (1.5) in the following form:
where
The linearized model (4.1) is
Let \(\tau=\tau_{0}+\mu\), \(\mu\in\mathbb{R}\), \(t=s\tau\), \(u_{1}(s\tau )=\hat{u}_{1}(s)\), \(u_{2}(s\tau)=\hat{u}_{2}(s)\), \(v(s\tau)=\hat {v}(s)\), denote \(u_{1}=\hat{u}_{1}\), \(u_{2}=\hat{u}_{2}\), \(v=\hat{v}\), then (4.1) is transformed into the model
where
Denote \(C^{k}[-1,0]=\{\varphi|\varphi:[-1,0]\rightarrow\mathbb{R}^{3}\} \), each component of φ has a Kth-order continuous derivative. Let \(\phi(\theta)=(\phi_{1}(\theta),\phi_{2}(\theta),\phi _{3}(\theta))^{T}\in C[-1,0]\) be the initial data of model (1.5).
Define the operators
with
and \(L_{\mu}:C[-1,0]\rightarrow\mathbb{R}^{3}\), \(f:R\times C[-1,0]\rightarrow\mathbb{R}^{3}\). Then (4.3) can be rewritten as \(u'_{t}=L_{\mu}(u_{t})+f(\mu,u_{t})\).
By the Riesz representation theorem there exists a function \(\eta(\theta,\mu)\) of bounded variation for \(\theta\in [-1,0]\) such that \(L_{\mu}\phi=\int_{-1} ^{0}d\eta(\theta,\mu)\phi(\theta)\), for \(\theta\in[-1,0]\). In fact, we can choose
where \(\delta(\theta)\) is the Dirac function.
For \(\phi\in C^{1}[-1,0]\), define
and
The model (4.3) is equivalent to \(u'_{t}=A_{\mu}u_{t}+R_{\mu }u_{t}\), where \(u_{t}=u(t+\theta)\), \(\theta\in[-1,0]\).
For \(\varphi\in C^{1}[-1,0]\), define
and the bilinear inner product
where \(\psi(\theta)\in C^{1}[-1,0]\), \(\eta(\theta)=\eta(\theta,0)\), and \(A_{0}\) and \(A^{\ast}\) are adjoint operators. From the discussion in Sect. 3, we know that \(\pm i\omega_{0}\tau_{0}\) are the eigenvalues of \(A_{0}\). Hence, they are also eigenvalues of \(A^{\ast}\).
Suppose that \(q(\theta)=(1,q_{1},q_{2})^{T}e^{i\omega_{0}\tau _{0}\theta}\) is the eigenvector of \(A_{0}\), corresponding to \(i\omega _{0}\tau_{0}\), then \(q(0)=(1,q_{1},q_{2})^{T}\), and \(q(-1)=q(0)e^{-i\omega_{0}\tau _{0}}\). By a direct calculation, we get
then
Similarly, we can calculate the eigenvector \(q^{\ast}(s)=D(1,q^{\ast }_{1},q^{\ast}_{2})e^{i\omega_{0}\tau_{0}s}\) of \(A^{\ast}\) belong to the eigenvector \(-i\omega_{0}\tau_{0}\), then we get
then
We normalize q and \(q^{\ast}\) by the condition \(\langle q^{\ast }(s),q(\theta)\rangle=1\). Clearly \(\langle q^{\ast}(s),q(\theta)\rangle =0\). In order to ensure that \(\langle q^{\ast}(s),q(\theta)\rangle =1\), we need to determine the value of D. By (4.4), we have
therefore \(\bar{D}=\frac{1}{1+\bar{q}^{\ast}_{1}q_{1}+\bar{q}^{\ast }_{2}q_{2}+\tau_{0}\bar{q}^{\ast }_{2}(b_{31}q_{1}+b_{32}q_{2})e^{-i\omega_{0}\tau_{0}}}\).
In the remainder of this section, following the algorithms given in [21] and using a similar computation process as in [22], we get the coefficients that will be used to determine several important qualities
where
and
Moreover, \(E_{1}\) and \(E_{2}\) satisfy the following equations:
Furthermore, \(g_{ij}\) is expressed by the parameters and delay in (1.5). Thus, we can compute the following values:
which determine the properties of bifurcation period solutions at \(\tau =\tau_{0}\) on the center manifold. From the above discussions, we have the following result.
Theorem 4.1
For model (1.5), the following results hold:
-
(i)
The sign of \(\mu_{2}\) determines the directions of the Hopf bifurcation: if \(\mu_{2}>0\), then the Hopf bifurcation is supercritical and the bifurcating periodic solutions exist for \(\tau >\tau_{0}\); if \(\mu_{2}<0\), then the Hopf bifurcation is subcritical and the bifurcating periodic solutions exist for \(\tau<\tau_{0} \).
-
(ii)
The sign of \(\beta_{2}\) determines the stability of the bifurcating periodic solutions: the bifurcating periodic solutions are stable if \(\beta_{2}<0 \); the bifurcating periodic solutions are unstable if \(\beta_{2}>0\).
-
(iii)
The sign of \(T_{2}\) determines the period of the bifurcating periodic solutions: the period increases if \(T_{2}>0\) and decreases \(T_{2}<0\).
5 Numerical simulations
We perform the numerical simulations of the model (1.5) to verify our theoretical results.
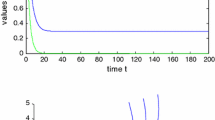
Taking \(a = 3\); \(b = \frac{1}{4}\); \(\alpha= \frac{1}{4}\); \(c = \frac{1}{8}\); \(d_{1} = \frac{1}{8}\); \(m = \frac{1}{2}\); \(k_{2} = \frac{3}{2}\); \(\xi= \frac{1}{3}\); \(\beta= \frac{1}{2}\); \(r = \frac{1}{4}\); we see that the conditions (\(\mathrm{H}_{1}\)) or (\(\mathrm{H}_{4}\)) hold. Theorem 3.1(i) is verified numerically in Fig. 1(a).
Time series of \(u_{1}(t)\), \(u_{2}(t)\) and \(v(t)\) generated by the model (1.5). Three initial values are chosen as \((u_{1}(0),u_{2}(0),v(0)) = (0.2, 0.4, 0.9), (0.6, 1.3, 1.7), (0.01, 1.5, 2.2)\) marked red points, blue points and black points, respectively. The dashed line stands for \(u_{1}(t) = 0\), \(u_{2}(t) = 0\) and \(v(t) = 0\), respectively. (a) The trivial equilibrium \(E_{0}(0,0,0)\) is unstable. (b) The trivial equilibrium \(E_{0}(0,0,0)\) is locally asymptotically stable
Taking \(a = 3\); \(b = \frac{1}{4}\); \(\alpha= \frac{1}{4}\); \(c = 2\); \(d_{1} = \frac{1}{8}\); \(m = \frac{1}{2}\); \(k_{2} = \frac{3}{2}\); \(\xi= \frac{1}{3}\); \(\beta= \frac{1}{2}\); \(r = 2\); it is clear that the conditions (\(\mathrm{H}_{2}\)) and (\(\mathrm{H}_{3}\)) hold. Theorem 3.1(ii) is verified numerically in Fig. 1(b).
If we choose \(a = 4.3\); \(b = \frac{1}{4}\); \(\alpha= \frac{2}{9}\); \(c = 2\); \(d_{1} = \frac{1}{8}\); \(m = \frac{1}{4}\); \(k_{2} = 3\); \(\xi= 5\); \(\beta= \frac{1}{2}\); \(r = 2\); then the conditions (\(\mathrm{H}_{4}\)) and (\(\mathrm{H}_{5}\)) hold. Theorem 3.2(i) is verified numerically by Fig. 2(a).
Time series of \(u_{1}(t)\), \(u_{2}(t)\) and \(v(t)\) generated by the model (1.5): (a) Three initial values are chosen as \((u_{1}(0),u_{2}(0),v(0)) = (1.75, 2, 0.5), (2.3, 0.3, 0.1), (1.1, 1.5, 0.8)\) marked red points, blue points and black points, respectively. The dashed line stands for \(u_{2}(t) = 0\). (b) Three initial values are chosen as \((u_{1}(0),u_{2}(0),v(0)) = (14, 5.2, 0.8), (10, 2, 2.4), (9, 1.3, 0.5)\) marked red points, blue points and black points, respectively. The dashed line stands for \(u_{1}(t) = 12.444444444446397\), \(u_{2}(t) = 2.666666666667100\) and \(v(t) = 0\), respectively
If we choose \(a = \frac{7}{2}\); \(b = \frac{1}{4}\); \(\alpha= \frac{1}{2}\); \(c = 2\); \(d_{1} = \frac{1}{8}\); \(m = \frac{1}{2}\); \(k_{2} = \frac{3}{2}\); \(\xi= \frac{1}{3}\); \(\beta= \frac{1}{2}\); \(r = 2\); then the conditions (\(\mathrm{H}_{3}\)) and (\(\mathrm{H}_{6}\)) hold. Theorem 3.2(ii) is verified numerically by Fig. 2(b).
Taking \(a = 1.1\); \(b = \frac{1}{10}\); \(\alpha= \frac{1}{2}\); \(c = \frac{1}{10}\); \(d_{1} = \frac{1}{12}\); \(m = \frac{1}{4}\); \(k_{2} = 0.5\); \(\xi= 3.5\); \(\beta= 5\); \(r = \frac{1}{8}\); we see that the conditions \(m < 1 - \frac{\xi}{1 + \beta\xi}\), (\(\mathrm{H}_{8}\)) and \((P_{1} - r)(P_{2} + P_{4}) - (P_{3} + P_{5}) > 0\) hold. The numerical result of Case 3.1 can be seen in Fig. 3.
Time series of \(u_{1}(t)\), \(u_{2}(t)\) and \(v(t)\) generated by the model (1.5): Three initial values are chosen as \((u_{1}(0),u_{2}(0),v(0)) = (8, 0.5, 21), (2, 4, 14), (1, 6, 12)\) marked red points, blue points and black points, respectively. The dashed line stands for \(u_{1}(t) = 4.125000892829194\), \(u_{2}(t) = 2.250000487010802\) and \(v(t) = 17.406948324710228\), respectively
When \(\tau\ge0\), taking \(a = 1.1\); \(b = 0.1\); \(\alpha= \frac{1}{2}\); \(c = \frac{1}{10}\); \(d_{1} = \frac{1}{4}\); \(m = \frac{1}{3}\); \(k_{2} = 0.5\); \(\xi= 3.5\); \(\beta= 4.5\); \(r = \frac{1}{8}\); we see that the conditions \(\beta= 4.5 > \frac{k_{2}}{r} - \frac{1}{\xi} = 3.714285714285714\), \(0 < m = \frac{1}{3} < \min \{1-\frac{r}{k_{2}}, 1-\frac{r}{k_{2}}-\frac {d_{1}[r+(r\beta-k_{2})\xi](b+\alpha)}{\alpha k_{2}(a-c)-bc} \} = 0.5351562500000000\), \(m = \frac{1}{3} < 1 - \frac{\xi}{1 + \beta\xi} = 0.7910447761194030\) and (\(\mathrm{H}_{9}\)) hold. The numerical result of Theorem 3.3(i) is presented by Fig. 4(a) for \(\tau= 0\) and Fig. 4(b) for \(\tau=10\).
Time series of \(u_{1}(t)\), \(u_{2}(t)\) and \(v(t)\) generated by the model (1.5): Three initial values are chosen as \((u_{1}(0),u_{2}(0),v(0)) = (7, 0.8, 16.5), (2, 4, 10), (0.3, 6, 12)\) marked red points, blue points and black points, respectively. The dashed line stands for \(u_{1}(t) = 3.025001035342410\), \(u_{2}(t) = 1.650000564732131\) and \(v(t) = 11.155001498913562\), respectively. (a) \(\tau= 0\). (b) \(\tau= 10\)
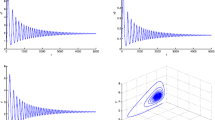
Taking \(a = 6\); \(b = 0.2\); \(\alpha= \frac{5}{3}\); \(c = \frac{1}{10}\); \(d_{1} = \frac{1}{4}\); \(m = \frac{1}{3}\); \(k_{2} = 0.5\); \(\xi= 3.5\); \(\beta= 4.5\); \(r = \frac{1}{8}\); we see that (\(\mathrm{H}_{1}\)), (\(\mathrm{H}_{3}\)), (\(\mathrm{H}_{5}\)), (\(\mathrm{H}_{7}\)), (\(\mathrm{H}_{10}\)) hold and \(\tau _{0}=0.1509514710143546\). The numerical result of Theorem 3.3(ii) is presented by Fig. 5 for \(\tau= 0.06\) and Fig. 6 for \(\tau=0.5\).
Time series of \(u_{1}(t)\), \(u_{2}(t)\), \(v(t)\) and phase portrait of the model (1.5) with \(\tau= 0.06 < \tau_{0} = 0.1509514710143546\). An orbit from the initial condition \((u_{1}(0),u_{2}(0),v(0)) = (7, 1.2, 125)\) located in a sufficiently small neighborhood of the equilibrium \(E_{2}(5.303571428572600, 1.650000000000400, 133.712142857161200)\) converges to the equilibrium \(E_{2}\). The simulation results indicate that the equilibrium \(E_{2}\) is locally asymptotically stable
Time series of \(u_{1}(t)\), \(u_{2}(t)\), \(v(t)\) and phase portrait of the model (1.5) with \(\tau= 0.5 > \tau_{0} = 0.1509514710143546\). An orbit from the initial condition \((u_{1}(0),u_{2}(0),v(0)) = (7, 1.2, 125)\) located in a sufficiently small neighborhood of the equilibrium \(E_{2}(5.303571428572600, 1.650000000000400, 133.712142857161200)\) converges to a periodic solution. The simulation results indicate that the equilibrium \(E_{2}\) is unstable and periodic solution is stable. The periodic attractor bifurcates from the equilibrium and surrounds the equilibrium \(E_{2}\) as the delay τ crosses the critical value \(\tau_{0} = 0.1509514710143546\)
6 Conclusions
In this paper, we study a delayed predator–prey model with stage structure for prey incorporating refuge and provide additional food to the predator. By analyzing the corresponding characteristic equations, we investigate the local stability of the equilibria of the model. We discuss the existence of Hopf bifurcation by choosing time delay as a parameter. We find that time delay can causes a stable equilibrium to become unstable one, even occur Hopf bifurcation, when time delay passes through some critical values. Furthermore, by applying the normal form method and center manifold theorem, we investigate the direction of Hopf bifurcation and the stability of the bifurcated periodic solutions. We give numerical simulations to show our main results.
From Theorem 3.3, we see that, for the stability of a coexisting equilibrium point, the refuge has to be bounded by a value which depends on the quantity and the quality of additional food. Results obtained in this paper provide a useful platform to understand the roles of refuge and additional food. Therefore, refuge and additional food can be taken as population controllers to study the prey–predator models.
Our results can be compared with the ones in Sahoo [17] which considered the role of additional food in eco-epidemiological system with disease in the prey. So, we can extend our predator–prey model to an eco-epidemiological system based on [17, 23].
References
Lotka, A.: Analytical note on certain rhythmic relations in organic systems. Proc. Natl. Acad. Sci. USA 6, 410–415 (1920)
Volterra, V.: Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem. R. Accad. Naz. Lincei, Ser VI 2, 31–113 (1926)
Freedman, H.: Deterministic Mathematical Models in Population Ecology. Dekker, New York (1980)
Kuang, Y.: Delay Differential Equation with Application in Population Dynamics. Academic Press, New York (1993)
Brauer, F., Castillo-Chavez, C.: Mathematical Models in Population Biology and Epidemiology. Springer, Berlin (2000)
Hu, D., Cao, H.: Stability and bifurcation analysis in a predator–prey system with Michaelis–Menten type predator harvesting. Nonlinear Anal., Real World Appl. 33, 58–82 (2017)
Yu, X., Wang, Q., Bai, Y.: Permanence and almost periodic solutions for N-species non-autonomous Lotka–Volterra competitive systems with delays and impulsive perturbations on time scales. Complexity 2018, Article ID 2658745 (2018)
Song, X., Hao, M., Meng, X.: A stage-structured predator–prey model with disturbing pulse and time delays. Appl. Math. Model. 33(1), 211–223 (2009)
Li, F., Li, H.: Hopf bifurcation of a predator–prey model with time delay and stage structure for the prey. Math. Comput. Model. 55(3–4), 672–679 (2012)
Devi, S.: Effects of prey refuge on a ratio-dependent predator–prey model with stage-structure of prey population. Appl. Math. Model. 37(6), 4337–4349 (2013)
Jana, D., Agrawal, R., Upadhyay, R.: Dynamics of generalist predator in a stochastic environment: effect of delayed growth and prey refuge. Appl. Math. Comput. 268(1), 1072–1094 (2015)
Dubey, B., Kumar, A., Maiti, A.: Global stability and Hopf-bifurcation of prey–predator system with two discrete delays including habitat complexity and prey refuge. Commun. Nonlinear Sci. Numer. Simul. 67, 528–554 (2019)
Wei, F., Fu, Q.: Hopf bifurcation and stability for predator–prey systems with Beddington–DeAngelis type functional response and stage structure for prey incorporating refuge. Appl. Math. Model. 40, 126–134 (2016)
Srinivasu, P., Prasad, B., Venkatesulu, M.: Biological control through provision of additional food to predators: a theoretical study. Theor. Popul. Biol. 72, 111–120 (2007)
Sahoo, B., Poria, S.: Effects of supplying alternative food in a predator–prey model with harvesting. Appl. Math. Comput. 234, 150–166 (2014)
Sahoo, B., Poria, S.: The chaos and control of a food chain model supplying additional food to top-predator. Chaos Solitons Fractals 58, 52–64 (2014)
Sahoo, B.: Role of additional food in eco-epidemiological system with disease in the prey. Appl. Math. Comput. 259, 61–79 (2015)
Ghosh, J., Sahoo, B., Poria, S.: Prey–predator dynamics with prey refuge providing additional food to predator. Chaos Solitons Fractals 96, 110–119 (2017)
Song, J., Hu, M., Bai, Y., Xia, Y.: Dynamic analysis of a non-autonomous ratio-dependent predator–prey model with additional food. J. Appl. Anal. Comput. 8(6), 1893–1909 (2018)
Hale, J.: Theory of Functional Differential Equation. Springer, Heidelberg (1977)
Hassard, B., Kazarinoff, N., Wan, Y.: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)
Wei, J., Ruan, S.: Stability and bifurcation in a neural net work model with two delays. Phys. D, Nonlinear Phenom. 130, 255–272 (1999)
Bai, Y., Mu, X.: Global asymptotic stability of a generalized SIRS epidemic model with transfer from infectious to susceptible. J. Appl. Anal. Comput. 8(2), 402–412 (2018)
Acknowledgements
The authors would like to express their gratitude to Prof. Yonghui Xia and Dr. Dongpo Hu for their help in doing numerical simulations. The authors are grateful to the anonymous reviewers for their valuable comments and suggestions.
Funding
This work was supported by China Postdoctoral Science Foundation (No. 2014M551873), Postdoctoral Science Foundation of Shandong Province of China (No. 201401008) and Distinguished Middle-Aged and Young Scientist Encourage and Reward Foundation of Shandong Province of China (No. ZR2018BF018).
Author information
Authors and Affiliations
Contributions
Both authors have equally contributed to obtaining new results in this paper and also read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bai, Y., Li, Y. Stability and Hopf bifurcation for a stage-structured predator–prey model incorporating refuge for prey and additional food for predator. Adv Differ Equ 2019, 42 (2019). https://doi.org/10.1186/s13662-019-1979-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-1979-6