1 Introduction

In the last few decades, many problems in finance [1, 2], physics [3,4,5,6], control theory [7], hydrology [8, 9] and viscoelasticity [10] were modeled mathematically by fractional partial differential equations. The biggest important advantage of using fractional partial differential equations in mathematical modeling is their non-local property in the sense that the next state of the system depends not only upon its current state but also upon all of its proceeding states. The fractional-order models are more adequate than the integral-order models to describe the memory and hereditary properties of different substances [11,12,13,14,15,16,17].

In practical physical applications, Brownian motion, the diffusion with an additional velocity field and diffusion under the influence of a constant external force field are both modeled by the advection–dispersion equation [18]. However, the advection–dispersion equation is not suitable for anomalous diffusion, i.e., the fractional generalization may be different for the advection case and the transport in an external force field [19]. A straightforward extension of the continuous time random walk (CTRW) model leads to a fractional advection–dispersion equation. The time-fractional advection–dispersion equation is obtained by replacing the time-derivative in the advection–dispersion equation by a generalized derivative of order α with \(0<\alpha \leq 1\) and can be used to simulate contaminant transport in porous media [20]. Direct problems for time-fractional advection–dispersion equations have been studied extensively in recent years [21,22,23,24]. By contrast, little has been done on the inverse problems for time-fractional advection–dispersion equations.

In this paper, the inverse problem of time-fractional advection–dispersion equation is given by

$$ \textstyle\begin{cases} {}_{0}D^{\alpha }_{t}u(x,t)+ b u_{x}(x,t)=a u_{xx}(x,t), &x>0, t>0, \\ u(x,0)=0, &x\geq 0, \\ u(x,t)|_{ x\rightarrow \infty }\quad \text{bounded}, &t\geq 0, \\ u(1,t)=g(t), &t\geq 0, \end{cases} $$
(1.1)

where u is the solute concentration, the constants a (\(a>0\)) and b (\(b\geq 0\)) represent the dispersion coefficient and the average fluid velocity, respectively. The time-fractional derivative \({}_{0}D^{\alpha }_{t}u(x,t)\) is the Caputo fractional derivative of order α (\(0<\alpha \leq 1\)) defined by [11]

$$ {}_{0}D^{\alpha }_{t}u(x,t)=\textstyle\begin{cases} \frac{1}{\varGamma (1-\alpha )}\int ^{t}_{0}\frac{\partial u(x,s)}{\partial s}\frac{ds}{(t-s)^{\alpha }}, & 0< \alpha < 1, \\ \frac{\partial u(x,t)}{\partial t}, & \alpha =1. \end{cases} $$

The problem is to detect the temperature for \(0\leq x<1\) by means of the current temperature measurement at \(x=1\). It is well known that this problem is ill-posed, since the small errors in the input data may cause large errors in the output solution.

Recently, time-fractional inverse diffusion problems have been considered by some authors; see [25,26,27,28,29]. Although there are many papers on time-fractional inverse diffusion problems, we only find a few results on inverse problems for time-fractional advection–dispersion equations. Zheng and Wei [30, 31] applied the spectral regularization method and the modified equation method to a time-fractional inverse advection–dispersion problem, respectively. Following the work of [30, 31], Zhao et al. [32] used an optimal filtering method to deal with a time-fractional inverse advection–dispersion problem. However, the theoretical studies in the literature [30,31,32] were only based on a priori regularization parameter choice rule. The main aim of this present work is to present a filter regularization method and prove the convergence estimates under both priori and posteriori regularization parameter choice rules. The advantages of the proposed approach over the other existing results available in the literature [30,31,32] are demonstrated in Remark 3.5, Remark 3.6, Remark 3.8 and Remark 4.6 in detail.

The idea of filter regularization method by modified ‘kernel’ is very simple and natural, since the ill-posedness of time-fractional inverse advection–dispersion problem is caused by the high frequency components of the ‘kernel’, the ‘kernel’ function can be modified. As long as the modified ‘kernel’ function satisfies som certain properties, a new regularization method can be established. In addition, the modified ‘kernel’ idea has been used to deal with several ill-posed problems [33,34,35,36].

This paper consists of six sections. Section 2 states the ill-posedness of the problem and presents a filter regularization method. In Sects. 3 and 4, the error estimates are proved under both prior and posterior regularization parameter choice rules. Numerical experiments are performed in Sect. 5. A brief conclusion is given in Sect. 6.

2 Ill-posedness of the problem and a filter regularization method

In order to apply the Fourier transform, all the functions are extended to the whole line \(-\infty < t<\infty \) by defining them to be zero for \(t<0\). Here, and in the following sections, \(\|\cdot \|\) denotes the \(L^{2}\)-norm, i.e.,

$$ \Vert f \Vert = \biggl( \int _{-\infty }^{\infty } \bigl\vert f(t) \bigr\vert ^{2}\,dt \biggr)^{\frac{1}{2}}. $$

The Fourier transform of the function \(f(t)\) is written as

$$ \widehat{f}(\xi )=\frac{1}{\sqrt{2\pi }} \int ^{\infty }_{-\infty }f(t)e ^{-i\xi t}\,dt, $$

and \(\|\cdot \|_{p}\) denotes the \(H^{p}\)-norm, i.e.,

$$ \Vert f \Vert _{H^{p}}= \biggl( \int _{-\infty }^{\infty }\bigl(1+\xi ^{2} \bigr)^{p} \bigl\vert \widehat{f}(\xi ) \bigr\vert ^{2}\,d \xi \biggr)^{\frac{1}{2}}. $$

Taking the Fourier transform to (1.1) with respect to t, one can easily get the solution of problem (1.1) in the frequency domain

$$ \widehat{u}(x,\xi )=e^{(1-x)k(\xi )}\widehat{g}(\xi ), $$
(2.1)

or equivalently

$$ u(x,t)=\frac{1}{\sqrt{2\pi }} \int _{-\infty }^{\infty }e^{i\xi t}e ^{(1-x)k(\xi )} \widehat{g}(\xi )\,d\xi , $$
(2.2)

where

$$\begin{aligned}& \begin{gathered}k(\xi )=\frac{1}{2a} \bigl(\sqrt{b^{2}+4a(i\xi )^{\alpha }}-b \bigr)=A+iB, \\ (i\xi )^{\alpha }=\textstyle\begin{cases} \vert \xi \vert ^{\alpha }(\cos \frac{\alpha \pi }{2}+i \sin \frac{\alpha \pi }{2}), & \xi \geq 0, \\ \vert \xi \vert ^{\alpha }(\cos \frac{\alpha \pi }{2}-i \sin \frac{\alpha \pi }{2}), & \xi < 0. \end{cases}\displaystyle \end{gathered} \end{aligned}$$
(2.3)

It is easy to see that the real part of \(k(\xi )\) is

$$ A=\Re \bigl(k(\xi )\bigr)=\frac{1}{2a} \biggl(\sqrt{\frac{r^{2}(\xi )+4a \vert \xi \vert ^{ \alpha }\cos \frac{\alpha \pi }{2}+b^{2}}{2}}-b \biggr), $$

and the imaginary part of \(k(\xi )\) is

$$ B=\Im \bigl(k(\xi )\bigr)=\operatorname{sign}(\xi )\cdot \frac{1}{2a}\sqrt{ \frac{r ^{2}(\xi )-4a \vert \xi \vert ^{\alpha }\cos \frac{\alpha \pi }{2}-b^{2}}{2}} $$

with

$$ r(\xi )= \bigl\vert b^{2}+4a(i\xi )^{\alpha } \bigr\vert ^{\frac{1}{2}}= \biggl(b^{4}+16a^{2} \vert \xi \vert ^{2\alpha }+8ab^{2} \vert \xi \vert ^{\alpha }\cos \frac{\alpha \pi }{2} \biggr)^{\frac{1}{4}}. $$

Note that \(k(\xi )\) has a positive real part and therefore the factor \(e^{(1-x)A}\) increases exponentially for \(0\leq x<1\) as \(|\xi |\rightarrow \infty \). The measured data function \(g^{\delta }(t)\in L^{2}( \mathbb{R})\) usually contains an error, and it satisfies

$$ \bigl\Vert g^{\delta }(t)-g(t) \bigr\Vert \leq \delta , $$
(2.4)

where \(\delta >0\) is a noise level. This mean a small error for the measured data \(g^{\delta }(t)\) will be amplified infinitely by the factor \(e^{(1-x)A}\) and destroy the solution of problem (1.1). Therefore, the time-fractional inverse advection–dispersion problem is severely ill-posed and some regularization methods are needed. Thus, a filter regularization method to solve problem (1.1) is presented in this paper.

To regularize the problem, our aim is to replace the term \(e^{(1-x)A}\) by another term. For this purpose, a regularized solution in frequency space is defined as follows:

$$ \widehat{u}^{\beta ,\delta }(x,\xi )=\frac{e^{(1-x)k(\xi )}}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }(\xi ), $$
(2.5)

or equivalently

$$ u^{\beta ,\delta }(x,t)=\frac{1}{\sqrt{2\pi }} \int ^{\infty }_{- \infty }e^{i\xi t}\frac{e^{(1-x)k(\xi )}}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }(\xi )\,d\xi . $$
(2.6)

In the following section, the error estimates between the regularized solution \(u^{\beta ,\delta }(x,t)\) and the exact solution \(u(x,t)\) will be proved under both prior and posterior regularization parameter choice rules.

3 Prior choice rule and error estimate

In this section, the \(L^{2}\)-estimate and \(H^{p}\)-estimate are discussed under a prior regularization parameter choice rule, respectively. Before obtaining the main theorems, some auxiliary lemmas firstly are given.

Lemma 3.1

([31])

If \(x\in [0,1)\), and \(k(\xi )\) is given by (2.3), then the following inequality holds:

$$ \bigl\vert k(\xi ) \bigr\vert \leq \frac{ \vert \xi \vert ^{\frac{\alpha }{2}}}{\sqrt{a}}. $$

Lemma 3.2

([37])

Let \(0< x< a\), \(0<\mu <1\), then

$$ \sup_{\eta \geq 0}\frac{e^{\eta x}}{1+\mu e^{\eta a}}\leq \mu ^{-\frac{x}{a}}. $$

3.1 \(L^{2}\)-Estimate

Theorem 3.3

Suppose that \(u(x,\cdot )\) is the exact solution of problem (1.1) and \(u^{\beta ,\delta }(x,\cdot )\) is the filter regularized solution of problem (1.1). Let the assumption (2.4) and the prior condition \(\|u(0,\cdot )\|\leq E\) hold. If the regularization parameter β is selected by

$$ \beta =\frac{\delta }{E}, $$
(3.1)

then we have the following error estimate:

$$ \bigl\Vert u^{\beta ,\delta }(x,\cdot )-u(x,\cdot ) \bigr\Vert \leq 2\delta ^{x}E^{1-x}, \quad 0< x< 1. $$
(3.2)

Proof

Due to Parseval’s formula and the triangle inequality, we have

$$\begin{aligned} \bigl\Vert u^{\beta ,\delta }(x,\cdot )-u(x,\cdot ) \bigr\Vert =& \bigl\Vert \widehat{u}^{\beta , \delta }(x,\cdot )-\widehat{u}(x,\cdot ) \bigr\Vert \\ =& \biggl\Vert e^{(1-x)k(\xi )}\widehat{g}(\xi )-\frac{e^{(1-x)k(\xi )}}{1+ \beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }(\xi ) \biggr\Vert \\ \leq & \biggl\Vert e^{(1-x)k(\xi )}\widehat{g}(\xi )-\frac{e^{(1-x)k( \xi )}}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}(\xi ) \biggr\Vert \\ &{}+ \biggl\Vert \frac{e^{(1-x)k(\xi )}}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g}( \xi )-\frac{e^{(1-x)k(\xi )}}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{ \delta }(\xi ) \biggr\Vert \\ =& \biggl\Vert \frac{\beta \vert e^{k(\xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert }e^{(1-x)k( \xi )}\widehat{g}(\xi ) \biggr\Vert \\ &{}+ \biggl\Vert \frac{e^{(1-x)k(\xi )}}{1+\beta \vert e^{k(\xi )} \vert }\bigl(\widehat{g}( \xi )- \widehat{g}^{\delta }(\xi )\bigr) \biggr\Vert \\ \leq &\sup_{\xi \in \mathbb{R}} \biggl\vert \frac{\beta \vert e^{k(\xi )} \vert }{1+ \beta \vert e^{k(\xi )} \vert }e^{-x k(\xi )} \biggr\vert E \\ &{}+\sup_{\xi \in \mathbb{R}} \biggl\vert \frac{e^{(1-x)k(\xi )}}{1+\beta \vert e ^{k(\xi )} \vert } \biggr\vert \bigl\Vert \widehat{g}(\xi )-\widehat{g}^{\delta }(\xi ) \bigr\Vert \\ \leq &E \sup_{A\geq 0}\frac{\beta e^{(1-x)A}}{1+\beta e^{A}}+\delta \sup _{A\geq 0}\frac{e^{(1-x)A}}{1+\beta e^{A}}. \end{aligned}$$
(3.3)

Let

$$ C(\xi )=\sup_{A\geq 0}\frac{\beta e^{(1-x)A}}{1+\beta e^{A}},\qquad D( \xi )=\sup _{A\geq 0}\frac{e^{(1-x)A}}{1+\beta e^{A}}. $$

According to Lemma 3.2, it is obvious that

$$\begin{aligned}& C(\xi )=\sup_{A\geq 0}\frac{\beta e^{(1-x)A}}{1+\beta e^{A}}\leq \beta \beta ^{x-1}=\beta ^{x}, \end{aligned}$$
(3.4)
$$\begin{aligned}& D(\xi )=\sup_{A\geq 0}\frac{e^{(1-x)A}}{1+\beta e^{A}}\leq \beta ^{x-1}. \end{aligned}$$
(3.5)

Combining the formulas (3.3)–(3.5), it follows that

$$ \bigl\Vert u^{\beta ,\delta }(x,\cdot )-u(x,\cdot ) \bigr\Vert \leq E \beta ^{x}+\delta \beta ^{x-1}, $$
(3.6)

using Eq. (3.1), the error estimate (3.2) is obtained. □

Remark 3.4

From (3.2), it is clear that a Hölder-type estimate in the interval \(0< x<1\) is obtained. However, the error estimate at \(x=0\) cannot be obtained. In order to obtain the error estimate at \(x=0\), a stronger prior bound is introduced as follows:

$$ \bigl\Vert u(0,\cdot ) \bigr\Vert _{H^{p}}\leq E. $$
(3.7)

Remark 3.5

The error estimate (3.2) is the same order as that of Theorem 1 in [30] and Theorem 2.1 in [32].

Remark 3.6

In [31], the authors regularize the time-fractional inverse advection–dispersion problem and derive the error estimate

$$ \bigl\Vert u^{\beta ,\delta }(x,\cdot )-u(x,\cdot ) \bigr\Vert \leq \varepsilon _{1}+\frac{C _{2}\cdot E}{(\ln \frac{E}{\delta })^{4}}. $$

Thus, the convergence rate in this work is better than the one in [31].

3.2 \(H^{p}\)-Estimate

Theorem 3.7

Suppose that \(u(0,\cdot )\) is the exact solution of problem (1.1) and \(u^{\beta ,\delta }(0,\cdot )\) is the filter regularized solution of problem (1.1). Let the assumption (2.3) and the prior condition \(\|u(0,\cdot )\|_{H^{p}}\leq E\) hold. If the regularization parameter β is selected by

$$ \beta = \biggl(\frac{\delta }{E} \biggr)^{\frac{1}{2}}, $$
(3.8)

then we have the following error estimate:

$$ \bigl\Vert u^{\beta ,\delta }(0,\cdot )-u(0,\cdot ) \bigr\Vert \leq \delta ^{\frac{1}{2}}E ^{\frac{1}{2}}+E\max \biggl\{ \biggl( \frac{1}{2}\ln \frac{E}{\delta } \biggr)^{-p}, \biggl( \frac{\delta }{E} \biggr)^{\frac{1}{2}-\frac{\alpha }{4 \sqrt{a}}} \biggr\} . $$
(3.9)

Proof

Using the analogous technique of Theorem 3.3, it is evident that

$$\begin{aligned} \bigl\Vert u^{\beta ,\delta }(0,\cdot )-u(0,\cdot ) \bigr\Vert =& \bigl\Vert \widehat{u}^{\beta , \delta }(0,\cdot )-\widehat{u}(0,\cdot ) \bigr\Vert \\ \leq & \bigl\Vert \widehat{u}^{\beta ,\delta }(0,\cdot )-\widehat{u}^{\beta }(0, \cdot ) \bigr\Vert + \bigl\Vert \widehat{u}^{\beta }(0,\cdot )- \widehat{u}(0,\cdot ) \bigr\Vert . \end{aligned}$$
(3.10)

For the first term on the right-hand side of (3.10), the following inequality holds:

$$ \bigl\Vert \widehat{u}^{\beta ,\delta }(0,\cdot )- \widehat{u}^{\beta }(0, \cdot ) \bigr\Vert \leq \delta \sup _{A\geq 0}\frac{e^{A}}{1+\beta e^{A}}\leq \delta \beta ^{-1}. $$
(3.11)

For the second term on the right-hand side of (3.10), and note that \(\|u(0,\cdot )\|_{H^{p}}\leq E\), we have

$$ \begin{aligned}[b] \bigl\Vert \widehat{u}^{\beta }(0, \cdot )-\widehat{u}(0,\cdot ) \bigr\Vert &= \biggl\Vert e ^{k(\xi )} \widehat{g}(\xi )-\frac{e^{k(\xi )}}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}(\xi ) \biggr\Vert \\ &= \biggl\Vert \frac{\beta \vert e^{k(\xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert }\bigl(1+ \vert \xi \vert ^{2} \bigr)^{-\frac{p}{2}}\bigl(1+ \vert \xi \vert ^{2} \bigr)^{\frac{p}{2}}e^{k(\xi )} \widehat{g}(\xi ) \biggr\Vert \\ &\leq E\sup_{\xi \in \mathbb{R}}\frac{\beta \vert e^{k(\xi )} \vert }{1+\beta \vert e ^{k(\xi )} \vert }\bigl(1+ \vert \xi \vert ^{2}\bigr)^{-\frac{p}{2}}, \end{aligned} $$
(3.12)

where E is the prior bound.

Now setting the function \(f(\xi ):=\frac{\beta |e^{k(\xi )}|}{1+ \beta |e^{k(\xi )}|}(1+|\xi |^{2})^{-\frac{p}{2}}\), and using Lemma 3.1, it is easy to see that:

  1. (i)

    \(f(\xi )\leq (1+|\xi |^{2})^{-\frac{p}{2}}\leq |\xi |^{-p}\leq ( \ln \frac{1}{\beta })^{-p}\), for \(|\xi |\geq \ln \frac{1}{ \beta }\),

  2. (ii)

    \(f(\xi )\leq \beta |e^{k(\xi )}|\leq \beta e^{\frac{|\xi |^{\frac{ \alpha }{2}}}{\sqrt{a}}}\leq \beta ^{1-\frac{\alpha }{2\sqrt{a}}}\), for \(|\xi |< \ln \frac{1}{\beta }\).

Then the following inequality can be obtained:

$$ \bigl\Vert \widehat{u}^{\beta }(0,\cdot )-\widehat{u}(0, \cdot ) \bigr\Vert \leq E\max \biggl\{ \biggl(\ln \frac{1}{\beta } \biggr)^{-p}, \beta ^{1-\frac{\alpha }{2\sqrt{a}}} \biggr\} . $$
(3.13)

Taking into account (3.8), (3.10), (3.11), (3.12) and (3.13), the error estimate (3.9) is obtained. □

Remark 3.8

In [30,31,32], the convergence estimates have been obtained under a prior regularization parameter choice rule. However, in practical computations, such choices do not work well for all cases. Therefore, it is better to provide a posterior regularization parameter choice rule. In the next section, this topic is considered.

4 Posterior choice rule and error estimate

This section presents a posterior regularization parameter choice by Morozov’s discrepancy principle. Choose the regularization parameter β as the solution of the equation

$$ \biggl\Vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }(\xi )- \widehat{g}^{\delta }(\xi ) \biggr\Vert =\tau \delta , $$
(4.1)

where \(\tau >1\) is a constant and β denotes the regularization parameter. To establish existence and uniqueness of solution for Eq. (4.1), the following lemmas are needed.

Lemma 4.1

Let \(\rho (\beta ):= \|\frac{1}{1+\beta |e^{k(\xi )}|}\widehat{g} ^{\delta }(\xi )-\widehat{g}^{\delta }(\xi ) \|\), if \(0<\tau \delta <\|\widehat{g}^{\delta }(\xi )\|\), then

  1. (a)

    \(\rho (\beta )\) is a continuous function;

  2. (b)

    \(\lim_{\beta \rightarrow 0}\rho (\beta )=0\);

  3. (c)

    \(\lim_{\beta \rightarrow +\infty }\rho (\beta )=\|\widehat{g}^{ \delta }\|\);

  4. (d)

    \(\rho (\beta )\) is a strictly increasing function.

The proof is very easy and we omit it here.

Remark 4.2

From Lemma 4.1, it is known that there exists a unique solution β satisfying Eq. (4.1).

Lemma 4.3

If β is the solution of Eq. (4.1), then the following inequality holds:

$$ \biggl\Vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }(\xi )- \widehat{g}(\xi ) \biggr\Vert \leq (\tau +1)\delta . $$
(4.2)

Proof

Due to the triangle inequality and Eq. (4.1), we have

$$ \begin{aligned}[b] & \biggl\Vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }(\xi )- \widehat{g}(\xi ) \biggr\Vert \\ &\quad \leq \biggl\Vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }( \xi )- \widehat{g}^{\delta }(\xi ) \biggr\Vert + \bigl\Vert \widehat{g}^{\delta }( \xi )-\widehat{g}(\xi ) \bigr\Vert \\ &\quad \leq (\tau +1)\delta . \end{aligned} $$
(4.3)

The lemma is proved. □

Lemma 4.4

If β is the solution of Eq. (4.1), the following inequality also holds:

$$ \beta ^{-1}\leq \frac{E}{(\tau -1)\delta }. $$
(4.4)

Proof

Due to the triangle inequality and Eq. (4.1), we have

$$\begin{aligned} \tau \delta =& \biggl\Vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g} ^{\delta }(\xi )-\widehat{g}^{\delta }(\xi ) \biggr\Vert \\ =& \biggl\Vert \frac{\beta \vert e^{k(\xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }(\xi ) \biggr\Vert \\ \leq & \biggl\Vert \frac{\beta \vert e^{k(\xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert }\bigl( \widehat{g}^{\delta }(\xi )- \widehat{g}(\xi )\bigr) \biggr\Vert + \biggl\Vert \frac{ \beta \vert e^{k(\xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}(\xi ) \biggr\Vert \\ \leq & \delta + \biggl\Vert \frac{\beta \vert e^{k(\xi )} \vert }{1+\beta \vert e^{k( \xi )} \vert }\widehat{g}(\xi ) \biggr\Vert \\ \leq & \delta +\beta E. \end{aligned}$$
(4.5)

Then (4.4) can be obtained. The lemma is proved. □

Now, the main theorem is given as follows.

Theorem 4.5

Suppose that the prior condition \(\|u(0,\cdot )\|\leq E\) and the assumption (2.4) hold, and there exists \(\tau >1\) such that \(0<\tau \delta <\|\widehat{g}^{\delta }\|\). The regularization parameter \(\beta >0\) is chosen by Morozov’s discrepancy principle (4.1). Then the following convergence estimate holds:

$$ \bigl\Vert u^{\beta ,\delta }(x,\cdot )-u(x,\cdot ) \bigr\Vert \leq \biggl(\frac{\tau }{ \tau -1} \biggr)^{1-x}(\tau +1)^{x} \delta ^{x}E^{1-x}. $$
(4.6)

Proof

Due to the Parseval formula and Lemma 4.3, we have

$$\begin{aligned} & \bigl\Vert u^{\beta ,\delta }(x,\cdot )-u(x,\cdot ) \bigr\Vert ^{2} \\ &\quad = \bigl\Vert \widehat{u}^{\beta ,\delta }(x,\cdot )-\widehat{u}(x,\cdot ) \bigr\Vert ^{2} \\ &\quad = \biggl\Vert \frac{e^{(1-x)k(\xi )}}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g} ^{\delta }(\xi )-e^{(1-x)k(\xi )}\widehat{g}(\xi ) \biggr\Vert ^{2} \\ &\quad = \biggl\Vert e^{(1-x)k(\xi )} \biggl(\frac{1}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }(\xi )-\widehat{g}(\xi ) \biggr) \biggr\Vert ^{2} \\ &\quad = \int ^{\infty }_{-\infty } \biggl\vert e^{(1-x)k(\xi )} \biggl( \frac{1}{1+ \beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi ) \biggr) \biggr\vert ^{2}\,d\xi \\ &\quad = \int ^{\infty }_{-\infty } \bigl\vert e^{(1-x)k(\xi )} \bigr\vert ^{2} \biggl\vert \frac{1}{1+ \beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }( \xi )-\widehat{g}(\xi ) \biggr\vert ^{2}\,d\xi \\ &\quad = \int ^{\infty }_{-\infty } \bigl\vert e^{(1-x)k(\xi )} \bigr\vert ^{2} \biggl\vert \frac{1}{1+ \beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }( \xi )-\widehat{g}(\xi ) \biggr\vert ^{2(1-x)}\cdot \biggl\vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g} ^{\delta }(\xi )-\widehat{g}(\xi ) \biggr\vert ^{2x}\,d\xi \\ &\quad \leq \biggl( \int ^{\infty }_{-\infty } \biggl( \bigl\vert e^{(1-x)k(\xi )} \bigr\vert ^{2} \biggl\vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }( \xi )- \widehat{g}(\xi ) \biggr\vert ^{2(1-x)} \biggr)^{\frac{1}{1-x}}\,d\xi \biggr)^{1-x} \\ & \qquad {}\cdot \biggl( \int ^{\infty }_{-\infty } \biggl( \biggl\vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }(\xi )-\widehat{g}(\xi ) \biggr\vert ^{2x} \biggr)^{\frac{1}{x}}\,d\xi \biggr)^{x} \\ &\quad \leq \biggl( \int ^{\infty }_{-\infty } \bigl\vert e^{2k(\xi )} \bigr\vert \biggl\vert \frac{1}{1+ \beta \vert e^{k(\xi )} \vert }\widehat{g}^{\delta }(\xi )- \widehat{g}(\xi ) \biggr\vert ^{2}\,d\xi \biggr)^{1-x} \\ &\qquad {}\cdot \biggl( \int ^{\infty }_{-\infty } \biggl\vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }(\xi )- \widehat{g}(\xi ) \biggr\vert ^{2}\,d \xi \biggr)^{x} \\ &\quad = \biggl\Vert \bigl\vert e^{k(\xi )} \bigr\vert \biggl( \frac{1}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }(\xi )-\widehat{g}(\xi ) \biggr) \biggr\Vert ^{2(1-x)} \cdot \biggl\Vert \frac{1}{1+\beta \vert e^{k(\xi )} \vert } \widehat{g}^{\delta }( \xi )-\widehat{g}(\xi ) \biggr\Vert ^{2x} \\ &\quad \leq \biggl\Vert \biggl(\frac{ \vert e^{k(\xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert }\bigl( \widehat{g}^{\delta }( \xi )-\widehat{g}(\xi )\bigr)+ \biggl(\frac{ \vert e^{k( \xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert }- \bigl\vert e^{k(\xi )} \bigr\vert \biggr)\widehat{g}(\xi ) \biggr) \biggr\Vert ^{2(1-x)}\cdot \bigl((\tau +1)\delta \bigr)^{2x} \\ &\quad \leq \biggl( \biggl\Vert \frac{ \vert e^{k(\xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert }\bigl( \widehat{g}^{\delta }( \xi )-\widehat{g}(\xi )\bigr) \biggr\Vert + \biggl\Vert \biggl( \frac{ \vert e ^{k(\xi )} \vert }{1+\beta \vert e^{k(\xi )} \vert }- \bigl\vert e^{k(\xi )} \bigr\vert \biggr)\widehat{g}( \xi ) \biggr\Vert \biggr)^{2(1-x)} \\ &\qquad {}\cdot \bigl((\tau +1)\delta \bigr)^{2x} \\ &\quad \leq \biggl(\delta \sup_{\xi \in \mathbb{R}}\frac{e^{A}}{1+ \beta e ^{A}}+E \biggr)^{2(1-x)}\cdot \bigl((\tau +1)\delta \bigr)^{2x} \\ &\quad \leq \bigl(\delta \beta ^{-1}+E\bigr)^{2(1-x)}\cdot \bigl((\tau +1)\delta \bigr)^{2x}. \end{aligned}$$
(4.7)

Using Lemma 4.4, it follows that

$$ \begin{aligned}[b] \bigl\Vert u^{\beta ,\delta }(x, \cdot )-u(x,\cdot ) \bigr\Vert ^{2} &\leq \bigl(\delta \beta ^{-1}+E\bigr)^{2(1-x)}\cdot \bigl((\tau +1)\delta \bigr)^{2x} \\ &\leq \biggl(\delta \frac{E}{(\tau -1)\delta }+E \biggr)^{2(1-x)}\cdot \bigl((\tau +1)\delta \bigr)^{2x} \\ &= \biggl(\frac{\tau }{\tau -1} \biggr)^{2(1-x)}(\tau +1)^{2x} \delta ^{2x}E ^{2(1-x)}. \end{aligned} $$
(4.8)

Therefore, the conclusion of the theorem can be obtained directly from (4.8). □

Remark 4.6

Obviously, If \(\alpha =1\), the problem (1.1) naturally corresponds to the standard inverse advection–dispersion problem [38]. If \(\alpha =1\) and \(b=0\), the problem (1.1) corresponds to the classical inverse heat conduction problem [39]. If \(b=0\), the problem (1.1) corresponds to the time-fractional inverse diffusion problem [40]. Thus, the results in the paper are valid for these special problems.

5 Numerical examples

In this section, three numerical examples are presented to illustrate the behavior of the proposed method. In our numerical experiment, we set \(a=1\) and \(b=1\) in (1.1).

The numerical examples are constructed in the following way. First, the initial data \(u(0,t)=f(t)\) of time-fractional advection–dispersion problem is presented at \(x=0\), and the function \(u(1,t)=g(t)\) is computed by solving a direct problem, which is a well-posed problem. Second, a randomly distributed perturbation to the data function obtaining vector \(g^{\delta }(t)\) is added, i.e.,

$$ g^{\delta }=g+\epsilon \operatorname{randn}\bigl( \operatorname{size}(g)\bigr). $$
(5.1)

Here, the function “\(\operatorname{randn}(\cdot )\)” generates arrays of random numbers whose elements are normally distributed with mean 0, variance \(\sigma ^{2}=1\) and standard deviation \(\sigma =1\), “\(\operatorname{randn}(\operatorname{size}(g))\)” returns array of random entries that is the same size as g, the magnitude ϵ indicates a relative noise level. Here, the total noise δ can be measured in the sense of the root mean square error according to

$$ \delta := \bigl\Vert g^{\delta }-g \bigr\Vert _{l^{2}}=\sqrt{\frac{1}{n}\sum ^{n}_{i=1}\bigl(g ^{\delta }_{i}-g_{i} \bigr)^{2}}. $$
(5.2)

Third, the regularized solution is obtained by solving the inverse problem. Finally, the regularized solution is compared with the exact solution.

In the experiments under the prior regularization parameter choice rule, the regularization parameter β is chosen by (3.1), and in the experiments under the posterior regularization parameter choice rule, the regularization parameter β is chosen by (4.1) with \(\tau =1.1\).

Example 5.1

Consider a smooth function

$$ f(t)=4\sin (2\pi t). $$
(5.3)

Example 5.2

Consider a piecewise smooth function

$$ f(t)=\textstyle\begin{cases} 0, & 0\leq t\leq 0.25, \\ 4t-1, & 0.25< t\leq 0.5, \\ 3-4t, & 0.5< t\leq 0.75, \\ 0, & 0.75< t\leq 1. \end{cases} $$
(5.4)

Example 5.3

Consider the following discontinuous function:

$$ f(t)=\textstyle\begin{cases} 0, & 0\leq t\leq \frac{1}{3}, \\ 1, & \frac{1}{3}< t\leq \frac{2}{3}, \\ 0, & \frac{2}{3}< t\leq 1. \end{cases} $$
(5.5)

Figures 1, 3 and 5 show the comparison between prior and posterior methods for different α for Examples 5.1, 5.2, 5.3, respectively. Figures 2, 4 and 6 show the comparison between prior and posterior methods for different ϵ for Examples 5.1, 5.2, 5.3, respectively.

Figure 1
figure 1

The comparison of the exact solution and its approximation solution for \(\epsilon =0.01\) at \(x=0.8\) with Example 5.1, (a) \(\alpha =0.1\), (b) \(\alpha =0.7\)

Full size image
Figure 2
figure 2

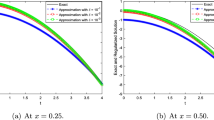
The comparison of the exact solution and its approximation solution for \(\alpha =0.3\) at \(x=0.1\) with Example 5.1, (a) \(\epsilon =0.01\), (b) \(\epsilon =0.001\)

Full size image
Figure 3
figure 3

The comparison of the exact solution and its approximation solution for \(\epsilon =0.001\) at \(x=0.8\) with Example 5.2, (a) \(\alpha =0.1\), (b) \(\alpha =0.7\)

Full size image
Figure 4
figure 4

The comparison of the exact solution and its approximation solution for \(\alpha =0.3\) at \(x=0.1\) with Example 5.2, (a) \(\epsilon =0.001\), (b) \(\epsilon =0.0001\)

Full size image
Figure 5
figure 5

The comparison of the exact solution and its approximation solution for \(\epsilon =0.001\) at \(x=0.8\) with Example 5.3, (a) \(\alpha =0.1\), (b) \(\alpha =0.7\)

Full size image
Figure 6
figure 6

The comparison of the exact solution and its approximation solution for \(\alpha =0.3\) at \(x=0.1\) with Example 5.3, (a) \(\epsilon =0.001\), (b) \(\epsilon =0.0001\)

Full size image

Figs. 1–6 show that the smaller the parameter ϵ is, the better the computed approximation is, and the smaller the parameter α is, the better the computed approximation is. Moreover, Figs. 1–6 also show that both prior and posterior parameter choice rules work well, but the result under a prior rule is better than the results under a posterior rule. Finally, these tests illustrate that the proposed method is not only effective for the smooth example, but it also works well for the continuous and discontinuous examples.

6 Conclusion

In this paper, an inverse problem of time-fractional advection–dispersion equations has been studied. A filter regularization method is suggested to deal with this problem, and its convergence is also discussed under both a prior regularization parameter choice rule and Morozov’s discrepancy principle. The numerical examples verify the efficiency and accuracy of the proposed computational method.

There are several potential extensions of the present method. On the one hand, the proposed method can be adapted to two-dimensional and three-dimensional inverse problems. On the other hand, the proposed method can be extended to the case with time-dependent coefficient. Towards this end, more vigorous investigations are needed in the future.