1 Introduction

Atmospheric blocking is an important large-scale weather phenomenon. When atmospheric blocking occurs at mid-high latitudes, it often causes extraordinary flood, extreme drought or extreme cold, and other abnormal phenomena. Usually an atmospheric blocking anticyclone has three types of patterns: monopole-type blocking, dipole-type blocking, and multi-pole type blocking. In the past decades, a large number of constant-coefficient nonlinear equations have been derived, for example, the famous Korteweg de Vries (KdV), modified KdV (mKdV), nonlinear Schrödinger (NLS) equations, and so on. However, analytical solutions of these deduced constant coefficient equations are impossible to describe the formation, development, and extinction of the complicated atmospheric blocking life cycle. The nonlinear variable coefficient equations can be used to explain atmospheric blocking phenomena. Ref. [1] used the derived variable coefficient KdV system to explain well the life cycle of a blocking system. In fact, blocking phenomena are related to beta effect, energy dispersion, topography, and other forcing factors. Yang and Chen [2,3,4] derived Boussinesq-BO equation, generalized Boussinesq equation, and generalized inhomogeneous KdV-Burgers equation considering dissipation effect and topography. The topography plays very important roles in atmospheric blocking evolution. A series of research works about topography forcing effect have been carried out [5,6,7,8], most of which still involved constant coefficient nonlinear equations.

In this paper, combining variable coefficient thought with the effect of topographic forcing, starting from barotropic and potential vorticity equation on a beta-plane including topographic effect, a variable coefficient KdV equation with time-dependent variable coefficient forced term is derived.

At present, there are many analytical methods [9,10,11,12,13,14,15] for solving nonlinear partial differential equations, for example, q-homotopy analysis transform method [16,17,18], homotopy analysis method [19, 20], homotopy perturbation method [21], and so on. However, solving analytical solutions of variable coefficient equation with forced term is a long-standing difficulty. Consider the KdV equation with forced term in Ref. [22]

$$ U_{T} + a(T)UU_{X} + b(T)U^{2}U_{X} + c(T)U_{XXX} + d(T)U_{X} + \gamma (T)U = \varGamma (T), $$
(1)

where the analytical solutions were obtained, and the interaction of multiple wave solutions was presented. In Ref. [23], the new exact solitary wave solution and periodic wave solution of Eq. (2) KdV-Burgers equation with forcing term were obtained.

$$ u_{t} + \alpha uu_{x} + \beta u_{xx} + \gamma u_{xxx} = f(t). $$
(2)

Obviously, forcing terms of Eqs. (1)–(2) are all functions of time. But research into exact analytical solutions of KdV type equation with forced term about variable x or X is almost blank. The homotopy analysis method (HAM) [24] is very powerful, we select it to solve the approximate analytic solution of the derived equation in this paper.

The main purpose of this paper is to derive a new variable coefficient KdV equation with forced term and investigate the evolution process of atmospheric blocking. The structure of this paper is as follows. A new model is derived from a non-dimensional barotropic and potential vorticity equation on a beta-plane including topography effect in Sect. 2. In Sect. 3, an approximate analytic solution of the derived equation is obtained by HAM, and the evolution process of stream function field is investigated in different parameters. In Sect. 4, discussion is presented. Finally, our conclusions are given.

2 Derivation of variable-coefficient KdV equation with time-dependent variable coefficient topographic forcing term

In barotropic atmosphere, the known barotropic and potential vorticity equation including topography effect on a beta-plane can be written in the form [25]

$$ \frac{\partial }{\partial t}\bigl(\nabla ^{2}\psi - F\psi \bigr) + J\bigl(\psi , \nabla ^{2}\psi + h\bigr) + \beta \frac{\partial \psi }{\partial x} = 0, $$
(3)

where \(\psi = \psi (x,y,t)\) is a non-dimensional stream function, \(\nabla ^{2} = \frac{\partial ^{2}}{\partial x^{2}} + \frac{\partial ^{2}}{\partial y^{2}}\) is the horizontal Laplace operator, \(J(a,b) = \frac{ \partial a}{\partial x}\frac{\partial b}{\partial y} - \frac{\partial a}{\partial y}\frac{\partial b}{\partial x}\) is the Jacobian of a and b, \(\beta = (L^{2}/U)\beta _{0}\) and \(\beta _{0} = (2\omega _{0}/a _{0})\cos \varphi _{0}\), \(\omega _{0}\) is the angular frequency of the earth’s rotation, \(a_{0}\) is the radius of the earth, \(\varphi _{0}\) is the latitude, \(F = (L/R_{0})^{2}\), U and L are the characteristic horizontal velocity and the characteristic horizontal length, respectively, \(R_{0}\) is the Rossby deformation radius, \(h = h(x,y)\) is non-dimensional topography height distribution.

In order to consider weakly nonlinear perturbations on a zonal flow, we introduce a small parameter \(\varepsilon \ll 1\), then assume

$$ \psi (x,y,t) = \varPsi _{0}(y,t) + \varepsilon \psi '(x,y,t), $$
(4)

where the basic flow \(\varPsi _{0}(y,t)\) is a function about y, t, \(\psi '(x,y,t)\) is a perturbation stream function.

Substituting Eq. (4) into Eq. (3) and omitting ′ of \(\psi '(x,y,t)\), we obtain the following equation for perturbation stream function:

$$\begin{aligned}& \frac{\partial }{\partial t}(\varPsi _{0yy} - F\varPsi _{0}) + \varepsilon \frac{ \partial }{\partial t}\bigl(\nabla ^{2}\psi - F\psi \bigr) + \varepsilon \frac{ \partial \psi }{\partial x}\varPsi _{0yyy} + \varepsilon ^{2} \frac{\partial \psi }{\partial x}\frac{\partial \nabla ^{2}\psi }{\partial y} \\& \quad {} - \varepsilon \varPsi _{0y}\frac{\partial \nabla ^{2}\psi }{\partial x} - \varepsilon ^{2}\frac{\partial \psi }{\partial y}\frac{\partial \nabla ^{2}\psi }{\partial x} \\& \quad {}+ \varepsilon \frac{\partial \psi }{\partial x}\frac{\partial h}{ \partial y} - \varPsi _{0y}\frac{\partial h}{\partial x} - \varepsilon \frac{ \partial \psi }{\partial y} \frac{\partial h}{\partial x} + \beta \varepsilon \frac{\partial \psi }{\partial x} = 0. \end{aligned}$$
(5)

We adopt the following transform:

$$ X = \varepsilon ^{\frac{1}{2}}(x - c_{0}t), \qquad T = \varepsilon ^{\frac{3}{2}}t, \qquad h(x,y) = \varepsilon ^{2}H(X,y). $$
(6)

Suppose topography can be separated as

$$ H(X,y) = H_{1}(X) + H_{2}(y), $$
(7)

where \(H_{2}(y)\) is a function of latitude, \(H_{1}(X)\) is a function about X.

According to Eq. (6), we obtain

$$ \frac{\partial }{\partial x} = \varepsilon ^{\frac{1}{2}}\frac{\partial }{\partial X}, \qquad \frac{\partial }{\partial t} = - \varepsilon ^{\frac{1}{2}}c_{0}\frac{ \partial }{\partial X} + \varepsilon ^{\frac{3}{2}}\frac{\partial }{ \partial T}, \qquad \frac{\partial ^{2}}{\partial x^{2}} = \varepsilon \frac{\partial }{ \partial X}. $$
(8)

Substitution of Eqs. (6)–(8) into Eq. (5) gives

$$\begin{aligned}& \varepsilon ^{\frac{3}{2}}\frac{\partial }{\partial T}(\varPsi _{0yy} - F \varPsi _{0}) + \varepsilon \biggl( - \varepsilon ^{\frac{1}{2}}c_{0} \frac{ \partial }{\partial X} + \varepsilon ^{\frac{3}{2}}\frac{\partial }{ \partial T}\biggr) \biggl( \varepsilon \frac{\partial ^{2}\psi }{\partial X^{2}} + \frac{ \partial ^{2}\psi }{\partial y^{2}} - F\psi \biggr) \\& \quad {} + \varepsilon ^{ \frac{3}{2}}\varPsi _{0yyy}\frac{\partial \psi }{\partial X} + \varepsilon ^{\frac{5}{2}}\frac{\partial \psi }{\partial X}\frac{ \partial }{\partial y}\biggl(\varepsilon \frac{\partial ^{2}\psi }{\partial X^{2}} + \frac{\partial ^{2}\psi }{\partial y^{2}}\biggr)- \varepsilon ^{\frac{5}{2}} \frac{\partial \psi }{\partial y}\frac{ \partial }{\partial X}\biggl(\varepsilon \frac{\partial ^{2}\psi }{\partial X^{2}} + \frac{\partial ^{2}\psi }{\partial y^{2}}\biggr) \\& \quad {}- \varepsilon ^{\frac{3}{2}}\varPsi _{0y}\frac{\partial }{\partial X} \biggl(\varepsilon \frac{\partial ^{2}\psi }{\partial X^{2}} + \frac{\partial ^{2}\psi }{ \partial y^{2}}\biggr) + \varepsilon ^{\frac{7}{2}}\frac{\partial \psi }{ \partial X}\frac{\partial H_{2}}{\partial y} - \varepsilon ^{ \frac{7}{2}} \frac{\partial \psi }{\partial y}\frac{\partial H_{1}}{ \partial X} - \varepsilon ^{\frac{5}{2}}\varPsi _{0y}\frac{\partial H_{1}}{ \partial X} \\& \quad {}+ \varepsilon ^{\frac{3}{2}}\beta \frac{\partial \psi }{\partial X} = 0. \end{aligned}$$
(9)

Equation (9) can be further simplified as follows:

$$\begin{aligned}& \frac{\partial }{\partial T}(\varPsi _{0yy} - F\varPsi _{0}) - (c_{0} + \varPsi _{0y})\frac{\partial }{\partial X}\frac{\partial ^{2}\psi }{\partial y ^{2}} + (c_{0}F + \varPsi _{0yyy} + \beta )\frac{\partial \psi }{\partial X} \\& \quad {} + \varepsilon \biggl[ - (c_{0} + \varPsi _{0y}) \frac{\partial ^{3}\psi }{ \partial X^{3}} + \frac{\partial }{\partial T}\biggl(\frac{\partial ^{2} \psi }{\partial y^{2}} - F\psi \biggr) \\& \quad {}+ \frac{\partial \psi }{\partial X}\frac{\partial }{\partial y}\frac{ \partial ^{2}\psi }{\partial y^{2}} - \frac{\partial \psi }{\partial y}\frac{\partial }{\partial X}\frac{ \partial ^{2}\psi }{\partial y^{2}} - \varPsi _{0y} \frac{\partial H_{1}}{ \partial X}\biggr] + O\bigl(\varepsilon ^{2}\bigr) = 0. \end{aligned}$$
(10)

The asymptotic expansion is imported for a perturbation stream function ψ in the form

$$ \psi = \psi _{0} + \varepsilon \psi _{1} + \varepsilon ^{2}\psi _{2} + \cdots . $$
(11)

Taking the substitution of Eq. (11) into Eq. (10) and requiring all the coefficients of different powers of ε to be zero yield

$$\begin{aligned}& \varepsilon ^{0}: (c_{0} + \varPsi _{0y}) \frac{\partial }{\partial X}\frac{ \partial ^{2}\psi _{0}}{\partial y^{2}} - (c_{0}F + \varPsi _{0yyy} + \beta )\frac{\partial \psi _{0}}{\partial X} = \frac{\partial }{\partial T}(\varPsi _{0yy} - F\varPsi _{0}), \end{aligned}$$
(12)
$$\begin{aligned}& \varepsilon ^{1}: (c_{0} + \varPsi _{0y}) \frac{\partial }{\partial X}\frac{ \partial ^{2}\psi _{1}}{\partial y^{2}} - (c_{0}F + \varPsi _{0yyy} + \beta )\frac{\partial \psi _{1}}{\partial X} \\& \quad = - (c_{0} + \varPsi _{0y})\frac{ \partial ^{3}\psi _{0}}{\partial X^{3}} + \frac{\partial }{\partial T}\biggl(\frac{ \partial ^{2}\psi _{0}}{\partial y^{2}} - F\psi _{0}\biggr) + \frac{\partial \psi _{0}}{\partial X}\frac{\partial }{\partial y}\frac{\partial ^{2} \psi _{0}}{\partial y^{2}} \\& \qquad {}- \frac{\partial \psi _{0}}{\partial y}\frac{\partial }{\partial X}\frac{ \partial ^{2}\psi _{0}}{\partial y^{2}} - \varPsi _{0y}\frac{\partial H_{1}}{ \partial X}. \end{aligned}$$
(13)

We suppose that Eq. (12) has the following variable separation solution:

$$ \psi _{0} = G_{0}(y ,T)A(X,T). $$
(14)

Taking the substitution of Eq. (14) into Eq. (12) yields

$$\begin{aligned}& \varPsi _{0yy} = F\varPsi _{0} + F_{1}(y), \end{aligned}$$
(15)
$$\begin{aligned}& (c_{0} + \varPsi _{0y})\frac{\partial ^{2}G_{0}}{\partial y^{2}} - (c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )G_{0} = 0, \end{aligned}$$
(16)

where \(F_{1}(y)\) is an arbitrary integration function about y, \(F_{1y}\) is the first order differential to y.

In order to derive an arbitrary variable coefficient KdV equation with forced term, we introduce the following higher order term \(\psi _{1}\) with forced term:

$$\begin{aligned} \psi _{1} =& B_{1}(y,T)A^{2} + B_{2}(y,T)A_{XX} + B_{3}(y,T) + B_{4}(y,T) \int A\,d X + B_{5}(y,T)H_{1}(X) \\ =& B_{1}A^{2} + B_{2}A_{XX} + B_{3} + B_{4} \int A\,d X + B_{5}H _{1}, \end{aligned}$$
(17)

where \(B_{i}\) (\(i = 1, 2, 3, 4, 5\)) are arbitrary functions about y and T.

By virtue of Eq. (17), we obtain

$$\begin{aligned}& \frac{\partial }{\partial X}\frac{\partial ^{2}\psi _{1}}{\partial y ^{2}} = B_{1yy}2AA_{X} + B_{2yy}A_{XXX} + B_{4yy}A + B_{5yy}H_{1X}, \end{aligned}$$
(18)
$$\begin{aligned}& \frac{\partial \psi _{1}}{\partial X} = B_{1}2AA_{X} + B_{2}A_{XXX} + B _{4}A + B_{5}H_{1X}. \end{aligned}$$
(19)

Suppose

$$\begin{aligned} F_{2} =& - (c_{0} + \varPsi _{0y}) \frac{\partial ^{3}\psi _{0}}{\partial X ^{3}} + \frac{\partial }{\partial T}\biggl(\frac{\partial ^{2}\psi _{0}}{ \partial y^{2}} - F\psi _{0}\biggr) \\ &{}+ \frac{\partial \psi _{0}}{\partial X}\frac{ \partial }{\partial y}\frac{\partial ^{2}\psi _{0}}{\partial y^{2}} - \frac{ \partial \psi _{0}}{\partial y}\frac{\partial }{\partial X}\frac{ \partial ^{2}\psi _{0}}{\partial y^{2}} - \varPsi _{0y} \frac{\partial H_{1}}{ \partial X}. \end{aligned}$$
(20)

Substituting Eqs. (14) and (16) into Eq. (20) leads to

$$\begin{aligned}& \frac{\partial \psi _{0}}{\partial X}\frac{\partial }{\partial y}\frac{ \partial ^{2}\psi _{0}}{\partial y^{2}} - \frac{\partial \psi _{0}}{ \partial y} \frac{\partial }{\partial X}\frac{\partial ^{2}\psi _{0}}{ \partial y^{2}} = AA_{X}G_{0}^{2} \biggl( \frac{c_{0}F + F \varPsi _{0y} + F_{1y} + \beta }{c_{0} + \varPsi _{0y}} \biggr)_{y}, \end{aligned}$$
(21)
$$\begin{aligned}& F_{2} = - (c_{0} + \varPsi _{0y})G_{0}A_{XXX} + A_{T}(G_{0yy} - FG_{0}) + (G_{0yy} - FG_{0})_{T}A \\& \hphantom{F_{2}=}{}+ G_{0}^{2} \biggl( \frac{c_{0}F + F\varPsi _{0y} + F_{1y} + \beta }{c_{0} + \varPsi _{0y}} \biggr)_{y}AA_{X} - \varPsi _{0y}H _{1X} \\& \hphantom{F_{2}}= - (c_{0} + \varPsi _{0y})G_{0}A_{XXX} + \frac{F_{1y} + \beta }{c_{0} + \varPsi _{0y}}G_{0}A_{T} + G_{0}^{2} \biggl( \frac{c_{0}F + F\varPsi _{0y} + F _{1y} + \beta }{c_{0} + \varPsi _{0y}} \biggr)_{y}AA_{X} \\& \hphantom{F_{2}=}{}+ \biggl( \frac{F _{1y} + \beta }{c_{0} + \varPsi _{0y}} \biggr)_{T}A - \varPsi _{0y}H_{1X} \\& \hphantom{F_{2}}= - (c_{0} + \varPsi _{0y})G_{0}A_{XXX} + \frac{F_{1y} + \beta }{c_{0} + \varPsi _{0y}}G_{0}A_{T} \\& \hphantom{F_{2}=}{} + \frac{(c_{0} + \varPsi _{0y})(F\varPsi _{0yy} + F_{1yy}) - \varPsi _{0yy}(c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )}{(c_{0} + \varPsi _{0y})^{2}}G_{0}^{2}AA_{X} \\& \hphantom{F_{2}=}{}- \frac{\varPsi _{0yT}(F_{1y} + \beta )G_{0}}{(c_{0} + \varPsi _{0y})^{2}}A - \varPsi _{0y}H_{1X}. \end{aligned}$$
(22)

Substituting Eqs. (18)–(19) and (22) into Eq. (13), we have

$$\begin{aligned}& A_{T} + \biggl[ \frac{(c_{0} + \varPsi _{0y})(F\varPsi _{0yy} + F_{1yy}) - \varPsi _{0yy}(c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )}{(c_{0} + \varPsi _{0y})^{2}}G _{0}^{2} \\& \quad {}- 2(c_{0} + \varPsi _{0y})B_{1yy} + 2(c_{0}F + F\varPsi _{0y} + F_{1y}+ \beta )B_{1} \biggr]\frac{c_{0} + \varPsi _{0y}}{(F_{1y} + \beta )G_{0}}AA_{X} \\& \quad {} - \bigl[ (c_{0} + \varPsi _{0y})G_{0} + (c_{0} + \varPsi _{0y})B_{2yy} - (c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )B_{2} \bigr] \frac{c _{0} + \varPsi _{0y}}{(F_{1y} + \beta )G_{0}}A_{XXX} \\& \quad {}- \biggl[ \frac{\varPsi _{0yT}(F_{1y} + \beta )}{(c_{0} + \varPsi _{0y})^{2}} + (c_{0} + \varPsi _{0y})B_{4yy} - (c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )B_{4} \biggr]\frac{c_{0} + \varPsi _{0y}}{(F_{1y} + \beta )G_{0}}A \\& \quad {} - \bigl[ \varPsi _{0y} + (c_{0} + \varPsi _{0y})B_{5yy} - (c_{0}F \\& \quad {} + F\varPsi _{0y} + F_{1y} + \beta )B_{5} \bigr]\frac{c_{0} + \varPsi _{0y}}{(F_{1y} + \beta )G_{0}}H_{1X} = 0. \end{aligned}$$
(23)

Therefore, when \(B_{i}\) (\(i = 1, 2, 3, 4, 5\)) satisfy the following equations:

$$\begin{aligned}& (c_{0} + \varPsi _{0y})^{2}(F\varPsi _{0yy} + F_{1yy}) - \varPsi _{0yy}(c_{0} + \varPsi _{0y}) (c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )G_{0}^{2} \\& \quad {}- 2(c_{0} + \varPsi _{0y})^{3}B_{1yy} + 2(c_{0} + \varPsi _{0y})^{2}(c_{0}F \\& \quad {}+ F\varPsi _{0y} + F_{1y} + \beta )B_{1} - a_{1}G_{0}(c_{0} + \varPsi _{0y}) (F _{1y} + \beta ) = 0, \end{aligned}$$
(24)
$$\begin{aligned}& (c_{0} + \varPsi _{0y})^{2}G_{0} + (c_{0} + \varPsi _{0y})^{2}B_{2yy} - (c _{0} + \varPsi _{0y}) (c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )B_{2} \\& \quad {} + a_{2}G _{0}(F_{1y} + \beta ) = 0, \end{aligned}$$
(25)
$$\begin{aligned}& \varPsi _{0yT}(F_{1y} + \beta ) + (c_{0} + \varPsi _{0y})^{3}B_{4yy} - (c_{0} + \varPsi _{0y})^{2}(c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )B_{4} \\& \quad {}+ a_{3}G _{0}(F_{1y} + \beta ) = 0, \end{aligned}$$
(26)
$$\begin{aligned}& \varPsi _{0y}(c_{0} + \varPsi _{0y}) + (c_{0} + \varPsi _{0y})^{2}B_{5yy} - (c _{0} + \varPsi _{0y}) (c_{0}F + F\varPsi _{0y} + F_{1y} + \beta )B_{5} \\& \quad {}- a_{4}G _{0}(F_{1y} + \beta ) = 0, \end{aligned}$$
(27)

where \(B_{3}\) is an arbitrary function, we can obtain a new variable coefficient KdV equation with forcing term

$$ \frac{\partial A}{\partial t} + a_{1}A\frac{\partial A}{\partial X} + a_{2} \frac{\partial ^{3}A}{\partial X^{3}} + a_{3}A = a_{4}\frac{ \partial H_{1}}{\partial X}. $$
(28)

In Eqs. (24)–(28), \(a_{i} = a_{i}(T)\) (\(i = 1, 2, 3, 4\)) are arbitrary functions about T. Obviously, forcing term of Eq. (28) contains time-dependent variable coefficient \(a_{4}(T)\) and topographic forcing term \(\frac{ \partial H_{1}}{\partial X}\). Consequently, Eq. (28) is called variable coefficient KdV equation with time-dependent variable coefficient topographic forcing term.

3 Approximate analytic solution of derived equation and complicated atmospheric blocking phenomena

In this section, we first solve approximate analytical solution of Eq. (28) by HAM in Ref. [24]. Equation (28) can be rewritten as

$$ LA(X,T) + PA(X,T) + BA(X,T) = 0, $$
(29)

where \(L = \frac{\partial }{\partial T}\) is a linear operator, \(LA(X,T) = \frac{\partial A}{\partial T}\), P is an auxiliary linear operator, \(PA(X,T) = a_{2}\frac{\partial ^{3}A}{\partial X^{3}} + a _{3}A\), B is a nonlinear operator, \(BA(X,T) = \frac{a_{1}}{2}\frac{ \partial A^{2}}{\partial X} - a_{4}\frac{\partial H}{\partial X}\).

Taking variable coefficients as

$$ \begin{aligned}&a_{1} = c_{1}\sin (T), \qquad a_{2} = c_{2}, \\ & a_{3} = c_{3}\cos (T), \qquad a_{4} = c_{4}, \end{aligned}$$
(30)

where \(c_{1}\), \(c_{2}\), \(c_{3}\), \(c_{4}\) are arbitrary constants, we take forced topography as

$$ H(X) = n_{0}\cos (mX), $$
(31)

where \(n_{0}\), m are arbitrary constants.

We make use of the strict solution of the standard constant coefficient KdV equation in the solitary theory as initial value, namely

$$ A_{0}(X,T) = 2k^{2}\operatorname{sech}^{2}(kX), $$
(32)

where \(k \ne 0\) is a constant.

When \(m = 1\), we obtain

$$\begin{aligned} A_{1}(X,T) =& \hbar \int _{0}^{T} \bigl[PA_{0}(X,T) + BA_{0}(X,T)\bigr]\,d\tau \\ =& \hbar \bigl[\tanh (kX)\operatorname{sech}^{4}(kX) \bigl(48k^{5}c_{2}T - 8k^{5}c _{1} + 8k^{5}c_{1}\cos (T)\bigr) \\ &{} + 2k^{2}c_{3}\operatorname{sech}^{2}(kX)\sin (T) + c_{4}mn_{0}\sin (Xm)T \\ &{}- 16k^{5}c_{2}\tanh (kX)\operatorname{sech}^{2}(kX)T \bigr], \end{aligned}$$
(33)

where ħ is an auxiliary parameter.

When \(m > 1\), we obtain the following equations:

$$\begin{aligned}& PA_{m - 1}(X,T) = a_{2}\frac{\partial ^{3}A_{m - 1}(X,T)}{\partial X ^{3}} + a_{3}A_{m - 1}(X,T), \end{aligned}$$
(34)
$$\begin{aligned}& BA_{m - 1}(X,T) = \frac{a_{1}}{2}\frac{\partial }{\partial X}\Biggl(\sum _{j = 0}^{m - 1} A_{j} (X,T)A_{m - 1 - j}(X,T)\Biggr) - a_{4}\frac{\partial H}{\partial X}, \end{aligned}$$
(35)
$$\begin{aligned}& A_{m}(X,T) = (1 + \hbar )A_{m - 1}(X,T) + \hbar \int _{0}^{t} \bigl[P A_{m - 1}(X,T) + BA_{m - 1}(X,T)\bigr]\,d\tau . \end{aligned}$$
(36)

Substituting Eqs. (33)–(35) into Eq. (36), we obtain

$$\begin{aligned} A_{2}(X,T) =& k^{2}\hbar ^{2} \operatorname{sech}^{2}(kX)\bigl[c_{3}^{2} - c _{3}^{2}\cos ^{2}(T) + 2c_{3}\sin (T) + 4c_{1}c_{4}mn_{0}\sin (Xm) \sin (T) \\ &{} - 4c_{1}c_{4}mn_{0}\sin (Xm)\cos (T)T+ 64k^{6}T^{2}c_{2}^{2} + 2c_{3}\sin (T)\bigr] \\ &{} + 1680k^{8}\hbar ^{2}c_{2} \operatorname{sech}^{8}(kX) \bigl(c_{1}T - 3T^{2}c_{2} - c_{1}\sin (T)\bigr) \\ &{} + 160k ^{8}\hbar ^{2}c_{2} \operatorname{sech}^{6}(kX)\bigl[13T^{2}c_{2}- 42c_{1}T + 42c_{1}\sin (T)\bigr] \\ &{} + 4k^{4} \hbar ^{2}\operatorname{sech} ^{4}(kX)\bigl[c_{1}c_{3}T - 504k^{4}c_{2}^{2}T^{2} \\ &{} + 103k^{4}c_{1}c_{2}T - 103k^{4}c_{1}c_{2}\sin (T) - 0.5c_{1}c_{3} \\ &{}\cdot \sin (2T)\bigr] + 2k^{5}\hbar \tanh (kX) \operatorname{sech}^{4}(kX)\bigl[4c _{1}\hbar \cos (T) - 4c_{1} \\ &{} + 24c_{2}T + 24\hbar c_{2}T + 4c_{1} \cos (T) + 2\hbar c_{1}c_{3}T - 4\hbar c_{1}c_{3} \\ &{}\cdot \sin (T) - 32k^{2}\hbar c_{1}c_{2}\sin (T) + c_{1}c_{3}\hbar \sin (2T) + 32k^{2}c_{1}c_{2} \hbar \cos (T)T \\ &{} + 24c_{2}c_{3}\hbar \sin (T)T\bigr] + 16k^{7}\hbar ^{2}c_{1}\tanh (kX) \\ &{}\cdot \operatorname{sech}^{6}(kX)\bigl[2c_{1}\cos (T) - c_{1} - c_{1}\cos ^{2}(T) + 12c_{2} \sin (T) - 12c_{2}\cos (T)T\bigr] \\ &{} - 16k^{5}\hbar c_{2} \tanh (kX)\operatorname{sech}^{2}(kX) \bigl[2T \\ &{}- c_{3}\hbar \sin (T)\bigr] + Tc_{4}\hbar ^{2}mn_{0}\sin (mX) - c_{3}c_{4} \hbar ^{2}mn_{0}\sin (mX) \\ &{} + 2c_{4}\hbar mn_{0}\sin (mX)T - 0.5T^{2}c _{2}c_{4}\hbar ^{2}m^{4}n_{0} \cos (mX) \\ &{}+ c_{3}c_{4}\hbar ^{2}mn_{0}\sin (mX)\cos (T) + c_{3}c_{4}\hbar ^{2}mn _{0}\sin (mX)\sin (T)T. \end{aligned}$$
(37)

Then the second-order HAM approximate analytical solution of Eq. (28) is as follows:

$$ A(X,T) = A_{0}(X,T) + A_{1}(X,T) + A_{2}(X,T). $$
(38)

When the basic flow \(\varPsi _{0}(y,t)\) is taken to be

$$ \varPsi _{0} = b_{0}y + b_{1}, $$
(39)

where \(b_{0}\), \(b_{1}\) are arbitrary constants, and using Eqs. (15)–(16), we obtain

$$ G_{0}(y,T) = R(T)\sin \biggl( \sqrt{ - \frac{c_{0}F + \beta }{b_{0} + c_{0}}} y \biggr), $$
(40)

where \(R(T)\) is an arbitrary function about T.

Substituting Eqs. (11) and (38)–(40) into Eq. (4) and returning the variables x and t, we obtain the first-order approximate solution of the original equation Eq. (3) in the form

$$\begin{aligned} \psi (x,y,t) \approx& b_{0}y + b_{1} + \varepsilon R \bigl( \varepsilon ^{\frac{3}{2}}t\bigr)\sin \biggl( \sqrt{ - \frac{c_{0}F + \beta }{b_{0} + c_{0}}} y \biggr) \bigl\{ 2k^{2}\operatorname{sech} ^{2}\bigl(k\sqrt{ \varepsilon } (x - c_{0}t)\bigr) \\ &{} + \hbar \bigl[\tanh \bigl(k\sqrt{ \varepsilon } (x - c_{0}t) \bigr) \\ &{}\cdot \operatorname{sech}^{4}\bigl(k\sqrt{\varepsilon } (x - c_{0}t)\bigr) \bigl(48k ^{5}c_{2}\varepsilon ^{\frac{3}{2}}t - 8k^{5}c_{1} + 8k^{5}c_{1} \cos \bigl( \varepsilon ^{\frac{3}{2}}t\bigr)\bigr) \\ &{} + 2k^{2}c_{3}\operatorname{sech}^{2}\bigl(k \sqrt{ \varepsilon } (x - c_{0}t)\bigr)\sin \bigl(\varepsilon ^{\frac{3}{2}}t\bigr) + c_{4}mn _{0}\cdot \sin \bigl(m \sqrt{\varepsilon } (x - c_{0}t)\bigr) \varepsilon ^{\frac{3}{2}}t \\ &{} - 16k^{5}c_{2}\tanh \bigl(k\sqrt{\varepsilon } (x - c_{0}t)\bigr)\operatorname{sech}^{2}\bigl(k\sqrt{\varepsilon } (x - c _{0}t)\bigr)\varepsilon ^{\frac{3}{2}}t\bigr]k^{2} \hbar ^{2} \\ &{}\cdot\operatorname{sech} ^{2}\bigl(k\sqrt{\varepsilon } (x - c_{0}t)\bigr)\bigl[c_{3}^{2}- c_{3}^{2} \cos ^{2}\bigl(\varepsilon ^{\frac{3}{2}}t\bigr) \\ &{} + 2c_{3}\sin \bigl( \varepsilon ^{\frac{3}{2}}t\bigr) + 4c_{1}c_{4}mn_{0}\sin \bigl(m\sqrt{\varepsilon } (x - c_{0}t)\bigr)\sin \bigl(\varepsilon ^{\frac{3}{2}}t\bigr) \\ &{} - 4c_{1}c_{4}mn_{0} \sin \bigl(m\sqrt{ \varepsilon } (x - c_{0}t)\bigr)\cos \bigl(\varepsilon ^{ \frac{3}{2}}t \bigr) \\ &{}\cdot \varepsilon ^{\frac{3}{2}}t + 64k^{6}\varepsilon ^{3}t^{2}c_{2} ^{2} + 2c_{3} \sin \bigl(\varepsilon ^{\frac{3}{2}}t\bigr)\bigr] \\ &{} + 1680k^{8}\hbar ^{2}c _{2} \operatorname{sech}^{8}\bigl(k\sqrt{\varepsilon } (x - c_{0}t)\bigr) \bigl(c _{1}\varepsilon ^{\frac{3}{2}}t - 3T^{2}c_{2} - c_{1}\sin \bigl( \varepsilon ^{\frac{3}{2}}t\bigr)\bigr) \\ &{}+ 160k^{8}\hbar ^{2}c_{2} \operatorname{sech}^{6}\bigl(k\sqrt{\varepsilon } (x - c_{0}t)\bigr)\bigl[13 \varepsilon ^{3}t^{2}c_{2} - 42c_{1}\varepsilon ^{\frac{3}{2}}t + 42c _{1}\sin \bigl( \varepsilon ^{\frac{3}{2}}t\bigr)\bigr] \\ &{} + 4k^{4}\hbar ^{2} \operatorname{sech}^{4} \bigl(k\sqrt{\varepsilon } (x - c_{0}t)\bigr)\bigl[c_{1}c _{3}\varepsilon ^{\frac{3}{2}}t - 504k^{4}c_{2}^{2} \cdot \varepsilon ^{3}t^{2} + 103k^{4}c_{1}c_{2} \varepsilon ^{\frac{3}{2}}t \\ &{}- 103k^{4}c _{1}c_{2}\sin \bigl(\varepsilon ^{\frac{3}{2}}t\bigr) - 0.5c_{1}c_{3}\sin \bigl(2 \varepsilon ^{\frac{3}{2}}t\bigr)\bigr] \\ &{} + 2k^{5}\hbar \tanh \bigl(k\sqrt{\varepsilon } (x - c_{0}t)\bigr)\operatorname{sech}^{4}\bigl(k\sqrt{ \varepsilon } (x - c _{0}t)\bigr) \\ &{}\cdot \bigl[4c_{1}\hbar \cos \bigl(\varepsilon ^{\frac{3}{2}}t \bigr) - 4c_{1} + 24\hbar c_{2}\varepsilon ^{\frac{3}{2}}t + 4c_{1}\cos \bigl( \varepsilon ^{\frac{3}{2}}t\bigr) + 2\hbar c_{1}c_{3}\varepsilon ^{ \frac{3}{2}}t \\ &{} - 4\hbar c_{1}c_{3}\sin \bigl(\varepsilon ^{\frac{3}{2}}t\bigr) - 32k ^{2}\hbar c_{1}c_{2} \sin \bigl(\varepsilon ^{\frac{3}{2}}t\bigr) + c_{1}c_{3} \hbar \\ &{}\cdot \sin \bigl(2\varepsilon ^{\frac{3}{2}}t\bigr) + 32k^{2}c_{1}c_{2} \hbar \cos \bigl(\varepsilon ^{\frac{3}{2}}t\bigr)\varepsilon ^{\frac{3}{2}}t + 24c_{2}c _{3}\hbar \sin \bigl(\varepsilon ^{\frac{3}{2}}t \bigr)\varepsilon ^{\frac{3}{2}}t\bigr] \\ &{} + 16k^{7}\hbar ^{2}c_{1}\tanh \bigl(k\sqrt{ \varepsilon } (x - c_{0}t)\bigr) \operatorname{sech}^{6} \bigl(k\sqrt{\varepsilon } (x \\ &{}- c_{0}t)\bigr)\bigl[2c_{1}\cos \bigl(\varepsilon ^{\frac{3}{2}}t\bigr) - c_{1} - c_{1}\cos ^{2} \bigl(\varepsilon ^{\frac{3}{2}}t\bigr) + 12c_{2}\sin \bigl(\varepsilon ^{ \frac{3}{2}}t\bigr) \\ &{}- 12c_{2}\cos \bigl(\varepsilon ^{\frac{3}{2}}t\bigr) \varepsilon ^{\frac{3}{2}}t\bigr] - 16k^{5}\hbar c_{2}\tanh (kX) \operatorname{sech}^{2}\bigl(k\sqrt{\varepsilon } (x \\ &{}- c_{0}t)\bigr)\bigl[2\varepsilon ^{\frac{3}{2}}t - c_{3}\hbar \sin \bigl( \varepsilon ^{\frac{3}{2}}t\bigr)\bigr] + Tc_{4}\hbar ^{2}mn_{0}\sin \bigl(m\sqrt{ \varepsilon } (x - c_{0}t)\bigr) \\ &{}- c_{3}c_{4}\hbar ^{2}mn_{0}\sin \bigl(m\sqrt{ \varepsilon } (x - c_{0}t)\bigr) + 2c_{4}\hbar mn_{0}\sin \bigl(m\sqrt{\varepsilon } \\ &{}\cdot (x - c_{0}t)\bigr)\varepsilon ^{\frac{3}{2}}t - 0.5T^{2}c_{2}c_{4} \hbar ^{2}m^{4}n_{0} \cos \bigl(m\sqrt{\varepsilon } (x - c_{0}t)\bigr) \\ &{} + c_{3}c _{4}\hbar ^{2}mn_{0}\sin \bigl(m\sqrt{\varepsilon } (x - c_{0}t)\bigr)\cos \bigl( \varepsilon ^{\frac{3}{2}}t\bigr) \\ &{} + c_{3}c_{4}\hbar ^{2}mn_{0} \sin \bigl(m\sqrt{\varepsilon } (x - c _{0}t)\bigr)\sin \bigl( \varepsilon ^{\frac{3}{2}}t\bigr)\varepsilon ^{\frac{3}{2}}t \bigr\} , \end{aligned}$$
(41)

where \(R(\varepsilon ^{\frac{3}{2}}t)\) is an arbitrary function about t.

When taking \(R(\varepsilon ^{\frac{3}{2}}t)\) in the form

$$ R\bigl(\varepsilon ^{\frac{3}{2}}t\bigr) = k_{1}\operatorname{sech} \bigl[20 \varepsilon ^{\frac{3}{2}}(t - 9)\bigr], $$
(42)

other parameters are as follows:

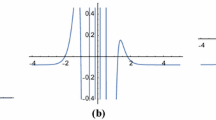
$$\begin{aligned}& \begin{aligned}&F = 1.5, \qquad c_{0} = - 2.4, \qquad c_{1} = 2.7, \qquad c_{2} = 5.3, \qquad c_{3} = 1.3, \qquad c_{4} = 0.6, \\ &\beta = 16.3, \qquad b_{0} = - 18, \\ &b_{1} = 5, \qquad n_{0} = 5.2, \qquad m = 1.4, \qquad \varepsilon = 0.1, \qquad k = 6, \qquad k_{1} = 10. \end{aligned} \end{aligned}$$
(43)

The evolution of stream function field is shown in Fig. 1.

Figure 1
figure 1figure 1

When \(a_{1} = c_{1}\sin (\varepsilon ^{3/2}t)\), \(a_{2} = c_{2}\), \(a_{3} = c_{3}\cos (\varepsilon ^{3/2}t)\), \(a_{4} = c_{4}\), the evolution of stream function field, the stream function analytic expression is Eq. (43), where \(R = k_{1}\operatorname{sech}[20\varepsilon ^{ \frac{3}{2}}(t - 9)]\), \(F = 1.5\), \(c_{0} = - 2.4\), \(c_{1} = 2.7\), \(c_{2} = 5.3\), \(c_{3} = 1.3\), \(c_{4} = 0.6\), \(\beta = 16.3\), \(b_{0} = - 18\), \(b_{1} = 5\), \(n_{0} = 5.2\), \(m = 1.4\), \(\varepsilon = 0.1\), \(k = 6\), \(k_{1} = 10\)

Full size image

When

$$ \begin{aligned}&a_{1} = c_{1}\sin \bigl(\varepsilon ^{3/2}t\bigr), \qquad a_{2} = c_{2}, \qquad a_{3} = c_{3}\cos \bigl(\varepsilon ^{3/2}t\bigr), \\ &a_{4} = c_{4}e^{\varepsilon ^{3/2}t}, \qquad R = k_{1}\operatorname{sech}\bigl[30\varepsilon ^{\frac{3}{2}}(t - 4) \bigr], \end{aligned} $$
(44)

where \(c_{1}\), \(c_{2}\), \(c_{3}\), \(c_{4}\) are arbitrary constants, and \(c _{4} = 9.6\), \(\beta = 16.3\), \(b_{0} = - 8\), \(b_{1} = 5\), \(n_{0} = 5.2\), \(m = 2.8\), \(\varepsilon = 0.05\), \(k_{1} = 20\), other parameters are the same as those for Fig. 1, \(\varPsi _{0}\), \(G_{0}\) are shown in Eqs. (39)–(40), solving process is similar to above, no longer repeated, the evolution of stream function field is shown in Fig. 2.

Figure 2
figure 2figure 2figure 2

When \(a_{1} = c_{1}\sin (\varepsilon ^{3/2}t)\), \(a_{2} = c_{2}\), \(a_{3} = c_{3}\cos (\varepsilon ^{3/2}t)\), \(a_{4} = c_{4}e^{ \varepsilon ^{3/2}t}\), the evolution of stream function field, \(R = k_{1}\operatorname{sech}[20\varepsilon ^{3/2}(t - 9)]\), \(F = 1.5\), \(c_{0} = - 2.4\), \(c_{1} = 2.7\), \(c_{2} = 5.3\), \(c_{3} = 1.3\), \(c_{4} = 9.6\), \(\beta = 16.3\), \(b_{0} = - 8\), \(b_{1} = 5\), \(n_{0} = 5.2\), \(m = 2.8\), \(\varepsilon = 0.05\), \(k = 6\), \(k_{1} = 20\)

Full size image

In order to enhance the practical significance of our work, we take a real observational blocking case that happened during 14 July 2003 to 27 July 2003 as a simple example. Making use of the National Centers for Environmental Prediction–National Center for Atmospheric Research (NCEP-NCAR) reanalysis data, a dipole blocking event is depicted in Fig. 3.

Figure 3
figure 3figure 3

Geopotential height at 300 hPa pressure level of a blocking case during 14 July 2003 to 27 July 2003. Contour interval is 4 gpdm. The x axis is longitude and the y axis is latitude

Full size image

4 Discussions

Figure 1 clearly demonstrates the formation, maintenance, and decay of a complicated dipole-type blocking, which gradually moves westward in the whole process. At the beginning (day 0), zonal flow flows from west to east (Fig. 1(a)). From the first day to the sixth day, stream function field presents north-south direction meridional flow in the form of multi-pole gradually moving westward (Fig. 1(b)–Fig. 1(e)), and then the multi-pole disappears (Fig. 1(f)). On the seventh day, monopoles appear (Fig. 1(g)); on the eighth day, dipoles appear (Fig. 1(h)); on the tenth day, they are at the strongest status (Fig. 1(j)) and then become weaker, finally disappearing after the fourth day (Fig. 1(h)). We still call it dipole blocking, and its life-time is fourteen days.

Figure 2 reveals a complicated dipole blocking process. At the initial time, a weak dipole is presented (Fig. 2(a)). From the second to sixth day, stream function field presents multi-pole status (Fig. 2(b)–(f)); on the seventh day, multi-dipoles appear (Fig. 2(g)), on the fourteenth day, multi-dipoles disappear (Fig. 2(n)), then a dipole appears (Fig. 2(o)). After the twenty-fourth day, the dipole disappears (Fig. 2(x)). Obviously, stream function field possesses a process from dipole to multi-pole then to multi-dipole, again to dipole, finally disappearing, but we still call it dipole blocking, and its life-time is twenty-four days.

From Fig. 3, it is easily found that geopotential height experiences the developing process of dipole (14 July 2003), multi-pole (15 July 2003), and the onset, maintenance, and collapse of dipole (16–27 July 2003). We still call it dipole blocking. Besides, from 16 July 2003 to 27 July 2003, the dipole gradually moves westward.

Figure 1 and Fig. 2 reveal the complexity of dipole blocking evolution. However, Fig. 2 basically corresponds well to the real observational blocking case (Fig. 3), although they have different life cycles, they have the same developing process, namely from dipole to multi-pole, then to dipole. Consequently, the introduction of a time-dependent variable coefficient topographic forcing term is more suitable to explain the complicated blocking phenomenon. Besides, we suspect that the real blocking process is very complicated and changeable, may be accompanied by monopole, dipole, and multi-pole three forms.

5 Conclusions

In this paper, combining topographic forcing effect with time-varying property and introducing a higher order term of the stream function with five arbitrary functions and forced topography, a variable coefficient KdV equation with time-dependent variable coefficient topographic forcing term is obtained. When selecting some proper parameters, stream function field presents a complicated and changeable dipole-type blocking. Consequently, time-dependent variable coefficient and forced topography have great influence on the evolution of stream function field. With appropriate selection of arbitrary functions and constants, many kinds of real atmospheric phenomena may be successfully explained.