The influence of commensalism on a Lotka–Volterra commensal symbiosis model with Michaelis–Menten type harvesting

Abstract

In this paper, we study the following Lotka–Volterra commensal symbiosis model of two populations with Michaelis–Menten type harvesting for the first species:

$$ \begin{gathered} \frac{dx}{dt} = r_{1}x \biggl(1- \frac{x}{K_{1}}+\alpha \frac{y}{K_{1}} \biggr)- \frac{qEx}{m_{1}E+m_{2}x}, \\ \frac{dy}{dt} = r_{2}y \biggl(1- \frac{y}{K_{2}} \biggr), \end{gathered} $$

where $r_{1}$, $r_{2}$, $K_{1}$, $K_{2}$, α, q, E, $m_{1}$ and $m_{2}$ are all positive constants. The local and global dynamic behaviors of the system are investigated, respectively. For the limited harvesting case (i.e., q is small enough), we show that the system admits a unique globally stable positive equilibrium. For the over harvesting case, if the cooperate intensity of the both species (α) and the capacity of the second species ($K_{2}$) are large enough, the two species could coexist in a stable state; otherwise, the first species will be driven to extinction. Numeric simulations are carried out to show the feasibility of the main results.

1 Introduction

Mutualism means that the different species exist in a relationship in which each species benefits from the activity of the other species. During the last decade, many scholars [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] investigated the dynamic behaviors of the mutualism model and some essential progress on persistent, extinction and stability of the system are obtained. Some scholars [1,2,3,4,5,6,7] focused on the persistent property of the cooperation system. Li and Yang [6] proposed a discrete model of mutualism with infinite deviating arguments, they showed that the system is permanent. Li and Zhang [1], Chen, Chen and Li [2], Chen and Xie [3], Chen, Xie, Chen [4] and Yang and Li [5] had studied the persistent property of the mutualism model with feedback control, and in [4], by applying a difference inequality of Fan and Wang, Chen, Xie and Chen showed that feedback control variables have influence on the permanence of the discrete N-species cooperative system, Li and Zhang [1] also obtained some similar results. Some scholars [8,9,10,11,12] focused on the stability property of the positive equilibrium of the mutualism model. For example, Xie, Chen, Yang et al. [12] showed that the unique positive equilibrium of an integrodifferential model of mutualism is globally attractive. Based on a difference inequality which was established by Fengde Chen, Xie, Xue and Wu [11] also investigated the stability property of the positive equilibrium of a discrete mutualism model with infinite deviating arguments. Some scholars [13,14,15] argued that non-autonomous case is more suitable, and such topics as the existence of the positive periodic solution and the persistence of the system were investigated. Recently, Chen, Xie and Chen [16] and Yang, Miao and Chen [17] focused on the extinction property of the mutualism model, in [16], Chen, Xie and Chen showed that the stage structure of the species plays important roles in the extinction of the species, despite the cooperation of the species. Yang, Miao, Chen et al. [17] proposed a mutualism model with single feedback control, and they found that the system admits more complicated dynamic behaviors, for example, by choosing suitable coefficients, the species may be driven to extinction.

Unlike the mutualism relationship, in which two species benefit from each other, commensalism is a long-term biological interaction (symbiosis) in which members of one species gain benefits while those of the other species neither benefit nor are harmed. Though such kinds of relationship are often observed in nature, only recently scholars [18,19,20,21,22,23,24,25,26,27,28,29] tried to propose the model to describe such kind of the relationship, and to study the dynamic behaviors of suck kind of model. Recently, Sun and Sun [18] proposed the following commensalism system:

$$ \begin{gathered} \frac{dx}{dt}=r_{1}x \biggl(1- \frac{x}{K_{1}}+\alpha \frac{y}{K_{1}} \biggr), \\ \frac{dy}{dt}=r_{2}y \biggl(1- \frac{y}{K_{2}} \biggr), \end{gathered} $$

(1.1)

where $r_{1}$, $r_{2}$, $K_{1}$, $K_{2}$, α are all positive constants. The system admits four equilibria:

$$ E_{1}(0,0),\qquad E_{2}(K_{1},0),\qquad E_{3}(0,K_{2}),\qquad E_{4}(K_{1}+\alpha K_{2}, K_{2}). $$

The authors showed that $E_{1}$, $E_{2}$ and $E_{3}$ are all unstable equilibria, and $E_{4}$ is a stable node. Han and Chen [19] incorporated the feedback control variables for the above system, and their study showed that feedback control variables have no influence on the stability property of the system (1.1). Corresponding to system (1.1), Xie, Miao and Xue [26] proposed a discrete commensal symbiosis model, they investigated the positive ω-periodic solution of the system. Xue and Xie et al. [22] further proposed a discrete commensalism model with delay, they investigated the almost periodic solution of the system. Miao, Xie and Pu [23] studied the persistent property of the periodic Lotka–Volterra commensal symbiosis model with impulsive action. Several scholars [24, 25] also argued that it may be more suitable to assume that the relationship between two species is of nonlinear type instead of linear, and they established the commensalism model with functional response. Lei [21] proposed a commensalism model with stage structure; by constructing some suitable Lyapunov function, he was able to show that under some suitable conditions, the system may admit a unique positive equilibrium which is globally asymptotically stable. Lin [28] considered the influence of the Allee effect on the Lotka–Volterra type commensalism model, and he found that the Allee effect could increase the final density of the species. Such a phenomenon is quite different from the predator–prey system incorporating the Allee efffect.

On the other hand, to obtain a resource for humans, harvesting of species is necessary. Already, many scholars investigated the influence of the harvesting on the population system [9, 10, 30,31,32,33,34,35,36,37,38].

There are three types of harvesting: (1) constant harvesting [39]; (2) linear harvesting [9, 10, 27, 31, 32]; (3) nonlinear harvesting [30, 33,34,35,36,37]. As is well known, nonlinear harvesting is more realistic from the biological and economical points of view [30]. Clark [11] proposed a harvesting term $h= \frac{qEx}{cE+lx}$, which is named the Michealis–Menten type functional form of the catch rate. Generally speaking, such kind of harvesting may lead to the complexity dynamic behaviors of the system; for example, Idlangoa, Shepherd and Gear [40] showed that the logistic model with Holling type II harvesting term may admit zero, one or two positive equilibria. Hu and Cao [35] showed that the predator–prey model with Michealis–Menten type harvesting in predator species may admit a rich bifurcation phenomenon.

In this paper, we will further incorporate the harvesting term for the first species in system (1.1), and this leads to the following model:

$$ \begin{gathered} \frac{dx}{dt}=r_{1}x \biggl(1- \frac{x}{K_{1}}+\alpha \frac{y}{K_{1}} \biggr)- \frac{qEx}{m_{1}E+m_{2}x}, \\ \frac{dy}{dt}=r_{2}y \biggl(1- \frac{y}{K_{2}} \biggr), \end{gathered} $$

(1.2)

where $r_{1}$, $r_{2}$, $K_{1}$, $K_{2}$, α, q, E, $m_{1}$, $m_{2}$ are all positive constants, $r_{1}$, $r_{2}$, $K_{1}$, $K_{2}$, α, have the same meaning as that of the system (1.1), E is the fishing effort used to harvest and q is the catchablity coefficient, $m_{1}$ and $m_{2}$ are suitable constants. One could refer to [35] and [40] for a more detailed discussion about the nonlinear harvesting term.

In system (1.2), without the commensalism of the second species, the first species will satisfy the following equation:

$$ \frac{dx}{dt}=r_{1}x \biggl(1- \frac{x}{K_{1}} \biggr)- \frac{qEx}{m_{1}E+m_{2}x}. $$

(1.3)

Similarly to the analysis of Idlangoa, Shepherd and Gear ([40], page 83), one could see that the model (1.3) may admit zero, one or two positive equilibrium. That is, by introducing the harvesting term, the first species may or may not exist in the long run, maybe the first species will be driven to extinction due to over harvesting. In this case, the commensalism of the second species to the first species may play the most important role in the persistence or extinction of the first species. It is the aim of this paper to find the answer to this problem.

The paper is arranged as follows. The local and global stability property of the equilibria of system (1.2) is investigated in Sects. 2 and 3, respectively. The extinction property of the system is investigated in Sect. 4. Some examples together with their numeric simulations are presented in Sect. 5 to show the feasibility of the main results. We end this paper by a brief discussion.

2 Local stability of the equilibria

The aim of this section is to investigate the existence and local stability property of the equilibrium of system (1.2).

Lemma 2.1

Assume that

$$ r_{1}> \frac{q}{m_{1}} $$

(2.1)

and

$$ \frac{qm_{2}}{Em_{1}^{2}}< \frac{r_{1}}{K_{1}} $$

(2.2)

hold, then

$$ F_{1}(x)=r_{1} \biggl(1- \frac{x}{K_{1}} \biggr)- \frac{qE}{m_{1}E+m_{2}x} =0 $$

(2.3)

admits a unique positive solution

$$ x_{1}= \frac{-B_{1}+\sqrt{B_{1}^{2}-4A_{1}C_{1}}}{2A_{1}}, $$

(2.4)

where

$$ A_{1}=m_{2}r_{1}, \qquad B_{1}= Em_{1}r_{1}-K_{2}m_{2}r_{1}, \qquad C_{1}=EK_{1}q-K_{1}m_{1}r_{1}. $$

(2.5)

Proof

It follows from the continuity of

$$ F_{1}(x)=r_{1} \biggl(1- \frac{x}{K_{1}} \biggr)- \frac{qE}{m_{1}E+m_{2}x} $$

and (2.1) that

$$ F_{1}(0)=r_{1}- \frac{q }{m_{1} }>0,\qquad F_{1}(K_{1})=- \frac{qE}{m_{1}E+m_{2}K_{1}}< 0, $$

hence $F_{1}(x)=0$ has at least one positive solution on the interval $(0,K_{1})$. Also, for $x\geq 0$, from (2.2)

$$ \frac{dF_{1}(x)}{dx}=- \frac{r_{1}}{K_{1}}+ \frac{qEm_{2}}{(Em_{1}+m_{2}x)^{2}}\leq - \frac{r_{1}}{K_{1}}+ \frac{qm_{2}}{Em_{1}^{2}}< 0. $$

Hence, $F_{1}(x)$ is strictly decreasing on the interval $(0,+\infty )$; therefore, $F_{1}(x)=0$ has at most one positive solution on the interval $(0,+\infty )$. The above analysis shows that under the assumption of Lemma 2.1, $F_{1}(x)=0$ has a unique positive solution on the interval $(0, K_{1})$.

The solution of the equation $F_{1}(x)=0$ is equivalent to the solution of the equation

$$ G_{1}(x)=A_{1}x^{2}+B_{1}x+C_{1}=0, $$

(2.6)

where $A_{1}$, $B_{1}$, $C_{1}$ is defined by (2.4). Noting that under the assumption (2.1), $C_{1}=EK_{1}q-EK_{1}m_{1}r_{2}<0$, (2.6) has only one positive solution,

$$ x_{1}= \frac{-B_{1}+\sqrt{B_{1}^{2}-4A_{1}C_{1}}}{2A_{1}}. $$

(2.7)

This ends the proof of Lemma 2.1. □

Lemma 2.2

Assume that

$$ r_{1} \biggl(1 +\alpha \frac{K_{2}}{K_{1}} \biggr)> \frac{q}{m_{1}} $$

(2.8)

and

$$ \frac{qm_{2}}{Em_{1}^{2}}< \frac{r_{1}}{K_{1}} $$

(2.9)

hold, then

$$ F_{2}(x)=r_{1} \biggl(1- \frac{x}{K_{1}}+\alpha \frac{K_{2}}{K_{1}} \biggr)- \frac{qE}{m_{1}E+m_{2}x} =0 $$

(2.10)

admits a unique positive solution

$$ x^{*}= \frac{-B_{2}+\sqrt{B_{2}^{2}-4A_{2}C_{2}}}{2A_{2}}, $$

(2.11)

where

$$\begin{aligned}& A_{2}=m_{2}r_{1}, \qquad B_{2}= Em_{1}r_{1}-K_{2}\alpha m_{2}r_{1}-K_{1}m_{2}r_{1}, \end{aligned}$$

(2.12)

$$\begin{aligned}& C_{2}=EK_{1}q-EK_{1}m_{1}r_{1}-EK_{2} \alpha m_{1}r_{1}. \end{aligned}$$

(2.13)

Proof

The proof of Lemma 2.2 is similar to that of Lemma 2.1 and we omit the details here. □

Under the assumption (2.8) and (2.9) hold, by using Lemma 2.2, system (1.2) admits three equilibria,

$$ E_{1}(0,0), \qquad E_{3}(0, K_{2}), \qquad E_{4}\bigl(x^{*}, y^{*}\bigr), $$

(2.14)

where $x^{*}$ is defined by (2.14) and $y^{*}=K_{2}$. If we further assume that (2.1) holds, then system (1.2) also admits the fourth equilibrium, $E_{2}(x_{1},0)$, where $x_{1}$ is defined by (2.4).

We shall now investigate the local stability property of the above equilibria.

Theorem 2.1

Assume that (2.8) and (2.9) hold, then $E_{1}(0,0)$ and $E_{3}(0,K_{2})$ are all unstable; $E_{4}(x^{*}, y ^{*})$ is locally asymptotically stable. Assume further that (2.1) holds, then $E_{2}(x_{1},0)$ is unstable.

Proof

The variational matrix of the system of Eq. (1.2) at $(x,y)$ is

$$J(x,y)=\left(\begin{array}{cc}\Gamma & \frac{r_1\alpha x}{K_1}\\ 0& r_2(1-\frac{y}{K_2})-\frac{r_{2}y}{K_2}\end{array}\right),$$

(2.15)

where

$$ \varGamma =r_{1}\biggl(1-\frac{x}{K_{1}}+\frac{\alpha y}{K_{1}} \biggr)- \frac{r_{1}x}{K _{1}}- \frac{qE}{Em_{1}+m_{2}x}+ \frac{qExm_{2}}{(Em_{1}+m_{2}x)^{2}}. $$

The characteristic equation of the variational matrix is

$$ \lambda ^{2}-\operatorname{tr}(J)\lambda +\det (J)=0. $$

(2.16)

• (1) For the steady-state solution $E_{1}(0,0)$, $\lambda _{1}=r_{1}- \frac{q}{m_{1}}$, $\lambda _{2}=r_{2}>0$, so $E_{1}(0,0)$ is unstable.

• (2) For the steady-state solution $E_{3}(0,K_{2})$, $\lambda _{1}=r _{1} (1+ \frac{\alpha K_{2}}{K_{1}} )- \frac{q}{m_{1}}>0$, $\lambda _{2}= -r_{2}<0$, and so, $E_{3}(0,K_{2})$ is unstable.

• (3) Noting that the positive equilibrium $E_{4}(x^{*}, y^{*})$ satisfies

  $$ \begin{gathered} r_{1} \biggl(1- \frac{x^{*}}{K_{1}}+\alpha \frac{y^{*}}{K_{1}} \biggr)- \frac{qE}{m_{1}E+m_{2}x^{*}}=0, \\ r_{2} \biggl(1- \frac{y^{*}}{K_{2}} \biggr)=0. \end{gathered} $$

  (2.17)

  By using (2.17), the Jacobian of the system about the equilibrium point $E_{4}(x^{*},y^{*})$ is given by

  $$J(x^{\ast },y^{\ast })=\left(\begin{array}{cc}-\frac{r_1{x}^{\ast }}{K_1}+\frac{qE{x}^{\ast }{m}_2}{{(E{m}_1+m_2{x}^{\ast })}^2}& \frac{r_1{x}^{\ast }\alpha }{K_1}\\ 0& -\frac{r_2{y}^{\ast }}{K_2}\end{array}\right).$$

  (2.18)

  Under the assumption (2.1) and (2.2), the two eigenvalues of the matrix satisfies

  $$\begin{aligned}& \lambda _{1}=- \frac{r_{1}x^{*}}{K_{1}} + \frac{qEx^{*}m_{2}}{(Em_{1}+m_{2}x^{*})^{2}}< x^{*} \biggl(-\frac{r_{1}}{K _{1}} + \frac{qm_{2}}{Em_{1}^{2}} \biggr)< 0, \\& \lambda _{2}=-\frac{r_{2}y^{*}}{K_{2}} < 0. \end{aligned}$$

  Consequently, $E_{4}(x^{*},y^{*})$ is locally asymptotically stable.

• (4) Noting that $x_{1}$ satisfies

  $$ r_{1} \biggl(1- \frac{x_{1}}{K_{1}} \biggr)- \frac{qE}{m_{1}E+m_{2}x_{1}}=0. $$

  The Jacobian of the system about the equilibrium point $E_{2}(x_{1},0)$ is given by

  $$\left(\begin{array}{cc}-\frac{r_1{x}_1}{K_1}+\frac{qE{x}_1{m}_2}{{(E{m}_1+m_2{x}_1)}^2}& \frac{r_1{x}_1\alpha }{K_1}\\ 0& r_2\end{array}\right).$$

  (2.19)

  Under the assumption (2.1), (2.8) and (2.9), the two eigenvalues of the matrix satisfies $\lambda _{1}=- \frac{r_{1}x_{1}}{K_{1}} + \frac{qEx_{1}m_{2}}{(Em_{1}+m_{2}x_{1})^{2}}<0$, $\lambda _{2}=r_{2}>0$. Consequently, $E_{2}(x_{1}, 0)$ is unstable.

The proof of Theorem 2.1 is finished. □

3 Global stability

The aim of this section is to investigate the global stability property of the equilibrium of system (1.2).

Theorem 3.1

Assume that (2.8) and (2.9) hold, then the positive equilibrium $E_{4}(x^{*},y^{*})$ of system (1.2) is globally stable.

Proof

Let $(x(t), y(t))^{T}$ be any positive solution of system (1.2). Noting that the second equation of system (1.2) is the traditional logistic equation, it immediately follows that

$$ \lim_{r\rightarrow +\infty }y(t)=K_{2}. $$

(3.1)

Condition (2.8) implies that, for small enough positive constant, $\varepsilon >0$, the inequality

$$ r_{1} \biggl(1 +\alpha \frac{K_{2}-\varepsilon }{K_{1}} \biggr)> \frac{q}{m_{1}} $$

(3.2)

holds. Let $\varepsilon >0$ be any small enough positive constant which satisfies (3.2) and $\varepsilon <\frac{1}{2}K_{2}$. It follows from (3.1) that there exists $T>0$ such that

$$ K_{2}-\varepsilon < y(t)< K_{2}+\varepsilon \quad \text{for all } t>T. $$

(3.3)

From the first equation of (1.2) and the right hand side of (3.2), we have

$$ \frac{dx}{dt}\leq r_{1}x \biggl(1- \frac{x}{K_{1}}+ \alpha \frac{K_{2}+\varepsilon }{K_{1}} \biggr)- \frac{qEx}{m_{1}E+m_{2}x}. $$

(3.4)

Now let us consider the equation

$$ \frac{du_{1}}{dt}=r_{1}u_{1} \biggl(1- \frac{u_{1}}{K_{1}}+\alpha \frac{K_{2}+\varepsilon }{K_{1}} \biggr)- \frac{qEu_{1}}{m_{1}E+m_{2}u_{1}}. $$

(3.5)

Condition (2.8) implies

$$ r_{1} \biggl(1 +\alpha \frac{K_{2}+\varepsilon }{K_{1}} \biggr)> \frac{q}{m_{1}} $$

(3.6)

holds. Let

$$ F_{3}(u_{1})=r_{1} \biggl(1- \frac{u_{1}}{K_{1}}+ \alpha \frac{K_{2}+\varepsilon }{K_{1}} \biggr)- \frac{qE}{m_{1}E+m_{2}u_{1}}. $$

(3.7)

From (3.6) and (2.9), with slightly revise of the proof of Lemma 2.1, we can show that:

• (1) There is a unique $u_{1\varepsilon }^{*}$, such that $F_{3}(u _{1\varepsilon }^{*}) = 0$, where, by simple computation,

  $$\begin{aligned}& u_{1\varepsilon }^{*}= \frac{-B_{21}+\sqrt{B_{21}^{2}-4A_{2}C_{21}}}{2A_{2}}. \end{aligned}$$

  (3.8)
  $$\begin{aligned}& \begin{aligned} &A_{2}=m_{2}r_{1}, \qquad B_{21}= Em_{1}r_{1}-(K_{2}+ \varepsilon )\alpha m_{2}r_{1}-K_{1}m_{2}r _{1}, \\ &C_{21}=EK_{1}q-EK_{1}m_{1}r_{1}-E(K_{2}+ \varepsilon )\alpha m_{1}r _{1}. \end{aligned} \end{aligned}$$

  (3.9)

• (2) For all $u_{1\varepsilon }^{*} > u_{1} > 0$, $F_{3}(u_{1}) > 0$.

• (3) For all $u_{1} > u_{1\varepsilon }^{*} > 0$, $F_{3}(u_{1}) < 0$.

Hence, it immediately follows from Lemma 2.1 in [38] that the unique positive equilibrium $u_{1\varepsilon }^{*}$ of system (3.5) has global stability. By the comparison theorem, it immediately follows from (3.4) and (3.5) that

$$ \limsup_{t\rightarrow +\infty } x(t)\leq u_{1\varepsilon }^{*}. $$

(3.10)

Since $\varepsilon >0$ is an arbitrary small positive constant, letting $\varepsilon \rightarrow 0$ in (3.10) leads to

$$ \limsup_{t\rightarrow +\infty } x(t)\leq x^{*}. $$

(3.11)

From the first equation of (1.2) and the left hand side of (3.2), we have

$$ \frac{dx}{dt}\geq r_{1}x \biggl(1- \frac{x}{K_{1}}+ \alpha \frac{K_{2}-\varepsilon }{K_{1}} \biggr)- \frac{qEx}{m_{1}E+m_{2}x}. $$

(3.12)

Now let us consider the equation

$$ \frac{dv_{1}}{dt}=r_{1}v_{1} \biggl(1- \frac{v_{1}}{K_{1}}+\alpha \frac{K_{2}-\varepsilon }{K_{1}} \biggr)- \frac{qEv_{1}}{m_{1}E+m_{2}v_{1}}. $$

(3.13)

Let

$$ F_{4}(v_{1})=r_{1} \biggl(1- \frac{v_{1}}{K_{1}}+ \alpha \frac{K_{2}-\varepsilon }{K_{1}} \biggr)- \frac{qE}{m_{1}E+m_{2}v_{1}}. $$

(3.14)

From (3.2) and (2.9), with slightly revision of the proof of Lemma 2.1, we can show that:

• (1) There is a unique $v_{1\varepsilon }^{*}$, such that $F_{4}(v _{1\varepsilon }^{*}) = 0$, where, by simple computation,

  $$ v_{1\varepsilon }^{*}= \frac{-B_{22}+\sqrt{B_{22}^{2}-4A_{2}C_{22}}}{2A_{2}}, $$

  (3.15)

  here

  $$ \begin{gathered} A_{2}=m_{2}r_{1}, \qquad B_{22}= Em_{1}r_{1}-(K_{2}- \varepsilon )\alpha m_{2}r_{1}-K_{1}m_{2}r _{1}, \\ C_{22}=EK_{1}q-EK_{1}m_{1}r_{1}-E(K_{2}- \varepsilon )\alpha m_{1}r _{1}. \end{gathered} $$

• (2) For all $v_{1\varepsilon }^{*} > v_{1} > 0$, $F_{4}(v_{1}) > 0$.

• (3) For all $v_{1} > v_{1\varepsilon }^{*} > 0$, $F_{4}(v_{1}) < 0$.

Hence, it immediately follows from Theorem 2.1 in [38] that the unique positive equilibrium $v_{1\varepsilon }^{*}$ of system (3.13) has global stability. By the comparison theorem, it immediately follows from (3.12) and (3.13) that

$$ \liminf_{t\rightarrow +\infty } x(t)\geq v_{1\varepsilon }^{*}. $$

(3.16)

Since $\varepsilon >0$ is an arbitrary small positive constant, letting $\varepsilon \rightarrow 0$ in (3.16) leads to

$$ \liminf_{t\rightarrow +\infty } x(t)\geq x^{*}. $$

(3.17)

It immediately follows from (3.11) and (3.17) that

$$ \lim_{t\rightarrow +\infty } x(t)= x^{*}. $$

(3.18)

This ends the proof of Theorem 3.1. □

One could easily see that (2.1) implies (2.8), hence, as a direct corollary of Theorem 3.1, we have the following.

Corollary 3.1

Assume that (2.1) and (2.2) hold, then system (1.2) admits a unique positive equilibrium $E_{4}(x^{*}, y^{*})$, which is globally stable.

Remark 3.1

Corollary 3.1 shows that if the harvesting is limited, the catchability is small enough (i.e., q is small enough), then the two species could coexist in a stable state.

Remark 3.2

Theorem 3.1 shows that, for the catchability large enough (i.e., q is large), then the cooperative intensity of the two species becomes the most important factor, if α is large enough, then two species could also coexist in a stable state.

4 Extinction of the first species

In Sect. 2, assumption (2.8) and (2.9) implies that the catchability coefficient q should be limited or the cooperative effect (α) should be large enough. One may be curious as to what would happen if the harvesting effort is large enough and the cooperative effect is limited. In this case, will the species be driven to extinction?

We will give an affirmative answer to this question. Indeed, we have the following result.

Theorem 4.1

Assume that

$$ r_{1} \biggl(1+ \frac{\alpha K_{2}}{K_{1}} \biggr)< \frac{qE}{m_{1}E+m_{2}(K_{1}+\alpha K_{2})} $$

(4.1)

holds, then

$$ \lim_{t\rightarrow +\infty }x(t)=0, \qquad \lim_{t\rightarrow +\infty }y(t)=K_{2}, $$

i.e., the first species will be driven to extinction due to the over harvesting.

Proof

From (4.1) we could choose $\varepsilon >0$ small enough, such that

$$ r_{1} \biggl(1+ \frac{\alpha ( K_{2}+\varepsilon )}{K_{1}} \biggr)< \frac{qE}{m_{1}E+m_{2} (K_{1}+\alpha (K_{2}+\varepsilon )+\varepsilon )}. $$

(4.2)

Noting that the second equation of system (1.2) is independent of the variable x and is the traditional logistic equation; we have

$$ \lim_{t\rightarrow +\infty }y(t)= K_{2}. $$

(4.3)

Hence, for $\varepsilon >0$ be defined by (4.1), there exists a large enough $T_{1}$ such that

$$ y(t)< K_{2}+\varepsilon \quad \text{for all } t\geq T_{1}. $$

(4.4)

For $t\geq T_{1}$, from the first equation of system (1.2) and (4.4), we also have

$$ \frac{dx}{dt}\leq r_{1}x \biggl(1+ \frac{\alpha (K_{2}+\varepsilon )}{K_{1}}- \frac{x}{K_{1}} \biggr). $$

(4.5)

Hence, it follows from Lemma 2.1 in [27] that

$$ \limsup_{t\rightarrow +\infty } x(t)\leq K_{1}+\alpha (K_{2}+ \varepsilon ). $$

Therefore, there exists a $T_{2}>T_{1}$ such that

$$ x(t)\leq K_{1}+\alpha (K_{2}+\varepsilon )+\varepsilon \quad \text{as } t\geq T_{2}. $$

(4.6)

For $t>T_{2}$, it follows from the first equation of system (1.2) and (4.6) that

$$ \frac{dx}{dt}\leq \varUpsilon x, $$

(4.7)

where

$$ \varUpsilon = r_{1} \biggl(1+ \frac{\alpha (K_{2}+\varepsilon )}{K_{1}}- \frac{qE}{r_{1} (m_{1}E+m_{2}(K_{1}+\alpha (K_{2}+\varepsilon )+ \varepsilon ) )} \biggr). $$

It follows from (4.2) and (4.7) that

$$ x(t)\leq x(T_{2})\exp \bigl\{ \varUpsilon (t-T_{2}) \bigr\} \rightarrow 0 \quad \text{as } t\rightarrow +\infty . $$

(4.8)

This ends the proof of Theorem 4.1. □

5 Numerical simulations

Example 5.1

Let us take $r_{1}= 1$, $E=1$, $q =1$, $\alpha =K _{1}=K_{2}=m_{2}=1$, $m_{1}=2$. In this case, by simple computation, one could easily see that

$$ 2=r_{1} \biggl(1 +\alpha \frac{K_{2}}{K_{1}} \biggr)> \frac{q}{m_{1}}=\frac{1}{2} $$

(5.1)

and

$$ \frac{1}{4}= \frac{qm_{2}}{Em_{1}^{2}}< \frac{r_{1}}{K_{1}}=1 $$

(5.2)

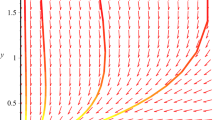
hold, that is, conditions (2.8) and (2.9) in Theorem 2.1 hold, and it follows from Theorems 2.1 and 3.1 that the unique positive equilibrium of the system is globally stable. Numeric simulations (Fig. 1, Fig. 2) also support this assertion.

Figure 1

Numeric simulations of the first component system (5.1), with the initial conditions $(x(0), y(0))=(5,0.1), (4,1), (0.3, 3)$ and $(0.7,2)$, respectively

Figure 2

Numeric simulations of the second component of system (5.1), with the initial conditions $(x(0), y(0))=(5,0.1), (4,1), (0.3, 3)$ and $(0.7,2)$, respectively

Example 5.2

Let us take $r_{1}= 1$, $E=1$, $q =5$, $r_{2}=2$, $\alpha =K_{1}=K_{2}=m_{2}=m_{1}=1$. In this case, by simple computation, one could easily see that

$$ \frac{3}{2}=r_{1} \biggl(1+ \frac{\alpha K_{2}}{K_{1}} \biggr)< \frac{5}{3}= \frac{qE}{m_{1}E+m_{2}(K_{1}+\alpha K_{2})}. $$

(5.3)

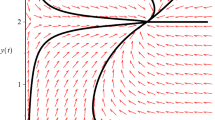
Hence, it follows from Theorem 4.1 that the first species will be driven to extinction, and the second species is globally stable. Numeric simulations (Fig. 3, Fig. 4) also support this assertion.

Figure 3

Numeric simulations of the second component of system (5.1), with the initial conditions $(x(0), y(0))=(5,0.1), (4,1), (0.3, 3)$ and $(0.7,2)$, respectively

Figure 4

Numeric simulations of the second component of system (5.1), with the initial conditions $(x(0), y(0))=(5,0.1), (4,1), (0.3, 3)$ and $(0.7,2)$, respectively

6 Discussion

Discussing the influence of harvesting is one of the main topics in the study of population dynamics, and many scholars (see [30,31,32,33,34,35,36,37,38,39,40]) have done work in this direction. Specially, recently, many scholars (see [30, 33,34,35,36]) studied the ecosystem with nonlinear harvesting term.

Stimulated by the work of [30, 33,34,35,36], in this paper, we try to incorporate the Michaelis–Menten type harvesting term for the first species of a Lotka–Volterra commensalism model, this seems more interesting and necessary, since more and more species become endangered due to the over harvesting by humans. It is natural to ask: Could the commensalism of the second species to the first species could avoid the extinction of the species? Theorem 3.1 shows that if the cooperative intensity is large enough, then the two species could really coexist in a stable state. However, Theorem 4.1 shows that if the cooperative effect is limited, the first species may still be driven to extinction due to the over harvesting.

Our study shows that to ensure the long run existence of the species, the harvesting effort should be limited.