1 Introduction

The aim of this paper is to investigate the dynamic behaviors of the following commensalism model with density dependent birth rate:

$$ \begin{aligned} &\frac{dx}{dt}=x \biggl( \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x+a_{12}y \biggr), \\ &\frac{dy}{dt}=y \biggl( \frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y \biggr), \end{aligned} $$
(1.1)

where \(b_{ij}, i=1, 2, j=1, 2,3, 4\), \(a_{11}\), \(a_{12} \), and \(a_{22}\) are all positive constants. \(x(t)\), \(y(t)\) are the densities of the first and second species at time t, respectively. Here we make the following assumptions:

  1. (a)

    \(\frac{b_{11}}{b_{12}+b_{13}x}\) is the birth rate of the first species which is density dependent, the birth rate of the species is declining as the density of the species is increasing;

  2. (b)

    \(b_{14}\) is the death rate of the first species, \(a_{11}\) is the density dependent coefficient of the first species;

  3. (c)

    \(\frac{b_{21}}{b_{22}+b_{23}y}\) is the birth rate of the second species, it is declining as the density of the species is increasing;

  4. (d)

    \(b_{24}\) is the death rate of the second species, \(a_{22}\) is the density dependent coefficient of the second species;

  5. (e)

    The relationship between the two species is commensalism, i.e., the second species has positive effect on the first species, while the first species has no influence on the second species, we describe such of relationship by using the bilinear function \(a_{12}xy\).

During the last decades, many scholars investigated the dynamic behaviors of the mutualism model or commensalism model [1, 2]. Some essential progress has been made in this direction. Such topics as the stability of the positive equilibrium [1, 3–20], the persistence of the system [21–27], the existence of the positive periodic solution [17, 28–30], the extinction of the species [2, 21, 31], the influence of harvesting [3, 9, 11, 12, 19], the influence of feedback control variables [1, 8, 18, 21, 22, 25, 26], the influence of stage structure [5, 7], etc. have been extensively investigated.

Sun and Wei [4] for the first time proposed and studied the following two species commensalism symbiosis model:

$$ \begin{aligned} & \frac{dx}{dt}=r_{1}x \biggl( \frac{k_{1}-x+\alpha y}{k_{1}} \biggr), \\ & \frac{dy}{dt}=r_{2}y \biggl( \frac{k_{2}-y}{k_{2}} \biggr), \end{aligned} $$
(1.2)

where x and y are the densities of the first and second species at time t, respectively. System (1.2) admits four equilibria \(E_{1}(0, 0), E_{2}(k_{1},0), E_{3}(0, k_{2})\), and \(E_{4}(k_{1}+\alpha k_{2} k_{2})\).

Concerned with the stability property of the above equilibria, Sun and Wei [4] obtained the following result:

Theorem A

\(E_{1}(0, 0), E_{2}(k_{1},0), E_{3}(0, k_{2})\) are all unstable, \(E_{4}(k_{1}+\alpha k_{2}, k_{2})\) is locally stable.

Noting that the authors of [4] did not give any global stability property of the equilibrium, with the aim of putting forward the study in this direction, Han and Chen [18] proposed the following commensalism model:

$$ \begin{aligned} &\frac{dx}{dt}=x (b_{1}-a_{11}x ) +a_{12}xy, \\ &\frac{dy}{dt}=y (b_{2}-a_{22}y ). \end{aligned} $$
(1.3)

System (1.3) admits a positive equilibrium \(P_{0}(x_{0},y_{0})\), where

$$ x_{0}= \frac{b_{1}a_{22}+b_{2}a_{12}}{a_{11}a_{22}},\qquad y_{0}= \frac{b_{2}}{a_{22}}. $$

Concerned with the stability property of this equilibrium, by constructing some suitable Lyapunov function, the authors obtained the following result:

Theorem B

The positive equilibrium \(P_{0}(x_{0},y_{0})\) of system (1.3) is globally stable.

It came to our attention that in system (1.3), if we did not consider the relationship of the two species, then the equations for both species reduce to the traditional logistic equation. For example, the first species takes the form

$$ \frac{dx}{dt}=x (b_{1}-a_{11}x ), $$
(1.4)

where \(b_{1}\) is the intrinsic growth rate and \(a_{11}\) is the density dependent coefficient. System (1.4) could be revised as

$$ \frac{dx}{dt}=x (b_{11}-b_{14}-ex ), $$
(1.5)

where \(b_{11}\) is the birth rate of the species and \(b_{14}\) is the death rate of the species. Already, Brauer and Castillo-Chavez [32], Tang and Chen [33], Berezansky et al. [34] have showed that in some cases the density dependent birth rate of the species is more suitable. If we take the famous Beverton–Holt function [34] as the birth rate, then system (1.5) should be revised to

$$ \frac{dx}{dt}=x \biggl(\frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x \biggr). $$
(1.6)

Similarly, the second species could be expressed as follows:

$$ \frac{dy}{dt}=y \biggl(\frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y \biggr). $$
(1.7)

(1.6), (1.7) together with the cooperation relationship between the species will lead to system (1.1).

As far as system (1.1) is concerned, one interesting issue is to find out the influence of the nonlinear density birth rate. Is it possible for system (1.1) to admit some similar dynamic behaviors as those of systems (1.2) and (1.3), or does system (1.1) admit some new characteristic property?

The aim of this paper is to find out the answers to the issues above. The rest of the paper is arranged as follows. In Sect. 2, we investigate the stability property of the equilibria of system (1.1); Sect. 3 presents some numerical simulations to show the feasibility of the main results. We end this paper with a brief discussion.

2 Global asymptotic stability

We first establish a lemma, which is useful for proving the main result.

Lemma 2.1

Consider the following equation:

$$ \frac{dy}{dt}= y \biggl(\frac{a}{b+cy}-d-ey \biggr). $$
(2.1)

Assume that \(a>bd\), then the unique positive equilibrium \(y^{*} \) of system (2.1) is globally asymptotically stable.

Proof

Set

$$ F(y)= \frac{a}{b+cy}-d-ey. $$

Since \(a>bd\), it follows that \(F(0)= \frac{a}{b}-d>0\). Also,

$$ \frac{dF(y)}{dy}=-\frac{ac}{(b+cy)^{2}}-e< 0, $$

hence \(F(y)\) is a strictly decreasing function. One could easily see that \(F(+\infty )=-\infty \), thus there exists a unique positive solution \(y^{*}\) such that \(F(y^{*})=0\). Indeed,

$$ y^{*}= \frac{-(eb+dc)+\sqrt{(eb+dc)^{2}-4ec(db-a)}}{2ec}. $$
(2.2)

The above analysis shows that

  1. (1)

    There is \(y^{*}\), as expressed by (2.2), such that \(F(y^{*}) = 0\);

  2. (2)

    For all \(y^{*} > y > 0, F(y)= \frac{a}{b+cy}-d-ey > 0\);

  3. (3)

    For all \(y > y^{*} > 0, F(y)= \frac{a}{b+cy}-d-ey < 0\).

Now let us consider the Lyapunov function

$$ V=y-y^{*}-y^{*}\ln \frac{y}{y^{*}}. $$

Direct calculation shows that

$$ \frac{dV}{dt}=\bigl(y-y^{*}\bigr)F(y)< 0. $$

Thus, \(y^{*}\) is globally asymptotically stable. This ends the proof of Lemma 2.1. □

Now we are in a position to consider the existence and stability property of the equilibria of system (1.1). The equilibrium of system (1.1) is determined by the equation

$$ \begin{aligned} &x \biggl( \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x+a_{12}y \biggr)=0, \\ &y \biggl( \frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y \biggr)=0. \end{aligned} $$
(2.3)

System (1.1) always admits a boundary equilibrium \(A_{1}(0,0)\). Assume that

$$ \frac{b_{11}}{b_{12}}>b_{14} $$
(2.4)

holds, then

$$ \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x=0 $$

admits a unique positive solution \(x^{*}\), where

$$ x^{*}= \frac{-(b_{14}b_{13}+a_{11}b_{12})+\sqrt{(b_{14}b_{13}+a_{11}b_{12})^{2}-4a_{11}b_{13}(b_{14}b_{12}-b_{11})}}{2a_{11}b_{13}}. $$
(2.5)

Assume that (2.4) and

$$ \frac{b_{21}}{b_{22}}< b_{24} $$
(2.6)

hold, then system (1.1) admits the nonnegative boundary equilibrium \(A_{2}(x^{*},0)\). Assume that

$$ \frac{b_{21}}{b_{22}}>b_{24} $$
(2.7)

holds, then

$$ \frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y=0 $$

admits a unique positive solution \(y^{*}\), where

$$ y^{*}= \frac{-(b_{24}b_{23}+a_{22}b_{22})+\sqrt{(b_{24}b_{23}+a_{22}b_{22})^{2}-4a_{22}b_{23}(b_{24}b_{22}-b_{21})}}{2a_{22}b_{23}}. $$
(2.8)

Assume that (2.7) and

$$ \frac{b_{11}}{b_{12}}+a_{12}y^{*}< b_{14} $$
(2.9)

hold, then system (1.1) admits the nonnegative boundary equilibrium \(A_{3}(0,y^{*})\). Assume that (2.7) and

$$ \frac{b_{11}}{b_{12}}+a_{12}y_{1}>b_{14} $$
(2.10)

hold, then system (1.1) admits the unique positive equilibrium \(A_{4}(x_{1},y_{1})\), where

$$ y_{1}= \frac{-(b_{24}b_{23}+a_{22}b_{22})+\sqrt{(b_{24}b_{23}+a_{22}b_{22})^{2}-4a_{22}b_{23}(b_{24}b_{22}-b_{21})}}{2a_{22}b_{23}}, $$
(2.11)

and \(x_{1}\) is the unique positive solution of the equation

$$ \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x+a_{12}y_{1}=0. $$
(2.12)

Remark 2.1

From the above discussion, one could easily see that the inequalities

$$ \frac{b_{11}}{b_{12}}>b_{14} $$
(2.13)

and

$$ \frac{b_{21}}{b_{22}}>b_{24} $$
(2.14)

is enough to ensure the existence of the unique positive equilibrium of system (1.1).

Concerned with the stability property of the above four nonnegative equilibria, we have the following result.

Theorem 2.1

  1. (1)

    Assume that (2.7) and (2.10) hold, then system (1.1) admits a unique positive equilibrium \(A_{4}(x_{1},y_{1})\), which is globally asymptotically stable;

  2. (2)

    Assume that (2.7) and (2.9) hold, then the boundary equilibrium \(A_{3}(0,y^{*})\) is globally asymptotically stable;

  3. (3)

    Assume that (2.4) and (2.6) hold, then the boundary equilibrium \(A_{2}(x^{*},0)\) is globally asymptotically stable;

  4. (4)

    Assume that

    $$ b_{11}< b_{12}b_{14} $$
    (2.15)

    and (2.6) hold, then the boundary equilibrium \(A_{1}(0,0)\) is globally asymptotically stable.

Remark 2.2

Conditions (2.7) and (2.10) are necessary to ensure that system (1.1) admits a positive equilibrium. Hence, it follows from Theorem 2.1(1) that if system (1.1) admits a positive equilibrium, it is globally asymptotically stable.

Remark 2.3

From Remark 2.2 it immediately follows that under the assumption that (2.13) and (2.14) hold, system (1.1) admits a unique globally asymptotically stable positive equilibrium.

Proof of Theorem 2.1

(1) Obviously, \(x_{1}\), \(y_{1}\) satisfy the equations

$$ \begin{aligned} & \frac{b_{11}}{b_{12}+b_{13}x_{1}}-b_{14}-a_{11}x_{1}+a_{12}y_{1} =0, \\ &\frac{b_{21}}{b_{22}+b_{23}y_{1}}-b_{24}-a_{22}y_{1} =0. \end{aligned} $$
(2.16)

Now let us consider the Lyapunov function

$$ V_{1}(x,y)= \frac{a_{11}a_{22}}{a_{12}^{2}} \biggl(x-x_{1}-x_{1} \ln \frac{x}{x_{1}} \biggr)+\frac{1}{4} \biggl(y-y_{1}-y_{1} \ln \frac{y}{y_{1}} \biggr). $$
(2.17)

One could easily see that the function \(V_{1}\) is zero at the positive equilibrium \(A_{4}(x_{1}, y_{1})\) and is positive for all other positive values of x, y. By applying (2.16), the time derivative of \(V_{1}\) along the trajectories of (1.1) is

$$\begin{aligned} D^{+}V_{1}(t)&= \frac{a_{11}a_{22}}{a_{12}^{2}} (x-x_{1}) \biggl( \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x+a_{12}y \biggr) \\ &\quad {}+ \frac{1}{4}(y-y_{1}) \biggl( \frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y \biggr) \\ &= \frac{a_{11}a_{22}}{a_{12}^{2}} (x-x_{1}) \biggl( \frac{b_{11}}{b_{12}+b_{13}x}- \frac{b_{11}}{b_{12}+b_{13}x_{1}} \\ &\quad {} +a_{11}x_{1}-a_{12}y_{1}-a_{11}x+a_{12}y \biggr) \\ &\quad {} + \frac{1}{4}(y-y_{1}) \biggl( \frac{b_{21}}{b_{22}+b_{23}y}- \frac{b_{21}}{b_{22}+b_{23}y_{1}}+a_{22}y_{1}-a_{22}y \biggr) \\ &= \frac{a_{11}a_{22}}{a_{12}^{2}} (x-x_{1}) \biggl( \frac{b_{11}b_{13}(x_{1}-x)}{(b_{12}+b_{13}x)(b_{12}+b_{13}x_{1})} \\ &\quad {} +a_{11}(x_{1}-x)+a_{12}(y-y_{1}) \biggr) \\ &\quad {} + \frac{1}{4}(y-y_{1}) \biggl( \frac{b_{21}b_{23}(y_{1}-y)}{(b_{22}+b_{23}y)(b_{22}+b_{23}y_{1})}+a_{22}(y_{1}- y) \biggr) \\ &= - \frac{a_{11}a_{22}}{a_{12}^{2}} \frac{b_{11}b_{13} }{(b_{12}+b_{13}x)(b_{12}+b_{13}x_{1})} (x-x_{1})^{2} \\ &\quad {}- \frac{a_{11}^{2}a_{22}}{a_{12}^{2}} (x-x_{1})^{2}+ \frac{a_{11}a_{22}}{a_{12}}(x-x_{1}) (y-y_{1}) \\ &\quad {}- \frac{1}{4} \frac{b_{21}b_{23}}{(b_{22}+b_{23}y)(b_{22}+b_{23}y_{1})}(y-y_{1})^{2} -\frac{1}{4}a_{22}(y- y_{1})^{2} \\ &= - \frac{a_{11}a_{22}}{a_{12}^{2}} \frac{b_{11}b_{13} }{(b_{12}+b_{13}x)(b_{12}+b_{13}x_{1})} (x-x_{1})^{2} \\ &\quad {}- \frac{1}{4} \frac{b_{21}b_{23}}{(b_{22}+b_{23}y)(b_{22}+b_{23}y_{1})}(y-y_{1})^{2} \\ &\quad {}-a_{22} \biggl[ \frac{a_{11}}{a_{12}} (x-x_{1})- \frac{1}{2}(y- y_{1}) \biggr]^{2}. \end{aligned}$$
(2.18)

It then follows from (2.18) that \(D^{+}V_{1}(t)<0\) strictly for all \(x, y>0\) except the positive equilibrium \(A_{4}(x_{1}, y_{1})\), where \(D^{+}V_{1}(t)=0\). Thus, \(V_{1}(x,y)\) satisfies Lyapunov’s asymptotic stability theorem [35], and the positive equilibrium \(A_{4}(x_{1}, y_{1})\) of system (1.1) is globally asymptotically stable.

(2) Inequality (2.9) implies that for enough small positive constant ε, one has

$$ \frac{b_{11}}{b_{12}}+a_{12}\bigl(y^{*}+\varepsilon \bigr)< b_{14} $$
(2.19)

holds. Obviously, \(y^{*}\) satisfies the equation

$$ \frac{b_{21}}{b_{22}+b_{23}y^{*}}-b_{24}-a_{22}y^{*} =0. $$
(2.20)

Also, it follows from Lemma 2.1 that the unique positive equilibrium \(y^{*}\) of system

$$ \frac{dy}{dt}= y \biggl( \frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y \biggr) $$
(2.21)

is globally asymptotically stable. That is,

$$ \lim_{t\rightarrow +\infty }y(t)=y^{*}. $$

Hence, for ε satisfies (2.19), there exists enough large \(T_{1}\) such that

$$ y(t)< y^{*}+\varepsilon \quad \mbox{for all } t\geq T_{1}. $$
(2.22)

Now let us consider the Lyapunov function

$$ V_{2}(x,y)= x+ \biggl(y-y^{*}-y^{*}\ln \frac{y}{x^{*}} \biggr). $$
(2.23)

One could easily see that the function \(V_{2}\) is zero at the boundary equilibrium \(A_{3}(0, y^{*})\) and is positive for all other positive values of x, y. By applying (2.20) and (2.23), for \(t>T_{1}\), the time derivative of \(V_{2}\) along the trajectories of (1.1) is

$$\begin{aligned} D^{+}V_{2}(t) &= x \biggl( \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x+a_{12}y \biggr) \\ &\quad {} +\bigl(y-y^{*}\bigr) \biggl( \frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y \biggr) \\ &\leq x \biggl( \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x+a_{12} \bigl(y^{*}+\varepsilon \bigr) \biggr) \\ &\quad {} +\bigl(y-y^{*}\bigr) \biggl( \frac{b_{21}}{b_{22}+b_{23}y}- \frac{b_{21}}{b_{22}+b_{23}y^{*}}+a_{22}y^{*}-a_{22}y \biggr) \\ &\leq x \biggl( \frac{b_{11}}{b_{12} }-b_{14}+a_{12} \bigl(y^{*}+\varepsilon \bigr) \biggr)-a_{11}x^{2} \\ & \quad{}- \biggl( \frac{b_{21}b_{23}}{(b_{22}+b_{23}y)(b_{22}+b_{23}y^{*})}+a_{22} \biggr) \bigl(y-y^{*}\bigr)^{2}. \end{aligned}$$
(2.24)

It then follows from (2.19) that \(D^{+}V_{2}(t)<0\) strictly for all \(x, y>0\) except the boundary equilibrium \(A_{3}(0, y^{*})\), where \(D^{+}V_{2}(t)=0\). Thus, \(V_{2}(x,y)\) satisfies Lyapunov’s asymptotic stability theorem [35], and the boundary equilibrium \(A_{3}(0, y^{*})\) of system (1.1) is globally asymptotically stable.

(3) Obviously, \(x^{*}\) satisfies the equation

$$ \begin{aligned} \frac{b_{11}}{b_{12}+b_{13}x^{*}}-b_{14}-a_{11}x^{*} =0. \end{aligned} $$
(2.25)

Now let us consider the Lyapunov function

$$ V_{3}(x,y)= \frac{a_{11}a_{22}}{a_{12}^{2}} \biggl(x-x^{*}-x^{*} \ln \frac{x}{x^{*}} \biggr)+\frac{1}{4}y. $$
(2.26)

One could easily see that the function \(V_{3}\) is zero at the boundary equilibrium \(A_{2}(x^{*}, 0)\) and is positive for all other positive values of x, y. By applying (2.25), the time derivative of \(V_{3}\) along the trajectories of (1.1) is

$$\begin{aligned} D^{+}V_{3}(t) &= \bigl(x-x^{*}\bigr) \frac{a_{11}a_{22}}{a_{12}^{2}} \biggl( \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x+a_{12}y \biggr) \\ &\quad {} + \frac{1}{4}y \biggl( \frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y \biggr) \\ &\leq \bigl(x-x^{*}\bigr) \frac{a_{11}a_{22}}{a_{12}^{2}} \biggl( \frac{b_{11}}{b_{12}+b_{13}x}- \frac{b_{11}}{b_{12}+b_{13}x^{*}}+a_{11}x^{*}-a_{11}x \biggr) \\ &\quad {} + \frac{a_{11}a_{22}}{a_{12}}\bigl(x-x^{*}\bigr)y + \frac{1}{4}y \biggl( \frac{b_{21}}{b_{22}}-b_{24} \biggr)- \frac{1}{4}a_{22}y^{2} \\ &= - \frac{a_{11}a_{22}}{a_{12}^{2}} \frac{b_{11}b_{13}}{(b_{12}+b_{13}x^{*})(b_{12}+b_{13}x)}\bigl(x-x^{*} \bigr)^{2}+ \frac{1}{4}y \biggl( \frac{b_{21}}{b_{22}}-b_{24} \biggr) \\ & \quad{}-a_{22} \biggl[ \frac{a_{11}}{a_{12}} (x-x_{1})- \frac{1}{2}y \biggr]^{2}. \end{aligned}$$
(2.27)

It then follows from (2.6) that \(D^{+}V_{3}(t)<0\) strictly for all \(x, y>0\) except the boundary equilibrium \(A_{2}(x^{*}, 0)\), where \(D^{+}V_{3}(t)=0\). Thus, \(V_{3}(x,y)\) satisfies Lyapunov’s asymptotic stability theorem [35], and the boundary equilibrium \(A_{2}(x^{*}, 0)\) of system (1.1) is globally asymptotically stable.

(4) Now let us consider the Lyapunov function

$$ V_{4}(x,y)= \frac{a_{11}a_{22}}{a_{12}^{2}} x+ \frac{1}{4}y. $$
(2.28)

One could easily see that the function \(V_{4}\) is zero at the boundary equilibrium \(A(0, 0)\) and is positive for all other positive values of x, y. The time derivative of \(V_{4}(x,y)\) along the trajectories of (1.1) is

$$\begin{aligned} D^{+}V_{4}(t)&= \frac{a_{11}a_{22}}{a_{12}^{2}} x \biggl( \frac{b_{11}}{b_{12}+b_{13}x}-b_{14}-a_{11}x+a_{12}y \biggr) \\ &\quad {} + \frac{1}{4} y \biggl( \frac{b_{21}}{b_{22}+b_{23}y}-b_{24}-a_{22}y \biggr) \\ &\leq \frac{a_{11}a_{22}}{a_{12}^{2}} x \biggl( \frac{b_{11}}{b_{12}}-b_{14} \biggr)- \frac{a_{11}^{2}a_{22}}{a_{12}^{2}} x^{2}+ \frac{a_{11}a_{22}}{a_{12}}xy \\ &\quad {} + \frac{1}{4} y \biggl( \frac{b_{21}}{b_{22} }-b_{24} \biggr)-\frac{1}{4}a_{22}y^{2} \\ &= \frac{a_{11}a_{22}}{a_{12}^{2}} \biggl( \frac{b_{11}}{b_{12}}-b_{14} \biggr) x -a_{22} \biggl[ \frac{a_{11}}{a_{12}} x-\frac{1}{2}y \biggr]^{2} + \frac{1}{4} y \biggl( \frac{b_{21}}{b_{22} }-b_{24} \biggr). \end{aligned}$$
(2.29)

It then follows from (2.6) and (2.15) that \(D^{+}V_{4}(t)<0\) strictly for all \(x, y>0\) except the boundary equilibrium \(A_{1}(0, 0)\), where \(D^{+}V_{4}(t)=0\). Thus, \(V_{4}(x,y)\) satisfies Lyapunov’s asymptotic stability theorem [35], and the boundary equilibrium \(A_{1}(0, 0)\) of system (1.1) is globally asymptotically stable.

This ends the proof of Theorem 2.1. □

3 Numeric simulations

Now let us consider the following four examples.

Example 3.1

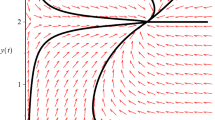
$$ \begin{aligned} &\frac{dx}{dt}=x \biggl( \frac{1}{2+x}-1- x+ y \biggr), \\ & \frac{dy}{dt}=y \biggl( \frac{1}{2+y}-1- y \biggr). \end{aligned} $$
(3.1)

In this system, corresponding to system (1.1), we take \(b_{11}=b_{13}=b_{14}=a_{11}=a_{12}=b_{21}=b_{23}=b_{24}=a_{22}=1, b_{12}=b_{22}=2\). Since \(b_{11}< b_{12}b_{14}, b_{21}< b_{22}b_{24}\), it follows from Theorem 2.1(4) that the boundary equilibrium \(A_{1}(0,0)\) is globally asymptotically stable. Figure 1 supports this assertion.

Figure 1
figure 1

Dynamic behaviors of system (3.1) with the initial condition \((x(0),y(0)) =(1,0.3),(0.4,2),(0.02,2),(1, 2)\), and \((0.1,2)\), respectively

Full size image

Example 3.2

$$ \begin{aligned} & \frac{dx}{dt}=x \biggl( \frac{2}{1+x}-1- x+ y \biggr), \\ &\frac{dy}{dt}=y \biggl( \frac{2}{1+y}-1- y \biggr). \end{aligned} $$
(3.2)

In this system, corresponding to system (1.1), we take \(b_{12}=b_{13}=b_{14}=a_{11}=a_{12}=b_{22}=b_{23}=b_{24}=a_{22}=1, b_{11}=b_{21}=2\). Since \(b_{11}>b_{12}b_{14}, b_{21}>b_{22}b_{24}\), it follows from Remark 2.3 that the unique positive equilibrium \(A_{4}(0.4142,0.6364)\) is globally asymptotically stable. Figure 2 supports this assertion.

Figure 2
figure 2

Dynamic behaviors of system (3.2) with the initial condition \((x(0),y(0)) =(1,0.3),(0.4,2),(0.02,2),(1, 2)\), and \((0.1,2)\), respectively

Full size image

Example 3.3

$$ \begin{aligned} &\frac{dx}{dt}=x \biggl( \frac{2}{1+x}-1- x+ y \biggr), \\ &\frac{dy}{dt}=y \biggl( \frac{1}{2+y}-1- y \biggr). \end{aligned} $$
(3.3)

In this system, corresponding to system (1.1), we take \(b_{12}=b_{13}=b_{14}=a_{11}=a_{12}=b_{21}=b_{23}=b_{24}=a_{22}=1, b_{11}=b_{22}=2\). Since \(b_{11}>b_{12}b_{14}, b_{21}< b_{22}b_{24}\), that is, inequalities (2.4) and (2.6) hold, it follows from Theorem 2.1(3) that the boundary equilibrium \(A_{2}(0.4142,0)\) is globally asymptotically stable. Figure 3 supports this assertion.

Figure 3
figure 3

Dynamic behaviors of system (3.3) with the initial condition \((x(0),y(0)) =(1,0.3),(0.4,2),(0.02, 2),(1, 2)\), and \((0.1,2)\), respectively

Full size image

Example 3.4

$$ \begin{aligned} &\frac{dx}{dt}=x \biggl( \frac{1}{2+x}-1- x+ y \biggr), \\ &\frac{dy}{dt}=y \biggl( \frac{2}{1+y}-1- y \biggr). \end{aligned} $$
(3.4)

In this system, corresponding to system (1.1), we take \(b_{11}=b_{13}=b_{14}=a_{11}=a_{12}=b_{22}=b_{23}=b_{24}=a_{22}=1, b_{12}=b_{21}=2\). Since \(b_{11}< b_{12}b_{14}, b_{21}>b_{22}b_{24}\), that is, inequalities (2.7) and (2.9) hold, it follows from Theorem 2.1(2) that the boundary equilibrium \(A_{2}(0, 0.4142)\) is globally asymptotically stable. Figure 4 supports this assertion.

Figure 4
figure 4

Dynamic behaviors of system (3.4) with the initial condition \((x(0),y(0)) =(0.4,1),(1,0.3),(0.02,1),(1, 1)\), and \((1,0.1)\), respectively

Full size image

4 Discussion

Recently, many scholars have studied the dynamic behaviors of the commensal symbiosis model [13–31]. All of the works of [13–31] are based on the traditional logistic model, as was showed in the introduction section. Especially, Han and Chen [18] showed that the unique positive equilibrium \(P_{0}(x_{0},y_{0})\) of system (1.3) is globally asymptotically stable (see Theorems A and B in the Introduction section for more details), this means that all other equilibria of system (1.3) are unstable.

In this paper, we argued that the birth rate of the species may be density dependent; indeed, this is one of the phenomena that could be observed in the nature and society. We propose system (1.1). Theorem 2.1 shows that under some suitable assumptions, all of the four equilibria may be globally asymptotically stable. That is, with introduction of the density dependent birth rate, the dynamic behaviors of the system become complicated. Such kind of phenomenon is not observed in [13–31].

Our study shows that the birth rate is one of the essential factors in determining the dynamic behaviors of the species. To control the number of the species, maybe one of the useful methods is to control the birth rate of the species.