Hopf-zero bifurcation of Oregonator oscillator with delay

Abstract

In this paper, we study the Hopf-zero bifurcation of Oregonator oscillator with delay. The interaction coefficient and time delay are taken as two bifurcation parameters. Firstly, we get the normal form by performing a center manifold reduction and using the normal form theory developed by Faria and Magalhães. Secondly, we obtain a critical value to predict the bifurcation diagrams and phase portraits. Under some conditions, saddle-node bifurcation and pitchfork bifurcation occur along M and N, respectively; Hopf bifurcation and heteroclinic bifurcation occur along H and S, respectively. Finally, we use numerical simulations to support theoretical analysis.

1 Introduction

An oscillatory chemical reaction refers to the reaction system of certain antileather concentration showing relatively stable cyclical changes. In 1921, Bray achieved a liquid oscillatory reaction in the experiment. In 1964, Zhabotinsky reported some other oscillatory reactions of this nature [14, 15, 21]. Until the 1970s, Field, Koros, and Noyes proposed the Oregonator model based on an in-depth study of the BZ reaction. According to Field and Noyes, the BZ reaction is simplified. In 1979, Tyson assumed that the concentration of the reactants $A=[\mathrm {BrO}_{3}^{-}]$ and $B=[\mathrm{BrCH(COOH)}_{2}]$ is independent of time. Therefore we can give the following reactant concentration equation:

$$\textstyle\begin{cases} \frac{dP}{dt}=k_{3}AQ-k_{2}PQ+k_{5}AP-2k_{4}P^{2} , \\ \frac{dQ}{dt}=k_{3}AQ-k_{2}PQ+\frac{1}{2}fk_{0}BW, \\ \frac{dW}{dt}=2k_{5}AP-k_{0}BW, \end{cases} $$

where $P=[\mathrm{HBrO}_{2}]$, $Q=[\mathrm{Br}]$, $W=[\mathrm {Ce(IV)}]$. We will make the following changes in this system:

$$x=\alpha{P},\qquad y=\beta{Q},\qquad z=\gamma{W},\qquad t=\delta{T}, $$

where

$$\begin{aligned} &\alpha\approx\frac{2k_{4}}{k_{3}A}\approx10^{6}~(\mathrm {mol/L})^{-1},\qquad \beta=\frac{k_{2}}{k_{3}A}\approx2\times 10^{7}~(\mathrm{mol/L})^{-1}, \\ &\gamma\approx\frac{k_{4}k_{5}B}{(k_{3}A)^{3}}\approx20~(\mathrm {mol/L})^{-1},\qquad \delta=k_{5}B\approx4\times10^{-3}~\mathrm{s}^{-1}. \end{aligned}$$

So we can obtain another form of the Oregonator oscillator, the so-called Tyson-type oscillator:

$$\textstyle\begin{cases} \varepsilon\frac{dx}{dt}=qy-xy+x(1-x), \\ \delta\frac{dy}{dt}=-qy-xy+h_{1}z, \\ \frac{dz}{dt}=x-z, \end{cases} $$

where

$$\varepsilon=\frac{k_{5}B}{k_{3}A}\approx4\times10^{-2},\qquad \delta= \varepsilon\frac{\alpha}{\beta}\approx2\times10^{-6},\qquad q= \frac{2k_{1}k_{4}}{k_{2}k_{3}}\approx10^{-5},\qquad h_{1}=2h_{1}. $$

Because δ is much smaller than ε, the second formula in the system can be approximated as

$$y\approx\frac{h_{1}z}{q+x}. $$

This yields a simplified two-dimensional Oregonator model [27] with respect to x and z:

$$ \textstyle\begin{cases} \varepsilon\frac{dx}{dt}=x(1-x)-h_{1}z\frac{x-q}{x+q} , \\ \frac{dz}{dt}=x-z, \end{cases} $$

(1.1)

where $x=[\mathrm{HBrO}_{2}]$, $z=\mathrm{Ce(IV)}$.

When electric current is applied, the catalyst Ce(IV) is perturbed, and other species are not affected (see [15]). Since the perturbation term is introduced in the equation $\frac{dz}{dt}=x-z$, we rewrite this equation in the following form:

$$\frac{dz}{dt}=x-z+kz(t-\tau). $$

We consider the Oregonator model with delay:

$$ \textstyle\begin{cases} \varepsilon\frac{dx}{dt}=x(1-x)-h_{1}z\frac{x-q}{x+q}, \\ \frac{dz}{dt}=x-z+kz(t-\tau), \end{cases} $$

(1.2)

where $\varepsilon=4\times10^{-2}$, $\delta=4\times10^{-4}$, $q=8\times 10^{-4}$, and $h_{1}\in(0,1)$ is an adjustable parameter.

Nowadays, many scholars study the Hopf bifurcation or Hopf-zero bifurcation in delay differential equations, and some results have been obtained (see [1, 2, 4, 5, 7,8,9,10, 12, 13, 17, 19, 22, 24, 26,27,28,29]). However, to the best of our knowledge, there are no studies on the Hopf-zero bifurcation of Oregonator oscillator with time delay. Therefore, it is the far-reaching significance to research the Hopf-zero bifurcation of Oregonator model.

The remainder of the paper is organized as follows. In Sect. 2, we provide stability and conditions of existence of the Hopf-zero bifurcation by taking the interaction coefficient and delay as two parameters. In Sect. 3, we use the center manifold theory and normal form method [6, 23] to investigate the Hopf-zero bifurcation with original parameters. In Sect. 4, we give several numerical simulations to support the analytic results. Finally, we draw the conclusion in Sect. 5.

2 Stability and existence of Hopf-zero bifurcation

Let $(x,z)$ be an equilibrium point of system (1.2). Obviously,

$$\textstyle\begin{cases} x(1-x)-h_{1}z\frac{x-q}{x+q}=0, \\ z=\frac{x}{1-k}. \end{cases} $$

Then we have

$$ x(1-x)-\frac{h_{1}}{1-k}x\frac{x-q}{x+q}=0. $$

(2.1)

There are three roots $x=0$, $x=x_{+}$, and $x=x_{-}$ of Eq. (2.1), where

$$ x_{\pm}=\frac{1-\frac{h_{1}}{1-k}-q\pm\sqrt{(1-\frac {h_{1}}{1-k}-q)^{2}+4q(1+\frac{h_{1}}{1-k})}}{2}. $$

(2.2)

Therefore we obtain that system (1.2) has three steady-state solutions, $(x_{-},z_{-})$, $(0,0)$, and $(x_{+},z_{+})$.

Obviously, there is a unique positive steady state.

Theorem 2.1

For any $\varepsilon>0$, $q>0$, and $h_{1}>0$, $(x_{+},z_{+})$ is the unique positive steady state of system (1.2).

Proof

Let $H(x)=x(1-x)-\frac{h_{1}}{1-k}x\frac{x-q}{x+q}$. From (2.1) and (2.2) we get that only $x_{+}$ satisfies $H(x)=0$, $H(x)>0$ for $0< x< x_{+}$, and $H(x)<0$ for $x>x_{+}$. Furthermore, we have $H(x_{+})=0$ and $H'(x_{+})<0$. □

We further mainly study the dynamics of the equilibrium point $(x_{+},z_{+})$. If the characteristic equation of system (1.2) has a simple pair of purely imaginary eigenvalues $\pm{i\omega}$, a simple root 0, and all other roots of the characteristic equation have negative real parts, then the Hopf-zero bifurcation will occur. Let $x=x-x_{+}$ and $z=z-z_{+}$. Then we can vary (1.2) as the following equivalent system:

$$ \textstyle\begin{cases} \frac{dx}{dt}=\frac{1}{\varepsilon }((x+x_{+})(1-x-x_{+})-h_{1}(z+z_{+})\frac{(x+x_{+})-q}{(x+x_{+})+q}),\\ \frac{dz}{dt}=x-z+kz(t-\tau). \end{cases} $$

(2.3)

The linearization equation of system (2.3) at $(0,0)$ is

$$ \textstyle\begin{cases} \frac{dx}{dt}=a_{1}x+a_{2}z, \\ \frac{dz}{dt}=x-z+kz(t-\tau), \end{cases} $$

(2.4)

where $a_{1}=\frac{1}{\varepsilon}(\frac {-2qh_{1}z_{+}}{(q+x_{+})^{2}}+1-2x_{+})$ and $a_{2}=\frac {1}{\varepsilon}\frac{qh_{1}-h_{1}x_{+}}{q+x_{+}}$. The characteristic equation of system (2.4) is

$$ E(\lambda)=\lambda^{2}-b_{1}\lambda-b_{2}-k \lambda{e}^{-\lambda\tau }+ka_{1}e^{-\lambda\tau}=0, $$

(2.5)

where $b_{1}=a_{1}-1$ and $b_{2}=a_{1}+a_{2}$.

If $\lambda=0$ is the root of Eq. (2.5), then $ka_{1}-b_{2}=0$. If $\tau=0$, then system (2.5) becomes

$$E(\lambda)=\lambda^{2}-(b_{1}+k)\lambda=0. $$

Therefore we obtain that if $\tau=0$ and $b_{1}+k<0$, then excluding a single zero eigenvalue, all the roots of Eq. (2.5) have negative real parts.

Next, we consider the case of $\tau\neq0$. Let iω with $\omega >0$ be a root of $\lambda^{2}-b_{1}\lambda-b_{2}-k\lambda{e}^{-\lambda \tau}+ka_{1}e^{-\lambda\tau}=0$. Then

$$-\omega^{2}-b_{1}i\omega-b_{2}-ki \omega{e}^{-i\omega\tau }+ka_{1}e^{-i\omega\tau}=0. $$

Separating the real and imaginary parts, we get

$$ \textstyle\begin{cases} -\omega^{2}-b_{2}=k\omega\sin\omega\tau-ka_{1}\cos\omega\tau, \\ -b_{1}\omega=k\omega\cos\omega\tau+ka_{1}\sin\omega\tau. \end{cases} $$

(2.6)

It follows that ω satisfies

$$ \omega^{4}+\bigl(2b_{2}+b_{1}^{2}-k^{2} \bigr)\omega^{2}+b_{2}^{2}-k^{2}a_{1}^{2}=0. $$

(2.7)

Suppose $m_{1}=\omega^{2}$ and denote $u_{1}=2b_{2}+b_{1}^{2}-k^{2}$, $r_{1}=b_{2}^{2}-k^{2}a_{1}^{2}$. Then Eq. (2.7) becomes

$$ m_{1}^{2}+u_{1}m_{1}+r_{1}=0. $$

(2.8)

Following [27], we consider the following cases:

(B1):

$r_{1}<0$.

Then we find that system (2.5) has a unique positive root $m_{1}=\frac {-u_{1}+\sqrt{u_{1}^{2}-4r_{1}}}{2}$.

(B2):

$r_{1}>0$, $u_{1}>0$.

Then system (2.5) has no positive root.

(B3):

$r_{1}>0$, $u_{1}<0$.

In this case, if system (2.5) has real positive roots, then $|k|$ is very large, and h is infinitely close to one, which is a contradiction.

Theorem 2.2

For the quadratic Eq. (2.8), we have:

• (i) if $r_{1}<0$, then Eq. (2.5) has a unique positive root $m_{1}=\frac{-u_{1}+\sqrt{u_{1}^{2}-4r_{1}}}{2}$.

• (ii) if $r_{1}>0$, then Eq. (2.5) has no positive root.

Suppose that Eq. (2.8) has positive roots. Without loss of generality, we assume that it has a positive root defined by m. Then Eq. (2.7) has a positive root ω, and ω must satisfy the equation

$$\biggl(\frac{\omega^{2}+a_{1}b_{2}}{k(\omega^{2}+a_{1}^{2})}\biggr)^{2}+\biggl(\frac {\omega^{3}+\omega(a_{1}^{2}+a_{2})}{k(\omega^{2}+a_{1}^{2})} \biggr)^{2}=1. $$

According to system (2.6), we obtain

$$\begin{aligned} &\cos(\omega\tau)=\frac{\omega^{2}+a_{1}b_{2}}{k(\omega^{2}+a_{1}^{2})}, \\ & \sin(\omega\tau)=-\frac{\omega^{3}+\omega(a_{1}^{2}+a_{2})}{k(\omega^{2}+a_{1}^{2})}. \end{aligned}$$

Denote

$$\tau_{j}= \textstyle\begin{cases} \frac{1}{\omega}(\arccos\beta_{1}+2j\pi), & \alpha_{1}\geq0,\\ \frac{1}{\omega}(2\pi-\arccos\beta_{1}+2j\pi),& \alpha_{1}\leq0, \end{cases} $$

where $\beta_{1}=\frac{\omega^{2}+a_{1}b_{2}}{k(\omega ^{2}+a_{1}^{2})}$, $\alpha_{1}=-\frac{\omega^{3}+\omega (a_{1}^{2}+a_{2})}{k(\omega^{2}+a_{1}^{2})}$, $j=0,1,2,\dots$. Then system (2.5) has a pair of purely imaginary roots $\pm{i}\omega$ with $\tau=\tau_{j}$, and $\tau=\tau_{j}, j=0,1,2,\ldots$ , satisfy the equation $\sin(\omega\tau)>0$.

We get $k<0$ when $(B1)$ holds, and then

$$\tau_{j}=\frac{1}{\omega}(\arccos\beta_{1}+2j\pi),\quad j\in \{0,1,2,\ldots\}. $$

We obtain the transversality conditions as follows.

Theorem 2.3

If $r<0$, then $\frac{d\operatorname{Re}\{\lambda(\tau_{j})\}}{d\tau}\neq0$.

Proof

Substituting $\lambda(\tau)$, $\tau=\tau_{j}$, into Eq. (2.5), we get

$$\frac{d\lambda}{d\tau}=\frac{\lambda{k}a_{1}{e}^{-\lambda\tau}-k\lambda ^{2}{e}^{-\lambda\tau}}{2\lambda-b_{1}\lambda+\tau{k}\lambda {e}^{-\lambda\tau}-k{e}^{-\lambda\tau}-\tau{a}_{1}\lambda{e}^{-\lambda \tau}}. $$

So

$$\biggl(\frac{d\lambda}{d\tau}\biggr)^{-1}=\frac{\tau(k-a_{1})}{k(a_{1}-\lambda )}- \frac{1}{\lambda(a_{1}-\lambda)}+\frac{(2-b_{1})e^{\lambda\tau }}{k(a_{1}-\lambda)}. $$

Consequently, we obtain

$$\begin{aligned} \biggl(\frac{d(\operatorname{Re}\lambda(\tau))}{d\tau}\biggr)^{-1}_{\tau=\tau_{j}}&=\operatorname{Re} \biggl\{ \frac{\tau (k-a_{1})}{k(a_{1}-\lambda)}-\frac{1}{\lambda(a_{1}-\lambda)}+\frac {(2-b_{1})e^{\lambda\tau}}{k(a_{1}-\lambda)}\biggr\} _{\tau=\tau_{j}} \\ &=\frac{\tau{a}_{1}(k-a_{1})}{k(a_{1}^{2}+\omega^{2})}+\frac{\omega ^{2}}{\omega^{4}+a_{1}^{2}\omega^{2}}+\frac{(2-b_{1})(\omega ^{2}+b_{2})}{k^{2}(a_{1}^{2}+\omega^{2})}\neq0. \end{aligned}$$

 □

Theorem 2.4

If $ka_{1}=b_{2}$, $b_{1}+k<0$, and $r_{1}<0$, then, for $\tau=\tau _{j}$ $(j=0,1,2,\ldots)$, system (1.2) undergoes a Hopf-zero bifurcation at equilibrium $(x_{+},z_{+})$.

3 Normal form for Hopf-zero bifurcation

In this section, we use the center manifold theory and normal form method [6, 23] to study Hopf-zero bifurcations. The normal form of a Hopf-zero bifurcation for a general delay-differential equations has been given in the following two papers: one is for a saddle-node-Hopf bifurcation [11], and the other is for a steady-state Hopf bifurcation [20]. After scaling $t\rightarrow{t/\tau}$, system (2.3) becomes

$$ \textstyle\begin{cases} \frac{dx}{dt}=\frac{\tau}{\varepsilon }((x+x_{+})(1-x-x_{+})-h_{1}(z+z_{+})\frac{(x+x_{+})-q}{(x+x_{+})+q}),\\ \frac{dz}{dt}=\tau(x-z+kz(t-1)). \end{cases} $$

(3.1)

Let $\tau=\tau_{1}+\mu_{1}$, $k=1+\frac{a_{2}}{a_{1}}+\mu_{2}$, where $\mu_{1}$ and $\mu_{2}$ are bifurcation parameters. Then system (3.1) can be written as

$$ \textstyle\begin{cases} \frac{dx}{dt}=(\tau_{1}+\mu_{1})(a_{1}x+a_{2}z+M_{1}), \\ \frac{dz}{dt}=(\tau_{1}+\mu_{1})(x-z+(1+\frac{a_{2}}{a_{1}}+\mu_{2})z(t-1)), \end{cases} $$

(3.2)

where $M_{1}=\frac{1}{\varepsilon}[\frac {h_{1}z_{+}(q-x_{+}+1)}{(q+x_{+})^{2}}]x^{2}+\frac{1}{\varepsilon}\frac {-2qh_{1}}{q+x_{+}}xz +\frac{1}{\varepsilon}\frac{-2qh_{1}x_{+}}{(x_{+}+q)^{4}}x^{3}+\frac {1}{\varepsilon}\frac{2qh_{1}}{(x_{+}+q)^{3}}x^{2}z$.

Choose the phase space $C=C([-1,0];R^{4})$ with supremum norm and define $X_{t}\in{C}$ by $X_{t}(\theta)=X(t+\theta)$, $-\tau\leq\theta \leq0$, and $\|X_{t}\|=\sup|X_{t}(\theta)|$. Then system (3.2) becomes

$$ \dot{X}(t)=L(\mu)X_{t}+F(X_{t},\mu), $$

(3.3)

where

$$L(\mu)X_{t}=(\tau_{1}+\mu_{1}) \begin{pmatrix} a_{1}x+a_{2}z \\ x-z+(1+\frac{a_{2}}{a_{1}}+\mu_{2})z(t-1) \end{pmatrix} $$

and

$$F(X_{t},\mu)= \begin{pmatrix} (\tau_{1}+\mu_{1})M_{1} \\ 0 \end{pmatrix}, $$

where $L(\mu)\varphi=\int_{-1}^{0}d\eta(\theta,\mu)\varphi(\xi)\,d\xi$ for $\varphi\in([-1,0],R^{4})$,

$$\eta(\theta,\mu)= \textstyle\begin{cases} 0, & \theta=0, \\ -(\tau_{1}+\mu_{1})A, & \theta\in(-1,0), \\ -(\tau_{1}+\mu_{1})(A+B), & \theta=-1, \end{cases} $$

with

$$A = \begin{pmatrix} a_{1} & a_{2} \\ 1 & -1 \end{pmatrix} \quad\mbox{and}\quad B= \begin{pmatrix} 0 & 0 \\ 0 & 1+\frac{a_{2}}{a_{1}} \end{pmatrix}. $$

Consider the linear system

$$\dot{X}(t)=L(0)X_{t}. $$

Between C and $C'=C([0,\tau],C^{n*})$, the bilinear form is defined by

$$\begin{aligned} \bigl(\psi(s),\varphi(\theta)\bigr) =&\psi(0)\varphi(0)- \int_{-1}^{0} \int _{0}^{\theta}\psi(\xi-\theta)\,d\eta(\theta,0) \varphi(\xi)\,d\xi \\ =&\psi(0)\varphi(0)- \int_{-1}^{0} \int_{0}^{\theta }\psi(\xi-\theta)\,d\bigl(A\varphi( \theta)+B\varphi(\theta+1)\bigr)\varphi(\xi)\,d\xi \\ =&\psi(0)\varphi(0)- \int_{-1}^{0}\psi(\xi+1)B\varphi(\xi)\,d\xi\quad \forall \psi\in{C}', \forall\varphi\in{C}, \end{aligned}$$

where $\varphi(\theta)=(\varphi_{1}(\theta),\varphi_{2}(\theta),\varphi _{3}(\theta))\in{C}$, $\psi (s)=(\begin{array}{c}{\psi }_1(s)\\ {\psi }_2(s)\\ {\psi }_3(s)\end{array})\in C^{\ast }$.

We know that $L(0)$ has a pair of purely imaginary eigenvalues $\pm {i\omega}$ $(\omega>0)$, a simple 0, and all other eigenvalues have negative real parts. Let $\varLambda=\{i\omega,-i\omega,0\}$, let P be the generalized eigenspace associated with Λ, and let $P^{*}$ is the space adjoint with P. Then C can be decomposed as $C=P\bigoplus{Q}$, where $Q= \{ \varphi\in{C}:(\psi,\varphi)=0 \mbox{ for all } \psi\in{P}^{*} \}$. We can choose the bases Φ and Ψ for P and $P^{*}$ such that $(\varPsi(s),\varPhi(\theta))=I$, $\dot{\varPhi}=\varPhi{J}$, and $-\varPsi=J\varPsi$, where $J=\operatorname{diag}(i\omega,-i\omega,0)$.

We calculate $\varPhi(\theta)$ and $\varPsi(s)$ as follows:

$$\varPhi(\theta) = \begin{pmatrix} \frac{a_{2}}{i\omega-a_{1}}e^{iw \tau_{1} \theta} & \frac{a_{2}}{-i\omega-a_{1}}e^{-iw \tau_{1} \theta} & -a_{2} \\ e^{iw \tau_{1} \theta} & e^{-iw \tau_{1} \theta} & a_{1} \end{pmatrix} $$

and

$$\varPsi(s) = \begin{pmatrix} \frac{D_{1}}{i\omega-a_{1}}e^{-iw \tau_{1} s} & D_{1}e^{-iw \tau_{1}s} \\ \frac{\overline{D_{1}}}{i\omega-a_{1}}e^{iw \tau_{1} s} & \overline{D_{1}}e^{-iw \tau_{1} s} \\ -D_{2} & a_{1}D_{2} \end{pmatrix}, $$

where

$$\begin{aligned} &D_{1}=\biggl(\frac{a_{2}}{(i\omega-a_{1})^{2}}+1+\tau_{1}\biggl(1+ \frac {a_{2}}{a_{1}}\biggr)\biggr)^{-1}, \\ &D_{2} = \bigl(a_{2}+a_{1}^{2}+a_{1} \tau_{1}b_{2}\bigr)^{ - 1}. \end{aligned}$$

Let us enlarge the space C to the following space:

$$BC= \Bigl\{ \varphi~\mbox{is a continuous function on } [-1,0), \mbox{ and } \lim_{\theta\rightarrow{0}^{-}}\varphi(\theta) \mbox{ exists} \Bigr\} . $$

Its elements can be written as $\psi=\varphi+X_{0}\alpha$ with $\varphi \in{C}$, $\alpha\in{\mathbb{C}^{n}}$, and

$$X_{0}(\theta)= \textstyle\begin{cases} 0, & \theta\in[-1,0), \\ I, & \theta=0. \end{cases} $$

In BC, system (3.3) varies an abstract ODE:

$$ \frac{d}{dt}X_{t}=Au+X_{0}\tilde{F}(u,\mu), $$

(3.4)

where $u\in{C}$, and A is defined by

$$A:C^{1}\rightarrow{BC},Au=\dot{u}+X_{0}\bigl[L(0)u- \dot{u}(0)\bigr] $$

and

$$\tilde{F}(u,\mu)=\bigl[L(\mu)-L_{0}\bigr]u+F(u,\mu). $$

Then the enlarged phase space BC can be decomposed as $BC=P\oplus {\operatorname{Ker}\pi}$. Let $X_{t}=\varPhi{x(t)}+\tilde{y}(\theta)$, where $x(t)=(x_{1},x_{2},x_{3})^{T}$, namely

$$\textstyle\begin{cases} x(\theta)=\frac{a_{2}}{i\omega-a_{1}}e^{iw \tau_{1} \theta}x_{1}+\frac {a_{2}}{-i\omega-a_{1}}e^{-iw \tau_{1} \theta }x_{2}-a_{2}x_{3}+y_{1}(\theta), \\ z(\theta)=e^{iw \tau_{1} \theta}x_{1}+e^{-iw \tau_{1} \theta }x_{2}+a_{1}x_{3}+y_{2}(\theta). \end{cases} $$

Let

$$\varPsi(0) = \begin{pmatrix} \psi_{11} & \psi_{12} \\ \psi_{21} & \psi_{22} \\ \psi_{31} & \psi_{32} \end{pmatrix} = \begin{pmatrix} \frac{D_{1}}{i\omega-a_{1}} & D_{1} \\ \frac{\overline{D_{1}}}{-i\omega-a_{1}} & \overline{D_{1}} \\ -D_{2} & a_{1}D_{2} \end{pmatrix}. $$

Equation (3.4) can be expressed as

$$ \begin{aligned} &\dot{x}=Jz+\varPsi(0)\tilde{F}\bigl(\varPhi{z}+\tilde{y}( \theta ),\mu\bigr), \\ &\dot{\tilde{y}}=A_{Q1}\tilde{y}+(I-\pi)Y_{0}\tilde{F} \bigl(\varPhi{z}+\tilde {y}(0),\mu\bigr), \end{aligned} $$

(3.5)

where $\tilde{y}(\theta)\in{Q^{1}}:=Q\bigcap{C^{1}}\subset{\operatorname{Ker}\pi}$, and $A_{Q1}$ is the restriction of A as an operator from $Q_{1}$ to the Banach space Kerπ.

System (3.5) can be rewritten as

$$\textstyle\begin{cases} \dot{x}=Jx+\frac{1}{2!}f_{2}^{1}(x,y,\mu)+\frac{1}{3!}f_{3}^{1}(x,y,\mu )+\mbox{h.o.t.}, \\ \dot{y}=A_{Q^{1}}y+\frac{1}{2!}f_{2}^{2}(x,y,\mu)+\frac {1}{3!}f_{3}^{2}(x,y,\mu)+\mbox{h.o.t.}, \end{cases} $$

where

$$\begin{aligned} &f_{2}^{1}(x,y,\mu)= \begin{pmatrix} \psi_{11}F_{2}^{1}(x,y,\mu)+\psi_{12}F_{2}^{2}(x,y,\mu) \\ \psi_{21}F_{2}^{1}(x,y,\mu)+\psi_{22}F_{2}^{2}(x,y,\mu) \\ \psi_{31}F_{2}^{1}(x,y,\mu)+\psi_{32}F_{2}^{2}(x,y,\mu) \end{pmatrix}, \\ &f_{3}^{1}(x,y,\mu)= \begin{pmatrix} \psi_{11}F_{3}^{1}(x,y,\mu)+\psi_{12}F_{3}^{2}(x,y,\mu) \\ \psi_{21}F_{3}^{1}(x,y,\mu)+\psi_{22}F_{3}^{2}(x,y,\mu) \\ \psi_{31}F_{3}^{1}(x,y,\mu)+\psi_{32}F_{3}^{2}(x,y,\mu) \end{pmatrix} \end{aligned}$$

with

$$\begin{aligned} &\begin{aligned} \frac{1}{2}F_{2}^{1}={}& \mu_{2}\biggl[a_{1}\biggl(\frac{a_{2}}{i\omega -a_{1}}x_{1}+ \frac{a_{2}}{-i\omega -a_{1}}x_{2}-a_{2}x_{3}+y_{1}(0) \biggr)+a_{2}\bigl(x_{1}+x_{2}+a_{1}x_{3}+y_{2}(0) \bigr)\biggr] \\ &{}+\tau_{1}\biggl[\frac{1}{\varepsilon}\biggl[\frac {hz_{+}(q-x_{+}+1)}{(q+x_{+})^{2}} \biggr]\biggl(\frac{a_{2}}{i\omega-a_{1}} x_{1}+\frac{a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3}+y_{1}(0) \biggr)^{2} \\ &{}+\frac{1}{\varepsilon}\frac{-2qh}{q+x_{+}}\biggl(\frac{a_{2}}{i\omega -a_{1}}x_{1}+ \frac{a_{2}}{-i\omega -a_{1}}x_{2}-a_{2}x_{3}+y_{1}(0) \biggr) \bigl(x_{1}+x_{2}+a_{1}x_{3}+y_{2}(0) \bigr)\biggr], \end{aligned} \\ &\begin{aligned} \frac{1}{2}F_{2}^{2}={}& \mu_{2}\biggl(\frac{a_{2}}{i\omega-a_{1}}x_{1}+\frac {a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3}+y_{1}(0) \biggr)-\mu _{2}\bigl(x_{1}+x_{2}+a_{1}x_{3}+y_{2}(0) \bigr) \\ &{}+\biggl(1+\frac{a_{2}}{a_{1}}\biggr)\mu_{2}\bigl(e^{-iw \tau_{1} }x_{1}+e^{iw \tau_{1} }x_{2}+a_{1}x_{3}+y_{2}(-1) \bigr) \\ &{}+\tau_{1}\mu_{1}\bigl(e^{-iw \tau_{1} }x_{1}+e^{iw \tau_{1} }x_{2}+a_{1}x_{3}+y_{2}(-1) \bigr), \end{aligned} \\ &\begin{aligned} \frac{1}{3!}F_{3}^{1}={}& \frac{\tau_{1}}{\varepsilon}\frac {-2qhx_{+}}{(q+x_{+})^{4}}\biggl(\frac{a_{2}}{i\omega-a_{1}}x_{1}+ \frac {a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3}+y_{1}(0) \biggr)^{3} \\ &{}+\frac{\tau_{1}}{\varepsilon}\frac{2qh}{(q+x_{+})^{3}}\biggl(\frac {a_{2}}{i\omega-a_{1}}x_{1}+ \frac{a_{2}}{-i\omega -a_{1}}x_{2}-a_{2}x_{3}+y_{1}(0) \biggr)^{2}\\ &{}\times\bigl(x_{1}+x_{2}+a_{1}x_{3}+y_{2}(0) \bigr), \end{aligned} \\ &F_{3}^{2}=0. \end{aligned}$$

According to [25], $(\operatorname{Im}(M_{2}^{1}))^{c}$ is spanned by

$$\bigl\{ z_{1}^{2}e_{1},z_{2}z_{3}e_{1},z_{1} \mu_{i}e_{1},\mu _{1}\mu_{2}e_{1},z_{1}z_{2}e_{2},z_{2} \mu _{i}e_{2},z_{1}z_{3}e_{3},z_{3} \mu_{i}e_{3} \bigr\} ,\quad i=1,2, $$

with $e_{1}=(1,0,0)^{T}$, $e_{2}=(0,1,0)^{T}$, $e_{3}=(0,0,1)^{T}$.

$(\operatorname{Im}(M_{3}^{1}))^{c}$ is spanned by

$$\bigl\{ z_{1}^{3}e_{1},z_{1}z_{2}z_{3}e_{1},z_{1}^{2}z_{2}e_{2},z_{2}^{2}z_{3}e_{2},z_{1}^{2}z_{3}e_{3},z_{2}z_{3}^{2}e_{3} \bigr\} . $$

Then we get

$$\begin{aligned} & g_{2}^{1}(x,0,\mu)=\mathrm{Proj}_{(\operatorname{Im}(M_{2}^{1}))^{c}}f_{2}^{1}(x,0, \mu )=\mathrm{Proj}_{S_{1}}f_{2}^{1}(x,0,\mu)+O\bigl( \vert \mu \vert ^{2}\bigr), \\ & g_{3}^{1}(x,0,\mu)=\mathrm{Proj}_{(\operatorname{Im}(M_{3}^{1}))^{c}} \tilde{f}_{3}^{1}(x,0,\mu)= \mathrm{Proj}_{S_{2}} \tilde{f}_{3}^{1}(x,0,0)+O\bigl( \vert \mu \vert ^{2} \vert x \vert + \vert \mu \vert \vert x \vert ^{2}\bigr), \end{aligned}$$

where $S_{1}$ and $S_{2}$ are spanned, respectively, by

$$z_{1}\mu_{i}e_{1},z_{2} \mu_{i}e_{2},z_{3}\mu_{i}e_{3}, \quad i=1,2, $$

and

$$z_{1}^{3}e_{1},z_{1}z_{2}z_{3}e_{1},z_{1}^{2}z_{2}e_{2},z_{2}^{2}z_{3}e_{2},z_{1}^{2}z_{3}e_{3},z_{2}z_{3}^{2}e_{3}. $$

System (3.5) can be transformed on the center manifold in the following normal form:

$$ \dot{x}=Jx+\frac{1}{2}g_{2}^{1}(x,0,\mu)+ \frac{1}{6}g_{3}^{1}(x,0,\mu)+\mbox{h.o.t.} $$

(3.6)

We need to compute $g_{2}^{1}(x,0,\mu)$ and $g_{3}^{1}(x,0,\mu)$ in (3.6). We can compute $\frac{1}{2}g_{2}^{1}(x,0,\mu)$:

$$\begin{aligned} \frac{1}{2}g_{2}^{1}(x,0,\mu) =&\frac{1}{2} \mathrm{Proj}_{S_{1}}f_{2}^{1}(x,0,\mu )+\vartheta \bigl( \vert u \vert ^{2}\bigr) \\ =& \begin{pmatrix} (a_{11}\mu_{1}+a_{12}\mu_{2})x_{1}+a_{13}x_{1}x_{3} \\ (\overline{a}_{11}\mu_{1}+\overline{a}_{12}\mu_{2})x_{1}+\overline {a}_{13}x_{1}x_{3} \\ (a_{21}\mu_{1}+a_{22}\mu_{2})x_{3}+a_{23}x_{1}x_{2}+a_{24}x_{3}^{2} \end{pmatrix} +\vartheta\bigl( \vert u \vert ^{2} \bigr) , \end{aligned}$$

where

$$\begin{aligned} &a_{11}=D_{1}\tau_{1}e^{-i\omega\tau_{1}}, \\ &a_{12}=D_{1}\biggl(\frac{a_{1}a_{2}}{(i\omega-a_{1})^{2}}+ \frac{2a_{2}}{i\omega -a_{1}}-1+\biggl(1+\frac{a_{2}}{a_{1}}\biggr)e^{-i\omega\tau_{1}}\biggr), \\ &a_{13}=\frac{D_{1}}{i\omega-a_{1}}\biggl[\frac{\tau_{1}}{\varepsilon} \frac {hz_{+}(q-x_{+}+1)}{(q+x_{+})^{2}}\biggl(-\frac{2a_{2}^{2}}{i\omega -a_{1}}\biggr)-\frac{2qh\tau_{1}}{\varepsilon(q+x_{+})}\biggl( \frac {a_{1}a_{2}}{i\omega-a_{1}}-a_{2}\biggr)\biggr], \\ &a_{21}=a_{1}^{2}\tau_{1}D_{2}, \qquad a_{22}=-a_{2}b_{1}D_{2}, \\ &a_{23}=-D_{2}\biggl[\frac{\tau_{1}}{\varepsilon}\frac {hz_{+}(q-x_{+}+1)}{(q+x_{+})^{2}} \biggl(\frac{2a_{2}^{2}}{a_{1}^{2}-\omega ^{2}}\biggr)-\frac{\tau_{1}}{\varepsilon}\frac{2qh}{q+x_{+}}\biggl( \frac {a_{2}}{i\omega-a_{1}}+\frac{a_{2}}{-i\omega-a_{1}}\biggr)\biggr], \\ &a_{24}=-\frac{\tau_{1}D_{2}}{\varepsilon}\biggl[\frac {hz_{+}(q-x_{+}+1)}{(q+x_{+})^{2}}a_{2}^{2}+ \frac{2qh}{q+x_{+}}a_{1}a_{2}\biggr]. \end{aligned}$$

Next, we compute $g_{3}^{1}(x,0,\mu)$:

$$\begin{aligned} \frac{1}{6}g_{3}^{1}(x,0,\mu) =&\frac{1}{6} \mathrm{Proj}_{\operatorname{Ker}(M_{2}^{1})}\tilde {f}_{3}^{1}(x,0,\mu) \\ =&\frac{1}{6}\mathrm{Proj}_{S_{2}}\tilde{f}_{3}^{1}(x,0,0)+ \vartheta \bigl( \vert x \vert \vert u \vert ^{2}+ \vert x \vert ^{2} \vert \mu \vert \bigr) \\ =&\frac{1}{6}\mathrm{Proj}_{S_{2}}f_{3}^{1}(x,0,0)\\ &{}+ \frac {1}{4}\mathrm{Proj}_{S_{2}}\bigl[\bigl(D_{x}f_{2}^{1} \bigr) (x,0,0)U_{2}^{1}(x,0) +\bigl(D_{y}f_{2}^{1} \bigr) (x,0,0)U_{2}^{2}(x,0)\bigr]\\ &{}+\vartheta \bigl( \vert x \vert \vert u \vert ^{2}+ \vert x \vert ^{2} \vert \mu \vert \bigr). \end{aligned}$$

We can get $\mathrm{Proj}_{S_{2}}f_{3}^{1}(x,0,0)$. Since

$$\frac{1}{6}f_{3}^{1}(x,0,0)=\frac{\tau_{1}}{\varepsilon} \left(\textstyle\begin{array}{l} \overline{D_{1}}\frac{-2qhx_{+}}{(x_{+}+q)^{4}}(\frac{a_{2}}{i\omega -a_{1}}x_{1}+\frac{a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3})^{3} \\ +\frac{2qh}{(x_{+}+q)^{3}}(\frac{a_{2}}{i\omega-a_{1}}x_{1}+\frac {a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3})^{2} \\ D_{1}\frac{-2qhx_{+}}{(x_{+}+q)^{4}}(\frac{a_{2}}{i\omega -a_{1}}x_{1}+\frac{a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3})^{3} \\ {}+\frac{2qh}{(x_{+}+q)^{3}}(\frac{a_{2}}{i\omega-a_{1}}x_{1}+\frac {a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3})^{2}(x_{1}+x_{2}+a_{1}x_{3}) \\ a_{1}D_{2}\frac{-2qhx_{+}}{(x_{+}+q)^{4}}(\frac{a_{2}}{i\omega -a_{1}}x_{1}+\frac{a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3})^{3} \\ {}+\frac{2qh}{(x_{+}+q)^{3}}(\frac{a_{2}}{i\omega-a_{1}}x_{1}+\frac {a_{2}}{-i\omega-a_{1}}x_{2}-a_{2}x_{3})^{2}(x_{1}+x_{2}+a_{1}x_{3}) \end{array}\displaystyle \right), $$

we have

$$\frac{1}{6}\mathrm{Proj}_{S_{2}}f_{3}^{1}(x,0,0)= \begin{pmatrix} b_{11}x_{1}^{2}x_{2}+b_{12}x_{1}x_{3}^{2} \\ \overline{b}_{11}x_{1}x_{2}^{2}+\overline{b}_{12}x_{2}x_{3}^{2} \\ b_{21}x_{1}x_{2}x_{3}+b_{22}x_{3}^{3} \end{pmatrix} + \vartheta\bigl( \vert u \vert ^{2}\bigr) , $$

where

$$\begin{aligned} & \begin{aligned} b_{11}={}&\frac{\tau_{1}}{\varepsilon}\overline{D}_{1} \frac {-2qhx_{+}}{(x_{+}+q)^{4}}\biggl(\frac{a_{2}^{2}}{\omega^{2}+a_{1}^{2}}+\frac {2a_{2}^{3}}{(\omega^{2}+a_{1}^{2})(i\omega-a_{1})}\biggr)\\ &{} + \frac{\tau_{1}}{\varepsilon}\overline{D}_{1}\frac {2qh}{(x_{+}+q)^{3}}\biggl( \frac{a_{2}}{i\omega-a_{1}}+\frac{a_{2}^{2}}{\omega ^{2}+a_{1}^{2}}\biggr), \end{aligned} \\ &b_{12}=\frac{\tau_{1}}{\varepsilon}\overline{D}_{1} \frac {-2qhx_{+}}{(x_{+}+q)^{4}}\frac{2a_{2}^{3}}{i\omega-a_{1}} -\frac{\tau_{1}}{\varepsilon}\overline{D}_{1} \frac {2qh}{(x_{+}+q)^{3}}\frac{2a_{2}^{2}a_{1}}{i\omega-a_{1}}, \\ &b_{21}=\frac{\tau_{1}}{\varepsilon}a_{1}D_{2} \frac {2qhx_{+}}{(x_{+}+q)^{4}}\frac{6a_{2}^{3}}{\omega^{2}+a_{1}^{2}} +\frac{\tau_{1}}{\varepsilon}a_{1}D_{2} \frac{2qh}{(x_{+}+q)^{3}}\biggl(\frac {2a_{2}^{2}a_{1}}{\omega^{2}+a_{1}^{2}}+\frac{4a_{1}^{2}}{i\omega -a_{1}}\biggr), \\ & b_{22}=\frac{\tau_{1}}{\varepsilon}a_{1}D_{2} \frac {2qhx_{+}}{(x_{+}+q)^{4}}a_{2}^{3}+\frac{\tau_{1}}{\varepsilon }a_{1}D_{2} \frac{2qh}{(x_{+}+q)^{3}}a_{1}a_{2}^{2}. \end{aligned}$$

Next, we compte $\mathrm{Proj}_{S_{2}}[(D_{x}f_{2}^{1}(x,0,0))U_{2}^{1}(x,0)]$.

From [25] we know that because J is a diagonal matrix, the operators $M_{j}^{1}, j\geq2$, are defined in $V_{j}^{5}(\mathbb {C}^{3})$, so we have a diagonal representation relative to the canonical basis $\{\mu^{p}x^{q}e_{k}:k=1,2,3,p\in\mathbb {{N}}_{0}^{2},q\in\mathbb{{N}}_{0}^{3},|p|+|q|=j\}$ of $V_{j}^{5}(\mathbb{{C}}^{3})$, where $e_{1}=(1,0,0)^{T}$, $e_{2}=(0,1,0)^{T}$, $e_{3}=(0,0,1)^{T}$. Clearly, we get

$$\begin{aligned} &M_{j}^{1}\bigl(\mu^{p}x^{q}e_{k} \bigr)=i\omega\bigl(q_{1}-q_{2}+(-1)^{k}\bigr) \mu^{p}x^{q}e_{k},\quad k=1,2, \\ &M_{j}^{1}\bigl(\mu^{p}x^{q}e_{3} \bigr)=i\omega(q_{1}-q_{2})\mu^{p}x^{q}e_{3}, \quad \vert p \vert + \vert q \vert =j. \end{aligned}$$

So

$$\operatorname{Ker}\bigl(M_{j}^{1}\bigr)= \operatorname{span}\bigl\{ \mu^{p}x^{q}e_{k}:(q, \overline{\lambda})=\lambda _{k},k=1,2,3,p\in\mathbb{{N}}_{0}^{2},q \in\mathbb {{N}}_{0}^{3}, \vert p \vert + \vert q \vert =j\bigr\} $$

with $\overline{\lambda}=(\lambda_{1},\lambda_{2},\lambda_{3})=(i\omega ,-i\omega,0)$. The elements of the canonical basis of $V_{2}^{5}(\mathbb {C}^{3})$ are

$$\begin{aligned} &\mu_{1}\mu_{2}e_{1}, \mu_{i}^{2}e_{1}, \mu_{i}x_{1}e_{1}, \mu _{i}x_{2}e_{1}, \mu_{i}x_{3}e_{1}, x_{1}x_{2}e_{1}, x_{1}x_{3}e_{1}, x_{2}x_{3}e_{1}, x_{1}^{2}e_{1}, x_{2}^{2}e_{1}, x_{3}^{2}e_{1}, \\ &\mu_{1}\mu_{2}e_{2}, \mu_{i}^{2}e_{2}, \mu_{i}x_{1}e_{2}, \mu _{i}x_{2}e_{2}, \mu_{i}x_{3}e_{2}, x_{1}x_{2}e_{2}, x_{1}x_{3}e_{2}, x_{2}x_{3}e_{2}, x_{1}^{2}e_{2}, x_{2}^{2}e_{2}, x_{3}^{2}e_{2}, \\ &\mu_{1}\mu_{2}e_{3}, \mu_{i}^{2}e_{3}, \mu_{i}x_{1}e_{3}, \mu _{i}x_{2}e_{3}, \mu_{i}x_{3}e_{3}, x_{1}x_{2}e_{3}, x_{1}x_{3}e_{3}, x_{2}x_{3}e_{3}, x_{1}^{2}e_{3}, x_{2}^{2}e_{3}, x_{3}^{2}e_{3},\quad i=1,2, \end{aligned}$$

the images of which under $\frac{1}{i\omega}M_{2}^{1}$ are

$$\begin{aligned} &{-}\mu_{1}\mu_{2}e_{1}, -\mu_{i}^{2}e_{1}, 0, -2\mu_{i}x_{2}e_{1}, -\mu _{i}x_{3}e_{1}, -x_{1}x_{2}e_{1}, 0, -2x_{2}x_{3}e_{1}, x_{1}^{2}e_{1}, -3x_{2}^{2}e_{1}, -x_{3}^{2}e_{1}, \\ &\mu_{1}\mu_{2}e_{2}, \mu_{i}^{2}e_{2}, 2\mu_{i}x_{1}e_{2}, 0, \mu _{i}x_{3}e_{2}, x_{1}x_{2}e_{2}, 2x_{1}x_{3}e_{2}, 0, 3x_{1}^{2}e_{2}, -x_{2}^{2}e_{2}, x_{3}^{2}e_{2}, \\ &0, 0, \mu_{i}x_{1}e_{3}, -\mu_{i}x_{2}e_{3}, 0, 0, x_{1}x_{3}e_{3}, -x_{2}x_{3}e_{3}, 2x_{1}^{2}e_{3}, -2x_{2}^{2}e_{3}, 0,\quad i=1,2. \end{aligned}$$

Hence

$$\begin{aligned} U_{2}^{1}(x,0)&=U_{2}^{1}(x, \mu)|_{\mu =0}=\bigl(M_{2}^{1}\bigr)^{-1} \mathrm{Proj}_{\operatorname{Im}(M_{2}^{1})}f_{2}^{1}(x,0,0) \\ &=\bigl(M_{2}^{1}\bigr)^{-1}\mathrm{Proj}_{\operatorname{Im}(M_{2}^{1})} \frac{\tau_{1}}{\varepsilon} \left(\textstyle\begin{array}{l} D_{1}h[(a_{2}hx_{1}+a_{2}\overline{h}x_{2}-a_{2}x_{3})^{2}\cdot{m} \\ {}+n\cdot(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3})(x_{1}+x_{2}+a_{1}x_{3})] \\ \overline{D}_{1}\overline{h}[(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3})^{2}\cdot{m} \\ {}+n\cdot(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3})(x_{1}+x_{2}+a_{1}x_{3})] \\ {}-D_{2}[(a_{2}hx_{1}+a_{2}\overline{h}x_{2}-a_{2}x_{3})^{2}\cdot{m} \\ {}+n\cdot(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3})(x_{1}+x_{2}+a_{1}x_{3})] \end{array}\displaystyle \right) \\ &=\frac{\tau_{1}}{i\omega\varepsilon} \left(\textstyle\begin{array}{l} D_{1}h[m(a_{2}^{2}h^{2}x_{1}^{2}-2a_{2}^{2}h\overline {h}x_{1}x_{2}+a_{2}^{2}\overline{h}x_{2}x_{3}-\frac {1}{3}a_{2}^{2}\overline{h}^{2}-a_{2}^{2}x_{3}^{2}) \\ {}+n(a_{2}hx_{1}^{2}-a_{2}(h+\overline{h})x_{1}x_{2}-\frac {1}{3}a_{2}\overline{h}x_{2}^{2}-\frac{1}{2}a_{2}(a_{1}\overline {h}+1)x_{2}x_{3}\\ {}+a_{1}a_{2}x_{3}^{2})] \\ \overline{D}_{1}\overline{h}[m(\frac {1}{3}a_{2}^{2}h^{2}x_{1}^{2}-a_{2}^{2}\overline {h}^{2}x_{2}^{2}+a_{2}^{2}x_{3}^{2}+2a_{2}^{2}h\overline {h}x_{1}x_{2}-a_{2}^{2}hx_{1}x_{3}) \\ {}+n(\frac{1}{3}a_{2}hx_{1}^{2}+\frac {1}{2}a_{2}(a_{1}h-1)x_{1}x_{3}-a_{2}\overline{h}x_{2}^{2}+\frac {1}{2}a_{1}a_{2}\overline {h}x_{2}x_{3}\\ {}-a_{1}a_{2}x_{3}^{2}+a_{2}(h+\overline{h})x_{1}x_{2})] \\ {}-D_{2}[m(\frac{1}{2}a_{2}^{2}h^{2}x_{1}^{2}-\frac {1}{2}a_{2}^{2}\overline {h}^{2}x_{2}^{2}-2a_{2}^{2}hx_{1}x_{3}+2a_{2}^{2}\overline {h}x_{2}x_{3}) \\ {}+n(\frac{1}{2}a_{2}hx_{1}^{2}+a_{1}a_{2}hx_{1}x_{3}-\frac {1}{2}a_{2}\overline{h}x_{2}^{2}-a_{1}a_{2}\overline {h}x_{2}x_{3}\\ {}-a_{2}x_{1}x_{3}+a_{2}x_{2}x_{3} \end{array}\displaystyle \right), \end{aligned}$$

where $m=\frac{hz_{+}(q-x_{+}+1)}{(q+x_{+})^{2}}$, $n=\frac {-2qh}{q+x_{+}}$, and $h=\frac{1}{i\omega-a_{1}}$.

Therefore we obtain

$$\frac{1}{4}\mathrm{Proj}_{S_{2}}\bigl[\bigl(D_{x}f_{2}^{1}(x,0,0) \bigr)U_{2}^{1}(x,0)\bigr]= \begin{pmatrix} c_{11}x_{1}^{2}x_{2}+c_{12}x_{1}x_{3}^{2} \\ \overline{c}_{11}x_{1}x_{2}^{2}+\overline{c}_{12}x_{2}x_{3}^{2} \\ c_{21}x_{1}x_{2}x_{3}+c_{22}x_{3}^{3} \end{pmatrix}, $$

where

$$\begin{aligned} &\begin{aligned} c_{11}={}&\frac{\tau_{1}^{2}}{i\omega\varepsilon ^{2}}\biggl[D_{1}^{2}h^{2}m^{2} \bigl(-2a_{2}^{4}h^{3}\overline {h} \bigr)+D_{1}^{2}h^{2}mn\bigl(-a_{2}^{3}h^{3} \bigr)+D_{1}^{2}h^{2}mn\bigl(-3a_{2}^{3}h^{2} \overline {h}\bigr)\\ &{} +D_{1}^{2}h^{2}n^{2}a_{2}^{2}h(-h- \overline{h})+D_{1}\overline {D}_{1}h\overline{h}m^{2} \biggl(\frac{16}{3}a_{2}^{4}h^{2} \overline{h}^{2}\biggr)\\ &{} +D_{1}\overline{D}_{1}h \overline{h}mn\biggl(\frac {14}{3}a_{2}^{3}h^{2} \overline{h}+\frac{14}{3}a_{2}^{3}h\overline {h}^{2}+a_{2}^{2}h^{2}+a_{2}^{2}h \overline{h}\biggr) +D_{1}\overline{D}_{1}h \overline{h}n^{2}\biggl(\frac{2}{3}a_{2}^{2}h \overline {h}\biggr)\\ &{}+D_{1}D_{2}hm^{2} \bigl(a_{2}^{4}h^{2}\overline {h} \bigr)+D_{1}D_{2}hmn\bigl(a_{2}^{3}h \overline{h}\bigr) -D_{1}D_{2}hmn\biggl(\frac{1}{2}a_{1}a_{2}^{3}h^{2} \overline{h}-\frac {1}{2}a_{2}^{3}h^{2} \biggr)\\ &{}-D_{1}D_{2}hn^{2}\biggl( \frac {1}{2}a_{1}a_{2}^{2}h\overline{h}- \frac{1}{2}a_{2}^{2}h\biggr)\biggr], \end{aligned} \\ &\begin{aligned} c_{12}={}&\frac{\tau_{1}^{2}}{i\omega\varepsilon ^{2}}\biggl[D_{1}^{2}h^{2}m^{2} \bigl(-2a_{2}^{4}h^{2}\bigr)+2D_{2}^{2}h^{2}mna_{2}^{3} \bigl(a_{1}h^{2}+h\bigr)+D_{1}h^{2}n^{2} \bigl(2a_{1}a_{2}^{2}h\bigr) \\ &{}+D_{1} \overline{D}_{1}h\overline{h}m^{2}\bigl(4a_{2}^{4}h \overline {h}\bigr)+D_{1}\overline{D}_{1}h\overline{h}mn \bigl(-4a_{1}a_{2}^{3}h\overline {h}+2a_{2}^{3}\overline{h}+2a_{2}^{3}h \bigr) \\ &{}+D_{1}\overline{D}_{1}h\overline{h}n^{2} \biggl(-\frac {3}{2}a_{1}a_{2}^{2}(h+ \overline{h})+\frac {1}{2}a_{2}^{2} \bigl(a_{1}^{2}h\overline{h}+1\bigr)\biggr) +D_{1}D_{2}hm^{2}\bigl(4a_{2}^{4}h \bigr)\\ &{}-D_{1}D_{2}hmn\bigl(6a_{1}a_{2}^{3}h-2a_{2}^{3} \bigr)+2D_{1}D_{2}hn^{2}\bigl(a_{1}^{2}a_{2}^{2}h-a_{1}a_{2}^{2} \bigr)\biggr], \end{aligned} \\ &\begin{aligned} c_{21}={}&\frac{\tau_{1}^{2}}{i\omega\varepsilon ^{2}}\bigl[-D_{1}D_{2}hm^{2} \bigl(6a_{2}^{4}h^{2}\overline {h} \bigr)-D_{1}D_{2}hmn\bigl(-3a_{1}a_{2}^{3}h^{2} \overline {h}+6a_{2}^{3}h\overline{h}+3a_{2}^{3}h^{2} \bigr) \\ &{}-D_{1}D_{2}hn^{2}\bigl(-2a_{1}a_{2}^{2}h \overline {h}+2a_{2}^{2}h-a_{1}a_{2}^{2}h^{2}+a_{2}^{2} \overline{h}\bigr)+\overline {D}_{1}D_{2} \overline{h}m^{2}\bigl(6a_{2}^{4}h \overline{h}^{2}\bigr)\\ &{} -\overline{D}_{1}D_{2} \overline{h}mn\bigl(3a_{1}a_{2}^{3}h\overline {h}^{2}-3a_{2}^{3}\overline{h}^{2}-6a_{2}^{3}h \overline{h}\bigr) \\ &{}-\overline{D}_{1}D_{2} \overline{h}n^{2}\bigl(2a_{1}a_{2}^{2}h \overline {h}-2a_{2}^{2}\overline{h}+a_{1}a_{2}^{2} \overline {h}^{2}-a_{2}^{2}h\bigr)\bigr], \end{aligned} \\ &\begin{aligned} c_{22}={}&\frac{\tau_{1}^{2}}{i\omega\varepsilon ^{2}}\bigl[-D_{1}D_{2}hm^{2} \bigl(2a_{2}^{4}h\bigr)-D_{1}D_{2}hmn \bigl(a_{2}^{3}-3a_{1}a_{2}^{3}h \bigr)-D_{1}D_{2}hn^{2}\bigl(a_{1}^{2}a_{2}^{2}h-a_{1}a_{2}^{2} \bigr)\\ &{} -D_{1}D_{2}\overline{h}m^{2} \bigl(-2a_{2}^{4}\overline{h}\bigr)-\overline {D}_{1}D_{2}\overline{h}mn\bigl(3a_{1}a_{2}^{3} \overline{h}-a_{2}^{3}\bigr) +\overline{D}_{1}D_{2} \overline{h}n^{2}\bigl(a_{1}^{2}a_{2}^{2} \overline {h}-a_{1}a_{2}^{2}\bigr)\bigr]. \end{aligned} \end{aligned}$$

Finally, we can compute $\mathrm{Proj}_{S_{2}}[(D_{y}f_{2}^{1})(x,0,0)U_{2}^{2}(x,0)]$. Define $h=h(x)(\theta)=U_{2}^{2}(x,0)$ and write

$$h(\theta)= \begin{pmatrix} h^{(1)}(\theta) \\ h^{(2)}(\theta) \end{pmatrix} =h_{200}x_{1}^{2}+h_{020}x_{2}^{2}+h_{002}x_{3}^{2}+h_{110}x_{1}x_{2}+h_{101}x_{1}x_{3}+h_{011}x_{2}x_{3}, $$

where $h_{200}, h_{020}, h_{002}, h_{110}, h_{101}, h_{011}\in{Q^{1}}$. $(M_{2}^{2}h)(x)=f_{2}^{2}(x,0,0)$ decides the coefficients of h, which is equivalent to

$$D_{x}hJx-A_{Q^{1}}(h)=(I-\pi)X_{0}F_{2}( \varPhi{x},0). $$

We use the definitions of $A_{Q^{1}}$ and π to obtain

$$\begin{aligned} &\dot{h}-D_{x}hJx=\varPhi(\theta)\varPsi(0)F_{2}(\varPhi{x},0), \\ &h(0)-Lh=F_{2}(\varPhi{x},0), \end{aligned}$$

where ḣ is the derivative of $h(\theta)$ with respect to θ. Let

$$F_{2}(\varPhi {x},0)=A_{200}x_{1}^{2}+A_{020}x_{2}^{2}+A_{002}x_{3}^{2}+A_{110}x_{1}x_{2}+A_{101}x_{1}x_{3}+A_{011}x_{2}x_{3}, $$

where $A_{ijk}\in{C}$, $0\leq{i,j,k}\leq2$, $i+j+k=2$. We can compare the coefficients of $x_{1}^{2}$, $x_{2}^{2}$, $x_{3}^{2}$, $x_{1}x_{2}$, $x_{1}x_{3}$, $x_{2}x_{3}$, and we get that $\overline{h}_{020}=h_{200}$, $\overline{h}_{011}=h_{101}$, and the following differential equations are satisfied by $h_{200}, h_{011}, h_{110}, h_{002}$, respectively:

$$\begin{aligned} &\textstyle\begin{cases} \dot{h}_{200}-2i\omega\tau_{1}h_{200}=\varPhi(\theta)\varPsi(0)A_{200},\\ \dot{h}_{200}(0)-L(h_{200})=A_{200}, \end{cases}\displaystyle \end{aligned}$$

(3.7)

$$\begin{aligned} & \textstyle\begin{cases} \dot{h}_{101}-i\omega\tau_{1}h_{101}=\varPhi(\theta)\varPsi(0)A_{101}, \\ \dot{h}_{101}(0)-L(h_{101})=A_{101}, \end{cases}\displaystyle \end{aligned}$$

(3.8)

$$\begin{aligned} & \textstyle\begin{cases} \dot{h}_{110}=\varPhi(\theta)\varPsi(0)A_{110}, \\ \dot{h}_{110}(0)-L(h_{110})=A_{110}, \end{cases}\displaystyle \end{aligned}$$

(3.9)

$$\begin{aligned} &\textstyle\begin{cases} \dot{h}_{002}=\varPhi(\theta)\varPsi(0)A_{002}, \\ \dot{h}_{002}(0)-L(h_{002})=A_{002}, \end{cases}\displaystyle \end{aligned}$$

(3.10)

where

$$\begin{aligned} &A_{200} = \begin{pmatrix} \tau_{1}a_{2}h(ma_{2}h+n) \\ 0 \end{pmatrix} ,\qquad A_{020}= \begin{pmatrix} \tau_{1}a_{2}\bar{h}(ma_{2}\bar{h}+n) \\ 0 \end{pmatrix}, \\ &A_{002} = \begin{pmatrix} \tau_{1}a_{2}(ma_{2}-na_{1}) \\ 0 \end{pmatrix}, \qquad A_{110}= \begin{pmatrix} \tau_{1}a_{2}\bar{h}(2mh\bar{h}+nh+\bar{h}n) \\ 0 \end{pmatrix}, \\ &A_{101} = \begin{pmatrix} \tau_{1}a_{2}(-2ma_{2}h+nha_{1}-n) \\ 0 \end{pmatrix},\qquad A_{011}= \begin{pmatrix} \tau_{1}a_{2}(-2ma_{2}\bar{h}+a_{1}n\bar{h}-n) \\ 0 \end{pmatrix}. \end{aligned}$$

Since

$$F_{2}(u_{t},0)= \begin{pmatrix} \frac{\tau_{1}}{\varepsilon}(mx^{2}+nxz) \\ 0 \end{pmatrix}, $$

we have

$$\begin{aligned} f_{2}^{1}(x,y,0) =&\varPsi(0)F_{1}(\varPhi{x}+y,0) \\ =&\frac{\tau_{1}}{\varepsilon} \begin{pmatrix} D_{1}h & D_{1} \\ \overline{D_{1}}\overline{h} & \overline{D_{1}} \\ -D_{2} & a_{1}D_{2} \end{pmatrix} \left(\textstyle\begin{array}{l} m(a_{2}hx_{1}+a_{2}\overline{h}x_{2}-a_{2}x_{3}+y_{1}(0))^{2} \\ {}+n(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}+y_{1}(0))\\ {}\times(x_{1}+x_{2}+a_{1}x_{3}+y_{2}(0)) \\ 0 \end{array}\displaystyle \right) \\ =&\frac{\tau_{1}}{\varepsilon}\left(\textstyle\begin{array}{l} D_{1}h[m(a_{2}hx_{1}+a_{2}\overline{h}x_{2}-a_{2}x_{3}+y_{1}(0))^{2}) \\ {}+n(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}+y_{1}(0))(x_{1}+x_{2}+a_{1}x_{3}+y_{2}(0))] \\ \overline{D_{1}}\overline{h}[m(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}+y_{1}(0))^{2}) \\ {}+n(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}+y_{1}(0))(x_{1}+x_{2}+a_{1}x_{3}+y_{2}(0))] \\ {}-D_{2}[m(a_{2}hx_{1}+a_{2}\overline{h}x_{2}-a_{2}x_{3}+y_{1}(0))^{2}) \\ {}+n(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}+y_{1}(0))(x_{1}+x_{2}+a_{1}x_{3}+y_{2}(0))] \end{array}\displaystyle \right) , \end{aligned}$$

which gives

$$\frac{1}{4}D_{y}f_{2}^{1}|_{y=0,\mu=0}(h)= \frac{\tau_{1}}{2\varepsilon }\left(\textstyle\begin{array}{l} D_{1}h[m(a_{2}hx_{1}+a_{2}\overline{h}x_{2}-a_{2}x_{3}) \\ {}+n(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}+x_{1}+x_{2}+a_{1}x_{3}]h^{(1)}(0) \\ \overline{D_{1}}\overline{h}[m(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}) \\ {}+n(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}+x_{1}+x_{2}+a_{1}x_{3}]h^{(1)}(0) \\ {}-D_{2}[m(a_{2}hx_{1}+a_{2}\overline{h}x_{2}-a_{2}x_{3}) \\ {}+n(a_{2}hx_{1}+a_{2}\overline {h}x_{2}-a_{2}x_{3}+x_{1}+x_{2}+a_{1}x_{3}]h^{(1)}(0) \end{array}\displaystyle \right) . $$

Thus

$$\frac{1}{4}\mathrm{Proj}_{S_{2}}D_{y}f_{2}^{1}|_{y=0,\mu=0}U_{2}^{2}= \begin{pmatrix} d_{11}x_{1}^{2}x_{2}+d_{12}x_{1}x_{3}^{2} \\ \overline{d}_{11}x_{1}x_{2}^{2}+\overline{d}_{12}x_{2}x_{3}^{2} \\ d_{21}x_{1}x_{2}x_{3}+d_{22}x_{1}x_{3}^{3} \end{pmatrix}, $$

where

$$\begin{aligned} &d_{11}=\frac{\tau_{1}}{\varepsilon}D_{1}h(m+n)a_{2} \bigl(h\cdot {h}_{110}^{(1)}(0)+\overline{h} \cdot{h}_{200}^{(1)}(0)\bigr)+\frac{\tau _{1}}{\varepsilon}D_{1}hn \bigl(h_{110}^{(1)}(0)+h_{200}^{(1)}(0)\bigr), \\ &d_{12}=\frac{\tau_{1}}{\varepsilon}D_{1}h(m+n)a_{2} \bigl(h\cdot {h}_{002}^{(1)}(0)-h_{101}^{(1)}(0) \bigr)+\frac{\tau_{1}}{\varepsilon }D_{1}hn\bigl(h_{002}^{(1)}(0)+a_{1}h_{101}^{(1)}(0) \bigr), \\ &\begin{aligned} d_{21}={}&\frac{\tau_{1}}{\varepsilon}D_{2}h(m+n)a_{2} \bigl(h\cdot {h}_{011}^{(1)}(0)+\overline{h}\cdot {h}_{101}^{(1)}(0)-h_{110}^{(1)}(0)\bigr) \\ &{}+\frac{\tau_{1}}{\varepsilon}D_{2}hn\bigl(a_{1}\cdot {h}_{011}^{(1)}(0)+h_{101}^{(1)}(0)+h_{011}^{(1)}(0) \bigr), \end{aligned} \\ &d_{22}=-D_{2}h(m+n)a_{2}h_{002}^{(1)}(0)+D_{2}hna_{1}h_{002}^{(1)}(0). \end{aligned}$$

So, we can obtain

$$\frac{1}{6}g_{3}^{1}(x,0,\mu)= \begin{pmatrix} (b_{11}+c_{11}+d_{11})x_{1}^{2}x_{2}+(b_{12}+c_{12}+d_{12})x_{1}x_{3}^{2} \\ (\overline{b}_{11}+\overline{c}_{11}+\overline {d}_{11})x_{1}x_{2}^{2}+(\overline{b}_{12}+\overline{c}_{12}+\overline {d}_{12})x_{2}x_{3}^{2} \\ (b_{21}+c_{21}+d_{21})x_{1}x_{2}x_{3}+(b_{22}+c_{22}+d_{22})x_{3}^{3} \end{pmatrix} +\vartheta\bigl( \vert x \vert \vert \mu \vert ^{2}+ \vert x \vert ^{2} \vert \mu \vert \bigr) . $$

Therefore, on the center manifold, the system $\dot{x}=Jx+\frac {1}{2}g_{2}^{1}(x,0,\mu)+\frac{1}{6}g_{3}^{1}(x,0,\mu)+\mbox{h.o.t.}$ becomes

$$ \left\{\textstyle\begin{array}{rcl} \dot{x}_{1}&=&(a_{11}\mu_{1}+a_{12}\mu _{2})x_{1}+a_{13}x_{1}x_{3}+(b_{11}+c_{11}+d_{11})x_{1}^{2}x_{2}\\ &&{}+(b_{12}+c_{12}+d_{12})x_{1}x_{3}^{2}+\mbox{h.o.t.}, \\ \dot{x}_{2}&=&(\overline{a}_{11}\mu_{1}+\overline{a}_{12}\mu _{2})x_{2}+\overline{a}_{13}x_{2}x_{3}+(\overline{b}_{11}+\overline {c}_{11}+\overline{d}_{11})x_{1}x_{2}^{2}\\ &&{}+(\overline{b}_{12}+\overline {c}_{12}+\overline{d}_{12})x_{2}x_{3}^{2}+\mbox{h.o.t.}, \\ \dot{x}_{3}&=&(a_{21}\mu_{1}+a_{22}\mu _{2})x_{3}+a_{23}x_{1}x_{2}+a_{24}x_{3}^{2}+(b_{21}+c_{21}+d_{21})x_{1}x_{2}x_{3}\\ &&{}+(b_{22}+c_{22}+d_{22})x_{3}^{3}+\mbox{h.o.t.} \end{array}\displaystyle \right. $$

(3.11)

By changing variables $x_{1}=\rho_{1}-i\rho_{2}$, $x_{2}=\rho_{1}+i\rho _{2}$, $x_{3}=\rho_{3}$, and introducing the cylindrical coordinates $\rho_{1}=r\cos\theta$, $\rho_{2}=r\sin\theta$, $\rho_{3}=\gamma$, $r>0$, system (3.11) becomes

$$\textstyle\begin{cases} \dot{r}=\alpha_{1}(\mu)r+\beta_{11}r\gamma+\beta_{30}r^{3}+\beta _{12}r\gamma^{2}+\mbox{h.o.t.}, \\ \dot{\gamma}=\alpha_{2}(\mu)\gamma+m_{20}r^{2}+m_{02}\gamma ^{2}+m_{21}r^{2}\gamma+m_{03}\gamma^{3}+\mbox{h.o.t.}, \\ \dot{\theta}=-\omega+(\operatorname{Im}[a_{11}]\mu_{1}+\operatorname{Im}[a_{12}]\mu_{2}), \end{cases} $$

where

$$\begin{aligned} &\alpha_{1}(\mu)=\operatorname{Re}[a_{11}] \mu_{1}+\operatorname{Re}[a_{12}]\mu_{2},\qquad \beta_{11}=\operatorname{Re}[a_{13}],\qquad \beta_{30}=\operatorname{Re}[b_{11}+c_{11}+d_{11}], \\ &\beta_{12}=\operatorname{Re}[b_{12}+c_{12}+d_{12}], \qquad \alpha_{2}(\mu)=a_{21}\mu_{1},\qquad m_{20}=a_{23},\qquad m_{02}=a_{24}, \\ &m_{21}=b_{21}+c_{21}+d_{21},\qquad m_{03}=b_{22}+c_{22}+d_{22}. \end{aligned}$$

Therefore we can get the system in the plane $(r,\gamma)$:

$$ \textstyle\begin{cases} \dot{r}=\alpha_{1}(\mu)r+\beta_{11}r\gamma+\beta_{30}r^{3}+\beta _{12}r\gamma^{2}+\mbox{h.o.t.}, \\ \dot{\zeta}=\alpha_{2}(\mu)\gamma+m_{20}r^{2}+m_{02}\gamma ^{2}+m_{21}r^{2}\gamma+m_{03}\gamma^{3}+\mbox{h.o.t.} \end{cases} $$

(3.12)

From [25] we know that Eq. (3.12) becomes

$$ \left\{\textstyle\begin{array}{rcl} \dot{r}&=&(\alpha_{1}(\mu)+\beta_{11}\delta+\beta_{12}\delta^{2})r+(\beta _{11}+2\beta_{12}\delta)r\gamma+\beta_{30}r^{3}+\beta_{12}r\gamma^{2},\\ \dot{\gamma}&=&(\alpha_{2}(\mu)\delta+m_{02}\delta^{2}+m_{03}\delta ^{3})+(\alpha_{2}(\mu)+2m_{02}\delta+3m_{03}\delta^{2})\gamma\\ &&{} +(m_{20}+m_{21}\delta)r^{2} +(m_{02}+3m_{03}\delta)\gamma^{2}+m_{21}r^{2}\gamma+m_{03}\gamma^{3}. \end{array}\displaystyle \right. $$

(3.13)

Choose $\delta=\delta(\mu)$ such that

$$\alpha_{2}(\mu)+2m_{02}\delta+3m_{03} \delta^{2}=0. $$

To simplify the above system, we only discuss the case of $m_{20}\neq0, m_{03}\neq0$. Clearly, for small $\alpha_{2}(\mu)$, the equation has two real roots. We take

$$\delta= \textstyle\begin{cases} \frac{1}{3m_{03}}[-m_{02}+\sqrt{m_{02}^{2}-3m_{03}\alpha_{2}(\mu)}] &\mbox{if } m_{02}>0, \\ \frac{1}{3m_{03}}[-m_{02}-\sqrt{m_{02}^{2}-3m_{03}\alpha_{2}(\mu)}] &\mbox{if } m_{02}< 0. \end{cases} $$

Then $\delta=\delta(\mu)$ is differentiable at $\mu=0$, and $\delta (0)=0$.

Define $k_{1}=\alpha_{1}(\mu)+\beta_{11}\delta+\beta_{12}\delta^{2}$, $k_{2}=\alpha_{2}(\mu)\delta+m_{02}\delta^{2}+m_{03}\delta^{3}$, $a=\beta_{11}+2\beta_{12}\delta$, $b=m_{20}+m_{21}\delta$, $c=m_{02}+3m_{03}\delta$ and choose $x=r, y=\gamma$. Then Eq. (3.13) becomes

$$ \textstyle\begin{cases} \dot{x}=k_{1}x+axy+\beta_{30}x^{3}+\beta_{12}xy^{2} , \\ \dot{y}=k_{2}+bx^{2}+cy^{2}+\gamma_{21}x^{2}y+\gamma_{03}y^{3}. \end{cases} $$

(3.14)

Let

$$x\rightarrow\sqrt{ \vert c \vert }x,\qquad y\rightarrow\sqrt{ \vert b \vert }y,\qquad t\rightarrow{-c}\sqrt{ \vert b \vert }t $$

and

$$\eta_{1}=-\frac{k_{1}}{c\sqrt{ \vert b \vert }},\qquad \eta_{2}=- \frac{k_{2}}{c \vert b \vert }. $$

Then system (3.14) becomes

$$ \textstyle\begin{cases} \dot{x}=\eta_{1}x+Bxy+d_{1}x^{3}+d_{2}xy^{2}, \\ \dot{y}=\eta_{2}+\eta{x}^{2}-y^{2}-y^{2}+d_{3}x^{2}y+d_{4}y^{3} , \end{cases} $$

(3.15)

where

$$B=-\frac{a}{c}\neq0,\qquad \eta=-\operatorname{sgn}(bc) $$

and

$$d_{1}=-\frac{\beta_{30} \vert c \vert }{c\sqrt{ \vert b \vert }},\qquad d_{2}= \frac{\sqrt{ \vert b \vert }\beta_{12}}{c},\qquad d_{3}=-\frac{m_{21} \vert c \vert }{c\sqrt{ \vert b \vert }},\qquad d_{4}=-\frac{\sqrt{ \vert b \vert }m_{03}}{c}. $$

According to [25], we assume that

$$K_{3}=\eta\biggl(\frac{2}{B}+2\biggr)d_{1}+ \frac{2}{B}d_{2}+\eta{d}_{3}+3d_{4}\neq0. $$

For small $\eta_{1}$ and $\eta_{2}$, the qualitative behavior of (3.15) near $(0,0)$ is the same as that of the following system (see [9]):

$$ \textstyle\begin{cases} \dot{x}=\eta_{1}x+Bxy+xy^{2}, \\ \dot{y}=\eta_{2}-x^{2}-y^{2}. \end{cases} $$

(3.16)

In Eq. (3.16), there are two trivial equilibrium points $E_{1,2}=(0,\pm\sqrt{\eta_{2}}), \eta_{2}>0$, and two nontrivial equilibrium points $E_{3,4}=(\sqrt{\frac{1}{2}B(-B\pm\sqrt{B^{2}-4\eta_{1}})+\eta_{1}+\eta _{2}},\frac{1}{2}(-B\pm\sqrt{B^{2}-4\eta_{1}}))$.

In [3] and [16], we can find the complete bifurcation diagrams of system (3.13). Here we list some of them.

Theorem 3.1

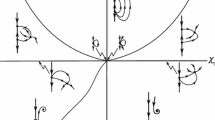
• (a) If $B<0$, then the bifurcation diagram of system (3.13) consists of the origin and the following curves:

  $$\begin{aligned} &M=\bigl\{ (\eta_{1},\eta_{2}):\eta_{2}=0, \eta_{1}\neq0\bigr\} , \\ &N=\biggl\{ (\eta_{1},\eta_{2}):\eta_{2}= \frac{1}{B^{2}}\eta_{1}^{2}+\vartheta \bigl( \eta_{1}^{3}\bigr),\eta_{1}\neq0\biggr\} . \end{aligned}$$

  Along M and N, a saddle-node bifurcation and pitchfork bifurcation occur, respectively. System (3.13) has no periodic orbits. Moreover, if $(\eta_{1},\eta_{2})$ is in the region between M and N, then the solution of system (3.13) goes asymptotically to one of the equilibrium points $E_{1}$, $E_{2}$, and $E_{3}$.

• (b) If $B>0$, then the bifurcation diagram of system (3.13) consists of the origin, the curves M and N, and the following curves:

  $$\begin{aligned} &H=\bigl\{ (\eta_{1},\eta_{2}):\eta_{1}=0, \eta_{2}>0\bigr\} , \\ &S=\biggl\{ (\eta_{1},\eta_{2}):\eta_{1}=- \frac{B}{3B+2}\eta_{2}+\vartheta \bigl( \vert \eta_{2} \vert ^{3/2}\bigr),\eta_{2}>0\biggr\} . \end{aligned}$$

  Along M and N, we have exactly the same bifurcation as in (a). Along H and S, a Hopf bifurcation and a heteroclinic bifurcation occur, respectively. If $(\eta_{1},\eta_{2})$ lies between the curves H and S, then system (3.13) has a unique limit cycle, which is unstable and becomes a heteroclinic orbit when $(\eta_{1},\eta_{2})\in{S}$.

Figures 1 and 2 show (a) and (b) of Theorem 3.1, respectively.

Figure 1

When $B<0$, the bifurcation diagrams and phase portraits of system (3.13) (see [18])

Figure 2

When $B>0$, the bifurcation diagrams and phase portraits of system (3.13) (see [18])

Figure 3

The system is asymptotically stable around the equilibrium point for $(\mu_{1},\mu_{2})=(-0.17,-0.10)$. The green line represents x, the red line represents z. Waveform diagram for variable of $x,z$ (left). Phase diagram for variable $(x,z)$ (right)

Figure 4

The system has an asymptotically stable periodic orbit near $\tau_{1}$ for $(\mu_{1},\mu_{2})=(0.11,0.10)$. The green line represents x, the red line represents z. Waveform diagram for variable of $x,z$ (left). Phase diagram for variable $(x,z)$ (right)

Figure 5

Waveform diagram for variable of $x,z$. The first two figures show that when $\tau=1.50<\tau_{10}$, the system is stable around the equilibrium point. When $\tau=1.80>\tau_{10}$, the next two figures show that the system is unstable around the equilibrium point

4 Numerical simulations

In this section, we give some examples to explain the theoretical results. Set $q=8\times10^{-4}$, $h=\frac{2}{3}$, $k=-2.5$, and $\varepsilon=4\times10^{-2}$ and consider the following system:

$$\textstyle\begin{cases} \frac{dx}{dt}=\frac{1}{\varepsilon}(x(1-x)-hz\frac{x-u}{x+u}), \\ \frac{dz}{dt}=x-z+kz(t-\tau). \end{cases} $$

By calculations we obtain $a_{11}=0.8842-0.76654i$, $a_{12}=-1.5560+1.1531$, $a_{13}=2.1439-1.3414i$, $a_{21}=2.9430$, $a_{22}=2.4523$, $a_{23}=-0.0483$, $a_{24}=-1.6154$, $b_{11}=-0.5236+0.0396i$, $b_{12}=-1.0801+1.4187i$, $b_{21}=-2.0122+0.0853i$, $b_{22}=-1.8473$, $c_{11}=0.0187-0.01301i$, $c_{12}=0.0046-0.0033i$, $c_{21}=-0.0171$, $c_{22}=-0.0130$, $d_{11}=-0.0005814-0.004575i$, $d_{12}=-0.0007235-0.002548i$, $d_{21}=-0.008275$, $d_{22}=-0.002301$; the equilibrium point is $(0.8075,0.2307)$, and $\tau_{1}=1.6735$. For small μ, we obtain $k_{3}\neq0$.

5 Conclusions

In this article, we have discussed the Hopf-zero bifurcation of Oregonator oscillator with delay. We thoroughly analyze the distribution of the eigenvalues of the corresponding characteristic equation and find some specific conditions ensuring that all the eigenvalues have negative real parts. We also can discover the factors that make system (1.2) undergo a Hopf-zero bifurcation at equilibrium $(x_{+},z_{+})$. Meanwhile, by using the normal form method and the center manifold theorem we have derived the normal form of the reduced system on the center manifold and discussed the Hopf-zero bifurcation with parameters in system (1.2). Besides, we have obtained bifurcation diagrams and phase portraits of system (3.13) when $B>0$ and $B<0$, respectively. We also note that a saddle-node bifurcation and pitchfork bifurcation occur along M and N, respectively, and a Hopf bifurcation and a heteroclinic bifurcation occur along H and S, respectively. Finally, numerical stimulations (see Figure 3, 4 and 5) have been given to illustrate the theoretical results.

Our work is a further study of the Oregonator oscillator, which will be useful in the research of the complex phenomenon caused by high codimensional bifurcation of a delay-differential equation.