Abstract
In this paper, a diffusive and delayed virus dynamics model with Crowley-Martin incidence function and CTL immune response is investigated. By constructing the Lyapunov functionals, the threshold conditions on the global stability of the infection-free, immune-free and interior equilibria are established if the space is assumed to be homogeneous. We show that the infection-free equilibrium is globally asymptotically stable if the basic reproductive number \(R_{0}\leq1\); the immune-free equilibrium is globally asymptotically stable if the immune reproduction number and the basic reproduction number satisfy \(R_{1}\leq1< R_{0}\); the interior equilibrium is globally asymptotically stable if \(R_{1}>1\).
Similar content being viewed by others
1 Introduction
Nowadays, virus infection is related to the global health problems. Many diseases which are caused by viruses, such as hepatitis B virus (HBV), human immunodeficiency virus (HIV), hepatitis C virus (HCV), have drawn the attention of researchers. Based on the virus infection models proposed in [1–18], several different mathematical models which are valuable to obtaining comprehensive views to the virus dynamics have been investigated, for example, in a form of ordinary differential equations (ODEs) [12, 19–21], delayed differential equations (DDEs) [1–5, 7, 9, 11, 22], partial differential equations (PDEs) [8, 22–28] and fractional-order differential equations (FODEs) [15–18]. Nowak and Bangham [19] pointed out the basic virus infection model which plays a critical role in understanding the virus replication dynamics in vivo. They considered the following basic mathematical model for uninfected host cells u, infected host cells w, free virus v and the magnitude of the CTL response z:
where the uninfected host cells are produced at rate λ, die at rate d and become infected at rate β. Infected host cells die at rate h and are killed by the CTL response at rate p. Free virus is produced from infected cells at rate k and is removed at rate μ. The magnitude of the CTL response, which expands in response to viral antigen derived from infected cells at rate c, decays in the absence of antigenic stimulation at rate q.
It should be mentioned here that, in model (1), the rate of infection is assumed to be bilinear, that is, \(\beta uv\). However, this assumption is not biologically sensible all the time. Recently, many researchers have performed the virus dynamics models with Crowley-Martin infection rate (see [20, 21]). The Crowley-Martin type of functional response, that is, \(\frac{\beta uv}{(1+au)(1+bv)}\), was introduced by Crowley and Martin in [29], where a, b are constants. Particularly, when \(a=0\), \(b=0\), the Crowley-Martin infection rate becomes bilinear infection rate. Thus, it is necessary to study virus infection model with Crowley-Martin infection rate. In addition, based on the epidemiological background, time delays play a critical role in the virus infection model. To incorporate the intracellular phase of the virus life-cycle, we assume that virus production occurs after the virus entry by the intracellular delay \(\tau_{1}\). The recruitment of virus producing cells at time t is given by the number of uninfected cells that were newly infected at time \(t-\tau_{1}\) and are still alive at time t (see [2, 5, 9, 11]). The constant m is assumed to be the death rate for newly infected cells during time period \([t-\tau_{1},t]\). \(e^{-m \tau_{1}}\) denotes the surviving rate of infected cells during the delay period. Virus replication delay \(\tau_{2}\) represents the time necessary for the newly produced viruses to become mature and then infectious (see [10, 14, 22]). The constant n is assumed to be the death rate of a new virus during time period \([t-\tau_{2},t]\). \(e^{-n \tau_{2}}\) denotes the surviving rate of a virus during the delay period.
Until now, there has been a large number of works about virus infection models which considered delays, but in many biological systems, the species under consideration may disperse spatially as well as evolve in time (see [30]). As a matter of fact, many models ignored the spatial mobility of cells and viruses. Recently, many authors argued that the virus moves freely in body and follows the Fickian diffusion (see [31]) and investigated the global stability properties of virus infection models with diffusion in [8, 22–28, 31]. But the research is relatively small, a lot of work needs to be further done to provide theoretical evidence for controlling disease.
In this paper, motivated by the work of [6, 22, 23], we further neglect the mobility of susceptible cells, infected cells and immune cells and consider a delayed virus infection model with Crowley-Martin infection rate and spatial diffusion:
for \(t>0\), \(x\in\Omega\subset\mathbb{R}^{n}\) with the initial conditions
and the homogeneous Neumann boundary conditions
where \(u(x, t)\), \(w(x, t)\), \(v(x, t)\) and \(z(x, t)\) represent the densities of uninfected cells, infected cells, free virus and immune cells at location x and time t, respectively. The Laplacian operator and the diffusion coefficient are denoted by Δ and D, respectively. \(\tau=\max\{\tau_{1}, \tau_{2}\}\), Ω is a connected, bounded domain in \(\mathbb{R}^{n}\) with smooth boundary ∂Ω. \(\frac{\partial}{\partial\vec{n}}\) denotes the outward normal derivative on ∂Ω. \(\phi_{i}(x,\theta)\) (\(i=1,2,3,4\)) are nonnegative and Hölder continuous in \(\bar{\Omega}\times[-\tau,0]\). The boundary conditions in (4) imply that the virus particles do not move across the boundary ∂Ω.
In this paper, the purpose is to investigate the dynamical properties of model (2), expressly the stability of equilibria. Our paper is organized as follows. In the next section, we discuss the positivity and boundedness of solutions, the threshold values and the existence of equilibria of model (2). In Section 3, by constructing Lyapunov functionals, we establish global stability of all equilibria of model (2). In Section 4, we further illustrate the dynamical behavior by numerical simulations. In the last section, we give brief conclusions.
2 Positivity, boundedness and equilibrium
In this section, our main purpose is to prove the existence, positivity and boundedness of solutions of model (2).
Theorem 2.1
For any given initial data satisfying condition (3), there exists a unique solution of model (2) defined on \([0,+\infty)\), and this solution remains nonnegative and bounded for all \(t\geq0\).
Proof
By standard existence theory [32–34], it is easy to establish the local existence of the unique solution \((u(x,t), w(x,t), v(x,t),z(x,t))\) of model (2) for \(x\in\overline{\Omega}\) and \(t\in[0,T_{\max}]\), where \(T_{\max}\) is the maximal existence time for solution of the model (2).
It is not hard to see that \(\textbf{0}=(0,0,0,0)\) and \(\textbf{M}=(M _{1}, M_{2}, M_{3}, M_{4})\) are a pair of coupled lower-upper solutions to model (2), where \(M_{1}\), \(M_{2}\), \(M_{3}\) and \(M_{4}\) satisfy
and \(l=\min\{q,h\}\). From the comparison principle [35], we have \(0\leq u(x,t)\leq M_{1}\), \(0\leq w(x,t)\leq M_{2}\), \(0\leq v(x,t) \leq M_{3}\), \(0\leq z(x,t)\leq M_{4}\) for \(x\in\overline{\Omega}\) and \(t\in[0, T_{\max}]\). Then \(u(x,t)\), \(w(x,t)\), \(v(x,t)\) and \(z(x,t)\) are bounded on \(\overline{\Omega}\times[0, T_{\max})\). By the standard theory for semilinear parabolic systems [36, 37], we can deduce that \(T_{\max}=+\infty\). This completes the proof.
In the following, we will discuss the existence of equilibria of model (2). Model (2) always has an infection-free equilibrium \(E_{0}=(u_{0}, 0, 0, 0)\), where \(u_{0}={\frac{\lambda}{d}}\). The basic reproduction number is given by
We can rewrite \(R_{0}\) in the following form:
Here, k is the rate of new virus particles produced by infected cells, \(\frac{1}{\mu}\) is the surviving period of virus, \(e^{-n\tau_{2}}\) is the surviving rate of a new virus in time period \([t-\tau_{2}, t]\), \(\frac{\beta\cdot\frac{\lambda}{d}}{1+a\cdot\frac{\lambda}{d}}\) denotes the newly infected cells which are infected by the first virus, \(e^{-m\tau_{1}}\) is the surviving rate of newly infected cells in time period \([t-\tau_{1}, t]\), and \(\frac{1}{h}\) is the surviving period of infected cells. Therefore, we easily see that \(R_{0}\) denotes the average number of the free viruses released by the infected cells which are infected by the first virus.
If \(R_{0}>1\), there exists a unique immune-free equilibrium \(E_{1}=(u_{1},w_{1},v_{1},0)\), where \(u_{1}\) is a positive root of the following equation:
and \(w_{1}={\frac{\mu e^{n\tau_{2}}}{kb}}(R^{*}-1)\), \(v_{1}={\frac{1}{b}}(R ^{*}-1)\) if and only if
Also, an immune response reproduction number is
Note that when \(R_{0}>1\) model (2) has a unique immune-free equilibrium \(E_{1}=(u_{1},w_{1},v_{1},0)\). This shows that virus infection is successful and the numbers of free viruses and infected cells at equilibrium \(E_{1}\) are \(v_{1}\) and \(w_{1}\), respectively. Furthermore, we have that \(\frac{1}{q}\) is the average life-span of CTL cells and c is the rate at which the CTL response is produced. Hence, \(R_{1}\) denotes the average number of the CTL immune cells activated by infected cells when virus infection is successful.
If \(R_{1}>1\), then model (2) has a unique interior equilibrium \(E_{2}=(u_{2}, w_{2}, v_{2}, z_{2})\), where \(u_{2}\) is a positive root of the following equation:
and
□
3 Stability analysis
In this section, we investigate the global stability of equilibria for model (2), namely, infection-free equilibrium \(E_{0}\), immune-free equilibrium \(E_{1}\) and interior equilibrium \(E_{2}\) of model (2), respectively. For the sake of convenience, we let \(y=y(x,t)\) and \(y_{\tau_{i}}=y(x,t-\tau_{i})\) for any \(y\in\{u, w, v, z\}\) and \(i\in{1,2}\).
3.1 Stability of equilibrium \(E_{0}\)
Theorem 3.1
If \(R_{0} \leq1\), then the infection-free equilibrium \(E_{0}\) of model (2) is globally asymptotically stable.
Proof
Construct a Lyapunov functional
where
We have
Calculating the derivative of \(W(t)\) along the positive solution of model (2), we get
Owing to the divergence theorem and the homogeneous Neumann boundary conditions (4), we obtain
Thus, we further have
Therefore, \(\frac{dW(t)}{dt}\leq0\) if \(R_{0} \leq1\). We have \(\frac{dW(t)}{dt}= 0\) if and only if \(u=u_{0}\), \(w=0\), \(v=0\) and \(z=0\). It follows that the largest invariant set \(\{(u,w,v,z)\in R ^{4}_{+}: \frac{dW(t)}{dt}=0\}\) is the singleton \(E_{0}\). By using LaSalle’s invariance principle [30], we see that the equilibrium \(E_{0}\) of model (2) is globally asymptotically stable when \(R_{0}\leq1\). □
3.2 Stability of equilibrium \(E_{1}\)
Theorem 3.2
If \(R_{1}\leq1< R_{0}\), then the immune-free equilibrium \(E_{1}\) of model (2) is globally asymptotically stable.
Proof
Let \(G(x,t)=g(x,t)-1-\ln g(x,t)\). We have that \(G(x,t)\geq0\) for all \(g(x,t)>0\) and \(G(x,t)=0\) if and only if \(g(x,t)=1\). Define a Lyapunov functional
where
We have
By using the equilibrium equation, we get \(\lambda=du_{1}+e^{m\tau _{1}}hw_{1}\), \({\frac{h\mu e^{n\tau_{2}}}{k}}={\frac{hw_{1}}{v_{1}}}\) and \({\frac{\beta u_{1}v_{1}}{(1+au_{1})(1+bv_{1})}}=hw _{1}e^{m\tau_{1}}\). Thus, we have
due to
Then we have
We know that
Thus,
Also, \(R_{1}\leq1\) implies that \(w_{1}\leq{\frac{q}{c}}\). Therefore, if \(R_{1}\leq1< R_{0}\), we can obtain \({\frac{dV(t)}{dt}}\leq0\). Obviously, \({\frac{dV(t)}{dt}}= 0\) if and only if \(u=u_{1}\), \(w=w_{1}\), \(v=v_{1}\) and \(z=0\). It follows that the largest invariant set \(\{(u,w,v,z)\in R ^{4}_{+}: \frac{dV(t)}{dt}=0\}\) is the singleton \(E_{1}\). By LaSalle’s invariance principle [30], we finally conclude that the equilibrium \(E_{1}\) is globally asymptotically stable when \(R_{1}\leq1< R_{0}\). □
3.3 Stability of equilibrium \(E_{2}\)
Theorem 3.3
If \(R_{1}>1\), then the interior equilibrium \(E_{2}\) of model (2) is globally asymptotically stable.
Proof
Consider a Lyapunov functional \(L(t)\) as follows:
where
By calculating the time derivative of \(L_{1}(x,t)\) and \(L_{2}(x,t)\), we have
and
Note that the interior equilibrium \(E_{2}(u_{2}, w_{2}, v_{2}, z_{2})\) satisfies the following equations:
We obtain that \(\lambda=du_{2}+e^{m\tau_{1}}(hw_{2}+pw_{2}z_{2})\), \({\frac{pw_{2}}{v_{2}}}={\frac{p\mu}{k}}\), \(w_{2}={\frac{q}{c}}\) and \(e^{m\tau_{1}}(hw _{2}+pw_{2}z_{2})={\frac{\beta u_{2}v_{2}}{(1+au_{2})(1+bv_{2})}}\). Thus, we have
Since
we further have
Therefore, we have \({\frac{dL(t)}{dt}}\leq0\) when \(R_{1}>1\). \({\frac{dL(t)}{dt}}=0\) if and only if \(u=u_{2}\), \(w=w_{2}\), \(v=v_{2}\) and \(z=z_{2}\). It follows that the largest invariant set \(\{(u,w,v,z) \in R^{4}_{+}: \frac{dL(t)}{dt}=0\}\) is the singleton \(E_{2}\). Based on LaSalle’s invariance principle [30], we conclude that the equilibrium \(E_{2}\) is globally asymptotically stable when \(R_{1}>1\). □
4 Numerical simulations
In the previous section, we analyzed the global stability of a model of virus infection with diffusion and time delay. The object of this section is to further illustrate the obtained theoretical results by some numerical simulations. The Runge-Kutta scheme of fourth order is applied for the reaction part and an explicit Euler scheme for the diffusion part of the PDE. Next, we consider model (2) with the homogeneous Neumann boundary conditions
and the initial conditions
In model (2), we choose β, c, q, \(\tau_{1}\), \(\tau_{2}\) as free parameters, and all remaining parameters are fixed as in Table 1.
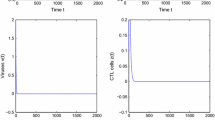
In Figures 1, 2 and 3, (a), (b), (c) and (d) denote time-series figures of \(u(x,t)\), \(w(x,t)\), \(v(x,t)\) and \(z(x,t)\).
Taking \(\pmb{\beta=0.3}\) , \(\pmb{c=0.01}\) , \(\pmb{q=0.15}\) , \(\pmb{\tau _{1}=10}\) , \(\pmb{\tau_{2}=5}\) , we have \(\pmb{R_{0}=6.2597>1}\) , \(\pmb{R_{1}=1.2303>1}\) , the infection equilibrium only with CTL immune response \(\pmb{E_{2}(10.9402,15,1.7214,0.1272)}\) is globally asymptotically stable.
5 Discussion
In this paper, we propose a delayed virus infection model with diffusion, CTL immune responses and Crowley-Martin incidence rate. We have showed the global asymptotic stability of infection-free equilibrium \(E_{0}\), immune-free equilibrium \(E_{1}\) and interior equilibrium \(E_{2}\). By the analysis, the infection-free equilibrium \(E_{0}\) is globally asymptotically stable if \(R_{0}\leq1\); in such circumstances, the viruses are cleared and the infection dies out. If \(R_{1}\leq1< R_{0}\), the immune-free equilibrium \(E_{1}\) is globally asymptotically stable, it is shown that immune response would not be activated and virus infection becomes vanished. If \(R_{1}>1\), model (2) has an interior equilibrium \(E_{2}\), which is globally asymptotically stable. Mathematically, in order to find treatment strategies, we have to find the analytical conditions under which trajectories of the model will converge to infection-free equilibrium. This condition is given in Theorem 3.1, that is, the infection-free equilibrium is globally asymptotically stable if \(R_{0}=\frac{\beta k \lambda}{\mu h(d+a \lambda) e^{m\tau_{1}+n\tau_{2}}}<1\). This relation relies on parameters β, \(\tau_{1}\) and \(\tau_{2}\). That is to say, the variation of these three parameters plays a vital role in disease treatment, and doctors have to adjust these parameters according to the above relation in order to eliminate virus infection. The parameters β, \(\tau_{1}\) and \(\tau_{2}\) might be changed as a consequence of disease treatment. The above analysis shows that \(R_{0}\) increases proportionally to parameter β and decreases proportionally to parameters \(\tau_{1}\) and \(\tau_{2}\). Thus, in order to eliminate the infection, we need to try to increase the value of \(\tau_{1}\) or \(\tau_{2}\). By decreasing infection rate β, immune-free and interior equilibria disappear and infection-free equilibrium will become stable, which implies the virus eradication and that the patient is cured.
Another important issue from medical point of view is to investigate the factors which cause growth of virus. Mathematically, the relations for existence and stability of interior equilibrium need to be investigated. This matter is solved in Theorem 3.3, which gives possible conditions for the existence of interior equilibrium and describes criteria for the stability of interior equilibrium.
Mathematical models can help physicians to choose a suitable dosage and check the effects of their therapeutic action. Virus infection progression has many variations from patient to patient, which is difficult to obtain by an ordinary differential equation. By choosing a relevant diffusive coefficient, the partial differential equation can be varied to best fit the real data according to the progression of different patients. Consequently, the clinician can recommend administration of drugs or treatment strategies to each individual by using the information from the delayed model with the relevant diffusive coefficient.
Our model considers a four-dimensional diffusive virus infection model with intracellular delay, virus replication delay and Crowley-Martin infection rate. It is considered whether the results also can be extended to five-dimensional diffusive virus infection model with mitosis transmission and immune delay. We leave this for the future work.
References
Miao, H, Teng, Z, Kang, C, Muhammadhaji, A: Stability analysis of a virus infection model with humoral immunity response and two time delays. Math. Methods Appl. Sci. 39, 3434-3449 (2016)
Shu, H, Wang, L, Watmoughs, J: Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL immune responses. SIAM J. Appl. Math. 73, 1280-1302 (2013)
Yuan, Z, Zou, X: Global threshold dynamics in an HIV virus model with nonlinear infection rate and distributed invasion and production delays. Math. Biosci. Eng. 10, 483-498 (2013)
Pawelek, K, Liu, S, Pahlevani, F, Rong, L: A model of HIV-1 infection with two time delays: mathematical analysis and comparison with patient data. Math. Biosci. 235, 98-109 (2012)
Nelson, P, Murray, J, Perelson, A: A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 163, 201-215 (2000)
Li, X, Fu, S: Global stability of the virus dynamics model with intracellular delay and CTL immune response. Math. Methods Appl. Sci. 38, 420-430 (2015)
Miao, H, Teng, Z, Li, Z: Global stability of delayed viral infection models with nonlinear antibody and CTL immune responses and general incidence rate. Comput. Math. Methods Med. 2016, Article ID 3903726 (2016). doi:10.1155/2016/3903726
Xu, R, Ma, Z: An HBV model with diffusion and time delay. J. Theor. Biol. 257, 499-509 (2009)
Zhu, H, Zou, X: Dynamics of a HIV-1 infection model with cell-mediated immune response and intracellular delay. Discrete Contin. Dyn. Syst., Ser. B 12, 511-524 (2009)
Ji, Y: Global stability of a multiple delayed viral infection model with general incidence rate and an application to HIV infection. Math. Biosci. Eng. 12, 525-536 (2015)
Wang, X, Elaiw, A, Song, X: Global properties of a delayed HIV infection model with CTL immune response. Appl. Math. Comput. 218, 9405-9414 (2012)
Wang, Y, Zhou, Y, Brauer, F, Heffernan, J: Viral dynamics model with CTL immune response incorporating antiretroviral therapy. J. Math. Biol. 67, 901-934 (2013)
Lu, X, Hui, L, Liu, S, Li, J: A mathematical model of HIV-I infection with two time delays. Math. Biosci. Eng. 12, 431-449 (2015)
Xiang, H, Feng, X, Huo, H: Stability of the virus dynamics model with Beddington-DeAngelis functional response and delays. Appl. Math. Model. 37, 5414-5423 (2013)
Arshad, S, Baleanu, D, Bu, W, Tang, Y: Effects of HIV infection on CD4+ T-cell population based on a fractional-order model. Adv. Differ. Equ. 2017, Article ID 92 (2017)
Singh, J, Kumar, D, Qurashi, M, Baleanu, D: A new fractional model for giving up smoking dynamics. Adv. Differ. Equ. 2017, Article ID 88 (2017)
Arshad, S, Baleanu, D, Huang, J, Tang, Y, Qurashi, M: Dynamical analysis of fractional order model of immunogenic tumors. Adv. Mech. Eng. 8, 1-13 (2016)
Khodabakhshi, N, Mansour, S, Baleanu, D: On dynamics of fractional-order model of HCV infection. J. Math. Anal. 8, 16-27 (2017)
Nowak, M, Bangham, C: Population dynamics of immune response to persistent viruses. Science 272, 74-79 (1996)
Zhou, X, Cui, J: Global stability of the virus dynamics model with Crowley-Martin functional response. Bull. Korean Math. Soc. 48, 555-574 (2011)
Xu, S: Global stability of the virus dynamics model with Crowley-Martin functional response. Electron. J. Qual. Theory Differ. Equ. 2012, Article ID 9 (2012). doi:10.14232/ejqtde.2012.1.9
Yang, Y, Xu, Y: Global stability of a diffusive and delayed virus dynamics model with Beddington-DeAngelis incidence function and CTL immune response. Comput. Math. Appl. 71, 922-930 (2016)
McCluskey, C, Yang, Y: Global stability of a diffusive virus dynamics model with general incidence function and time delay. Nonlinear Anal., Real World Appl. 25, 64-78 (2015)
Wang, S, Feng, X, He, Y: Global asymptotical properties for a diffused HBV infection model with CTL immune response and nonlinear incidence. Acta Math. Sci. 31, 1959-1967 (2011)
Hattaf, K, Yousfi, N: A generalized HBV model with diffusion and two delays. Comput. Math. Appl. 69, 31-40 (2015)
Zhang, Y, Xu, Z: Dynamics of a diffusive HBV model with delayed Beddington-DeAngelis response. Nonlinear Anal., Real World Appl. 15, 118-139 (2014)
Wang, F, Huang, Y, Zou, X: Global dynamics of a PDE in-host viral model. Appl. Anal. 93, 2312-2329 (2014)
Hattaf, K, Yousfi, N: Global stability for reaction-diffusion equations in biology. Comput. Math. Appl. 66, 1488-1497 (2013)
Crowley, P, Martin, E: Functional responses and interferences within and between year classes of a dragonfly population. J. North Am. Benthol. Soc. 8, 211-221 (1989)
Wu, J: Theory and Applications of Partial Functional Differential Equations. Springer, NewYork (1996)
Gourley, S, So, J: Dynamics of a food-limited population model incorporating nonlocal delays on a finite domain. J. Math. Biol. 44, 49-78 (2002)
Amann, H: Dynamics theory of quasilinear parabolic equations-I: abstract evolution equations. Nonlinear Anal. 12, 895-919 (1988)
Amann, H: Dynamics theory of quasilinear parabolic equations-II: reaction-diffusion. Differ. Integral Equ. 3, 13-75 (1990)
Amann, H: Dynamics theory of quasilinear parabolic equations-III: global existence. Math. Z. 202, 219-250 (1989)
Protter, M, Weinberger, H: Maximum Principles in Differential Equations. Prentice Hall International, Englewood Cliffs (1967)
Redlinger, R: Existence theorems for semilinear parabolic systems with functionals. Nonlinear Anal., Theory Methods Appl. 8, 667-682 (1984)
Henry, D: Geometric Theory of Semilinear Parabolic Equations. Lecture Notes in Mathematics, vol. 840. Springer, Berlin (1993). doi:10.1007/BFb0089647
Acknowledgements
This work was supported by 2016xgy041812, NSFXJ (No. 2015211B005), NSFC (No. 11661077), NSFC (No. 11301452), the Youth Cultivation Project for Innovative Talents of Xinjiang (No. qn2015bs013).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
KC and MH provided the subject, wrote the introduction and the conclusion and verified some calculations. CX and XJ conceived the study and computed the equilibria and their global stabilities. HD checked the proofs and verified the calculation. All the authors read and approved the final manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kang, C., Miao, H., Chen, X. et al. Global stability of a diffusive and delayed virus dynamics model with Crowley-Martin incidence function and CTL immune response. Adv Differ Equ 2017, 324 (2017). https://doi.org/10.1186/s13662-017-1332-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1332-x