1 Introduction

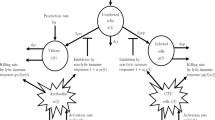
Mathematical models have been developed to explore mechanisms and dynamical behaviors in host virus infection process, and these provide insights into our understanding of HIV and other viruses; for example, HBV, HCV, influenza, SARS and Ebola are formulated and studied in many articles. Mathematical analysis for these models are necessary to obtain an integrated view for the virus dynamics in vivo. Nowak and Bangham (1996) pointed out that cytotoxic T-lymphocyte (CTL) immune responses play a critical part in antiviral defense by attacking virus-infected cells in most virus infections. They proposed the basic mathematical model describing immune responses against infected cells

$$\begin{aligned} \begin{aligned} \displaystyle {\displaystyle \frac{\mathrm{d}u(t)}{\mathrm{d}t}}&=\displaystyle \lambda -\mathrm{d}u(t)- \beta u(t)v(t),\\ \displaystyle {\displaystyle \frac{\mathrm{d}w(t)}{\mathrm{d}t}}&=\displaystyle \beta u(t)v(t) -a w(t)-pw(t)z(t),\\ \displaystyle {\displaystyle \frac{\mathrm{d}v(t)}{\mathrm{d}t}}&=\displaystyle kw(t)-mv(t),\\ \displaystyle {\displaystyle \frac{\mathrm{d}z(t)}{\mathrm{d}t}}&=\displaystyle cw(t)z(t)-bz(t), \end{aligned} \end{aligned}$$
(1)

where the uninfected susceptible host cells u are produced at a rate \(\lambda \), die at rate d, and become infected at rate \(\beta \). Infected host cells, w, die at rate a and are killed by the CTL response at rate p. Free virus v are produced from infected cells at rate k and are removed at rate m. The variable z denotes the magnitude of the CTL response, which expands in response to viral antigen derived from infected cells at rate c, and decays in the absence of antigenic stimulation at rate b.

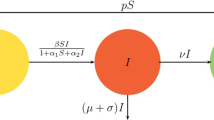
Usually the rate of infection in most virus infection models is assumed to be bilinear in the virus v and the uninfected cells u. However, the actual incidence rate is probably not linear over the entire range of v and u. Thus, it is reasonable to assume that the infection rate is given by the Beddington–DeAngelis functional response, \(\frac{\beta u(t)v(t)}{1+a_1u(t)+a_2v(t)}\), where \(a_1,a_2>0\) are constants. The functional response \(\frac{\beta u(t)v(t)}{1+a_1u(t)+a_2v(t)}\) was introduced by Beddington (1975) and DeAngelis et al. (1975). It is similar to the well-known Holling type II functional response but has an extra term \(a_2v\) in the denominator which models mutual interference between virus. When \(a_1>0; a_2=0\), the Beddington–DeAngelis functional response is simplified to Holling type II functional response (Li and Ma 2007). And when \(a_1=0\) and \(a_2>0\), it expresses a saturation response (Song and Neumann 2007). They obtained some criterion for the local asymptotic stability of the positive equilibrium of model (1) and gave the global stability of the positive equilibrium by constructing Lyapunov functions. Balasubramaniam et al. (2015) and Pawelek et al. (2012) performed detailed qualitative and bifurcation analysis such as the stability of equilibria and Hopf bifurcation.

Note that it is implicitly assumed that cells and viruses are well mixed, and the spatial mobility of cells and viruses has been ignored in model (1). Model (1) has been traditionally formulated in relation to the time evolution of uniform population distributions in a habitat and areas such governed by ordinary differential equations. However, as discussed by Wu (1996), in many biological systems, the species under consideration may disperse spatially as well as evolving in time. The mobility of susceptible cells, infected cells and immune cells is further neglected under normal conditions, but viruses move freely in body in McCluskey and Yang (2015), Gourley and So (2002), Xu and Ma (2009), Hattaf and Yousfi (2013, 2015), Wang et al. (2011, 2014) and Zhang and Xu (2014). They introduced the random mobility for viruses into model (1) and assume that the motion of virus follows the Fickian diffusion. Yang and Xu (2016) proposed the following virus infection model with spatial dependence

$$\begin{aligned} {\displaystyle \frac{\partial u(x,t)}{\partial t}}= & {} \displaystyle \lambda -\mathrm{d}u(x,t)- {\displaystyle \frac{\beta u(x,t)v(x,t)}{1+a_1u(x,t)+a_2v(x,t)}},\nonumber \\ {\displaystyle \frac{\partial w(x,t)}{\partial t}}= & {} \displaystyle {\displaystyle \frac{\mathrm{e}^{-\alpha \tau }\beta u(x,t-\tau )v(x,t-\tau )}{1+a_1u(x,t-\tau )+a_2v(x,t-\tau )}}\nonumber \\&-\,a w(x,t)-pw(x,t)z(x,t),\nonumber \\ {\displaystyle \frac{\partial v(x,t)}{\partial t}}= & {} \displaystyle D\triangle v(x,t)+kw(x,t)-mv(x,t),\\ {\displaystyle \frac{\partial z(x,t)}{\partial t}}= & {} \displaystyle cw(x,t)z(x,t)-bz(x,t),\nonumber \end{aligned}$$
(2)

where \(u(x, t),\; w(x, t),\; v(x, t)\) and z(x, t) represent the densities of uninfected cells, infected cells, free virus and immune cells at location x and time t, respectively. The Laplacian operator and the diffusion coefficient are denoted by \(\triangle \) and D, respectively. It is demonstrated in model (2) that by constructing Lyapunov functionals and using LaSalle’s invariance principle, the global stability of the model is established. More recently, the global dynamics of diffusive virus dynamic models have been studied in McCluskey and Yang (2015), Gourley and So (2002), Xu and Ma (2009), Hattaf and Yousfi (2013, 2015), Wang et al. (2011, 2014) and Zhang and Xu (2014).

During viral infections, the immune system reacts against virus. The antibody and CTLs play the crucial roles in preventing and modulating infections. The antibody response is implemented by the functioning of immunocompetent B lymphocytes. The CTL response has the ability to suppress the virus replication in vivo. Hence, an effective vaccine to prevent virus infection needs both strong neutralizing antibody and CTL responses (Balasubramaniam et al. 2015; Wodarz 2003; Yan and Wang 2012; Wang et al. 2014). Therefore, some of the typical HIV infection models are described by delay differential equations, considering the dynamics of target cell, virus populations and immune response has been studied in recent years (Nelson and Perelson 2000; Yan and Wang 2012; Zhu and Zou 2009; Shu et al. 2013; Yuan and Zou 2013; Balasubramaniam et al. 2015; Wang et al. 2012, 2014; Pawelek et al. 2012; Huang et al. 2011; Ji 2015; Lu et al. 2015; Xiang et al. 2013). There are some models which include intracellular delay (Nelson and Perelson 2000; Yan and Wang 2012; Zhu and Zou 2009; Shu et al. 2013; Wang et al. 2012, 2014; Pawelek et al. 2012; Huang et al. 2011); some authors believe that time delays cannot be ignored in models for production viruses (Shu et al. 2013; Wang et al. 2014; Ji 2015; Xiang et al. 2013). Therefore, it is more realistic to investigate delayed virus infection models with antibody and CTL responses and nonlinear incidences. However, to our knowledge, there are few works on diffusive virus dynamics model with time delay and adaptive immune response.

Motivated by the works of Yang and Xu (2016), Yan and Wang (2012), Wang et al. (2014) and McCluskey and Yang (2015), we propose a delayed virus infection model with generalized incidence rate and spatial diffusion

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\partial u}{\partial t}}&=\displaystyle \lambda -\mathrm{d}u(x,t)-f(u(x,t),w(x,t),v(x,t))v(x,t),\\ {\displaystyle \frac{\partial w}{\partial t}}&=\displaystyle \mathrm{e}^{-a_1\tau _1}f(u(x,t-\tau _1),w(x,t-\tau _1),v(x,t-\tau _1))v(x,t-\tau _1)\\&\quad \displaystyle -aw(x,t)-pw(x,t)z(x,t),\\ {\displaystyle \frac{\partial v}{\partial t}}&=\displaystyle D\triangle v(x,t)+k\mathrm{e} ^{-a_2\tau _2}w(x,t-\tau _2)-mv(x,t)-qv(x,t)y(x,t),\\ {\displaystyle \frac{\partial z}{\partial t}}&=\displaystyle cw(x,t)z(x,t)-bz(x,t),\\ {\displaystyle \frac{\partial y}{\partial t}}&=\displaystyle gv(x,t)y(x,t)-hy(x,t), \end{aligned} \end{aligned}$$
(3)

for \(t>0,x\in \Omega \), where y(x, t) represents the densities of antibody cells at location x and time t, h represents the death rate of the antibody response, q is the antibody cells neutralize rate, g is the birth rate of the antibody response. And the other parameters are the same meaning as model (1).

In model (3), based on the epidemiological background, to incorporate the intracellular phase of the virus life cycle, we assume that virus production occurs after the virus entry by the intracellular delay \(\tau _1\). The recruitment of virus-producing cells at time t is given by the number of the uninfected cells that were newly infected at time \(t-\tau _1\) and are still alive at time t (Nelson and Perelson 2000; Yan and Wang 2012; Zhu and Zou 2009; Shu et al. 2013; Wang et al. 2012, 2014; Pawelek et al. 2012; Huang et al. 2011). The constant \(a_1\) is assumed to be the death rate for newly infected cells during time period \([t-\tau _1,t]\). \(\mathrm{e}^{-a_1\tau _1}\) denotes the surviving rate of infected cells during the delay period. Virus replication delay \(\tau _2\) represents the time necessary for the newly produced viruses to become mature and then infectious, that is, the maturation time of the newly produced viruses (Shu et al. 2013; Wang et al. 2014; Ji 2015; Xiang et al. 2013). The constant \(a_2\) is assumed to be the death rate for new virus during time period \([t-\tau _2,t]\). \(\mathrm{e}^{-a_2\tau _2}\) denotes the surviving rate of virus during the delay period.

We assume that the contacts between target cells, infected cells and viruses are given by an incidence function f(u, w, v),  which is assumed to satisfy the following conditions:

\((A_1)\) Function \(f:\mathbb {R}_{+}^5\rightarrow \mathbb {R}_{+}\) is continuously differentiable; \(f(0,w,v)=0\) for all \(w\ge 0\) and \(v\ge 0;\) \(\frac{\partial f(u,w,v)}{\partial u}>0,\;\frac{\partial f(u,w,v)}{\partial w}\le 0\) and \(\frac{\partial f(u,w,v)}{\partial v}\le 0\) for all \(u\ge 0,\; w\ge 0\) and \(v\ge 0.\)

From assumption \((A_1)\), we easily obtain that there are no new infected cells (i.e., \(f(u,w,v)=0\)) without healthy cells (\(u= 0\)) or virus (\(v=0\)). If the total number of virus is constant, the more the amount of cell is, then the more the average number of cells which are infected by each virus in the unite time will be. If the total number of cells is constant, the more the amount of infected cells or virus is, then the less the average number of cells which are infected by each infected cell or virus in the unite time will be.

It is easy to check that class of functions f(u, w, v) satisfying \((A_1)\) include incidence functions such as \(f(u,w,v) =\frac{\beta uv}{1+bv}\) (Wang et al. 2013), \(f(u,w,v)=\frac{\beta uv}{1+au+bv}\) (Huang et al. 2011) and \(f(u,w,v) = \frac{\beta uv}{1+au+bv+cuv}\) (Zhou and Cui 2011), where constants \(\beta , a, b, c >0\).

We consider model (3) with initial conditions

$$\begin{aligned} u(x,\theta )= & {} \phi _1(x,\theta )\ge 0,\quad w(x,\theta )=\phi _2(x,\theta )\ge 0,\nonumber \\ v(x,\theta )= & {} \phi _3(x,\theta )\ge 0,\quad z(x,\theta )=\phi _4(x,\theta )\ge 0,\\ y(x,\theta )= & {} \phi _5(x,\theta )\ge 0,\quad x\in \bar{\Omega },\quad \;\theta \in [-\tau ,0],\nonumber \end{aligned}$$
(4)

and homogeneous Neumann boundary conditions

$$\begin{aligned} \frac{\partial v}{\partial \vec {n}}=0,\quad \; t>0,\quad \;x\in \partial \Omega , \end{aligned}$$
(5)

where \(\tau =\max \{\tau _1,\;\tau _2\},\) \(\Omega \) is a connected, bounded domain in \(\mathbb {R}^n\) with smooth boundary \(\partial \Omega .\) \(\frac{\partial }{\partial \vec {n}}\) denotes the outward normal derivative on \(\partial \Omega .\) \(\phi _i(x,\theta )(i=1,2,3,4,5)\) is H\(\ddot{o}\)lder continuous in \(\bar{\Omega }\times [-\tau ,0].\) The boundary conditions in (5) imply that the virus particles do not move across the boundary \(\partial \Omega \). \(\Delta \) is the Laplacian operator. D is the diffusion coefficient of the virus particles.

In this paper, our purpose is to investigate the dynamical properties of model (3), expressly the stability of equilibria. The reproduction numbers for viral infection, antibody immune response, CTL immune response, CTL immune competition and antibody immune competition, respectively, are calculated. By using Lyapunov functionals and LaSalle’s invariance principle, the threshold conditions for the global asymptotic stability of equilibria for infection-free \(E_0\), immune-free \(E_1\), antibody response \(E_2\), and infection only with CTL response \(E_3\) and infection with both antibody and CTL responses \(E_4\) are established, respectively. By using the linearization method, the instability of equilibria for \(E_0, E_1, E_2\) and \(E_3\), respectively, also is established.

The organization of this paper is as follows. In the next section, the basic properties of model (3) for the positivity and boundedness of solutions, the threshold values and the existence of equilibria are discussed. In Section 3, under the additional assumptions \((A_1)\)–\((A_2)\), the threshold conditions on the global stability and instability for \(E_0, E_1, E_2, E_3\) and \(E_4\) are stated and proved. In Sect. 4, the numerical simulations are given to further illustrate the dynamical behavior of the model. In the last section, we will give a conclusion.

2 Positivity, boundedness and equilibrium

In this section, we show the existence, positivity and boundedness of solutions of model (3)–(5) as they represent the densities of uninfected cells, infected cells, free virus, CTL immune cells and antibody cells. Further, we discuss the existence of equilibria of model (3).

Let \(C= C([-\tau ,0],X)\) be the Banach space of continuous functions from \([-\tau ,0]\) into X with the norm \(\parallel \phi \parallel \,=\,\max _{\theta \in [-\tau ,0]}\parallel \phi (\theta )\parallel _{X}\). In our case, X is the Banach space \(C(\overline{\Omega }, R^5)\) and C(E, F) denotes the space of continuous functions from the topological space E into the space F. For convenience, we identify an element \(\phi \in C\) as a function from \(\overline{\Omega }\times [-\tau ,0]\) into \(R^5\) defined by \(\phi (x,s)=\phi (s)(x)\).

For any continuous function \(\omega (\cdot ): [-\tau ,b)\rightarrow X\) for \(b>0\), we define \(\omega _t\in C\) by \(\omega _t(s) = \omega (t+s),\; s\in [-\tau ,0]\). It is not hard to see that \(t\rightarrow \omega _t\) is a continuous function from [0, b) to C.

Theorem 2.1

For any given initial data \(\phi \in C\) satisfying the condition (4), there exists a unique solution of model (3)–(5) defined on \([0,+\infty )\) and this solution remains nonnegative and bounded for all \(t\ge 0\).

Proof

For any \(\phi = (\phi _1,\phi _2,\phi _3,\phi _4,\phi _5)^T\in C\) and \(x\in \overline{\Omega }\), we define \(F=(F_1,F_2,F_3,F_4, F_5):C\rightarrow X\) by

$$\begin{aligned} \begin{aligned} F_1(\phi )(x)&=\displaystyle \lambda -\mathrm{d}\phi _1(x,0)-f(\phi _1(x,0),\phi _2(x,0),\phi _3(x,0))\phi _3(x,0),\\ F_2(\phi )(x)&=\displaystyle \mathrm{e}^{-a_1\tau _1}f(\phi _1(x,-\tau _1),\phi _2(x,-\tau _1),\phi _3(x,-\tau _1))\phi _3(x,-\tau _1)\\&\quad \displaystyle -a\phi _2(x,0)-p\phi _2(x,0)\phi _4(x,0),\\ F_3(\phi )(x)&=\displaystyle k\mathrm{e} ^{-a_2\tau _2}\phi _2(x,-\tau _2)-m\phi _3(x,0)-q\phi _3(x,0)\phi _5(x,0),\\ F_4(\phi )(x)&=\displaystyle c\phi _2(x,0)\phi _4(x,0)-b\phi _4(x,0),\\ F_5(\phi )(x)&=\displaystyle g\phi _3(x,0)\phi _5(x,0)-h\phi _5(x,0). \end{aligned} \end{aligned}$$

Then, model (3)–(5) can be rewritten as the following abstract functional differential equation:

$$\begin{aligned} \omega '(t)= & {} \displaystyle A\omega +F(\omega _t),\quad \;t>0,\nonumber \\ \omega (0)= & {} \displaystyle \phi \in X, \end{aligned}$$
(6)

where \(\omega = (u,w,v,z,y)^\mathrm{T} , \phi = (\phi _1,\phi _2,\phi _3,\phi _4,\phi _5)^\mathrm{T}\) and \(A\omega =(0,0,D\triangle v,0,0)^\mathrm{T}\). It is clear that F is locally Lipschitz in X. From Wu (1996), we deduce that model (6) admits a unique local solution on \([0, T_{\mathrm{max}})\), where \(T_{\mathrm{max}}\) is the maximal existence time for solution of model (6).

Therefore, we have \(u(x, t)\ge 0,\;w(x, t)\ge 0,\; v(x, t)\ge 0,\;z(x, t)\ge 0\) and \(y(x, t)\ge 0\) because 0 is a sub-solution of each equation of model (3).

Next, we prove the boundedness of solutions. Denote

$$\begin{aligned} T_1(x,t)=\mathrm{e}^{-a_1\tau _1}u(x,t-\tau _1)+w(x,t)+\frac{p}{c}z(x,t). \end{aligned}$$

So we have

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\partial T_1(x,t)}{\partial t}}&=\displaystyle \lambda \mathrm{e}^{-a_1\tau _1}- -d\mathrm{e}^{-a_1\tau _1}u(x,t-\tau _1)-aw(x,t) -{\displaystyle \frac{pb}{c}}z(x,t)\\&\le \lambda \mathrm{e}^{-a_1\tau _1}-l_1T_1(x,t), \end{aligned} \end{aligned}$$

where \(l_1= \min \{d,a,b\}\). Hence,

$$\begin{aligned} T_1(x,t)\le \max \left( \frac{\lambda \mathrm{e}^{-a_1\tau _1}}{l_1},\max _{x\in \overline{\Omega }} \left\{ \mathrm{e}^{-a_1\tau _1}\phi _1(x,\tau _1)+\phi _2(x,0)+\frac{p}{c}\phi _4(x,0)\right\} \right) . \end{aligned}$$

This implies that \(u,\;w\) and z are bounded for large t.

From the boundedness of w and (3)–(5), we deduce that v satisfies the following system

$$\begin{aligned} \begin{aligned}&{\displaystyle \frac{\partial v}{\partial t}}-D\triangle v(x,t)\le k\mathrm{e} ^{-a_2\tau _2}\xi -mv(x,t)-qv(x,t)y(x,t),\\&{\displaystyle \frac{\partial v}{\partial \vec {n}}}=0,\\&v(x,0)=\phi _3(x,0)\ge 0, \end{aligned} \end{aligned}$$

where \(\xi =\max (\frac{\lambda \mathrm{e}^{-a_1\tau _1}}{l_1},\max _{x\in \overline{\Omega }} \{\mathrm{e}^{-a_1\tau _1}\phi _1(x,\tau _1)+\phi _2(x,0)+\frac{p}{c}\phi _4(x,0)\}).\)

Let \(v_1(t)\) be a solution to the ordinary differential equation

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\mathrm{d} v_1}{\mathrm{d} t}}&= k\mathrm{e} ^{-a_2\tau _2}\xi -mv-qvy,\\ v_1(0)&=\max _{x\in \overline{\Omega }}\phi _3(x,0). \end{aligned} \end{aligned}$$

Denote

$$\begin{aligned} T_2(x,t)=\mathrm{e}^{-a_1\tau _1}v_1(t)+\frac{q}{g}y(x,t). \end{aligned}$$

So we can get

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\partial T_2(x,t)}{\partial t}}&=\displaystyle k\mathrm{e} ^{-a_2\tau _2}\xi -mv_1-\frac{qh}{g}y\\&\le k \mathrm{e}^{-a_2\tau _2}\xi -l_2T_2(x,t), \end{aligned} \end{aligned}$$

where \(l_2= \min \{m,h\}\). Hence,

$$\begin{aligned} T_2(x,t)\le \max \left( \frac{k\mathrm{e} ^{-a_2\tau _2}\xi }{l_2},\max _{x\in \overline{\Omega }} \left\{ \phi _3(x,0)+\frac{q}{g}\phi _5(x,0)\right\} \right) . \end{aligned}$$

Then \(v_1(t)\le \max (\frac{k\mathrm{e} ^{-a_2\tau _2}\xi }{l_2},\max _{x\in \overline{\Omega }} \{\phi _3(x,0)+\frac{q}{g}\phi _5(x,0)\}).\)

From the comparison principle Protter and Weinberger (1967), we get \(v(x, t)\le v_1(t)\). Hence,

$$\begin{aligned} v(x,t)\le \max \left( \frac{k\mathrm{e} ^{-a_2\tau _2}\xi }{l_2},\max _{x\in \overline{\Omega }} \left\{ \phi _3(x,0)+\frac{q}{g}\phi _5(x,0)\right\} \right) . \end{aligned}$$

From the above, we have proved that \(u(x,t),\;w(x, t),\;v(x, t),\;z(x, t)\) and y(x, t) are bounded on \(\overline{\Omega }\times [0, T_{\mathrm{max}})\). Therefore, it follows from the standard theory for semilinear parabolic systems (Henry 1993; Redlinger 1984) that \(T_{\mathrm{max}} = +\infty \). This completes the proof. \(\square \)

Now, we discuss the existence of equilibria of model (3). It is easy to know that any equilibrium \(E =(u, w, v, z,y)\) of model (3) satisfies

$$\begin{aligned} \begin{aligned}&\displaystyle \lambda -\mathrm{d}u(x)-f(u(x),w(x),v(x))v(x)=0,\\&\displaystyle \mathrm{e}^{-a_1\tau _1}f(u(x),w(x),v(x))v(x) -aw(x)-pw(x)z(x)=0,\\&\displaystyle k\mathrm{e} ^{-a_2\tau _2}w(x)-mv(x)-qv(x)y(x)=0,\\&\displaystyle cw(x)z(x)-bz(x)=0,\\&\displaystyle gv(x)y(x)-hy(x)=0. \end{aligned} \end{aligned}$$
(7)

It is clear from (7) that model (3) always has a unique infection-free equilibrium \(E_0=(u_0,0,0,0,0)\) with \(u_0=\frac{\lambda }{d}.\)

The basic reproductive number of viral infection for model (3) is

$$\begin{aligned} R_0=\frac{k f\left( \frac{\lambda }{d},0,0\right) }{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}}. \end{aligned}$$
(8)

If \(z=0\) and \(y=0,\) then we get the following equation

$$\begin{aligned}&f\left( u,\frac{\lambda -\mathrm{d}u}{a \mathrm{e}^{a_1\tau _1}},\frac{k(\lambda -\mathrm{d}u)}{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}} \right) =\frac{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k},\\&\qquad w=\frac{\lambda -\mathrm{d}u}{a \mathrm{e}^{a_1\tau _1}}\quad \;\text{ and }\quad \; v=\frac{k(\lambda -\mathrm{d}u)}{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}}. \end{aligned}$$

Since \(w\ge 0,\) we have \(u\le \frac{\lambda }{d}.\) Denote

$$\begin{aligned} F_1(u)=f\left( u,\frac{\lambda -\mathrm{d}u}{a \mathrm{e}^{a_1\tau _1}},\frac{k(\lambda -\mathrm{d}u)}{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}} \right) -\frac{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}. \end{aligned}$$

We have

$$\begin{aligned} F_1(0)= & {} -\frac{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}<0,\\ F_1\left( \frac{\lambda }{d}\right)= & {} \frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}(R_0-1) \end{aligned}$$

and

$$\begin{aligned} F_1'(u)=\frac{\partial f}{\partial u}-\frac{d}{a\mathrm{e}^{a_1\tau _1}}\cdot \frac{\partial f}{\partial w}-\frac{kd}{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}}\cdot \frac{\partial f}{\partial v}>0. \end{aligned}$$

Because of \((A_1)\), we know that the function \(F_1(u)\) is strictly monotonically increasing with respect to u. When \(R_0 > 1,\) there exists a unique \(u_1\in (0,\frac{\lambda }{d})\) such that \(F_1(u_1)=0.\) Thus, we obtain a unique immune-free equilibrium \(E_1=(u_1,w_1,v_1,0,0)\) with \(u_1\in (0,\frac{\lambda }{d}), w_1=\frac{\lambda -\mathrm{d}u_1}{a \mathrm{e}^{a_1\tau _1}}\) and \(v_1=\frac{k(\lambda -\mathrm{d}u_1)}{am \mathrm{e}^{a_1\tau _1+a_2\tau _2}}.\)

If \(y\ne 0\) and \(z=0,\) we have \(v=\frac{h}{g}.\) From the first and second equations of (7), we have

$$\begin{aligned} f\left( u,\frac{\lambda -\mathrm{d}u}{a\mathrm{e}^{a_1\tau _1}},\frac{h}{g}\right) =\frac{g}{h}(\lambda -\mathrm{d}u). \end{aligned}$$

Since \(y=\frac{kg(\lambda -\mathrm{d}u)-amh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{aqh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}\ge 0,\) we get \(u\le \frac{\lambda }{d}-\frac{amh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kgd}.\) Denote

$$\begin{aligned} F_2(u)=f\left( u,\frac{\lambda -\mathrm{d}u}{a\mathrm{e}^{a_1\tau _1}},\frac{h}{g}\right) -\frac{g}{h}(\lambda -\mathrm{d}u). \end{aligned}$$

We have \(F_2(0)=-\frac{\lambda g}{h}<0\) and \(F_2'(u)=\frac{\partial f}{\partial v}-\frac{{ d}}{a\mathrm{e}^{a_1\tau _1}}\cdot \frac{\partial f}{\partial w}+\frac{{ d}g}{h}>0.\)

Now, we define the antibody immune reproductive number for model (3) given by

$$\begin{aligned} R_1=\frac{g}{h}v_1. \end{aligned}$$
(9)

Note that when \(R_0>1\) model (3) has a unique immune-free equilibrium \(E_1=(u_1,w_1,v_1,\) 0, 0). This shows that virus infection is successful and the numbers of free viruses at equilibrium \(E_1\) is \(v_1\). Furthermore, we have that \(\frac{1}{h}\) is the average life span of antibody cells, g is birth rate of the antibody response. Hence, \(R_1\) denotes the average number of the antibody immune cells activated by virus when virus infection is successful and CTL responses have not been established.

If \(R_1>1,\) then \(v_1>\frac{h}{g},\) \(u_1<\frac{\lambda }{d}-\frac{amh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kdg}\) and

$$\begin{aligned} \begin{aligned} F_2\left( \frac{\lambda }{d}-\frac{amh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kdg}\right)&=\displaystyle f\left( \frac{\lambda }{d}-\frac{amh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kdg}, \frac{mh\mathrm{e}^{a_2\tau _2}}{kg},\frac{h}{g}\right) \\&\quad -\frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}\\&=\displaystyle F_1\left( \frac{\lambda }{d}-\frac{amh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kdg}\right) >F_1(u_1). \end{aligned} \end{aligned}$$

Thus, if \(R_1>1,\) there exists a unique infection equilibrium with only antibody response \(E_2=(u_2,w_2,v_2,0,y_2)\) with \(u_2\in (0,\frac{\lambda }{d}-\frac{amh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kgd}),\; w_2=\frac{\lambda -\mathrm{d}u_2}{a\mathrm{e}^{a_1\tau _1}},\;v_2=\frac{h}{g}\) and \(y_2=\frac{kg(\lambda -\mathrm{d}u_2)-amh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{aqh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}.\)

If \(y=0\) and \(z\ne 0\), we have \(w=\frac{b}{c}\) and \(v=\frac{kb\mathrm{e}^{-a_2\tau _2}}{cm}\). From the first equation of (7), we obtain

$$\begin{aligned} f\left( u,\frac{b}{c},\frac{kb\mathrm{e}^{-a_2\tau _2}}{cm}\right) =\frac{cm}{kb\mathrm{e}^{-a_2\tau _2}}(\lambda -\mathrm{d}u). \end{aligned}$$

As \(z=\frac{c(\lambda -\mathrm{d}u)\mathrm{e}^{-a_1\tau _1}-ab}{pb}\ge 0\) then \(u\le \frac{\lambda }{d}-\frac{ab\mathrm{e}^{a_1\tau _1}}{cd}.\) Denote

$$\begin{aligned} F_3(u)=f\left( u,\frac{b}{c},\frac{kb\mathrm{e}^{-a_2\tau _2}}{cm}\right) -\frac{cm}{kb\mathrm{e}^{-a_2\tau _2}}(\lambda -\mathrm{d}u). \end{aligned}$$

We have \(F_3(0)=-\frac{\lambda cm}{kb\mathrm{e}^{-a_2\tau _2}}<0\) and \(F_3'(u)=\frac{\partial f}{\partial u}+\frac{cmd}{kb\mathrm{e}^{-a_2\tau _2}}>0.\) Denote

$$\begin{aligned} R_2=\frac{c}{b}w_1, \end{aligned}$$
(10)

which \(R_2\) denotes the average number of the CTL immune cells activated by infected cells when virus infection is successful and antibody immune responses have not been established. Note that the number of infected cells at equilibrium \(E_1\) is \(w_1, \frac{1}{b}\) is the average life span of CTL cells and c is the rate at which the CTL responses are produced.

We see that \(R_2>1\) is equivalent to \(w_1>\frac{b}{c},\;u_1<\frac{\lambda }{d}-\frac{ab}{cd\mathrm{e}^{-a_1\tau _1}}\) and

$$\begin{aligned} \begin{aligned} F_3\left( \frac{\lambda }{d}-\frac{ab}{cd\mathrm{e}^{-a_1\tau _1}}\right)&=\displaystyle f\left( \frac{\lambda }{d}-\frac{ab}{cd\mathrm{e}^{-a_1\tau _1}}, \frac{b}{c},\frac{kb\mathrm{e}^{-a_2\tau _2}}{cm}\right) -\frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}\\&>\displaystyle f(u_1,w_1,v_1)-\frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}=0. \end{aligned} \end{aligned}$$

Hence, \(R_2>1\), there exists a unique infection equilibrium with only CTL response \(E_3=(u_3,w_3,v_3,z_3,0)\) with \(u_3\in (0,\frac{\lambda }{d}-\frac{ab}{cd\mathrm{e}^{-a_1\tau _1}}),\;w_3=\frac{b}{c},\; v_3=\frac{kb\mathrm{e}^{-a_2\tau _2}}{cm}\) and \(z_3=\frac{c(\lambda -\mathrm{d}u)\mathrm{e}^{-a_1\tau _1}-ab}{pb}.\)

If \(z\ne 0\) and \(y\ne 0\), we have \(w=\frac{b}{c}\) and \(v=\frac{h}{g}\). From the first equation of (7), we have

$$\begin{aligned} f\left( u,\frac{b}{c},\frac{h}{g}\right) =\frac{g}{h}(\lambda -\mathrm{d}u). \end{aligned}$$

According to \(z=\frac{(\lambda -\mathrm{d}u)\mathrm{e}^{-a_1\tau _1}-aw}{pw}\ge 0,\) we deduce that \(u\le \frac{\lambda }{d}-\frac{ab\mathrm{e}^{a_1\tau _1}}{cd}.\) Define

$$\begin{aligned} F_4(u)=f\left( u,\frac{b}{c},\frac{h}{g}\right) -\frac{g}{h}(\lambda -\mathrm{d}u). \end{aligned}$$

We have \(F_4(0)=-\frac{\lambda g}{h}<0\) and \(F_4'(u)=\frac{\partial f}{\partial u}+\frac{dg}{h}>0.\)

The CTL immune competitive reproductive number for model (3) is

$$\begin{aligned} R_3=\frac{cw_2}{b}. \end{aligned}$$
(11)

In fact, when \(R_1>1\), model (3) has a unique infection equilibrium with only antibody response \(E_2=(u_2,w_2,v_2,0,y_2)\). This predicates that CTL immune responses have been established, and the number of infected cells at equilibrium \(E_2\) is \(w_2\). Hence, \(R_3\) denotes the average number of the CTL immune cells activated by infected cells under the condition that antibody immune responses have been established.

If \(R_3>1\), then \(w_2>\frac{b}{c},\; u_2<\frac{\lambda }{d}-\frac{ab\mathrm{e}^{a_1\tau _1}}{cd}\) and

$$\begin{aligned} \begin{aligned} F_4\left( \frac{\lambda }{d}-\frac{ab\mathrm{e}^{a_1\tau _1}}{cd}\right)&=\displaystyle f\left( \frac{\lambda }{d}-\frac{ab\mathrm{e}^{a_1\tau _1}}{cd}, \frac{b}{c},\frac{h}{g}\right) -\frac{abg\mathrm{e}^{a_1\tau _1}}{ch}\\&=\displaystyle F_2\left( \frac{\lambda }{d}-\frac{ab\mathrm{e}^{a_1\tau _1}}{cd}\right) >F_2(u_2)=0. \end{aligned} \end{aligned}$$

Thus, there exists a unique \(u_4\in (0,\frac{\lambda }{d}-\frac{ab\mathrm{e}^{a_1\tau _1}}{cd})\) such that \(F_4(u_4)=0.\) From the third equation of (7), we obtain that \(y_4=\frac{m}{q}(R_4-1),\) where \(R_4\) is the antibody immune competitive reproductive number defined by

$$\begin{aligned} R_4=\frac{gv_3}{h}. \end{aligned}$$
(12)

In fact, when \(R_2>1\), model (3) has a unique infection equilibrium with only CTL response \(E_3=(u_3,w_3,v_3,z_3,0)\). This predicates that antibody immune responses have been established, and the numbers of the viruses at equilibrium \(E_3\) is \(v_3\). Hence, \(R_4\) denotes the average number of the antibody immune cells activated by viruses under the condition that CTL immune responses have been established.

When \(R_3 > 1\) and \(R_4 > 1\), model (3) has a unique infection equilibrium with CTL and antibody response \(E_4=(u_4,w_4,v_4,z_4,y_4)\) with \(u_4\in (0,\frac{\lambda }{d}-\frac{ab\mathrm{e}^{a_1\tau _1}}{cd}),\) \(w_4=\frac{b}{c},\;v_4=\frac{h}{g}, z_4=\frac{(\lambda -\mathrm{d}u_4)\mathrm{e}^{-a_1\tau _1}-aw_4}{pw_4}\) and \(y_4=\frac{m}{q}(R_4-1).\)

3 Stability analysis

In this section, we discuss global stability of equilibria for infection-free, immune-free, antibody response, and infection only with CTL response and infection with both antibody and CTL responses, respectively.

We further introduce the following assumption

\((A_2)\) \((1-\frac{f(u,w,v)}{f(u,w_i,v_i)})(\frac{f(u,w_i,v_i)}{f(u,w,v)}-\frac{v}{v_i})\le 0\) for all \(u,\;w,\;v>0\), where \(w_i\) and \(v_i\) are the components of equilibrium \(E_i \;(i=1,2,3,4).\)

For convenience, for any solution (u(x, t), w(x, t), v(x, t), z(x, t), y(x, t)) of model (3) we let

$$\begin{aligned} u(x,t)= & {} u,\; u(x,t-\tau _2)=u_{\tau _2},\; w(x,t)=w,\; w(x,t-\tau _2)=w_{\tau _2},\\ v(x,t)= & {} v,\; v(x,t-\tau _2)=v_{\tau _2},\; z(x,t)=z,\; z(x,t-\tau _2)=z_{\tau _2},\\ y(x,t)= & {} y,\; y(x,t-\tau _2)=y_{\tau _2}, f(u(x,t-\tau _1),w(x,t-\tau _1),\\&v(x,t-\tau _1))v(x,t-\tau _1)=f_{\tau _1}. \end{aligned}$$

3.1 Stability of equilibrium \(E_0\)

Theorem 3.1

  1. (a)

    If \(R_0 \le 1\), then the infection-free equilibrium \(E_0\) is globally asymptotically stable.

  2. (b)

    If \(R_0>1\), then the equilibrium \(E_0\) is unstable.

Proof

Consider conclusion (a). Define a Lyapunov functional \(L_1(t)=\int _{\Omega } (V_1(x,t)+V_2(x,t))\,\mathrm {d}x,\) where

$$\begin{aligned} \begin{aligned} V_1(x,t)&=\displaystyle u-u_0-\int _{u_0}^{u} {\displaystyle \frac{f(u_0,0,0)}{f(s,0,0)}}\,\mathrm {d}s +\mathrm{e}^{a_1\tau _1}w +{\displaystyle \frac{a\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v\\&\quad \displaystyle +\,{\displaystyle \frac{p\mathrm{e}^{a_1\tau _1}}{c}}z+{\displaystyle \frac{aq\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y \end{aligned} \end{aligned}$$

and

$$\begin{aligned} V_2(x,t)= & {} \displaystyle \int _0^{\tau _1} f(u_\theta ,w_\theta ,v_\theta )v_\theta \,\mathrm {d}\theta \\&+\,a\mathrm{e} ^{a_1\tau _1}\int _0^{\tau _2} w_\theta \,\mathrm {d}\theta . \end{aligned}$$

By calculation, we have

$$\begin{aligned} {\displaystyle \frac{\partial V_1(x,t)}{\partial t}}+{\displaystyle \frac{\partial V_2(x,t)}{\partial t}}= & {} \left( 1-{\displaystyle \frac{f(u_0,0,0)}{f(u,0,0)}}\right) (\lambda -\mathrm{d}u-f(u,w,v)v)\\&+\,\mathrm{e}^{a_1\tau _1}(\mathrm{e} ^{-a_1\tau _1}f_{\tau _1}-aw-pwz)\\&+\,{\displaystyle \frac{a\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}(D\triangle v+k\mathrm{e}^{-a_2\tau _2}w_{\tau _2}-mv-qvy)\\&+\,{\displaystyle \frac{p\mathrm{e}^{a_1\tau _1}}{c}}(cwz-bz) +{\displaystyle \frac{aq\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}(gvy-hy)\\&+\,f(u,w,v)v-f_{\tau _1}+a\mathrm{e}^{a_1\tau _1}w-a\mathrm{e}^{a_1\tau _1}w_{\tau _2}\\= & {} \mathrm{d}u_0\left( 1-{\displaystyle \frac{u}{u_0}}\right) \left( 1-{\displaystyle \frac{f(u_0,0,0)}{f(u,0,0)}}\right) -{\displaystyle \frac{aqh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y\\&+\,v\left( f(u,w,v)\cdot {\displaystyle \frac{f(u_0,0,0)}{f(u,0,0)}}-{\displaystyle \frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}\right) \\&-\,{\displaystyle \frac{pb\mathrm{e}^{a_1\tau _1}}{c}}z+{\displaystyle \frac{aD\mathrm{e}^{a_1\tau _1+a_2\tau _2}\triangle v}{k}}\\= & {} \mathrm{d}u_0\left( 1-{\displaystyle \frac{u}{u_0}}\right) \left( 1-{\displaystyle \frac{f(u_0,0,0)}{f(u,0,0)}}\right) - {\displaystyle \frac{pb\mathrm{e}^{a_1\tau _1}}{c}}z\\&-\,{\displaystyle \frac{aqh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y\\&+\,{\displaystyle \frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v\left( {\displaystyle \frac{f(u,w,v)}{f(u,0,0)}}R_0-1\right) +{\displaystyle \frac{aD\mathrm{e}^{a_1\tau _1+a_2\tau _2}\triangle v}{k}}\\\le & {} \mathrm{d}u_0\left( 1-{\displaystyle \frac{u}{u_0}}\right) \left( 1-{\displaystyle \frac{f(u_0,0,0)}{f(u,0,0)}}\right) +{\displaystyle \frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v(R_0-1)\\&-\,{\displaystyle \frac{aqh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y-{\displaystyle \frac{pb\mathrm{e}^{a_1\tau _1}}{c}}z +{\displaystyle \frac{aD\mathrm{e}^{a_1\tau _1+a_2\tau _2}\triangle v}{k}}. \end{aligned}$$

Calculating the time derivative of \(L_1(t)\) along any positive solution of model (3) and noticing that \(u_0=\frac{\lambda }{d}\), we can obtain

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\mathrm{d}L_1(t)}{\mathrm{d}t}}&\le \int _{\Omega } \mathrm{d}u_0\left( 1-{\displaystyle \frac{u}{u_0}}\right) \left( 1-{\displaystyle \frac{f(u_0,0,0)}{f(u,0,0)}}\right) \,\mathrm {d}x\\&\quad +\int _{\Omega } {\displaystyle \frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v(R_0-1)\,\mathrm {d}x\\&\quad -\int _{\Omega } {\displaystyle \frac{aqh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y\,\mathrm {d}x\\&\quad -\int _{\Omega } {\displaystyle \frac{pb\mathrm{e}^{a_1\tau _1}}{c}}z\,\mathrm {d}x +\int _{\Omega } {\displaystyle \frac{aD\mathrm{e}^{a_1\tau _1+a_2\tau _2}\triangle v}{k}}\,\mathrm {d}x. \end{aligned} \end{aligned}$$

Using the divergence theorem and the homogeneous Neumann boundary conditions, we get

$$\begin{aligned} \int _{\Omega } \triangle v\,\mathrm {d}x=\int _{\partial \Omega } \frac{\partial v}{\partial \vec {n}}\,\mathrm {d}x=0. \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\mathrm{d}L_1(t)}{\mathrm{d}t}}&\le \int _{\Omega } \mathrm{d}u_0\left( 1-{\displaystyle \frac{u}{u_0}}\right) \left( 1-{\displaystyle \frac{f(u_0,0,0)}{f(u,0,0)}}\right) \,\mathrm {d}x\\&\quad +\int _{\Omega } {\displaystyle \frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v(R_0-1)\,\mathrm {d}x\\&\quad -\int _{\Omega } {\displaystyle \frac{aqh\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y\,\mathrm {d}x\\&\quad -\int _{\Omega } {\displaystyle \frac{pb\mathrm{e}^{a_1\tau _1}}{c}}z\,\mathrm {d}x. \end{aligned} \end{aligned}$$

Obviously, if \(R_0 \le 1\), then \(\frac{\mathrm{d}L_1(t)}{\mathrm{d}t}\le 0\) for any (u, w, v, z, y). We have \(\frac{\mathrm{d}L_1(t)}{\mathrm{d}t}= 0\) if and only if \( u=u_0, v=0, z=0\) and \(y=0\). Let M be the largest invariant set of \(\{(x,y,v,z,w)\in R^5_+: \frac{\mathrm{d}L_1(t)}{\mathrm{d}t}=0\}\). From the third equation of model (3), we easily obtain \(M=\{E_0\}.\) It follows from LaSalle’s invariance principle Hale and Verduyn (1993) that the equilibrium \(E_0\) of model (3) is globally asymptotically stable when \(R_0\le 1\).

Next, we consider conclusion (b). To do so, we determine the characteristic equation about the equilibrium \(E_0\).

Let \(0 =\mu _1<\mu _2< \cdots< \mu _{n} < \cdots \) be the eigenvalues of the operator \(-\Delta \) on \(\Omega \) with the homogeneous Neumann boundary conditions, and \(E(\mu _{i})\) be the eigenfunction space corresponding to \(\mu _{i}\) in \(C^1(\Omega )\). Let \(\{\varphi _{ij} : j = 1, 2,\ldots , \text{ dim }E(\mu _{i})\}\) be an orthonormal basis of \(E(\mu _{i}), \mathbb {X} = [C^1(\Omega )]^5\), and \(\mathbb {X}_{ij} = \{c\varphi _{ij }: c \in \mathbb {R}^5\}\). Then

$$\begin{aligned} \mathbb {X}=\bigoplus _{i=1}^{\infty }\mathbb {X}_i\; \quad \text{ and } \quad \mathbb {X}_i= \bigoplus _{i=1}^{\text{ dim }E(\mu _{i})}\mathbb {X}_{ij}. \end{aligned}$$

Let \(E^*(u^*,w^*,v^*,z^*,y^*)\) be an arbitrary equilibrium, and consider the following change

$$\begin{aligned} \begin{aligned} U(x,t)&=u(x,t)-u^*,\\ W(x,t)&=w(x,t)-w^*,\\ V(x,t)&=v(x,t)-v^*,\\ Z(x,t)&=z(x,t)-z^*,\\ Y(x,t)&=y(x,t)-y^*. \end{aligned} \end{aligned}$$

By substituting U(x, t), W(x, t), V(x, t), Z(x, t) and Y(x, t) into model (3) and linearizing, we obtain the following system

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\partial U}{\partial t}}&=\displaystyle -\left( d+\frac{\partial f }{\partial u}v^*\right) U(x,t)-\frac{\partial f }{\partial w}v^*W(x,t)\\&\quad -\left( \frac{\partial f }{\partial v}v^*+f(u^*,w^*,v^*)\right) V(x,t),\\ {\displaystyle \frac{\partial W}{\partial t}}&=\displaystyle \mathrm{e}^{-a_1\tau _1}\frac{\partial f }{\partial u}v^*U(x,t-\tau _1)+\mathrm{e}^{-a_1\tau _1}\frac{\partial f }{\partial w}v^*W(x,t-\tau _1)-pw^*Z(x,t)\\&\quad \displaystyle +\,\mathrm{e}^{-a_1\tau _1}\left( \frac{\partial f }{\partial v}v^*+f(u^*,w^*,v^*)\right) V(x,t-\tau _1)-(a+pz^*)W(x,t),\\ {\displaystyle \frac{\partial V}{\partial t}}&=\displaystyle D\triangle v(x,t)+k\mathrm{e}^{-a_2\tau _2}W(x,t-\tau _2)\\&\quad -\,(m+qy^*)V(x,t)-qv^*Y(x,t),\\ {\displaystyle \frac{\partial Z}{\partial t}}&=\displaystyle cz^*W(x,t)+(cw^*-b)Z(x,t),\\ {\displaystyle \frac{\partial Y}{\partial t}}&=\displaystyle gy^*V(x,t)+(gv^*-h)Y(x,t), \end{aligned} \end{aligned}$$
(13)

This system is equivalent to

$$\begin{aligned} {\displaystyle \frac{\partial \mathbb {Z}}{\partial t}}=\mathbb {D}\triangle \mathbb {Z}+\mathbb {A}\mathbb {Z}(x,t) +\mathbb {B}\mathbb {Z}(x,t-\tau _1)+\mathbb {C}\mathbb {Z}(x,t-\tau _2), \end{aligned}$$

where

$$\begin{aligned} \mathbb {A}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -\left( d+\frac{\partial f }{\partial u}v^*\right) &{} - \frac{\partial f }{\partial w}v^* &{} -\left( \frac{\partial f }{\partial v}v^*+f(u^*,w^*,v^*)\right) &{} 0 &{} 0\\ 0 &{} -(a+pz^*)&{} 0 &{} -pw^* &{} 0\\ 0 &{} 0 &{} -(m+qy^*) &{} 0 &{} -qv^*\\ 0 &{} cz^* &{} 0 &{} cw^*-b &{} 0\\ 0 &{} 0 &{} gy^* &{} 0 &{} gv^*-h\\ \end{array} \right) ,\\ \mathbb {B}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \frac{\partial f }{\partial u}v^*\mathrm{e}^{-a_1\tau _1} &{} \frac{\partial f }{\partial w}v^*\mathrm{e}^{-a_1\tau _1} &{} \left( \frac{\partial f }{\partial v}v^*+f(u^*,w^*,v^*)\right) \mathrm{e}^{-a_1\tau _1} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} \right) ,\\ \mathbb {C}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} k\mathrm{e}^{-a_2\tau _2} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} \right) , \quad \; \mathbb {D}=\mathrm{diag}(0,0,D,0,0). \end{aligned}$$

We put \(\mathbb {L}\mathbb {Z} = \mathbb {D}\triangle \mathbb {Z}+\mathbb {A}\mathbb {Z}(x,t) +\mathbb {B}\mathbb {Z}(x,t-\tau _1)+\mathbb {C}\mathbb {Z}(x,t-\tau _2).\) For each \(i\ge 1, \mathbb {X}_{i}\) is invariant under the operator \(\mathbb {L}\), and s is an eigenvalue of \(\mathbb {L}\) if and only if it is a root of the characteristic equation det\((sI-\mathbb {A}-\mathbb {B}\mathrm{e}^{-a_1\tau _1}-\mathbb {C}\mathrm{e}^{-a_2\tau _2}+\mu _{i}\mathbb {D}) = 0\) for some \(i\ge 1\), in which case, there is an eigenvector in \(\mathbb {X}_{i}\).

From (13), by computing, we obtain the characteristic equation of the corresponding linearized system of model (3) at the equilibrium \(E_0\) as follows

$$\begin{aligned} (s+h)(s+b)(s+d)f_i(s)=0, \end{aligned}$$
(14)

where

$$\begin{aligned} f_i(s)= & {} s^2+(a+m+\mu _{i}D)s+a(m+\mu _{i}D)\nonumber \\&-kf\left( \frac{\lambda }{d},0,0\right) \mathrm{e}^{-(a_1+s)\tau _1-(a_2+s)\tau _2}. \end{aligned}$$
(15)

Obviously, \(s_1=-d, s_2 =-b\) and \(s_3 =-h\) are the roots of this equation. It is easy to prove that Eq. (15) has a real positive root when \(R_0>1\).

When \(R_0>1\), we have \(f_1(0)=am(1-R_0)<0\), as \(\mu _1=0\) when \(i=1.\) Since \(\lim _{s\rightarrow +\infty }f_i(s)=+\infty \), there is a \(s^*>0\) such that \(f_i(s^*)=0\). Therefore, when \(R_0>1,\) the equilibrium \(E_0\) is unstable. This completes the proof. \(\square \)

Biologically, Theorem 3.1 shows that the viruses are cleared and the infection dies out.

3.2 Stability of equilibrium \(E_1\)

Theorem 3.2

Assume \((A_2)\) holds, if \(R_0>1\) (a) \(R_1\le 1\) and \(R_2\le 1,\) then the immune-free equilibrium \(E_1\) is globally asymptotically stable.

(b) If \(R_1>1\) or \(R_2>1\), then the equilibrium \(E_1\) is unstable.

Proof

Define firstly function \(H(\xi )=\xi -1-\ln \xi \). We have that \(H(\xi )\ge 0\) for all \(\xi >0\) and \(H(\xi )=0\) if and only if \(\xi =1\). Consider conclusion (a). Define a Lyapunov functional

$$\begin{aligned} L_2(t)=\int _{\Omega } (V_1(x,t)+V_2(x,t))\,\mathrm {d}x, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} V_1(x,t)&=\displaystyle u-u_1-\int _{u_1}^{u} {\displaystyle \frac{f(u_1,w_1,v_1)}{f(s,w_1,v_1)}}\,\mathrm {d}s +\mathrm{e}^{a_1\tau _1}w_1H\left( \frac{w}{w_1}\right) \\&\quad \displaystyle +\,{\displaystyle \frac{a\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v_1H\left( \frac{v}{v_1}\right) +{\displaystyle \frac{p\mathrm{e}^{a_1\tau _1}}{c}}z+{\displaystyle \frac{aq\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} V_2(x,t)&=\displaystyle f(u_1,w_1,v_1)v_1\int _0^{\tau _1} H\left( \frac{f(u_\theta ,w_\theta ,v_\theta )v_\theta }{f(u_1,w_1,v_1)v_1}\right) \,\mathrm {d}\theta \\&\quad \quad \displaystyle +\,a\mathrm{e} ^{a_1\tau _1}w_1\int _0^{\tau _2} H\left( \frac{w_\theta }{w_1}\right) \,\mathrm {d}\theta . \end{aligned} \end{aligned}$$

It is obvious that \(L_2(t)>0\) for all \((u(t),w(t),v(t),z(t),y(t))>0\) and \((u(t),w(t),v(t),z(t),y(t))\ne (u_1,w_1,v_1,0,0)\).

Calculating the time derivative of \(V_1(x,t)\) and \(V_2(x,t)\) along any positive solution of model (3), we can obtain

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\partial V_1(x,t)}{\partial t}}&=\left( 1-{\displaystyle \frac{f(u_1,w_1,v_1)}{f(u,w_1,v_1)}}\right) (\lambda -\mathrm{d}u-f(u,w,v)v)\\&\quad +\,\mathrm{e}^{a_1\tau _1}\left( 1-{\displaystyle \frac{w_1}{w}}\right) (\mathrm{e} ^{-a_1\tau _1}f_{\tau _1} -aw-pwz)\\&\quad + {\displaystyle \frac{a\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}\left( 1-{\displaystyle \frac{v_1}{v}}\right) (D\triangle v+k\mathrm{e}^{-a_2\tau _2}w_{\tau _2}\\&\quad -mv-qvy) +{\displaystyle \frac{p\mathrm{e}^{a_1\tau _1}}{c}}(cwz-bz)\\&\quad +{\displaystyle \frac{aq\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}(gvy-hy) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\partial V_2(x,t)}{\partial t}}&=f(u,w,v)v -f_{\tau _1} +f(u_1,w_1,v_1)v_1\ln {\displaystyle \frac{f_{\tau _1}}{f(u,w,v)v}} \\&\quad +\,a\mathrm{e}^{a_1\tau _1}w-a\mathrm{e}^{a_1\tau _1}w_{\tau _2}+a\mathrm{e}^{a_1\tau _1}w_1\ln {\displaystyle \frac{w_{\tau _2}}{w}}. \end{aligned} \end{aligned}$$

By using

$$\begin{aligned} f(u_1,w_1,v_1)v_1=a\mathrm{e}^{a_1\tau _1}w_1={\displaystyle \frac{am\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v_1. \end{aligned}$$

Since

$$\begin{aligned}\int _{\Omega } \triangle v\,\mathrm {d}x=0,\quad \; \int _{\Omega } {\displaystyle \frac{\triangle v}{v}}\,\mathrm {d}x=\int _{\Omega } {\displaystyle \frac{\parallel \nabla v\parallel ^2}{v^2}}\,\mathrm {d}x, \end{aligned}$$

we have

$$\begin{aligned} {\displaystyle \frac{\mathrm{d}L_2(t)}{\mathrm{d}t}}= & {} \displaystyle \int _{\Omega } {\displaystyle \frac{\partial V_1(x,t)}{\partial t}}+{\displaystyle \frac{\partial V_2(x,t)}{\partial t}}\,\mathrm {d}x\\= & {} \displaystyle \int _{\Omega } \mathrm{d}u_1\left( 1-{\displaystyle \frac{u}{u_1}}\right) \left( 1-{\displaystyle \frac{f(u_1,w_1,v_1)}{f(u,w_1,v_1)}}\right) \,\mathrm {d}x\\&\displaystyle +f(u_1,w_1,v_1)v_1\int _{\Omega } \left[ 4-{\displaystyle \frac{f_{\tau _1}}{f(u_1,w_1,v_1)v_1}} \cdot {\displaystyle \frac{w_1}{w}}-{\displaystyle \frac{f(u_1,w_1,v_1)}{f(u,w_1,v_1)}}\right. \\&\left. \displaystyle -{\displaystyle \frac{v_1w_{\tau _2}}{vw_1}} -{\displaystyle \frac{f(u,w_1,v_1)}{f(u,w,v)}}\right] \,\mathrm {d}x+{\displaystyle \frac{aD\mathrm{e}^{a_1\tau _1+a_2\tau _2}\triangle v}{k}}\left( 1-{\displaystyle \frac{v_1}{v}}\right) \\&\displaystyle +f(u_1,w_1,v_1)v_1\int _{\Omega } \left[ -1+{\displaystyle \frac{f(u,w_1,v_1)}{f(u,w,v)}}-{\displaystyle \frac{v}{v_1}} +{\displaystyle \frac{vf(u,w,v)}{v_1f(u,w_1,v_1)}}\right] \,\mathrm {d}x\\&\displaystyle +\int _{\Omega } p\mathrm{e}^{a_1\tau _1}\left( w_1-{\displaystyle \frac{b}{c}}\right) z\,\mathrm {d}x +\int _{\Omega } {\displaystyle \frac{aq\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}\left( v_1-{\displaystyle \frac{h}{g}}\right) y\,\mathrm {d}x\\&\displaystyle +f(u_1,w_1,v_1)v_1\int _{\Omega }\left[ \ln {\displaystyle \frac{f_{\tau _1}}{f(u_1,w_1,v_1)v_1}}\cdot {\displaystyle \frac{w_{\tau _2}}{w}}\right] \,\mathrm {d}x\\= & {} \displaystyle \int _{\Omega } \mathrm{d}u_1\left( 1-{\displaystyle \frac{u}{u_1}}\right) \left( 1-{\displaystyle \frac{f(u_1,w_1,v_1)}{f(u,w_1,v_1)}}\right) \,\mathrm {d}x\\&\displaystyle -f(u_1,w_1,v_1)v_1\int _{\Omega } \left[ H({\displaystyle \frac{f(u_1,w_1,v_1)}{f(u,w_1,v_1)}}) +H\left( {\displaystyle \frac{f_{\tau _1}}{f(u_1,w_1,v_1)v_1}}\cdot {\displaystyle \frac{w_1}{w}}\right) \right. \\&\left. \displaystyle +H\left( {\displaystyle \frac{v_1w_{\tau _2}}{vw_1}}\right) +H\left( {\displaystyle \frac{f(u,w_1,v_1)}{f(u,w,v)}}\right) \right] \,\mathrm {d}x+p\mathrm{e}^{a_1\tau _1}\left( w_1-{\displaystyle \frac{b}{c}}\right) \int _{\Omega }z \,\mathrm {d}x\\&\displaystyle +{\displaystyle \frac{aq\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}\left( v_1-{\displaystyle \frac{h}{g}}\right) \int _{\Omega } y\,\mathrm {d}x-{\displaystyle \frac{aD\mathrm{e}^{a_1\tau _1+a_2\tau _2}v_1}{k}}\int _{\Omega } {\displaystyle \frac{\parallel \nabla v\parallel ^2}{v^2}}\,\mathrm {d}x\\&\displaystyle +f(u_1,w_1,v_1)v_1\int _{\Omega }\left( 1-{\displaystyle \frac{f(u,w,v)}{f(u_1,w_1,v_1)}}\right) \left( {\displaystyle \frac{f(u,w_1,v_1)}{f(u,w,v)}}-{\displaystyle \frac{v}{v_1}}\right) \,\mathrm {d}x. \end{aligned}$$

Obviously, we always have \(\frac{\mathrm{d}L_2(t)}{\mathrm{d}t}\le 0,\) and \(\frac{\mathrm{d}L_2(t)}{\mathrm{d}t}=0\) if and only if \(u(t)=u_1,w(t)=w_1,v(t)=v_1, z(t)=0\) and \(y(t)=0.\) From LaSalle’s invariance principle Hale and Verduyn (1993), we finally have that the immune-free equilibrium \(E_1\) of model (3) is globally asymptotically stable when \(R_0>1, R_1\le 1\) and \(R_2\le 1\).

Next, we consider conclusion (b). From (13), by computing, we obtain the characteristic equation of the corresponding linearized system of model (3) at the equilibrium \(E_1\) as follows

$$\begin{aligned} (s+h-gv_1)(s+b-cw_1)f(s)=0, \end{aligned}$$

where

$$\begin{aligned} f(s)=\left| \begin{array}{c@{\quad }c@{\quad }c} s+d+\frac{\partial f }{\partial u}v_1 &{} \frac{\partial f }{\partial w}v_1 &{} \left( \frac{\partial f }{\partial v}v_1+f(u_1,w_1,v_1)\right) \\ -\mathrm{e}^{-(a_1+s)\tau _1}\frac{\partial f }{\partial u}v_1 &{} s+a-\frac{\partial f }{\partial w}v_1\mathrm{e}^{-(a_1+s)\tau _1} &{} -\mathrm{e}^{-(a_1+s)\tau _1}\left( \frac{\partial f }{\partial v}v_1+f(u_1,w_1,v_1)\right) \\ 0 &{} -k\mathrm{e}^{-(a_2+s)\tau _2} &{} s+m+\mu _{i}D \end{array}\right| . \end{aligned}$$

When \(R_1>1\), we have \(h-gv_1<0\). Hence, there is a positive root \(s_1=gv_1-h\). When \(R_2>1\), there is also a positive root \(s_2=cw_1-b\). Therefore, when \(R_1>1\) or \(R_2>1,\) the equilibrium \(E_1\) is unstable. This completes the proof. \(\square \)

Biologically, Theorem 3.2 implies that when \(R_0>1, R_1\le 1\) and \(R_2\le 1\) then the establishments of both CTLs and antibody immune responses are unsuccessful.

3.3 Stability of equilibrium \(E_2\)

Theorem 3.3

Assume \((A_2)\) holds, if \(R_0>1\) and \(R_1>1\) (a) If \(R_3\le 1,\) then the antibody response equilibrium \(E_2\) is globally asymptotically stable.

(b) If \(R_3>1\), then the equilibrium \(E_2\) is unstable.

Proof

Consider conclusion (a). Define a Lyapunov functional \(L_3(t)\) as follows

$$\begin{aligned} L_3(t)=\int _{\Omega } (V_1(x,t)+V_2(x,t))\,\mathrm {d}x, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} V_1(x,t)&=\displaystyle u-u_2-\int _{u_2}^{u} {\displaystyle \frac{f(u_2,w_2,v_2)}{f(s,w_2,v_2)}}\,\mathrm {d}s +\mathrm{e}^{a_1\tau _1}w_2H\left( \frac{w}{w_2}\right) \\&\quad \displaystyle +\,{\displaystyle \frac{a\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v_2H\left( \frac{v}{v_2}\right) +{\displaystyle \frac{p\mathrm{e}^{a_1\tau _1}}{c}}z+{\displaystyle \frac{aq\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y_2H\left( \frac{y}{y_2}\right) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} V_2(x,t)= & {} \displaystyle f(u_2,w_2,v_2)v_2\int _0^{\tau _1} H\left( \frac{f(u_\theta ,w_\theta ,v_\theta )v_\theta }{f(u_2,w_2,v_2)v_2}\right) \,\mathrm {d}\theta \\&+a\mathrm{e} ^{a_1\tau _1}w_2\int _0^{\tau _2} H\left( \frac{w_\theta }{w_2}\right) \,\mathrm {d}\theta . \end{aligned}$$

It is obvious that \(L_3(t)>0\) for all \((u(t),w(t),v(t),z(t),y(t))>0\) and \((u(t),w(t),v(t), z(t),y(t))\ne (u_2,w_2,v_2,0,y_2)\), where \(u_2,w_2,v_2\) and \(y_2\) satisfy the following equations

$$\begin{aligned} f(u_2,w_2,v_2)v_2=a\mathrm{e}^{a_1\tau _1}w_2={\displaystyle \frac{a(m+qy_2)\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v_2. \end{aligned}$$

Calculating the time derivative of \(L_3(t)\) along any positive solution of model (3), we can obtain

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\mathrm{d}L_3(t)}{\mathrm{d}t}}&=\displaystyle \int _{\Omega } \mathrm{d}u_2\left( 1-{\displaystyle \frac{u}{u_2}}\right) \left( 1-{\displaystyle \frac{f(u_2,w_2,v_2)}{f(u,w_2,v_2)}}\right) \,\mathrm {d}x\\&\quad +f(u_2,w_2,v_2)v_2\int _{\Omega } \left[ 4-{\displaystyle \frac{v_2w_{\tau _2}}{vw_2}}\right. \\&\quad \left. \displaystyle -{\displaystyle \frac{f_{\tau _1}}{f(u_2,w_2,v_2)v_2}} \cdot {\displaystyle \frac{w_2}{w}}-{\displaystyle \frac{f(u_2,w_2,v_2)}{f(u,w_2,v_2)}} -{\displaystyle \frac{f(u,w_2,v_2)}{f(u,w,v)}}\right] \,\mathrm {d}x\\&\quad \displaystyle +f(u_2,w_2,v_2)v_2\int _{\Omega } \left[ -1+{\displaystyle \frac{f(u,w_2,v_2)}{f(u,w,v)}}-{\displaystyle \frac{v}{v_2}} +{\displaystyle \frac{vf(u,w,v)}{v_2f(u,w_2,v_2)}}\right] \,\mathrm {d}x\\&\quad \displaystyle +\int _{\Omega } p\mathrm{e}^{a_1\tau _1}\left( w_2-{\displaystyle \frac{b}{c}}\right) z\,\mathrm {d}x +{\displaystyle \frac{aD\mathrm{e}^{a_1\tau _1+a_2\tau _2}\triangle v}{k}}\left( 1-{\displaystyle \frac{v_2}{v}}\right) \\&\quad \displaystyle +f(u_2,w_2,v_2)v_2\int _{\Omega } \left[ \ln {\displaystyle \frac{f_{\tau _1}}{f(u_2,w_2,v_2)v_2}}\cdot {\displaystyle \frac{w_{\tau _2}}{w}}\right] \,\mathrm {d}x\\&=\displaystyle \int _{\Omega } \mathrm{d}u_2\left( 1-{\displaystyle \frac{u}{u_2}}\right) \left( 1-{\displaystyle \frac{f(u_2,w_2,v_2)}{f(u,w_2,v_2)}}\right) \,\mathrm {d}x\\&\quad -f(u_2,w_2,v_2)v_2\int _{\Omega } \left[ H\left( {\displaystyle \frac{v_2w_{\tau _2}}{vw_2}}\right) \right. \\&\quad \left. \displaystyle +H\left( {\displaystyle \frac{f(u_2,w_2,v_2)}{f(u,w_2,v_2)}}\right) +H\left( {\displaystyle \frac{f_{\tau _1}}{f(u_2,w_2,v_2)v_2}}\cdot {\displaystyle \frac{w_2}{w}}\right) +H\left( {\displaystyle \frac{f(u,w_2,v_2)}{f(u,w,v)}}\right) \right] \,\mathrm {d}x\\&\quad \displaystyle +p\mathrm{e}^{a_1\tau _1}\left( w_2-{\displaystyle \frac{b}{c}}\right) \int _{\Omega }z \,\mathrm {d}x-{\displaystyle \frac{aD\mathrm{e}^{a_1\tau _1+a_2\tau _2}v_2}{k}}\int _{\Omega } {\displaystyle \frac{\parallel \nabla v\parallel ^2}{v^2}}\,\mathrm {d}x\\&\quad \displaystyle +f(u_2,w_2,v_2)v_2\int _{\Omega }\left( 1-{\displaystyle \frac{f(u,w,v)}{f(u_2,w_2,v_2)}}\right) \left( {\displaystyle \frac{f(u,w_2,v_2)}{f(u,w,v)}}-{\displaystyle \frac{v}{v_2}}\right) \,\mathrm {d}x. \end{aligned} \end{aligned}$$

Obviously, we always have \(\frac{\mathrm{d}L_3(t)}{\mathrm{d}t}\le 0,\) and \(\frac{\mathrm{d}L_3(t)}{\mathrm{d}t}=0\) if and only if \(u(t)=u_2,w(t)=w_2,v(t)=v_2, z(t)=0\) and \(y(t)=y_2.\) From LaSalle’s invariance principle (Hale and Verduyn 1993), we finally have that the equilibrium \(E_2\) of model (3) is globally asymptotically stable when \(R_0>1, R_1\le 1\) and \(R_2\le 1\).

Next, we consider conclusion (b). From (13), by computing, we obtain the characteristic equation of the corresponding linearized system of model (3) at the equilibrium \(E_2\) as follows

$$\begin{aligned} (s-cw_2+b)f(s)=0, \end{aligned}$$

where

$$\begin{aligned} f(s)=\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{11} &{} a_{12} &{} a_{13} &{} 0\\ a_{21} &{} a_{22} &{} a_{23} &{} 0\\ 0 &{} a_{32} &{} a_{33} &{} a_{34}\\ 0 &{} 0 &{} a_{43} &{} a_{44} \end{array}\right| , \end{aligned}$$

where

$$\begin{aligned} a_{11}= & {} s+d+\frac{\partial f }{\partial u}v_2,\\ a_{12}= & {} \frac{\partial f }{\partial w}v_2,\\ a_{13}= & {} \frac{\partial f }{\partial v}v_2+f(u_2,w_2,v_2),\\ a_{21}= & {} -\mathrm{e}^{-(a_1+s)\tau _1}\frac{\partial f }{\partial u}v_2,\\ a_{22}= & {} s+a-\frac{\partial f }{\partial w}v_2\mathrm{e}^{-(a_1+s)\tau _1},\\ a_{23}= & {} -\mathrm{e}^{-(a_1+s)\tau _1}\left( \frac{\partial f }{\partial v}v_2+f(u_2,w_2,v_2)\right) ,\\ a_{32}= & {} -k\mathrm{e}^{-(a_2+s)\tau _2},\\ a_{33}= & {} s+m+\mu _{i}D+qy_2,\; a_{34}= qv_2,\; a_{43}=-gy_2,\;a_{44}=s-gv_2+h. \end{aligned}$$

When \(R_3>1\), we have \(s=cw_2-b>0.\) Therefore, when \(R_3>1\) equilibrium \(E_2\) is unstable. This completes the proof. \(\square \)

Biologically, Theorem 3.3 implies that when \(R_0>1, R_1>1\) and \(R_3\le 1\), the antibody response can be established, but the infected cells are too weak so that it cannot stimulate CTL immune response.

3.4 Stability of equilibrium \(E_3\)

Theorem 3.4

Assume \((A_2)\) holds, if \(R_0>1\) and \(R_2>1\) (a) If \(R_4\le 1\), then the infection equilibrium \(E_3\) with only CTL response is globally asymptotically stable.

(b) If \(R_4>1\), then the equilibrium \(E_3\) is unstable.

Proof

Consider conclusion (a). Define a Lyapunov functional \(L_4(t)\) as follows

$$\begin{aligned} L_4(t)=\int _{\Omega } (V_1(x,t)+V_2(x,t))\,\mathrm {d}x, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} V_1(x,t)&=\displaystyle u-u_3-\int _{u_3}^{u} {\displaystyle \frac{f(u_3,w_3,v_3)}{f(s,w_3,v_3)}}\,\mathrm {d}s\\&\quad +\,\mathrm{e}^{a_1\tau _1}w_3H\left( \frac{w}{w_3}\right) + {\displaystyle \frac{p\mathrm{e}^{a_1\tau _1}}{c}}z_3H\left( \frac{z}{z_3}\right) \\&\quad \displaystyle +\,{\displaystyle \frac{(a+pz_3)\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v_3H\left( \frac{v}{v_3}\right) \\&\quad +\,{\displaystyle \frac{(a+pz_3)q\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} V_2(x,t)&=\displaystyle f(u_3,w_3,v_3)v_3\int _0^{\tau _1} H\left( \frac{f(u_\theta ,w_\theta ,v_\theta )v_\theta }{f(u_3,w_3,v_3)v_3}\right) \,\mathrm {d}\theta \\&\quad \displaystyle +(a+pz_3)\mathrm{e} ^{a_1\tau _1}w_3\int _0^{\tau _2} H\left( \frac{w_\theta }{w_3}\right) \,\mathrm {d}\theta . \end{aligned} \end{aligned}$$

We easily prove that \(L_4(t)>0\) for all \((u(t),w(t),v(t),z(t),y(t))>0\) and \((u(t),w(t), v(t),z(t),y(t))\ne (u_3,w_3,v_3,z_3,0)\).

By using

$$\begin{aligned} f(u_3,w_3,v_3)v_3= & {} (a+pz_3)\mathrm{e}^{a_1\tau _1}w_3\\= & {} {\displaystyle \frac{m(a+pz_3)\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v_3. \end{aligned}$$

Calculating the time derivative of \(L_4(t)\) along any positive solution of model (3), we can obtain

$$\begin{aligned} {\displaystyle \frac{\mathrm{d}L_4(t)}{\mathrm{d}t}}= & {} \displaystyle \int _{\Omega } \mathrm{d}u_3\left( 1-{\displaystyle \frac{u}{u_3}}\right) \left( 1-{\displaystyle \frac{f(u_3,w_3,v_3)}{f(u,w_3,v_3)}}\right) \,\mathrm {d}x\\&+f(u_3,w_3,v_3)v_3\int _{\Omega } \left[ 4-{\displaystyle \frac{v_3w_{\tau _2}}{vw_3}}\right. \\&\left. \displaystyle -{\displaystyle \frac{f_{\tau _1}}{f(u_3,w_3,v_3)v_3}} \cdot {\displaystyle \frac{w_2}{w}}-{\displaystyle \frac{f(u_3,w_3,v_3)}{f(u,w_3,v_3)}} -{\displaystyle \frac{f(u,w_3,v_3)}{f(u,w,v)}}\right] \,\mathrm {d}x\\&\displaystyle +f(u_3,w_3,v_3)v_3\int _{\Omega } \left[ -1+{\displaystyle \frac{f(u,w_3,v_3)}{f(u,w,v)}}-{\displaystyle \frac{v}{v_3}} +{\displaystyle \frac{vf(u,w,v)}{v_3f(u,w_3,v_3)}}\right] \,\mathrm {d}x\\&\displaystyle +\int _{\Omega } {\displaystyle \frac{(a+pz_3)}{k}}\mathrm{e}^{a_1\tau _1+ a_2\tau _2}\left( y_3-{\displaystyle \frac{h}{g}}\right) y\,\mathrm {d}x +{\displaystyle \frac{(a+pz_3)D\mathrm{e}^{a_1\tau _1+a_2\tau _2}\triangle v}{k}}\left( 1-{\displaystyle \frac{v_3}{v}}\right) \\&\displaystyle +f(u_3,w_3,v_3)v_3\int _{\Omega } \left[ \ln {\displaystyle \frac{f_{\tau _1}}{f(u_3,w_3,v_3)v_3}}\cdot {\displaystyle \frac{w_{\tau _2}}{w}}\right] \,\mathrm {d}x\\= & {} \displaystyle \int _{\Omega } \mathrm{d}u_3\left( 1-{\displaystyle \frac{u}{u_3}}\right) \left( 1-{\displaystyle \frac{f(u_3,w_3,v_3)}{f(u,w_3,v_3)}}\right) \,\mathrm {d}x -f(u_3,w_3,v_3)v_3\int _{\Omega } \left[ H\left( {\displaystyle \frac{v_3w_{\tau _2}}{vw_3}}\right) \right. \\&\left. \displaystyle +H\left( {\displaystyle \frac{f(u_3,w_3,v_3)}{f(u,w_3,v_3)}}\right) + H\left( {\displaystyle \frac{f_{\tau _1}}{f(u_3,w_3,v_3)v_3}}\cdot {\displaystyle \frac{w_3}{w}}\right) + H\left( {\displaystyle \frac{f(u,w_3,v_3)}{f(u,w,v)}}\right) \right] \,\mathrm {d}x\\&\displaystyle +f(u_3,w_3,v_3)v_3\int _{\Omega }\left( 1-{\displaystyle \frac{f(u,w,v)}{f(u_3,w_3,v_3)}}\right) \left( {\displaystyle \frac{f(u,w_3,v_3)}{f(u,w,v)}}-{\displaystyle \frac{v}{v_3}}\right) \,\mathrm {d}x\\&\displaystyle -{\displaystyle \frac{(a+pz_3)D\mathrm{e}^{a_1\tau _1+a_2\tau _2}v_3}{k}}\int _{\Omega } {\displaystyle \frac{\parallel \nabla v\parallel ^2}{v^2}}\,\mathrm {d}x\\&\displaystyle +{\displaystyle \frac{(a+pz_3)}{k}}\mathrm{e}^{a_1\tau _1+a_2\tau _2} \left( y_3-{\displaystyle \frac{h}{g}}\right) \int _{\Omega } y\,\mathrm {d}x. \end{aligned}$$

Obviously, we always have \(\frac{\mathrm{d}L_4(t)}{\mathrm{d}t}\le 0,\) and \(\frac{\mathrm{d}L_4(t)}{\mathrm{d}t}=0\) if and only if \(u(t)=u_3,w(t)=w_3,v(t)=v_3, z(t)=z_3\) and \(y(t)=0.\) From LaSalle’s invariance principle (Hale and Verduyn 1993), we finally have that the equilibrium \(E_3\) of model (3) is globally asymptotically stable when \(R_0>1, R_2>1\) and \(R_4\le 1\).

Next, we consider conclusion (b). From (13), by computing, we obtain the characteristic equation of the linearization system of model (3) at the equilibrium \(E_3\) as follows

$$\begin{aligned} (s+h-gv_3)f(s)=0, \end{aligned}$$

where

$$\begin{aligned} f(s)=\left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_{11} &{} a_{12} &{} a_{13} &{} 0\\ a_{21} &{} a_{22} &{} a_{23} &{} a_{24}\\ 0 &{} a_{32} &{} a_{33} &{} 0\\ 0 &{} a_{42} &{} 0 &{} a_{44} \end{array}\right| , \end{aligned}$$

where

$$\begin{aligned} a_{11}= & {} s+d+\frac{\partial f }{\partial u}v_3,\\ a_{12}= & {} \frac{\partial f }{\partial w}v_3,\; a_{13}=\frac{\partial f }{\partial v}v_3+f(u_3,w_3,v_3),\\ a_{21}= & {} -\mathrm{e}^{-(a_1+s)\tau _1}\frac{\partial f }{\partial u}v_3,\; a_{22}=s+a-\mathrm{e}^{-(a_1+s)\tau _1}\frac{\partial f }{\partial w}v_3+pz_3,\\ a_{23}= & {} -\mathrm{e}^{-(a_1+s)\tau _1}\left( \frac{\partial f }{\partial v}v_3+f(u_2,w_2,v_2)\right) ,\;a_{24}=pw_3,\; a_{32}=-k\mathrm{e}^{-(a_2+s)\tau _2},\\ a_{33}= & {} s+m+\mu _{i}D,\; a_{42}=-cz_3,\;a_{44}=s-cw_3+b. \end{aligned}$$

When \(R_4>1\), we have there is a positive root \(s_1=gv_3-h\). Therefore, when \(R_4>1\) equilibrium \(E_3\) is unstable for any \(\tau _1\ge 0\) and \(\tau _2\ge 0\). This completes the proof. \(\square \)

Biologically, Theorem 3.4 implies that, when \(R_0>1, R_2>1\) and \(R_4\le 1\), the CTL immune response can be determined, but the viral loads are so small that it cannot activate the antibody responses.

3.5 Stability of equilibrium \(E_4\)

Theorem 3.5

Assume \((A_2)\) holds, if \(R_0>1, R_1>1, R_3>1\) and \(R_4>1\), then the infection equilibrium with CTL and antibody responses \(E_4\) is globally asymptotically stable.

Proof

Define a Lyapunov functional \(L_5(t)\) as follows

$$\begin{aligned} L_5(t)=\int _{\Omega } (V_1(x,t)+V_2(x,t))\,\mathrm {d}x, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} V_1(x,t)&=\displaystyle u-u_4-\int _{u_4}^{u} {\displaystyle \frac{f(u_4,w_4,v_4)}{f(s,w_4,v_4)}}\,\mathrm {d}s +\mathrm{e}^{a_1\tau _1}w_4H\left( \frac{w}{w_4}\right) +{\displaystyle \frac{p\mathrm{e}^{a_1\tau _1}}{c}}z_4H\left( \frac{z}{z_4}\right) \\&\quad \displaystyle +{\displaystyle \frac{(a+pz_4)\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{k}}v_4H\left( \frac{v}{v_4}\right) +{\displaystyle \frac{(a+pz_4)q\mathrm{e}^{a_1\tau _1+a_2\tau _2}}{kg}}y_4H\left( \frac{y}{y_4}\right) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} V_2(x,t)&=\displaystyle f(u_4,w_4,v_4)v_4\int _0^{\tau _1} H\left( \frac{f(u_\theta ,w_\theta ,v_\theta )v_\theta }{f (u_4,w_4,v_4)v_4}\right) \,\mathrm {d}\theta \\&\quad \displaystyle +(a+pz_4)\mathrm{e} ^{a_1\tau _1}w_4\int _0^{\tau _2} H\left( \frac{w_\theta }{w_4}\right) \,\mathrm {d}\theta . \end{aligned} \end{aligned}$$

It is obvious that \(L_5(t)>0\) for all \((u(t),w(t),v(t),z(t),y(t))>0\) and \((u(t),w(t),v(t), z(t),y(t))\ne (u_4,w_4,v_4,z_4,y_4)\).

Calculating the time derivative of \( L_5(t) \) along any positive solution of model (3), we can obtain

$$\begin{aligned} \begin{aligned} {\displaystyle \frac{\mathrm{d}L_5(t)}{\mathrm{d}t}}&=\displaystyle \int _{\Omega } \mathrm{d}u_4\left( 1-{\displaystyle \frac{u}{u_4}}\right) \left( 1-{\displaystyle \frac{f(u_4,w_4,v_4)}{f(u,w_4,v_4)}}\right) \,\mathrm {d}x\\&\quad -f(u_4,w_4,v_4)v_4\int _{\Omega } \left[ H\left( {\displaystyle \frac{v_4w_{\tau _2}}{vw_4}}\right) \right. \\&\left. \quad \displaystyle +H\left( {\displaystyle \frac{f(u_4,w_4,v_4)}{f(u,w_4,v_4)}}\right) +H\left( {\displaystyle \frac{f_{\tau _1}}{f(u_4,w_4,v_4)v_4}}\cdot {\displaystyle \frac{w_4}{w}}\right) \right. \\&\left. \quad +H\left( {\displaystyle \frac{f(u,w_4,v_4)}{f(u,w,v)}}\right) \right] \,\mathrm {d}x\\&\quad \displaystyle +f(u_4,w_4,v_4)v_4\int _{\Omega }\left( 1-{\displaystyle \frac{f(u,w,v)}{f(u_4,w_4,v_4)}}\right) \left( {\displaystyle \frac{f(u,w_4,v_4)}{f(u,w,v)}}-{\displaystyle \frac{v}{v_4}}\right) \,\mathrm {d}x\\&\quad \displaystyle -{\displaystyle \frac{(a+pz_4)D\mathrm{e}^{a_1\tau _1+a_2\tau _2}v_4}{k}}\int _{\Omega } {\displaystyle \frac{\parallel \nabla v\parallel ^2}{v^2}}\,\mathrm {d}x. \end{aligned} \end{aligned}$$

Obviously, we always have \(\frac{\mathrm{d}L_5(t)}{\mathrm{d}t}\le 0,\) and \(\frac{\mathrm{d}L_5(t)}{\mathrm{d}t}=0\) if and only if \(u=u_4,\;w=w_4,\;v=v_4.\) From the LaSalle’s invariance principle Hale and Verduyn (1993), we finally have that the equilibrium \(E_4\) of model (3) is globally asymptotically stable when \(R_0>1, R_1>1, R_3>1\) and \(R_4>1\). This completes the proof. \(\square \)

Biologically, Theorem 3.5 implies that, if CTL immune response has not any delay, then the susceptible cells, infected cells, free virus, CTL immune response and antibody immune response can coexist in vivo.

4 Numerical simulations

In this section, we perform some numerical simulations to illustrate the results obtained in Sect. 3. We consider model (3) under the homogeneous Neumann boundary conditions

$$\begin{aligned} \frac{\partial v}{\partial \vec {n}}=0,\; t>0,\;x=0,\;1 \end{aligned}$$
(16)

and initial conditions

$$\begin{aligned} \begin{aligned} u(x,\theta )&=\phi _1(x,\theta )\ge 0,\;w(x,\theta )=\phi _2(x,\theta )\ge 0,\\ v(x,\theta )&=\phi _3(x,\theta )\ge 0,\;z(x,\theta )=\phi _4(x,\theta )\ge 0,\\ y(x,\theta )&=\phi _5(x,\theta )\ge 0,\;x\in [0,1],\;\theta \in [-\tau ,0]. \end{aligned} \end{aligned}$$
(17)

In model (3), we choose a nonlinear incidence \(f(u,w,v)=\frac{\beta u}{1+m_1u+n_1v+m_1n_1uv}\). Furthermore, \(\beta , g, h, \tau _1, \tau _2, c\) and b are chosen as free parameters and all remaining parameters are fixed as in Table 1.

Table 1 List of parameters
Full size table

In Figs. 1, 2, 3, 4 and 5a–e are denoted time series figures of u(x, t), w(x, t), v(x, t), z(x, t) and y(x, t).

5 Discussion

In this paper, we have discussed a delayed virus infection model (3) with diffusion, adaptive immune responses and general incidence rate. During viral infection, CTL immune responses which attack infected cells, and antibody responses which attack viruses. Hence, we assume that the production of CTL immune response depends on the infected cells and CTL immune responses. We see that similar assumption also is given in Nowak and Bangham (1996), Yan and Wang (2012), Zhu and Zou (2009), Shu et al. (2013), Wang et al. (2013, 2014, 2012) and Balasubramaniam et al. (2015). Similarly, the production of antibody response depends on the virus and antibody (Yan and Wang 2012; Wang et al. 2013; Balasubramaniam et al. 2015; Wang et al. 2014). Assumptions \((A_1)\) and \((A_2)\) for nonlinear function f(u, w, v)v are introduced and a combination of the basic reproduction number for viral infection \(R_0\), for CTL response \(R_1\), for antibody immune response \(R_2\), for CTL immune competition \(R_3\) and for humoral immune competition \(R_4\) defined by (8)–(12), respectively, also are defined. Under \((A_1)\) and \((A_2)\), the global stability and instability of the equilibria of model (3) by utilizing the method of constructing suitable Lyapunov functionals which are motivated by recent works of Pawelek et al. (2012), Zhu and Zou (2009), Shu et al. (2013), Yuan and Zou (2013) and Huang et al. (2011) are completely determined by the basic reproduction numbers \(R_0, R_1, R_2, R_3\) and \(R_4\).

Fig. 1
figure 1

Taking \(\beta =0.01,\; c=0.1,\; b=0.15,\; g=1.5,\; h=0.1,\;\tau _1=10,\;\tau _2=5\), we have \(R_0=0.2087<1\), the infection-free equilibrium \(E_0(1000,0,0,0,0)\) is asymptotically stable

Full size image
Fig. 2
figure 2

Taking \(\beta =0.15,\; c=0.01,\; b=0.2,\; g=0.5,\; h=1.5,\;\tau _1=3,\;\tau _2=15\), we have \(R_0=3.0373>1,\;R_1= 0.7098<1\) and \(R_2=0.9277<1\), the immune-free equilibrium \(E_1(44.0253,18.5544,2.1293,0,0)\) is asymptotically stable

Full size image

By the analysis, we have shown that when \(R_0\le 1\), the infection-free equilibrium \(E_0\) is globally asymptotically stable, which means that the viruses are cleared and the infection dies out. When \(R_0>1, R_1\le 1\) and \(R_2\le 1\) the immune-free equilibrium \(E_1\) is globally asymptotically stable, which means that immune response would not be activated and viral infection becomes vanished. When \(R_0>1, R_1>1\) and \(R_3\le 1\), the infection equilibrium with only antibody cells response \(E_2\) is globally asymptotically stable. As respect to the analysis of infection equilibrium \(E_3\) with only CTL response, when \(R_0>1,\) \(R_2>1\) and \(R_4\le 1, E_3\) is globally asymptotically stable, which means that the antibody response would not be activated and viral infection becomes vanished. About the stability of infection equilibrium \(E_4\) with both CTL and antibody response we have obtained that when \(R_3>1\) and \(R_4>1, E_4\) is globally asymptotically stable. We see that \((A_1)\) is basic for model (3). Particularly, when \(f(u,w,v)=\frac{\beta u}{1+m_1u+n_1v+m_1n_1uv}\) then \((A_1)\) naturally hold. But \((A_2)\) is a mathematical assumption. It is only used in the proofs of theorems on the global stability of equilibria \(E_1, E_2, E_3\) and \(E_4\) to obtain \(\frac{dL_n(t)}{dt}\) for the Lyapunov function \(L_n\) (see the proofs of Theorems 3.2–3.5). Furthermore, the numerical simulations given in Sect. 4 show the stability. Moreover, the effect of diffusion is considered as an important factor, which will be closer to reality. Compared to the case without diffusion, the approach is to construct Lyapunov functionals for partial differential equations (PDEs) or delayed partial differential equations (DPDEs) using Lyapunov functionals for ordinary differential equations (ODEs) or delayed differential equations (DDEs). Research on diffusion will be more complicated. Moreover, all the five state variables are influenced by multi-time delays and diffusion can better impact the virus infection problems. Therefore, research in this paper can be seen as an improvement and a supplementary of model (2), and it might be helpful to understand the virus infection model. Finally, under homogeneous Neumann boundary conditions, our results imply that diffusion, the intracellular delay and virus replication delay have no effect on the global behaviors of such virus dynamics model.

Fig. 3
figure 3

Taking \(\beta =0.25,\; c=0.01,\; b=0.18,\; g=1.5,\; h=1,\;\tau _1=10,\;\tau _2=5\), we have \(R_0=5.2164>1,\;R_1= 3.3682>1\) and \(R_3=0.8899<1\), the infection equilibrium only with CTL immune response \(E_2(114.8758,16.0179,0.6667,0,6.1420)\) is asymptotically stable

Full size image
Fig. 4
figure 4

Taking \(\beta =0.35,\; c=0.1,\; b=0.15,\; g=1.5,\; h=1,\;\tau _1=10,\;\tau _2=5\), we have \(R_0=7.3030>1,\;R_2= 11.8885>1\) and \(R_4=0.2854<1\), the infection equilibrium only with antibody response \(E_3(455.1241,1.5000,0.1902,2.7868,0)\) is asymptotically stable

Full size image
Fig. 5
figure 5

Taking \(\beta =0.45,\; c=0.15,\; b=0.15,\; g=0.1,\; h=0.01,\;\tau _1=2,\;\tau _2=5\), we have \(R_0=10.1716>1,\;R_3= 7.5777>1\) and \(R_4=1.2683>1\), the infection equilibrium with both antibody and CTL immune responses \(E_4(613.4595,1.0000,0.1000,3.2889,0.8049)\) is asymptotically stable

Full size image

Observing all obtained results in this paper, we can directly put forward the following open question which need to be further studied in the future.

In this paper, we only discuss a five-dimensional diffusive virus infection model with intracellular delay, virus replication delay and general incidence rate. Based on different practical backgrounds, the immune response delay and mitotic proliferation terms for both uninfected and infected target cells are considered in modeling the viral infection of disease. Therefore, whether the results obtained in this paper also can be extended to five-dimensional diffusive virus infection model with mitosis transmission and immune delay. In other words, with immune delay as a bifurcation parameter, whether we also can obtain that the global asymptotic stability of equilibria for infection-free, immune-free, antibody response, infection with CTL response and infection with both antibody and CTL response, respectively, will also be a very estimable and significative subject.