Abstract
Nonlinear differential equations with non-instantaneous impulses are studied. The impulses start abruptly at some points and their actions continue on given finite intervals. We pursue the study of Lipschitz stability using Lyapunov functions. Some sufficient conditions for Lipschitz stability, uniform Lipschitz stability, and uniform global Lipschitz stability are obtained. Examples are given to illustrate the results.
Similar content being viewed by others
1 Introduction
The problems of stability of solutions of differential equations via Lyapunov functions have been successfully investigated in the past. One type of stability, very useful in real world problems, is the so-called Lipschitz stability. Dannan and Elaydi [1] introduced the notion of Lipschitz stability for ordinary differential equations. As is mentioned in [1] this type of stability is important only for nonlinear problems, since it coincides with uniform stability in linear systems.
There are a few different real life processes and phenomena that are characterized by rapid changes in their state. We will emphasize two main types of such kind of changes:
-
The duration of these changes is relatively short compared to the overall duration of the whole process and the changes turn out to be irrelevant to the development of the studied process. The mathematical models in such cases can be adequately created with the help of impulsive equations (see, for example, [2–5], the monographs [6, 7] and the references therein).
-
The duration of these changes is not negligible short, i.e. these changes start impulsively at arbitrary fixed points and remain active on finite initially time intervals. The model of this situation is the non-instantaneous impulsive differential equation. Hernandez and O’Regan [8] introduced this new class of differential equations where the impulses are not instantaneous and they investigated the existence of mild and classical solutions. We refer the reader for some recent results such as existence to [9, 10], to stability [11–16], to periodic boundary value problems [17, 18].
Some examples of such processes can be found in physics, biology, population dynamics, ecology, pharmacokinetics, and others.
In this paper Lipschitz stability of solutions of nonlinear non-instantaneous impulsive differential equations is defined and studied. Several sufficient conditions for Lipschitz stability, uniform Lipschitz stability, and global uniform Lipschitz stability are obtained. Some examples illustrating the results are given. Note that non-instantaneous impulsive differential equations are natural generalizations of impulsive differential equations and some of the obtained sufficient conditions are a generalization of some results in [19]. Also, Lipschitz stability of impulsive functional-differential equations is studied in [20].
2 Preliminaries
In this paper we assume two increasing sequences of points \(\{t_{i}\} _{i=1}^{\infty}\) and \(\{s_{i}\}_{i=0}^{\infty}\) are given such that \(0 < s_{0}<t_{i}<s_{i}<t_{i+1}<s_{i+1}\), \(i=1,2, \ldots\) , and \(\lim_{k\rightarrow \infty}t_{k}=\infty\).
Let \(t_{0} \in\bigcup_{k=0}^{\infty}[s_{k},t_{k+1})\) be a given arbitrary point. Without loss of generality we will assume that \(t_{0} \in[0,s_{0})\).
Consider the initial value problem (IVP) for the system of non-instantaneous impulsive differential equation (NIDE)
where \(x,x_{0} \in\mathbb{R}^{n}\), \(f:\bigcup_{k=0}^{\infty}[t_{k}, s_{k}]\times \mathbb{R}^{n} \rightarrow\mathbb{R}^{n}\), \(\Psi_{k}:[s_{k},t_{k+1}] \times \mathbb{R}^{n} \times\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}\) (\(k = 1,2,3,\ldots\)).
Remark 1
The functions \(\Psi_{k}\) are called impulsive functions and the intervals \((s_{k},t_{k+1}]\), \(k=0, 1,2,\ldots\) are called intervals of non-instantaneous impulses.
Remark 2
In the partial case \(s_{k}=t_{k+1}\), \(k=0,1,2,\ldots\) each interval of non-instantaneous impulses is reduced to a point, and the problem (1) is reduced to an IVP for an impulsive differential equation with points of jump \(t_{k}\) and impulsive condition \(x(t_{k}+0)=I_{k}(x(t_{k}-0))\equiv\Psi_{k}(t_{k},x(t_{k}-0),x(t_{k}-0))\).
The solution \(x(t;t_{0},x_{0})\) of IVP for NIDE (1) is given by
where
-
for any \(k=0,1,2,\ldots\) the function \(X_{k}(t)\), \(t\in[t_{k},s_{k}]\) is a solution of the initial value problem for ODE \(x'=f(t,x)\), \(x(t_{k})=x(t_{k};t_{0},x_{0})\), respectively;
-
on any interval \((s_{k},t_{k+1}]\), \(k=0,1,2,\ldots\) the solution \(x(t;t_{0},x_{0})\) satisfies the algebraic equation \(x(t;t_{0},x_{0})=\Psi _{k}(t,x(t;t_{0},x_{0}), X_{k}(t_{1}-0))\).
Let \(J \subset\mathbb{R}^{+}\) be a given interval. Introduce the following classes of functions:
Remark 3
According to the above description any solution of (1) might have a discontinuity at any point \(s_{k}\), \(k =0, 1,2, \ldots\) .
Now we will illustrate the influence of the impulsive condition on the behavior of the solution.
Example 1
Consider the IVP for the NIDE
Case 1. Let \(\Psi_{k}(t,x,y)=2y\). Then the impulsive condition is \(x(t)=2 x(2k+1-0)\) and the solution of (3) is
The graph of the solutions of (3) on \([0,8]\) with various initial values \(x_{0}=0.5\), \(x_{0}=1\), \(x_{0}=1.5\) is given in Figure 1.
Graphs of solutions of ( 3 ) for various \(\pmb{x_{0}}\) .
Case 2. Let \(\Psi_{k}(t,x,y)=2x\). Then the impulsive condition is \(x(t)=2x(t)\) for \(t \in(2k-1,2k]\), \(k=1,2,\ldots\) with a solution \(x(t)\equiv0\), \(t \in(2k-1,2k]\), \(k=1,2,\ldots\) . The solution of (3) with the new impulsive condition is
Case 3. Let \(\Psi_{k}(t,x,y)=t-x\). Then the impulsive condition is \(x(t)=t-x(t)\) for \(t \in(2k-1,2k]\), \(k=1,2,\ldots\) with a solution \(x(t)=0.5 t\), \(t \in(2k-1,2k]\), \(k=1,2,\ldots\) . The solution of (3) with the new impulsive condition is
Therefore, if any impulsive function \(\Psi_{k}(t,x,y)\) do not depend on y the solution does not depend on the initial value \(x_{0}\) for \(t>s_{k}\) (see Cases 2 and 3).
Remark 4
Note in some papers (see, for example [14]) the functions of non-instantaneous impulses are given in the form \(g_{k}(t,x(t))\), i.e. they do not depend on the value of the solution before the jump \(x(s_{k}-0)\). Then the solution will depend on the initial value only on the interval \([t_{0},s_{0}]\). Then the meaning of the stability as well dependence of the solution on the initial value is lost.
Introduce the following condition.
-
(H1)
The function \(f \in C(\bigcup_{k=0}^{\infty}[t_{k}, s_{k}]\times\mathbb{R}^{n}, \mathbb{R}^{n})\) and \(f(t,0)\equiv0\).
-
(H2)
For any \(k=0,1,2,\ldots\) and any fixed \(t\in [s_{k},t_{k+1}]\) and \(y\in\mathbb{R}^{n}\) the algebraic equation \(x=\Psi _{k}(t,x,y)\) has unique solution \(x=\phi_{k}(t,y)\) with \(\phi_{k} \in C([s_{k},t_{k+1}] \times\mathbb{R}^{n}, \mathbb{R}^{n})\) and \(\phi_{k}(t,0)\equiv0\).
If condition (H2) is satisfied then IVP for NIDE (1) could be written in the form
Let \(J\subset\mathbb{R}_{+}\), \(0\in J\), \(\rho>0\). Introduce the following sets:
Remark 5
The function \(a(u)=K_{1}u\), \(K_{1}\in(0,1]\) is from the class \(K(\mathbb{R}_{+})\) with \(q(u)\equiv u\). The function \(a(u)=K_{1} u^{2}\), \(K_{1}>0\) is from the class \(M([0,1])\).
We will use the class Λ of Lyapunov-like functions, defined and used for impulsive differential equations in [7].
Definition 1
Let \(J \subset\mathbb{R}_{+}\) be a given interval, and \(\Delta\subset \mathbb{R}^{n} \) be a given set. We will say that the function \(V(t,x):J \times\Delta\rightarrow\mathbb{R}_{+}\), belongs to the class \(\Lambda(J, \Delta)\) if:
-
the function \(V(t,x)\) is a continuous on \(J/\{t_{k} \in J\}\times\Delta\) and it is locally Lipschitz with respect to its second argument;
-
for each \(s_{k} \in J\) and \(x \in\Delta\) there exist finite limits
$$ V(s_{k},x)=V(s_{k}-0,x)= \lim_{t \uparrow s_{k}}V(t,x) \quad \text{and}\quad V(s_{k}+0,x)= \lim_{t \downarrow s_{k}}V(t,x). $$
For any \(t \in(t_{k}, s_{k})\), \(k=0,1,2,\ldots\) , we define the Dini derivative of the function \(V(t,x)\in\Lambda(J, \Delta)\) by
where \(x \in\Delta\), and for any \(t \in(t_{k},s_{k})\) there exists \(h_{t}>0\): \(t-h \in(t_{k},s_{k})\), \(x-hf(t,x) \in\Delta\) for \(0< h< h_{t}\).
3 Main results
We define Lipschitz stability [1] of systems of differential equations with non-instantaneous impulses.
Definition 2
Lipschitz stability
The zero solution of (7) is said to be:
-
Lipschitz stable if there exists \(M \geq1\) and for every \(t_{0} \geq0\) there exists \(\delta=\delta(t_{0})>0\) such that, for any \(x_{0} \in\mathbb{R}^{n}\), the inequality \(|x_{0}|<\delta\) implies \(|x(t;t_{0},x_{0})| \leq M|x_{0}|\) for \(t \geq t_{0}\);
-
uniformly Lipschitz stable if there exist \(M \geq1\) and \(\delta>0\) such that for any \(t_{0}\geq0\) and \(x_{0} \in\mathbb{R}^{n}\) the inequality \(|x_{0}|<\delta\) implies \(|x(t;t_{0},x_{0})| \leq M|x_{0}|\) for \(t \geq t_{0}\);
-
globally uniformly Lipschitz stable if there exists \(M \geq1\) such that for any \(t_{0} \geq0\) and \(x_{0} \in \mathbb{R}^{n}\) the inequality \(|x_{0}|<\infty\) implies \(|x(t;t_{0},x_{0})| \leq M|x_{0}|\) for \(t \geq t_{0}\).
Example 2
Let \(t_{0}\geq0\) be an arbitrary point and without loss of generality we can assume \(0\leq t_{0}< s_{0}\). Consider the IVP for the NIDE
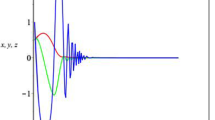
The solution of ODE \(x'=\frac{x}{(1+t)^{2}}\), \(x(\tau _{0})=x_{0}\) is \(x(t)=x_{0}e^{\frac{1}{1+\tau _{0}}-\frac{1}{1+t}}\), \(t\geq\tau _{0}\). Note, for any finite initial value \(x_{0}\) the inequality \(|x(t)|=x_{0}e^{\frac {1}{1+\tau _{0}}-\frac{1}{1+t}}\leq M|x_{0}|\) for \(t\geq\tau _{0}\) holds with \(M=e\), i.e. the zero solution of ODE is globally Lipschitz stable but not asymptotically stable (see the graphs for \(\tau _{0}=0\), \(x_{0}=0.1,0.5,1,1.5\) in Figure 2).
Graphs of solutions of ( 8 ), Case 1, for various \(\pmb{x_{0}}\) .
Case 1. Let \(\Psi_{k}(t,x,y)=xy\), \(k=0,1,2,\ldots\) . Then the impulsive condition is \(x(t)=x(t)x(s_{k}-0)\) which unique solution is \(x(t)=0\) since \(x(s_{k}-0)= x_{0}e^{\frac{1}{1+t_{0}}-\frac{1}{1+s_{0}}}\neq0\) iff \(x_{0}\neq0 \) and \(t_{0}< s_{0}\). Then the solution of NIDE (8) will be
The zero solution is globally Lipschitz stable, since \(x_{0}e^{\frac {1}{1+t_{0}}-\frac{1}{1+t}}\leq M|x_{0}|\) for \(t\geq t_{0}\) with \(M=e^{\frac {1}{1+t_{0}}-\frac{1}{1+t}}=e>1\). In this case the solution is also asymptotically stable.
Case 2. Let \(\Psi_{k}(t,x,y)=y\), \(k=0,1,2,\ldots\) . Then the impulsive condition is \(x(t)=x(s_{k}-0)\) and the solution of (8) is
The solution is a continuous function. The graphs of solutions for \(t_{0}=0\), \(s_{k}=2k-1\), \(t_{k}=2k\), \(k=1,2,\ldots\) and various initial values \(x_{0}\) are given in Figure 3. There exists \(M=e>1\) such that \(x(t)< M|x_{0}|\), \(t\geq t_{0}\) for any finite value of \(x_{0}\). Therefore the zero solution of (8) is globally uniformly Lipschitz stable but not asymptotically stable.
Graphs of solutions of ( 8 ), Case 2, for various \(\pmb{x_{0}}\) .
Case 3. Let \(\Psi_{k}(t,x,y)=y-x\), \(k=0,1,2,\ldots\) . Then the impulsive condition is \(x(t)=x(s_{k}-0)-x(t)\) which unique solution is \(x(t)=0.5 x(s_{k}-0)\). The solution of (8) is
The graphs of solutions for \(t_{0}=0\), \(s_{k}=2k-1\), \(t_{k}=2k\), \(k=1,2,\ldots\) , and various initial values \(x_{0}\) are given in Figure 4. There exists \(M=e>1\) such that \(x(t)< M|x_{0}|\), \(t\geq t_{0}\) for any finite value of \(x_{0}\). Therefore the zero solution of (8) is globally uniformly Lipschitz stable. Also it is asymptotically stable.
Graphs of solutions of ( 8 ), Case 3, for various \(\pmb{x_{0}}\) .
The above example shows the presence of non-instantaneous impulses and the type of impulsive functions that have influence on the behavior of the solution.
We study the Lipschitz stability using the following scalar comparison differential equation with non-instantaneous impulses:
where \(u,u_{0} \in\mathbb{R}\), \(g:\bigcup_{k=0}^{\infty}[t_{k}, s_{k}]\times \mathbb{R} \rightarrow\mathbb{R}\), \(\psi_{k}:[s_{k},t_{k+1}] \times \mathbb {R} \rightarrow\mathbb{R}\) (\(k = 0,1,2,3,\ldots\)).
We introduce the following condition.
-
(H3)
The function \(g(t,u) \in C(\bigcup_{k=0}^{\infty }[t_{k},s_{k}] \times\mathbb{R}_{+}, \mathbb{R})\), \(g(t,0)=0\), and for any \(k=0,1,2,\ldots\) the functions \(\psi_{k}:[s_{k},t_{k+1}] \times\mathbb{R}_{+} \rightarrow\mathbb{R}_{+}\) are nondecreasing with respect to their second argument and \(\psi_{k}(t,0)=0\).
In the main study we will use the following result.
Proposition 1
Theorem 3.1.1 [21]
Let the function \(V \in C([t_{0},T]\times\mathbb{R}^{n},\mathbb{R}_{+})\) and \(V(t,x)\) be locally Lipschitz in x and \(D_{+}V(t,x)\leq g(t,V(t,x))\) for \((t,x) \in[t_{0},T]\times\mathbb{R}^{n}\), where \(g\in C([t_{0},T] \times\mathbb{R}_{+},\mathbb{R})\). Let \(\tilde {r}(t)=r(t;t_{0},u_{0})\) be the maximal solution of the scalar differential equation \(u'=g(t,u)\) with initial condition \(u(t_{0})=u_{0}\geq0\), existing on \([t_{0},T]\). If \(x(t)=x(t;t_{0},x_{0})\) is any solution of the IVP for ODE \(x'=f(t,x)\), \(x(t_{0})=x_{0}\) existing on \([t_{0},T]\) such that \(V(t_{0},x_{0})\leq u_{0}\), then the inequality \(V(t,x(t)) \leq \tilde{r}(t)\) for \(t \in[t_{0},T]\) holds.
Lemma 1
Assume the following conditions are satisfied:
-
1.
Conditions (H1), (H2), and (H3) are satisfied.
-
2.
The function \(x^{*}(t)=x(t;t_{0},x_{0}) \in NPC^{1}([t_{0},T], \Delta)\) is a solution of (7), where \(T \geq t_{0}\) is a given constants, \(\Delta\subset\mathbb{R}^{n}\).
-
3.
The function \(V \in\Lambda([t_{0},T], \Delta)\) is such that:
-
(i)
the inequality \(D_{+}V(t,x^{*}(t))\leq g(t,V(t,x^{*}(t)))\) for \(t \in[t_{0},T] \cap(\bigcup_{k=0}^{\infty}(t_{k},s_{k})) \) holds;
-
(ii)
for all \(k=0, 1, 2,3, \ldots\) the inequality
$$V\bigl(t, \phi_{k}\bigl(t,x^{*}(s_{k}-0)\bigr)\bigr)\leq \psi_{k}\bigl(t,V\bigl(s_{k}-0,x^{*}(s_{k}-0)\bigr) \bigr)\quad \textit{for } t \in[t_{0},T]\cap(s_{k},t_{k+1}] $$holds.
-
(i)
If \(V(t_{0},x_{0})\leq u_{0}\), then the inequality \(V(t,x^{*}(t))\leq r(t)\) for \(t \in[t_{0},T]\) holds, where \(r(t)=r(t;t_{0},u_{0})\) is the maximal solution of (12) with \(u_{0}\geq0\).
Proof
We use induction to prove Lemma 1.
The function \(x^{*}(t) \in C^{1}([t_{0},s_{0}]\cap[t_{0},T],\Delta)\). According to condition 3(i) and Proposition 1 applied to the interval \([t_{0},s_{0}]\cap[t_{0},T]\) the inequality
holds.
Let \(T>s_{0}\) and \(t \in(s_{0},t_{1}] \cap[t_{0},T]\). From condition 3(ii)
From the inequality (13) we get \(V(s_{0}-0,x^{*}(s_{0}-0))\leq r(s_{0}-0;t_{0},u_{0})\) and the monotonicity of \(\psi_{0}\) we get
i.e. \(V(t,x^{*}(t))\leq r(t;t_{0},u_{0})\) for \(t \in(s_{0},t_{1}] \cap [t_{0},T]\).
Let \(T>t_{1}\) and \(t \in(t_{1},s_{1}] \cap[t_{0},T]\). Consider the function \(\overline{x}(t)=x^{*}(t)\) for \(t \in(t_{1},s_{1}]\) and \(\overline {x}(t_{1})=x^{*}(t_{1})=\phi_{0}(t_{1},x^{*}(s_{0}-0))\). Since \(\lim_{t \to t_{1}+0}\overline{x}(t)=\overline{x}(t_{1}+0)=\phi_{0}(t_{1},\overline {x}(s_{1}-0))=\overline{x}(t_{1}+0)\), \(\overline{x}(t) \in C^{1}([t_{1},s_{1}],\Delta)\). From condition \(3(ii)\) for the interval \([t_{1},s_{1}] \cap[t_{0},T]\) and the proof above we obtain
Apply Proposition 1 to the interval \([t_{1},s_{1}] \cap[t_{0},T]\) with the initial value \(u_{0}=r(t_{1};t_{0},u_{0})\) and \(V(t_{1},\overline{x}(t_{1}))\leq r(t_{1};t_{0},u_{0})\) and we obtain \(V(t,\overline{x}(t))\leq r(t)\), \(t\in[t_{1},s_{1}] \cap[t_{0},T]\). Therefore \(V(t,x^{*}(t))\leq r(t;t_{0},u_{0})\), \(t\in(t_{1},s_{1}] \cap[t_{0},T]\).
Let \(T>s_{1}\) and \(t \in(s_{1},t_{2}] \cap[t_{0},T]\). From condition 3(ii)
From the proof above and monotonicity of \(\psi_{1}\) we get
i.e. \(V(t,x^{*}(t))\leq r(t;t_{0},u_{0})\) for \(t \in(s_{1},t_{2}] \cap [t_{0},T]\).
Continue this process and an induction argument proves the claim of Lemma 1 is true for \(t \in[t_{0},T]\). □
Remark 6
Proposition 1 and Lemma 1 are true for \(T=\infty\) for the interval \([t_{0},\infty)\).
Theorem 1
Let the following conditions be satisfied:
-
1.
Conditions (H1)-(H3) are fulfilled.
-
2.
There exists a function \(V(t,x) \in\Lambda(\mathbb{R}^{+}, \mathbb{R}^{n})\) with Lipschitz constant L in \(S_{\rho}\), \(V(t,0)=0\), and:
-
(i)
the inequality
$$b\bigl(\Vert x\Vert \bigr)\leq V(t,x), \quad x \in\mathbb{R}^{n}, t \in\mathbb{R}_{+}, $$holds, where \(b\in K (\mathbb{R}_{+})\);
-
(ii)
the inequality \(D^{+}V(t,x) \leq g(t,V(t,x))\), \(t \in\bigcup_{k=0}^{\infty}(t_{k},s_{k}) \), \(x \in\mathbb{R}^{n}\), holds;
-
(iii)
for any \(k=1,2, \ldots\) the inequality
$$V\bigl(t,\phi_{k}(t,y)\bigr)\leq\psi_{k} \bigl(t,V(s_{k}-0,y)\bigr),\quad t \in(s_{k},t_{k+1}], y \in \mathbb{R}^{n}, $$holds.
-
(i)
-
3.
The zero solution of (12) is Lipschitz stable.
Then the zero solution of (7) is Lipschitz stable.
Proof
Let \(t_{0}\geq0\) be an arbitrary. Without loss of generality we assume \(t_{0}\in[0,s_{0})\). From condition 3 there exist \(M\geq1\), \(\delta_{1}=\delta_{1}(t_{0},M)>0\) such that for any \(u_{0}\in\mathbb{R}: |u_{0}|<\delta_{1}\) the inequality
holds, where \(u(t;t_{0},u_{0})\) is a solution of (12).
Since \(V(t_{0},0)=0\) there exists a \(\delta_{2}=\delta_{2}(t_{0},\delta_{1})>0\) such that \(V(t_{0},x)<\delta_{1}\) for \(\Vert x\Vert <\delta_{2}\). The function \(V(t,x)\) is Lipschitz on \(S_{\rho}\) then \(\|x\|<\rho\) implies \(|V(t,x)|=|V(t,x)-V(t,0)|\leq L\|x\|\).
Let \(\delta=\min \{ \delta_{1},\delta_{2},\rho \} \) and choose \(M_{1}\geq1\) such that \(M_{1}> M L\) and let \(M_{2}=q(M_{1})\). Note since \(M_{1}\geq1\) we have \(M_{2}\geq1\) and δ depends on \(t_{0}\) and M, therefore on \(M_{2}\).
Now let the initial value be such that \(\Vert x_{0}\Vert <\delta\). Consider a solution \(x(t)=x(t;t_{0},x_{0})\) of system (7). Let \(u_{0}^{\ast}=V(t_{0},x_{0})\). Then from the choice of \(x_{0}\) it follows that \(u_{0}^{\ast }=V(t_{0},x_{0})<\delta_{1}\) for \(\Vert x_{0}\Vert <\delta\). Therefore, the function \(u^{\ast}(t)\) satisfies (14) for \(t\geq t_{0}\) with \(u_{0}=u^{*}_{0}\), where \(u^{\ast }(t)=u(t;t_{0},u_{0}^{\ast})\) is a solution of (12).
Using condition 2(ii) and applying Lemma 1 for \(\Delta=\mathbb{R}^{n}\), \(T=\infty\) we get
From inequalities (14), (15), Lipschitz property of \(V(t,x)\), condition 2(i), and Lemma 1 we obtain, for any \(t\geq t_{0}\),
From the properties of \(b\in K \) and \(M_{1}>1\) it follows that \(b^{-1}(M_{1}u)< M_{1}q(u)\), and
From \(M_{1}\geq1\) its follows that \(q(M_{1})\geq1\) and therefore
□
Corollary 1
Let the conditions of Theorem 1 be satisfied with \(b(u)=K_{1} u\), \(K_{1}>0\).
Then the zero solution of (7) is Lipschitz stable.
Proof
The proof is similar to the one of Theorem 1 with \(M_{1}\geq1: M_{1}> M \frac{L}{K_{1}}\) and \(M_{2}=M_{1}\). □
Theorem 2
Let the following conditions be satisfied:
-
1.
Conditions (H1)-(H3) are fulfilled.
-
2.
There exists a function \(V(t,x) \in\Lambda(\mathbb{R}_{+}, \mathbb{R}^{n})\) and:
-
(i)
the inequalities
$$b\bigl(\Vert x\Vert \bigr)\leq V(t,x)\leq a\bigl(\Vert x\Vert \bigr), \quad x \in S_{\rho}, t \in\mathbb{R}_{+} $$holds, where \(b\in K ([0,\rho])\), \(a\in M ([0,\rho])\), \(\rho>0\);
-
(ii)
the inequality \(D^{+}V(t,x) \leq g(t,V(t,x))\), \(t \in\bigcup_{k=0}^{\infty}(t_{k},s_{k}) \), \(x \in S_{\rho}\) holds;
-
(iii)
for any \(k=0,1,2, \ldots\) the inequality
$$V\bigl(t,\phi_{k}(t,y)\bigr)\leq\psi_{k} \bigl(t,V(s_{k}-0,y)\bigr),\quad t \in(s_{k},t_{k+1}], y \in S_{\rho}, $$holds.
-
(i)
-
3.
The zero solution of (12) is uniformly Lipschitz stable (uniformly globally Lipschitz stable).
Then the zero solution of (7) is uniformly Lipschitz stable (uniformly globally Lipschitz stable).
Proof
Let the zero solution of (12) be uniformly Lipschitz stable. Let \(t_{0}\geq0\) be an arbitrary. Without loss of generality we assume \(t_{0}\in[0,s_{0})\). From condition 3 there exist \(M\geq1\), \(\delta _{1}>0\) such that for any \(t_{0} \in\bigcup_{k=0}^{\infty}[s_{k},t_{k+1})\) and any \(u_{0}\in\mathbb{R}: |u_{0}|<\delta_{1}\) the inequality
holds, where \(u(t;t_{0},u_{0})\) is a solution of (12).
From the inclusions \(b\in K ([0,\rho])\) and \(a\in {M}([0,\rho])\) there exist a function \(q_{b}(u)\) and a positive constant \(K_{a}\). Choose \(M_{1}\geq1\) such that \(M_{1}>q_{b}(M) K_{a}\) and \(\delta_{2}\leq \frac{\rho}{M_{1}}\). Therefore, \(\delta_{2}\leq\rho\).
Let \(\delta=\min \{ \delta_{1},\delta_{2},\frac{\delta _{1}}{K_{a}} \} \). Choose the initial value \(x_{0}\): \(\Vert x_{0}\Vert <\delta\). Therefore, \(\|x_{0}\|<\delta\leq\delta _{2}\leq\rho\), i.e. \(x_{0}\in S_{\rho}\). Consider the solution \(x(t)=x(t;t_{0},x_{0})\) of system (7) for the chosen initial data. Let \(u_{0}^{\ast}=V(t_{0},x_{0})\). From the choice of \(x_{0}\) and the properties of the function \(a(u)\) applying condition 2(i) we get \(u_{0}^{\ast }=V(t_{0},x_{0})\leq a(\|x_{0}\|)\leq K_{a}\|x_{0}\|< K_{a} \delta\leq\delta _{1}\). Therefore, the function \(u^{\ast}(t)\) satisfies (17) for \(t\geq t_{0}\) with \(u_{0}=u^{*}_{0}\), where \(u^{\ast }(t)=u(t;t_{0},u_{0}^{\ast})\) is a solution of (12).
We will prove
Assume (18) is not true. Therefore, there exists a point \(T>t_{0}\) such that \(\|x(t)\|\leq M_{1}\|x_{0}\|\) for \(t\in[t_{0},T]\), \(\|x(T)\|= M_{1}\|x_{0}\|\) and \(\|x(t)\|> M_{1}\|x_{0}\|\) for \(t\in(T,T+\epsilon]\), where \(\epsilon>0\) is a small enough number. Then for \(t\in[t_{0},T]\) the inequalities \(\|x(t)\|\leq M_{1}\|x_{0}\|< M_{1}\delta\leq M_{1}\delta_{2} \leq\rho\) hold, i.e. \(x(t)\in S_{\rho}\) for \(t\in[t_{0},T]\).
Using condition 2(ii) and applying Lemma 1 on \([t_{0},T]\) for \(\Delta=S_{\rho}\) we get
From inequality (19) and condition 2(i) we obtain
The contradiction obtained proves the validity of (18).
The proof of globally uniformly Lipschitz stability is analogous and we omit it. □
Corollary 2
Let (H1)-(H3) and condition 2 of Theorem 2 be satisfied with \(g(t,x)\equiv0\) and \(\psi_{k}(t,x)\equiv x\).
Then the zero solution of (7) is uniformly Lipschitz stable.
Corollary 3
Let (H1), (H2) be satisfied and the inequality
holds and for any \(k=0,1,2, \ldots\) the inequality
holds.
Then the zero solution of (7) is uniformly Lipschitz stable.
Proof
Consider the quadratic Lyapunov function \(V(t,x)=x^{2}\) for which \(D^{+}V(t,x) =2xf(t,x)\) and condition 2 of Theorem 2 is satisfied with \(K_{1}\leq1\), \(K_{2}\geq1\), \(g(t,x)=0\), and \(\psi_{k}(t,x)\equiv x\). □
Theorem 3
Let the conditions of Theorem 2 be satisfied where 2(i) is replaced by
-
2.
-
(i)
the inequalities \(\lambda_{1}(t)\|x\|^{2}\leq V(t,x)\leq\lambda _{2}(t)\|x\|^{2}\), \(x \in S_{\rho}\), \(t \in\mathbb{R}^{+} \) holds, where \(\lambda _{1},\lambda_{2}\in C(\mathbb{R}_{+},(0,\infty))\) and there exist positive constants \(A_{1}\), \(A_{2}\): \(A_{1}< A_{2}\) such that \(\lambda_{1}(t)\geq A_{1}\), \(\lambda _{2}(t)\leq A_{2}\) for \(t\geq0\), and \(\rho>0\).
-
(i)
If the zero solution of (12) is uniformly Lipschitz stable (uniformly globally Lipschitz stable) then the zero solution of (7) is uniformly Lipschitz stable(uniformly globally Lipschitz stable).
Proof
The proof is similar to the one of Theorem 2 where \(M_{1}=\sqrt {M\frac{A_{2}}{A_{1}}}\). □
4 Applications
Let two increasing sequences of points \(\{t_{i}\}_{i=1}^{\infty}\) and \(\{ s_{i}\}_{i=0}^{\infty}\) be given such that \(t_{0}=0\), \(0< s_{0}< t_{i}\leq s_{i}< t_{i+1}\), \(i=1,2, \ldots\) , and \(\lim_{k\rightarrow\infty }t_{k}=\infty\). Consider the following single species model exhibiting the so-called Allee effect in which the per-capita growth rate is a quadratic function of the density:
where \(a,c>0\), \(b\in\mathbb{R}\). The impulsive functions \(\psi_{k}(t, x)\leq C_{k}x\), \(k=0,1,2,\ldots\) , where \(C_{k}\in(0,1]\).
Define the function \(V(t,x)=x^{2}\).
Then condition 2(i) of Theorem 3 is satisfied for \(\lambda_{1}(t)=0.5\), \(\lambda_{2}(t)=1.5\).
For any \(x: |x|\leq\rho\), \(\rho=|\frac{b-\sqrt{b^{2}+4 ac}}{2c}|>0\) we have \(D^{+}V(t,x)=2x^{2} (cx^{2}-bx-a ) \leq0\), \(t \in\bigcup_{k=0}^{\infty}(t_{k},s_{k}) \), \(x \in S_{\rho}\). Therefore, condition 2(ii) is satisfied with \(g(t,x)\equiv0\).
The condition 2(ii) is satisfied for \(\psi_{k}(t,x)\equiv C_{k}x\).
Therefore, the comparison equation is
which solution is \(u(t;t_{0},u_{0}) =u_{0}\prod_{i=1}^{k}C_{i} \), for \(t\in (s_{k}, s_{k+1}]\), \(k=0,1,2,\ldots\) . Therefore, the zero solution of (21) according to Corollary 2 is uniformly Lipschitz stable.
References
Dannan, FM, Elaydi, S: Lipschitz stability of nonlinear systems of differential equations. J. Math. Anal. Appl. 113, 562-577 (1986)
Agarwal, RP, Hristova, S: Strict stability in terms of two measures for impulsive differential equations with ‘supremum’. Appl. Anal. 91(7), 1379-1392 (2012)
Hristova, S: Stability on a cone in terms of two measures for impulsive differential equations with ‘supremum’. Appl. Math. Lett. 23(5), 508-511 (2010)
Hristova, SG, Georgieva, A: Practical stability in terms of two measures for impulsive differential equations with ‘supremum’. Int. J. Differ. Equ. 2011, Article ID 703189 (2011)
Hristova, S, Stefanova, K: Practical stability of impulsive differential equations with ‘supremum’ by integral inequalities. Eur. J. Pure Appl. Math. 5(1), 30-44 (2012)
Hristova, S: Qualitative Investigations and Approximate Methods for Impulsive Equations. Nova Science Publishers, New York (2009)
Lakshmikantham, V, Bainov, DD, Simeonov, PS: Theory of Impulsive Differential Equations. World Scientific, Singapore (1989)
Hernandez, E, O’Regan, D: On a new class of abstract impulsive differential equations. Proc. Am. Math. Soc. 141, 1641-1649 (2013)
Pandey, DN, Das, S, Sukavanam, N: Existence of solutions for a second order neutral differential equation with state dependent delay and not instantaneous impulses. Int. J. Nonlinear Sci. 18(2), 145-155 (2014)
Pierri, M, O’Regan, D, Rolnik, V: Existence of solutions for semi-linear abstract differential equations with not instantaneous impulses. Appl. Math. Comput. 219, 6743-6749 (2013)
Agarwal, R, O’Regan, D, Hristova, S: Stability by Lyapunov like functions of nonlinear differential equations with non-instantaneous impulses. Appl. Math. Comput. (2015). doi:10.1007/s12190-015-0961-z
Liao, YM, Wang, JR: A note on stability of impulsive differential equations. Bound. Value Probl. 2014, 67 (2014)
Lin, Z, Wei, W, Wang, JR: Existence and stability results for impulsive integro-differential equatons. Facta Univ., Ser. Math. Inform. 29(2), 119-130 (2014)
Sood, A, Srivastava, SK: On stability of differential systems with noninstantaneous impulses. Math. Probl. Eng. 2015, Article ID 691687 (2015)
Wang, J, Lin, Z: A class of impulsive nonautonomous differential equations and Ulam-Hyers-Rassias stability. Math. Methods Appl. Sci. 38(5), 868-880 (2015)
Wang, Z, Zang, Y: Existence and stability of solutions to nonlinear impulsive differential equations in β-normed space. Electron. J. Differ. Equ. 2014, 83 (2014)
Feckan, M, Wang, JR, Zhou, Y: Periodic solutions for nonlinear evolution equations with non-istantaneous impulses. Nonauton. Dyn. Syst. 1, 93-101 (2014)
Wang, JR, Li, X: Periodic BVP for integer/fractional order nonlinear differential equations with non-instantaneous impulses. J. Appl. Math. Comput. 46(1-2), 321-334 (2014)
Soliman, AA: On stability of perturbed impulsive differential systems. Appl. Math. Comput. 133, 105-117 (2002)
Bainov, DD, Stamova, IM: Lipschitz stability of impulsive functional-differential equations. ANZIAM J. 42(4), 504-514 (2001)
Lakshmikantham, V, Leela, S: Differential and Integral Inequalities, vol. I. Academic Press, New York (1969)
Acknowledgements
The research is partially supported by the Fund NPD, Plovdiv University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
Each of the authors SH and RT contributed to each part of the work equally and read and approved the final version of the manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hristova, S., Terzieva, R. Lipschitz stability of differential equations with non-instantaneous impulses. Adv Differ Equ 2016, 322 (2016). https://doi.org/10.1186/s13662-016-1045-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-016-1045-6