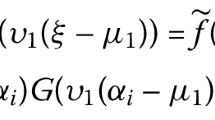A note on stability of impulsive differential equations

Abstract

In this note, we study a new class of ordinary differential equations with non-instantaneous impulses. Both existence and generalized Ulam-Hyers-Rassias stability results are established. Finally, an example is given to illustrate our theoretical results.

1 Introduction

Many evolution processes studied in applied sciences are represented by differential equations. However, the situation is quite different in many modeled phenomena which have a sudden change in their states such as population dynamics, biotechnology processes, chemistry, engineering, medicine and so on. One of the mathematical models about such processes can be formulated by the following impulsive differential equations:

$$\{\begin{array}{l}{x}^{\prime }(t)=f(t,x(t)),t\in J^{\prime }:=J\setminus \{t_1,\dots ,t_m\},J:=[0,T],\\ x(t_k^{+})=x(t_k^{-})+I_k(x(t_k^{-})),k=1,2,\dots ,m,\end{array}$$

(1)

where the function $f:J\times \mathbb{R}\to \mathbb{R}$ and impulsive conditions $I_k:\mathbb{R}\to \mathbb{R}$, $k=1,2,\dots ,m$. We set $t_0=0$ and $t_{m+1}=T$. The fixed time sequence ${\{t_k\}}_{k=1,2,\dots ,m}$ is increasing, i.e., $t_k<t_{k+1}$. $x(t_k^{+})={lim}_{ϵ\to 0^{+}}x(t_k+ϵ)$ and $x(t_k^{-})={lim}_{ϵ\to 0^{-}}x(t_k+ϵ)$ represent the right and left limits of $x(t)$ at $t=t_k$, respectively. Here, the impulsive conditions are the combination of the traditional initial value problems and the short-term perturbations whose duration can be negligible in comparison with the duration of such a process.

However, the above short-term perturbations could not show the dynamic change of evolution processes completely in pharmacotherapy. As we know, the introduction of the drugs in the bloodstream and the consequent absorption for the body are a gradual and continuous process. Thus, we have to use a new model to describe such an evolution process. In fact, the above situation has fallen in a new impulsive action, which starts at an arbitrary fixed point and keeps active on a finite time interval. To achieve this aim, Hernández and O’Regan [1] introduced a new class of abstract semilinear impulsive differential equations with non-instantaneous impulses. Then, the concept of mild solutions and existence results are presented. Next, Pierri et al. [2] continued the work and developed the results in [1] and obtained new existence results in a fractional power space.

In 1940, the famous stability of functional equations was firstly offered by Ulam at Wisconsin University and concerned approximate homomorphisms. Thereafter, Ulam’s stability problem [3] has attracted many famous researchers, one can refer to the interesting monographs of Hyers [4, 5], Rassias [6], Jung [7], Cădariu [8], and an important survey of Brillouët-Belluot et al. [9] via the recent special issue on Ulam-type stability edited by Brzdȩk et al. [10]. For the recent Ulam’s stability concepts and results on ordinary differential equations (with impulses), one can see [11, 12] and reference therein.

Motivated by [1, 2, 11, 12], we introduce a new Ulam-type stability concept for the following semilinear differential equations with non-instantaneous impulses:

$$\{\begin{array}{l}{x}^{\prime }(t)=f(t,x(t)),t\in (s_i,t_{i+1}],i=0,1,2,\dots ,m,\\ x(t)=g_i(t,x(t)),t\in (t_i,s_i],i=1,2,\dots ,m,\end{array}$$

(2)

where $0=t_0=s_0<t_1\le s_1\le t_2<\cdots <s_{m-1}\le t_m\le s_m\le t_{m+1}=T$ are pre-fixed numbers, $f:[0,T]\times \mathbb{R}\to \mathbb{R}$ is continuous, and $g_i:[t_i,s_i]\times \mathbb{R}\to \mathbb{R}$ is continuous for all $i=1,2,\dots ,m$.

The novelty of our paper is considering a new type of equation (2), then presenting a generalized Ulam-Hyers-Rassias stability definition and finding reasonable conditions on equation (2) to show that equation (2) is generalized Ulam-Hyers-Rassias stable.

In Section 2, we introduce a new Ulam-type stability concept for equation (2) (see Definition 2.2). In Section 3, we mainly prove a generalized Ulam-Hyers-Rassias stability result for equation (2) on a compact interval. Finally, an example is given to illustrate our theoretical results.

2 Preliminaries

Throughout this paper, let $C(J,\mathbb{R})$ be the Banach space of all continuous functions from J into ℝ with the norm ${\parallel x\parallel }_C:=sup\{|x(t)|:t\in J\}$ for $x\in C(J,\mathbb{R})$. We introduce the Banach space $PC(J,\mathbb{R})$ := {$x:J\to \mathbb{R}:x\in C((t_k,t_{k+1}],\mathbb{R})$, $k=0,1,\dots ,m$, and there exist $x(t_k^{-})$ and $x(t_k^{+})$, $k=1,\dots ,m$, with $x(t_k^{-})=x(t_k)$} with the norm ${\parallel x\parallel }_{PC}:=sup\{|x(t)|:t\in J\}$. Meanwhile, we set $P{C}^1(J,\mathbb{R}):=\{x\in PC(J,\mathbb{R}):x^{\prime }\in PC(J,\mathbb{R})\}$ with ${\parallel x\parallel }_{P{C}^1}:=max\{{\parallel x\parallel }_{PC},{\parallel x^{\prime }\parallel }_{PC}\}$. Clearly, $P{C}^1(J,\mathbb{R})$ endowed with the norm ${\parallel \cdot \parallel }_{P{C}^1}$ is also a Banach space.

By virtue of the concept about the solutions in [1], we can introduce the following definition.

Definition 2.1 A function $x\in P{C}^1(J,\mathbb{R})$ is called a classical solution of the problem

$$\{\begin{array}{l}{x}^{\prime }(t)=f(t,x(t)),t\in (s_i,t_{i+1}],i=0,1,2,\dots ,m,\\ x(t)=g_i(t,x(t)),t\in (t_i,s_i],i=1,2,\dots ,m,\\ x(0)=x_0\in \mathbb{R},\end{array}$$

(3)

if x satisfies

$$\begin{array}{c}x(0)=x_0;\hfill \\ x(t)=g_i(t,x(t)),t\in (t_i,s_i],i=1,2,\dots ,m;\hfill \\ x(t)=x_0+{\int }_0^{t}f(s,x(s))ds,t\in [0,t_1];\hfill \\ x(t)=g_i(s_i,x(s_i))+{\int }_{s_i}^{t}f(s,x(s))ds,t\in [s_i,t_{i+1}],i=1,2,\dots ,m.\hfill \end{array}$$

Next, we adopt the idea in [12] and introduce a new Ulam-type stability concept for equation (2). Set $PC(J,{\mathbb{R}}_{+}):=\{x\in PC(J,\mathbb{R}):x(t)\ge 0\}$. Let $\psi \ge 0$ and $\phi \in PC(J,{\mathbb{R}}_{+})$. We consider the following inequality:

$$\{\begin{array}{l}|y^{\prime }(t)-f(t,y(t))|\le \phi (t),t\in (s_i,t_{i+1}],i=0,1,2,\dots ,m,\\ |y(t)-g_i(t,y(t))|\le \psi ,t\in (t_i,s_i],i=1,2,\dots ,m.\end{array}$$

(4)

Definition 2.2 Equation (2) is generalized Ulam-Hyers-Rassias stable with respect to $(\phi ,\psi )$ if there exists $c_{f,g_i,\phi ,m}>0$ such that for each solution $y\in P{C}^1(J,\mathbb{R})$ of inequality (4), there exists a solution $x\in P{C}^1(J,\mathbb{R})$ of equation (2) with

$$|y(t)-x(t)|\le c_{f,g_i,\phi ,m}(\phi (t)+\psi ),t\in J.$$

Remark 2.3 Definition 2.2 has practical meaning in the following sense. Consider an evolution process with not sudden changes of states but acting on an interval, which can be modeled by equation (2). Assume that we can measure the state of the process at any time to get a function $x(\cdot )$. Putting this $x(\cdot )$ into equation (2), in general, we do not expect to get a precise solution of equation (2). All what is required is to get a function which satisfies the suitable approximation inequality (4). Our result of Section 3 will guarantee that there is a solution $y(\cdot )$ of inequality (4) close to the measured output $x(\cdot )$ and closeness is defined in the sense of generalized Ulam-Hyers-Rassias stability. This technique is quite useful in many applications such as numerical analysis, optimization, biology and economics, where it is quite difficult to find the exact solution.

Remark 2.4 A function $y\in P{C}^1(J,\mathbb{R})$ is a solution of inequality (4) if and only if there is $G\in PC(J,\mathbb{R})$ and a sequence $G_i$, $i=1,2,\dots ,m$ (which depend on y) such that

• (i) $|G(t)|\le \phi (t)$, $t\in J$ and $|G_i|\le \psi$, $i=1,2,\dots ,m$;

• (ii) $y^{\prime }(t)=f(t,y(t))+G(t)$, $t\in (s_i,t_{i+1}]$, $i=0,1,2,\dots ,m$;

• (iii) $y(t)=g_i(t,y(t))+G_i$, $t\in (t_i,s_i]$, $i=1,2,\dots ,m$.

Remark 2.5 If $y\in P{C}^1(J,\mathbb{R})$ is a solution of inequality (4), then y is a solution of the following integral inequality:

$$\{\begin{array}{l}|y(t)-g_i(t,y(t))|\le \psi ,t\in (t_i,s_i],i=1,2,\dots ,m;\\ |y(t)-y(0)-{\int }_0^{t}f(s,y(s))ds|\le {\int }_0^t\phi (s)ds,t\in [0,t_1];\\ |y(t)-g_i(s_i,y(s_i))-{\int }_{s_i}^{t}f(s,y(s))ds|\le \psi +{\int }_{s_i}^t\phi (s)ds,t\in [s_i,t_{i+1}],i=1,2,\dots ,m.\end{array}$$

(5)

In fact, by Remark 2.4 we get

$$\{\begin{array}{l}{y}^{\prime }(t)=f(t,y(t))+G(t),t\in (s_i,t_{i+1}],i=1,2,\dots ,m,\\ y(t)=g_i(t,y(t))+G_i,t\in (t_i,s_i],i=1,2,\dots ,m.\end{array}$$

(6)

Clearly, the solution of equation (6) is given by

$$\begin{array}{c}y(t)=g_i(t,y(t))+G_i,t\in (t_i,s_i],i=1,2,\dots ,m;\hfill \\ y(t)=y(0)+{\int }_0^t(f(s,y(s))+G(s))ds,t\in [0,t_1];\hfill \\ y(t)=(g_i(s_i,y(s_i))+G_i)+{\int }_{s_i}^t(f(s,y(s))+G(s))ds,t\in (s_i,t_{i+1}],i=1,2,\dots ,m.\hfill \end{array}$$

For each $t\in (s_i,t_{i+1}]$, $i=0,1,2,\dots ,m$, we get

$$|y(t)-g_i(s_i,y(s_i))-{\int }_{s_i}^{t}f(s,y(s))ds|\le |G_i|+{\int }_{s_i}^t|G(s)|ds\le \psi +{\int }_{s_i}^t\phi (s)ds.$$

Proceeding as above, we derive that

$$\begin{array}{c}|y(t)-g_i(t,y(t))|\le |G_i|\le \psi ,t\in (t_i,s_i],i=1,2,\dots ,m;\hfill \\ |y(t)-y(0)-{\int }_0^{t}f(s,y(s))ds|\le {\int }_0^t|G(s)|ds\le {\int }_0^t\phi (s)ds,t\in [0,t_1].\hfill \end{array}$$

In order to deal with Ulam-type stability, we need the following result (see Theorem 16.4, [13]).

Lemma 2.6 Let the following inequality hold:

$$u(t)\le a(t)+{\int }_0^{t}b(s)u(s)ds+\sum _{0<t_k<t}{\beta }_{k}u\left(t_k^{-}\right),t\ge 0,$$

where $u,a,b\in PC({\mathbb{R}}_{+},{\mathbb{R}}_{+}):=\{x\in PC({\mathbb{R}}_{+},\mathbb{R}):x(t)\ge 0\}$, a is nondecreasing and $b(t)>0$, ${\beta }_k>0$, $k=1,\dots ,m$.

Then, for $t\in {\mathbb{R}}_{+}$, the following inequality is valid:

$$u(t)\le a(t){(1+\beta )}^{k}exp({\int }_0^{t}b(s)ds),t\in (t_k,t_{k+1}],k\in \{1,\dots ,m\},$$

where $\beta =max\{{\beta }_k:k=1,\dots ,m\}$.

3 Main results

We introduce the following assumptions:

(H₁) $f\in C(J\times \mathbb{R},\mathbb{R})$.

(H₂) There exists a positive constant $L_f$ such that

$$|f(t,u_1)-f(t,u_2)|\le L_f|u_1-u_2|\text{for each }t\in J\text{ and all }{u}_1,u_2\in \mathbb{R}.$$

(${\mathrm{H}}_2^{\prime }$) $f:J\times \mathbb{R}\to \mathbb{R}$ is strongly measurable for the first variable and is continuous for the second variable. There exists a positive constant $L_f^{\prime }$ and a nondecreasing function $W_f\in C([0,\mathrm{\infty }),{\mathbb{R}}_{+})$ such that

$$|f(t,u)|\le L_f^{\prime }{W}_f(|u|)\text{for each }t\in J\text{ and all }u\in \mathbb{R}.$$

(H₃) $g_i\in C([t_i,s_i]\times \mathbb{R},\mathbb{R})$ and there are positive constants $L_{g_i}$, $i=1,2,\dots ,m$, such that

$$|g_i(t,u_1)-g_i(t,u_2)|\le L_{g_i}|u_1-u_2|\text{for each }t\in [t_i,s_i]\text{ and all }{u}_1,u_2\in \mathbb{R}.$$

(H₄) There exists a constant $c_{\phi }>0$ and a nondecreasing function $\phi \in PC(J,{\mathbb{R}}_{+})$ such that

$${\int }_0^t\phi (s)ds\le c_{\phi }\phi (t)\text{for each }t\in J.$$

Concerning the existence results for the solutions about problem (3), one can repeat the same procedure in Theorems 2.1 and 2.2 of Hernández and O’Regan [1] to derive the following results. So we omit the proof here.

Theorem 3.1 Assume that (H₁), (H₂) and (H₃) are satisfied. Then problem (3) has the unique solution $x\in P{C}^1(J,\mathbb{R})$ provided that

$$max\{L_{g_i}+L_f(t_{i+1}-s_i),L_f{t}_1:i=1,2,\dots ,m\}<1.$$

(7)

Theorem 3.2 Assume that (${\mathrm{H}}_2^{\prime }$) and (H₃) are satisfied, the functions $g_i(\cdot ,0)$ are bounded. Then problem (3) has at least one solution $x\in P{C}^1(J,\mathbb{R})$ provided that

$$lim\underset{r\to \mathrm{\infty }}{sup}\frac{W_f(r)}{r}max\{2L_{g_i}+L_f^{\prime }(t_{i+1}-s_i),L_f^{\prime }{t}_1:i=1,2,\dots ,m\}<1.$$

Now, we discuss the stability of equation (2) by using the concept of generalized Ulam-Hyers-Rassias in the above section.

Theorem 3.3 Assume that (H₁), (H₂), (H₃) and (H₄) are satisfied. Then equation (2) is generalized Ulam-Hyers-Rassias stable with respect to $(\phi ,\psi )$ provided that (7) holds.

Proof Let $y\in P{C}^1(J,\mathbb{R})$ be a solution of inequality (4). Denote by x the unique solution of the impulsive Cauchy problem

$$\{\begin{array}{l}{x}^{\prime }(t)=f(t,x(t)),t\in (s_i,t_{i+1}],i=0,1,2,\dots ,m,\\ x(t)=g_i(t,x(t)),t\in (t_i,s_i],i=1,2,\dots ,m,\\ x(0)=y(0).\end{array}$$

(8)

Then we get

$$x(t)=\{\begin{array}{ll}{g}_i(t,x(t)),& t\in (t_i,s_i],i=1,2,\dots ,m;\\ y(0)+{\int }_0^{t}f(s,x(s))ds,& t\in [0,t_1];\\ g_i(s_i,x(s_i))+{\int }_{s_i}^{t}f(s,x(s))ds,& t\in (s_i,t_{i+1}],i=0,1,2,\dots ,m.\end{array}$$

Keeping in mind (5), for each $t\in [s_i,t_{i+1}]$, $i=1,2,\dots ,m$, we have

$$|y(t)-g_i(s_i,y(s_i))-{\int }_{s_i}^{t}f(s,y(s))ds|\le \psi +{\int }_{s_i}^t\phi (s)ds\le \psi +c_{\phi }\phi (t),$$

and for each $t\in (t_i,s_i]$, $i=1,2,\dots ,m$, we have

$$|y(t)-g_i(t,y(t))|\le \psi ,$$

and for each $t\in [0,t_1]$, we have

$$|y(t)-y(0)-{\int }_0^{t}f(s,y(s))ds|\le c_{\phi }\phi (t).$$

Hence, for each $t\in (s_i,t_{i+1}]$, $i=1,2,\dots ,m$, we get

$$\begin{array}{rcl}|y(t)-x(t)|& \le & |y(t)-g_i(s_i,y(s_i))-{\int }_{s_i}^{t}f(s,y(s))ds|\\ +|g_i(s_i,y(s_i))-g_i(s_i,x(s_i))|+{\int }_{s_i}^t|f(s,y(s))-f(s,x(s))|ds\\ \le & (1+c_{\phi })[\psi +\phi (t)]+L_{g_i}|y(s_i)-x(s_i)|+L_f{\int }_{s_i}^t|y(s)-x(s)|ds\\ \le & (1+c_{\phi })(\psi +\phi (t))+L_{g_i}\sum _{0<s_i<t}|y(s_i)-x(s_i)|+L_f{\int }_0^t|y(s)-x(s)|ds.\end{array}$$

Thus, by Lemma 2.6, we have

$$|y(t)-x(t)|\le (1+c_{\phi })(\psi +\phi (t)){(1+L_g)}^m{e}^{L_f{t}_{i+1}}$$

(9)

for each $t\in (s_i,t_{i+1}]$, $i=1,2,\dots ,m$.

Further, for each $t\in (t_i,s_i]$, $i=1,2,\dots ,m$, we have

$$|y(t)-x(t)|\le |y(t)-g_i(t,y(t))|+|g_i(t,y(t))-g_i(t,x(t))|\le \psi +L_{g_i}|y(t)-x(t)|,$$

which yields that

$$|y(t)-x(t)|\le \frac{1}{1-L_g}\psi ((\text{7})⟹L_g=max\{L_{g_i}:i=1,2,\dots ,m\}<1).$$

(10)

Moreover, for each $t\in [0,t_1]$, we have

$$|y(t)-x(t)|\le c_{\phi }\phi (t)+L_f{\int }_0^t|y(s)-x(s)|ds.$$

By Gronwall’s inequality, we obtain

$$|y(t)-x(t)|\le c_{\phi }\phi (t)e^{L_f{t}_1},t\in [0,t_1].$$

(11)

Summarizing, we combine (9), (10) and (11) and derive that

$$\begin{array}{rcl}|y(t)-x(t)|& \le & ((1+c_{\phi }){(1+L_g)}^m{e}^{L_f{t}_{m+1}}+\frac{1}{1-L_g}+c_{\phi }{e}^{L_f{t}_1})(\psi +\phi (t))\\ :=& c_{f,g_i,\phi ,m}(\psi +\phi (t))\end{array}$$

for all $t\in J$, which implies that equation (2) is generalized Ulam-Hyers-Rassias stable with respect to $(\phi ,\psi )$. The proof is completed. □

4 Example

Let $J=[0,2]$ and $0=t_0=s_0<t_1=1<s_1=2$. Denote $f(t,x(t))=\frac{|x(t)|}{(1+9e^t)(1+|x(t)|)}$ with $L_f=\frac{1}{10}$ for $t\in (0,1]$ and $g_1(t,x(t))=\frac{|x(t)|}{(5-e+e^t)(2+|x(t)|)}$ with $L_{g_1}=\frac{1}{10}$ for $t\in (1,2]$. We set $\phi (t)=e^t$ and $\psi =1$.

Consider

$$\{\begin{array}{l}{x}^{\prime }(t)=\frac{|x(t)|}{(1+9e^t)(1+|x(t)|)},t\in (0,1],\\ x(t)=\frac{|x(t)|}{(5-e+e^t)(2+|x(t)|)},t\in (1,2],\end{array}$$

(12)

and

$$\{\begin{array}{l}|y^{\prime }(t)-\frac{|y(t)|}{(1+9e^t)(1+|y(t)|)}|\le e^t,t\in (0,1],\\ |y(t)-\frac{|y(t)|}{(5-e+e^t)(2+|y(t)|)}|\le 1,t\in (1,2].\end{array}$$

(13)

Let $y\in P{C}^1([0,2],\mathbb{R})$ be a solution of inequality (13). Then there exist $G(\cdot )\in P{C}^1([0,2],\mathbb{R})$ and $G_1\in \mathbb{R}$ such that

$$\begin{array}{r}|G(t)|\le e^t,t\in (0,1],|G_1|\le 1,\\ y^{\prime }(t)=\frac{|y(t)|}{(1+9e^t)(1+|y(t)|)}+G(t),t\in (0,1],\\ y(t)=\frac{|y(t)|}{(5-e+e^t)(2+|y(t)|)}+G_1,t\in (1,2].\end{array}$$

(14)

For $t\in [0,1]$, integrating (14) from 0 to t, we have

$$y(t)=y(0)+{\int }_0^t(\frac{|y(s)|}{(1+9e^s)(1+|y(s)|)}+G(s))ds.$$

For $t\in (1,2]$, we have

$$y(t)=\frac{|y(t)|}{(5-e+e^t)(2+|y(t)|)}+G_1.$$

After checking the conditions in Theorem 3.1, we find that

$$\{\begin{array}{l}{x}^{\prime }(t)=\frac{|x(t)|}{(1+9e^t)(1+|x(t)|)},t\in (0,1],\\ x(t)=\frac{|x(t)|}{(5-e+e^t)(2+|x(t)|)},t\in (1,2],\\ x(0)=y(0)\end{array}$$

(15)

has a unique solution. Let us take the solution x of problem (15) given by

$$\begin{array}{c}x(t)=y(0)+{\int }_0^t\frac{|x(s)|}{(1+9e^s)(1+|x(s)|)}ds,t\in [0,1],\hfill \\ x(t)=\frac{|x(t)|}{(5-e+e^t)(2+|x(t)|)},t\in (1,2].\hfill \end{array}$$

For $t\in [0,1]$, we have

$$|y(t)-x(t)|\le {\int }_0^t|G(s)|ds\le {\int }_0^t{e}^{s}ds=e^t-1\le e^t.$$

For $t\in (1,2]$, we have

$$|y(t)-x(t)|\le \frac{1}{10}|y(t)-x(t)|+|G_1|\le \frac{1}{10}|y(t)-x(t)|+1,$$

which yields that

$$|y(t)-x(t)|\le \frac{10}{9}.$$

Summarizing, we have

$$|y(t)-x(t)|\le \frac{10}{9}(1+e^t),t\in J,$$

which yields that equation (12) is generalized Ulam-Hyers-Rassias stable with respect to $(e^t,1)$.