1 Introduction

Many complex phenomena of nature can be described by a large number of nonlinear evolution equations [1–10], so studying soliton solutions of nonlinear evolution equations is significant [9–13]. In recent years, the research of soliton theory has been penetrated into different areas, for instance, the plasma physics, fluid mechanics, and optics [11–20].

In nonlinear optics, many equations have been modeled to structure the propagation of optical pulses in various media [21–27]; the most famous equation of which is nonlinear Schrödinger equation (NLSE) [28, 29]. However, the Fokas-Lenells (FL) equation (1.1) was first proposed and derived by Fokas and Lenells via the bi-Hamiltonian method, which is a generalization of the NLSE [30–32],

$$\begin{aligned} i q_{y}+\alpha q_{yy}+\beta q_{yt}+ q q^{*}(\gamma q+i \sigma r q_{y})=0, \end{aligned}$$
(1.1)

where \(q(y,t)\) represents soliton profile, and asterisk denotes conjugate complex, α represents velocity dispersion, γ represents the self-phase modulation coefficient, β the Space-time dispersion coefficient, and σ the nonlinear dispersion coefficient, while y and t denote space and time variables, respectively. Equation (1.1) and NLSE is equivalent to the Camassa-Holm equation and KdV equation in correlation [33, 34]. By gauge transformation, Eq. (1.1) can be reduced to a simple form,

$$\begin{aligned} i q_{yt}-i q_{yy}+2q_{y}-q_{y} q q^{*}+i q=0. \end{aligned}$$
(1.2)

As all we know, many scholars have done a lot of work on the solution of FL system [35–44]. For example, the bright, dark, and singular soliton solutions of Eq. (1.2) are found by extended trial function method [35, 36]. Different kinds of exact solutions and analytical representation for the rogue waves of Eq. (1.2) are derived via the Darboux transformation [37–40]. A class of exact combined soliton solutions of Eq. (1.2) is obtained by the complex envelope function method [41]. The general dark N-soliton solution of Eq. (1.2) is constructed by the Hirota direct method [42]. Singular and combo-soliton solutions are presented using \(\exp(-\varphi (\xi ))\) function approach [43]. Exact explicit travelling wave solutions are given by the method of dynamical systems [44].

The Jacobi elliptic function expansion method takes the form of constructing solution to get new exact solutions, which plays an important role in obtaining exact solutions of many equations and models [45–49]. However, many researchers use the extended Jacobian elliptic function expansion method to obtain more general and richer solitary wave solutions of different physical models [50–55]. In this paper, we apply the extended Jacobian elliptic function method to solve new exact solutions of Eq. (1.2).

The overall framework of this paper will be designed as below. In Sect. 2, steps and hints of the method are listed. In Sect. 3, the periodic solutions and exact solutions of Eq. (1.2) are presented. Meanwhile, we draw some figures for those soliton solutions; the conclusion is given in the last section.

2 Program description

First, we state the general process of the Jacobi elliptic function expansion method [50–55]:

Suppose a nonlinear equation with two independent variable:

$$\begin{aligned} F\bigl(\phi , \phi ^{2}, \phi _{y}, \phi _{t}, \phi _{yy}, \phi _{tt},\ldots\bigr)=0. \end{aligned}$$
(2.1)

Applying the following transformation to Eq. (2.1)

$$\begin{aligned} \phi (y,t)=\Phi (\varsigma ), \quad \varsigma =k(y-ct), \end{aligned}$$
(2.2)

we can get

$$\begin{aligned} L\bigl(\Phi (\varsigma ), \Phi ^{2}(\varsigma ), \Phi ^{\prime }(\varsigma ), \Phi ^{\prime \prime }(\varsigma ),\ldots\bigr)=0, \end{aligned}$$
(2.3)

here k shows wave number, and c is for wave speed.

Assume that the solution of Eq. (2.3) has a limited form of the extended Jacobi elliptic function:

$$\begin{aligned} \Phi (\varsigma )=\sum_{j=-M}^{M}d_{j}Y^{j}( \varsigma ), \end{aligned}$$
(2.4)

where \(Y(\varsigma )=sn(\varsigma ,m)\) or \(cn(\varsigma ,m)\) or \(dn(\varsigma ,m)\) (\(0< m<1\)). The value of M can be solved by equating the highest order of the nonlinear term and the linear derivative term in Eq. (2.3). The value of \(d_{j}\) (\(j=-M,\ldots ,M\)) can be obtained by solving a system of equations, resulting from the substitution of Eq. (2.4) into (2.3), with a computer. Taking \(Y(\varsigma )\), M, and \(d_{j}\) into Eq. (2.4), we obtain a general expression for the solution of Eq. (2.1) in terms of the Jacobi elliptic function.

To make better use of this method, we note the following points:

1. Decision of the highest order

$$ \begin{aligned} &O(V)=M,\qquad O\bigl(V^{r} \bigr)=rM, \qquad O\biggl(\frac{d^{s}V}{d\varsigma ^{s}}\biggr)=M+s, \\ &O\biggl(V^{r}\frac{d^{s}V}{d\varsigma ^{s}}\biggr)=(r+1)M+s. \end{aligned} $$
(2.5)

2. Identical relation

$$ \begin{aligned} &sn^{2}(\varsigma ,m)+cn^{2}(\varsigma ,m)=1, \\ &dn^{2}( \varsigma ,m)+m^{2} sn^{2}(\varsigma ,m)=1, \\ & m^{2} cn^{2}(\varsigma ,m)+1-m^{2}=dn^{2}( \varsigma ,m), \\ &cn^{2}(\varsigma ,m)+\bigl(1-m^{2}\bigr) sn^{2}( \varsigma ,m)=dn^{2}( \varsigma ,m). \end{aligned} $$
(2.6)

3. Derivative relations

$$ \begin{aligned} &sn^{\prime }(\varsigma ,m)=cn( \varsigma ,m) dn(\varsigma ,m), \\ &cn^{\prime }(\varsigma ,m)=-sn(\varsigma ,m) dn(\varsigma ,m), \\ & dn^{\prime }(\varsigma ,m)=-m^{2}sn(\varsigma ,m) cn(\varsigma ,m). \end{aligned} $$
(2.7)

4. Limit relation

$$ \begin{aligned} &m\rightarrow 1, \qquad sn(\varsigma ,m) \rightarrow \tanh \varsigma , \\ & cn(\varsigma ,m) \rightarrow \operatorname{sech} \varsigma , \qquad dn( \varsigma ,m) \rightarrow \operatorname{sech} \varsigma . \\ & m\rightarrow 0, \qquad sn(\varsigma ,m) \rightarrow \sin \varsigma ,\qquad cn( \varsigma ,m) \rightarrow \cos \varsigma ,\qquad dn(\varsigma ,m) \rightarrow 1. \end{aligned} $$
(2.8)

3 Application to FLE

The solution of Eq. (1.2) can be supposed to be:

$$\begin{aligned} q(y,t) =&Q(\varsigma ) e^{i\varphi}, \quad \varsigma =k ( y-ct ) , \varphi =ay-\omega t, \end{aligned}$$
(3.1)

here k, c, a, and ω refer to real arbitrary constants.

Taking Eq. (3.1) into (1.2) and simplifying, we can obtain real and imaginary parts:

$$\begin{aligned}& (c+1) k^{2} Q^{\prime \prime }-\bigl(a \omega +a^{2}+2a+1\bigr) Q+a Q^{3}=0, \end{aligned}$$
(3.2)
$$\begin{aligned}& \bigl(a c + \omega +2 a +2 - Q^{2}\bigr)k Q^{\prime }=0. \end{aligned}$$
(3.3)

Using (2.5) in Eq. (3.2), we can obtain \(M=1\).

So, we can get:

$$\begin{aligned} Q(\varsigma ) =&d_{-1}Y^{-1}(\varsigma ) +d_{0}+d_{1}Y(\varsigma ). \end{aligned}$$
(3.4)

3.1 Periodic solutions of FLE

Case 1: If \(Y ( \varsigma ) =sn ( \varsigma ,m )\)

Set 1:

$$\begin{aligned}& \biggl\{ d_{-1}=\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}}, d_{0}=0, d_{1}=\mp \frac{\sqrt{2} ik m \sqrt{1+c}}{\sqrt{a}}, \\& \quad \omega = \frac{-(1+a)^{2}-k^{2}(1+c)(1+6m+m^{2})}{a} \biggr\} . \end{aligned}$$
(3.5)

Using Eq. (3.4) and (3.5), we obtain

$$\begin{aligned} q ( y,t ) =& \biggl(\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}}sn^{-1}\bigl( k(y-ct )\bigr)\mp \frac{\sqrt{2} ik m \sqrt{1+c}}{\sqrt{a}}sn \bigl( k (y-ct ) \bigr) \biggr) \\ &{}\times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(1+6m+m^{2})}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.6)

Set 2:

$$\begin{aligned}& \biggl\{ d_{-1}=\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}}, d_{0}=0, d_{1}=0, \omega =\frac{-(1+a)^{2}-k^{2}(1+c)(1+m^{2})}{a} \biggr\} . \end{aligned}$$
(3.7)

Using Eq. (3.4) and (3.7), we obtain

$$\begin{aligned} q ( y,t ) =&\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}}sn^{-1}\bigl( k(y-ct )\bigr) \\ &{} \times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(1+m^{2})}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.8)

Set 3:

$$\begin{aligned}& \biggl\{ d_{-1}=\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}}, d_{0}=0, d_{1}=\pm \frac{\sqrt{2} ik m \sqrt{1+c}}{\sqrt{a}}, \\& \quad \omega = \frac{-(1+a)^{2}-k^{2}(1+c)(1-6m+m^{2})}{a} \biggr\} . \end{aligned}$$
(3.9)

Using Eq. (3.4) and (3.9), we obtain

$$\begin{aligned} q ( y,t ) =& \biggl(\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}}sn^{-1}\bigl( k(y-ct )\bigr)\pm \frac{\sqrt{2} ik m \sqrt{1+c}}{\sqrt{a}}sn \bigl( k (y-ct ) \bigr) \biggr) \\ &{}\times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(1-6m+m^{2})}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.10)

Set 4:

$$\begin{aligned}& \biggl\{ d_{-1}=0, d_{0}=0, d_{1}= \mp \frac{\sqrt{2} ik m \sqrt{1+c}}{\sqrt{a}}, \omega = \frac{-(1+a)^{2}-k^{2}(1+c)(1+m^{2})}{a} \biggr\} . \end{aligned}$$
(3.11)

Using Eq. (3.4) and (3.11), we obtain

$$\begin{aligned} q ( y,t ) =&\mp \frac{\sqrt{2} ik m \sqrt{1+c}}{\sqrt{a}}sn \bigl( k (y-ct ) \bigr) \\ &{}\times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(1+m^{2})}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.12)

Case 2: If \(Y ( \varsigma ) =cn ( \varsigma ,m )\)

Set 1:

$$\begin{aligned}& \biggl\{ d_{-1}=- \frac{\sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{ \sqrt{a}}, d_{0}=0, d_{1}= \mp \frac{\sqrt{2} k m \sqrt{1+c}}{\sqrt{a}}, \\& \quad \omega = \frac{-(1+a)^{2}+k^{2}(1+c)(-1+2m^{2}\pm 6m\sqrt{-1+m^{2}})}{a} \biggr\} . \end{aligned}$$
(3.13)

Using Eq. (3.4) and (3.13), we obtain

$$\begin{aligned} q ( y,t ) =& \biggl(- \frac{\sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{ \sqrt{a}}cn^{-1}\bigl( k(y-ct )\bigr) \mp \frac{\sqrt{2} k m \sqrt{1+c}}{\sqrt{a}}cn \bigl( k (y-ct ) \bigr) \biggr) \\ &{}\times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(1-2m^{2}\mp 6m\sqrt{-1+m^{2}})}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.14)

Set 2:

$$\begin{aligned}& \biggl\{ d_{-1}=\mp \frac{\sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{ \sqrt{a}}, d_{0}=0, d_{1}=0, \\& \quad \omega =\frac{-(1+a)^{2}-k^{2}(1+c)(1-2m^{2})}{a} \biggr\} . \end{aligned}$$
(3.15)

Using Eq. (3.4) and (3.15), we obtain

$$\begin{aligned} q ( y,t ) =&\mp \frac{\sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{ \sqrt{a}}cn^{-1}\bigl( k(y-ct )\bigr) \\ &{}\times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(1-2 m^{2})}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.16)

Set 3:

$$\begin{aligned}& \biggl\{ d_{-1}= \frac{\sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{ \sqrt{a}}, d_{0}=0, d_{1}= \mp \frac{\sqrt{2} k m \sqrt{1+c}}{\sqrt{a}}, \\& \quad \omega = \frac{-(1+a)^{2}+k^{2}(1+c)(-1+2m^{2}\mp 6m\sqrt{-1+m^{2}})}{a} \biggr\} . \end{aligned}$$
(3.17)

Using Eq. (3.4) and (3.17), we obtain

$$\begin{aligned} q ( y,t ) =& \biggl( \frac{\sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{ \sqrt{a}}cn^{-1}\bigl( k(y-ct )\bigr) \mp \frac{\sqrt{2} k m \sqrt{1+c}}{\sqrt{a}}cn \bigl( k (y-ct ) \bigr) \biggr) \\ &{}\times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(1-2m^{2}\pm 6m\sqrt{-1+m^{2}})}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.18)

Set 4:

$$\begin{aligned}& \biggl\{ d_{-1}=0, d_{0}=0, d_{1}= \mp \frac{\sqrt{2} k m \sqrt{1+c}}{\sqrt{a}}, \omega = \frac{-(1+a)^{2}+k^{2}(1+c)(-1+2m^{2})}{a} \biggr\} . \end{aligned}$$
(3.19)

Using Eq. (3.4) and (3.19), we obtain

$$\begin{aligned} q ( y,t ) =&\mp \frac{\sqrt{2} k m \sqrt{1+c}}{\sqrt{a}}cn \bigl( k (y-ct ) \bigr) \\ &{} \times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(1-2m^{2})}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.20)

Case 3: If \(Y ( \varsigma ) =dn ( \varsigma ,m )\)

Set 1:

$$\begin{aligned}& \biggl\{ d_{-1}=- \frac{i \sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{\sqrt{a}}, d_{0}=0, d_{1}= \mp \frac{\sqrt{2} \sqrt{k^{2}(1+c)}}{\sqrt{a}}, \\& \quad \omega = \frac{-(1+a)^{2}+k^{2}(1+c)(2-m^{2})\pm 6i k \sqrt{-1+m^{2}} \sqrt{k^{2}(1+c)^{2}}}{a} \biggr\} . \end{aligned}$$
(3.21)

Using Eq. (3.4) and (3.21), we obtain

$$\begin{aligned}& q ( y,t ) \\& \quad = \biggl(- \frac{i \sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{\sqrt{a}}dn^{-1}\bigl( k(y-ct )\bigr)\mp \frac{\sqrt{2} \sqrt{k^{2}(1+c)}}{\sqrt{a}}dn \bigl( k (y-ct ) \bigr) \biggr) \\& \qquad {}\times \exp \biggl( i \\& \qquad {}\times \biggl( ay+ \frac{-(1+a)^{2}+k^{2}(1+c)(2-m^{2})\mp 6i k \sqrt{-1+m^{2}} \sqrt{k^{2}(1+c)^{2}}}{a}t \biggr) \biggr). \end{aligned}$$
(3.22)

Set 2:

$$\begin{aligned}& \biggl\{ d_{-1}= \frac{i \sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{\sqrt{a}}, d_{0}=0, d_{1}= \mp \frac{\sqrt{2} \sqrt{k^{2}(1+c)}}{\sqrt{a}}, \\& \quad \omega = \frac{-(1+a)^{2}+k^{2}(1+c)(2-m^{2})\mp 6i k \sqrt{-1+m^{2}} \sqrt{k^{2}(1+c)^{2}}}{a} \biggr\} . \end{aligned}$$
(3.23)

Using Eq. (3.4) and (3.23), we obtain

$$\begin{aligned}& q ( y,t ) \\& \quad = \biggl( \frac{i \sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{\sqrt{a}}dn^{-1}\bigl( k(y-ct )\bigr)\mp \frac{\sqrt{2} \sqrt{k^{2}(1+c)}}{\sqrt{a}}dn \bigl( k (y-ct ) \bigr) \biggr) \\& \qquad {}\times \exp \biggl( i \\& \qquad {}\times \biggl( ay+ \frac{-(1+a)^{2}+k^{2}(1+c)(2-m^{2})\mp 6i k \sqrt{-1+m^{2}} \sqrt{k^{2}(1+c)^{2}}}{a}t \biggr) \biggr). \end{aligned}$$
(3.24)

Set 3:

$$\begin{aligned}& \biggl\{ d_{-1}=0, d_{0}=0, d_{1}= \mp \frac{\sqrt{2} \sqrt{k^{2}(1+c)}}{\sqrt{a}}, \omega = \frac{-(1+a)^{2}+k^{2}(1+c)(2-m^{2})}{a} \biggr\} . \end{aligned}$$
(3.25)

Using Eq. (3.4) and (3.25), we obtain

$$\begin{aligned} q ( y,t ) =& \biggl(\mp \frac{\sqrt{2} \sqrt{k^{2}(1+c)}}{\sqrt{a}}dn\bigl( k(y-ct ) \bigr) \biggr) \\ &{}\times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(m^{2}-2)}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.26)

Set 4:

$$\begin{aligned}& \biggl\{ d_{-1}=\mp \frac{i \sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{\sqrt{a}}, d_{0}=0, d_{1}=0, \end{aligned}$$
(3.27)
$$\begin{aligned}& \quad \omega =\frac{-(1+a)^{2}+k^{2}(1+c)(2-m^{2})}{a} \biggr\} . \end{aligned}$$
(3.28)

Using Eq. (3.4) and (3.27), we obtain

$$\begin{aligned} q ( y,t ) =& \biggl( \frac{i \sqrt{2} k \sqrt{1+c}\sqrt{-1+m^{2}}}{\sqrt{a}}dn^{-1}\bigl( k(y-ct )\bigr) \biggr) \\ &{} \times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)(m^{2}-2)}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.29)

3.2 Degradation

The following are degenerative forms of the above periodic solutions when \(m\rightarrow 1\):

Case 1: \(sn ( \varsigma ,m ) \rightarrow \tanh \varsigma \), then Eq. (3.6), (3.8), (3.10), and (3.12) are simplified to the following:

$$\begin{aligned}& q ( y,t ) = \mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}} \bigl(\coth\bigl( k(y-ct ) \bigr)+\tanh\bigl( k(y-ct )\bigr) \bigr) \\& \hphantom{q ( y,t ) =} {} \times \exp{ \biggl( i \biggl( ay+\frac{(1+a)^{2}+8k^{2}(1+c)}{a}t \biggr) \biggr)}, \end{aligned}$$
(3.30)
$$\begin{aligned}& q ( y,t ) =\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}}\coth\bigl( k(y-ct )\bigr) \\& \hphantom{q ( y,t ) =}{} \times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+2k^{2}(1+c)}{a}t \biggr) \biggr)}, \end{aligned}$$
(3.31)
$$\begin{aligned}& q ( y,t ) =\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}} \bigl(\coth\bigl( k(y-ct ) \bigr)+\tanh\bigl( k(y-ct )\bigr) \bigr) \\& \hphantom{q ( y,t ) =}{} \times \exp{ \biggl( i \biggl( ay+\frac{(1+a)^{2}-4k^{2}(1+c)}{a}t \biggr) \biggr)}, \end{aligned}$$
(3.32)
$$\begin{aligned}& q ( y,t ) =\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}}\tanh\bigl( k(y-ct )\bigr) \\& \hphantom{q ( y,t ) =}{} \times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+2k^{2}(1+c)}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.33)

Case 2: \(cn ( \varsigma ,m ) \rightarrow \operatorname{sech} \varsigma \), then Eq. (3.14), (3.18), and (3.20) are simplified to the following:

$$\begin{aligned} q ( y,t ) =&\mp \frac{\sqrt{2} k \sqrt{1+c}}{\sqrt{a}}\operatorname{sech}\bigl( k(y-ct )\bigr) \times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}-k^{2}(1+c)}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.34)

Case 3: \(dn ( \varsigma ,m ) \rightarrow \operatorname{sech} \varsigma \), then Eq. (3.22), (3.24), and (3.26) are simplified to the following:

$$\begin{aligned} q ( y,t ) =& \biggl(\mp \frac{\sqrt{2} \sqrt{k^{2}(1+c)}}{\sqrt{a}}\operatorname{sech} \bigl( k(y-ct )\bigr) \biggr) \\ &{}\times \exp{ \biggl( i \biggl( ay+\frac{(1+a)^{2}-k^{2}(1+c))}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.35)

The following are degenerative forms of the above periodic solutions when \(m\rightarrow 0\):

Case 1: \(sn ( \varsigma ,m ) \rightarrow \sin \varsigma \), then Eq. (3.6), (3.8), and (3.10) are simplified to the following:

$$\begin{aligned} q ( y,t ) =&\mp \frac{\sqrt{2} ik \sqrt{1+c}}{\sqrt{a}} \csc\bigl( k(y-ct )\bigr) \times \exp{ \biggl( i \biggl( ay+ \frac{(1+a)^{2}+k^{2}(1+c)}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.36)

Case 2: \(cn ( \varsigma ,m ) \rightarrow \cos \varsigma \), then Eq. (3.14), (3.16), and (3.18) are simplified to the following:

$$\begin{aligned} q ( y,t ) =&-i \frac{\sqrt{2} k \sqrt{1+c}}{\sqrt{a}}\sec\bigl( k(y-ct )\bigr) \times \exp{ \biggl( i \biggl( ay+\frac{(1+a)^{2}+k^{2}(1+c)}{a}t \biggr) \biggr)}. \end{aligned}$$
(3.37)

3.3 Figure

In this part, we present some two- and three-dimensional graphs of Eq. (1.2) that we have solved in part 3.2.

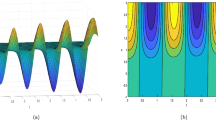
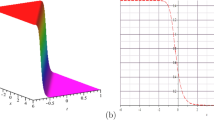
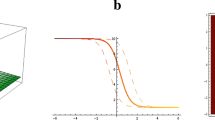
By selecting particular parameters, Figs. 1–5 show the solitary wave of \(q ( y,t )\). From the two-dimensional graphs, the amplitude of the solition wave doesn’t change over time, but their spatial position shifts.

Figure 1
figure 1

Graphs of the solitary wave for (3.33) with \(m\rightarrow 1\), \(a=1\), \(c=1\), \(k=1\)

Full size image
Figure 2
figure 2

Graphs of the solitary wave for (3.36) with \(m\rightarrow 0\), \(a=1\), \(c=0.1\), \(k=1\)

Full size image
Figure 3
figure 3

Graphs of the solitary wave for (3.34) with \(m\rightarrow 1\), \(a=2\), \(c=0.6\), \(k=0.01\)

Full size image
Figure 4
figure 4

Graphs of the solitary wave for (3.37) with \(m\rightarrow 0\), \(a=2\), \(c=0.6\), \(k=0.01\)

Full size image
Figure 5
figure 5

Graphs of the solitary wave for (3.35) with \(m\rightarrow 1\), \(a=1\), \(c=1\), \(k=1\)

Full size image

4 Summary

We apply the extended Jacobi elliptic function expansion scheme to the Fokas-Lenells equation; moreover, the periodic wave solutions are obtained. In particular, when \(m\rightarrow 1\) and \(m\rightarrow 0\), these periodic solutions are degraded to solitary solutions, and their graphs are drawn in two cases.