Abstract
The nonlocal competition in prey and schooling behavior among predators are incorporated in a delayed diffusive predator–prey model. Our main interest is to study the dynamic properties of the model generated by nonlocal competition and delay. We mainly concentrate on the stability and Hopf bifurcation at the coexisting equilibrium. Compared with the model without nonlocal competition, our results suggest that nonlocal competition can affect the stability of the coexisting equilibrium, and induce the stably spatial bifurcating periodic solutions.
Similar content being viewed by others
1 Introduction
In the ecological environment, schooling behavior among predators widely exists, such as wolves, African wild dogs, and lions [1–3]. In [4], Cosner et al. proposed the following functional response
The biological meanings of the parameters are given in Table 1. Unlike the traditional functional response (Holling I–III [5]), it is dependent on predator density and increases with prey and predator densities. This functional response can reflect the schooling behavior among predators. Incorporating this functional response, Ryu et al. [6] studied the following model:
By the scaling
model (1.1) changed to (dropping the bars)
All parameters are positive. They mainly studied the saddle-node, Hopf, and Bogdanov–Takens types of bifurcations at coexisting equilibrium.
In the real world, the living region of prey and predator is inhomogeneous, and diffusion often occurs. Therefore, it is necessary to consider the spatial effect, such as reaction diffusion. Some work shows that space will affect the dynamic properties of the predator–prey model, such as spatial pattern, inhomogeneous periodic solution, etc. [7–10]. In addition, time delays often occur in predator–prey models, such as maturity delay and resource constraint delay. Time delays often cause spatial oscillations, such as periodic solutions [11–14].
The resources in nature are limited, there will be competition within the population, and this competition is usually nonlocal. In [15, 16], the authors modified the \(\frac{u}{K}\) as \(\frac{1}{K} \int _{\Omega}G(x,y)u(y,t)\,dy\) to represent the nonlocal competition, where \(G(x,y)\) is some kernel function. In [17], Wu and Song studied a diffusive predator–prey model with nonlocal effect and delay, and suggested that steady-state, Hopf, and steady-state Hopf bifurcations may occur. In [18], Geng et al. studied Hopf, Turing, double-Hopf, and Turing–Hopf bifurcations of a diffusive predator–prey model with nonlocal competition. In [19–22], all the authors show that the nonlocal competition may induce stably spatially inhomogeneous bifurcating periodic solutions, which is different from the model without nonlocal competition. Inspired by the above work, we want to analyze the effect of nonlocal competition, time delay, and spatial diffusion on the model (1.1). Consider the following model
The biological descriptions of the parameters are given in Table 1. \(\int _{\Omega}G(x,y)u(y,t)\,dy\) represents the nonlocal competition effect.
The rest of this paper is organized as follows. In Sect. 2, we study the stability of coexisting equilibrium and the existence of a Hopf bifurcation. In Sect. 3, we study the property of a Hopf bifurcation. In Sect. 4, we give some numerical simulations to illustrate the theoretical results. In Sect. 5, we give a short conclusion.
2 Stability analysis
Choose \(\Omega =(0,l\pi )\), and the kernel function \(G(x,y)=\frac{1}{l\pi}\). Denote as a positive integer set, and as a nonnegative integer set. \((0,0)\) and \((K,0)\) are boundary equilibria of system (1.4). The existence of positive equilibria of system (1.4) has been studied in [6], that is
Lemma 2.1
([6])
The existence of positive equilibria of system (1.4) can be divided into three cases:
• \(\alpha >\alpha _{bt}:=\frac{4 (1 -\gamma )}{27 \gamma ^{2}}\): no positive equilibrium.
• \(\alpha =\alpha _{bt}\) and \(\beta >\gamma \): one positive equilibrium \((\frac{2}{3}, \frac{3\gamma }{2(1 -\gamma )})\).
• \(\alpha <\alpha _{bt}\) and \(\beta >\gamma \): two distinct equilibria \((u_{1}, v_{1})\) and \((u_{2}, v_{2})\), where \(u_{1}<\frac{2}{3}<u_{2}\), and \(u_{1,2}\) are two roots of \(u^{3}-u^{2}+\frac{\alpha \gamma ^{2}}{1 - \gamma }=0\), \(v_{1,2}=\frac{\gamma}{(1-\gamma )u_{1,2}}\).
2.1 Model with nonlocal competition
Make the following hypothesis
If \({\mathbf{(H_{0})}}\) holds, then system (1.4) has one or two coexisting equilibria. Hereinafter, for brevity, we denote \(E_{*}(u_{*},v_{*})\) as the coexisting equilibrium. Linearize system (1.4) at \(E_{*}(u_{*},v_{*})\)
where
and \(a_{1}=\frac{u_{*} v_{*}^{3} \alpha }{(1+u_{*} v_{*})^{2}}>0\), \(a_{2}=- \frac{u_{*} v_{*} (2+u_{*} v_{*}) \alpha }{(1+u_{*} v_{*})^{2}}<0\), \(b_{1}=\frac{v_{*}^{2} \beta }{(1+u_{*} v_{*})^{2}}>0\), \(b_{2}=\frac{u_{*} v_{*} (2+u_{*} v_{*}) \beta }{(1+u_{*} v_{*})^{2}}>0\), \(\hat{u}=\frac{1}{l\pi}\int _{0}^{l\pi}u(y,t)\,dy\). The characteristic equations are
where
When \(\tau =0\), the characteristic equations (2.2) are
where
Make the following hypothesis
Theorem 2.1
For system (1.4), assume \(\tau =0\) and \({\mathbf{(H_{0})}}\) hold. Then, \(E_{*}(u_{*},v_{*})\) is locally asymptotically stable under \({\mathbf{(H_{1})}}\).
Proof
If \({\mathbf{(H_{1})}}\) holds, we can obtain that the characteristic roots of (2.4) all have negative real parts. Then, \(E_{*}(u_{*},v_{*})\) is locally asymptotically stable. □
Let iω (\(\omega >0\)) be a solution of Eq. (2.2), then
We can obtain \(\text{cos}\omega \tau = \frac{\omega ^{2} ( b_{2} A_{n}+C_{n})-B_{n} C_{n}}{C_{n}^{2}+d^{2} \omega ^{2}}\), \(\text{sin}\omega \tau = \frac{\omega (A_{n} C_{n}+B_{n} b_{2}-b_{2} \omega ^{2} )}{C_{n}^{2}+b_{2}^{2} \omega ^{2}}\). This leads to
Let \(z = \omega ^{2}\), then (2.6) becomes
and the roots of (2.7) are \(z^{\pm}=\frac{1}{2}[-P_{n} \pm \sqrt{P_{n}^{2}-4Q_{n}R_{n}}] \), where \(P_{n}=A_{k}^{2}-2 B_{k}-b_{2}^{2}\), \(Q_{n}=B_{n}+C_{n}\), and \(R_{n}=B_{n}-C_{n}\). If \({\mathbf{(H_{0})}}\) and \({\mathbf{(H_{1})}}\) hold, \(Q_{n}>0\) (). By direct calculation, we have
Define
and
We have the following lemma.
Lemma 2.2
Assume \({\mathbf{(H_{0})}}\) and \({\mathbf{(H_{1})}}\) hold, then the following results hold.
• Eq. (2.2) has a pair of purely imaginary roots \(\pm i\omega ^{+}_{n}\) at \(\tau ^{j,+}_{n}\) for and .
• Eq. (2.2) has two pairs of purely imaginary roots \(\pm i\omega ^{\pm}_{n}\) at \(\tau ^{j,\pm}_{n}\) for and .
• Eq. (2.2) has no purely imaginary root for .
Lemma 2.3
Assume \({\mathbf{(H_{0})}}\) and \({\mathbf{(H_{1})}}\) hold. Then, \(\operatorname{Re}(\frac{d \lambda}{d \tau})|_{\tau =\tau ^{j,+}_{n}}>0\), \(\operatorname{Re} ( \frac{d \lambda}{d \tau})|_{\tau =\tau ^{j,-}_{n}}<0\) for and .
Proof
By (2.2), we have
Then,
Therefore, \(\operatorname{Re}(\frac{d \lambda}{d \tau})|_{\tau =\tau ^{j,+}_{n}}>0\), \(\operatorname{Re} ( \frac{d \lambda}{d \tau})|_{\tau =\tau ^{j,-}_{n}}<0\). □
Denote . Note that \(\tau =\tau ^{j,+}_{m}(\tau =\tau ^{j,-}_{m})\) may be equal to \(\tau =\tau ^{j,+}_{n}(\tau =\tau ^{j,-}_{n})\), for some \(m\neq n\). In this case, high codimensional bifurcation will occur. In this paper, we do not consider this case. Then, we have the following theorem.
Theorem 2.2
Assume \({\mathbf{(H_{0})}}\) and \({\mathbf{(H_{1})}}\) hold, then the following statements are true for system (1.4).
• \(E_{*}(u_{*},v_{*})\) is locally asymptotically stable for \(\tau >0\) when .
• \(E_{*}(u_{*},v_{*})\) is locally asymptotically stable for \(\tau \in [0,\tau _{*})\) when .
• \(E_{*}(u_{*},v_{*})\) is unstable for \(\tau \in (\tau _{*},\tau _{*}+\varepsilon )\) for some \(\varepsilon >0\) when .
• Hopf bifurcation occurs at \((u_{*},v_{*})\) when \(\tau =\tau ^{j,+}_{n}\) \((\tau =\tau ^{j,-}_{n})\), , .
2.2 Model without nonlocal competition
The model (1.4) without nonlocal competition is
Linearizing system (1.4) at \((u_{*},v_{*})\) gives:
where
The characteristic equations of (2.10) are
where
When \(\tau =0\), the characteristic Eq. (2.11) reduces to the following equation:
where
Make the following hypothesis
Theorem 2.3
For system (2.9), assume \(\tau =0\) and \({\mathbf{(H_{0})}}\) holds. Then, \(E_{*}(u_{*},v_{*})\) is locally asymptotically stable under \({\mathbf{(H_{2})}}\).
Let iω (\(\omega >0\)) be a solution of Eq. (2.10), and \(z = \omega ^{2}\). Similarly, we can obtain \(z_{n,w}^{\pm}=\frac{1}{2}[-P'_{n} \pm \sqrt{(P'_{n})^{2}-4Q'_{n}R'_{n}}] \), where \(P'_{n}=(A'_{k})^{2}-2 B'_{k}-b_{2}^{2}\), \(Q'_{n}=B'_{n}+C'_{n}\), and \(R'_{n}=B'_{n}-C'_{n}\). If \({\mathbf{(H_{0})}}\) and \({\mathbf{(H_{2})}}\) hold, \(Q'_{n}>0\) (). By direct calculation, we have
Define
and
We have the following lemma.
Lemma 2.4
Assume \({\mathbf{(H_{0})}}\) and \({\mathbf{(H_{1})}}\) hold, then the following results hold.
• Eq. (2.11) has a pair of purely imaginary roots \(\pm i\omega ^{+}_{n,w}\) at \(\tau ^{j,+}_{n,w}\) for and .
• Eq. (2.11) has two pairs of purely imaginary roots \(\pm i\omega ^{\pm}_{n,w}\) at \(\tau ^{j,\pm}_{n,w}\) for and .
• Eq. (2.11) has no purely imaginary root for .
Lemma 2.5
Assume \({\mathbf{(H_{0})}}\) and \({\mathbf{(H_{1})}}\) hold. Then, \(\operatorname{Re}(\frac{d \lambda}{d \tau})|_{\tau =\tau ^{j,+}_{n,w}}>0\), \(\operatorname{Re} ( \frac{d \lambda}{d \tau})|_{\tau =\tau ^{j,-}_{n,w}}<0\) for and .
Proof
By (2.11), we have
Then,
Therefore, \(\operatorname{Re}(\frac{d \lambda}{d \tau})|_{\tau =\tau ^{j,+}_{n,w}}>0\), \(\operatorname{Re} ( \frac{d \lambda}{d \tau})|_{\tau =\tau ^{j,-}_{n,w}}<0\). □
Denote . We have the following theorem.
Theorem 2.4
Assume \({\mathbf{(H_{0})}}\) and \({\mathbf{(H_{1})}}\) hold, then the following statements are true for system (2.9).
• \(E_{*}(u_{*},v_{*})\) is locally asymptotically stable for \(\tau >0\) when .
• \(E_{*}(u_{*},v_{*})\) is locally asymptotically stable for \(\tau \in [0,\tau '_{*})\) when .
• \(E_{*}(u_{*},v_{*})\) is unstable for \(\tau \in (\tau '_{*},\tau _{*}+\varepsilon )\) for some \(\varepsilon >0\) when .
• Hopf bifurcation occurs at \((u_{*},v_{*})\) when \(\tau =\tau ^{j,+}_{n,w}\) (\(\tau =\tau ^{j,-}_{n,w}\)), , .
3 Property of Hopf bifurcation
By the work [23, 24], we study the property of Hopf bifurcation. For fixed and , we denote \(\tilde{\tau}=\tau ^{j,\pm}_{n}\). Let \(\bar{u}(x,t)=u(x,\tau t)-u_{*}\) and \(\bar{v}(x,t)=v(x,\tau t)-v_{*}\). Dropping the bar, (1.4) can be written as
We rewrite system (3.1) as the following system:
where \(\alpha _{1}=\frac{v_{*}^{3} \alpha }{(1+u_{*} v_{*})^{3}}\), \(\alpha _{2}=-\frac{2 v_{*} \alpha }{(1+u_{*} v_{*})^{3}}\), \(\alpha _{3}=-\frac{u_{*} \alpha }{(1+u_{*} v_{*})^{3}}\), \(\alpha _{4}=-\frac{v_{*}^{4} \alpha }{(1+u_{*} v_{*})^{4}}\), \(\alpha _{5}=\frac{v_{*}^{2} \alpha }{(1+u_{*} v_{*})^{4}}\), \(\alpha _{6}=\frac{(-1+2 u_{*} v_{*}) \alpha }{(1+u_{*} v_{*})^{4}}\), \(\alpha _{7}=\frac{u_{*}^{2} \alpha }{(1+u_{*} v_{*})^{4}}\), \(\beta _{1}=-\frac{v_{*}^{3} \beta }{(1+u_{*} v_{*})^{3}}\), \(\beta _{2}=\frac{2 v_{*} \beta }{(1+u_{*} v_{*})^{3}}\), \(\beta _{3}=\frac{u_{*} \beta }{(1+u_{*} v_{*})^{3}}\), \(\beta _{4}=\frac{v_{*}^{4} \beta }{(1+u_{*} v_{*})^{4}}\), \(\beta _{5}=-\frac{3 v_{*}^{2} \beta }{(1+u_{*} v_{*})^{4}}\), \(\beta _{6}=\frac{(1-2 u_{*} v_{*}) \beta }{(1+u_{*} v_{*})^{4}}\), \(\beta _{7}=-\frac{6 u_{*}^{2} \beta }{(1+u_{*} v_{*})^{4}}\).
Define the real-valued Sobolev space \(X:= \{(u,v)^{T}: u,v\in H^{2}(0,l\pi ), (u_{x},v_{x})|_{x=0,l \pi}=0 \} \), the complexification of X , and the inner product \(\langle \tilde{u},\tilde{v}\rangle :=\int _{0}^{l\pi} \overline{u_{1}} v_{1}\,dx+ \int _{0}^{l\pi} \overline{u_{2}} v_{2}\,dx \) for \(\tilde{u}=(u_{1},u_{2})^{T}\), \(\tilde{v}=(v_{1},v_{2})^{T}\), . The phase space \(\mathscr{C}:=C([-1,0],X)\) is with the sup norm, then we can write \(\phi _{t} \in \mathscr{C}\), \(\phi _{t}(\theta )=\phi (t+\theta )\) or \(-1\leq \theta \leq 0\). Denote \(\beta _{n}^{(1)}(x)=(\gamma _{n}(x),0)^{T}\), \(\beta _{n}^{(2)}(x)=(0,\gamma _{n}(x))^{T}\), and \(\beta _{n}=\{\beta _{n}^{(1)}(x),\beta _{n}^{(2)}(x) \}\), where \(\{\beta _{n}^{(i)}(x) \}\) is an orthonormal basis of X. We define the subspace of \(\mathscr{C}\) as , . There exists a \(2\times 2\) matrix function \(\eta ^{n}(\sigma , \tilde{\tau})\) \(-1\le \sigma \le 0\), such that \(-\tilde{\tau} D\frac{n^{2}}{l^{2}} \phi (0)+\tilde{\tau}L(\phi )= \int _{-1}^{0}\,d\eta ^{n}(\sigma , \tau ) \phi (\sigma )\) for \(\phi \in \mathscr{C}\). The bilinear form on \(\mathscr{C}^{*} \times \mathscr{C}\) is defined by
for \(\phi \in \mathscr{C}\), \(\psi \in \mathscr{C}^{*}\). Define \(\tau =\tilde{\tau}+\mu \), then the system undergoes a Hopf bifurcation at \((0,0)\) when \(\mu =0\), with a pair of purely imaginary roots \(\pm \text{i}\omega _{n_{0}}\). Let A denote the infinitesimal generators of the semigroup, and \(A^{*}\) be the formal adjoint of A under the bilinear form (3.3). Define the following function
Choose \(\eta _{n_{0}}(0,\tilde{\tau})=\tilde{\tau}[(-n_{0}^{2}/l^{2})D+L_{1}+L_{3} \delta (n_{n_{0}})]\), \(\eta _{n_{0}}(-1,\tilde{\tau})=-\tilde{\tau} L_{2}\), \(\eta _{n_{0}}(\sigma ,\tilde{\tau})=0\) for \(-1< \sigma <0\). Let \(p(\theta )=p(0)e^{\text{i}\omega _{n_{0}} \tilde{\tau} \theta}\) (\(\theta \in [-1,0]\)), \(q(\vartheta )=q(0)e^{-\text{i}\omega _{n_{0}} \tilde{\tau} \vartheta}\) (\(\vartheta \in [0,1]\)) be the eigenfunctions of \(A(\tilde{\tau})\) and \(A^{*}\) corresponds to \(i \omega _{n_{0}} \tilde{\tau}\), respectively. We can choose \(p(0)=(1,p_{1})^{T}\), \(q(0)=M(1,q_{2})\), where \(p_{1}=\frac{1}{a_{2}}(\text{i}\omega _{n_{0}}+d_{1} n_{0}^{2}/l^{2}-a_{1}+u_{*} \delta (n_{0}))\), \(q_{2}=a_{2}/(\text{i} \omega _{n_{0}}-b_{2} e^{\text{i} \tau \omega _{n_{0}} }+\beta \gamma +\frac{d_{2} n^{2}}{l^{2}})\), and \(M=(1+p_{1} q_{2}+\tilde{\tau}q_{2}(b_{1} +b_{2} p_{1})e^{-\text{i} \omega _{n_{0}} \tilde{\tau}})^{-1}\). Then, (3.1) can be rewritten in an abstract form
where
respectively, for \(\phi =(\phi _{1}, \phi _{2})^{T} \in \mathscr{C}\) and \(\hat{\phi}_{1}=\frac{1}{l\pi}\int _{0}^{l\pi}\phi \,dx\). Then, the space \(\mathscr{C}\) can be decomposed as \(\mathscr{C}=P\oplus Q\), where  , \(Q=\{\phi \in \mathscr{C} | (q\gamma _{n_{0}}(x),\phi )=0 \text{ and } ( \bar{q}\gamma _{n_{0}}(x),\phi )=0 \}\). Then, system (3.6) can be rewritten as \(U_{t}=z(t)p(\cdot )\gamma _{n_{0}}(x) +\bar{z}(t)\bar{p}(\cdot ) \gamma _{n_{0}}(x)+ \omega (t, \cdot )\) and \(\hat{U_{t}}=\frac{1}{l\pi}\int _{0}^{l\pi} U_{t}\,dx\), where
, \(Q=\{\phi \in \mathscr{C} | (q\gamma _{n_{0}}(x),\phi )=0 \text{ and } ( \bar{q}\gamma _{n_{0}}(x),\phi )=0 \}\). Then, system (3.6) can be rewritten as \(U_{t}=z(t)p(\cdot )\gamma _{n_{0}}(x) +\bar{z}(t)\bar{p}(\cdot ) \gamma _{n_{0}}(x)+ \omega (t, \cdot )\) and \(\hat{U_{t}}=\frac{1}{l\pi}\int _{0}^{l\pi} U_{t}\,dx\), where
Then, we have \(\dot{z}(t)=\text{i}\omega ){n_{0}} \tilde{\tau} z(t)+\bar{q}(0)\langle F(0,U_{t}), \beta _{n_{0}}\rangle \). There exists a center manifold \(\mathcal{C}_{0}\) and ω can be written as follows near \((0,0)\):
Then, restrict the system to the center manifold: \(\dot{z}(t)=\text{i}\omega _{n_{0}} \tilde{\tau} z(t)+g(z,\bar{z})\). Denote \(g(z,\bar{z})=g_{20}\frac{z^{2}}{2}+g_{11}z\bar{z} +g_{02} \frac{\bar{z}^{2}}{2}+g_{21}\frac{z^{2}\bar{z}}{2}+\cdots \) . By direct computation, we have
where \(I_{2}=\int _{0}^{l\pi} \gamma ^{2}_{n_{0}}(x)\,dx\), \(I_{3}=\int _{0}^{l\pi} \gamma ^{3}_{n_{0}}(x)\,dx\), \(I_{4}=\int _{0}^{l\pi} \gamma ^{4}_{n_{0}}(x)\,dx\), \(\varsigma _{1}=-\delta \mathrm{n}+\alpha _{1}+\alpha _{2} \xi + \alpha _{3} \xi ^{2}\), \(\varsigma _{2}=e^{-2 i \tau \omega _{n}} (\beta _{1}+\xi (\beta _{2}+ \beta _{3} \xi ))\), \(\varrho _{1}=\frac{1}{4} (2 \alpha _{1}-2 \delta \mathrm{n}+\alpha _{2} \bar{\xi} +\alpha _{2} \xi +2 \alpha _{3} \bar{\xi} \xi )\), \(\varrho _{2} =\frac{1}{4} (2 \beta _{1}+2 \beta _{3} \bar{\xi} \xi + \beta _{2} (\bar{\xi} +\xi ))\), \(\kappa _{11}=2 W_{11}^{(1)}(0) (-1+2 \alpha _{1}-\delta \mathrm{n}+ \alpha _{2} \xi )+2 W_{11}^{(2)}(0) (\alpha _{2}+2 \alpha _{3} \xi )+W_{20}^{(1)}(0) (-1+2 \alpha _{1}-\delta \mathrm{n}+\alpha _{2} \bar{\xi} )+W_{20}^{(2)}(0) (\alpha _{2}+2 \alpha _{3} \bar{\xi} )\), \(\kappa _{12}=\frac{1}{2} (3 \alpha _{4}+\alpha _{5} (\bar{\xi} +2 \xi )+\xi (2 \alpha _{6} \bar{\xi} +\alpha _{6} \xi +3 \alpha _{7} \bar{\xi} \xi ))\), \(\kappa _{21}=2 e^{-i \tau \omega _{n}} W_{11}^{(1)}(-1) (2 \beta _{1}+ \beta _{2} \xi )+2 e^{-i \tau \omega _{n}} W_{11}^{(2)}(-1) (\beta _{2}+2 \beta _{3} \xi )+e^{i \tau \omega _{n}} W_{20}^{(1)}(-1) (2 \beta _{1}+ \beta _{2} \bar{\xi} )+e^{i \tau \omega _{n}} W_{20}^{(2)}(-1) ( \beta _{2}+2 \beta _{3} \bar{\xi} )\), \(\kappa _{22}=\frac{1}{2} e^{-i \tau \omega _{n}} (3 \beta _{4}+ \beta _{5} (\bar{\xi} +2 \xi )+\xi (2 \beta _{6} \bar{\xi} +\beta _{6} \xi +3 \beta _{7} \bar{\xi} \xi ))\).
Now, we compute \(W_{20}(\theta )\) and \(W_{11}(\theta )\) for \(\theta \in [-1,0]\) to give \(g_{21}\). By (3.7), we have
where
Compared the coeffcients of (3.8) with (3.9), we have
Then, we have
where \(E_{1}=\sum_{n=0}^{\infty}E_{1}^{(n)}\), \(E_{2}=\sum_{n=0}^{\infty}E_{2}^{(n)}\),
and \(\hat{F}_{20}=2(\varsigma _{1},\varsigma _{2})^{T}\), \(\hat{F}_{11}=2(\varrho _{1},\varrho _{2})^{T}\).
Thus, we can obtain
Theorem 3.1
For any critical value \(\tau ^{j}_{n}\) (, ), we have the following results:
• When \(\mu _{2}>0\) (resp., <0), the Hopf bifurcation is forward (resp., backward).
• When \(\beta _{2}<0\) (resp., >0), the bifurcating periodic solutions on the center manifold are orbitally asymptotically stable (resp., unstable).
• When \(T_{2}>0\) (resp., \(T_{2}<0\)), the period increases (resp., decreases).
4 Numerical simulations
To study the effect of nonlocal competition, we also give numerical simulations for models (1.4) and (2.9). Fix the following parameters:
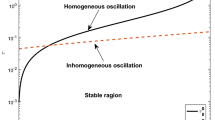
System (1.4) has two positive equilibria \(E_{1}\approx (0.4126,0.8079)\) and \(E_{2}\approx (0.8670,0.3845)\). Since \(E_{2}\) is always unstable, we mainly analyze the stability of \(E_{1}\). We can obtain the bifurcation diagrams of systems (1.4) and (2.9) with β (Fig. 1), where \(\beta _{1}\approx 0.1929\) and \((\beta _{2},\tau _{2} )\approx (0.2064,80.1787)\). We also compute some parameters for model (1.4) with different β (Table 2).
From Fig. 1, we can see that increasing β is no benefit to the stability of coexisting equilibrium. For the model (2.9), a spatially inhomogeneous periodic solution curve does not exist. For the model (1.4), when \(0<\beta <\beta _{1}\), the stability of the coexistence equilibrium \(E_{1}\) is similar to model (2.9). When \(\beta >\beta _{1}\), the spatially inhomogeneous periodic solution curve (\(\tau _{1}^{0}\)) exists, and is larger than the spatially homogeneous periodic solution curve (\(\tau _{0}^{0}\)) for \(\beta _{1}<\beta <\beta _{2}\). This means that the spatially homogeneous periodic solution will appear first, and the spatially inhomogeneous periodic solution is usually unstable. However, when \(\beta >\beta _{2}\), the spatially inhomogeneous periodic solution curve (\(\tau _{1}^{0}\)) is smaller than the spatially homogeneous periodic solution curve (\(\tau _{0}^{0}\)). This means that the spatially inhomogeneous periodic solution will appear first, and may be asymptotically stable.
Choose \(\beta =0.18\), when \(\tau < \tau _{*}\approx 89.9073\), the coexistence equilibrium \(E_{1}\) is asymptotically stable for models (1.4) and (2.9) (Fig. 2). When \(\tau >\tau _{*}\), the coexistence equilibrium \(E_{1}\) is unstable and the spatial homogeneous periodic solution appears for models (1.4) and (2.9) (Fig. 3).
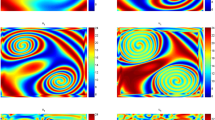
Choose \(\beta =0.5\), when \(\tau < \tau _{*}\approx 10.3066\), the coexistence equilibrium \(E_{1}\) is asymptotically stable for models (1.4) and (2.9) (Fig. 4). However, when \(\tau _{*}< \tau < \tau _{0}^{0} \approx 19.7545\), for model (1.4) the coexistence equilibrium \(E_{1}\) is unstable and the spatial homogeneous periodic solution does not exist. The stably spatial inhomogeneous periodic solution appears (Fig. 5 left). However, for the model (2.9), the coexistence equilibrium \(E_{1}\) is still asymptotically stable (Fig. 5 right). When \(\tau >\tau _{0}^{0}\), for model (1.4), the coexistence equilibrium \(E_{1}\) is unstable and the unstably spatial homogeneous periodic solution exists. The stably spatial inhomogeneous periodic solution still exists (Fig. 6 left). However, for the model (2.9), the coexistence equilibrium \((u_{*}, v_{*})\) is unstable, and the stably spatial homogeneous periodic solution appears (Fig. 6 right).
5 Conclusion
In this paper, we study a delayed diffusive predator–prey model with nonlocal competition in prey and schooling behavior among predators. We mainly study the local stability of coexisting equilibrium and the existence of Hopf bifurcation. We also studied the property of bifurcating periodic solutions by the normal form method and center manifold theorem. Our results show that diffusion and delay can induce a spatially inhomogeneous periodic solution, which is usually unstable. However, the model incorporating nonlocal competition may have a stably spatially inhomogeneous periodic solution.
Availability of data and materials
Data sharing is not applicable to this article as no data sets were generated or analyzed during the current study.
References
Schmidt, P., Mech, L.: Wolf pack size and food acquisition. Am. Nat. 150(4), 513–517 (1997)
Courchamp, F., Macdonald, D.: Crucial importance of pack size in the African wild dog lycaon pictus. Anim. Conserv. 4(2), 169–174 (2010)
Scheel, D., Packer, C.: Group hunting behaviour of lions: a search for cooperation. Anim. Behav. 41(4), 697–709 (1991)
Cosner, C., Deangelis, D.L., Ault, J.S., et al.: Effects of spatial grouping on the functional response of predators. Theor. Popul. Biol. 56(1), 65–75 (1999)
Holling, C.S.: The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 97(45), 1–60 (1965)
Ryu, K., Ko, W., Haque, M.: Bifurcation analysis in a predator-prey system with a functional response increasing in both predator and prey densities. Nonlinear Dyn. 94, 1639–1656 (2018)
Song, Y., Peng, Y., Zhang, T.: The spatially inhomogeneous Hopf bifurcation induced by memory delay in a memory-based diffusion system. J. Differ. Equ. 300, 597–624 (2021)
Arancibia-Ibarra, C., Bode, M., Flores, J., et al.: Turing patterns in a diffusive Holling-Tanner predator-prey model with an alternative food source for the predator. Commun. Nonlinear Sci. Numer. Simul. 99, 105802 (2021)
Mukherjee, N., Volpert, V.: Bifurcation scenario of Turing patterns in prey-predator model with nonlocal consumption in the prey dynamics. Commun. Nonlinear Sci. Numer. Simul. 96, 105677 (2020)
Yi, F.: Turing instability of the periodic solutions for reaction-diffusion systems with cross-diffusion and the patch model with cross-diffusion-like coupling. J. Differ. Equ. 281, 379–410 (2021)
Yang, R., Zhang, C.: Dynamics in a diffusive predator-prey system with a constant prey refuge and delay. Nonlinear Anal., Real World Appl. 31, 1–22 (2016)
Duan, D., Niu, B., Wei, J.: Coexistence of periodic oscillations induced by predator cannibalism in a delayed diffusive predator-prey model. Int. J. Bifurc. Chaos 29(7), 1950089 (2019)
Yang, R., Zhao, X., An, Y.: Dynamical analysis of a delayed diffusive predator-prey model with additional food provided and anti-predator behavior. Mathematics 10, 469 (2022)
Yang, R., Song, Q., An, Y.: Spatiotemporal dynamics in a predator-prey model with functional response increasing in both predator and prey densities. Mathematics 10, 17 (2022)
Britton, N.F.: Aggregation and the competitive exclusion principle. J. Theor. Biol. 136(1), 57–66 (1989)
Furter, J., Grinfeld, M.: Local vs. non-local interactions in population dynamics. J. Math. Biol. 27(1), 65–80 (1989)
Wu, S., Song, Y.: Spatiotemporal dynamics of a diffusive predator-prey model with nonlocal effect and delay. Commun. Nonlinear Sci. Numer. Simul. 89, 105310 (2020)
Geng, D., Jiang, W., Lou, Y., et al.: Spatiotemporal patterns in a diffusive predator-prey system with nonlocal intraspecific prey competition. Stud. Appl. Math. 148(1), 396–432 (2022)
Chen, S., Yu, J.: Stability and bifurcation on predator-prey systems with nonlocal prey competition. Discrete Contin. Dyn. Syst. 38(1), 43–62 (2018)
Liu, Y., Duan, D., Niu, B.: Spatiotemporal dynamics in a diffusive predator-prey model with group defense and nonlocal competition. Appl. Math. Lett. 103, 106175 (2020)
Yang, R., Nie, C., Jin, D.: Spatially inhomogeneous bifurcating periodic solutions induced by nonlocal competition in a predator-prey system with additional food. Nonlinear Dyn. (2022). https://doi.org/10.1007/s11071-022-07625-x
Yang, R., Wang, F., Jin, D.: Spatiotemporal dynamics induced by nonlocal competition in a diffusive predator-prey system with habitat complexity. Math. Methods Appl. Sci. (2022). https://doi.org/10.1002/mma.8349
Wu, J.: Theory and Applications of Partial Functional Differential Equations. Springer, Berlin (1996)
Hassard, B.D., Kazarinoff, N.D., Wan, Y.H.: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)
Acknowledgements
Not applicable.
Funding
This research is supported by the Fundamental Research Funds for the Central Universities (Grant No. 2572022DJ05), the Postdoctoral program of Heilongjiang Province (No. LBH-Q21060), and the College Students Innovations Special Project funded by Northeast Forestry University (No. 202210225160).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation, data collection, and analysis were performed by RY. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, R., Zhang, X. & Jin, D. Spatiotemporal dynamics in a delayed diffusive predator–prey system with nonlocal competition in prey and schooling behavior among predators. Bound Value Probl 2022, 56 (2022). https://doi.org/10.1186/s13661-022-01638-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-022-01638-6