Bifurcation analysis in a diffusive phytoplankton–zooplankton model with harvesting

Abstract

A diffusive phytoplankton–zooplankton model with nonlinear harvesting is considered in this paper. Firstly, using the harvesting as the parameter, we get the existence and stability of the positive steady state, and also investigate the existence of spatially homogeneous and inhomogeneous periodic solutions. Then, by applying the normal form theory and center manifold theorem, we give the stability and direction of Hopf bifurcation from the positive steady state. In addition, we also prove the existence of the Bogdanov–Takens bifurcation. These results reveal that the harvesting and diffusion really affect the spatiotemporal complexity of the system. Finally, numerical simulations are also given to support our theoretical analysis.

1 Introduction

In marine ecosystems, the plankton consist of two species, phytoplankton and zooplankton, which are the basis of the aquatic food chain [1]. Plankton is very important to the marine ecosystems, and the accumulation of plankton can cause “red tide” [2]. It is one of the most serious environmental problems faced by the whole world. A red tide is badly endangering the health of marine and human life.

In order to better understand plankton and explain the cause of “red tide”, the dynamics of plankton systems have been studied by a number of authors [3–7]. The results of studies suggested that plankton systems could exhibit complex dynamic behaviors, such as Hopf bifurcation, global Hopf-bifurcation, Hopf-transcritical bifurcation, and so on. Other references [8–11] discussed the persistence, positivity, boundedness, and chaos of phytoplankton–zooplankton models. Most of these models were governed by ordinary or delay differential equations.

The level of plankton species changes not only in time but also in space. Hence, interaction and spatial processes of phytoplankton and zooplankton should be taken into account in mathematical models of plankton population dynamic systems [12–14]. Consequently, the construction of phytoplankton and zooplankton (prey and predator) models was commonly used by reaction–diffusion systems. According to a widely accepted approach [15–18], the functioning of phytoplankton and zooplankton (prey and predator) can be described by the following reaction–diffusion system:

$$ \textstyle\begin{cases} \frac{\partial P(X,T)}{\partial T}=D_{1}\Delta P+f(P,Z)-g(P,Z), \\ \frac{\partial Z(X,T)}{\partial T}=D_{2}\Delta Z+kg(P,Z)-d Z , \end{cases}$$

(1.1)

where

• (1) P and Z describe the densities of phytoplankton and zooplankton (prey and predator) at moment T and position X, respectively;

• (2) $D_{1}$ and $D_{2}$ are diffusivities;

• (3) $f(P,Z)$ is the local growth and natural mortality of the prey, $g(P,Z)$ describes the functional response for the grazing of phytoplankton by zooplankton;

• (4) k is the ratio of biomass conversion. The parameter d is the mortality rate of the predator.

The choice of the functional response $f(P,Z)$ and $g(P,Z)$ in (1.1) can pick various combinations, which depend on the type of the prey and predator population. Based on the results of field and laboratory observations for plankton systems [19], we assume that the growth of the prey is logistic and $g(P,Z)$ takes the Holling type II functional response [20, 21]. According to the above facts, the model system (1.1) can be expressed in the following form:

$$ \textstyle\begin{cases} \frac{\partial P(X,T)}{\partial T}=D_{1}\Delta P+rP(1-\frac{P}{K})- \frac{a_{1} PZ}{n+P}, \\ \frac{\partial Z(X,T)}{\partial T}=D_{2}\Delta Z+ \frac{a_{2}PZ}{n+P}-dZ, \end{cases}$$

(1.2)

where $a_{1}$ describes the maximum predation rate, n is the self-saturation prey density.

For system (1.2), a lot of results have been obtained, such as local stability, Hopf bifurcation, chaotic attractor, and Turing singularity [20, 22–24].

Furthermore, some phytoplankton and zooplankton can be harvested for food. Hence, the stocks of edible plankton play an important role for fishery management. For system (1.2), considering constant harvesting, Chang et al. [25] discussed the existence and stability of Hopf bifurcation from the positive constant steady state and derived the direction and stability of bifurcating periodic solutions, and also considered an optimal control problem.

In several types of harvesting, Michaelis–Menten type harvesting is more realistic from biological and economic points of view [26]. In this paper, we investigate the following model with Michaelis–Menten type prey harvesting:

$$ \textstyle\begin{cases} \frac{\partial P(X,T)}{\partial T}=D_{1}\Delta P+rP(1-\frac{P}{K})- \frac{a_{1} PZ}{n+P}-\frac{qEP}{m_{1}E+m_{2}P}, \\ \frac{\partial Z(X,T)}{\partial T}=D_{2}\Delta Z+ \frac{a_{2}PZ}{n+P}-dZ, \end{cases}$$

(1.3)

where E measures the harvest effort, q represents the catchability, and $m_{1}$ and $m_{2}$ are appropriate constants.

For simplicity, dimensionless variables are introduced. Let

$$ u=\frac{P}{K}, \qquad v=\frac{a_{1}Z}{K},\qquad t=tT, \qquad x=\sqrt{l}X, $$

then we can obtain the following reaction–diffusion phytoplankton–zooplankton model:

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t} =d_{1}\Delta u +u(1-u)- \frac{\beta uv}{\alpha +u}-\frac{h u}{c+u}, \\ \frac{\partial v(x,t)}{\partial t} =d_{2}\Delta v+ \frac{\beta _{1}uv}{\alpha +u}-mv, \end{cases}$$

(1.4)

where

$$\begin{aligned}& \beta =\frac{1}{r},\qquad c=\frac{m_{1}E}{m_{2}K},\qquad m=\frac{d}{r},\qquad \alpha = \frac{n}{K},\qquad \beta _{1}=\frac{a_{2}}{r}, \\& h= \frac{qE}{m_{2}rK},\qquad d_{1}= \frac{D_{1}}{r},\qquad d_{2}=\frac{D_{2}}{r}. \end{aligned}$$

In this paper, we consider the following homogeneous reaction–diffusion phytoplankton–zooplankton system with homogeneous Neumann boundary condition:

$$ \textstyle\begin{cases} \frac{\partial u}{\partial t}=d_{1}\Delta u+u(1-u)- \frac{\beta uv}{\alpha +u}-\frac{h u}{c+u}, & x\in \Omega , t>0, \\ \frac{\partial v}{\partial t}=d_{2}\Delta v+ \frac{\beta _{1}uv}{\alpha +u}-mv, & x\in \Omega , t>0, \\ \frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=0, &x \in \partial \Omega , t>0, \\ u(x,0)=u_{0}(x)\geq 0, \qquad v(x,0)=v_{0}(x)\geq 0, & x\in \Omega , \end{cases} $$

(1.5)

where Ω is bounded in $\mathbb{R}$ with smooth boundary ∂Ω, Δ denotes the Laplacian operator.

The organization of the rest of the paper is as follows: In Sect. 2, we obtain global existence and boundedness of system (1.5) and demonstrate the asymptotic behavior of system (1.5). In Sect. 3, we give bifurcation analysis of system (1.5) under different parameters, including Hopf bifurcation, Bogdanov–Takens bifurcation. In Sect. 4, some numerical simulations are included to test and verify our theoretical analysis. Finally, we end the paper with a brief conclusion in Sect. 5.

2 Dynamical behavior

2.1 Global existence and boundedness

In this subsection, we prove the global existence of solutions of (1.5) and establish a priori bound of the solution.

Theorem 2.1

• (a) If $u_{0}(x)\geq 0$, $v_{0}(x)\geq 0$ in Ω, then system (1.5) has a unique, nonnegative, globally defined, bounded solution $(u,v)$ for all $(x,t) \in \Omega \times \mathbb{R}_{+}$.

• (b) Any nonnegative solution $(u(x,t),v(x,t))$ of system (1.5) satisfies

  $$ \limsup_{t\rightarrow +\infty } u(x,t)\leq 1,\qquad \limsup_{t \rightarrow +\infty } \int _{\Omega }v(x,t)\,dx\leq \biggl(1+ \frac{c^{2}+4(c-h) }{4cm} \biggr) \vert \Omega \vert . $$

Proof

(a) Define

$$ \Phi (u,v)=u(1-u)-\frac{\beta uv}{\alpha +u}-\frac{h u}{c+u},\qquad \Psi (u,v)= \frac{\beta _{1}uv}{\alpha +u}-mv, $$

then $\Phi _{v}\leqslant 0$ and $\Psi _{u}\geqslant 0$ in $\overline{\mathbb{R}^{2}_{+}}=\{u\geqslant 0,v\geqslant 0\}$ and (1.5) is a mixed quasi-monotone system (see [27, 28]). Let $(\underline{u}(x,t), \underline{v}(x,t))=(0,0)$, $(\overline{u}(x,t), \overline{v}(x,t))=(u^{*}(t),v^{*}(t))$, where $(u^{*}(t),v^{*}(t))$ is the unique solution of the following system:

$$ \textstyle\begin{cases} \frac{du}{dt}=u(1-u)-\frac{h u}{c+u}, \\ \frac{dv}{dt}=\frac{\beta _{1}uv}{\alpha +u}-mv, \\ u(0)=u^{*},\qquad v(0)=v^{*}, \end{cases} $$

(2.1)

where $u^{*}=\sup_{x\in \bar{\Omega }}u(x,0)$, $v^{*}=\sup_{x\in \bar{\Omega }}v(x,0)$. Since $u(1-u)-\frac{h u}{c+u}<0$ for $u\geq 1$, then $u(t)$ exists globally, and there exists sufficiently small $\varepsilon >0$ such that $u(t) < 1 +\varepsilon$ for $t > T$; this implies that $\limsup_{t\rightarrow +\infty } u(x,t)\leq 1$ for $(x,t)\in \bar{\Omega }\times [T,\infty )$. On the basis of Definition 5.3.1 in [28], we claim that $(\underline{u}(x,t), \underline{v}(x,t))=(0,0)$ and $(\overline{u}(x,t), \overline{v}(x,t))=(u^{*}(t),v^{*}(t))$ are the lower-solution and upper-solution to (1.5), respectively, since

$$ \begin{aligned} &\frac{\partial \overline{u}}{\partial t}-\Delta \overline{u}(x,t)- \Phi \bigl(\overline{u}(x,t),\underline{v}(x,t)\bigr) \\ &\quad =0\geq 0=\frac{\partial \underline{u}}{\partial t}-\Delta \underline{u}(x,t)- \Phi \bigl( \underline{u}(x,t),\overline{v}(x,t)\bigr) \end{aligned} $$

and

$$ \begin{aligned} &\frac{\partial \overline{v}}{\partial t}-\Delta \overline{v}(x,t)- \Psi \bigl(\overline{u}(x,t),\overline{v}(x,t)\bigr) \\ &\quad = \frac{\beta _{1}\overline{u}\overline{v}}{\alpha +\overline{u}}-m \overline{v}=0 \geq 0=\frac{\partial \underline{v}}{\partial t}-\Delta \underline{v}(x,t)- \Psi \bigl( \underline{u}(x,t),\underline{v}(x,t)\bigr), \end{aligned} $$

then $0\leq u_{0}(x)\leq u^{*}$ and $0\leq v_{0}(x)\leq v^{*}$, and they satisfy the boundary conditions. Therefore, by using Theorem 5.3.3 in [28], system (1.5) has a unique globally defined solution $(u(x,t),v(x,t))$ which satisfies

$$ 0\leq u(x,t)\leq u^{*}(t),\qquad 0\leq v(x,t)\leq v^{*}(t). $$

In addition, by the strong maximum principle, we know that $u(x,t)>0$, $v(x,t)>0$ for $t>0$ and $x\in \bar{\Omega }$. This completes the proof of (a).

(b) Let $\int _{\Omega }u(x,t)\,dx=U(t)$, $\int _{\Omega }v(x,t)\,dx=V(t)$, then

$$\begin{aligned}& \frac{dU}{dt}= \int _{\Omega }u_{t}\,dx= \int _{\Omega }d_{1}\Delta u\,dx+ \int _{\Omega } \biggl[u(1-u)-\frac{\beta uv}{\alpha +u}- \frac{h u}{c+u} \biggr]\,dx, \end{aligned}$$

(2.2)

$$\begin{aligned}& \frac{dV}{dt}= \int _{\Omega }v_{t}\,dx= \int _{\Omega }d_{2}\Delta u\,dx-mV+ \int _{\Omega }\frac{\beta _{1} uv}{\alpha +u}\,dx. \end{aligned}$$

(2.3)

By using the Neumann boundary condition and adding (2.2) and (2.3), we can obtain

$$ \begin{aligned} (U+V)_{t}&=-mV+ \int _{\Omega } \biggl[u(1-u)- \frac{(\beta -\beta _{1}) uv}{\alpha +u}- \frac{h u}{c+u} \biggr]\,dx \\ &\leq -m(U+V)+mU+ \int _{\Omega }u \biggl[1-u-\frac{h }{c+u} \biggr]\,dx \\ &=-m(U+V)+mU+ \int _{\Omega }u \biggl[1- \frac{(u+\frac{c}{2})^{2} }{c+u}+ \frac{\frac{c^{2}}{4}-h }{c+u} \biggr]\,dx \\ &\leq -m(U+V)+ \biggl[m+\biggl(1+\frac{c^{2}-4h }{4c}\biggr) \biggr]U. \end{aligned} $$

Since $\limsup_{t\rightarrow +\infty } u(x,t)\leq 1$, we can obtain $\limsup_{t\rightarrow +\infty } U(x,t)\leq |\Omega |$. Thus, for small $\varepsilon >0$, there exists $T_{1}>0$ such that

$$ (U+V)_{t}\leq -m(U+V)+ \biggl[m+\biggl(1+ \frac{c^{2}-4h }{4c}\biggr) \biggr](1+ \varepsilon ) \vert \Omega \vert ,\quad t>T_{1}. $$

(2.4)

From (2.4), we can obtain

$$ \int _{\Omega }v(x,t)\,dx=V(t)< U(t)+V(t)\leq \frac{1+\varepsilon }{m} \biggl[m+\biggl(1+\frac{c^{2}-4h }{4c}\biggr) \biggr] \vert \Omega \vert ,\quad t>T_{2}. $$

(2.5)

Hence, we get

$$ \limsup_{t\rightarrow +\infty } \int _{\Omega }v(x,t)\,dx\leq \biggl(1+ \frac{c^{2}+4(c-h) }{4cm} \biggr) \vert \Omega \vert , $$

which completes the proof of (b). □

2.2 Existence and stability of the positive constant steady state solution

The steady state solutions of (1.5) satisfy:

$$ \textstyle\begin{cases} -d_{1}\Delta u=u(1-u)-\frac{\beta uv}{\alpha +u}-\frac{h u}{c+u}, & x\in \Omega , \\ -d_{2}\Delta v=\frac{\beta _{1}uv}{\alpha +u}-mv, & x\in \Omega , \\ \frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=0, &x \in \partial \Omega . \end{cases} $$

(2.6)

Then (1.5) has the unique positive constant solution $(\sigma ,v_{\sigma })$ by mathematical calculation, where

$$ \sigma =\frac{\alpha m}{\beta _{1}-m},\qquad v_{\sigma }= \frac{(\alpha +\sigma )((c+\sigma )(1-\sigma )-h)}{\beta (c+\sigma )}. $$

The positive constant solution exists if and only if

$$ {\mathbf{(C{1})}}\quad \beta _{1}>m,\qquad 0< h< h^{*}=(c+ \sigma ) (1-\sigma ). $$

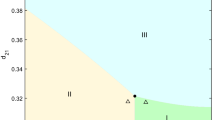
Further in this section, we fix α, β, $\beta _{1}$, c, m, σ and take h as the bifurcation parameter. We have discussed the existence and stability of the positive constant steady state solutions, and the bifurcating periodic solutions were affected by the variance of h. The local stability of the positive constant steady state solution can be summarized as follows.

Theorem 2.2

Suppose $\alpha >0$, $\beta _{1}>0$, $m>0$, $c>0$, $d_{1}>0$, $d_{2}>0$,

• (a) if $c>1$,

  • (1) when $\max\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}<\alpha < \frac{\beta _{1}-m}{m}$, $\beta _{1}>2m$, then $(\sigma , v_{\sigma })$ is locally asymptotically stable for $0< h<\bar{h}$ and is unstable for $\bar{h}< h< h^{*}$;

  • (2) when $0<\alpha <\min\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}$, $\beta _{1}>2m$, then $(\sigma , v_{\sigma })$ is locally asymptotically stable for $\bar{h}< h< h^{*}$ and is unstable for $0< h<\bar{h}$.

• (b) if $0< c<1$,

  • (1) when $\max\{c,\frac{\beta _{1}-m}{\beta _{1}+m}, \frac{(1-c)(\beta _{1}-m)}{2m}\}<\alpha <\frac{\beta _{1}-m}{m}$, $\beta _{1}>2m$, then $(\sigma , v_{\sigma })$ is locally asymptotically stable for $0< h<\bar{h}$ and is unstable for $\bar{h}< h< h^{*}$;

  • (2) when $\frac{(1-c)(\beta _{1}-m)}{2m}<\alpha <\min\{c, \frac{\beta _{1}-m}{\beta _{1}+m}\}$, $\beta _{1}>2m$, then $(\sigma , v_{\sigma })$ is locally asymptotically stable for $\bar{h}< h< h^{*}$ and is unstable for $0< h<\bar{h}$;

  • (3) when $\max\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}<\alpha < \frac{(1-c)(\beta _{1}-m)}{2m}$, $m<\beta _{1}<2m$, then $(\sigma , v_{\sigma })$ is locally asymptotically stable for $0< h<\bar{h}$ and is unstable for $\bar{h}< h< h^{*}$;

  • (4) when $0<\alpha <\min\{c,\frac{\beta _{1}-m}{\beta _{1}+m}, \frac{(1-c)(\beta _{1}-m)}{2m}\}$, $m<\beta _{1}<2m$, then $(\sigma , v_{\sigma })$ is locally asymptotically stable for $\bar{h}< h< h^{*}$ and is unstable for $0< h<\bar{h}$,

where h̄ is given by

$$ \bar{h}=\frac{(2\sigma +\alpha -1)(c+\sigma )^{2}}{\alpha -c}. $$

(2.7)

Proof

The linearized system of (1.5) at a positive constant solution $(\sigma ,v_{\sigma })$ has the form

$$\left(\begin{array}{c}{\varphi }_t\\ {\psi }_t\end{array}\right)=L\left(\begin{array}{c}\varphi \\ \psi \end{array}\right):=D\left(\begin{array}{c}\mathrm{△}\varphi \\ \mathrm{△}\psi \end{array}\right)+J_{(\sigma ,v_{\sigma })}\left(\begin{array}{c}\varphi \\ \psi \end{array}\right)$$

with the domain $X=\{(\phi ,\psi )\in H^{2}(\Omega )\times H^{2}(\Omega ): \frac{\partial \phi }{\partial n}=\frac{\partial \psi }{\partial n}=0 \}$, where

$$D:=\left(\begin{array}{cc}{d}_1& 0\\ 0& d_2\end{array}\right),J_{(\sigma ,v_{\sigma })}:=\left(\begin{array}{cc}{A}^{\ast }(\sigma ,v_{\sigma })& B^{\ast }(\sigma ,v_{\sigma })\\ C^{\ast }(\sigma ,v_{\sigma })& D^{\ast }(\sigma ,v_{\sigma })\end{array}\right)$$

and

$$\begin{aligned}& A^{*}(\sigma ,v_{\sigma })=1-2\sigma - \frac{\beta \alpha v_{\sigma }}{(\alpha +\sigma )^{2}}- \frac{h c}{(c+\sigma )^{2}}, \\& B^{*}(\sigma ,v_{\sigma })=-\frac{\beta \sigma }{\alpha +\sigma }, \\& C^{*}(\sigma ,v_{\sigma })= \frac{\beta _{1} \alpha v_{\sigma }}{(\alpha +\sigma )^{2}}, \\& D^{*}(\sigma ,v_{\sigma })=\frac{\beta _{1} \sigma }{\alpha +\sigma }-m=0. \end{aligned}$$

Recall that −△ under the Neumann boundary condition has eigenvalues $\mu _{0}=0$, $\mu _{k}=k^{2}$, $k=1,2,3,\ldots$ . λ is an eigenvalue of L if and only if λ is an eigenvalue of the matrix $J_{k}=-\mu _{k}D+J_{(\sigma ,v_{\sigma })}$ for some $k\geq 0$. The characteristic equation of L is

$$ \lambda ^{2}-T_{k}\lambda +D_{k}=0,\quad k=0,1,2,\ldots , $$

(2.8)

where

$$ \begin{aligned} &T_{k}:= \operatorname{tr}J_{k}=-k^{2}(d_{1}+d_{2})+A^{*}( \sigma ,v_{\sigma }), \\ &D_{k}:=\operatorname{det}J_{k}=k^{4}d_{1}d_{2}-A^{*}( \sigma ,v_{\sigma })d_{2}k^{2}-B^{*}( \sigma ,v_{\sigma })C^{*}(\sigma ,v_{\sigma }), \end{aligned} $$

(2.9)

and we notice that $\bar{h}\in (0,h^{*})$ defined in (2.7) is the root of $A^{*}(\sigma ,v_{\sigma })=0$.

By direct calculations, if $\alpha <\frac{\beta _{1}-m}{m}$, we observe that $h^{*}>0$. When $\max\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}<\alpha$ or $\alpha <\min\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}$, then $\bar{h}>0$. And if $c>1$, it is clear that $\bar{h}< h^{*}$ for $\beta _{1}>2m$. If $0< c<1$, we can get $\bar{h}< h^{*}$ for $\beta _{1}>2m$, $\alpha >\frac{(1-c)(\beta _{1}-m)}{2m}$ or $\beta _{1}<2m$, $\alpha <\frac{(1-c)(\beta _{1}-m)}{2m}$. Next, we note that $\frac{dA^{*}(h)}{dh}= \frac{(\alpha -c)\sigma }{(c+\sigma )^{2}(\alpha +\sigma )}$. Obviously, $A^{*}(h)$ is monotone increasing for $\alpha >c$ and monotone decreasing for $\alpha < c$. Hence, according to the above analysis, when $c>1$, $\max\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}<\alpha < \frac{\beta _{1}-m}{m}$, $\beta _{1}>2m$ or $\max\{c,\frac{\beta _{1}-m}{\beta _{1}+m}, \frac{(1-c)(\beta _{1}-m)}{2m}\}<\alpha <\frac{\beta _{1}-m}{m}$, $\beta _{1}>2m$ or $\max\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}< \alpha <\frac{(1-c)(\beta _{1}-m)}{2m}$, $m<\beta _{1}<2m$, we can obtain, for $0< h<\bar{h}$, $k\geq 0$,

$$ \begin{aligned} &T_{k}:=\operatorname{tr}J_{k}=-k^{2}(d_{1}+d_{2})+A^{*}( \sigma ,v_{\sigma })< 0, \\ &D_{k}:=\operatorname{det}J_{k}=k^{4}d_{1}d_{2}-A^{*}( \sigma ,v_{\sigma })d_{2}k^{2}-B^{*}( \sigma ,v_{\sigma })C^{*}(\sigma ,v_{\sigma })>0. \end{aligned} $$

Hence $(\sigma , v_{\sigma })$ is a locally asymptotically stable steady state solution of (1.5). When $\bar{h}< h< h^{*}$, then $A^{*}(\sigma ,v_{\sigma })>0$. For $k=0$,

$$ T_{k}:=\operatorname{tr}J_{k}=A^{*}(\sigma ,v_{\sigma })>0, $$

which implies that (2.8) has at least one root with positive real part. Hence $(\sigma , v_{\sigma })$ is an unstable steady state solution of (1.5). This completes $a(1)$, $b(1)$, $b(3)$.

The proofs of $a(2)$, $b(2)$, $b(4)$ are similar to the above, thus they are omitted here. The proof is completed. □

Remark 2.3

If $\min\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}<\alpha < \max\{c,\frac{\beta _{1}-m}{\beta _{1}+m}\}$, then $\bar{h}<0$. Based on the biological significance, we abandon this case.

3 Bifurcation analysis in a diffusive system

3.1 Bifurcation analysis using the harvesting h as the parameter

Next, we study Hopf bifurcations from the constant steady state of (1.5) with the Neumann boundary condition on the spatial domain $\Omega =(0, \pi )$.

In this subsection, we show the existence of the spatial homogeneous and nonhomogeneous periodic solutions of system (1.5), and we also obtain the conditions for direction and stability of the Hopf bifurcation. As is well known, the eigenvalue problem

$$ -\psi ''=\mu \psi ,\quad x\in (0,\pi ),\qquad \psi '(0)=\psi '(\pi )=0 $$

has eigenvalues $\mu _{n}= k^{2}$ ($k=0,1,2,\ldots$) corresponding to the eigenfunction $\psi _{n}(x)=\cos kx$. From the proof of Theorem 2.2, the eigenvalues $\lambda (k)$ of $J_{k}$ ($k\geq 0$) are given by

$$ \lambda _{k}=\frac{T_{k}\pm \sqrt{T_{k}^{2}-4D_{k}}}{2},\quad k=0,1,2, \ldots. $$

In the following, we will identify the Hopf bifurcation points $h^{H}$ that satisfy the necessary and sufficient condition $(\mathbf{{H1})}$ in [20]:

$(\mathbf{{H1})}$:

There exists $k\in \mathbb{N}_{0}=\mathbb{N}\cup \{0\}$ such that

$$ \begin{aligned} &T_{k}\bigl(h^{H}\bigr)=0,\qquad D_{k}\bigl(h^{H}\bigr)>0 \quad \text{and} \\ &T_{j}\bigl(h^{H}\bigr) \neq 0,\qquad D_{j} \bigl(h^{H}\bigr)\neq 0 \quad \text{for } j\neq k, \end{aligned} $$

(3.1)

and the following transversality condition holds:

$$ \alpha '\bigl(h^{H}\bigr)\neq 0. $$

(3.2)

Since

$$ T_{0}\bigl(h_{0}^{H}\bigr)=0,\quad \text{and}\quad T_{k}\bigl(h_{0}^{H} \bigr)=-k^{2}(d_{1}+d_{2})< 0 \quad \text{for any } k\geq 1 $$

and

$$ D_{k}\bigl(h_{0}^{H}\bigr)=d_{1}d_{2}k^{4}-B^{*}C^{*}>0 $$

for any $k\in \mathbb{N}_{0}=\mathbb{N}\cup \{0\}$. Hence $h=\bar{h}=h_{0}^{H}$ is a Hopf bifurcation point which corresponds to the spatially homogeneous periodic orbits.

And then we discuss the spatially nonhomogeneous Hopf bifurcation for $k\geq 1$ $(\mathbf{{H1})}$. In the following, we assume that the condition of Theorem 2.2 ($a(1)$, $b(1)$, $b(3)$) is satisfied. The case of the conditions of Theorem 2.2 ($a(2)$, $b(2)$, $b(4)$) is similar, thus they are omitted here. From $T_{k}=0$, we have

$$ h(k)=h_{0}^{H}+ \frac{k^{2}(d_{1}+d_{2})(\alpha +\sigma )(c+\sigma )^{2}}{\sigma (\alpha -c)}, $$

then

$$ h'(k)= \frac{2k(d_{1}+d_{2})(\alpha +\sigma )(c+\sigma )^{2}}{\sigma (\alpha -c)}>0. $$

Obviously, $h(k)$ is increasing for all $k>0$ if $a>c$.

For $j\geq 1$, define

$$ h_{j}^{H}=h_{0}^{H}+ \frac{j^{2}(d_{1}+d_{2})(\alpha +\sigma )(c+\sigma )^{2}}{\sigma (\alpha -c)}, $$

(3.3)

then $T_{j}(h_{j}^{H})=0$ and $T_{i}(h_{j}^{H})\neq 0$ for any $i\neq j$. These $h_{j}^{H}$ satisfy the following inequality:

$$ 0< h_{0}^{H}< h_{1}^{H}< \cdots < h_{m}^{H}< h^{*}, $$

so that $h_{0}^{H}=\bar{h}< h_{m}^{H}< h^{*}$, where m is the largest integer.

We next testify $D_{i}(h_{j}^{H})\neq 0$ for all $i\in \mathbb{N}_{0}$. Since $(A^{*})'(h)= \frac{(\alpha -c)\sigma }{(c+\sigma )^{2}(\alpha +\sigma )}>0$, hence $A^{*}(h)$ can achieve a local maximum at $h_{m}^{H}$. Let $A^{*}(h_{m}^{H})=M_{*}>0$, when $i\geq 1$, then

$$ \begin{aligned} D_{i}(h) & = d_{1}d_{2}i^{4}-d_{2}A^{*}(h)i^{2}- BC \\ & \geq -d_{2}M_{*}i^{2}+d_{1}d_{2}i^{4}:=g \bigl(i^{2}\bigr). \end{aligned} $$

Apparently, if

$$ (\mathbf{{C2}})\quad M_{*}< d_{1} $$

holds, then for all $x\geq 1$, $g(x)=-d_{2}M_{*}x+d_{2}d_{2}x^{2}$ is positive.

Finally, we verify that the transversality condition holds:

$$ \alpha '\bigl(h_{j}^{H}\bigr)= \frac{(\alpha -c)\sigma }{2(c+\sigma )^{2}(\alpha +\sigma )}>0. $$

By applying the Hopf bifurcation theorem [20] and our analysis, we get the following results.

Theorem 3.1

Suppose that $d_{1},d_{2},\beta , \beta _{1}, \alpha , c, m>0$ and satisfy the conditions of Theorem 2.2, $(\mathbf{C1})$ and $(\mathbf{C2})$. Then there exist $m+1$ points h satisfying $0< h_{0}^{H}< h_{1}^{H}<\cdots <h_{m}^{H}<h^{*}$ such that system (1.5) undergoes a Hopf bifurcation near $h=h_{j}^{H}$ ($1\leq j\leq m$). In addition,

• (a) the bifurcating periodic solutions are spatially homogeneous if they are bifurcated from $h=h_{0}^{H}$. The direction of Hopf bifurcation is supercritical (subcritical), and the bifurcating periodic solutions are asymptotically stable (unstable) if $\operatorname{Re}(c_{1}(\lambda _{0}^{H}))<0$ ($\operatorname{Re}(c_{1}(\lambda _{0}^{H}))>0$);

• (b) the bifurcating periodic solutions are spatially nonhomogeneous if they are bifurcated from $h=h_{j}^{H}$ ($1\leq j\leq m$).

Proof

Above we have already discussed the existence of Hopf bifurcation. In the following, we will calculate the direction of Hopf bifurcation and the stability of spatially homogeneous periodic solutions by using the method in [20, 29]. Take

$$q:=\left(\begin{array}{c}{a}_0\\ b_0\end{array}\right)=\left(\begin{array}{c}1\\ i{\omega }_0/B^{\ast }\end{array}\right),\text{and}{q}^{\ast }:=\left(\begin{array}{c}{a}_0^{\ast }\\ b_0^{\ast }\end{array}\right)=\left(\begin{array}{c}1/2\pi \\ B^{\ast }i/2{\omega }_0\pi \end{array}\right),$$

(3.4)

where $\omega _{0}=\sqrt{-B^{*}C^{*}}$ ($-B^{*}C^{*}>0$). Define the inner product in $X_{C}$ by

$$ \langle U_{1},U_{2}\rangle = \int _{0}^{\pi }(\bar{u}_{1}u_{2}+ \bar{v}_{1}v_{2})\,dx, $$

where $U_{i}=(u_{i},v_{i})\in X_{C}$ ($i=1,2$).

Let $f(u,v)=u(1-u)-\frac{\beta uv}{\alpha +u}-\frac{h u}{c+u}$ and $g(u,v)=\frac{\beta _{1}uv}{\alpha +u}-mv$, at a positive constant solution $(\sigma ,v_{\sigma })$, by calculation, we obtain

$$ \textstyle\begin{cases} f_{uu}=A_{20}=\frac{\beta \alpha v_{\sigma }}{(\alpha +\sigma )^{3}}+ \frac{h c}{(c+\sigma )^{3}}-1, \qquad f_{uv}=A_{11}=- \frac{\beta \alpha }{(\alpha +\sigma )^{2}}, \\ f_{uuu}=A_{30}=- \frac{\beta \alpha v_{\sigma }}{(\alpha +\sigma )^{4}}- \frac{h c}{(c+\sigma )^{4}},\qquad f_{uuv}=A_{21}= \frac{\beta \alpha }{(\alpha +\sigma )^{3}}, \\ g_{uu}=B_{20}=- \frac{\beta _{1} \alpha v_{\sigma }}{(\alpha +\sigma )^{3}}, \qquad g_{uv}=B_{11}= \frac{\beta _{1} \alpha }{(\alpha +\sigma )^{2}}, \\ g_{uuu}=B_{30}= \frac{\beta _{1} \alpha v_{\sigma }}{(\alpha +\sigma )^{4}},\qquad g_{uuv}=B_{21}= -\frac{\beta _{1} \alpha }{(\alpha +\sigma )^{3}}. \end{cases} $$

Then

$$ \begin{aligned} &c_{0}=2A_{20}+2A_{11}b_{0},\qquad d_{0}=2B_{20}+2B_{11}b_{0}, \\ &e_{0}=2A_{20}+A_{11}(b_{0}+ \bar{b}_{0}),\qquad f_{0}=2B_{20}+B_{11}(b_{0}+ \bar{b}_{0}), \\ &g_{0}=6A_{30}+2A_{21}(2b_{0}+ \bar{b}_{0}),\qquad h_{0}=6B_{30}+2B_{21}(2b_{0}+ \bar{b}_{0}). \end{aligned} $$

Then we get the following formulas by simple calculation:

$$\begin{aligned}& g_{20} =\bigl\langle q^{*},(c_{0},d_{0})^{\top } \bigr\rangle =(A_{20}+B_{11})+\biggl( \frac{A_{11}\omega _{0}}{B^{*}}-\frac{B_{20}B^{*}}{\omega _{0}}\biggr)i, \\& g_{02} =\bar{g}_{20}, \\& g_{11} =\bigl\langle q^{*},(e_{0},f_{0})^{\top } \bigr\rangle = A_{20}- \frac{B_{20}B^{*}}{\omega _{0}}i, \\& g_{21} =\bigl\langle q^{*},(g_{0},h_{0})^{\top } \bigr\rangle =(3A_{30}+B_{21})+\biggl( \frac{A_{21}\omega _{0}}{B^{*}}-\frac{3B_{30}B^{*}}{\omega _{0}}\biggr)i. \end{aligned}$$

Therefore,

$$ \begin{aligned} \operatorname{Re}\bigl(c_{1} \bigl(h_{0}^{H}\bigr)\bigr)&=\operatorname{Re}\biggl\{ \frac{i}{2\omega _{0}}\biggl(g_{20}g_{11}-2 \vert g_{11} \vert ^{2}-\frac{1}{3} \vert g_{02} \vert ^{2}\biggr)+\frac{g_{21}}{2}\biggr\} \\ &=\frac{A_{20}B_{20}B^{*}}{\omega _{0}^{2}}+ \frac{B_{11}B_{20}B^{*}}{2\omega _{0}^{2}}- \frac{A_{20}A_{11}}{2B^{*}}+ \frac{3A_{30}+B_{21}}{2}. \end{aligned} $$

According to the results of [20, 29], we know that the Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solutions are stable (unstable) when $\operatorname{Re}(c_{1}(\lambda _{0}^{H}))<0$ ($\operatorname{Re}(c_{1}(\lambda _{0}^{H}))>0$). In Sect. 4, we test and verify the direction of Hopf bifurcation and the stability of the spatially homogeneous periodic solutions by numerical simulations. □

3.2 Bifurcation analysis with k as the parameter

In this section, we investigate bifurcation analysis arising at the positive constant steady-state solution by using k as the parameter. Based on (2.8) and the conclusions in [20, 30–32], we have the following results.

Theorem 3.2

Suppose $d_{1},d_{2},\beta , \beta _{1}, \alpha , c, m>0$, there exist $k_{0}$, $k_{1}\in \mathbb{N}$ such that

• (1) when $k=0$, if $h=h_{0}^{H}$, Eq. (2.8) has a pair of purely imaginary roots, and all other roots of Eq. (2.8) have negative real parts. Then system (1.5) undergoes a Hopf bifurcation at $h=h_{0}^{H}$;

• (2) when $k>0$,

  • (a) we denote $k_{0}=\sqrt{\frac{A^{*}}{d_{1}+d_{2}}}$. If $k_{0}^{4}d_{2}^{2}+B^{*}C^{*}<0$ and $j> k_{0}$, Eq. (2.8) has a pair of purely imaginary roots, and all other roots of Eq. (2.8) have negative real parts. System (1.5) undergoes a Hopf bifurcation at $k_{0}$;

  • (b) if $k_{0}=\sqrt{\frac{A^{*}}{d_{1}+d_{2}}}$, and take the appropriate parameters such that $k_{0}^{4}d_{2}^{2}+B^{*}C^{*}=0$, $j> k_{0}$, and $d_{1}\geq d_{2}$, Eq. (2.8) has a double zero root, and all other roots of Eq. (2.8) have negative real parts. System (1.5) undergoes a Bogdanov–Takens bifurcation at $k_{0}$.

Proof

(1) Based on (2.8), we know that there is $k_{0}=0$ such that $T_{k_{0}}=A^{*}$, $D_{k_{0}}=-B^{*}C^{*}>0$. According to the analysis of Sect. 3.1, we know that when $h=h_{0}^{H}$, then $T_{k_{0}}=A^{*}=0$. For $j\neq k_{0}$, $T_{j}(h_{0}^{H})=-j^{2}(d_{1}+d_{2})<0$, $D_{j}(h_{0}^{H})=d_{1}d_{2}j^{4}-B^{*}C^{*}>0$, hence, when $h=h_{0}^{H}$, Eq. (2.8) has a pair of purely imaginary roots, and all other roots of Eq. (2.8) have negative real parts. System (1.5) undergoes a Hopf bifurcation at $h=h_{0}^{H}$.

(2) (a) There exists $k_{0}>0$, when $k_{0}^{2}=\frac{A^{*}}{d_{1}+d_{2}}$, $k_{0}^{4}d_{2}^{2}+B^{*}C^{*}<0$, then $T_{k_{0}}=0$, $D_{k_{0}}>0$. For $j\neq k_{0}$, when $j>k_{0}$,

$$\begin{aligned}& T_{j}=k_{0}^{2}(d_{1}+d_{2})-j^{2}(d_{1}+d_{2})< 0, \\& \begin{aligned} D_{j}&=d_{1}d_{2}j^{4}-k_{0}^{2}(d_{1}+d_{2})d_{2}j^{2}-B^{*}C^{*} \\ &>d_{1}d_{2}j^{4}-k_{0}^{2}d_{1}d_{2}j^{2}-d_{2}^{2}k_{0}^{2}j^{2}+d_{2}^{2}k_{0}^{4} \\ &>d_{2}^{2}k_{0}^{2} \bigl(j^{2}-k_{0}^{2}\bigr)>0. \end{aligned} \end{aligned}$$

Hence, Eq. (2.8) has a pair of purely imaginary roots, and all other roots of Eq. (2.8) have negative real parts. Following [20, 31], system (1.5) undergoes a Hopf bifurcation at $k_{0}$, which completes the proof.

(b) There exists $k_{0}>0$, when $k_{0}^{2}=\frac{A^{*}}{d_{1}+d_{2}}$, $k_{0}^{4}d_{2}^{2}+B^{*}C^{*}=0$, then $T_{k_{0}}=0$, $D_{k_{0}}=0$. For $j\neq k_{0}$, when $j>k_{0}$, $d_{1}\geq d_{2}$,

$$\begin{aligned}& \begin{aligned} T_{j}&=A-j^{2}(d_{1}+d_{2}) \\ &=k_{0}^{2}(d_{1}+d_{2})-j^{2}(d_{1}+d_{2})< 0, \end{aligned} \\& \begin{aligned} D_{j}&=d_{1}d_{2}j^{4}-k_{0}^{2}(d_{1}+d_{2})d_{2}j^{2}-B^{*}C^{*} \\ &=d_{1}d_{2}j^{4}-k_{0}^{2}(d_{1}+d_{2})d_{2}j^{2}+d_{2}^{2}k_{0}^{4}. \end{aligned} \end{aligned}$$

We know that $D_{j^{2}}=0$ has two roots $j^{2}=k_{0}^{2}$, $j^{2}=\frac{k_{0}^{2}d_{2}}{d_{1}}$, since $d_{1}\geq d_{2}$, hence, when $j>k_{0}$, then $D_{j}>0$. Hence Eq. (2.8) has a double zero root, and all other roots of Eq. (2.8) have negative real parts. Following [30, 32], system (1.5) undergoes a Bogdanov–Takens bifurcation at $k_{0}$, which completes the proof. □

4 Numerical simulations

In this section, we illustrate several conclusions by numerical simulations with Matlab. In model (1.5), we choose the following parameters:

$$\begin{aligned}& d_{1}=0.7,\qquad d_{2}=0.3,\qquad \alpha =0.29, \\& \beta =0.26,\qquad \beta _{1}=0.91,\qquad m=0.43,\qquad c=0.78. \end{aligned}$$

Then model (1.5) has a unique positive equilibrium $(\sigma ,v_{\sigma }) \approx (0.2598,1.1585)$. By direct computation, we have $h^{*}=0.7697$, $\bar{h}=0.4201$. By Theorem 2.2, we know that $(\sigma ,v_{\sigma })$ is locally asymptotically stable when $\bar{h}< h< h^{*}$ (shown in Fig. 1), the positive solution $(\sigma ,v_{\sigma })$ is unstable for $0< h<\bar{h}$. By Theorem 3.1, we know that when h crosses $\bar{h}=h_{0}^{H}$, the positive solution $(\sigma ,v_{\sigma })$ loses its stability and Hopf bifurcation occurs (see Fig. 2).

Figure 1

When the initial values $u(x,0)=0.8$, $v(x,0)=0.3$, $h=0.45$, the coexistence equilibrium is locally asymptotically stable

Figure 2

When the initial values $u(x,0)=0.25$, $v(x,0)=0.65$, $h=0.2$, a spatial homogeneous periodic solution is stable

In model (1.5), we choose the following parameters:

$$\begin{aligned}& d_{1}=0.4, \qquad d_{2}=0.3,\qquad \alpha =0.4, \\& \beta =0.65,\qquad \beta _{1}=0.6,\qquad m=0.23,\qquad c=0.58,\qquad h=0.3. \end{aligned}$$

Model (1.5) has a unique positive equilibrium $(\sigma ,v_{\sigma }) \approx (0.2486,0.3885)$. By direct computation, we have $h^{*}=0.6226$, $\bar{h}=0.3918$. By Theorem 3.2, we know that the diffusive system can undergo the Bogdanov–Takens bifurcation, this indicates that diffusion plays an important role in leading to complex dynamic behaviors. In this paper, the universal unfolding of the system near the Bogdanov–Takens bifurcation point is still not obtained, but we found that system (1.5) can exhibit some complex dynamic behaviors by numerical simulations such as quasi-periodic solutions (shown in Fig. 3).

Figure 3

When the initial values $u(x,0)=0.25$, $v(x,0)=0.68$, spatial quasi-periodic solutions

5 Conclusion

In this paper, we investigated the dynamics of a diffusive phytoplankton–zooplankton model with nonlinear harvesting. By choosing different parameters, we obtained the parameter ranges of the existence of bifurcations. We have shown that the harvesting and the diffusion have a combined effect on the dynamic behaviors of the system.

According to the analysis of the above, we know that if the harvesting h overruns $h^{*}$, then zooplankton will die out. It means overfishing can break the coexistence of phytoplankton and zooplankton. We have also shown that the system can undergo Hopf bifurcation, Bogdanov–Takens bifurcation, when the parameters of the harvesting and diffusion cross certain critical values. It turns out that, by adjusting the parameters of the harvesting and diffusion, the planktonic ecological system can develop towards a healthy direction which can avoid “red tide”. Furthermore, we also studied the stability of Hopf bifurcation by applying the normal form theory and the center manifold theorem.

According to Sect. 3, we know that the diffusive system can exhibit Bogdanov–Takens bifurcation (see Theorem 3.2). Meanwhile, the system may have a quasi-periodic solution near the Bogdanov–Takens bifurcation, which has been verified by some numerical simulations (see Fig. 3). This indicates that diffusion and harvesting can increase the dynamic complexity of system (1.5). The universal unfolding of system (1.5) near the Bogdanov–Takens bifurcation is still not obtained. This is an issue that needs to be addressed in our further study.