New analytical method based on dynamic response of planar mechanical elastic systems

Abstract

An important stage in an analysis of a multibody system (MBS) with elastic elements by the finite element method is the assembly of the equations of motion for the whole system. This assembly, which seems like an empirical process as it is applied and described, is in fact the result of applying variational formulations to the whole considered system, putting together all the finite elements used in modeling and introducing constraints between the elements, which are, in general, nonholonomic. In the paper, we apply the method of Maggi’s equations to realize the assembly of the equations of motion for a planar mechanical systems using finite two-dimensional elements. This presents some advantages in the case of mechanical systems with nonholonomic liaisons.

1 Introduction

In the dynamic analysis of an MBS that has one or more elastic elements, the method used mainly in the study is the finite element method (FEM). The main step in this study is obtaining the equations of motion for the finite elements. For this purpose, there are several methods that can be applied, but the method of Lagrange equations [1–3] remains the most used one. The advantages of this method are:

• The generalized coordinates need not be the Cartesian coordinates;

• Use only with scalar quantities (kinetic energy, potential energy, mechanical work) instead of vectors;

• Once the Lagrangian is determined, the problem solving is reduced to the calculation of partial derivatives in a certain order.

• Most of the works in the field studying the mechanical response of elastic systems with FEM use the method of Lagrange equations, mainly because the researchers are familiar with this approach and obtaining the equations of motion is easy [4–6].

However, analytical mechanics offers alternative formalism to be applied in the analysis of elastic mechanical systems. In recent years, there are papers that analyze the known methods from analytical mechanics to determine the mechanical response of some MBS with elastic elements. The Gibbs–Appell, Hamilton, Maggi, Jacobi, or equivalent formulations are possible.

Gibbs–Appell equations have started to be used lately in calculating the dynamic response of an MBS. These equations present the main advantage that the number of operations required to be applied in this case for a system is smaller than in the case of applying Lagrange equations. A disadvantage and explanation of the small-scale application of the method is that researchers are less familiar with these methods.

The Gibbs–Appell method is convenient in solving the problems related to the dynamics of nonholonomic systems. Developed independently by Gibbs (1879) [7] and Appell (1899) [8], the method consists of replacing a Lagrange function by the energy of accelerations and is essentially based on the Gauss principle of least constraint. In recent years, the Gibbs–Appell formalism has begun to be applied more often to a class of MBS systems [9–12]. For nonholonomic systems, Kane’s equations can also be used, and it seems that in the last decade, their use has begun to be applied to problems that require the dynamic analysis of complex systems. The latest research on applying the method to MBS systems with elastic elements can be found in [13–17].

2 Maggi’s equations

Maggi’s equations [7, 18], although little applied, are known from (1896), and the way of obtaining this alternative formalism from the analytical mechanics is found in numerous works [19–23]. We will point out only the main steps and notions to understand the application in this paper. We consider a nonholonomic mechanical system whose behavior is described by means of n parameters. These parameters are linked by m linear relationships

$$ \sum_{j = 1}^{n} b_{ij} (q_{1},q_{2}, \ldots ,q_{n},t) \dot{q}_{j} + b_{i}(q_{1},q_{2}, \ldots ,q_{n},t) = 0 ,\quad i = \overline{1,m}, $$

(1)

or, explicitly,

$$\left[\begin{array}{cccc}{b}_{11}& b_{12}& \dots & b_{1n}\\ b_{21}& c_{22}& \cdots & b_{2n}\\ ⋮& & & ⋮\\ b_{m1}& b_{m2}& \cdots & b_{mn}\end{array}\right]\left\{\begin{array}{c}{\dot{q}}_1\\ {\dot{q}}_2\\ ⋮\\ {\dot{q}}_n\end{array}\right\}+\left\{\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_n\end{array}\right\}=0.$$

(2)

By a virtual displacement of the n coordinates $q_{1},q_{2}, \ldots ,q_{n}$ relation (2) becomes [7, 8]

$$\left[\begin{array}{cccc}{b}_{11}& b_{12}& \dots & b_{1n}\\ b_{21}& b_{22}& \cdots & b_{2n}\\ ⋮& & & ⋮\\ b_{m1}& b_{m2}& \cdots & b_{mn}\end{array}\right]\left\{\begin{array}{c}\delta q_1\\ \delta q_2\\ ⋮\\ \delta q_n\end{array}\right\}=0.$$

(3)

The m relations (1) give us the expression of all coordinates according to n-m of them, which will be independent coordinates. We renumber these coordinates in the following manner: the independent coordinates will be $\delta q_{1}, \delta q_{2}, \ldots, \delta q_{n - m}$, and the dependent ones are renumbered as $\delta q_{n - m + 1}, \delta q_{n - m + 2}, \ldots ,\delta q_{n}$. With these notations, we get the following relations:

$$\left\{\begin{array}{c}\delta q_{n-m+1}\\ \delta q_{n-m+2}\\ ⋮\\ \delta q_n\end{array}\right\}=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \dots & c_{1,n-m}\\ c_{21}& c_{22}& \cdots & c_{2,n-m}\\ ⋮& & & ⋮\\ c_{m,1}& c_{m,2}& \cdots & c_{m,n-m}\end{array}\right]\left\{\begin{array}{c}\delta q_1\\ \delta q_2\\ ⋮\\ \delta q_{n-m}\end{array}\right\}=[C_{mx(m-n)}]\{\delta \tilde{q}\},$$

(4)

or

$$[C_{mx(n-m)}]=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \dots & c_{1,n-m}\\ c_{21}& c_{22}& \cdots & c_{2,n-m}\\ ⋮& & & ⋮\\ c_{m,1}& c_{m,2}& \cdots & c_{m,n-m}\end{array}\right];\{\delta \tilde{q}\}=\left\{\begin{array}{c}\delta q_1\\ \delta q_2\\ ⋮\\ \delta q_{n-m}\end{array}\right\}.$$

(5)

So the coordinate vector $\{ \delta q \}$, using (4), can be expressed as

$$\{\delta q\}=\left\{\begin{array}{c}\delta q_1\\ \delta q_2\\ ⋮\\ \delta q_n\end{array}\right\}=\left[\begin{array}{c}{E}_{n-m}\\ C_{mx(n-m)}\end{array}\right]\left\{\begin{array}{c}\delta q_1\\ \delta q_2\\ ⋮\\ \delta q_{n-m}\end{array}\right\}=[A_{nx(n-m)}]\left\{\begin{array}{c}\delta q_1\\ \delta q_2\\ ⋮\\ \delta q_{n-m}\end{array}\right\}=[A_{nx(n-m)}]\{\delta \tilde{q}\}$$

(6)

or

$$ \delta q_{k} = \sum_{j = 1}^{n - m} a_{kj} \delta q_{j},\quad k = \overline{1,n}. $$

(7)

If $\{ \mathrm{Ma} \}$ represents the Maggi vector with the components

$$ \mathrm{Ma}(k) = \biggl( \frac{d}{dt} \biggl( \frac{\partial T}{\partial \dot{q}_{k}} \biggr) - \frac{\partial T}{\partial q_{k}} \biggr) - F_{k} ,\quad k = \overline{1,n}, $$

(8)

then Maggi’s equations are obtained if the following condition is satisfied [7–9]:

$$ \{ \mathrm{Ma} \} ^{T} \{ \delta q \} = 0, $$

(9)

or, equivalently,

$$ \{ \delta q \} ^{T} \{ \mathrm{Ma} \} = 0. $$

(10)

Using relation (10) in relation (7), we obtain

$$ \sum_{k = 1}^{n} \Biggl\{ \biggl[ \biggl( \frac{d}{dt} \biggl( \frac{\partial T}{\partial \dot{q}_{k}} \biggr) - \frac{\partial T}{\partial q_{k}} \biggr) - F_{k} \biggr]\sum_{j = 1}^{n - m} a_{kj} \delta q_{j} \Biggr\} = 0. $$

(11)

The coordinates $q_{1},q_{2}, \ldots ,q_{n - m}$ being independent, this results in

$$ \sum_{\boldsymbol{k}=\boldsymbol{1}}^{\boldsymbol{n}} \boldsymbol{a}_{\boldsymbol{kj}} \biggl[\biggl( \frac{\boldsymbol{d}}{\boldsymbol{dt}} \biggl( \frac{\boldsymbol{\partial T}}{\boldsymbol{\partial } \dot{\boldsymbol{q}}_{\boldsymbol{k}}} \biggr)- \frac{\boldsymbol{\partial T}}{\boldsymbol{\partial q}_{\boldsymbol{k}}} \biggr)- \boldsymbol{F}_{\boldsymbol{k}} \biggr] =\boldsymbol{0},\quad \boldsymbol{j}= \overline{\mathbf{1},\boldsymbol{n}-\boldsymbol{m}}, $$

(12)

or

$$ [ A ]^{T} \{ \mathrm{Ma} \} = 0. $$

(13)

Relation (13) represents the Maggi equations, a system of n-m second-order differential equations, where

$$ [ A ] = \begin{bmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}. $$

(14)

These equations offer the unknown independent coordinates $\boldsymbol{q}_{\boldsymbol{1}}, \boldsymbol{q}_{\boldsymbol{2}}, \boldsymbol{\dots }, \boldsymbol{q}_{\boldsymbol{n}-\boldsymbol{m}}$ and then the dependent coordinates $\delta q_{n - m + 1},\delta q_{n - m + 2},\dots , \delta q_{n}$.

3 Kinematics and kinetic energy

In the application of the methods of analytical mechanics a fundamental role is played by the kinetic energy, which must be calculated for the studied system. Applying Maggi’s method, the calculation of kinetic energy is the essential step. Therefore, for the study of a solid elastic body discretized into finite elements, kinetic energy calculation is required. Then the kinetic energy calculation for a single element is done, after which the calculation of the kinetic energy for the whole assembly is obtained by a simple summation. The calculation is done for two-dimensional finite elements. In the analysis with finite elements the displacement of a certain point of the element is described by means of nodal displacements and, possibly, their derivatives, which are the generalized coordinates. For this, a set of shape functions is used.

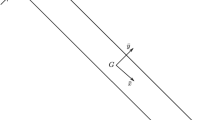
The speed of an arbitrary point of the finite element is given (see Fig. 1) by the relation [15, 17]

$$ \{ v_{M'} \} _{G} = \{ \dot{r}_{M'} \} _{G} = \{ v_{O} \} _{G} + [ \dot{R} ] \{ r \} _{L} + [ \dot{R} ] [ N ] \{ \delta \} _{L} + [ R ] [ N ] \{ \dot{\delta } \} _{L}, $$

(15)

where $\{ v_{O} \} _{G} = \{ \dot{r}_{O} \} _{G}$ represents the velocity vector of the origin of the mobile reference system with components expressed in the global system, $\{ r \} _{L}$ is the position vector of the current point with the coordinates expressed in the mobile system, $\{ \delta \} _{L}$ is the vector of nodal coordinates, $[ N ]$ is the shape function matrix, $[ R ]$ represents the rotation matrix that makes the transition from the mobile reference system to the fixed reference system, and $[ \dot{R} ]$ is the derivative of $[ R ]$ with respect to time.

Figure 1

Two-dimensional finite element

In the following, the quantities that are expressed in the global reference frame will be indexed by G, and those expressed in the local reference frame will be indexed by L. In the case of a vector the transformation from one reference system to another is done through the matrix $[ R ]$:

$$ \{ t \} _{G} = [ R ] \{ t \} _{L}, $$

(16)

where

$$ [ R ] = \begin{bmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}. $$

(17)

The transformation matrix $[ R ]$ is orthonormal, thereby

$$ [ R ] [ R ]^{T} = [ R ]^{T} [ R ] = [ E ] = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, $$

(18)

where $[ E ]$ is the unit matrix. By differentiating (18) we get

$$ [ \dot{R} ] [ R ]^{T} + [ R ] [ \dot{R} ]^{T} = [ \dot{R} ]^{T} [ R ] + [ R ]^{T} [ \dot{R} ] = [ 0 ], $$

(19)

where

$$ [ \omega ]_{G} = [ \dot{R} ] [ R ]^{T} = - [ R ] [ \dot{R} ]^{T} = \begin{bmatrix} 0 & - \omega \\ \omega & 0 \end{bmatrix} $$

(20)

is the skew symmetric operator angular velocity expressed in the global coordinate system, corresponding to the vector angular velocity ω. We have the relation

$$ [ \omega ]_{G} = - [ \omega ]_{G}^{T}. $$

(21)

The operator angular acceleration is

$$ [ \varepsilon ]_{G} = [ \dot{\omega } ]_{G} = \begin{bmatrix} 0 & - \dot{\omega } \\ \dot{\omega } & 0 \end{bmatrix} = [ \ddot{R} ] [ R ]^{T} + [ \dot{R} ] [ \dot{R} ]^{T} = \begin{bmatrix} 0 & - \varepsilon \\ \varepsilon & 0 \end{bmatrix}. $$

(22)

The following relations are valuable too:

$$ [ R ]^{T} [ \ddot{R} ] = [ \varepsilon ]_{L} - [ \dot{R} ]^{T} [ \dot{R} ] = [ \varepsilon ]_{L} + [ \omega ]_{L} [ \omega ]_{L} = \begin{bmatrix} - \omega ^{2} & - \varepsilon \\ \varepsilon & - \omega ^{2} \end{bmatrix} $$

(23)

and

$$ [ \dot{R} ]^{T} [ \dot{R} ] = - [ \omega ]_{L} [ \omega ]_{L} = \omega ^{2} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}. $$

(24)

The kinetic energy is (see the expanded form in Appendix A)

$$ T = \frac{1}{2} \int _{V} \rho \{ v_{M'} \} _{G}^{T} \{ v_{M'} \} _{G} \,dV. $$

(25)

The relation between the independent coordinate vector in the mobile and global reference frames is obtain by the relations [6]

$$ \{ \delta \} _{G} = [ S ] \{ \delta \} _{L},\qquad \{ \delta \} _{L} = [ S ]^{T} \{ \delta \} _{G}, $$

(26)

where $[ S ]$ provides this transformation.

The kinetic energy for an arbitrary element e becomes, after some elementary calculus (Appendix A),

$$\begin{aligned}& \begin{aligned}[b] T_{e} &= \frac{1}{2}mv_{O}^{2} + \{ v_{O} \} _{G}^{T} [ \dot{R} ] \{ S_{O} \} _{L} + \{ v_{O} \} _{G}^{T} [ \dot{R} ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} \{ \delta \} _{G} + \{ \dot{r}_{O} \} _{G}^{T} [ R ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} \{ \dot{ \delta } \} _{G} \\ &\quad {} + \frac{1}{2}\omega ^{2} [ J_{O} ] + \omega ^{2} \bigl( [ m_{1x} ] + [ m_{2y} ] \bigr) [ S ]^{T} \{ \delta \} _{G} + \omega \bigl( [ m_{2x} ] - [ m_{1y} ] \bigr) [ S ]^{T} \{ \dot{ \delta } \} _{G} \\ &\quad {} + \frac{1}{2}\omega ^{2} \{ \delta \} _{G}^{T} [ S ] [ m ] [ S ] \{ \delta \} _{G} + \omega \{ \delta \} _{G}^{T} [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T} \{ \dot{ \delta } \} _{G} \\ &\quad {}+ \frac{1}{2} \{ \dot{\delta } \} _{G}^{T} [ S ] [ m ] [ S ]^{T} \{ \dot{\delta } \} _{G}. \end{aligned} \end{aligned}$$

(27)

The notations and intermediate calculus are presented in Appendix B. For ease of presentation, we do not put the index e in expression (27) since all the quantities are expressed for the eth finite element. The index e will be further added in the chapter dedicated to Maggi equations. The following notations will be further used:

$$ \begin{aligned}[b] T_{e0} &= \{ v_{O} \} _{G}^{T} [ \dot{R} ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} \{ \delta \} _{G} + \omega ^{2} \bigl( [ m_{1x} ] + [ m_{2y} ] \bigr) [ S ]^{T} \{ \delta \} _{G}\\ &\quad {} + \frac{\omega ^{2}}{2} \{ \delta \} _{G}^{T} [ S ] [ m ] [ S ]^{T} \{ \delta \} _{G} \end{aligned} $$

(28)

represents the part of kinetic energy that contains $\{ \delta \}$ but not $\{ \dot{\delta } \} _{G}$.

$$ T_{e10} = \omega \{ \delta \} _{G}^{T} [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T} \{ \dot{\delta } \} _{G} $$

(29)

is the term that contains both $\{ \delta \}$ and $\{ \dot{\delta } \} _{G}$.

$$ T_{e1} = \{ \dot{r}_{O} \} _{G}^{T} [ R ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} \{ \dot{ \delta } \} _{G} - \omega \bigl( [ - m_{1y} ] + [ m_{2x} ] \bigr) [ S ]^{T} \{ \dot{\delta } \} _{G} + \{ \dot{\delta } \} _{G}^{T} [ S ] [ m ] [ S ]^{T} \{ \dot{\delta } \} _{G} $$

(30)

represents the part of kinetic energy that contains $\{ \dot{\delta } \} _{G}$ but not $\{ \delta \}$, and $T_{er}$ is the term that contains neither $\{ \delta \}$ nor $\{ \dot{\delta } \} _{G}$. Then

$$ T_{e} = T_{e0} + T_{e1} + T_{e01} + T_{er}. $$

(31)

To determine the equations of motion for the finite element, Lagrange equations will be applied. The Lagrangian for the element is

$$ L_{e} = T_{e} - V_{e} + W_{e}^{\mathrm{ext}} + W_{e}^{\mathrm{liaison}}. $$

(32)

We first calculate

$$\begin{aligned}& \begin{aligned}[b] \biggl\{ \frac{\partial T_{e}}{\partial \{ \delta \} _{G}} \biggr\} & = \biggl\{ \frac{\partial ( T_{e0} + T_{e01} )}{\partial \{ \delta \} _{G}} \biggr\} \\ &= \{ v_{O} \} _{G}^{T} [ \dot{R} ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} - \bigl\{ Q_{e}^{i}(\omega ) \bigr\} - \bigl[ K_{e} \bigl( \omega ^{2} \bigr) \bigr] + \frac{1}{2} [ C_{e} ] \{ \dot{\delta } \} _{G}, \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned}& \begin{aligned}[b] \biggl\{ \frac{\partial T_{e}}{\partial \{ \dot{\delta } \} _{G}} \biggr\} &= \biggl\{ \frac{\partial ( T_{e01} + T_{e1} )}{\partial \{ \dot{\delta } \} _{G}} \biggr\} \\ &= \{ \dot{r}_{O} \} _{G}^{T} [ R ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} + \omega \bigl( [ - m_{1y} ] + [ m_{2x} ] \bigr) [ S ]^{T}\\ &\quad {} + [ S ] [ m ] [ S ]^{T} \{ \dot{\delta } \} _{G} + \omega [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T} \{ \delta \} _{G}, \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned}& \begin{aligned}[b] \frac{d}{dt} \biggl\{ \frac{\partial T_{e}}{\partial \{ \dot{\delta } \} _{G}} \biggr\} &= \frac{d}{dt} \biggl\{ \frac{\partial ( T_{e01} + T_{e1} )}{\partial \{ \dot{\delta } \} _{G}} \biggr\} \\ &= \bigl[ M_{Oe}^{i} \bigr] \{ \ddot{r}_{O} \} _{G}^{T} + \bigl\{ Q_{e}^{i} ( \varepsilon ) \bigr\} + [ M_{e} ] \{ \ddot{\delta } \} _{G} + \bigl[ K_{e} ( \varepsilon ) \bigr] \{ \delta \} _{G} + \frac{1}{2} [ C_{e} ] \{ \dot{\delta } \} _{G}. \end{aligned} \end{aligned}$$

(35)

Using the notations presented in Appendix B, after some calculus, from (33), (34), and (35) we get

$$\begin{aligned}& \begin{aligned}[b] &\frac{d}{dt} \biggl\{ \frac{\partial T_{e}}{\partial \{ \dot{\delta }_{e} \} _{G}} \biggr\} - \biggl\{ \frac{\partial T_{e}}{\partial \{ \delta _{e} \} _{G}} \biggr\} \\ &\quad = [ M_{e} ] \{ \ddot{\delta }_{e} \} _{G} + [ C_{e} ] \{ \dot{\delta }_{e} \} _{G} + \bigl( \bigl[ K_{e} ( \varepsilon ) \bigr] + \bigl[ K_{e} ( \omega ) \bigr] \bigr) \{ \delta _{e} \} _{G}\\ &\qquad {} + \bigl\{ Q_{e}^{i}(\varepsilon ) \bigr\} + \bigl\{ Q_{e}^{i}(\omega ) \bigr\} + \bigl[ M_{Oe}^{i} \bigr] \{ \ddot{r}_{Oe} \} _{G}, \end{aligned} \end{aligned}$$

(36)

where the following notations are used:

$$\begin{aligned}& \begin{gathered} {}[ M_{e} ] = [ S ] [ m ] [ S ]^{T};\qquad [ C_{e} ] = 2 \omega [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T};\\ \bigl[ K_{e} ( \varepsilon ) \bigr] = [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T}; \qquad \bigl[ K_{e} ( \omega ) \bigr] = \omega ^{2} [ S ] [ m ] [ S ]^{T};\\ \bigl[ M_{Oe}^{i} \bigr] = [ S ] \bigl[ m_{O}^{i} \bigr]^{T} [ R ]^{T};\qquad \bigl\{ Q_{e}^{i}(\omega ) \bigr\} = \omega ^{2} \bigl( [ m_{1x} ] + [ m_{2y} ] \bigr) [ S ]^{T}; \\ \bigl\{ Q_{e}^{i}(\varepsilon ) \bigr\} = \varepsilon \bigl( [ - m_{1y} ] + [ m_{2x} ] \bigr) [ S ]^{T}. \end{gathered} \end{aligned}$$

(37)

By $\{ \frac{\partial T}{\partial \{ \delta \} } \}$ and $\{ \frac{\partial T}{\partial \{ \dot{\delta } \} } \}$ we denote

$$ \begin{bmatrix} \frac{\partial T}{\partial \delta _{1}} & \frac{\partial T}{\partial \delta _{2}} & \ldots & \ldots & \frac{\partial T}{\partial \delta _{se}} \end{bmatrix}^{T} $$

and

$$ \begin{bmatrix} \frac{\partial T}{\partial \dot{\delta }_{1}} & \frac{\partial T}{\partial \dot{\delta }_{2}} & \ldots & \ldots & \frac{\partial T}{\partial \dot{\delta }_{se}} \end{bmatrix}^{T}, $$

respectively.

Taking into account the expression of the potential energy and the work of the concentrated and distributed forces, in this case, Lagrange equations give the following equations of motion of the finite element:

$$\begin{aligned}& \begin{aligned}[b] &[ M_{e} ] \{ \ddot{\delta }_{e} \} _{G} + [ C_{e} ] \{ \dot{\delta }_{e} \} _{G} + \bigl( [ K ] + \bigl[ K_{e} ( \varepsilon ) \bigr] + \bigl[ K_{e} ( \omega ) \bigr] \bigr) \{ \delta _{e} \} _{G} \\ &\quad = \bigl\{ Q_{e}^{\mathrm{ext}} \bigr\} + \bigl\{ Q_{e}^{\mathrm{liaison}} \bigr\} + \bigl\{ Q_{e}^{i}(\varepsilon ) \bigr\} + \bigl\{ Q_{e}^{i}(\omega ) \bigr\} + \bigl[ M_{Oe}^{i} \bigr] \{ \ddot{r}_{Oe} \} _{G}. \end{aligned} \end{aligned}$$

(38)

4 Maggi’s formalism applied to MBS

To apply Maggi’s methodm it is necessary to write the kinetic energy for the whole system. This kinetic energy is the sum of the kinetic energies written for each element (rel. (22)). It follows that

$$ T = \frac{1}{2}\sum_{e = 1}^{Ne} T_{e}, $$

(39)

where $N_{e}$ is the number of elements, and $T_{0}$ represents the part of kinetic energy that contains the coordinates of the nodes but not their derivatives:

$$ \begin{aligned}[b] T_{0} &= \sum_{e = 1}^{Ne} \biggl( \{ v_{Oe} \} _{G}^{T} [ \dot{R}_{e} ] \bigl[ m_{Oe}^{i} \bigr] [ S_{e} ]^{T} \{ \delta _{e} \} _{G} + \omega _{e}^{2} \bigl( [ m_{1x,e} ] + [ m_{2y,e} ] \bigr) [ S_{e} ]^{T} \{ \delta _{e} \} _{G} \\ &\quad {}+ \frac{\omega _{e}^{2}}{2} \{ \delta _{e} \} _{G}^{T} [ S_{e} ] [ m_{e} ] [ S_{e} ]^{T} \{ \delta _{e} \} _{G} \biggr). \end{aligned} $$

(40)

$T_{10}$ represents the terms that contain both the coordinates and their derivatives:

$$ T_{10} = \sum_{e = 1}^{Ne} \omega _{e} \{ \delta _{e} \} _{G}^{T} [ S_{e} ] \bigl( [ m_{12,e} ] - [ m_{21,e} ] \bigr) [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G}. $$

(41)

$T_{1}$ represents the part of kinetic energy containing no coordinates but containing their derivatives, and $T_{r}$ is the term that does not contain coordinates and their derivatives:

$$ \begin{aligned}[b] T_{1} &= \sum_{e = 1}^{Ne} \bigl[ \{ \dot{r}_{Oe} \} _{G}^{T} [ R_{e} ] \bigl[ m_{Oe}^{i} \bigr] [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} - \omega _{e} \bigl( [ - m_{1y,e} ] + [ m_{2x,e} ] \bigr) [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} \\ &\quad {}+ \{ \dot{ \delta }_{e} \} _{G}^{T} [ S_{e} ] [ m_{e} ] [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} \bigr]. \end{aligned} $$

(42)

Note that

$$[A(B_i)]=\left[\begin{array}{ccccc}{B}_1& & & & \\ & B_2& & 0& \\ & & \ddots & & \\ & 0& & & \\ & & & & B_n\end{array}\right];\{A(B_i)\}=\left\{\begin{array}{c}{B}_1\\ B_2\\ ⋮\\ B_n\end{array}\right\}.$$

(43)

To apply the Maggi equations, we first calculate

$$\begin{aligned}& \begin{aligned}[b] \biggl\{ \frac{\partial T}{\partial \{ \Delta \} } \biggr\} &= \sum_{e = 1}^{Ne} \biggl\{ \frac{\partial ( T_{0,e} + T_{01,e} )}{\partial \{ \delta _{e} \} _{G}} \biggr\} \\ &= \sum_{e = 1}^{Ne} \biggl( \{ v_{Oe} \} _{G}^{T} [ \dot{R}_{e} ] \bigl[ m_{Oe}^{i} \bigr] [ S_{e} ]^{T} - \bigl\{ Q_{e}^{i}(\omega _{e}) \bigr\} - \bigl[ K_{e} \bigl( \omega _{e}^{2} \bigr) \bigr] + \frac{1}{2} [ C_{e} ] \{ \dot{\delta }_{e} \} _{G} \biggr), \end{aligned} \end{aligned}$$

(44)

$$\begin{aligned}& \begin{aligned}[b] &\frac{d}{dt} \biggl\{ \frac{\partial T}{\partial \{ \dot{\Delta } \} } \biggr\} \\ &\quad = \sum _{e = 1}^{Ne} \frac{d}{dt} \biggl\{ \frac{\partial ( T_{e01} + T_{e1} )}{\partial \{ \dot{\delta }_{e} \} _{G}} \biggr\} \\ &\quad = \sum_{e = 1}^{Ne} \biggl( \bigl[ M_{Oe}^{i} \bigr] \{ \ddot{r}_{O} \} _{G}^{T} + \bigl\{ Q_{e}^{i} ( \varepsilon ) \bigr\} + [ M_{e} ] \{ \ddot{\delta } \} _{G} + \bigl[ K_{e} ( \varepsilon ) \bigr] \{ \delta \} _{G} + \frac{1}{2} [ C_{e} ] \{ \dot{\delta } \} _{G} \biggr). \end{aligned} \end{aligned}$$

(45)

This results in

$$\begin{aligned}& \begin{aligned}[b] &\frac{d}{dt} \biggl\{ \frac{\partial T}{\partial \{ \dot{\Delta } \} } \biggr\} - \biggl\{ \frac{\partial T}{\partial \{ \Delta \} } \biggr\} \\ &\quad = \sum_{e = 1}^{Ne} \bigl( [ M_{e} ] \{ \ddot{\delta }_{e} \} _{G} + [ C_{e} ] \{ \dot{\delta }_{e} \} _{G} + \bigl( \bigl[ K_{e} ( \varepsilon ) \bigr] + \bigl[ K_{e} ( \omega ) \bigr] \bigr) \{ \delta _{e} \} _{G} \\ &\qquad {}+ \bigl\{ Q_{e}^{i}( \varepsilon ) \bigr\} + \bigl\{ Q_{e}^{i}(\omega ) \bigr\} + \bigl[ M_{Oe}^{i} \bigr] \{ \ddot{r}_{Oe} \} _{G} \bigr).\end{aligned} \end{aligned}$$

(46)

Considering the notations from Appendix B and

$$\begin{aligned}& \begin{gathered} {}[ M ] = \bigl[ A ( M_{e} ) \bigr],\qquad [ C ] = \bigl[ A(C_{e}) \bigr],\qquad [ K ] = \bigl[ A(K_{e}) \bigr], \qquad \bigl[ K ( \varepsilon ) \bigr] = \bigl[ A(K_{e}(\varepsilon _{e}) \bigr], \\ \bigl[ K ( \omega ) \bigr] = \bigl[ A(K_{e}(\omega _{e}) \bigr],\qquad \{ Q \} = \bigl\{ A ( Q_{e} ) \bigr\} ,\qquad \bigl\{ Q^{i}(\varepsilon ) \bigr\} = \bigl\{ A \bigl( Q_{e}^{i} ( \varepsilon _{e} ) \bigr) \bigr\} , \\ \bigl\{ Q^{i}(\omega ) \bigr\} = \bigl\{ A \bigl( Q_{e}^{i} ( \omega _{e} ) \bigr) \bigr\} ,\qquad \bigl\{ Q_{O}^{i} \bigr\} = \bigl\{ A \bigl( \bigl[ M_{Oe}^{i} \bigr] \{ \ddot{r}_{Oe} \} _{G} \bigr) \bigr\} , \\ \{ \Delta \} = \bigl\{ A \bigl( \{ \delta _{e} \} _{G} \bigr) \bigr\} ,\qquad \{ \dot{\Delta } \} = \bigl\{ A \bigl( \{ \dot{\delta }_{e} \} _{G} \bigr) \bigr\} ,\qquad \{ \ddot{\Delta } \} = \bigl\{ A \bigl( \{ \ddot{\delta }_{e} \} _{G} \bigr) \bigr\} ,\end{gathered} \end{aligned}$$

(47)

we can write:

$$\sum _{e=1}^{Ne}[M_e]{\{{\ddot{\delta }}_e\}}_G=\left[\begin{array}{ccccc}{M}_1& & & & \\ & M_2& & 0& \\ & & \ddots & & \\ & 0& & & \\ & & & & M_{Ne}\end{array}\right]\left\{\begin{array}{c}{\{{\ddot{\delta }}_1\}}_G\\ {\{{\ddot{\delta }}_2\}}_G\\ ⋮\\ {\{{\ddot{\delta }}_{Ne}\}}_G\end{array}\right\}=[M]\{\ddot{\mathrm{\Delta }}\},$$

(48)

$$\sum _{e=1}^{Ne}[C_e]{\{{\ddot{\delta }}_e\}}_G=\left[\begin{array}{ccccc}{C}_1& & & & \\ & C_2& & 0& \\ & & \ddots & & \\ & 0& & & \\ & & & & C_{Ne}\end{array}\right]\left\{\begin{array}{c}{\{{\dot{\delta }}_1\}}_G\\ {\{{\dot{\delta }}_2\}}_G\\ ⋮\\ {\{{\dot{\delta }}_{Ne}\}}_G\end{array}\right\}=[C]\{\dot{\mathrm{\Delta }}\},$$

(49)

and so on. Finally, we obtain

$$ \begin{aligned}[b] \frac{d}{dt} \biggl\{ \frac{\partial T}{\partial \{ \dot{\Delta } \} } \biggr\} - \biggl\{ \frac{\partial T}{\partial \{ \Delta \} } \biggr\} &= [ M ] \{ \ddot{\Delta } \} + [ C ] \{ \dot{\Delta } \} + \bigl( [ K ] + \bigl[ K ( \varepsilon ) \bigr] + \bigl[ K ( \omega ) \bigr] \bigr) \{ \Delta \} \\ &\quad {}+ \bigl\{ Q^{i}(\varepsilon ) \bigr\} + \bigl\{ Q^{i}(\omega ) \bigr\} + \bigl\{ Q_{O}^{i} \bigr\} .\end{aligned} $$

(50)

The finite elements are connected to each other. Some nodes may belong to several elements. In this case the displacements for the elements connected through a common node are equal. These liaisons between nodes can be expressed by linear relationships of form (51), which, in this case, are written as:

$$\{\mathrm{\Delta }\}=\left\{\begin{array}{c}{\mathrm{\Delta }}_1\\ {\mathrm{\Delta }}_2\\ ⋮\\ ⋮\\ {\mathrm{\Delta }}_M\end{array}\right\}=[A]\{q\};\{\dot{\mathrm{\Delta }}\}=\left\{\begin{array}{c}{\dot{\mathrm{\Delta }}}_1\\ {\dot{\mathrm{\Delta }}}_2\\ ⋮\\ ⋮\\ {\dot{\mathrm{\Delta }}}_M\end{array}\right\}=[A]\{\dot{q}\};\{\ddot{\mathrm{\Delta }}\}=\left\{\begin{array}{c}{\ddot{\mathrm{\Delta }}}_1\\ {\ddot{\mathrm{\Delta }}}_2\\ ⋮\\ ⋮\\ {\ddot{\mathrm{\Delta }}}_M\end{array}\right\}=[A]\{\ddot{q}\}.$$

(51)

Here $\{ q \}$ is the vector of independent coordinates of the whole system. Considering (50), it is possible to write

$$\begin{aligned}& \begin{aligned}[b] &\frac{d}{dt} \biggl\{ \frac{\partial T}{\partial \dot{\Delta }} \biggr\} - \biggl\{ \frac{\partial T}{\partial \Delta } \biggr\} - \bigl\{ Q^{\mathrm{ext}} \bigr\} - \bigl\{ Q^{\mathrm{liaison}} \bigr\} \\ &\quad = [ M ] \{ \ddot{\Delta } \} + [ C ] \{ \dot{\Delta } \} + \bigl( [ K ] + \bigl[ K ( \varepsilon ) \bigr] + \bigl[ K ( \omega ) \bigr] \bigr) \{ \Delta \}\\ &\qquad {}- \bigl\{ Q^{i}(\varepsilon ) \bigr\} - \bigl\{ Q^{i}(\omega ) \bigr\} - \bigl\{ Q_{O}^{i} \bigr\} - \bigl\{ Q^{\mathrm{ext}}) \bigr\} - \bigl\{ Q^{\mathrm{liaison}}) \bigr\} . \end{aligned} \end{aligned}$$

(52)

Applying the Maggi equations (A.1) and (A.2) using relation (52), we finally obtain:

$$\begin{aligned}& \begin{aligned}[b] &[ A ]^{T} [ M ] \{ \ddot{\Delta } \} + [ A ]^{T} [ C ] \{ \dot{\Delta } \} + [ A ]^{T} \bigl( [ K ] + \bigl[ K ( \varepsilon ) \bigr] + \bigl[ K ( \omega ) \bigr] \bigr) \{ \Delta \} \\ &\quad {}- [ A ]^{T} \bigl\{ Q^{i}(\varepsilon ) \bigr\} - [ A ]^{T} \bigl\{ Q^{i}(\omega ) \bigr\} - [ A ]^{T} \bigl\{ Q_{O}^{i} \bigr\} - [ A ]^{T} \bigl\{ Q^{\mathrm{ext}}) \bigr\} - [ A ]^{T} \bigl\{ Q^{\mathrm{liaison}}) \bigr\} = 0. \end{aligned} \end{aligned}$$

(53)

The work of the liaison forces is null [17]:

$$ [ A ]^{T} \bigl\{ Q^{\mathrm{liaison}} \bigr\} = 0. $$

(54)

Taking into account relation (54), the Maggi equations become

$$\begin{aligned}& \begin{aligned}[b] &[ A ]^{T} [ M ] [ A ] \{ \ddot{q} \} + [ A ]^{T} [ C ] [ A ] \{ \dot{q} \} + [ A ]^{T} \bigl( [ K ] + \bigl[ K ( \varepsilon ) \bigr] + \bigl[ K ( \omega ) \bigr] \bigr) [ A ] \{ q \} \\ &\quad = - [ A ]^{T} \bigl\{ Q^{i}(\varepsilon ) \bigr\} - [ A ]^{T} \bigl\{ Q^{i}(\omega ) \bigr\} - [ A ]^{T} \bigl\{ Q_{O}^{i} \bigr\} - [ A ]^{T} \bigl\{ Q^{\mathrm{ext}} \bigr\} . \end{aligned} \end{aligned}$$

(55)

Using the notations

$$ \begin{aligned} &{}[ \tilde{M} ] = [ A ]^{T} [ M ] [ A ] \{ \ddot{q} \} ,\qquad [ C ] = [ A ]^{T} [ C ] [ A ],\\ &[ \tilde{K} ] = [ A ]^{T} [ K ] [ A ],\qquad \bigl[ \tilde{K} ( \varepsilon ) \bigr] = [ A ]^{T} \bigl[ K ( \varepsilon ) \bigr] [ A ], \end{aligned} $$

(56)

we arrive at the final form of the motion equations:

$$\begin{aligned}& \begin{gathered} {}[ \tilde{M} ] \{ \ddot{q} \} + [ \tilde{C} ] \{ \dot{q} \} + \bigl( [ \tilde{K} ] + \bigl[ \tilde{K} ( \varepsilon ) \bigr] + \bigl[ \tilde{K} ( \omega ) \bigr] \bigr) \{ q \} \\ \quad =- \bigl\{ \tilde{Q}^{i}(\varepsilon ) \bigr\} - \bigl\{ \tilde{Q}^{i}(\omega ) \bigr\} - \bigl\{ \tilde{Q}_{O}^{i} \bigr\} - \bigl\{ \tilde{Q}^{\mathrm{ext}} \bigr\} . \end{gathered} \end{aligned}$$

(57)

These equations have the same form as those obtained by using Lagrange equations [17].

5 Conclusions

Maggi’s equations have been used sporadically in applications, but in the case of finite element analysis of a planar mechanism, it is their first use. In the analysis of MBS with elastic elements, one of the steps that has to be completed is the assembly of the equations of motion, to obtain a complete system of differential equations that describes the evolution of the considered mechanical system. To do this, several methods can be used, equivalent to each other: Lagrange equations, Newton–Euler equations, Kane’s Mmethod, or Maggi’s equations. Each of these methods has advantages and disadvantages that have been highlighted, more or less, in different works presented in the Introduction. For example, the Newton–Euler method offers the advantage of being able to obtain equations that are formally independent of geometry, inertia, or bonds. The main disadvantage is that the liaison forces and moments must be determined. When dealing with a system with a reduced number of degrees of freedom, this method can proved to be very useful. If, however, we deal with a system with a large number of degrees of freedom, then it may be advantageous to use the Lagrange equation method. In this case, it can be difficult to determine the generalized liaison forces, and Lagrange equations offer a useful formalism in this stage. Another advantage is that Lagrange equations have a homogeneous form, which suits to generalizations for large systems. This is why the method was used by software developers (ADAMS, DADS, DYMAC).

There are other developers that offer an equivalent form from the point of view of analytical mechanics, namely the use of Kane’s equations (i.e. SD-EXACT, NBOD2, SD / FAST). In essence, Kane’s equations represent a formalism equivalent to Maggi’s equations, a development of this method. As a result, it is natural to study whether it can be more advantageous to apply Maggi’s equations directly to MBS systems with elastic elements, resulting in a computational economy. In the paper, we presented the possibility of using Maggi’s equations for MBS systems with two-dimensional elastic elements having a plane motion. This type of systems meets current in engineering practice; there are numerous mechanisms that operate in industries and belong to this category. In this way, a unitary and simple approach of such systems can be made, which could allow the development of software that uses this method. Maggi’s equations can provide a simple solution to the problem of assembling the equations of motion of individual finite elements. Thus, it is sufficient to know the kinetic energy of the system and the internal and external forces. Then the kinematic relations of liaison between the independent coordinates and the equations of motion of the whole system can be obtained in a simple way.

We can conclude that the application of this method has an advantage over the use of Lagrange equations because the number of unknowns involved is lower. It is no longer need to calculate the Lagrange multipliers. For this reason, the number of equations to be solved and computer time are reduced. It is worth mentioning that the Maggi method is very suitable for systems with nonholonomic constraints.

Appendices

Appendix A

$$\begin{aligned}& T = \frac{1}{2} \int _{V} \rho \{ v_{M'} \} _{G}^{T} \{ v_{M'} \} _{G} \,dV \\& \hphantom{T }= \frac{1}{2} \int _{V} \rho \bigl( \{ \dot{r}_{O} \} _{G}^{T} \{ \dot{r}_{O} \} _{G} + 2 \{ \dot{r}_{O} \} _{G}^{T} [ \dot{R} ] \{ r \} _{L} + 2 \{ \dot{r}_{O} \} _{G}^{T} [ \dot{R} ] [ N ] \{ \delta \} _{L} \\& \hphantom{T =} {}+ 2 \{ \dot{r}_{O} \} _{G}^{T} [ R ] [ N ] \{ \dot{\delta } \} _{L} \bigr)\,d V + \frac{1}{2} \int _{V} \rho \bigl( \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ \dot{R} ] \{ r \} _{L} \\& \hphantom{T =} {} + 2 \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ \dot{R} ] [ N ] \{ \delta \} _{L} + 2 \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ R ] [ N ] \{ \dot{\delta } \} _{L} \bigr)\,dV \\& \hphantom{T =} {}+ \frac{1}{2} \int _{V} \rho \bigl( \{ \delta \} _{L}^{T} [ N ]^{T} [ \dot{R} ]^{T} [ \dot{R} ] [ N ] \{ \delta \} _{L} \\& \hphantom{T =} {}+ 2 \{ \delta \} _{L}^{T} [ N ]^{T} [ \dot{R} ]^{T} [ R ] [ N ] \{ \dot{\delta } \} _{L} + \{ \dot{\delta } \} _{L}^{T} [ N ]^{T} [ N ] \{ \dot{\delta } \} _{L} \bigr) \,dV, \end{aligned}$$

(A.1)

$$\begin{aligned}& \begin{aligned}[b] T_{e} &= \frac{1}{2} \int _{V} \rho \bigl( \{ \dot{r}_{O} \} _{G}^{T} \{ \dot{r}_{O} \} _{G} + 2 \{ \dot{r}_{O} \} _{G}^{T} [ \dot{R} ] \{ r \} _{L} + 2 \{ \dot{r}_{O} \} _{G}^{T} [ \dot{R} ] [ N ] [ S ]^{T} \{ \delta \} _{G} \\ &\quad {}+ 2 \{ \dot{r}_{O} \} _{G}^{T} [ R ] [ N ] [ S ]^{T} \{ \dot{\delta } \} _{G} \bigr)\,d V + \frac{1}{2} \int _{V} \rho \bigl( \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ \dot{R} ] \{ r \} _{L} \\ &\quad {}+ 2 \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ \dot{R} ] [ N ] [ S ]^{T} \{ \delta \} _{G} + 2 \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ R ] [ N ] [ S ]^{T} \{ \dot{\delta } \} _{G} \bigr)\,dV \\ &\quad {}+ \frac{1}{2} \int _{V} \rho \bigl( \{ \delta \} _{G}^{T} [ S ] [ N ]^{T} [ \dot{R} ]^{T} [ \dot{R} ] [ N ] [ S ]^{T} \{ \delta \} _{G} \\ &\quad {}+ 2 \{ \delta \} _{G}^{T} [ S ] [ N ]^{T} [ \dot{R} ]^{T} [ R ] [ N ] [ S ]^{T} \{ \dot{\delta } \} _{G} + \{ \dot{ \delta } \} _{G}^{T} [ S ] [ N ]^{T} [ N ] [ S ]^{T} \{ \dot{\delta } \} _{G} \bigr) \,dV; \end{aligned} \end{aligned}$$

(A.2)

$$\begin{aligned}& \begin{aligned}[b] \biggl\{ \frac{\partial T_{e}}{\partial \{ \delta \} _{G}} \biggr\} &= \biggl\{ \frac{\partial ( T_{e0} + T_{e01} )}{\partial \{ \delta \} _{G}} \biggr\} \\ & = \{ v_{O} \} _{G}^{T} [ \dot{R} ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} - \omega ^{2} \bigl( [ m_{1x} ] + [ m_{2y} ] \bigr) [ S ]^{T} \\ &\quad {}- \omega ^{2} [ S ] [ m ] [ S ]^{T} \{ \delta \} _{G} + \omega [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T} \{ \dot{\delta } \} _{G} \\ &= \{ v_{O} \} _{G}^{T} [ \dot{R} ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} - \bigl\{ Q_{e}^{i}(\omega ) \bigr\} - \bigl[ K_{e} \bigl( \omega ^{2} \bigr) \bigr] + \frac{1}{2} [ C_{e} ] \{ \dot{\delta } \} _{G}; \end{aligned} \end{aligned}$$

(A.3)

$$\begin{aligned}& \begin{aligned}[b] \biggl\{ \frac{\partial T_{e}}{\partial \{ \dot{\delta } \} _{G}} \biggr\} &= \biggl\{ \frac{\partial ( T_{e01} + T_{e1} )}{\partial \{ \dot{\delta } \} _{G}} \biggr\} \\ &= \{ \dot{r}_{O} \} _{G}^{T} [ R ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} + \omega \bigl( [ - m_{1y} ] + [ m_{2x} ] \bigr) [ S ]^{T}\\ &\quad {}+ [ S ] [ m ] [ S ]^{T} \{ \dot{\delta } \} _{G} + \omega [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T} \{ \delta \} _{G}; \end{aligned} \end{aligned}$$

(A.4)

$$\begin{aligned}& \begin{aligned}[b] \frac{d}{dt} \biggl\{ \frac{\partial T_{e}}{\partial \{ \dot{\delta } \} _{G}} \biggr\} &= \frac{d}{dt} \biggl\{ \frac{\partial ( T_{e01} + T_{e1} )}{\partial \{ \dot{\delta } \} _{G}} \biggr\} \\ &= \{ \ddot{r}_{O} \} _{G}^{T} [ R ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} + \varepsilon \bigl( [ - m_{1y} ] + [ m_{2x} ] \bigr) [ S ]^{T}\\ &\quad {} + [ S ] [ m ] [ S ]^{T} \{ \ddot{\delta } \} _{G} + \varepsilon [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T} \{ \delta \} _{G} \\ &\quad {}+ \omega [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T} \{ \dot{\delta } \} _{G} = \bigl[ M_{Oe}^{i} \bigr] \{ \ddot{r}_{O} \} _{G}^{T}\\ &\quad {} + \bigl\{ Q_{e}^{i} ( \varepsilon ) \bigr\} + [ M_{e} ] \{ \ddot{\delta } \} _{G} + \bigl[ K_{e} ( \varepsilon ) \bigr] \{ \delta \} _{G} + \frac{1}{2} [ C_{e} ] \{ \dot{ \delta } \} _{G}; \end{aligned} \end{aligned}$$

(A.5)

$$\begin{aligned}& T = \frac{1}{2}\sum_{e = 1}^{Ne} T_{e} \\& \hphantom{T}= \sum_{e = 1}^{Ne} \biggl( \frac{1}{2}m_{e}v_{Oe}^{2} + \{ v_{Oe} \} _{G}^{T} [ \dot{R}_{e} ] \{ S_{Oe} \} _{L} + \{ v_{Oe} \} _{G}^{T} [ \dot{R}_{e} ] \bigl[ m_{Oe}^{i} \bigr] [ S_{e} ]^{T} \{ \delta _{e} \} _{G} \\& \hphantom{T =} {} + \{ \dot{r}_{Oe} \} _{G}^{T} [ R_{e} ] \bigl[ m_{Oe}^{i} \bigr] [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} \biggr) \\& \hphantom{T =} {} + \sum _{e = 1}^{Ne} \biggl( \frac{1}{2}\omega _{e}^{2} [ J_{Oe} ] + \omega _{e}^{2} \bigl( [ m_{1x,e} ] + [ m_{2y,e} ] \bigr) [ S_{e} ]^{T} \{ \delta _{e} \} _{G} \\& \hphantom{T =} {} + \omega _{e} \bigl( [ m_{2x,e} ] - [ m_{1y,e} ] \bigr) [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} \biggr) \\& \hphantom{T =} {} + \sum_{e = 1}^{Ne} \biggl( \frac{1}{2}\omega _{e}^{e} \{ \delta _{e} \} _{G}^{T} [ S_{e} ] [ m_{e} ] [ S_{e} ] \{ \delta _{e} \} _{G} \\& \hphantom{T =} {} + \omega _{e} \{ \delta _{e} \} _{G}^{T} [ S_{e} ] \bigl( [ m_{12,e} ] - [ m_{21,e} ] \bigr) [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} \biggr) \\& \hphantom{T =} {}+ \frac{1}{2}\sum_{e = 1}^{Ne} \{ \dot{\delta }_{e} \} _{G}^{T} [ S_{e} ] [ m_{e} ] [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G}; \end{aligned}$$

(A.6)

$$\begin{aligned}& \begin{aligned}[b] T_{0} &= \sum_{e = 1}^{Ne} \biggl( \{ v_{Oe} \} _{G}^{T} [ \dot{R}_{e} ] \bigl[ m_{Oe}^{i} \bigr] [ S_{e} ]^{T} \{ \delta _{e} \} _{G} + \omega _{e}^{2} \bigl( [ m_{1x,e} ] + [ m_{2y,e} ] \bigr) [ S_{e} ]^{T} \{ \delta _{e} \} _{G} \\ &\quad {}+ \frac{\omega _{e}^{2}}{2} \{ \delta _{e} \} _{G}^{T} [ S_{e} ] [ m_{e} ] [ S_{e} ]^{T} \{ \delta _{e} \} _{G} \biggr); \end{aligned} \\& T_{10} = \sum_{e = 1}^{Ne} \omega _{e} \{ \delta _{e} \} _{G}^{T} [ S_{e} ] \bigl( [ m_{12,e} ] - [ m_{21,e} ] \bigr) [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G}; \\& \begin{aligned}[b] T_{1} &= \sum_{e = 1}^{Ne} \bigl[ \{ \dot{r}_{Oe} \} _{G}^{T} [ R_{e} ] \bigl[ m_{Oe}^{i} \bigr] [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} - \omega _{e} \bigl( [ - m_{1y,e} ] + [ m_{2x,e} ] \bigr) [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} \\ &\quad {}+ \{ \dot{ \delta }_{e} \} _{G}^{T} [ S_{e} ] [ m_{e} ] [ S_{e} ]^{T} \{ \dot{\delta }_{e} \} _{G} \bigr]. \end{aligned} \end{aligned}$$

(A.7)

Appendix B

Let us consider the ten terms of kinetic energy (31):

$$ \bullet \quad \frac{1}{2} \int _{V} \rho \{ \dot{r}_{O} \} _{G}^{T} \{ \dot{r}_{O} \} _{G}\,d V = \frac{v_{O}^{2}}{2} \int _{V} \rho \,d V = \frac{mv_{O}^{2}}{2}, $$

(B.1)

where m is the mass of the finite element;

$$ \bullet \quad \int _{V} \rho \{ \dot{r}_{O} \} _{G}^{T} [ \dot{R} ] \{ r \} _{L}\,d V = \{ \dot{r}_{O} \} _{G}^{T} [ \dot{R} ] \int _{V} \rho \{ r \} _{L}\,d V = \{ v_{O} \} _{G}^{T} [ \dot{R} ] \{ S_{O} \} _{L}, $$

(B.2)

where $\{ S_{O} \}$ is the static moment of the finite element;

$$ \begin{aligned}[b] \bullet \quad \int _{V} \rho \bigl( \{ \dot{r}_{O} \} _{G}^{T} [ \dot{R} ] [ N ] [ S ]^{T} \{ \delta \} _{G} \bigr)\,d V &= \{ \dot{r}_{O} \} _{G}^{T} [ \dot{R} ] \biggl( \int _{V} \rho [ N ]\,d V \biggr) [ S ]^{T} \{ \delta \} _{G} \\ &= \{ v_{O} \} _{G}^{T} [ \dot{R} ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} \{ \delta \} _{G},\end{aligned} $$

(B.3)

where $[ m_{O}^{i} ] = \int _{V} \rho [ N ]\,d V$ is the mass of the element;

$$\begin{aligned}& \begin{aligned}[b] \bullet \quad \int _{V} \rho \bigl( \{ \dot{r}_{O} \} _{G}^{T} [ R ] [ N ] [ S ]^{T} \{ \dot{\delta } \} _{G} \bigr)\,d V &= \{ \dot{r}_{O} \} _{G}^{T} [ R ] \biggl( \int _{V} \rho [ N ]\,d V \biggr) [ S ]^{T} \{ \dot{ \delta } \} _{G} \\ &= \{ v_{O} \} _{G}^{T} [ R ] \bigl[ m_{O}^{i} \bigr] [ S ]^{T} \{ \dot{ \delta } \} _{G};\end{aligned} \end{aligned}$$

(B.4)

$$\begin{aligned}& \bullet \quad \frac{1}{2} \int _{V} \rho \bigl( \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ \dot{R} ] \{ r \} _{L} \bigr)\,dV = \frac{1}{2}\omega ^{2} \int _{V} \rho \{ r \} _{L}^{T} \{ r \} _{L}\,dV = \frac{1}{2}\omega ^{2}J_{o}, \end{aligned}$$

(B.5)

$$\begin{aligned}& \text{where }J_{O} = \int _{V} \rho \{ r \} _{L}^{T} \{ r \} _{L}\,dV; \end{aligned}$$

(B.6)

$$\begin{aligned}& \begin{gathered}[b] \bullet \quad \int _{V} \rho \bigl( \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ \dot{R} ] [ N ] [ S ]^{T} \{ \delta \} _{G} \bigr)\,dV \\ \hphantom{\bullet \quad}\quad = \omega ^{2} \biggl[ \int _{V} \rho \bigl( [ N_{(1)} ]x + [ N_{(2)} ]y \bigr)\,dV \biggr] [ S ]^{T} \{ \delta \} _{G} = \omega ^{2} \bigl( [ m_{1x} ] + [ m_{2y} ] \bigr) [ S ]^{T} \{ \delta \} _{G}; \end{gathered} \end{aligned}$$

(B.7)

$$\begin{aligned}& \text{where } [ m_{1x} ]= \int _{V} \rho [ N_{(1)} ]x \,dV \quad \text{and} \quad [ m_{2y} ]= \int _{V} \rho [ N_{(2)} ]y \,dV; \end{aligned}$$

(B.8)

$$\begin{aligned}& \begin{aligned}[b] \int _{V} \rho \bigl( \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ R ] [ N ] \bigr)\,dV &= \int _{V} \rho \bigl( \{ r \} _{L}^{T} [ \dot{R} ]^{T} [ R ] [ N ] \bigr)\,dV [ S ]^{T} \{ \dot{\delta } \} _{G} \\ &= \int _{V} \rho \left( \{ r \} _{L}^{T} \begin{bmatrix} 0 & \omega \\ - \omega & 0 \end{bmatrix} [ N ] \right)\,dV [ S ]^{T} \{ \dot{ \delta } \} _{G}\\ & = \omega \biggl[ \int _{V} \rho \bigl( [ N_{(2)} ]x - [ N_{(1)} ]y \bigr)\,dV \biggr] [ S ]^{T} \{ \dot{\delta } \} \\ &= \omega \bigl[ [ m_{2x} ] - [ m_{1y} ] \bigr] [ S ]^{T} \{ \dot{\delta } \} , \end{aligned} \end{aligned}$$

(B.9)

$$\begin{aligned}& \text{where } [ m_{2x} ]= \int _{V} \rho [ N_{(2)} ]x \,dV \quad \text{and}\quad [ m_{1y} ]= \int _{V} \rho [ N_{(1)} ]y \,dV; \end{aligned}$$

(B.10)

$$\begin{aligned}& \begin{aligned}[b] &\frac{1}{2} \int _{V} \rho \bigl( \{ \delta \} _{G}^{T} [ S ] [ N ]^{T} [ \dot{R} ]^{T} [ \dot{R} ] [ N ] [ S ]^{T} \{ \delta \} _{G} \bigr) \,dV \\ &\quad = \frac{\omega ^{2}}{2} \{ \delta \} _{G}^{T} [ S ] \biggl( \int _{V} [ N ]^{T} [ N ] \,dV \biggr) [ S ]^{T} \{ \delta \} _{G} \\ &\quad = \frac{\omega ^{2}}{2} \{ \delta \} _{G}^{T} [ S ] [ m ] [ S ]^{T} \{ \delta \} _{G}.\end{aligned} \end{aligned}$$

(B.11)

The following notations were also used:

$$\begin{aligned}& [ m_{11} ] = \int _{V} \rho [ N_{(1)} ]^{T} [ N_{(1)} ] \,dV ;\qquad [ m_{12} ] = \int _{V} \rho [ N_{(1)} ]^{T} [ N_{(2)} ]y \,dV; \end{aligned}$$

(B.12)

$$\begin{aligned}& [ m_{21} ] = \int _{V} \rho [ N_{(2)} ]^{T} [ N_{(1)} ] \,dV ;\qquad [ m_{22} ] = \int _{V} \rho [ N_{(2)} ]^{T} [ N_{(2)} ]y \,dV; \end{aligned}$$

(B.13)

$$\begin{aligned}& [m]= \int _{V} \rho \bigl( [ N_{(1)} ]^{T} [ N_{(1)} ]+ [ N_{(2)} ]^{T} [ N_{(2)} ]\bigr) \,dV =[ m_{11} ]+[ m_{22} ] , \end{aligned}$$

(B.14)

$$\begin{aligned}& \begin{aligned}[b] &\bullet \quad \int _{V} \rho \{ \delta \} _{G}^{T} [ S ] [ N ]^{T} [ \dot{R} ]^{T} [ R ] [ N ] [ S ]^{T} \{ \dot{\delta } \} _{G} \,dV \\ &\hphantom{\bullet \quad}\quad = \{ \delta \} _{G}^{T} [ S ] \biggl( \int _{V} \rho [ N ]^{T} [ \dot{R} ]^{T} [ R ] [ N ] \,dV \biggr) [ S ]^{T} \{ \dot{\delta } \} _{G} \\ &\hphantom{\bullet \quad}\quad= \omega \{ \delta \} _{G}^{T} [ S ] \biggl[ \int _{V} \rho \bigl( [ N_{(1)} ]^{T} [ N_{(2)} ] - [ N_{(2)} ]^{T} [ N_{(1)} ] \bigr) \,dV \biggr] [ S ]^{T} \{ \dot{\delta } \} _{G}\\ &\hphantom{\bullet \quad}\quad = \omega \{ \delta \} _{G}^{T} [ S ] \bigl( [ m_{12} ] - [ m_{21} ] \bigr) [ S ]^{T} \{ \dot{\delta } \} _{G};\end{aligned} \end{aligned}$$

(B.15)

$$\begin{aligned}& \begin{aligned}[b] &\bullet \quad \frac{1}{2} \int _{V} \rho \bigl( \{ \dot{\delta } \} _{G}^{T} [ S ] [ N ]^{T} [ N ] [ S ]^{T} \{ \dot{\delta } \} _{G} \bigr) \,dV \\ &\hphantom{\bullet \quad}\quad = \frac{1}{2} \{ \dot{\delta } \} _{G}^{T} [ S ] \biggl( \int _{V} \rho [ N ]^{T} [ N ] \,dV \biggr) [ S ]^{T} \{ \dot{\delta } \} _{G} = \frac{1}{2} \{ \dot{ \delta } \} _{G}^{T} [ S ] [ m ] [ S ]^{T} \{ \dot{ \delta } \} _{G}.\end{aligned} \end{aligned}$$

(B.16)

The internal energy has the classical form

$$ E_{p} = \{ \delta \} _{G}^{T} [ K_{e} ] \{ \delta \} _{G}. $$

(B.17)

The work of the concentrated and distributed external forces is

$$ \begin{aligned}[b] W^{\mathrm{ext}} &= \{ Q \} ^{T} \{ \delta \} _{G} + \biggl( \int _{V} \{ p \} _{G}^{T} [ N ]\,dV \biggr) \{ \delta \} _{G}\\ & = \biggl[ \{ Q \} ^{T} + \biggl( \int _{V} \{ p \} _{G}^{T} [ N ]\,dV \biggr) \biggr] \{ \delta \} _{G} = \bigl\{ Q^{\mathrm{ext}} \bigr\} ^{T} \{ \delta \} _{G}.\end{aligned} $$

(B.18)

The work of the liaison forces is

$$ W^{\mathrm{liaison}} = \bigl\{ Q^{\mathrm{liaison}} \bigr\} ^{T} \{ \delta \} _{G}. $$

(B.19)