1 Introduction

Mathematical modeling of the processes associated with deformations of solids with inhomogeneities in the form of inclusions or cracks is an actively studied research topic. Technological progress leads to a remarkable growth of research interest in the development and analysis of new mathematical models of mechanics describing the deformation of bodies with such inhomogeneities, as well as in the improvement of computational methods for solving them. It is well known that both inclusions and cracks in loaded solids can cause significant stress concentrations. When stress concentrations locally exceed critical values, inclusions can delaminate at some part of the interface between different materials. In addition, cracks may appear along the boundaries of inclusions under the influence of the temperature regimes of the operating environment. Analysis of problems for cracked solids is hampered by nonsmoothness of domains in which the problems are formulated. For inhomogeneous bodies with a crack along the boundary of a rigid or elastic inclusion, problems are further complicated by relations describing mechanical interaction of the inclusion and the supporting matrix. For various types of rigid inclusions and cracks, different models of composite solids with cracks subject to both linear and nonlinear boundary conditions have been under active study [1,2,3,4,5,6,7,8,9]. Other models of deformable solids can be found in [10,11,12,13].

In this paper, we follow an approach that uses inequality-type boundary conditions on the crack faces [14,15,16,17,18,19,20,21,22]. This determines the nonlinearity of boundary conditions and leads to the formulation of the problems as variational inequalities. The use of such boundary conditions, in contrast to the classical formulations of the problems of the crack theory [23, 24], does not impose an a priori known zone of contact for the crack faces. The wide range of applicability of variational methods enables successful formulation and investigation of various problems for solids with rigid or elastic inclusions, see, for example [25,26,27,28,29,30,31,32,33,34,35,36,37]. In particular, a foundational reference for two-dimensional elasticity problems with Signorini-type conditions on a part of the boundary of a thin delaminated rigid inclusion is [4]. The three-dimensional case was proposed in [22]. The papers [5, 26, 31] are devoted to optimal control problems for the shapes of cracks or rigid inclusions in elastic bodies. As for the framework of equilibrium problems, we refer to [38] with the references quoted therein.

In the present article, we investigate the connection between two different two-dimensional models describing the equilibrium of an elastic body with a rigid inclusion. Following [27], we will use the following characterizations for inclusions: the term “thin inclusion” is used when the dimension of the inclusion set is strictly less than the dimension of the body, while the term “volume inclusion” is used when the dimensions coincide. For the first model, we assume that the body contains a volume rigid inclusion described by a domain. In addition, we suppose that the body has an interfacial crack lying on a part of the inclusion boundary. The second model also describes equilibrium of an elastic body with a rigid inclusion and a crack, but unlike the first case, the inclusion is modeled as a union of a finite number of straight line segments and a curve joining these segments. The crack is given by the same curve in both models. We prove that the equilibrium problem for the first model can be viewed as the limit of problems corresponding to the second model as the number of line segments in the inclusion tends to infinity. For a suitable Sobolev space, the strong convergence of solutions of the corresponding problems is established.

2 Equilibrium problem for an elastic body with a volume rigid inclusion

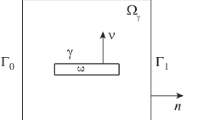
Let us formulate an equilibrium problem for an elastic body containing a volume rigid inclusion. We consider the case of the partly delaminated inclusion. In this case we have an interfacial crack passing along the inclusion boundary. In addition, we suppose that the rest of the crack can be situated inside the elastic medium. Consider a bounded domain \(\varOmega \subset \mathbf{R}^{2}\) with the boundary \(\varGamma \in C^{0,1}\). We consider a strictly inner subdomain ω of Ω (\(\overline{\omega }\subset \varOmega \)) having the shape of a curvilinear rectangle of width a:

$$ \omega =\bigl\{ (x_{1},x_{2})\mid 0< x_{1}< 1, g(x_{1})< x_{2}< g(x_{1})+a \bigr\} , \quad a>0, $$

where \(g\in C^{0,1}(0,2)\). The crack in the body is defined by the unclosed Lipschitz curve

$$ \gamma =\bigl\{ (x_{1},x_{2})\mid 0< x_{1}< 1+\lambda , x_{2}=g(x_{1})+a \bigr\} ,\quad \bar{\gamma }\subset \varOmega , -1< \lambda < 1, $$

which lies on the part of the boundary of ω (see Fig. 1). We assume that the domain Ω can be split into two subdomains \(\varOmega _{1}\) and \(\varOmega _{2}\) with Lipschitz boundaries such that \(\gamma \subset \partial \varOmega _{1}\cap \partial \varOmega _{2}\), \(\operatorname{meas}(\partial \varOmega _{i}\cap \varGamma )>0\), \(i=1,2\). This condition guarantees the validity of the Korn inequality in the non-Lipschitz domain \(\varOmega _{\gamma }=\varOmega \backslash \bar{\gamma }\). Depending on the direction of the normal \(\nu =(\nu _{1},\nu _{2})\) to γ, we will speak about a positive face \(\gamma ^{+}\) or a negative face \(\gamma ^{-}\) of the curve γ.

Figure 1
figure 1

Geometry of the cracked body with a volume rigid inclusion

Full size image

The domain ω fits a volume rigid inclusion, while the domain \(\varOmega _{\gamma }\backslash \overline{\omega }\) corresponds to an elastic part of the body.

Denote by \(W=(w_{1},w_{2})\) the displacement vector. Introduce the Sobolev spaces

$$ H^{1,0}(\varOmega _{\gamma })=\bigl\{ v\in H^{1}(\varOmega _{\gamma }) \mid v=0 \text{ on } \varGamma \bigr\} . $$

Introduce the tensors describing the deformation of the body

$$\begin{aligned}& \varepsilon _{ij}(W)=\frac{1}{2}(w_{i,j}+w_{j,i}), \quad i,j=1,2, \biggl(w_{i,j}=\frac{\partial w_{i}}{\partial x_{j}}\biggr), \\& \sigma _{ij}(W)=c_{ijkl}\varepsilon _{ij}(W), \quad i,j=1,2, \end{aligned}$$

where \(c_{ijkl}\) is the given elasticity tensor, assumed to be symmetric and positive definite:

$$\begin{aligned}& c_{ijkl}=c_{klij}=c_{jikl}, \quad i,j,k,l=1,2, c_{ijkl}=\mathit{const}., \\& c_{ijkl}\xi _{ij}\xi _{kl}\geq c_{0} \vert \xi \vert ^{2}, \quad \forall \xi , \xi _{ij}= \xi _{ji}, i,j=1,2, c_{0}=\mathit{const}., c_{0}>0. \end{aligned}$$

For further consideration, we should note that the well-known Korn inequality provides

$$ \int _{\varOmega _{\gamma }}\sigma _{ij}(W)\varepsilon _{ij}(W)\geq c \Vert W \Vert ^{2}, \quad \forall W \in {H^{1,0}(\varOmega _{\gamma })^{2}}, $$
(1)

where \(\|\cdot \|=\|\cdot \|_{H^{1}(\varOmega _{\gamma })^{2}}\), the constant \(c>0\) is independent of W [14, 39].

Remark 1

Inequality (1) yields the equivalence of the standard norm in the Sobolev space \({H^{1,0}(\varOmega _{\gamma })^{2}}\) and the semi-norm determined by the left-hand side of (1).

Due to the presence of the rigid inclusion in the body, the displacement field satisfies a special kind of relations on the corresponding domain ω. The linear space of infinitesimal rigid displacements \(R(\omega )\) is defined as follows [40]:

$$ R(\omega )=\bigl\{ \rho =(\rho _{1},\rho _{2})\mid \rho (x)=b(x_{2},-x_{1})+(c _{1},c_{2}); b,c_{1},c_{2}\in \mathbf{R}, x\in \omega \bigr\} . $$

The condition of mutual nonpenetration of opposite faces of the crack is given by [14, 40]

$$ [W]\nu \geq 0\quad \text{on } \gamma , $$

where \([W]=W|_{\gamma ^{+}}-W|_{\gamma ^{-}}\) is the jump of W on γ with two opposite crack faces \(\gamma ^{+}\) and \(\gamma ^{+}\).

In order to provide a variational formulation describing the equilibrium state for the body with the rigid inclusion ω and the crack γ, we introduce the energy functional

$$ \varPi (W)=\frac{1}{2} \int _{\varOmega _{\gamma }}\sigma _{ij}(W) \varepsilon _{ij}(W) - \int _{\varOmega _{\gamma }}FW, $$
(2)

where the vector \(F=(f_{1},f_{2})\in L^{2}(\varOmega _{\gamma })^{2}\) describes the external forces acting on the body, \(FW=f_{i} w_{i}\). Consider the minimization problem:

$$ \text{find}\quad U_{\omega }\in K\quad \text{such that } \varPi (U _{\omega })=\inf_{W\in K}\varPi (W), $$
(3)

where

$$ K=\bigl\{ W\in H^{1,0}(\varOmega _{\gamma })^{2}\mid [W]\nu \geq 0\text{ on } \gamma ; W|_{\omega }\in R(\omega )\bigr\} . $$

Problem (3) is known to have a unique solution \(U_{\omega }\in K\), which satisfies the variational inequality [40]

$$ \int _{\varOmega _{\gamma }\backslash \overline{\omega }}\sigma _{ij}( {U_{\omega }}) \varepsilon _{ij}({W}-{U_{\omega }})\geq \int _{\varOmega _{\gamma }}F(W-{U_{\omega }})\quad \forall W\in K. $$
(4)

We note that because of the structure of the displacement in the domain ω, we have \(\varepsilon _{ij}(W)=0\), \(i,j=1,2\), for all \(W\in K\). Therefore, inequality (4) can be rewritten as

$$ U_{\omega }\in K, \quad \int _{\varOmega _{\gamma }}\sigma _{ij}( {U_{\omega }}) \varepsilon _{ij}({W}-{U_{\omega }})\geq \int _{\varOmega _{\gamma }}F(W-{U_{\omega }})\quad \forall W\in K. $$
(5)

3 Family of equilibrium problems for an elastic bodies with a thin rigid inclusion

Along with the equilibrium problem (3), we will consider the following equilibrium problems for a special thin rigid inclusion. We start with a description of the geometrical properties of the inclusions’ shape. We suppose that \(Q_{n}\) is a union of line segments and a special Lipschitzian curve \(\mathcal{L}\), so that (see Fig. 2)

$$ Q_{n}=\Biggl(\bigcup_{k=1}^{k=2^{n}}l^{n}_{k} \Biggr)\cup \mathcal{L},\quad n=1,2,\ldots , $$

where \(2^{n}\) is a quantity of the following similar line segments:

$$ l^{n}_{k}=\bigl\{ (x_{1},x_{2})\mid x_{1}=k/2^{n}, g(x_{1})< x_{2}< g(x_{1})+a\bigr\} ,\quad k=1,2,\ldots2^{n}, $$

and \(\mathcal{L}\) is the curve

$$ \mathcal{L}=\bigl\{ (x_{1},x_{2})\mid 0\leq x_{1} \leq 1, x_{2}=\psi (x _{1})\bigr\} $$

defined by the function \(\psi \in C^{0,1}[0,1]\) satisfying

$$ g(x_{1})< \psi (x_{1})< g(x_{1})+a,\quad 0\leq x_{1}\leq 1. $$
Figure 2
figure 2

Geometry of the cracked body with a system of joined thin inclusions (example of \(Q_{3}\))

Full size image

Next we fix \(n\in \mathbf{N}\) and assume that the set \(Q_{n}\) fits the rigid inclusion, so that the corresponding space of infinitesimal rigid displacements has the form

$$ R(Q_{n})=\bigl\{ \rho =(\rho _{1},\rho _{2})\mid \rho (x)=b(x_{2},-x_{1})+(c _{1},c_{2}); b,c_{1},c_{2}\in \mathbf{R}, x\in Q_{n}\bigr\} . $$

A variational statement of the equilibrium problem for an elastic body with a system of joined thin rigid inclusions and a crack has the following form:

$$ \begin{gathered} \text{find}\quad U_{n}\in K_{n}\quad \text{such that } \varPi (U_{n}, \varOmega )=\inf_{W\in K_{n}}\varPi (W,\varOmega ), \\ K_{n}=\bigl\{ W\in H^{1,0}(\varOmega _{\gamma })^{2} \mid [W]\nu \geq 0 \text{ on }\gamma ; W|_{Q_{n}}\in R(Q_{n})\bigr\} . \end{gathered} $$
(6)

The existence and uniqueness of solution \(U_{n}\) of problem (6) can be proven as in the case for one delaminated inclusion, see [4]. The corresponding variational inequality takes the form

$$ U_{n}\in K_{n}, \quad \int _{\varOmega _{\gamma }}\sigma _{ij}({U} _{n})\varepsilon _{ij}({W}-{U}_{n})\geq \int _{\varOmega _{\gamma }}F(W- {U}_{n})\quad \forall W\in K_{n}. $$
(7)

4 Passage to the limit for the second model as the number of line inclusions tends to infinity

We consider the limiting case when the number of line inclusions tends to infinity, i.e., \(n\to \infty \). We want to answer the following questions:

  1. 1.

    Can we get problem (4) as a limit for the family of problems (7) depending on \(n\in \mathbf{N}\)?

  2. 2.

    Does the sequence of solutions \(\{U_{n}\}\) of problems (7) converge to \(U_{\omega }\) as \(n\to \infty \) in \(H^{1,0}(\varOmega _{\gamma })^{2}\)?

We formulate the following theorem, in the proof of which we answer the questions posed.

Theorem 1

The sequence of solutions \(\{U_{n}\}\) of problems (7) strongly converges to \(U_{\omega }\) as \(n\to \infty \) in \(H^{1,0}(\varOmega _{\gamma })^{2}\).

Proof

We first obtain a uniform estimate for the norms of solutions. We can substitute \(W=0\) for all inequalities (7), which gives

$$ \int _{\varOmega _{\gamma }}\sigma _{ij}({U}_{n})\varepsilon _{ij}( {U}_{n})\leq \int _{\varOmega _{\gamma }}F{U}_{n}\quad \forall n \in \mathbf{N}. $$
(8)

From this, using the Korn inequality, we get the following uniform estimate:

$$ \Vert U_{n} \Vert \leq C $$
(9)

for some constant C independent of n. Since \(H^{1}({\varOmega _{ \gamma }})\) is a Hilbert space, we can extract a weakly convergent subsequence (denoted as previously) \(\{U_{n}\}\) to some Ũ in \(H^{1,0}({\varOmega _{\gamma }})^{2}\).

Next we will show that \(\tilde{U}\in K\). For the traces on \(\gamma ^{+}\), \(\gamma ^{-}\), and \(Q_{m}\), by the compactness property, we have the following convergences:

$$\begin{aligned}& U_{n}\to \tilde{U} \quad \text{strongly in } L_{2}(\gamma )^{2}, \end{aligned}$$
(10)
$$\begin{aligned}& U_{n}\to \tilde{U} \quad \text{strongly in } L_{2}(Q_{m})^{2}, \end{aligned}$$
(11)

for all fixed \(m\in \mathbf{N}\). Bearing in mind the last relations, we can extract once again subsequences (retain notations) and obtain the convergences \(U_{n}|_{\gamma }\to \tilde{U}|_{\gamma }\), \(U_{n}|_{Q _{m}}\to \tilde{U}|_{Q_{m}}\) a.e. on \(\gamma ^{\pm }\) and \({Q_{m}}\). This fact allows us to pass to the limit in the following inequality:

$$ [U_{n}]\nu \geq 0\quad \text{on } \gamma \text{ as } n\to \infty . $$

This leads to \([\tilde{U}]\nu \geq 0\) on γ.

It remains to prove that \(\tilde{U}\in R(\omega )\) to show that Ũ belongs to K. For instance, we fix some natural number m. The convergence (11) allows us to conclude that each of the numerical sequences \(\{b^{n}\}\), \(\{c_{1}^{n}\}\), \(\{c_{2}^{n} \}\) defining the structure of \(\rho _{n}\) on \({Q_{m}}\) is bounded in absolute value. Thus, we can extract subsequences (retain notation) such that

$$ b^{n}\to b,\qquad c_{i}^{n}\to c_{i}, \quad i=1,2, \text{ as }n\to \infty . $$

Consequently, we have for this subsequence the convergence

$$ {U}_{n}|_{Q_{m}}\to (bx_{2}+c_{1},-bx_{1}+c_{2}) \quad \text{ a.e. on } {Q_{m}}. $$

Due to arbitrariness of m, we can see that

$$ {\tilde{U}}|_{Q_{m}}=(bx_{2}+c_{1},-bx_{1}+c_{2}) \quad \forall m \in \mathbf{N}. $$
(12)

For an arbitrary value of \(x_{s}\in (0,1)\), we consider the traces of Ũ on the line segment

$$ I_{s}=\bigl\{ (x_{1},x_{2})\mid x_{1}=x_{s}, g(x_{s})< x_{2}< g(x_{s})+a\bigr\} . $$

Since the function g is continuous, for an arbitrary positive number ϵ, there is \(\delta _{\epsilon }>0\) such that

$$ \bigl\vert g(x)-g(x_{s}) \bigr\vert < \epsilon , \quad \forall x: \vert x-x_{s} \vert \leq \delta _{\epsilon }. $$

Consider the following line segment:

$$ C_{\epsilon }=\bigl\{ (x_{1},x_{2})\mid x_{1}=x_{s}, g(x_{s})+\epsilon \leq x_{2}\leq g(x_{s})-\epsilon +a\bigr\} . $$

For sufficiently small h satisfying \(|h|<\delta _{\epsilon }\), we have the uniform estimate

$$ \bigl\Vert \tilde{U}\bigl(x^{h}\bigr)-\tilde{U}(x) \bigr\Vert _{L^{2}(C_{\epsilon })}\leq C \sqrt{ \vert h \vert } \Vert \tilde{U} \Vert , $$
(13)

where \(x^{h}(x)=x^{h}(x_{1},x_{2})=(x_{1}+h,x_{2})\) [41]. Now choosing as h the numbers of a convergent sequence \(\{h_{m}\}\) satisfying

$$\begin{aligned}& (x_{s}+h_{m},x_{2})\in Q_{m},\quad \forall x_{2} : g(x_{s}+h_{m})< x_{2}< g(x_{s}+h_{m})+a, \end{aligned}$$
(14)
$$\begin{aligned}& h_{m}\to 0 \quad \text{as } m\to \infty , \end{aligned}$$
(15)

from (12) and (13), we establish that \(\tilde{U}(x)=(bx _{2}+c_{1},-bx_{1}+c_{2})\) on \(C_{\epsilon }\). Due to arbitrariness of ϵ, the relation \(\tilde{U}(x)|_{I_{s}}=(bx_{2}+c_{1},-bx _{1}+c_{2})\) is fulfilled a.e. on each line segment \(I_{s}\), \(s\in (0,1)\). Therefore,

$$ \tilde{U}|_{\omega }=(bx_{2}+c_{1},-bx_{1}+c_{2}), $$

and Ũ belongs to the set K.

Now we fix some test function \(W\in K\), which also belongs to \(K_{n}\) for all \(n\in \mathbf{N}\). For this function we rewrite (7) as follows:

$$ U_{n}\in K_{n}, \quad \int _{\varOmega _{\gamma }}\sigma _{ij}({U} _{n})\varepsilon _{ij}({W}-{U}_{n})\geq \int _{\varOmega _{\gamma }}F(W- {U}_{n})\quad \forall n\in \mathbf{N}. $$
(16)

Next, without loss of generality, we can assume that \(\{U_{n}\}\) weakly converges to Ũ. Then we can pass to the limit in inequalities (16) as \(n\to \infty \). As a result, we obtain

$$ \int _{\varOmega _{\gamma }}\sigma _{ij}(\tilde{U})\varepsilon _{ij}( {W}-\tilde{U})\geq \int _{\varOmega _{\gamma }}F(W-\tilde{U}). $$
(17)

Taking into account that \(W\in K\) is arbitrary, and \(\tilde{U}\in K\), by uniqueness of solution to the variational inequality (4), we have that \(\tilde{U}=U_{\omega }\). By analogous arguments, it can be shown that from any subsequence of solutions \(\{U_{k}\}\subset \{U_{n}\}\) we can extract a subsequence \(\{U_{k_{n}}\}\) that weakly converges to \(U_{\omega }\) in \(H^{1,0}( \varOmega _{\gamma })^{2}\) as \(n\to \infty \). This means that the initial sequence \(\{U_{n}\}\) weakly converges to \(U_{\omega }\) in \(H^{1,0}( \varOmega _{\gamma })^{2}\) as \(n\to \infty \).

Let us prove that \(U_{n}\to U_{\omega }\) strongly in \(H^{1,0}( \varOmega _{\gamma })^{2}\) as \(n\to \infty \). Comparing two inequalities that correspond to (4) with the following test functions \(W=0\) and \(W=2U_{\omega }\), we have

$$ \int _{\varOmega _{\gamma }}\sigma _{ij}({U_{\omega }})\varepsilon _{ij}({U_{\omega }})= \int _{\varOmega _{\gamma }}F{U_{\omega }}. $$

Analogously, we get from (7)

$$ \int _{\varOmega _{\gamma }}\sigma _{ij}({U}_{n})\varepsilon _{ij}( {U}_{n})= \int _{\varOmega _{\gamma }}F{U}_{n}. $$

In virtue of the weak convergence \(U_{n}\to U_{\omega }\) in \(H^{1,0}(\varOmega _{\gamma })^{2}\) as \(n\to \infty \), the last two equations yield the following chain of equalities:

$$ \lim_{n\to \infty } \int _{\varOmega _{\gamma }}\sigma _{ij}( {U}_{n}) \varepsilon _{ij}({U}_{n})= \lim_{n\to \infty } \int _{\varOmega _{\gamma }} F{U}_{n}= \int _{\varOmega _{\gamma }}F {U_{\omega }}= \int _{\varOmega _{\gamma }}\sigma _{ij}({U_{\omega }}) \varepsilon _{ij}({U_{\omega }}). $$

Finally, recalling Remark 1, we see that these equalities provide \(\|{U}_{n}\|\to \|{U}_{\omega }\|\) as \(n\to \infty \) in \(H^{1,0}( \varOmega _{\gamma })^{2}\). This, together with the weak convergence \(U_{n}\to U_{\omega }\) in \(H^{1,0}(\varOmega _{\gamma })^{2}\), gives \(U_{n}\to U_{\omega }\) strongly in \(H^{1,0}(\varOmega _{\gamma })^{2}\) as \(n\to \infty \) as was to be shown. Theorem is proved. □

5 Conclusion

Convergence result for the solutions \(U_{n}\) of the variational problems (6) is proved. These problems correspond to the model describing the equilibrium of the elastic body with the system of the joined thin rigid inclusions. Each thin inclusion is prescribed by a curve, and the system of the joined inclusions fits the set \(Q_{n}\) being a union of curves. We prove that \(U_{n}\to U_{\omega }\) strongly in \(H^{1,0}(\varOmega _{\gamma })^{2}\) as \(n\to \infty \), where the number n is associated with the quantity of inclusions, and the limiting function \(U_{\omega }\) is the solution of problem (3) corresponding to the model with the volume rigid inclusion. The volume inclusion fits a domain in \(\mathbf{R}^{2}\). The considered problems are nonlinear due to the nonpenetration condition of inequality type on the crack γ.