Abstract
This paper is devoted to identifying an unknown source for a time-fractional diffusion equation with variable coefficients in a general bounded domain. This is an ill-posed problem. Firstly, we obtain a regularization solution by the Landweber iterative regularization method. The convergence estimates between regularization solution and exact solution are given under a priori and a posteriori regularization parameter choice rules, respectively. The convergence estimates we obtain are optimal order for any p in two parameter choice rules, i.e., it does not appear to be a saturating phenomenon. Finally, the numerical examples in the one-dimensional and two-dimensional cases show our method is feasible and effective.
Similar content being viewed by others
1 Introduction
Nowadays, the study of time-fractional diffusion equations has drawn attention from various disciplines of science and engineering, such as mechanical engineering [1, 2], viscoelasticity [3], Lévy motion [4], electron transport [5], dissipation [6], heat conduction [7–11] and high-frequency financial data [12]. A number of experiments have shown that, in the process of modeling real physical phenomena such as Brownian motion [13], fractional calculus and derivatives provide more accurate simulations than traditional calculus with integer order derivatives. Fractional derivatives have also proved to be more flexible in describing viscoelastic behavior. In particular, fractional models are believed to be more realistic in describing anomalous diffusion in heterogeneous porous media.
In recent years, people gradually find that the fractional derivative in describing the memory and genetic of material has a natural advantage. The slow diffusion can be characterized by the long-tailed profile in the spatial distribution of densities as time passes and continuous-time random walk has been applied to the underground environmental problem. Thus fractional derivatives are applied to many science fields, especially in the analytical [14–18] and numerical [19–22]. However, in practical problems, we need to retrieve the part boundary data or source term of the equation by measuring the data. This leads to the inverse problem of the fractional diffusion equation. In this respect, some work has been published. In [10], the authors studied the inverse problem for restoration of the initial data of a solution, classical in time and with values in a space of periodic spatial distributions for a time-fractional diffusion equation and diffusion-wave equation. In [23], the authors considered the problem of identifying an unknown coefficient in a nonlinear diffusion equation. In [24], the authors considered the backward inverse problem for a time-fractional diffusion equation. In [25], Liu and Yamamoto used the quasi-reversibility method to solve a backward problem for a time-fractional diffusion equation in the one-dimensional case. In [26], Murio used the mollification technique to solve source terms identification for a time-fractional diffusion equation. In [27], Wang solved a backward problem for a time-fractional diffusion equation with variable coefficients in a general bounded domain by the Tikhonov regularization method. In [28], Zhang considered an inverse source problem for a fractional diffusion equation.
In this paper, we consider the following problem:
where Ω is a bounded domain in \(\mathbb{R}^{d}\) with sufficient smooth boundary ∂Ω and \(D_{t}^{\alpha}\) is the Caputo fractional derivative of order α defined by
−L is a symmetric uniformly elliptic operator and its expression is
where the coefficient
and, for any given constant \(c>0\), we have
Denote the eigenvalues of −L by \(\lambda_{n}\). We suppose \(\lambda_{n}\) (see [29]) satisfy
and the corresponding eigenfunction \(\varphi_{n}(x)\in H^{2}(\Omega )\cap H_{0}^{1}(\Omega)\).
The source function \(f(x)\) is unknown in problem (1.1). We use the additional condition \(u(x,T)=g(x)\) to identify the unknown source \(f(x)\). In practice, measurable data \(g(x)\) are never known exactly. We assume that the exact data \(g(x)\) and the measured data \(g^{\delta}(x)\) satisfy
where \(\|\cdot\|\) is the \(L^{2}(\Omega)\) norm and \(\delta>0\) is a noise level.
If \(\alpha=1\), the equation of problem (1.1) is a standard heat conduction equation. There have been published a lot of research results (see [30–35], etc.). In this paper, we only consider \(0<\alpha<1\) for identifying the unknown source of the time-fractional diffusion equation. In [36], Zhang used a truncation method to identify the unknown source for the time-fractional diffusion equation, and in [37], Wang simplified the Tikhonov regularization method to solve it, but they consider an inverse source problem for the time-fractional diffusion equation in a regular domain. In [38], the author used the quasi-reversibility method to solved problem (1.1). However, the error estimates from [37, 38] are not optimal order, which will lead to a saturating phenomenon.
In this article, the Landweber iterative method is used to deal with the ill-posedness problem (1.1) in a general region and convergence estimates are all obtained under a priori and a posteriori choice regularization parameter rules. Moreover, convergence estimates are all optimal order according to our method. The Landweber iteration method [39], proposed by Landweber, Friedman and Bialy, is a kind of iterative algorithm for solving the operator equation \(Kx=y\).
The structure of this paper is as follows. In Section 2, some basic lemmas and results are given. In Section 3, the Landweber iterative regularization method and regularization solution are given. In Section 4, the convergence estimates under the a priori and a posteriori regularization parameter choice rules are given. In Section 5, numerical implementation and numerical examples are given. In Section 6, some conclusions as regards this paper are given.
2 Lemma and results
Definition 2.1
([40])
The Mittag-Leffler function is defined by
where \(\alpha>0\) and \(\beta\in\mathbb{R}\) are arbitrary constants.
Lemma 2.2
([41])
For the Mittag-Leffler function, we have
Lemma 2.3
([40])
Let \(\lambda>0\), that is,
where \(E_{\gamma,\beta}^{(k)}(y):=\frac{d^{k}}{dy^{k}}E_{\gamma,\beta }(y)\).
Lemma 2.3 implies that the Laplace transform of \(t^{\gamma k+\beta -1}E_{\gamma,\beta}^{(k)}(\pm at^{\gamma})\) is \(\frac{k!p^{\gamma-\beta }}{(p^{\gamma}\mp a)^{k+1}}\).
Lemma 2.4
([42])
For \(0<\alpha<1\), \(\eta>0\), we have \(0\leq E_{\alpha ,1}(-\eta)\leq1\) and \(E_{\alpha,1}(-\eta)\) is a completely monotonic function, i.e.,
Lemma 2.5
Suppose \(\lambda_{n}\) are the eigenvalues of operator −L. If \(\lambda_{n} \geq\cdots\lambda_{1}\geq0\), then there exists a positive constant \(C_{1}\) which depends on α, T, \(\lambda_{1}\) such that
where \(C_{1}(\alpha,T,\lambda_{1})=1-E_{\alpha,1}(-\lambda_{1}T^{\alpha})\).
Proof
From Lemma 2.2 and Lemma 2.4, we easily get
From Lemma 2.4, we know \(E_{\alpha,1}(-\lambda_{n}T^{\alpha})\leq E_{\alpha,1}(-\lambda_{1}T^{\alpha})\) when \(\lambda_{n} \geq\lambda _{1}\), so
where \(C_{1}(\alpha,T,\lambda_{1})=1-E_{\alpha,1}(-\lambda_{1}T^{\alpha})\). □
3 Regularization method
where \((\cdot,\cdot)\) is the inner product in \(L^{2}(\Omega)\) and \(D((-L)^{\gamma})\) is a Hilbert space with the norm
Now using separation of variables and Lemma 2.3, we get the solution of problem (1.1) as follows:
Denote \(f_{n}=(f(x),\varphi_{n}(x))\), \(g_{n}=(g(x),\varphi_{n}(x))\) and let \(t=T\). Then
and
Hence we obtain
and
Using Lemma 2.5, we have
Consequently,
Small errors in the high-frequency components for \(g^{\delta}(x)\) will be amplified by \(\frac{1}{T^{\alpha}E_{\alpha,1+\alpha}(-\lambda _{n}T^{\alpha})}\), so problem (1.1) is ill-posed. We must use the regularization method to solve it. We first impose the a priori bound for the exact solution \(f(x)\) as follows:
where E is the positive constant.
A conditional stability estimate of the inverse source problem (1.1) is given below.
Theorem 3.1
([27])
If \(\|f(x)\|_{D((-L)^{\frac{p}{2}})}\leq E\), then
where \(C_{2}:=C_{1}^{-\frac{p}{p+2}}\) is a constant.
To find \(f(x)\), we need to solve the following integral equation:
For \(k(x,\xi)=k(\xi,x)\), K is a self-adjoint operator. From Theorem 2.4 of [29], if \(f\in L^{2}(\Omega)\), then \(g\in H^{2}(\Omega)\). Because \(H^{2}(\Omega)\) compacts embedding \(L^{2}(\Omega)\), we know \(K:L^{2}(\Omega)\rightarrow L^{2}(\Omega)\) is compact operator.
For \(\varphi_{n}(x)\) being an orthonormal basis in \(L^{2}(\Omega)\),
are singular values of K and \(\varphi_{n}\) is the corresponding eigenvector.
Now, we use the Landweber iterative method to obtain the regularization solution for (1.1). We rewrite the equation \(Kf=g\) in the form \(f=(I-aK^{*}K)f+aK^{*}g\) for some \(a>0\) and give the following iterative form:
where m is the iterative step number, which is also the selected regularization parameter. a is called the relaxation factor and satisfies \(0< a<\frac{1}{\|K\|^{2}}\). For K is a self-adjoint operator, we obtain
Using (3.12), we get
where \(g_{n}^{\delta}=(g^{\delta}(x),\varphi_{n}(x))\).
Because \(\sigma_{n}=T^{\alpha}E_{\alpha,1+\alpha}(-\lambda _{n}T^{\alpha})\) are singular values of K and \(0< a<\frac{1}{\|K\| ^{2}}\), we can easily see \(0< aT^{2\alpha}E_{\alpha,1+\alpha }^{2}(-\lambda_{n}T^{\alpha})<1\).
4 Error estimate under two parameter choice rules
In this section, we will give error estimates under the a priori choice rule and the a posteriori choice rule.
-
An a priori choice rule
Theorem 4.1
Let \(f(x)\), given by (3.6), be the exact solution of problem (1.1). Let \(f^{m,\delta}(x)\) be the regularization solution. Let conditions (1.5) and (3.9) hold. If we choose regularization parameter \(m=[b]\), where
then we have the following error estimate:
where \([b]\) denotes the largest integer less than or equal to b and \(C_{3}=\sqrt{a}+(\frac{p}{aC_{1}^{2}})^{\frac{p}{4}}\) is constant.
Proof
Using the triangle inequality, we have
Using conditions (1.5), we get
where \(A(n):=\frac{1-(1-aT^{2\alpha}E_{\alpha,1+\alpha}^{2}(-\lambda _{n}T^{\alpha}))^{m}}{T^{\alpha}E_{\alpha,1+\alpha}(-\lambda _{n}T^{\alpha})}\).
Because \(0< x<1\), we have
and
Using (4.3) and (4.4), we obtain
i.e.,
so
On the other hand, using (3.9), we get
where \(B(n):=(1-aT^{2\alpha}E_{\alpha,1+\alpha}^{2}(-\lambda _{n}T^{\alpha}))^{m}(\lambda_{n})^{-\frac{p}{2}}\).
Using Lemma 2.5, we have
Let
Let \(s_{0}\) satisfy \(F'(s_{0})=0\). Then we easily get
so
i.e.,
Thus we obtain
Hence
Combining (4.7) and (4.14), we choose \(m=[b]\) and we get
where \(C_{3}:=\sqrt{a}+(\frac{p}{aC_{1}^{2}})^{\frac{p}{4}}\). The theorem is proved. □
-
An a posteriori selection rule
We construct regularization solution sequences \(f^{m,\delta}(x)\) by the Landweber iterative method. Let \(r>1\) be a fixed constant. Stop the algorithm at the first occurrence of \(m=m(\delta)\in\mathbb{N}_{0}\) with
where \(\|g^{\delta}\|\geq r\delta\).
Lemma 4.2
Let \(\rho(m)=\|Kf^{m,\delta}(\cdot)-g^{\delta}(\cdot)\|\). Then we have the following conclusions:
-
(a)
\(\rho(m)\) is a continuous function;
-
(b)
\(\lim_{m\rightarrow0}\rho(m)=\|g^{\delta}\|\);
-
(c)
\(\lim_{m\rightarrow+\infty}\rho(m)=0\);
-
(d)
\(\rho(m)\) is a strictly decreasing function, for any \(m\in(0,+\infty)\).
Lemma 4.2 shows that there exists a unique solution for inequality (4.16).
Lemma 4.3
Let (4.16) hold, so the regularization parameter m satisfies
Proof
From (3.15), we show the representation
for every \(g\in H^{2}(\Omega)\), so
Because \(|1-aT^{2\alpha}E_{\alpha,1+\alpha}^{2}(-\lambda_{n}T^{\alpha })|<1\), we obtain \(\|KR_{m-1}-I\|\leq1\). Using (4.16), we obtain
On the other hand, using (3.9), we obtain
Let
so
Using Lemma 2.5, we have
Let
Suppose \(s_{\ast}\) satisfies \(G'(s_{\ast})=0\). Then we get
so
Using (4.21) and (4.25), we get
Thus
□
Theorem 4.4
Let \(f(x)\), given by (3.6), be the exact solution of problem (1.1). Let \(f^{m,\delta}(x)\) be the regularization solution. The conditions (1.5) and (3.10) hold and the regularization parameter is given by (4.16). Then we have the following error estimate:
where \(C_{4}=(\frac{p+2}{2C_{1}^{2}})^{\frac{1}{2}}(\frac {1}{r-1})^{\frac{2}{p+2}}\).
Proof
Using the triangle inequality, we obtain
Using (4.7) and Lemma 4.3, we get
where \(C_{4}:=(\frac{p+2}{2C_{1}^{2}})^{\frac{1}{2}}(\frac {1}{r-1})^{\frac{2}{p+2}}\).
For the second part of the right side of (4.28), we know
Using (1.5) and (4.16), we have
We also have
Using Theorem 3.1, we have
Therefore
□
5 Numerical implementation and numerical examples
In this section, we will use several numerical examples to show effectiveness of the Landweber iterative method.
5.1 One-dimensional case
Since the exact solution of problem (1.1) is difficult to give, we get the data function \(g(x)\) by solving the following direct problem:
When the source function \(f(x)\) is given, we use the finite difference method to obtain data function \(g(x)\).
The time and space step size of the grid are \(\Delta t=\frac{T}{N}\) and \(\Delta x=\frac{1}{M}\), respectively. \(t_{n}=n\Delta t\), \(n=0,1,2,\ldots,N\), indicates grid points on time interval \([0,T]\) and \(x_{i}=i\Delta x\), \(i=0,1,2,\ldots,M\), is the grid point of space interval \([0,1]\). The value of each grid point is denoted by \(u_{i}^{n}=u(x_{i}, t_{n})\).
The following time-fractional differential is given in [18, 19]:
where \(i=1,\ldots,M-1\), \(n=1,\ldots,N\) and \(b_{j}=(j+1)^{1-\alpha}-j^{1-\alpha}\).
The spatial derivative difference scheme is given as follows [27]:
where \(a_{i+\frac{1}{2}}=a(x_{i+\frac{1}{2}})\), \(x_{i+\frac{1}{2}}=\frac {x_{i}+x_{i+1}}{2}\).
For the inverse problem, we need to obtain a matrix K such that \(Kf=u_{i}^{N}\). In order to obtain it, we use the same method as in [27], that is,
where \(h:=\frac{(\Delta t)^{-\alpha}}{\Gamma(2-\alpha)}\),
and
where \(d_{i}=\frac{1}{(\Delta x)^{2}}(a_{i+\frac {1}{2}}+a_{i-\frac{1}{2}})-c(x_{i})+h\), \(i=1,\ldots, M-1\). Then we obtain the regularization solution by
Noise data are generated by adding random perturbation, i.e.,
The relative error level and absolute error level are computed by
5.2 Two-dimensional case
Let \(\Omega=(0,l_{1})\times(0,l_{2})\) be a rectangle domain. Consider the following time-fractional diffusion equation:
Let \(x_{i}=i \Delta x\), \(i=0,1,\ldots,M_{1}\); \(y_{j}=j \Delta y\), \(j=0,1,\ldots,M_{2}\); \(t_{n}=n\Delta t\), \(n=0,1,\ldots,N\), where \(\Delta x=\frac{l_{1}}{M_{1}}\), \(\Delta y=\frac{l_{2}}{M_{2}}\) and \(\Delta t=\frac{T}{N}\) are space and time steps, respectively. The approximate values of each grid point u are denoted by \(u_{i,j}^{n}\approx u(x_{i},y_{j},t_{n})\). Thus, we use initial and boundary conditions of equation (5.6) to get \(u_{i,j}^{0}=0\), \(u_{0,j}^{n}=u_{M_{1},j}^{n}=0\), \(u_{i,0}^{n}=u_{i,M_{2}}^{n}=0\).
Let the integer order derivative difference scheme be given as follows:
It is easy to obtain the numerical solution of \(u(x,y,T)=g(x,y)\) by the scheme
where \(p_{x}=\frac{1}{(\Delta x)^{2}}\), \(p_{y}=\frac{1}{(\Delta y)^{2}}\) and h and \(b_{k}\) are defined in the one-dimensional case.
Denote \(U^{n}=(u_{1,1}^{n},\ldots,u_{M_{1}-1,1}^{n},u_{1,2}^{n},\ldots ,u_{M_{1}-1,2}^{n}, \ldots,u_{1,M_{2}-1}^{n},\ldots,u_{M_{1}-1,M_{2}-1}^{n})\) and \(f=(f_{1,1},\ldots, f_{M_{1}-1,1},f_{1,2},\ldots,f_{M_{1}-1,2},\ldots ,f_{1,M_{2}-1},\ldots,f_{M_{1}-1,M_{2}-1})\). Then we obtain the following iterative scheme:
where \(\omega_{i}=b_{i-1}-b_{i}\) and
where I is the unit matrix with order \((M_{1}-1)\times(M_{1}-1)\).
For the inverse problem, we can obtain a matrix \(\mathcal{K}\) such that \(\mathcal{K}f=u_{i,j}^{N}\) by
We take \(g^{\delta}\) as noise data by adding a random perturbation, i.e.,
Then we obtain the regularization solution in the two-dimensional case by
For practical problems, the a priori bound is very difficult to obtain. We only give numerical effectiveness under the a posteriori regularization parameter choice rule. The iterative steps are given to solve (4.16) with \(r=1.1\).
In the one-dimensional computational procedure, we choose \(T=1\). Let \(\Omega=(0,1)\), \(a(x)=x^{2}+1\) and \(c(x)=-(x+1)\). We use the algorithm in [44] to compute the Mittag-Leffler function. In discrete format, we compute the direct problem with \(M=100\), \(N=200\) and we choose \(M=50\), \(N=100\) for solving the inverse problem.
Example 1
Take the smooth function \(f(x)=x^{\alpha }(1-x)^{\alpha}\sin(2\pi x)\).
Example 2
We take the piecewise smooth function
Figure 1 shows the comparisons between the exact solution and its regularized solution for various noise levels \(\varepsilon=0.05,0.01,0.001\) in the case of \(\alpha=0.2,0.5,0.9\). The iterative step \(m=41\text{,}336, 94\text{,}936, 1\text{,}040\text{,}301\) for \(\alpha=0.2\), in the case of \(\alpha=0.5\), \(m=61\text{,}244, 235\text{,}887,167\text{,}709\) and \(m=80\text{,}991, 219\text{,}401,2\text{,}248\text{,}377\) for \(\alpha=0.9\).
The comparison of numerical effects between the exact solution and its regularized solution for Example 1 .
Example 3
Consider the following discontinuous function:
Figure 2 shows the comparison between the exact solution and its regularized solution for various noise levels \(\varepsilon=0.05,0.01,0.001\) in the case of \(\alpha=0.2,0.5,0.9\). The iterative step \(m=46\text{,}890,213\text{,}120,902\text{,}941\) for \(\alpha=0.2\), in the case of \(\alpha=0.5\), \(m=48\text{,}184,248\text{,}462,1\text{,}514\text{,}062\) and \(m=47\text{,}244, 182\text{,}142, 1\text{,}782\text{,}127\) for \(\alpha=0.9\).
The comparison of numerical effects between the exact solution and its regularized solution for Example 2 .
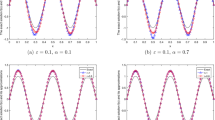
Figure 3 shows the comparison between the exact solution and its regularized solution for various noise levels \(\varepsilon =0.05,0.01,0.001\) in the case of \(\alpha=0.2,0.5,0.9\). The iterative step \(m=293\text{,}388, 3\text{,}111\text{,}053, 70\text{,}256\text{,}177\) for \(\alpha=0.2\), in the case of \(\alpha=0.5\), \(m=289\text{,}029, 3\text{,}059\text{,}035, 69\text{,}693\text{,}245 \) and \(m=446\text{,}047, 2\text{,}986\text{,}943, 69\text{,}181\text{,}622\) for \(\alpha=0.9\).
The comparison of numerical effects between the exact solution and its regularized solution for Example 3 .
In Figures 1-3, we see that the smaller ε and α, the better the regularized solution is. Moreover, we see that the a posteriori parameter choice also works well.
Example 4
Take source function \(f(x,y)=xy\).
In Example 4, we take \(T=0.5\), \(M_{1}=M_{2}=25\), \(N=50\) and \(l_{1}=l_{2}=1\). Figure 4 shows the comparison between the exact solution and its regularized solution for various noise levels \(\varepsilon=0.01,0.001\) in the case of \(\alpha =0.2\). The iterative step \(m=443\text{,}531\) for \(\varepsilon=0.01\), \(m=6\text{,}572\text{,}432\) when the error level \(\varepsilon=0.001\).
The comparison of numerical effects between the exact solution and its regularized solution for Example 4 .
Example 5
Take source function \(f(x,y)=\sin(x)\sin(y)+\sin(2x)\sin(2y)\).
In Example 5, we take \(T=1\), \(M_{1}=M_{2}=40\), \(N=60\) and \(l_{1}=l_{2}=\pi \). Figure 5 shows the comparison between the exact solution and its regularized solution for various noise levels \(\varepsilon=0.01,0.001\) in the case of \(\alpha =0.5\). The iterative step \(m=354\) for \(\varepsilon=0.01\), \(m=538\) when error level \(\varepsilon=0.001\).
The comparison of numerical effects between the exact solution and its regularized solution for Example 5 .
In Figure 4 and Figure 5, we see that the numerical results are in good agreement with the exact shape. We see that the smaller ε, the better the computed approximation is.
6 Conclusion
In this paper, we consider an inverse problem for identifying an unknown source for a time-fractional diffusion equation with variable coefficients defined in a general domain. This problem is ill-posed, i.e., the solution (if it exists) does not depend continuous on the data. The Landweber regularization is first used to solve this problem. Moreover, under two regularization parameter choice rules, we obtain Hölder type error estimates. Especially, the a posteriori regularization parameter choice is selected. In [37], the authors used two regularization methods to identify the spatial variable source for the time-fraction diffusion equation. In [38], the authors used quasi-reversibility regularization methods to identify the spatial variable source for the time-fraction diffusion equation. From [37], under the a priori regularization parameter choice rule, the authors found the orders of error estimate convergence are \(\mathcal{O}(\delta^{\frac{p}{p+2}})\) (\(0< p\leq4\)) and \(\mathcal{O}(\delta^{\frac{2}{3}})\) (\(p>4\)) and under the a posteriori regularization parameter choice rule, the authors found the orders of error estimate convergence are \(\mathcal{O}(\delta^{\frac {p}{p+2}})\) (\(0< p\leq2\)) and \(\mathcal{O}(\delta^{\frac{2}{3}})\) (\(p>2\)). In [38], under the a priori and a posteriori regularization parameter choice rules, the authors found the orders of error estimate convergence are \(\mathcal{O}(\delta^{\frac {p}{p+2}})\) (\(0< p\leq2\)) and \(\mathcal{O}(\delta^{\frac{2}{3}})\) (\(p>2\)), but in our paper, under the a priori and a posteriori regularization parameter choice rules, we found the order of error estimate convergence is \(\mathcal{O}(\delta^{\frac{p}{p+2}})\). Comparing references [37, 38], under the a posteriori regularization parameter choice, as \(p>2\), the authors found the error estimate convergence is \(\mathcal{O}(\delta^{\frac{1}{2}})\) (\(p>2\)), which is a saturating phenomenon, i.e., if we add the smoothness of the solution, the error estimate order does not improve. In our method, the error estimate convergence is \(\mathcal{O}(\delta^{\frac {p}{p+2}})\), which does not appear to be a saturating phenomenon. Finally, three numerical results show that the Landweber iterative method is very effective for this kind of ill-posed problems.
References
Chen, W, Ye, LJ, Sun, HG: Fractional diffusion equations by the Kansa method. Comput. Math. Appl. 59, 1614-1620 (2010)
Agarwal, RP, Asma, Lupulescu, V, O’Regan, D: Fractional semilinear equations with causal operators. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 111, 257-269 (2017)
Yu, Z, Lin, J: Numerical research on the coherent structure in the viscoelastic second-order mixing layers. Appl. Math. Mech. 19, 671-677 (1998)
Laskin, N, Lambadaris, I, Harmantzis, FC, Devetsikiotis, M: Fractional Lévy motion and its application to network traffic modeling. Comput. Netw. 40(3), 363-375 (2002)
Scher, H, Montroll, EW: Anomalous transit-time dispersion in amorphous. Phys. Rev. B 12(6), 2455-2477 (1975)
Szabo, TL, Wu, J: A model for longitudinal and shear wave propagation in viscoelastic media. J. Acoust. Soc. Am. 107(5), 2437-2446 (2000)
Gorenflo, R, Mainardi, F, Moretti, D, Pagnini, G, Paradisi, P: Discrete random walk models for space-time fractional diffusion. Chem. Phys. 284, 521-541 (2002)
Metzler, R, Klafter, J: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339, 1-77 (2000)
Sokolov, IM, Klafter, J, Blumen, A: Fractional kinetics. Phys. Today 55, 48-54 (2002)
Lopushanska, H, Lopushansky, A, Myaus, O: Inverse problems of periodic spatial distributions for a time fractional diffusion equation. Electron. J. Differ. Equ. 2016, 14 (2016)
Nemat, D: Numerical study of entropy generation for forced convection flow and heat transfer of a Jeffrey fluid over a stretching sheet. Alex. Eng. J. 53, 769-778 (2014)
Mendes, RV: A fractional calculus interpretation of the fractional volatility model. Nonlinear Dyn. 55, 395-399 (2009)
Muhammad, MB, Tehseen, A, Mohammad, MR: Entropy generation as a practical tool of optimisation for non-Newtonian nanofluid flow through a permeable stretching surface using SLM. J. Comput. Des. Eng. 4, 21-28 (2017)
Wyss, W: The fractional diffusion equation. J. Math. Phys. 27(11), 2782-2785 (1986)
Schneider, WR, Wyss, W: Fractional diffusion and wave equations. J. Math. Phys. 30(1), 134-144 (1989)
Agrawal, OP: Solution for a fractional diffusion-wave equation defined in a bounded domain. Nonlinear Dyn. 29(1), 145-155 (2002)
Murio, DA: Time fractional IHCP with Caputo fractional derivatives. Comput. Math. Appl. 56(9), 2371-2381 (2008)
Murio, DA: Implicit finite difference approximation for time-fractional diffusion equations. Comput. Math. Appl. 56(4), 1138-1145 (2008)
Zhuang, P, Liu, F: Implicit difference approximation for the time fractional diffusion equation. J. Appl. Math. Comput. 22(3), 87-99 (2006)
Zhang, H, Liu, FW, Anh, V: Galerkin finite element approximation of symmetric space-fractional partial differential equations. Appl. Math. Comput. 217(6), 2534-2545 (2010)
Li, XJ, Xu, CJ: Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and spectral method approximation. Commun. Comput. Phys. 8(5), 1016-1051 (2010)
Fulger, D, Scalas, E, Germano, G: Monte Carlo simulation of uncoupled continuous-time random walks yielding a stochastic solution of the space-time fractional diffusion equation. Phys. Rev. E 77(2), 021122 (2008)
Tatar, S, Ulusoy, S: An inverse coefficient problem for a nonlinear reaction diffusion equation with a nonlinear source. Electron. J. Differ. Equ. 2015, 245 (2015)
Tuan, NH, Kirane, M, Luu, VCH, Bin-Mohsin, B: A regularization method for time-fractional linear inverse diffusion problems. Electron. J. Differ. Equ. 2016, 290 (2016)
Liu, JJ, Yamamoto, M: A backward problem for the time-fractional diffusion equation. Appl. Anal. 89(11), 1769-1788 (2010)
Murio, DA, Mejía, CE: Source terms identification for time fractional diffusion equation. Rev. Colomb. Mat. 42(1), 25-46 (2008)
Wang, JG, Wei, T, Zhou, YB: Tikhonov regularization method for a backward problem for the time-fractional diffusion equation. Appl. Math. Model. 37(18), 8518-8532 (2013)
Zhang, Y, Xu, X: Inverse source problem for a fractional diffusion equation. Inverse Probl. 27(3), 035010 (2011)
Sakamoto, K, Yamamoto, M: Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 382(1), 426-447 (2011)
Yang, F, Fu, CL: A simplified Tikhonov regularization method for determining the heat source. Appl. Math. Model. 34(11), 3286-3299 (2010)
Dou, FF, Fu, CL: Determining an unknown source in the heat equation by a wavelet dual least squares method. Appl. Math. Lett. 22, 661-667 (2009)
Farcas, A, Lesnic, D: The boundary-element method for the determination of a heat source dependent on one variable. J. Eng. Math. 54, 375-388 (2006)
Johansson, T, Lesnic, D: Determination of a spacewise dependent heat source. J. Comput. Appl. Math. 20, 966-980 (2007)
Liu, CH: A two-stage LGSM to identify time-dependent heat source through an internal measurement of temperature. Int. J. Heat Mass Transf. 52, 1635-1642 (2009)
Dou, FF, Fu, CL, Yang, FL: Optimal error bound and Fourier regularization for identifying an unknown source in the hear equation. J. Comput. Appl. Math. 230, 728-737 (2009)
Zhang, ZQ, Wei, T: Identifying an unknown source in time-fractional diffusion equation by a truncation method. Appl. Math. Comput. 219(11), 5972-5983 (2013)
Wang, JG, Zhou, YB, Wei, T: Two regularization methods to identify a space-dependent source for the time-fractional diffusion equation. Appl. Numer. Math. 68, 39-57 (2013)
Wang, JG, Wei, T: Quasi-reversibility method to identify a space-dependent source for the time-fractional diffusion equation. Appl. Math. Model. 39, 6139-6149 (2015)
Landweber, L: An iteration formula for Fredholm integral equations of the first kind. Am. J. Math. 73(3), 615-624 (1951)
Podlubny, I: Fractional Differential Equations. Academic Press, San Diego (1999)
Haubold, HJ, Mathai, AM, Saxena, RK: Mittag-Leffler functions and their applications. J. Appl. Math. 2011, Article ID 298628 (2011)
Pollard, H: The completely monotonic character of the Mittag-Leffler function \(E_{\alpha}(-x)\). Bull. Am. Math. Soc. 54, 1115-1116 (1948)
Wei, T, Wang, JG: A modified quasi-boundary value method for the backward time-fractional diffusion problem. ESAIM: Math. Model. Numer. Anal. 48(2), 603-621 (2014)
Podlubny, I, Kaccenak, M: Mittag-Leffler function. The matlab routine (2006). http://www.mathworks.com/matlabcentral/fileexchange
Acknowledgements
The authors would like to thanks the editor and the referees for their valuable comments and suggestions, that improved the quality of our paper.
Availability of data and materials
Not applicable.
Funding
The work is supported by the National Natural Science Foundation of China (11561045, 11501272) and the Doctor Fund of Lan Zhou University of Technology.
Author information
Authors and Affiliations
Contributions
The main idea of this paper was proposed by FY. Y-PR prepared the manuscript initially and performed all the steps of the proofs in this research. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Abbreviations
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yang, F., Ren, YP., Li, XX. et al. Landweber iterative method for identifying a space-dependent source for the time-fractional diffusion equation. Bound Value Probl 2017, 163 (2017). https://doi.org/10.1186/s13661-017-0898-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-017-0898-2