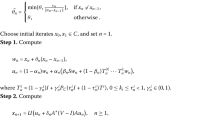Modified Krasnoselski–Mann iterative method for hierarchical fixed point problem and split mixed equilibrium problem

Abstract

In this paper, we introduce a modified Krasnoselski–Mann type iterative method for capturing a common solution of a split mixed equilibrium problem and a hierarchical fixed point problem of a finite collection of k-strictly pseudocontractive nonself-mappings. Many of the algorithms for solving the split mixed equilibrium problem involve a step size which depends on the norm of a bounded linear operator. Since the computation of the operator norm is very difficult, we formulate our iterative algorithm in such a way that the implementation of the proposed algorithm does not require any prior knowledge of operator norm. Weak convergence results are established under mild conditions. We also establish strong convergence results for a certain class of hierarchical fixed point and split equilibrium problem. Our results generalize some important results in the recent literature.

1 Introduction

Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces with inner product $\langle \cdot ,\cdot \rangle$ and norm $\|\cdot \|$. Let C and D be two nonempty closed and convex subsets of $H_{1}$ and $H_{2}$, respectively. A nonself-mapping $T:C\mapsto H_{1}$ is said to be k-strictly pseudocontractive if there exists a constant $k\in [0,1)$ such that

$$ \Vert Tx-Ty \Vert ^{2}\leq \Vert x-y \Vert ^{2}+k \bigl\Vert (I-T)x-(I-T)y \bigr\Vert ^{2},\quad \forall x,y \in H_{1}. $$

If $k=0$, then T is a nonexpansive nonself-mapping.

For a mapping $T:C\mapsto H_{1}$, the fixed point problem is to find $x\in C$ such that $x=Tx$. The set of all fixed points of T is denoted by $\operatorname{Fix}(T)$.

Moudafi and Mainge [24] considered the following hierarchical fixed point problem (in short, HFPP) for a nonexpansive self-mapping T with respect to another nonexpansive self-mapping S on C in the following way: Find $x^{*}\in \operatorname{Fix}(T)$ such that

$$ \bigl\langle x^{*}-Sx^{*},x^{*}-x \bigr\rangle \leq 0, \quad \forall x\in \operatorname{Fix}(T). $$

(1.1)

Let us denote the solution set of the HFPP (1.1) as $\mathcal{S}=\{x^{*} \in \operatorname{Fix}(T):\langle x^{*}-Sx^{*},x^{*}-x\rangle \leq 0, \forall x\in \operatorname{Fix}(T)\}$.

We can check that $x^{*}$ is a solution of the HFPP (1.1) if and only if $x^{*}=P_{\operatorname{Fix}(T)}\circ Sx^{*}$, where $P_{\operatorname{Fix}(T)}$ is the metric projection of $H_{1}$ onto $\operatorname{Fix}(T)$.

By using the definition of the normal cone to $\operatorname{Fix}(T)$, i.e.,

$$ N_{\operatorname{Fix}(T)}= \textstyle\begin{cases} \{u\in H_{1}:\langle y-x,u\rangle \leq 0, \forall y\in \operatorname{Fix}(T) \}, &\text{if } x\in \operatorname{Fix}(T), \\ \emptyset ,& \text{otherwise}, \end{cases} $$

(1.2)

we can easily prove that HFPP (1.1) is equivalent to the variational inclusion

$$ 0\in (I-S)x^{*}+N_{\operatorname{Fix}(T)}x^{*}. $$

We note that based on the relation $x^{*}=P_{\operatorname{Fix}(T)}\circ Sx^{*}$, HFPP (1.1) has an iterative algorithm $x_{n+1}=P_{\operatorname{Fix}(T)}\circ Sx_{n}$. This iterative method converges if the mapping $P_{\operatorname{Fix}(T)}\circ S$ has a fixed point and S is averaged not just nonexpansive. Disadvantage of this method is that the calculation of $P_{\operatorname{Fix}(T)}\circ S$ is usually not easy. To overcome this, Moudafi [22] introduced an algorithm which uses T itself, rather than $P_{\operatorname{Fix}(T)}\circ S$. Moudafi introduced the iterative method in the following way: For starting point $x_{0}\in C$, define $\{x_{n}\}$ by

$$ x_{n+1}=(1-\alpha _{n})x_{n}+ \alpha _{n}\bigl(\sigma _{n}Sx_{n}+(1- \sigma _{n})Tx_{n}\bigr), $$

(1.3)

where $\{\alpha _{n}\}$ and $\{\sigma _{n}\}$ are two real sequences in $(0,1)$.

Problems (1.1) are often used in the area of optimization and related fields, such as signal processing and image reconstruction (see [4, 6, 11, 14–20, 25, 27–30, 32–36] and the references therein).

On the other hand, for a bifunction $F:C\times C\rightarrow \mathbb{R}$, an equilibrium problem is defined by

$$ \text{find } x \in C \text{ such that } F(x,y)\geq 0,\quad \text{for all } y\in C. $$

The solution set of this problem is denoted as $\operatorname{EP}(F,C)$. Equilibrium problem includes variational inequality problem, optimization problem, the Nash equilibrium problem, saddle point problem, complementarity problem, convex differential optimization etc. as special cases (see Blum and Oettli [1]).

In 2009, Marino et al. [21] introduced an iterative method to find common solutions of the following system of equilibrium problem and hierarchical fixed point problem:

$$ \textstyle\begin{cases} \text{find } x^{*} \in C \text{ such that } F(x^{*},y) \geq 0,\quad \forall y\in C;\quad \text{and} \\ x^{*} \in \operatorname{Fix}(T) \text{ such that } \langle x^{*}-f(x^{*}),x^{*}-y \rangle \leq 0, \quad \forall y\in \operatorname{Fix}(T), \end{cases} $$

(1.4)

where F is a bifunction, f is a ρ-contraction and T is a nonexpansive self-mapping.

In 2011, Moudafi [23] introduced and studied the following split equilibrium problem S_pEP: Suppose $F_{1}:C\times C\rightarrow \mathbb{R}$ and $F_{2}: D\times D \rightarrow \mathbb{R}$ are two bifunctions and $A:H_{1}\rightarrow H_{2}$ is a bounded linear operator. Then the split equilibrium problem is to find $x^{*}\in C$ such that

$$ F_{1}\bigl(x^{*},x\bigr)\geq 0,\quad \forall x\in C. $$

(1.5)

and $y^{*}=Ax^{*}\in D$ solves

$$ F_{2}\bigl(y^{*},y\bigr)\geq 0,\quad \forall y\in D. $$

(1.6)

In 2012, Censor et al. [7] introduced and studied the following split variational inequality problem S_pVIP: Find $x^{*}\in C$ such that

$$ \bigl\langle g_{1}\bigl(x^{*} \bigr),y-x^{*}\bigr\rangle \geq 0, \quad \forall x\in C, $$

(1.7)

and $y^{*}=Ax^{*}\in Q$ solves

$$ \bigl\langle g_{2}\bigl(x^{*} \bigr),y-x^{*}\bigr\rangle \geq 0, \quad \forall y\in D, $$

(1.8)

where $g_{1}:C\rightarrow H_{1}$ and $g_{2}:D\rightarrow H_{2}$ are two nonlinear mappings, and $A:H_{1}\rightarrow H_{2}$ is a bounded linear operator.

Very recently, Kazmi et al. [13] have introduced and analyzed a Krasnoselski–Mann iteration method for finding a common solution of HFPP (1.1) and the following split mixed equilibrium problem S_pMEP: Find $x^{*}\in C$ such that

$$ F_{1}\bigl(x^{*},x\bigr)+\bigl\langle g_{1}\bigl(x^{*}\bigr),y-x^{*}\bigr\rangle \geq 0,\quad \forall x \in C, $$

(1.9)

and $y^{*}=Ax^{*}\in Q$ solves

$$ F_{2}\bigl(y^{*},y\bigr)+\bigl\langle g_{2}\bigl(x^{*}\bigr),y-x^{*}\bigr\rangle \geq 0,\quad \forall y \in D. $$

(1.10)

The solution set of S_pMEP is denoted by $\Gamma =\{p\in \operatorname{MEP}(F_{1}, g_{1}) : Ap \in \operatorname{MEP}(F_{2}, g_{2})\}$. To solve the S_pMEP (1.9)–(1.10) and HFPP (1.1), Kazmi et al. [13] introduced the following algorithm: For the starting point $x_{0}\in C$, define $\{x_{n}\}$ by

$$ \textstyle\begin{cases} u_{n}=(1-\alpha _{n})x_{n}+\alpha _{n}(\sigma _{n}Sx_{n}+(1- \sigma )Tx_{n}), \\ x_{n+1}=U(u_{n}+\gamma A^{*}(V-I)Au_{n} ),\quad n\geq 1, \end{cases} $$

(1.11)

where S, T are nonexpansive self-mappings on C and the step size $\gamma \in (0, \frac{1}{L})$, L is the spectral radius of the operator $A^{*}A$ and $A^{*}$ is the adjoint of the bounded linear operator A.

Motivated by the above results, we revisit the problem considered by Kazmi et al. [13]. We introduce and analyze a modified Krasnoselski–Mann type iterative method with the help of averaged mappings for finding a common solution of the HFPP (1.1) of a finite collection of k-strictly pseudocontractive non-self-mappings and S_pMEP (1.9)–(1.10). Our work can be seen as an extension of HFPP (1.1) [13, 22] from single nonexpansive self-mapping to a finite collection of k-strictly pseudocontractive nonself-mappings. The authors in [10, 13] have selected the step size γ in the interval $(0,\frac{1}{L})$, where L is the spectral radius of the operator $A^{*}A$ and $A^{*}$ is the adjoint of the bounded linear operator A.

It is well known that the computation or an estimate of the spectral radius of a given operator is very difficult at times. This makes the implementation of the proposed algorithm very difficult. In our iterative method, we give an explicit formula to choose the step size, which does not require any prior knowledge of operator norm. We also establish strong convergence results for a certain class of hierarchical fixed point and split equilibrium problem.

We organize the paper in the following way. Some basic definitions and lemmas are given in Sect. 2. In Sect. 3, we present our modified iterative methods for a split mixed equilibrium problem and hierarchical fixed point problem. Finally, we make some remarks to highlight the main contribution of this paper.

2 Preliminaries

In order to prove our main results, we recall some basic definitions and lemmas, which will be needed in the sequel. Let $H_{1}$ be a real Hilbert space and C be a nonempty closed convex subset of $H_{1}$. Let the symbols “⇀” and “→” denote the weak and strong convergence, respectively. We know that in a Hilbert space $H_{1}$, the following properties hold:

$$ \Vert x-y \Vert ^{2}\leq \Vert x \Vert ^{2}- \Vert y \Vert ^{2}-2\langle x-y,y\rangle ,\quad \forall x,y\in H_{1} $$

(2.1)

and

$$ 2\langle x,y\rangle = \Vert x \Vert ^{2}+ \Vert y \Vert ^{2}- \Vert x-y \Vert ^{2}= \Vert x+y \Vert ^{2}- \Vert x \Vert ^{2}- \Vert y \Vert ^{2}, \quad \forall x,y\in H_{1}. $$

(2.2)

It is well known that every nonexpansive mapping $T:H_{1} \rightarrow H_{1}$ satisfies the inequality:

$$ \bigl\langle (x-Tx)-(y-Ty),Ty-Tx\bigr\rangle \leq \frac{1}{2} \bigl\Vert (Tx-x)-(Ty-y) \bigr\Vert ^{2},\quad \forall (x,y)\in H_{1}\times H_{1}. $$

Therefore for all $(x,y)\in H_{1}\times \operatorname{Fix}(T)$, we get

$$ \langle x-Tx,y-Tx\rangle \leq \frac{1}{2} \bigl\Vert (Tx-x) \bigr\Vert ^{2}. $$

(2.3)

A mapping $T: H_{1}\rightarrow H_{1}$ is said to be monotone if

$$ \langle Tx-Ty,x-y\rangle \geq 0, \quad \forall x,y\in H_{1}. $$

T is said to be α-inverse strongly monotone if there exists a $\alpha >0$ such that

$$ \langle Tx-Ty,x-y\rangle \geq \alpha \Vert Tx-Ty \Vert ^{2},\quad \forall x,y\in H_{1}. $$

T is said to be firmly nonexpansive if

$$ \langle Tx-Ty,x-y\rangle \geq \Vert Tx-Ty \Vert ^{2},\quad \forall x,y\in H_{1}. $$

A mapping $P_{C}$ is said to be metric projection from $H_{1}$ onto C if for every $x\in H_{1}$, there exists a unique nearest point in C denoted by $P_{C}(x)$ such that

$$ \bigl\Vert x-P_{C}(x) \bigr\Vert \leq \Vert x-y \Vert ,\quad \forall y\in C. $$

(2.4)

It is well known that $P_{C}$ is nonexpansive and firmly nonexpansive. Moreover, $P_{C}$ is characterized by the following property:

$$ \bigl\langle x-P_{C}(x),y-P_{C}(x) \bigr\rangle \leq 0,\quad \forall x\in H_{1},y \in C. $$

(2.5)

A multivalued mapping $M:H_{1}\rightarrow 2^{H_{1}}$ is called monotone if for any $x,y\in H_{1}$

$$ \langle u-v,x-y\rangle \geq 0,\quad \forall u\in Mx, v\in My. $$

For a multivalued mapping M, $\operatorname{graph}(M)$ is defined by $\operatorname{graph}(M):=\{(x,u)\in H_{1}\times H_{1}: u\in Mx\}$. A multivalued monotone mapping $M:H_{1}\rightarrow 2^{H_{1}}$ is said to be maximal monotone if $\operatorname{graph}(M)$ is not properly contained in the graph of any other monotone mapping. It is well known that a multivalued monotone mapping is maximal monotone if for $(x,u)\in H_{1}\times H_{1}$, $\langle x-y,u-v\rangle \geq 0$ for every $(y,v)\in \operatorname{graph}(M)$ implies that $u\in Mx$. Let $M:H_{1}\rightarrow 2^{H_{1}}$ be a multivalued maximal monotone operator. Then the resolvent mapping $J_{\lambda }^{M}:H_{1}\rightarrow H_{1}$ associated with M is defined by

$$ J_{\lambda }^{M}(x):=(I+\lambda M)^{-1}(x),\quad \forall x\in H_{1}, $$

for some $\lambda >0$, where I is the identity operator on $H_{1}$. It is well known that for all $\lambda >0$ the resolvent operator is single-valued, nonexpansive and firmly nonexpansive. Also, we know that $\operatorname{Fix}(J_{\lambda }^{M})=M^{-1}(0)$.

Definition 2.1

A mapping $T:H_{1}\rightarrow H_{1}$ is said to be an averaged mapping if there exists some number $\alpha \in (0,1)$ such that $T=(1-\alpha )I+\alpha S$, where $I:H_{1}\rightarrow H_{1}$ is the identity mapping and $S:H_{1}\rightarrow H_{1}$ is a nonexpansive mapping. An averaged mapping is also nonexpansive and $\operatorname{Fix}(S)=\operatorname{Fix}(T)$.

Lemma 2.2

([3, 4])

If the mappings $\{T_{i}\}_{i=1}^{N}$are averaged and have a common fixed point, then

$$ \bigcap_{i=1}^{N} \operatorname{Fix}(T_{i})=\operatorname{Fix}(T_{1}T_{2} \cdots T_{N}). $$

In particular, for $N=2$, $\operatorname{Fix}(T_{1})\cap \operatorname{Fix}(T_{2})= \operatorname{Fix}(T_{1}T_{2})=\operatorname{Fix}(T_{2}T_{1})$.

Lemma 2.3

([37])

Assume that $S:C\rightarrow H_{1}$is a k-strictly pseudocontractive mapping. Define a mapping T by $Tx=\alpha x+(1-\alpha )Sx$for all $x\in H_{1}$, where $\alpha \in [k,1)$. Then T is a nonexpansive mapping with $\operatorname{Fix}(T)=\operatorname{Fix}(S)$.

Lemma 2.4

([37])

Let $T:C\rightarrow H_{1}$be a k-strictly pseudocontractive mapping with $\operatorname{Fix}(T)\neq \emptyset$. Then $\operatorname{Fix}(P_{C}T)=\operatorname{Fix}(T)$.

Lemma 2.5

(Demiclosedness principle [12])

Let C be a nonempty closed convex subset of a real Hilbert space $H_{1}$and let $T:C\rightarrow C$be a nonexpansive mapping. If $\{x_{n}\}$is a sequence in C weakly converging to $x\in C$and $\{(I-T)x_{n}\}$converges strongly to $y\in C$, then $(I-T)x=y$. In particular, if $y=0$, then $x\in \operatorname{Fix}(T)$.

Assumption A

([1])

Let $F:C\times C\rightarrow \mathbb{R}$ be a bifunction which satisfies the following assumptions:

• (i) $F(x,x)\geq 0$, $\forall x\in C$;

• (ii) F is monotone, i.e., $F(x,y)+F(y,x)\leq 0$, $\forall x,y\in C$;

• (iii) F is upper hemicontinuous, i.e., for each $x,y,z \in C$,

  $$ \limsup_{t\to 0}F\bigl(tz+(1-t)x,y\bigr)\leq F(x,y); $$

  (2.6)

• (iv) For each $x\in C$ fixed, the function $y\mapsto F(x,y)$ is convex and lower semicontinuous.

Lemma 2.6

([9])

Assume that the bifunction $F :C\times C\rightarrow \mathbb{R}$satisfies Assumption A. For $r>0$and $x\in H_{1}$, define a mapping $T_{r}^{F}:H_{1}\rightarrow C$as follows:

$$ T_{r}^{F}(x):= \biggl\{ z\in C: F(z,y)+\frac{1}{r}\langle y-z,z-x \rangle \geq 0, \forall y\in C \biggr\} . $$

(2.7)

Then the following properties hold:

• (i) $T_{r}^{F}$is nonempty and single-valued.

• (ii) $T_{r}^{F}$is firmly nonexpansive, i.e., $\|T_{r}^{F}x-T_{r}^{F}y\|^{2}\leq \langle T_{r}^{F}x-T_{r}^{F}y,x-y \rangle$, $\forall x,y\in H_{1}$.

• (iii) $\operatorname{Fix}(T_{r}^{F})=\operatorname{EP}(F,C)$.

• (iv) $\operatorname{EP}(F,C)$is closed and convex.

Furthermore, assume that $F_{2} :D\times D\rightarrow \mathbb{R}$ satisfy the conditions in Assumption A. For $s>0$ and for all $w\in H_{2}$, define a mapping $T_{s}^{F_{2}}:H_{2}\rightarrow D$ as follows:

$$ T_{s}^{F_{2}}(w):= \biggl\{ d\in D: F(d,e)+\frac{1}{s}\langle e-d,d-w \rangle \geq 0, \forall e\in D \biggr\} . $$

(2.8)

Then we easily observe that $T_{s}^{F_{2}}$ is nonempty, single-valued and firmly nonexpansive. Also, $\operatorname{EP}(F_{2},D)$ is closed and convex, and $\operatorname{Fix}(T_{s}^{F_{2}})=\operatorname{EP}(F_{2},D)$, where $\operatorname{EP}(F_{2},D)$ is the solution of the following equilibrium problem: Find $y^{*}\in D$ such that

$$ F_{2}\bigl(y^{*},y\bigr)\geq 0,\quad \forall y\in D. $$

Lemma 2.7

([8])

Let $\{\delta _{n}\}$and $\{\gamma _{n}\}$be non-negative sequences satisfying $\sum_{n=0}^{\infty }\delta _{n}<+\infty$and $\gamma _{n+1}\leq \gamma _{n}+\delta _{n}$for all $n\in \mathbb{N}$. Then $\{\gamma _{n}\}$is a convergent sequence.

Definition 2.8

([2, 24])

A sequence $\{M_{n}\}$ of maximal monotone mappings defined on $H_{1}$ is said to be graph convergent to a multivalued mapping M if $\{\operatorname{graph}(M_{n})\}$ converges to $\operatorname{graph}(M)$ in the Kuratowski–Painlevé sense, that is,

$$ \limsup_{n\rightarrow \infty } \operatorname{graph}(M_{n}) \subset \operatorname{graph}(M) \subset \liminf_{n\rightarrow \infty } \operatorname{graph}(M_{n}). $$

Lemma 2.9

([9])

We have the following statements:

• (i) Let M be a maximal monotone mapping on $H_{1}$. Then $\{{t_{n}}^{-1}M\}$is graph convergent to $N_{M^{-1}0}$as $t_{n}\to 0$provided that $M^{-1}0\neq \emptyset$.

• (ii) Let $\{M_{n}\}$be a sequence of maximal monotone mappings on $H_{1}$which is graph convergent to a mapping M defined on $H_{1}$. If B is a Lipschitz maximal monotone mapping on $H_{1}$, then $\{B+M_{n}\}$is graph convergent to $B+M$and $B+M$is maximal monotone.

3 Main results

In this section, we state and prove our main results of the paper. First we will study the weak convergence theorem.

Theorem 3.1

Let $H_{1}$and $H_{2}$be two Hilbert spaces. Let C and D be nonempty closed and convex subset of $H_{1}$and $H_{2}$, respectively. Let $A: H_{1} \rightarrow H_{2}$be a bounded linear operator. Suppose $F_{1}: C\times C\rightarrow \mathbb{R}$and $F_{2}: D\times D\rightarrow \mathbb{R}$are two bifunctions which satisfy Assumption Aand $F_{2}$is upper semicontinuous. Let $g_{1}:C\rightarrow H_{1}$and $g_{2}: D\rightarrow H_{2}$be $\eta _{1}$- and $\eta _{2}$-inverse strongly monotone mappings, respectively. Let $S:C\rightarrow C$be a nonexpansive self-mapping and $\{T_{i}\}_{i=1}^{N}:C\rightarrow H_{1}$be $k_{i}$-strictly pseudocontractive nonself-mappings. Assume that

$$ \mathcal{F}=\Gamma \cap \mathcal{S}\neq \emptyset . $$

Define a sequence $\{x_{n}\}$as follows:

$$ \textstyle\begin{cases} x_{0} \in C, \\ u_{n}=(1-\alpha _{n})x_{n}+\alpha _{n}(\tau _{n}Sx_{n}+(1-\tau _{n})T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n}), \\ x_{n+1}=U(u_{n}+\gamma _{n} A^{*}(V-I)Au_{n}),\quad n\geq 1, \end{cases} $$

(3.1)

where $U=T_{r_{n}}^{F_{1}}(I-r_{n}g_{1})$, $V=T_{r_{n}}^{F_{2}}(I-r_{n}g_{2})$, $T_{i}^{n}=(1-\delta _{n}^{i})I+\delta _{n}^{i}P_{C}(\beta _{i}I +(1- \beta _{i})T_{i})$, $0\leq k_{i}\leq \beta _{i}<1$, $\delta _{n}^{i}\in (0,1)$for $i=1,2,\ldots,N$and

$$ \gamma _{n}= \frac{\sigma _{n} \Vert (T_{r_{n}}^{F_{2}}(I-r_{n}g_{2})-I)Ax_{n} \Vert }{ \Vert A^{*}(T_{r_{n}}^{F_{2}}(I-r_{n}g_{2})-I)Ax_{n} \Vert },\quad 0< a\leq \sigma _{n}\leq b< 1. $$

Let $\{\alpha _{n}\}$, $\{\tau _{n}\}$be two real sequences in $(0,1)$and $\{r_{n}\}\subset (0,\alpha )$, where $\alpha =2\min \{\eta _{1},\eta _{2}\}$. Suppose the following conditions are satisfied:

• (i) $\sum_{n=0}^{\infty }\tau _{n}<\infty$;

• (ii) $\lim_{n\rightarrow \infty } \frac{\|x_{n}-u_{n}\|}{\alpha _{n}\tau _{n}}=0$;

• (iii) $\liminf_{n\rightarrow \infty }r_{n}>0$;

• (iv) $\lim_{n\rightarrow \infty }|\delta _{n+1}^{i}-\delta _{n}^{i}|=0$for $i=1,2,\ldots,N$.

Then the sequence $\{x_{n}\}$converges weakly to $x^{*} \in \mathcal{F}$

Proof

Since our method easily deduce the general case, we only prove the theorem for $N=2$. Since $g_{1}:H_{1}\rightarrow H_{1}$ is $\eta _{1}$-strongly monotone mapping, for any $x,y\in H_{1}$, we get

$$\begin{aligned} \begin{aligned} \bigl\Vert (I-r_{n}g_{1})x-(I-r_{n}g_{1})y \bigr\Vert ^{2} &= \bigl\Vert (x-y)-r_{n}(g_{1}x-g_{1}y) \bigr\Vert ^{2} \\ &\leq \Vert x-y \Vert ^{2}-r_{n}(2\eta _{1}-r_{n}) \Vert g_{1}x-g_{1}y \Vert ^{2} \\ &\leq \Vert x-y \Vert ^{2}. \end{aligned} \end{aligned}$$

This means that $(I-r_{n}g_{1})$ is nonexpansive. Similarly, we can show that $(I-r_{n}g_{2})$ is a nonexpansive mapping. Thus, U and V are also nonexpansive mappings. Let $x^{*}\in \mathcal{F}$. From Lemma 2.2, Lemma 2.3 and Lemma 2.4, we get $x^{*}=T_{2}^{n}T_{1}^{n}x^{*}$. Hence, we have

$$\begin{aligned} \bigl\Vert u_{n}-x^{*} \bigr\Vert &= \bigl\Vert (1-\alpha _{n})x_{n}+\alpha _{n}\bigl(\tau _{n}Sx_{n}+(1-\tau _{n})T_{2}^{n}T_{1}^{n}x_{n} \bigr)-x^{*} \bigr\Vert \\ &\leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n}\bigl[\tau _{n} \bigl\Vert Sx_{n}-x^{*} \bigr\Vert +(1-\tau _{n}) \bigl\Vert T_{2}^{n}T_{1}^{n}x_{n}-x^{*} \bigr\Vert \bigr] \\ &\leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n}\bigl[\tau _{n} \bigl\Vert x_{n}-x^{*} \bigr\Vert +(1-\tau _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert \bigr] \\ &\quad {} +\alpha _{n}\tau _{n} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert \\ &= \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n}\tau _{n} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert . \end{aligned}$$

(3.2)

Also, since $x^{*}\in \mathcal{F}$, we have $Ux^{*}=x^{*}$ and $VAx^{*}=Ax^{*}$.

Let $v_{n}=u_{n}+\gamma A^{*}(V-I)Au_{n}$. Then we have

$$\begin{aligned} \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2} &= \bigl\Vert u_{n}+\gamma _{n} A^{*}(V-I)Au_{n}-x^{*} \bigr\Vert ^{2} \\ &= \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}+\gamma _{n}^{2} \bigl\Vert A^{*}(V-I)Au_{n} \bigr\Vert ^{2} \\ &\quad {} +2\gamma _{n}\bigl\langle u_{n}-x^{*},A^{*}(V-I)Au_{n} \bigr\rangle . \end{aligned}$$

(3.3)

Since $VAx^{*}=Ax^{*}$, we get

$$\begin{aligned} &\bigl\langle u_{n}-x^{*},A^{*}(V-I)Au_{n} \bigr\rangle \\ &\quad =\bigl\langle Au_{n}-Ax^{*},(V-I)Au_{n} \bigr\rangle \\ &\quad =\bigl\langle Au_{n}-Ax^{*}+(V-I)Au_{n}-(V-I)Au_{n},(V-I)Au_{n} \bigr\rangle \\ &\quad =\bigl\langle VAu_{n}-Ax^{*},(V-I)Au_{n} \bigr\rangle - \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2} \\ &\quad =\frac{1}{2} \bigl[ \bigl\Vert VAu_{n}-Ax^{*} \bigr\Vert ^{2}+ \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2}- \bigl\Vert Au_{n}-Ax^{*} \bigr\Vert ^{2}\bigr] \\ &\qquad {} - \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2} \\ &\quad \leq \frac{1}{2} \bigl[ \bigl\Vert Au_{n}-Ax^{*} \bigr\Vert ^{2}- \bigl\Vert Au_{n}-Ax^{*} \bigr\Vert ^{2}\bigr]- \frac{1}{2} \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2} \\ &\quad =-\frac{1}{2} \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2}. \end{aligned}$$

(3.4)

From (3.3) and (3.4), we obtain

$$ \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2}\leq \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}-\gamma _{n}\bigl( \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2}-\gamma _{n} \bigl\Vert A^{*}(V-I)Au_{n} \bigr\Vert ^{2}\bigr). $$

(3.5)

Now

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} &= \bigl\Vert U\bigl(u_{n}+\gamma _{n} A^{*}(V-I)Au_{n}\bigr)-x^{*} \bigr\Vert ^{2} \\ &\leq \bigl\Vert u_{n}+\gamma _{n} A^{*}(V-I)Au_{n}-x^{*} \bigr\Vert ^{2} \\ &= \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}-\gamma _{n}\bigl( \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2}-\gamma _{n} \bigl\Vert A^{*}(V-I)Au_{n} \bigr\Vert ^{2}\bigr). \end{aligned}$$

(3.6)

From (3.2), (3.3) and (3.4), we get

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} &\leq \bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n}\tau _{n} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert \bigr)^{2} \\ &\quad {} -\gamma _{n}\bigl( \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2}-\gamma _{n} \bigl\Vert A^{*}(V-I)Au_{n} \bigr\Vert ^{2}\bigr). \end{aligned}$$

(3.7)

Now, using the definition of $\gamma _{n}$, we get

$$ \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \leq \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n}\tau _{n} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert . $$

(3.8)

Since $\sum_{n=0}^{\infty }\tau _{n}<\infty$, we have $\sum_{n=0}^{\infty }\alpha _{n}\tau _{n}<\infty$. Thus, by using Lemma 2.7 to (3.8), we conclude that $\lim_{n\rightarrow \infty }\|x_{n}-x^{*}\|$ exists and the value is finite. Hence, $\{x_{n}\}$ is bounded and so are $\{u_{n}\}$ and $\{v_{n}\}$.

Now, from (3.7), we get

$$\begin{aligned} &\gamma _{n}\bigl( \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2}-\gamma _{n} \bigl\Vert A^{*}(V-I)Au_{n} \bigr\Vert ^{2}\bigr) \\ &\quad \leq \bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert + \alpha _{n}\tau _{n} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert \bigr)^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ &\quad = \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}+\alpha _{n}^{2}\tau _{n}^{2} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert ^{2} \\ &\qquad {} +2\alpha _{n}\tau _{n} \bigl\Vert x_{n}-x^{*} \bigr\Vert \bigl\Vert Sx^{*}-x^{*} \bigr\Vert . \end{aligned}$$

Since $\lim_{n\rightarrow \infty }\tau _{n}=0$, we get

$$ \gamma _{n}\bigl( \bigl\Vert (V-I)Au_{n} \bigr\Vert ^{2}-\gamma _{n} \bigl\Vert A^{*}(V-I)Au_{n} \bigr\Vert ^{2}\bigr) \rightarrow 0 \quad \text{as } n\rightarrow \infty , $$

which by definition of $\gamma _{n}$, implies that

$$ \frac{\sigma _{n}(1-\sigma _{n}) \Vert (V-I)Au_{n} \Vert ^{4}}{ \Vert A^{*}(V-I)Au_{n} \Vert ^{2}} \rightarrow 0\quad \text{as } n\rightarrow \infty . $$

Since $0< a\leq \sigma _{n}\leq b<1$ and $\|A^{*}(V-I)Au_{n}\|$ is bounded, we get

$$ \bigl\Vert (V-I)Au_{n} \bigr\Vert \rightarrow 0\quad \text{as } n \rightarrow \infty . $$

Now

$$ \bigl\Vert A^{*}(V-I)Au_{n} \bigr\Vert = \bigl\Vert A^{*} \bigr\Vert \bigl\Vert (V-I)Au_{n} \bigr\Vert \rightarrow 0 \quad \text{as } n\rightarrow \infty . $$

(3.9)

So,

$$ \Vert u_{n}-v_{n} \Vert = \bigl\Vert A^{*}(V-I)Au_{n} \bigr\Vert \rightarrow 0\quad \text{as } n \rightarrow \infty . $$

(3.10)

Now, we estimate

$$\begin{aligned} \Vert x_{n+1}-x_{n} \Vert &= \bigl\Vert x_{n+1}-x^{*}-\bigl(x_{n}-x^{*} \bigr) \bigr\Vert \\ &= \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}-2\bigl\langle x_{n+1}-x_{n},x_{n}-x^{*} \bigr\rangle \\ &= \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}-2\bigl\langle x_{n+1}-p,x_{n}-x^{*} \bigr\rangle \\ &\quad {} +2\bigl\langle x_{n}-p,x_{n}-x^{*}\bigr\rangle , \end{aligned}$$

where p is a weak limit point of $\{x_{n}\}$. Since $\lim_{n\rightarrow \infty }\|x_{n}-x^{*}\|$ exists, we get

$$ \Vert x_{n+1}-x_{n} \Vert \rightarrow 0 \quad \text{as } n\rightarrow \infty . $$

(3.11)

Since $\liminf_{n\rightarrow \infty }r_{n}>0$, there exists a number $r>0$ such that $r_{n}>r$. Hence, we get

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}&= \bigl\Vert Uv_{n}-Ux^{*} \bigr\Vert ^{2} \\ &= \bigl\Vert T_{r_{n}}^{F_{1}}(I-r_{n}g_{1})v_{n}-T_{r_{n}}^{F_{1}}(I-r_{n}g_{1})x^{*} \bigr\Vert ^{2} \\ &\leq \bigl\Vert (I-r_{n}g_{1})v_{n}-(I-r_{n}g_{1})x^{*} \bigr\Vert ^{2} \\ &\leq \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2}-r_{n}(2\eta _{1}-r_{n}) \bigl\Vert g_{1}v_{n}-g_{1}x^{*} \bigr\Vert ^{2} \\ &\leq \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2}-r(2\eta _{1}-\alpha ) \bigl\Vert g_{1}v_{n}-g_{1}x^{*} \bigr\Vert ^{2}, \end{aligned}$$

that is,

$$\begin{aligned} r(2\eta _{1}-\alpha ) \bigl\Vert g_{1}v_{n}-g_{1}x^{*} \bigr\Vert ^{2} &\leq \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ &\leq \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ &\leq \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}+\alpha _{n}^{2}\tau _{n}^{2} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert ^{2} \\ &\quad {} +2\alpha _{n}\tau _{n} \bigl\Vert x_{n}-x^{*} \bigr\Vert \bigl\Vert Sx^{*}-x^{*} \bigr\Vert \\ &\leq \Vert x_{n}-x_{n+1} \Vert \bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert + \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \bigr) \\ &\quad {} +\alpha _{n}^{2}\tau _{n}^{2} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert ^{2} +2\alpha _{n} \tau _{n} \bigl\Vert x_{n}-x^{*} \bigr\Vert \bigl\Vert Sx^{*}-x^{*} \bigr\Vert . \end{aligned}$$

Since $\lim_{n\rightarrow \infty }\tau _{n}=0$, $\|x_{n}-x^{*}\|$ is bounded and $r(2\eta _{1}-\alpha )>0$, we get

$$ \lim_{n\rightarrow \infty } \bigl\Vert g_{1}v_{n}-g_{1}x^{*} \bigr\Vert =0. $$

(3.12)

Now, from the firmly nonexpansivity of $T_{r_{n}}^{F_{1}}$, we get

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} &\leq \bigl\langle (I-r_{n}g_{1})v_{n}-(I-r_{n}g_{1})x^{*},x_{n+1}-x^{*} \bigr\rangle \\ &=\frac{1}{2} \bigl[ \bigl\Vert (I-r_{n}g_{1})v_{n}-(I-r_{n}g_{1})x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ &\quad {} - \bigl\Vert v_{n}-x_{n+1}-r_{n} \bigl(g_{1}v_{n}-g_{1}{x^{*}} \bigr) \bigr\Vert ^{2} \bigr] \\ &\leq \frac{1}{2} \bigl[ \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}- \Vert v_{n}-x_{n+1} \Vert ^{2} \\ &\quad {} +2r_{n}\bigl\langle v_{n}-x_{n+1},g_{1}v_{n}-g_{1}{x^{*}} \bigr\rangle -r_{n}^{2} \bigl\Vert g_{1}v_{n}-g_{1}{x^{*}} \bigr\Vert ^{2} \bigr] \\ &\leq \frac{1}{2} \bigl[ \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}- \Vert v_{n}-x_{n+1} \Vert ^{2} \\ &\quad {} +2r_{n} \Vert v_{n}-x_{n+1} \Vert \bigl\Vert g_{1}v_{n}-g_{1}{x^{*}} \bigr\Vert \bigr], \end{aligned}$$

this implies that

$$ \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}\leq \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2}- \Vert v_{n}-x_{n+1} \Vert ^{2}+2r_{n} \Vert v_{n}-x_{n+1} \Vert \bigl\Vert g_{1}v_{n}-g_{1}{x^{*}} \bigr\Vert . $$

That is,

$$ \Vert v_{n}-x_{n+1} \Vert ^{2}\leq \bigl\Vert v_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}+2r_{n} \Vert v_{n}-x_{n+1} \Vert \bigl\Vert g_{1}v_{n}-g_{1}{x^{*}} \bigr\Vert . $$

Hence, we have

$$\begin{aligned} \Vert v_{n}-x_{n+1} \Vert ^{2} &\leq \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}+ \alpha _{n}^{2}\tau _{n}^{2} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert ^{2} \\ &\quad {} +2\alpha _{n}\tau _{n} \bigl\Vert x_{n}-x^{*} \bigr\Vert \bigl\Vert Sx^{*}-x^{*} \bigr\Vert +2r_{n} \Vert v_{n}-x_{n+1} \Vert \bigl\Vert g_{1}v_{n}-g_{1}{x^{*}} \bigr\Vert \\ &\leq \Vert x_{n}-x_{n+1} \Vert \bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert + \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \bigr)+\alpha _{n}^{2} \tau _{n}^{2} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert ^{2} \\ & \quad {}+2\alpha _{n}\tau _{n} \bigl\Vert x_{n}-x^{*} \bigr\Vert \bigl\Vert Sx^{*}-x^{*} \bigr\Vert +2r_{n} \Vert v_{n}-x_{n+1} \Vert \bigl\Vert g_{1}v_{n}-g_{1}{x^{*}} \bigr\Vert . \end{aligned}$$

Using (3.11) and (3.12), we get

$$ \lim_{n\rightarrow \infty } \Vert v_{n}-x_{n+1} \Vert =0. $$

(3.13)

Now

$$ \Vert x_{n}-v_{n} \Vert \leq \Vert x_{n}-x_{n+1} \Vert + \Vert x_{n+1}-v_{n} \Vert \rightarrow 0\quad \text{as } n \rightarrow \infty . $$

(3.14)

Again, by using (3.10) and (3.14), we get

$$ \Vert x_{n}-u_{n} \Vert \leq \Vert x_{n}-v_{n} \Vert + \Vert v_{n}-u_{n} \Vert \rightarrow 0 \quad \text{as } n \rightarrow \infty . $$

(3.15)

Now, we show that $p\in \mathcal{F}$. Since $T_{2}^{n}T_{1}^{n}$ is an averaged mapping, it is nonexpansive. Using the boundedness of $\{x_{n}\}$ and nonexpansivity of S, there exists a $K>0$ such that $\|Sx_{n}-T_{2}^{n}T_{1}^{n}x_{n}\|\leq K$ for all $n\geq 0$. Now, we know that

$$\begin{aligned} \bigl\Vert u_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert &=\bigl\| (1-\alpha _{n})x_{n}+\alpha _{n}\bigl( \tau _{n}Sx_{n}+(1-\tau _{n})T_{2}^{n}T_{1}^{n}x_{n}\bigr)-T_{2}^{n}T_{1}^{n}x_{n} \bigr\| \\ &\leq (1-\alpha _{n}) \bigl\Vert x_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert +\alpha _{n} \tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert \\ &\leq (1-\alpha _{n}) \Vert x_{n}-u_{n} \Vert +(1-\alpha _{n}) \bigl\Vert u_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert \\ &\quad {} +\alpha _{n}\tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert , \end{aligned}$$

this implies that

$$\begin{aligned} \begin{aligned} \alpha _{n} \bigl\Vert u_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert &\leq (1-\alpha _{n}) \Vert x_{n}-u_{n} \Vert +\alpha _{n}\tau _{n}K \\ &\leq \Vert x_{n}-u_{n} \Vert +\alpha _{n}\tau _{n}K. \end{aligned} \end{aligned}$$

Hence, we have

$$ \bigl\Vert u_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert \leq \frac{ \Vert x_{n}-u_{n} \Vert }{\alpha _{n}}+\tau _{n}K. $$

(3.16)

It follows from the conditions (i)–(ii) that

$$ \lim_{n\rightarrow \infty } \frac{ \Vert x_{n}-u_{n} \Vert }{\alpha _{n}}=\lim_{n\rightarrow \infty } \tau _{n}\frac{ \Vert x_{n}-u_{n} \Vert }{\tau _{n}\alpha _{n}}=0. $$

Hence from (3.16), we get

$$ \lim_{n\rightarrow \infty } \bigl\Vert u_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert =0. $$

Now, by using (3.15), we get

$$ \bigl\Vert x_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert \leq \Vert x_{n}-u_{n} \Vert + \bigl\Vert u_{n}-T_{2}^{n}T_{1}^{n}x_{n} \bigr\Vert \rightarrow 0 \quad \text{as } n\rightarrow \infty . $$

(3.17)

Since $\{x_{n}\}$ is bounded, there exists a subsequence $\{x_{n_{j}}\}$ of $\{x_{n}\}$ such that $x_{n_{j}}\rightharpoonup p$ as $j\to \infty$. Noticing that $\{\delta _{n}^{i}\}$ is bounded for $i=1,2$, we can assume that $\delta _{n_{j}}^{i}\to \delta _{\infty }^{i}$ as $j\to \infty$, where $0<\delta _{\infty }^{i}<1$ for $i=1,2$. Define, for $i = 1, 2$,

$$ T_{i}^{\infty }=\bigl(1-\delta _{\infty }^{i} \bigr)I+\delta _{\infty }^{i}P_{C}\bigl( \beta _{i}I+(1-\beta _{i})T_{i}\bigr). $$

Now, by Lemma 2.3 and Lemma 2.4, $\operatorname{Fix}(P_{C}(\beta _{i}I+(1-\beta _{i})T_{i}))=\operatorname{Fix}(T_{i})$. Again, since $P_{C}(\beta _{i}I+(1-\beta _{i})T_{i})$ is a nonexpansive mapping, $T_{i}^{\infty }$ is averaged and $\operatorname{Fix}(T_{i}^{\infty })=\operatorname{Fix}(T_{i})$ for $i=1,2$.

Furthermore, since

$$ \operatorname{Fix}\bigl(T_{1}^{\infty }\bigr)\cap \operatorname{Fix}\bigl(T_{2}^{\infty }\bigr)= \operatorname{Fix}(T_{1})\cap \operatorname{Fix}(T_{2})= \operatorname{Fix}( \mathcal{S})\neq \emptyset , $$

by Lemma 2.2, we get

$$ \operatorname{Fix}\bigl(T_{2}^{\infty }T_{1}^{\infty } \bigr)=\operatorname{Fix}\bigl(T_{1}^{\infty }\bigr)\cap \operatorname{Fix}\bigl(T_{2}^{\infty }\bigr)= \operatorname{Fix}(\mathcal{S}). $$

Note that

$$ \bigl\Vert T_{i}^{n_{j}}t-T_{i}^{\infty }t \bigr\Vert \leq \bigl\vert \delta _{n_{j}}^{i}-\delta _{ \infty }^{i} \bigr\vert \bigl( \Vert t \Vert + \bigl\Vert P_{C}\bigl(\beta _{i}t+(1-\beta _{i})T_{i}(t)\bigr) \bigr\Vert \bigr). $$

Hence, we get

$$ \lim_{j\to \infty }\sup_{t\in B} \bigl\Vert T_{i}^{n_{j}}t-T_{i}^{ \infty }t \bigr\Vert =0, $$

(3.18)

where B is an arbitrary bounded subset of $H_{1}$. Also, we have

$$\begin{aligned} \bigl\Vert x_{n_{j}}-T_{2}^{\infty }T_{1}^{\infty }x_{n_{j}} \bigr\Vert &\leq \bigl\Vert x_{n_{j}}-T_{2}^{n_{j}} T_{1}^{n_{j}} x_{n_{j}} \bigr\Vert + \bigl\Vert T_{2}^{n_{j}} T_{1}^{n_{j}} x_{n_{j}}-T_{2}^{\infty }T_{1}^{n_{j}} x_{n_{j}} \bigr\Vert \\ &\quad {} + \bigl\Vert T_{2}^{\infty }T_{1}^{n_{j}} x_{n_{j}}-T_{2}^{\infty }T_{1}^{\infty }x_{n_{j}} \bigr\Vert \\ &\leq \bigl\Vert x_{n_{j}}-T_{2}^{n_{j}} T_{1}^{n_{j}} x_{n_{j}} \bigr\Vert + \bigl\Vert T_{2}^{n_{j}} T_{1}^{n_{j}} x_{n_{j}}-T_{2}^{\infty }T_{1}^{n_{j}} x_{n_{j}} \bigr\Vert \\ &\quad {} + \bigl\Vert T_{1}^{n_{j}} x_{n_{j}}-T_{1}^{\infty }x_{n_{j}} \bigr\Vert \\ &\leq \bigl\Vert x_{n_{j}}-T_{2}^{n_{j}} T_{1}^{n_{j}} x_{n_{j}} \bigr\Vert +\sup _{t\in B_{1}} \bigl\Vert T_{2}^{n_{j}} t-T_{2}^{\infty }t \bigr\Vert \\ &\quad {} +\sup_{t\in B_{2}} \bigl\Vert T_{1}^{n_{j}} t-T_{1}^{\infty }t \bigr\Vert , \end{aligned}$$

(3.19)

where $B_{1}$ is a bounded subset including $\{T_{1}^{n_{j}}x_{n_{j}}\}$ and $B_{2}$ is a bounded subset including $\{x_{n_{j}}\}$. It follows from (3.17), (3.18) and (3.19) that

$$ \lim_{j\to \infty } \bigl\Vert x_{n_{j}}-T_{2}^{\infty }T_{1}^{\infty }x_{n_{j}} \bigr\Vert =0. $$

Hence, from Lemma 2.5, we get $p\in \operatorname{Fix}(T_{2}^{\infty }T_{1}^{\infty })= \operatorname{Fix}(T_{1})\cap \operatorname{Fix}(T_{2})$.

Now, we show that $x^{*}\in \mathcal{S}$. It follows from (3.1) that

$$ u_{n}-x_{n}=\alpha _{n}\bigl(\tau _{n}(Sx_{n}-x_{n})+(1-\tau _{n}) \bigl(T_{2}^{n}T_{1}^{n}x_{n}-x_{n} \bigr)\bigr), $$

and hence,

$$ \frac{1}{\alpha _{n}\tau _{n}}(x_{n}-u_{n})= \biggl((I-S)x_{n}+ \biggl( \frac{1-\tau _{n}}{\tau _{n}} \biggr) \bigl(I-T_{2}^{n}T_{1}^{n} \bigr)x_{n} \biggr). $$

(3.20)

By using Lemma 2.9(i), it follows that the operator sequence $\{ (\frac{1-\tau _{n}}{\tau _{n}} ) (I-T_{2}^{n}T_{1}^{n} ) \}$ is graph convergent to $N_{\operatorname{Fix}(T_{1})\cap \operatorname{Fix}(T_{2})}$, and hence, from Lemma 2.9(ii), it follows that the operator sequence $\{(I-S)+ (\frac{1-\tau _{n}}{\tau _{n}} ) (I-T_{2}^{n}T_{1}^{n} ) \}$ is graph convergent to $(I-S)+N_{\operatorname{Fix}(T_{1})\cap \operatorname{Fix}(T_{2})}$. Now, by replacing n by $n_{j}$ and letting the limit in (3.20) and considering the fact that $\lim_{n\to \infty }\frac{1}{\alpha _{n}\tau _{n}}\|x_{n}-u_{n} \|=0$ and the graph of $(I-S)+N_{\operatorname{Fix}(T_{1})\cap \operatorname{Fix}(T_{2})}$ is weakly–strongly closed, we get

$$ 0\in {(I-S)p+N_{\operatorname{Fix}(T_{1})\cap \operatorname{Fix}(T_{2})}p}, $$

that is, $p\in \mathcal{S}$.

We now show that $p\in \Gamma$. Since $u_{n}=U(v_{n})=T_{r_{n}}^{F_{1}}(I-r_{n}g_{1})(v_{n})$, we have

$$ F_{1}(x_{n+1},y)+\langle g_{1}v_{n},y-x_{n+1} \rangle + \frac{1}{r_{n}}\langle y-x_{n+1},x_{n+1}-v_{n} \rangle \geq 0,\quad \forall y\in C. $$

From the monotonicity of $F_{1}$, we get

$$ \langle g_{1}v_{n},y-x_{n+1}\rangle + \frac{1}{r_{n}}\langle y-x_{n+1},x_{n+1}-v_{n} \rangle \geq F_{1}(y,x_{n+1}),\quad \forall y\in C. $$

Replacing n with $n_{j}$ in the above inequality, we get

$$ \langle g_{1}v_{n_{j}},y-x_{{n_{j}}+1}\rangle + \frac{1}{r_{n_{j}}} \langle y-x_{{n_{j}}+1},x_{{n_{j}}+1}-v_{n_{j}} \rangle \geq F_{1}(y,x_{{n_{j}}+1}),\quad \forall y\in C. $$

For t with $0< t\leq 1$ and $y\in C$, let $y_{t}=ty+(1-t)p$. Since $y\in C$ and $p\in C$, we get $y_{t}\in C$ and hence $F_{1}(y_{t},p)\leq 0$. So, from the above inequality, we get

$$\begin{aligned} \langle y_{t}-x_{n+1},g_{1}y_{t} \rangle &\geq \langle y_{t}-x_{n+1},g_{1}y_{t} \rangle -\langle y_{t}-x_{n+1},g_{1}v_{t} \rangle \\ &\quad {} -\frac{1}{r_{n_{j}}}\biggl\langle y_{t}-x_{{n_{j}}+1}, \frac{x_{{n_{j}}+1}-v_{n_{j}}}{r_{n_{j}}}\biggr\rangle + F_{1}(y_{t},x_{{n_{j}}+1}) \\ &=\langle y_{t}-x_{n+1},g_{1}y_{t}-g_{1}x_{{n_{j}}+1} \rangle + \langle y_{t}-x_{{n_{j}}+1},g_{1}x_{{n_{j}}+1}-g_{1}v_{t} \rangle \\ &\quad {} -\frac{1}{r_{n_{j}}}\biggl\langle y_{t}-x_{{n_{j}}+1}, \frac{x_{{n_{j}}+1}-v_{n_{j}}}{r_{n_{j}}}\biggr\rangle + F_{1}(y_{t},x_{{n_{j}}+1}). \end{aligned}$$

Since $\{x_{n}\}$, $\{u_{n}\}$ and $\{v_{n}\}$ have the same asymptotic behavior and $x_{n_{j}}\rightharpoonup p$, there exist subsequences $\{u_{n_{j}}\}$ of $\{u_{n}\}$ and $\{v_{n_{j}}\}$ of $\{v_{n}\}$ such that $u_{n_{j}}\rightharpoonup p$ and $v_{n_{j}}\rightharpoonup p$. Since $\lim_{j\to \infty }\|x_{{n_{j}}+1}-v_{n_{j}}\|=0$ and $f_{1}$ is Lipschitz continuous, we have $\lim_{j\to \infty }\|g_{1}x_{{n_{j}}+1}-g_{1}v_{n_{j}}\|=0$. Since $\liminf_{n\rightarrow \infty }r_{n}>0$, there exists a number $r>0$ such that $\liminf_{n\rightarrow \infty }r_{n}=r$. Hence, we have

$$\begin{aligned} \lim_{j\to \infty } \frac{ \Vert x_{{n_{j}}+1}-v_{n_{j}} \Vert }{r_{n_{j}}} &\leq \frac{\lim_{j\to \infty } \Vert x_{{n_{j}}+1}-v_{n_{j}} \Vert }{\liminf_{n\rightarrow \infty }r_{n_{j}}} \\ &=\frac{1}{r}\lim_{j\to \infty } \Vert x_{{n_{j}}+1}-v_{n_{j}} \Vert \\ &=0. \end{aligned}$$

Furthermore, from the monotonicity of $g_{1}$ and lower semicontinuity of $F_{1}$, we have

$$ \langle y_{t}-p,g_{1}y_{t}\rangle \geq F_{1}(y_{t},p), $$

as $j\to \infty$. And also, from the convexity of $F_{1}$, we have

$$\begin{aligned} 0&=F_{1}(y_{t},y_{t}) \\ &\leq tF_{1}(y_{t},y)+(1-t)\langle y_{t}-p,g_{1}y_{t}\rangle \\ &\leq tF_{1}(y_{t},y)+(1-t)t\langle y-p,g_{1}y_{t}\rangle . \end{aligned}$$

Hence, $0\leq F_{1}(y_{t},y)+(1-t)\langle y-p,g_{1}y_{t}\rangle$. Letting $t\to 0_{+}$, for each $y\in C$, we have

$$ F_{1}(p,y)+\langle y-p,g_{1}p\rangle \geq 0. $$

This implies that $p\in \operatorname{Sol}(\operatorname{MEP}\text{(1.9)})$.

Now, we need to show that $Ap\in \operatorname{Sol}(\operatorname{MEP}\text{(1.10)})$. Since A is bounded linear operator, we have $Ax_{n_{j}}\rightharpoonup Ap$. Now, setting $d_{n_{j}}=Au_{n_{j}}-VAu_{n_{j}}$, we get $d_{n_{j}}\to 0$ and $Au_{n_{j}}-d_{n_{j}}=VAu_{n_{j}}$. Therefore, from Lemma 2.6, we have

$$\begin{aligned} &F_{2}(Au_{n_{j}}-d_{n_{j}},z)+\bigl\langle g_{2}Au_{n_{j}},z-(Au_{n_{j}}-d_{n_{j}}) \bigr\rangle \\ &\quad {}+\frac{1}{r_{n_{j}}}\bigl\langle z-(Au_{n_{j}}-d_{n_{j}}),Au_{n_{j}}-d_{n_{j}}-Au_{n_{j}} \bigr\rangle \geq 0 ,\quad \forall z\in D. \end{aligned}$$

Since $F_{2}$ is upper semicontinuous in the first argument, taking lim sup to the above inequality as $j\to \infty$ and using $\liminf_{n\rightarrow \infty }r_{n}>0$, we get

$$ F_{2}(Ap,z)+\langle z-Ap,g_{2}Ap\rangle \geq 0,\quad \forall z\in D, $$

which implies that $Ap\in \operatorname{Sol}(\operatorname{MEP}\text{(1.10)})$. This shows that $p\in \Gamma$ and thus $p\in \mathcal{F}$. It follows from the existence of $\lim_{n\to \infty }\|x_{n}-p\|$ and the fact that Hilbert space satisfies Opial’s conditions, the sequence $\{x_{n}\}$ has only one weak limit point, and hence $\{x_{n}\}$ converges weakly to $p\in \mathcal{F}$. □

The following consequence is a weak convergence theorem for computing a common solution of a mixed equilibrium problem and a hierarchical fixed point problem in a real Hilbert space.

Corollary 3.2

Let $H_{1}$be a Hilbert spaces. Let C be a nonempty closed and convex subset of $H_{1}$. Suppose $F_{1}: C\times C\rightarrow \mathbb{R}$is a bifunction which satisfy Assumption A. Let $g_{1}:C\rightarrow H_{1}$be $\eta _{1}$-inverse strongly monotone mapping. Let $S:C\rightarrow C$be a nonexpansive self-mapping and $\{T_{i}\}_{i=1}^{N}:C\rightarrow H_{1}$be $k_{i}$-strictly pseudocontractive nonself-mappings. Assume that $\mathcal{F}=\operatorname{MEP}(F_{1},g_{1}) \cap \mathcal{S}\neq \emptyset$. Define a sequence $\{x_{n}\}$as follows:

$$ \textstyle\begin{cases} x_{0} \in C, \\ u_{n}=(1-\alpha _{n})x_{n}+\alpha _{n}(\tau _{n}Sx_{n}+(1-\tau _{n})T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}x_{n}), \\ x_{n+1}=T_{r_{n}}^{F_{1}}(I-r_{n}g_{1}) (u_{n}),\quad n\geq 1, \end{cases} $$

(3.21)

where $T_{i}^{n}=(1-\delta _{n}^{i})I+\delta _{n}^{i}P_{C}(\beta _{i}I+(1- \beta _{i})T_{i})$, $0\leq k_{i}\leq \beta _{i}<1$, $\delta _{n}^{i}\in (0,1)$for $i=1,2,\ldots,N$. Let $\{\alpha _{n}\}$, $\{\tau _{n}\}$be two real sequences in $(0,1)$and $\{r_{n}\}\subset (0,2\eta _{1})$. Suppose the following conditions (i)–(iv) of Theorem 3.1are satisfied. Then the sequence $\{x_{n}\}$converges weakly to $x^{*} \in \mathcal{F}$

Proof

Taking $A=0$ in Theorem 3.1, the conclusion of Corollary 3.2 is followed. □

In the above theorem, the sequence generated by algorithm (3.1) converges weakly to a common solution of a split mixed equilibrium problem and a hierarchical fixed point problem.

In this section, our other aim is to prove a strong convergence theorem for a hierarchical fixed point problem and split equilibrium problem for some special cases.

We consider the following hierarchical fixed point and split equilibrium problem: Find $x^{*} \in \Gamma \cap \mathcal{S}$ such that

$$ \begin{aligned} \bigl\langle x^{*}-Sx^{*},x^{*}-y \bigr\rangle \leq 0,\quad \forall y \in \Gamma \cap \mathcal{S}, \end{aligned} $$

(3.22)

where $\mathcal{S}=\bigcap_{i=1}^{N} \operatorname{Fix}(T_{i})$ and Γ is the solution set of the split equilibrium problem (1.5)–(1.6). When S is a contraction mapping, a special case of nonexpansive mappings, we prove a strong convergence theorem for the above problem. We need the following results for our study.

Lemma 3.3

([8])

Let $F_{1}:C\times C\rightarrow \mathbb{R}$be a bifunction satisfying Assumption Aand $T_{r}^{F_{1}}$be defined as in Lemma 2.6. Let $x,y\in H_{1}$and $r_{1},r_{2}>0$. Then

$$ \bigl\Vert T_{r_{2}}^{F_{1}}y-T_{r_{1}}^{F_{1}}x \bigr\Vert \leq \Vert y-x \Vert + \biggl\vert \frac{r_{2}-r_{1}}{r_{2}} \biggr\vert \bigl\Vert T_{r_{2}}^{F_{1}}y-y \bigr\Vert . $$

Lemma 3.4

([26])

Let $\{x_{n}\}$and $\{z_{n}\}$be bounded sequences in a Banach space X. Let $\{\beta _{n}\}$be a sequence in $[0,1]$which satisfies the condition $0<\liminf_{n\rightarrow \infty }\beta _{n}\leq \limsup_{n\rightarrow \infty }\beta _{n}<1$. Suppose $x_{n+1}=(1-\beta _{n}) z_{n}+\beta _{n} x_{n}$for all integer $n\geq 0$and $\limsup_{n\rightarrow \infty }(\|z_{n+1}-z_{n}\|-\|x_{n+1}-x_{n} \|)\leq 0$. Then $\lim_{n\rightarrow \infty }\|x_{n}-z_{n}\|=0$.

Lemma 3.5

([31])

Let $\{\alpha _{n}\}$be a sequence of non-negative real numbers such that

$$ \alpha _{n+1}\leq (1-\gamma _{n})\alpha _{n}+\delta _{n}, $$

where $\{\gamma _{n}\}$is a sequence in $(0,1)$and $\{\delta _{n}\}$is a sequence such that

• (i) $\sum_{n=1}^{\infty }\gamma _{n}=\infty$;

• (ii) $\limsup_{n\to \infty }\frac{\delta _{n}}{\gamma _{n}} \leq 0$or $\sum_{n=1}^{\infty }|\delta _{n}|<\infty$.

Then $\lim_{n\to \infty } \alpha _{n}=0$.

Now we are in a position to state our second main result for strong convergence.

Theorem 3.6

Let $H_{1}$and $H_{2}$be two Hilbert spaces. Let C and D be nonempty closed and convex subset of $H_{1}$and $H_{2}$, respectively. Let $A: H_{1} \rightarrow H_{2}$be a bounded linear operator. Let $F_{1}: C \times C\rightarrow \mathbb{R}$and $F_{2}: D \times D\rightarrow \mathbb{R}$be two bifunctions satisfying Assumption Aand $F_{2}$be upper semicontinuous. Let $S:C\rightarrow C$be a contraction mapping with coefficient $\rho \geq 0$and $\{T_{i}\}_{i=1}^{N}:C\rightarrow H_{1}$be $k_{i}$-strictly pseudocontractive nonself-mappings. Assume that the solution set of problem (3.22) is nonempty. Define a sequence $\{x_{n}\}$as follows:

$$ \textstyle\begin{cases} x_{0} \in C, \\ u_{n}=U(x_{n}+\gamma A^{*}(V-I)Ax_{n} ),\quad n\geq 1, \\ x_{n+1}=(1-\alpha _{n})x_{n}+\alpha _{n}(\tau _{n}Sx_{n}+(1-\tau _{n})T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}u_{n}), \end{cases} $$

(3.23)

where $U=T_{r_{n}}^{F_{1}}$, $V=T_{r_{n}}^{F_{2}}$, $T_{i}^{n}=(1-\delta _{n}^{i})I+\delta _{n}^{i}P_{C}(\beta _{i}I+(1- \beta _{i})T_{i})$, $0\leq k_{i}\leq \beta _{i}<1$, and $\delta _{n}^{i}\in (0,1)$for $i=1,2,\ldots,N$. Also let $\gamma \in (0,\frac{1}{L})$where L is the spectral radius of the operator $A^{*}A$and $A^{*}$is the adjoint operator of A. Let $\{\alpha _{n}\}$and $\{\tau _{n}\}$be two real sequences in $(0,1)$. Suppose the following conditions are satisfied:

• (i) $\liminf_{n\rightarrow \infty } r_{n} >0$and $\lim_{n\to \infty }|r_{n+1}- r_{n}| = 0$;

• (ii) $0\leq \alpha _{n}\leq b<1$for some $b\in (0,1)$and $0<\liminf_{n\rightarrow \infty }\alpha _{n}\leq \limsup_{n\rightarrow \infty }\alpha _{n}<1$;

• (iii) $\lim_{n\rightarrow \infty }\tau _{n}=0$and $\sum_{n=0}^{\infty }\tau _{n}=\infty$;

• (iv) $\lim_{n\rightarrow \infty }|\delta _{n+1}^{i}-\delta _{n}^{i}|=0$for $i=1,2,\ldots,N$.

Then the sequence $\{x_{n}\}$converges strongly to $p \in \Gamma \cap \mathcal{S}$, which is the unique solution of the following variational inequality:

$$\begin{aligned} \langle p-Sp, p-y\rangle \leq 0, \quad \forall y\in \Gamma \cap \mathcal{S}. \end{aligned}$$

(3.24)

Proof

We will prove the theorem for $N=2$. Then our method can be easily extended to the general case. First we show that the sequence $\{x_{n}\}$ is bounded.

Let $x^{*}$ be a solution of problem (3.22). Then $T_{r_{n}}^{F_{1}}x^{*}=x^{*}$ and $T_{r_{n}}^{F_{2}}Ax^{*}=Ax^{*}$. So, by (3.23) we get

$$\begin{aligned} \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}&= \bigl\Vert T_{r_{n}}^{F_{1}} \bigl(x_{n}+\gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr)-x^{*} \bigr\Vert ^{2} \\ & = \bigl\Vert T_{r_{n}}^{F_{1}}\bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr)-T_{r_{n}}^{F_{1}}x^{*} \bigr\Vert ^{2} \\ &\leq \bigl\Vert x_{n}+\gamma A^{*} \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n}-x^{*} \bigr\Vert \\ &\leq \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+\gamma ^{2} \bigl\Vert A^{*} \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert ^{2} \\ & +2\gamma \bigl\langle x_{n}-x^{*},A^{*} \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\rangle . \end{aligned}$$

(3.25)

Then

$$\begin{aligned} \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}&\leq \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+\gamma ^{2} \bigl\langle \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n}, A^{*}A\bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\rangle \\ &\quad {} +2\gamma \bigl\langle x_{n}-x^{*},A^{*} \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\rangle . \end{aligned}$$

(3.26)

Now, we have

$$\begin{aligned} \gamma ^{2} \bigl\langle \bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}, A^{*}A\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n} \bigr\rangle &\leq L\gamma ^{2} \bigl\langle \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n}, \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\rangle \\ &=L\gamma ^{2}\bigl\| (T_{r_{n}}^{F_{2}}-I)Ax_{n} \bigr\| ^{2}. \end{aligned}$$

(3.27)

Denoting $\Lambda :=2\gamma \langle x_{n}-x^{*},A^{*}(T_{r_{n}}^{F_{2}}-I)Ax_{n} \rangle$ and using (2.3), we have

$$\begin{aligned} \Lambda &=2\gamma \bigl\langle x_{n}-x^{*},A^{*} \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\rangle \\ &=2\gamma \bigl\langle A\bigl(x_{n}-x^{*}\bigr), \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\rangle \\ &=2\gamma \bigl\langle A\bigl(x_{n}-x^{*}\bigr)+ \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n}- \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n}, \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\rangle \\ &=2\gamma \bigl\{ \bigl\langle \bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax^{*},\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n} \bigr\rangle - \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n} \bigr\Vert ^{2}\bigr\} \\ &=2\gamma \biggl\{ \frac{1}{2} \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n} \bigr\Vert ^{2} - \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert ^{2} \biggr\} \\ &=-\gamma \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n} \bigr\Vert ^{2}. \end{aligned}$$

(3.28)

Using (3.26), (3.27) and (3.28), we get

$$ \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}\leq \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+\gamma (L\gamma -1) \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert ^{2}. $$

(3.29)

From the definition of γ, we obtain

$$ \bigl\Vert u_{n}-x^{*} \bigr\Vert \leq \bigl\Vert x_{n}-x^{*} \bigr\Vert . $$

(3.30)

Now

$$\begin{aligned} & \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \\ &\quad = \bigl\Vert (1-\alpha _{n}) \bigl(x_{n}-x^{*} \bigr)+\alpha _{n}\bigl[\tau _{n}\bigl(Sx_{n}-x^{*} \bigr)+(1- \tau _{n}) \bigl(T_{2}^{n}T_{1}^{n}u_{n}-x^{*} \bigr)\bigr] \bigr\Vert \\ &\quad \leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n}\bigl[\tau _{n} \bigl\Vert Sx_{n}-x^{*} \bigr\Vert +(1-\tau _{n}) \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-x^{*} \bigr\Vert \bigr] \\ &\quad \leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n}\bigl[\tau _{n} \bigl\Vert Sx_{n}-Sx^{*} \bigr\Vert +(1-\tau _{n}) \bigl\Vert u_{n}-x^{*} \bigr\Vert \bigr] \\ &\qquad {} +\alpha _{n}\tau _{n} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert \\ &\quad \leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n}\bigl[\tau _{n}\rho \bigl\Vert x_{n}-x^{*} \bigr\Vert +(1-\tau _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert \bigr] \\ &\qquad {} +\alpha _{n}\tau _{n} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert \\ &\quad \leq \bigl(1-(1-\rho )\alpha _{n}\tau _{n}\bigr) \bigl\Vert x_{n}-x^{*} \bigr\Vert +\alpha _{n} \tau _{n} \bigl\Vert Sx^{*}-x^{*} \bigr\Vert \\ &\quad \leq \max \biggl\{ \bigl\Vert x_{n}- x^{*} \bigr\Vert , \frac{ \Vert Sx^{*}-x^{*} \Vert }{(1-\rho )} \biggr\} \\ &\quad \leq \cdots \leq \max \biggl\{ \bigl\Vert x_{0}- x^{*} \bigr\Vert , \frac{ \Vert Sx^{*}-x^{*} \Vert }{(1-\rho )} \biggr\} . \end{aligned}$$

(3.31)

Hence the sequence $\{x_{n}\}$ is bounded.

Now, we show that

$$ \lim_{x\to \infty } \Vert x_{n+1}-x_{n} \Vert =0. $$

Let us consider $y_{n}=\tau _{n}Sx_{n}+(1-\tau _{n})T_{2}^{n}T_{1}^{n}u_{n}$. Then

$$\begin{aligned} \Vert y_{n+1}-y_{n} \Vert &\leq \tau _{n+1} \Vert Sx_{n+1}-Sx_{n} \Vert + \vert \tau _{n+1}- \tau _{n} \vert \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \\ & \quad {}+(1-\tau _{n+1}) \bigl\Vert T_{2}^{n+1}T_{1}^{n+1}u_{n+1}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert . \end{aligned}$$

(3.32)

In addition, we have

$$\begin{aligned} & \bigl\Vert T_{2}^{n+1}T_{1}^{n+1}u_{n+1}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \\ &\quad \leq \bigl\Vert T_{2}^{n+1}T_{1}^{n+1}u_{n+1}-T_{2}^{n}T_{1}^{n}u_{n+1} \bigr\Vert + \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n+1}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \\ &\quad \leq \bigl\Vert T_{2}^{n+1}T_{1}^{n+1}u_{n+1}-T_{2}^{n+1}T_{1}^{n}u_{n+1} \bigr\Vert \\ &\qquad {} + \bigl\Vert T_{2}^{n+1}T_{1}^{n}u_{n+1}-T_{2}^{n}T_{1}^{n}u_{n+1} \bigr\Vert + \Vert u_{n+1}-u_{n} \Vert \\ &\quad \leq \bigl\Vert T_{1}^{n+1}u_{n+1}-T_{1}^{n}u_{n+1} \bigr\Vert + \bigl\Vert T_{2}^{n+1}T_{1}^{n}u_{n+1}-T_{2}^{n}T_{1}^{n}u_{n+1} \bigr\Vert \\ &\qquad {} + \Vert u_{n+1}-u_{n} \Vert . \end{aligned}$$

(3.33)

It follows from the definition $T_{i}^{n}$ that

$$\begin{aligned} & \bigl\Vert T_{1}^{n+1}u_{n+1}-T_{1}^{n}u_{n+1} \bigr\Vert \\ &\quad = \bigl\Vert \bigl(1-\delta _{n+1}^{1} \bigr)u_{n+1}+\delta _{n+1}^{1}P_{C} \bigl(\beta _{1}I+(1- \beta _{1})T_{1} \bigr)u_{n+1} \\ &\qquad {} -\bigl(1-\delta _{n}^{1}\bigr)u_{n+1}+ \delta _{n}^{1}P_{C}\bigl(\beta _{1}I+(1- \beta _{1})T_{1} \bigr)u_{n+1} \bigr\Vert \\ &\quad \leq \bigl\vert \delta _{n+1}^{1}-\delta _{n}^{1} \bigr\vert \bigl( \Vert u_{n+1} \Vert + \bigl\Vert P_{C}\bigl(\beta _{1}I+(1- \beta _{1})T_{1}\bigr)u_{n+1} \bigr\Vert \bigr). \end{aligned}$$

Since $\lim_{n \to +\infty }|\delta _{n+1}^{1}-\delta _{n}^{1}|=0$, and $\{u_{n}\}$, $\{P_{C}(\beta _{1}I+(1-\beta _{1})T_{1})u_{n}\}$ are bounded, we get

$$ \lim_{n \to +\infty } \bigl\Vert T_{1}^{n+1}u_{n+1}-T_{1}^{n}u_{n+1} \bigr\Vert =0. $$

(3.34)

Similarly, we have

$$\begin{aligned} & \bigl\Vert T_{2}^{n+1}T_{1}^{n}u_{n+1}-T_{2}^{n}T_{1}^{n}u_{n+1} \bigr\Vert \\ &\quad \leq \bigl\vert \delta _{n+1}^{2}-\delta _{n}^{2} \bigr\vert \bigl( \bigl\Vert T_{1}^{n}u_{n+1} \bigr\Vert + \bigl\Vert P_{C}\bigl( \beta _{2}I+(1-\beta _{2})T_{2} \bigr)T_{1}^{n}u_{n+1} \bigr\Vert \bigr), \end{aligned}$$

from which it follows that

$$ \lim_{n \to +\infty } \bigl\Vert T_{2}^{n+1}T_{1}^{n+1}u_{n+1}-T_{2}^{n}T_{1}^{n}u_{n+1} \bigr\Vert =0. $$

(3.35)

Since

$$ u_{n}=T_{r_{n}}^{F_{1}}\bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr) $$

and

$$ u_{n+1}=T_{r_{n+1}}^{F_{1}}\bigl(x_{n+1}+ \gamma A^{*}\bigl(T_{r_{n+1}}^{F_{2}}-I \bigr)Ax_{n+1}\bigr), $$

it follows from Lemma 3.3 that

$$\begin{aligned} & \Vert u_{n+1}-u_{n} \Vert \\ &\quad = \bigl\Vert T_{r_{n+1}}^{F_{1}}\bigl(x_{n+1}+ \gamma A^{*}\bigl(T_{r_{n+1}}^{F_{2}}-I \bigr)Ax_{n+1}\bigr)-T_{r_{n}}^{F_{1}} \bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr) \bigr\Vert \\ &\quad \leq \bigl\Vert T_{r_{n+1}}^{F_{1}}\bigl(x_{n+1}+ \gamma A^{*}\bigl(T_{r_{n+1}}^{F_{2}}-I \bigr)Ax_{n+1}\bigr)-T_{r_{n+1}}^{F_{1}} \bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr) \bigr\Vert \\ &\qquad {} + \bigl\Vert T_{r_{n+1}}^{F_{1}}\bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr)-T_{r_{n}}^{F_{1}} \bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr) \bigr\Vert \\ &\quad \leq \bigl\Vert \bigl(x_{n+1}+\gamma A^{*} \bigl(T_{r_{n+1}}^{F_{2}}-I\bigr)Ax_{n+1}\bigr)- \bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr) \bigr\Vert \\ &\qquad {} + \biggl\vert \frac{r_{n+1}-r_{n}}{r_{n+1}} \biggr\vert \bigl\Vert T_{r_{n+1}}^{F_{1}}\bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr)-\bigl(x_{n}+\gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr) \bigr\Vert \\ &\quad \leq \bigl\Vert x_{n+1}-x_{n}-\gamma A^{*}A(x_{n+1}-x_{n}) \bigr\Vert +\gamma \Vert A \Vert \bigl\Vert T_{r_{n+1}}^{F_{2}}Ax_{n+1}-T_{r_{n}}^{F_{2}}Ax_{n} \bigr\Vert +\delta _{n} \\ &\quad \leq \bigl\{ \Vert x_{n+1}-x_{n} \Vert ^{2}-2\gamma \Vert Ax_{n+1}-Ax_{n} \Vert ^{2}+ \gamma ^{2} \Vert A \Vert ^{4} \Vert x_{n+1}-x_{n} \Vert ^{2} \bigr\} ^{\frac{1}{2}} \\ &\qquad {} +\gamma \Vert A \Vert \biggl\{ \Vert Ax_{n+1}-Ax_{n} \Vert + \biggl\vert \frac{r_{n+1}-r_{n}}{r_{n+1}} \biggr\vert \bigl\Vert T_{r_{n+1}}^{F_{2}}Ax_{n+1}-Ax_{n} \bigr\Vert \biggr\} +\delta _{n} \\ &\quad \leq \bigl(1-2\gamma \Vert A \Vert ^{2}+\gamma ^{2} \Vert A \Vert ^{4} \bigr)^{\frac{1}{2}} \Vert x_{n+1}-x_{n} \Vert +\gamma \Vert A \Vert ^{2} \Vert x_{n+1}-x_{n} \Vert +\gamma \Vert A \Vert \sigma _{n}+\delta _{n} \\ &\quad =\bigl(1-\gamma \Vert A \Vert ^{2}\bigr) \Vert x_{n+1}-x_{n} \Vert +\gamma \Vert A \Vert ^{2} \Vert x_{n+1}-x_{n} \Vert +\gamma \Vert A \Vert \sigma _{n}+\delta _{n} \\ &\quad = \Vert x_{n+1}-x_{n} \Vert +\gamma \Vert A \Vert \sigma _{n}+\delta _{n}, \end{aligned}$$

(3.36)

where

$$ \sigma _{n}= \biggl\vert \frac{r_{n+1}-r_{n}}{r_{n+1}} \biggr\vert \bigl\Vert T_{r_{n+1}}^{F_{2}}Ax_{n+1}-Ax_{n} \bigr\Vert $$

and

$$ \delta _{n}= \biggl\vert \frac{r_{n+1}-r_{n}}{r_{n+1}} \biggr\vert \bigl\Vert T_{r_{n+1}}^{F_{1}}\bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr)-\bigl(x_{n}+\gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr) \bigr\Vert . $$

Hence, using (3.34), (3.35) and (3.36) to (3.32) with the conditions (i) and (ii), we get

$$ \limsup_{n \to +\infty }\bigl( \Vert y_{n+1}-y_{n} \Vert - \Vert x_{n+1}-x_{n} \Vert \bigr) \leq 0. $$

Thus by Lemma 3.4, we conclude that $\lim_{n \to +\infty }\|y_{n}-x_{n}\|=0$, which implies that

$$ \lim_{n \to +\infty } \Vert x_{n+1}-x_{n} \Vert =0. $$

Since $T_{r_{n}}^{F_{1}}x^{*}=x^{*}$ and $T_{r_{n}}^{F_{1}}$ is firmly nonexpansive, we get

$$\begin{aligned} \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}&= \bigl\Vert T_{r_{n}}^{F_{1}} \bigl(x_{n}+\gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr)-x^{*} \bigr\Vert ^{2} \\ &= \bigl\Vert T_{r_{n}}^{F_{1}}\bigl(x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr)-T_{r_{n}}^{F_{1}}x^{*} \bigr\Vert ^{2} \\ &\leq \bigl\langle u_{n}-x^{*},x_{n}+ \gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}-x^{*} \bigr\rangle \\ &=\frac{1}{2} \bigl\{ \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}+\gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n}-x^{*} \bigr\Vert ^{2} \\ &\quad {} - \bigl\Vert \bigl(u_{n}-x^{*}\bigr)- \bigl[x_{n}+\gamma A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}-x^{*}\bigr] \bigr\Vert ^{2} \bigr\} \\ &=\frac{1}{2} \bigl\{ \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+\gamma (L \gamma -1) \bigl\Vert A^{*} \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert ^{2} \\ &\quad {} - \bigl\Vert u_{n}-x_{n}-\gamma A^{*} \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert ^{2} \bigr\} \\ &=\frac{1}{2} \bigl\{ \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \bigl[ \Vert u_{n}-x_{n} \Vert ^{2} \\ &\quad {} +\gamma ^{2} \bigl\Vert A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n} \bigr\Vert ^{2}-2\gamma \bigl\langle u_{n}-x_{n},A^{*}\bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n}\bigr\rangle \bigr] \bigr\} \\ &=\frac{1}{2} \bigl\{ \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \Vert u_{n}-x_{n} \Vert ^{2} \\ &\quad {} +2\gamma \bigl\Vert A(u_{n}-x_{n}) \bigr\Vert \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert \bigr\} . \end{aligned}$$

Hence, we obtain

$$ \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2}\leq \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \Vert u_{n}-x_{n} \Vert ^{2} +2 \gamma \bigl\Vert A(u_{n}-x_{n}) \bigr\Vert \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I \bigr)Ax_{n} \bigr\Vert . $$

(3.37)

Again,

$$\begin{aligned} & \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ &\quad = \bigl\Vert (1-\alpha _{n}) \bigl(x_{n}-x^{*} \bigr)+\alpha _{n}\bigl[\tau _{n}\bigl(Sx_{n}-x^{*} \bigr)+(1- \tau _{n}) \bigl(T_{2}^{n}T_{1}^{n}u_{n}-x^{*} \bigr)\bigr] \bigr\Vert ^{2} \\ &\quad = \bigl\Vert (1-\alpha _{n}) \bigl(x_{n}-x^{*} \bigr)+\alpha _{n}\bigl(T_{2}^{n}T_{1}^{n}u_{n}-x^{*} \bigr) +\alpha _{n}\tau _{n}\bigl(Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr) \bigr\Vert ^{2} \\ &\quad \leq \bigl\Vert (1-\alpha _{n}) \bigl(x_{n}-x^{*} \bigr)+\alpha _{n}\bigl(T_{2}^{n}T_{1}^{n}u_{n}-x^{*} \bigr) \bigr\Vert ^{2} \\ &\qquad {} +2\tau _{n}\bigl\langle Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n}, x_{n+1}-x^{*} \bigr\rangle \\ &\quad \leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+\alpha _{n} \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-x^{*} \bigr\Vert ^{2} \\ &\qquad {} +2\tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \\ &\quad \leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+\alpha _{n} \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2} \\ &\qquad {} +2\tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \bigl\Vert x_{n+1}-x^{*} \bigr\Vert . \end{aligned}$$

(3.38)

Hence, we have

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}&\leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} \\ &\quad {} +\alpha _{n}\bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+\gamma (L\gamma -1) \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert ^{2}\bigr) \\ &\quad {} +2\tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \bigl\Vert x_{n+1}-x^{*} \bigr\Vert , \end{aligned}$$

(3.39)

which gives

$$\begin{aligned} \alpha _{n}(1-L\gamma ) \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert ^{2}&\leq \Vert x_{n+1}-x_{n} \Vert \bigl( \Vert x_{n}-p \Vert + \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \bigr) \\ &\quad {} +2\tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \bigl\Vert x_{n+1}-x^{*} \bigr\Vert . \end{aligned}$$

(3.40)

Using the condition (iii) in (3.40), we get

$$ \lim_{n\to \infty } \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert =0. $$

(3.41)

Again,

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}&\leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+\alpha _{n} \bigl\Vert u_{n}-x^{*} \bigr\Vert ^{2} \\ &\quad {} +2\tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \bigl\Vert x_{n+1}-x^{*} \bigr\Vert . \end{aligned}$$

(3.42)

So, using (3.37) we get

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} &\leq (1-\alpha _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} +\alpha _{n}\bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \Vert u_{n}-x_{n} \Vert ^{2} \\ &\quad {} +2\gamma \bigl\Vert A(u_{n}-x_{n}) \bigr\Vert \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert \bigr) \\ &\quad {} +2\tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \bigl\Vert x_{n+1}-x^{*} \bigr\Vert , \end{aligned}$$

(3.43)

which gives

$$\begin{aligned} \alpha _{n} \Vert u_{n}-x_{n} \Vert ^{2} &\leq \Vert x_{n+1}-x_{n} \Vert \bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert + \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \bigr) \\ &\quad {} +2\tau _{n} \bigl\Vert Sx_{n}-T_{2}^{n}T_{1}^{n}u_{n} \bigr\Vert \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \\ &\quad {} +2\gamma \bigl\Vert A(u_{n}-x_{n}) \bigr\Vert \bigl\Vert \bigl(T_{r_{n}}^{F_{2}}-I\bigr)Ax_{n} \bigr\Vert . \end{aligned}$$

(3.44)

Using the condition (iii) to (3.44), we get

$$ \lim_{n\to \infty } \Vert u_{n}-x_{n} \Vert =0. $$

(3.45)

Using (3.45) we get

$$ \Vert x_{n+1}-u_{n} \Vert \leq \Vert x_{n+1}-x_{n} \Vert + \Vert x_{n}-u_{n} \Vert \to 0 \quad \text{as } n\to \infty . $$

(3.46)

Now

$$\begin{aligned} \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-u_{n} \bigr\Vert &\leq \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-y_{n} \bigr\Vert + \Vert y_{n}-u_{n} \Vert \\ &\leq \tau _{n} \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-Sx_{n} \bigr\Vert + \Vert y_{n}-u_{n} \Vert \\ &\leq \tau _{n} \Vert x_{n}-Sx_{n} \Vert +\tau _{n} \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-x_{n} \bigr\Vert + \Vert y_{n}-u_{n} \Vert \\ &\leq \tau _{n} \Vert x_{n}-Sx_{n} \Vert +\tau _{n} \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-u_{n} \bigr\Vert +\tau _{n} \Vert u_{n}-x_{n} \Vert \\ &\quad {} + \Vert y_{n}-u_{n} \Vert . \end{aligned}$$

Therefore, we have

$$\begin{aligned} \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-u_{n} \bigr\Vert &\leq \frac{\tau _{n}}{1-\tau _{n}} \Vert x_{n}-Sx_{n} \Vert +\frac{\tau _{n}}{1-\tau _{n}} \Vert u_{n}-x_{n} \Vert \\ &\quad {} +\frac{1}{1-\tau _{n}} \Vert y_{n}-u_{n} \Vert . \end{aligned}$$

(3.47)

Since $\alpha _{n}\|x_{n}-y_{n}\|=\|x_{n+1}-x_{n}\|$, $\|x_{n}-y_{n}\|\to 0$ as $n\to \infty$. So,

$$ \Vert y_{n}-u_{n} \Vert \leq \Vert y_{n}-x_{n} \Vert + \Vert x_{n}-u_{n} \Vert \to 0\quad \text{as } n\to \infty . $$

(3.48)

Hence,

$$ \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-u_{n} \bigr\Vert \to 0\quad \text{as } n\to \infty . $$

(3.49)

Now, we show that

$$ \limsup_{n\to \infty }\langle Sp-p, x_{n}-p\rangle \leq 0, $$

where p is the unique solution of the variational inequality (3.24). Since $\{x_{n}\}$ is bounded, there exists a subsequence $\{x_{n_{j}}\}$ of $\{x_{n}\}$ such that $x_{n_{j}}\rightharpoonup \bar{x}$ as $j\to \infty$ and

$$ \limsup_{n\to \infty }\langle Sp-p, x_{n}-p\rangle =\lim _{j\to \infty }\langle Sp-p, x_{n_{j}}-p\rangle . $$

Since $\|x_{n}-u_{n}\| \to 0$ as $n\to \infty$, $u_{n_{j}} \rightharpoonup \bar{x}$. Now, following similar steps to Theorem 3.1, we can show that $\bar{x}\in \Gamma \cap \mathcal{S}$. Hence

$$ \lim_{j\to \infty }\langle Sp-p, x_{n_{j}}-p\rangle =\langle Sp-p, \bar{x}-p\rangle \leq 0. $$

(3.50)

Finally, we show that $x_{n}\to p$ and $n\to \infty$. From (2.1) and (3.23), we have

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} &= \bigl\Vert (1-\alpha _{n}) (x_{n}-p)+\alpha _{n}\bigl[\tau _{n}Sx_{n}+(1- \tau _{n})T_{2}^{n}T_{1}^{n}u_{n}-p \bigr] \bigr\Vert ^{2} \\ &= \bigl\Vert (1-\alpha _{n}) (x_{n}-p)+\alpha _{n}(1-\tau _{n}) \bigl(T_{2}^{n}T_{1}^{n}u_{n}-p \bigr)+ \alpha _{n}\tau _{n}(Sx_{n}-p) \bigr\Vert ^{2} \\ &\leq \bigl\Vert (1-\alpha _{n}) (x_{n}-p)+\alpha _{n}(1-\tau _{n}) \bigl(T_{2}^{n}T_{1}^{n}u_{n}-p \bigr) \bigr\Vert ^{2} \\ &\quad {} + 2\alpha _{n}\tau _{n}\langle Sx_{n}-p,x_{n+1}-p \rangle \\ &\leq (1-\alpha _{n}) \Vert x_{n}-p \Vert ^{2}+\alpha _{n}(1-\tau _{n})^{2} \bigl\Vert T_{2}^{n}T_{1}^{n}u_{n}-p \bigr\Vert ^{2} \\ &\quad {} + 2\alpha _{n}\tau _{n}\langle Sx_{n}-p,x_{n+1}-p \rangle \\ &\leq \bigl(1-\alpha _{n}+\alpha _{n}(1-\tau _{n})^{2}\bigr) \Vert x_{n}-p \Vert ^{2}+2 \alpha _{n}\tau _{n}\langle Sx_{n}-Sp,x_{n+1}-p\rangle \\ &\quad {} +2\alpha _{n}\tau _{n}\langle Sp-p,x_{n+1}-p \rangle \\ &\leq \bigl(1-\alpha _{n}+\alpha _{n}(1-\tau _{n})^{2}\bigr) \Vert x_{n}-p \Vert ^{2}+2 \alpha _{n}\tau _{n} \Vert Sx_{n}-Sp \Vert \Vert x_{n+1}-p \Vert \\ &\quad {} +2\alpha _{n}\tau _{n}\langle Sp-p,x_{n+1}-p \rangle \\ &\leq \bigl(1-\alpha _{n}+\alpha _{n}(1-\tau _{n})^{2}\bigr) \Vert x_{n}-p \Vert ^{2} \\ &\quad {} +\alpha _{n}\tau _{n}\bigl[ \Vert Sx_{n}-Sp \Vert ^{2}+ \Vert x_{n+1}-p \Vert ^{2}\bigr]+2 \alpha _{n}\tau _{n} \langle Sp-p,x_{n+1}-p\rangle \\ &\leq \bigl(1-\alpha _{n}+\alpha _{n}(1-\tau _{n})^{2}+\alpha _{n}\tau _{n} \rho \bigr) \Vert x_{n}-p \Vert ^{2}+\alpha _{n}\tau _{n} \Vert x_{n+1}-p \Vert ^{2} \\ &\quad {} +2\alpha _{n}\tau _{n}\langle Sp-p,x_{n+1}-p \rangle \\ &=\bigl(1-\alpha _{n}\tau _{n}-\alpha _{n}\tau _{n}(1-\rho -\tau _{n})\bigr) \Vert x_{n}-p \Vert ^{2}+\alpha _{n}\tau _{n} \Vert x_{n+1}-p \Vert ^{2} \\ &\quad {} +2\alpha _{n}\tau _{n}\langle Sp-p,x_{n+1}-p \rangle . \end{aligned}$$

From the above inequality, it follows that

$$\begin{aligned} \Vert x_{n+1}-p \Vert ^{2} &\leq \biggl(1- \frac{\alpha _{n}\tau _{n}(1-\rho -\tau _{n})}{1-\alpha _{n}\tau _{n}}\biggr) \Vert x_{n}-p \Vert ^{2} \\ &\quad {} +2\frac{\alpha _{n}\tau _{n}}{1-\alpha _{n}\tau _{n}}\langle Sp-p,x_{n+1}-p \rangle . \end{aligned}$$

(3.51)

Considering $a_{n}=\|x_{n}-p\|^{2}$, $b_{n}= \frac{\alpha _{n}\tau _{n}(1-\rho -\tau _{n})}{1-\alpha _{n}\tau _{n}}$ and $c_{n}=2\frac{\alpha _{n}\tau _{n}}{1-\alpha _{n}\tau _{n}}\langle Sp-p,x_{n+1}-p \rangle$, we get $a_{n+1}\leq (1-b_{n})a_{n}+c_{n}$. Hence, from Lemma 3.5, we conclude that $\{x_{n}\}$ converges strongly to p. □

The following consequence is a strong convergence theorem for computing a common solution of an equilibrium problem and a hierarchical fixed point problem in a real Hilbert space.

Corollary 3.7

Let $H_{1}$be a Hilbert spaces. Let C be nonempty closed and convex subset of $H_{1}$. Let $F_{1}: C \times C\rightarrow \mathbb{R}$and be a bifunction satisfying Assumption A. Let $S:C\rightarrow C$be a contraction mapping with coefficient $\rho \geq 0$and $\{T_{i}\}_{i=1}^{N}:C\rightarrow H_{1}$be $k_{i}$-strictly pseudocontractive nonself-mappings. Assume that $EP(F,C)\cap \mathcal{S}\neq \emptyset$. Define a sequence $\{x_{n}\}$as follows:

$$ \textstyle\begin{cases} x_{0} \in C, \\ u_{n}=T_{r_{n}}^{F_{1}}(x_{n}), \quad n \geq 1, \\ x_{n+1}=(1-\alpha _{n})x_{n}+\alpha _{n}(\tau _{n}Sx_{n}+(1-\tau _{n})T_{N}^{n}T_{N-1}^{n} \cdots T_{1}^{n}u_{n}), \end{cases} $$

(3.52)

where $T_{i}^{n}=(1-\delta _{n}^{i})I+\delta _{n}^{i}P_{C}(\beta _{i}I+(1- \beta _{i})T_{i})$, $0\leq k_{i}\leq \beta _{i}<1$, and $\delta _{n}^{i}\in (0,1)$for $i=1,2,\ldots,N$. Let $\{\alpha _{n}\}$and $\{\tau _{n}\}$be two real sequences in $(0,1)$. Suppose the following conditions (i)–(iv) of Theorem 3.6are satisfied. Then the sequence $\{x_{n}\}$converges strongly to $p \in EP(F,C)\cap \mathcal{S}$, which is the unique solution of the following variational inequality:

$$ \langle p-Sp, p-y\rangle \leq 0,\quad \forall y\in EP(F,C)\cap \mathcal{S}. $$

(3.53)

Proof

Taking $A=0$ in Theorem 3.6, the conclusion of Corollary 3.7 is followed. □

4 Conclusions

In this paper, we have introduced a modified Krasnoselski–Mann type iterative method for approximating a common solution of a split mixed equilibrium problem and a hierarchical fixed point problem of a finite collection of k-strictly pseudocontractive nonself-mappings.

Our main results improve and extend the corresponding results of Moudafi and Mainge [24], Moudafi [22] and Kazmi et al. [13] from single nonexpansive self-mapping to a finite collection of $k_{i}$-strictly pseudocontractive nonself-mappings. Also, we have studied our iterative algorithm by giving an explicit formula for selecting the step size so that the implementation of the proposed algorithm does not require any prior information of operator norm. We also have established strong convergence results for a special class of hierarchical fixed point and split mixed equilibrium problem.

In [5], Ceng and Petruşel have introduced a cyclic algorithm for HFPP of a finite collection of nonexpansive nonself-mappings in Banach spaces. Whether we can extend Theorems 3.1 and 3.6 to Banach spaces will be an issue of future research.