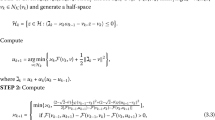Abstract
In this paper, we introduce a new algorithm for finding a common element of the set of fixed points of N strict pseudocontractions and the set of solutions of equilibrium problems with a pseudomonotone and Lipschitz-type continuous bifunction. The scheme is motivated by the idea of extragradient methods and fixed point iteration methods. We show that the iterative sequences generated by this algorithm converge strongly to the above mentioned common element under some suitable conditions on algorithm parameters in a real Hilbert space. And also, we consider the variational inequality problems as an application.
MSC:46H09, 47H10, 47J25, 65K10.
Similar content being viewed by others
1 Introduction
Let C be a nonempty closed convex subset of a real Hilbert space H with the inner product and the norm , and let f be a bifunction from into R such that for all . We consider the equilibrium problem in the sense of Blum and Oettli [1]: Find such that

for all .
We denote by the set of solutions of the equilibrium problem .
We know that the problem covers many important problems in optimization and nonlinear analysis. It has also found many applications in economics, transportation and engineering (see [1, 2] and the references quoted therein). Theory and methods for solving this problem have been developed by many authors [3–7]. Alternatively, the problem of finding a common fixed point of a sequence of finite self-mappings () is described as follows: Find such that

where is the set of fixed points of the mappings () on C. This problem has now become a mature subject in nonlinear analysis. The theory and solution methods of this problem can be found in many research papers and monographs (see [8–10]).
We are interested in the problem of finding a common element of the set of solutions of the equilibrium problem and the set of solutions of the fixed problem (FP), namely: Find such that
A special case of problem (1.1) is that , and this problem is reduced to finding a common element of the set of solutions of variational inequalities, i.e., find such that

and the set solutions of a fixed point problem (see [11–17]).
In this paper, we introduce a new iterative scheme for solving problem (1.1). This method can be considered to be an improvement of the viscosity approximation method in [15, 18, 19] and the iterative method in [20] via an improvement of the extragradient methods [3, 4, 21–23].
The paper is organized as follows. Section 2 recalls some concepts in equilibrium problems and fixed point problems that are used in the sequel and an iterative algorithm for solving problem (1.1). In Section 3, we prove the convergence theorems for the algorithms which are defined in Section 2 as the main results of this paper. In Section 4, we consider the variational inequality problems as an application of the main theorem.
2 Preliminaries
We first recall the following definitions that will be used for the main theorem.
Definition 2.1 Let C be a nonempty closed convex subset of a real Hilbert space H. A bifunction is said to be
-
(a)
monotone on C if , ;
-
(b)
pseudomonotone on C if implies , ;
-
(c)
Lipschitz-type continuous on C with two constants and if
(2.1)
We know that every monotone bifunction f is pseudomonotone, but the converse is not true (see [24]).
Definition 2.2 Let C be a nonempty closed convex subset of a real Hilbert space H. A mapping is said to be a strict pseudocontraction if there exists a constant such that
where I is the identity mapping on H. If , then S is called nonexpansive on C.
Now, we define the projection on C, denoted by , i.e.,
And we use the symbols ⇀ and → to denote weak convergence and strong convergence, respectively. The following proposition gives some useful properties for strict pseudocontractions.
Proposition 2.3 [25]
Let C be a nonempty closed convex subset of a real Hilbert space H, let be an L-strict pseudocontraction, and for each , let be an -strict pseudocontraction for some . Then we have the following.
-
(a)
S satisfies the following Lipschitz condition:
-
(b)
is demiclosed at zero. That is, if the sequence is in C such that and , then ;
-
(c)
The set is closed and convex;
-
(d)
If () and , then is an -strict pseudocontraction, where ;
-
(e)
If is the same as in (d) and has a common fixed point, then
Many authors studied the problem of finding a common fixed point of a finite family of mappings. For instance, Marino and Xu [26] constructed an iterative algorithm for finding a common fixed point of N strict pseudocontractions (). They defined the sequence starting from and taking
where the control sequence of parameters was made in order to get the guarantee for the convergence of the iterative sequence . And they proved that the sequence converges weakly to the point .
Recently, Chen et al. [20] introduced a new iterative scheme for finding a common element of the set of common fixed points of a sequence of strict pseudocontractions and the set of solutions of the equilibrium problem in a real Hilbert space H. Given a starting point , three iterative sequences , and are generated as the following scheme:
Here, two sequences and are given as control parameters. The authors proved that the sequences , and converged strongly to the same point , under certain conditions on and , such that
where S is a nonexpansive mapping of C into itself defined by
for all .
The methods for finding a common element of the sets and in a real Hilbert space have been studied in many research papers (see [7, 17, 21, 22, 27–30]).
We need the following assumptions for the main theorems.
Assumption 2.4 The bifunction f satisfies the following conditions:
-
(i)
f is pseudomonotone and weakly continuous on C;
-
(ii)
f is Lipschitz-type continuous on C;
-
(iii)
for each , is convex and subdifferentiable on C.
Assumption 2.5 Every is an -strict pseudocontraction for some .
Assumption 2.6 The solution set of (1.1) is nonempty, i.e.,
Note that if , where is the set of relative interior points of the domain of , then Assumption 2.4(iii) is satisfied. Now we construct the new algorithms as follows.
Algorithm 2.7 Initialization: Choose positive sequences , , , and satisfying the following conditions:
Take an initial point and set .
Iteration k: Carry out three steps below continuously.
-
Step 1. Solve two strongly convex programs:
-
Step 2. Compute the iterations
-
Step 3. Set
Compute .
Increase k by one and go back to Step 1.
3 Convergence of the algorithms
In this section, we study the convergence of Algorithm 2.7. We need the following useful lemmas for the main theorems.
Lemma 3.1 [2]
Let C be a nonempty closed convex subset of a real Hilbert space H, and let be subdifferentiable on C. Then is a solution of the following convex problem:
if and only if
where denotes the subdifferential of g and is the (outward) normal cone of C at .
Lemma 3.2 [8]
Let C be a nonempty closed convex subset of a real Hilbert space H and . Let be a bounded sequence such that every weakly cluster point of belongs to C and
Then converges strongly to as .
Now, we are in a position to prove the main theorem.
Theorem 3.3 Let C be a nonempty closed convex subset of a real Hilbert space H. Suppose that Assumptions 2.4-2.6 are satisfied. Then the sequences , and generated by Algorithm 2.7 converge strongly to the same point , where
Proof The proof of this theorem is divided into several steps.
Step 1. Suppose that . Then we have
Since is convex on C for each , by Lemma 3.1, we see that
if and only if
where is the (outward) normal cone of C at .
Since is subdifferentiable on C, by the well-known Moreau-Rockafellar theorem (see [31]), there exists such that
Substituting into this inequality, we obtain
And also, it follows from (3.3) that , where and . By the definition of the normal cone , we have
Substituting into the last inequality, we obtain
Combining (3.4) and (3.6), we have
Since , for all , and f is pseudomonotone on C, we have . Hence, (3.7) implies that
From Lipschitz condition (2.1) for f with , and , we have
Combining (3.8) and (3.9), we get
Similarly, since is the unique solution of the strongly convex program
we have
Substituting into the last inequality, we have
Since
from (3.10), (3.11), we have
Hence, we have
The implies that the inequality (3.2) holds.
Step 2. Next, we show that
for all .
Using Step 1 and , we have
where .
Set
Let , using Proposition 2.3(d), (3.12) and the relation
and , we have
where . This means that . Hence
Step 3. Now, we have to prove that
for all .
We show this assertion by mathematical induction. For we have . Hence by Step 2, we obtain
Assume that for some ,
From it follows that
Using this and (3.14), we have
Hence we have
Then it follows from Step 2 that
Consequently, we have
Step 4. Next, we claim that
It follows from Step 2 and that
Hence, we get that is bounded. By Step 1, also the sequences and are bounded. Otherwise, we have
and hence . Using this and , we have
Therefore, there exists
Using , and the property of projections
we have
Combining this and (3.16), we get
It follows from that , i.e.,
Hence
Then, by (3.17), we have
Step 2 and (3.16) imply that is bounded, and hence and are also bounded.
By (3.13), we have
From this and (3.18), we obtain
Using (3.13), we also have
and hence
Similarly, we have
Combining (3.20), (3.21) and , we have
This completes the proof of Step 4.
In Step 5 and Step 6 of this theorem, we consider weakly clusters of . It follows from (3.15) that the sequence is bounded, and hence there exists a subsequence converging weakly to as . By Step 4, also the sequences , and converge weakly to .
Step 5. Claim that .
For each , we suppose that converges as such that . Then we have
Since , from Step 4 and
we obtain that . By Proposition 2.3(b), we have
Then, it implies that from Proposition 2.3(e).
Step 6. Now we prove that if as , then we have .
Since is the unique strongly convex problem
from Lemma 3.1, we have
It follows that
where and . The definition of the normal cone implies that
On the other hand, since is subdifferentiable on C, by the Moreau-Rockafellar theorem [32], there exists such that
Combining this with (3.23), we have
Hence
Then, using , Step 2, as and weak continuity of f, we have
This means that .
Step 7. Finally, we claim that the sequences , , and converge strongly to the same point , where
From Step 5 and Step 6 it follows that for every weakly cluster point of the sequence ,
On the other hand, using the definition of , we have
Combining this with (3.15), we obtain
for all . For , we have
By Lemma 3.2, we know that the sequence converges strongly to as , where
We also have that as by Step 4. □
4 Applications
Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a function from C into H. In this section, we consider the variational inequality problem which is presented as follows:
Find such that

Let be defined by . Then problem can be written in . The set of solutions of is denoted by .
The function F is called
-
strongly monotone on C with if
-
monotone on C if
-
pseudomonotone on C if
-
Lipschitz continuous on C with constants if
Since
from Algorithm 2.7, we obtain the algorithm for finding a common element of the set of fixed points of p strict pseudocontractions and the solution set of variational inequality problem .
Algorithm 4.1 Initialization: Choose positive sequences , , , and satisfying the conditions:
Find an initial point .
Iteration k: Perform the three steps below.
-
Step 1. Solve two strongly convex programs:
-
Step 2. Compute the iterations
-
Step 3. Set
Compute .
Increase k by one and go back to Step 1.
Now, we can prove the following convergence theorem with respect to from Theorem 3.3.
Theorem 4.2 Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a function from C into H such that F is pseudomonotone, weakly continuous and L-Lipschitz continuous on C. If each , is -strict pseudocontraction for some and
then the sequences , and generated by Algorithm 4.1 converge strongly to the same point , where
References
Blum E, Oettli W: From optimization and variational inequality to equilibrium problems. Math. Stud. 1994, 63: 127–149.
Daniele P, Giannessi F, Maugeri A: Equilibrium Problems and Variational Models. Kluwer Academic, Dordrecht; 2003.
Anh PN: A logarithmic quadratic regularization method for solving pseudo-monotone equilibrium problems. Acta Math. Vietnam. 2009, 34: 183–200.
Anh PN: An LQP regularization method for equilibrium problems on polyhedral. Vietnam J. Math. 2008, 36: 209–228.
Chang SS, Cho YJ, Kim JK: Approximation methods of solutions for equilibrium problem in Hilbert spaces. Dyn. Syst. Appl. 2008, 17: 503–508.
Mastroeni G: Gap function for equilibrium problems. J. Glob. Optim. 2004, 27: 411–426.
Peng JW: Iterative algorithms for mixed equilibrium problems, strict pseudocontractions and monotone mappings. J. Optim. Theory Appl. 2010, 144: 107–119. 10.1007/s10957-009-9585-5
Goebel K, Kirk WA: Topics on Metric Fixed Point Theory. Cambridge University Press, Cambridge; 1990.
Kim JK, Sahu DR, Nam YM: Convergence theorem for fixed points of nearly uniformly L -Lipschitzian asymptotically generalized ϕ -hemicontractive mappings. Nonlinear Anal. TMA 2009, 71: 2833–2838. doi:10.1016/j.na.2009.06.091 10.1016/j.na.2009.06.091
Kim JK, Nam YM, Sim JY: Convergence theorem of implicit iterative sequences for a finite family of asymptotically quasi-nonexpansive type mappings. Nonlinear Anal. TMA 2009, 71: 2839–2848. doi:10.1016/j.na.2009.06.090 10.1016/j.na.2009.06.090
Chang SS, Lee HWJ, Chan CK, Kim JK: Approximating solutions of variational inequalities for asymptotically nonexpansive mappings. Appl. Math. Comput. 2009, 212: 51–59. 10.1016/j.amc.2009.01.078
Kim JK: Strong convergence theorems by hybrid projection methods for equilibrium problems and fixed point problems of the asymptotically quasi- ϕ -nonexpansive mappings. Fixed Point Theory Appl. 2011. doi:10.1186/1687–1812–2011–10
Kim JK, Cho SY, Qin X: Some results on generalized equilibrium problems involving strictly pseudocontractive mappings. Acta Math. Sci., Ser. B 2011, 31(5):985–996.
Nadezhkina N, Takahashi W: Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings. J. Optim. Theory Appl. 2006, 128: 191–201. 10.1007/s10957-005-7564-z
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J. Math. Anal. Appl. 2007, 331: 506–515. 10.1016/j.jmaa.2006.08.036
Takahashi S, Toyoda M: Weakly convergence theorems for nonexpansive mappings and monotone mappings. J. Optim. Theory Appl. 2003, 118: 417–428. 10.1023/A:1025407607560
Zeng LC, Yao JC: Strong convergence theorem by an extragradient method for fixed point problems and variational inequality problems. Taiwan. J. Math. 2010, 10: 1293–1303.
Li XS, Huang J, Kim JK: General viscosity approximation methods for common fixed points of nonexpansive semigroup in Hilbert spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 783502. doi:10.1155/2011/783502
Li XS, Kim JK, Huang NJ: Viscosity approximation of common fixed points for L -Lipschitzian semigroup of pseudocontractive mappings in Banach spaces. J. Inequal. Appl. 2009., 2009: Article ID 936121. doi:10.1155/2009/936121
Chen R, Shen X, Cui S: Weak and strong convergence theorems for equilibrium problems and countable strict pseudocontractions mappings in Hilbert space. J. Inequal. Appl. 2010. doi:10.1155/2010/474813
Kim JK, Buong N: Regularization inertial proximal point algorithm for monotone hemicontinuous mapping and inverse strongly monotone mappings in Hilbert spaces. J. Inequal. Appl. 2010., 2010: Article ID 451916. doi:10.1155/2010/451916
Kim JK, Anh PN, Nam YM: Strong convergence of an extended extragradient method for equilibrium problems and fixed point problems. J. Korean Math. Soc. 2011, 47: 187–200.
Kim JK, Tuyen TM: Regularization proximal point algorithm for finding a common fixed point of a finite family of nonexpansive mappings in Banach spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 52. doi:10.1186/1687–1812–2011–52
Schaible S, Karamardian S, Crouzeix JP: Characterizations of generalized monotone maps. J. Optim. Theory Appl. 1993, 76: 399–413. 10.1007/BF00939374
Acedo GL, Xu HK: Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Anal. 2007, 67: 2258–2271. 10.1016/j.na.2006.08.036
Marino-Yanes C, Xu HK: Strong convergence of the CQ method for fixed point processes. Nonlinear Anal. 2006, 64: 2400–2411. 10.1016/j.na.2005.08.018
Ceng LC, Petrusel A, Lee C, Wong MM: Two extragradient approximation methods for variational inequalities and fixed point problems of strict pseudo-contractions. Taiwan. J. Math. 2009, 13: 607–632.
Wang S, Cho YJ, Qin X: A new iterative method for solving equilibrium problems and fixed point problems for infinite family of nonexpansive mappings. Fixed Point Theory Appl. 2010. doi:10.1155/2010/165098
Wang S, Guo B: New iterative scheme with nonexpansive mappings for equilibrium problems and variational inequality problems in Hilbert spaces. J. Comput. Appl. Math. 2010, 233: 2620–2630. 10.1016/j.cam.2009.11.008
Yao Y, Liou YC, Wu YJ: An extragradient method for mixed equilibrium problems and fixed point problems. Fixed Point Theory Appl. 2009. doi:10.1155/2009/632819
Rockafellar RT: Convex Analysis. Princeton University Press, Princeton; 1970.
Kim JK, Cho SY, Qin X: Hybrid projection algorithms for generalized equilibrium problems and strictly pseudocontractive mappings. J. Inequal. Appl. 2010., 2010: Article ID 312602. doi:10.1155/2010/312602
Acknowledgements
This work was supported by the Kyungnam University Foundation Grant 2011.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The main idea of this paper was proposed by JKK. JKK and WHL prepared the manuscript initially and performed all the steps of proof in this research. Both authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, J.K., Lim, W.H. A new iterative algorithm of pseudomonotone mappings for equilibrium problems in Hilbert spaces. J Inequal Appl 2013, 128 (2013). https://doi.org/10.1186/1029-242X-2013-128
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-128