Abstract
We consider a hybrid projection method for finding a common element in the fixed point set of an asymptotically quasi-ϕ-nonexpansive mapping and in the solution set of an equilibrium problem. Strong convergence theorems of common elements are established in a uniformly smooth and strictly convex Banach space which has the Kadec-Klee property.
2000 Mathematics subject classification: 47H05, 47H09, 47H10, 47J25
Similar content being viewed by others
1. Introduction and Preliminaries
Let E be a real Banach space, E* the dual space of E and C a nonempty closed convex subset of E. Let f be a bifunction from C × C to ℝ, where ℝ denotes the set of real numbers.
In this paper, we consider the following equilibrium problem. Find p ∈ C such that

We denote EP(f) the solution set of the equilibrium problem (1.1). That is,

Given a mapping Q : C → E*, let

Then p ∈ EP(f) if and only if p is a solution of the following variational inequality problem. Find p such that

Numerous problems in physics, optimization and economics reduce to find a solution of (1.1) (see [1–4]). Let T : C → C be a mapping.
The mapping T is said to be asymptotically regular on C if for any bounded subset K of C,

The mapping T is said to be closed if for any sequence {x n } ⊂ C such that

and

then Tx0 = y0.
A point x ∈ C is a fixed point of T provided Tx = x. In this paper, we denote F(T) the fixed point set of T and denote → and ⇀ the strong convergence and weak convergence, respectively.
Recall that the mapping T is said to be nonexpansive if

T is said to be quasi-nonexpansive if F(T) ≠ Ø and

T is said to be asymptotically nonexpansive if there exists a sequence {k n } ⊂ [1, ∞) with k n → 1 as n → ∞ such that

T is said to be asymptotically quasi-nonexpansive if F(T) ≠ Ø and there exists a sequence {k n } ⊂ [1, ∞) with k n → 1 as n → ∞ such that

The class of asymptotically nonexpansive mappings was introduced by Goebel and Kirk [5] in 1972. They proved that if C is nonempty bounded closed and convex then every asymptotically nonexpansive self-mapping T on C has a fixed point in uniformly convex Banach spaces. Further, the fixed point set of T is closed and convex.
Recently, many authors considered the problem of finding a common element in the set of fixed points of a nonexpansive mapping and in the set of solutions of the equilibrium problem (1.1) based on iterative methods in the framework of real Hilbert spaces; see, for instance [4, 6–14] and the references therein. However, there are few results presented in Banach spaces.
In this paper, we will consider the problem in a Banach space. Before proceeding further, we give some definitions and propositions in Banach spaces.
Let E be a Banach space with the dual E*. We denote by J the normalized duality mapping from E to 2E*defined by

where 〈•,•〉 denotes the generalized duality pairing.
A Banach space E is said to be strictly convex if  for all x, y ∈ E with ||x|| = ||y|| = 1 and x ≠ y. It is said to be uniformly convex if limn→∞||x
n
- y
n
|| = 0 for any two sequences {x
n
} and {y
n
} in E such that ||x
n
|| = ||y
n
|| = 1 and
for all x, y ∈ E with ||x|| = ||y|| = 1 and x ≠ y. It is said to be uniformly convex if limn→∞||x
n
- y
n
|| = 0 for any two sequences {x
n
} and {y
n
} in E such that ||x
n
|| = ||y
n
|| = 1 and

Let U E = {x ∈ E : ||x|| = 1} be the unit sphere of E. Then the Banach space E is said to be smooth provided

exists for each x, y ∈ U E . It is said to be uniformly smooth if the limit (1.3) is attained uniformly for x, y ∈ U E . It is well known that if E is uniformly smooth, then J is uniformly norm-to-norm continuous on each bounded subset of E. It is also well known that if E is uniformly smooth if and only if E* is uniformly convex.
Recall that a Banach space E has the Kadec-Klee property [15–17], if for any sequence {x n } ⊂ E and x ∈ E with x n ⇀ x and ||x n || → ||x||, then ||x n - x|| → 0 as n → ∞. It is well known that if E is a uniformly convex Banach space, then E has the Kadec-Klee property.
As we all know that if C is a nonempty closed convex subset of a Hilbert space H and P C : H → C is the metric projection of H onto C, then P C is nonexpansive. This fact actually characterizes Hilbert spaces and consequently, it is not available in more general Banach spaces. In this connection, Alber [18] recently introduced a generalized projection operator Π C in a Banach space E which is an analogue of the metric projection in Hilbert spaces.
Next, we assume that E is a smooth Banach space. Consider the functional defined by

Observe that, in a Hilbert space H, (1.4) is reduced to ϕ(x, y) = ||x-y||2 , x, y ∈ H. The generalized projection Π
C
: E → C is a mapping that assigns to an arbitrary point x ∈ E the minimum point of the functional ϕ(x, y), that is,  , where
, where  is the solution to the minimization problem
is the solution to the minimization problem

The existence and uniqueness of the operator Π C follows from the properties of the functional ϕ(x, y) and strict monotonicity of the mapping J (see, for example, [15, 17–19]). We know that Π C = P C in Hilbert spaces. It is obvious from the definition of function ϕ that

Remark 1.1. Let E be a reflexive, strictly convex and smooth Banach space. Then for x, y ∈ E, ϕ(x, y) = 0 if and only if x = y. It is sufficient to show that if ϕ(x, y) = 0 then x = y. From (1.5), we have ||x|| = ||y||. This implies that 〈x, Jy〉 = ||x||2 = ||Jy||2. From the definition of J, we have Jx = Jy. Therefore, we have x = y (see [15, 17]).
Let C be a nonempty closed convex subset of E and T a mapping from C into itself. A point p in C is said to be an asymptotic fixed point of T[20] if C contains a sequence {x n } which converges weakly to p such that

The set of asymptotic fixed points of T will be denoted by 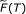 .
.
A mapping T from C into itself is said to be relatively nonexpansive [21–23] if  and
and

for all x ∈ C and p ∈ F(T).
The mapping T is said to be relatively asymptotically nonexpansive [24] if  and there exists a sequence {k
n
} ⊂ [1, ∞) with k
n
→ 1 as n → ∞ such that
and there exists a sequence {k
n
} ⊂ [1, ∞) with k
n
→ 1 as n → ∞ such that

for all x ∈ C, p ∈ F(T) and n ≥ 1. The asymptotic behavior of a relatively nonexpansive mapping was studied in [21–23].
The mapping T is said to be ϕ-nonexpansive if

for all x, y ∈ C.
The mapping T is said to be quasi-ϕ-nonexpansive [25–27] if F(T) ≠ ∅ and

for all x ∈ C and p ∈ F(T).
The mapping T is said to be asymptotically ϕ-nonexpansive if there exists a sequence {k n } ⊂ [1, ∞) with k n → 1 as n → ∞ such that

for all x, y ∈ C.
The mapping T is said to be asymptotically quasi-ϕ-nonexpansive [27, 28] if F(T) ≠ ∅ and there exists a sequence {k n } ⊂ [0, ∞) with k n → 1 as n → ∞ such that

for all x ∈ C, p ∈ F(T) and n ≥ 1.
Remark 1.2. The class of (asymptotically) quasi-ϕ-nonexpansive mappings is more general than the class of relatively (asymptotically) nonexpansive mappings which requires the restriction:  . In the framework of Hilbert spaces, (asymptotically) quasi-ϕ-nonexpansive mappings is reduced to (asymptotically) quasi-nonexpansive mappings (cf. [29–32]).
. In the framework of Hilbert spaces, (asymptotically) quasi-ϕ-nonexpansive mappings is reduced to (asymptotically) quasi-nonexpansive mappings (cf. [29–32]).
We assume that f satisfies the following conditions for studying the equilibrium problem (1.1).
(A1): f(x, x) = 0∀x ∈ C;
(A2): f is monotone, i.e., f(x, y) + f(y, x) ≤ 0∀x, y ∈ C;
(A3): lim supt↓0f (tz + (1 - t)x, y) ≤ f(x, y)∀x, y, z ∈ C;
(A4): for each x ∈ C, y α f(x, y) is convex and weakly lower semi-continuous.
Recently, Takahashi and Zembayshi [33] considered the problem of finding a common element in the fixed point set of a relatively nonexpansive mapping and in the solution set of the equilibrium problem (1.1) (cf. [32]).
Theorem TZ. ([33]) Let E be a uniformly smooth and uniformly convex Banach space and let C be a nonempty closed convex subset of E. Let f be a bifunction from C × C to ℝ satisfying (A 1)-(A 4) and let T be a relatively nonexpansive mapping from C into itself such that F(T) ∩ EP(f) ≠ Ø. Let {x n } be a sequence generated by

for every n ≥ 0, where J is the duality mapping on E, {α n } ⊂ [0, 1] satisfies

and {r n } ⊂ [a, ∞) for some a > 0. Then {x n } converges strongly to ∏F(T)∩EP(f)x, where ∏F(T)∩EP(f)is the generalized projection of E onto F (T) ∩ EP (f ).
Very recently, Qin et al. [25] further improved Theorem TZ by considering shrinking projection methods which were introduced in [34] for quasi-ϕ-nonexpansive mappings in a uniformly convex and uniformly smooth Banach space.
Theorem QCK. [25]Let C be a nonempty closed convex subset of a uniformly convex and uniformly smooth Ban ach space E. Let f be a bifunction from C × C to ℝ satisfying (A 1)-(A 4) and let T : C → C be a closed quasi-ϕ-nonexpansive mappings such that . Let {x
n
} be a sequence generated in the following manner:
. Let {x
n
} be a sequence generated in the following manner:

where J is the duality mapping on E and {α n } is a sequence in [0, 1] satisfying

and {r
n
} ⊂ [a, ∞) for some a > 0. Then {x
n
} converges strongly to .
.
In this paper, we considered the problem of finding a common element in the fixed point set of an asymptotically quasi-ϕ-nonexpansive mapping which is an another generalization of asymptotically nonexpansive mappings in Hilbert spaces and in the solution set of the equilibrium problem (1.1). The results presented this paper mainly improve the corresponding results announced in [33].
In order to prove our main results, we need the following lemmas.
Lemma 1.3. [18]Let C be a nonempty closed convex subset of a smooth Banach space E and x ∈ E. Then x0 = ∏ C x if and only if

Lemma 1.4. [18]Let E be a reflexive, strictly convex and smooth Banach space, C a nonempty closed convex subset of E and x ∈ E. Then

Lemma 1.5. Let E be a strictly convex and smooth Banach space, C a nonempty closed convex subset of E and T : C → C a quasi- ϕ -nonexpansive mapping. Then F(T) is a closed convex subset of C.
Proof. Let {p n } be a sequence in F(T ) with p n → p as n → ∞. Then we have to prove that p ∈ F(T) for the closedness of F(T). From the definition of T, we have

which implies that ϕ(p n , Tp) → 0 as n → ∞. Note that

Letting n → ∞ in the above equality, we see that ϕ(p, Tp) = 0. This shows that p = Tp.
Next, we show that F(T) is convex. To end this, for arbitrary p1, p2 ∈ F (T), t ∈ (0, 1), putting p3 = tp1 + (1 - t)p2, we prove that Tp3 = p3. Indeed, from the definition of ϕ, we see that

This implies that p3 ∈ F (T ). This completes the proof.
Now we will improve the above Lemma 1.6 as follows.
Lemma 1.6. Let E be a uniformly smooth and strictly convex Banach space which has the Kadec-Klee property, C a nonempty closed convex subset of E and T : C → C a closed and asymptotically quasi- ϕ -nonexpansive mapping. Then F(T) is a closed convex subset of C.
Proof. It is easy to check that the closedness of F(T) can be deduced from the closedness of T. We mainly show that F(T) is convex. To end this, for arbitrary p1, p2 ∈ F(T), t ∈ (0, 1), putting p3 = tp1 + (1 - t)p2, we prove that Tp3 = p3.
Indeed, from the definition of ϕ, we see that

This implies that

From (1.5), we see that

It follows that

This shows that the sequence {J(Tnp3)}is bounded. Note that E* is reflexive; we may, without loss of generality, assume that J(Tnp3) ⇀ e* ∈ E*. In view of the reflexivity of E, we have J(E) = E*. This shows that there exists an element e ∈ E such that Je = e*. It follows that

Taking lim infn→ ∞on the both sides of above equality, we obtain that

This implies that p3 = e, that is, Jp3 = e*. It follows that J(Tnp3) ⇀ Jp3 ∈ E*.
In view of the Kadec-Klee property of E* and (1.9), we have

Note that J-1 : E* → E is demi-continuous, we see that Tn p3 ⇀ p3. By virtue of the Kadec-Klee property of E and (1.8), we have Tnp3 → p3 as n → ∞. Hence

as n → ∞. In view of the closedness of T, we can obtain that p3 ∈ F (T). This shows that F(T) is convex. This completes of proof
Lemma 1.7. [35, 36]Let E be a smooth and uniformly convex Banach space and let r > 0. Then there exists a strictly increasing, continuous and convex function g : [0, 2r] → R such that g(0) = 0 and

for all x, y ∈ B r = {x ∈ E : ||x|| ≤ r} and t ∈ [0, 1].
Lemma 1.8. Let C be a closed convex subset of a smooth, strictly convex and reflexive Banach space E. Let f be a bifunction from C × C to ℝ satisfying (A 1)-(A 4). Let r > 0 and x ∈ E. Then we have the followings.
(a): ([1]) There exists z ∈ C such that

(b): (Refs. [25, 33]) Define a mapping T r : E → C by

Then the following conclusions hold:
(1): S r is single-valued;
(2): S r is a firmly nonexpansive-type mapping, i.e., for all x, y ∈ E,

(3): F(S r ) = EP)(f);
(4): S r is quasi- ϕ -nonexpansive;
(5): ϕ(q, S r x) + ϕ(S r x, x) ≤ ϕ (q, x), ∀q ∈ F(S r );
(6): EP(f) is closed and convex.
2. Main Results
Theorem 2.1. Let E be a uniformly smooth and strictly convex Banach space which has the Kadec-Klee property and C a nonempty closed convex subset of E. Let f be a bifunction from C × C to ℝ satisfying (A 1)-(A 4) and T : C → C a closed and asymptotically quasi-ϕ-nonexpansive mapping. Assume that T is asymptotically regular on C and is nonempty and bounded. Let {x
n
} be a sequence generated in the following manner:
is nonempty and bounded. Let {x
n
} be a sequence generated in the following manner:

where for each n ≥ 1, {α
n
} is a real sequence in [0, 1] such that lim infn→ ∞α
n
(1 - α
n
) > 0, {r
n
} is a real sequence in [a, ∞), where a is some positive real number and J is the duality mapping on E. Then the sequence {x
n
} converges strongly to
for each n ≥ 1, {α
n
} is a real sequence in [0, 1] such that lim infn→ ∞α
n
(1 - α
n
) > 0, {r
n
} is a real sequence in [a, ∞), where a is some positive real number and J is the duality mapping on E. Then the sequence {x
n
} converges strongly to , where
, where is the generalized projection from E onto
is the generalized projection from E onto .
.
Proof. First, we show that C n is closed and convex by induction on n ≥ 1. It is obvious that C1 = C is closed and convex. Suppose that C m is closed and convex for some integer m. For z ∈ C m , we see that ϕ(z, u m ) ≤ ϕ(z, x m ) + (k m -1)M m is equivalent to

It is easy to see that Cm+1is closed and convex. This proves that C
n
is closed and convex for each n ≥ 1. This in turn shows that  x0 is well defined. Putting
x0 is well defined. Putting  , we from Lemma 1.8 see that
, we from Lemma 1.8 see that  is quasi-ϕ-nonexpansive.
is quasi-ϕ-nonexpansive.
Now, we are in a position to prove that  for each n ≥ 1. Indeed,
for each n ≥ 1. Indeed,  is obvious. Suppose that
is obvious. Suppose that  for some positive integer m. Then,
for some positive integer m. Then,  , we have
, we have

which shows that w ∈ Cm+1. This implies that  for each n ≥ 1.
for each n ≥ 1.
On the other hand, it follows from Lemma 1.4 that

for each  and for each n ≥ 1. This shows that the sequence ϕ(x
n
, x0) is bounded. From (1.5), we see that the sequence {x
n
} is also bounded. Since the space is reflexive, we may, without loss of generality, assume that x
n
⇀ p. Not that C
n
is closed and convex for each n ≥ 1. It is easy to see that p ∈ C
n
for each n ≥ 1. Note that
and for each n ≥ 1. This shows that the sequence ϕ(x
n
, x0) is bounded. From (1.5), we see that the sequence {x
n
} is also bounded. Since the space is reflexive, we may, without loss of generality, assume that x
n
⇀ p. Not that C
n
is closed and convex for each n ≥ 1. It is easy to see that p ∈ C
n
for each n ≥ 1. Note that

It follows that

This implies that

Hence, we have ||x n || → ||p|| as n → ∞. In view of the Kadec-Klee property of E, we obtain that x n → p as n → ∞.
Next, we show that p ∈ F(T). By the construction of C
n
, we have that Cn+1⊂ C
n
and  . It follows that
. It follows that

Letting n → ∞, we obtain that ϕ(xn+1, x n ) → 0. In view of xn+1∈ Cn+1, we have

It follows that

From (1.5), we see that

It follows that

This implies that {Ju n } is bounded. Note that E is reflexive and E* is also reflexive. We may assume that Ju n → x* ∈ E*. In view of the reflexivity of E, we see that J(E) = E*. This shows that there exists an x ∈ E such that Jx = x*. It follows that

Taking lim infn→∞the both sides of above equality yields that

That is, p = x, which in turn implies that x* = Jp. It follows that Ju n → Jp ∈ E*. From (2.4) and E* has the Kadec-Klee property, we obtain that

Note that J-1 : E* → E is demi-continuous. It follows that u n → p. From (2.3) and E has the Kadec-Klee property, we obtain that

Note that

It follows that

Since J is uniformly norm-to-norm continuous on any bounded sets, we have

Let r = supn≥0{||x n ||, ||Tnx n ||}. Since E is uniformly smooth, we know that E* is uniformly convex. In view of Lemma 1.7, we see that

It follows that

On the other hand, we have

It follows from (2.6) and (2.7) that

In view of limn→∞(k n -1) M n = 0 and (2.8) and the assumption lim infn→∞α n (1 - α n ) > 0, we see that

It follows from the property of g that

Since x n → p as n →∞ and J : E → E* is demi-continuous, we obtain that Jx n → Jp ∈ E*. Note that

This implies that ||Jx n || → ||Jp|| as n → ∞. Since E* has the Kadec-Klee property, we see that

Note that

From (2.9) and (2.10), we obtain at

Note that J-1 : E* → E is demi-continuous. It follows that Tnx n → p. On the other hand, we have

In view of (2.11), we obtain that ||Tnx n || → ||p|| as n → ∞. Since E has the Kadec-Klee property, we obtain that

Note that

It follows from the asymptotic regularity of T and (2.12) that

That is, TTnx n - p → 0 as n → ∞: It follows from the closedness of T that Tp = p:
Next, we show that p ∈ EF(f): From (2.1), we have

In view of  and Lemma 1.8, we obtain
and Lemma 1.8, we obtain

It follows from (2.8) that

From (1.5), we see that ||u n || - ||y n || → 0 as n → ∞. In view of u n → p as n → ∞, we have

It follows that

Since E* is reflexive, we may assume that Jy n → q*∈ E*: In view of J(E) = E*, we see that there exists q ∈ E such that Jq = q*. It follows that

Taking lim infn→∞the both sides of above equality yields that

That is, p = q, which in turn implies that q* = Jp. It follows that Jy n → Jp ∈ E*. From (2.16) and E* has the Kadec-Klee property, we obtain that

Note that J-1 : E* → E is demi-continuous. It follows that y n → p. From (2.15) and E has the Kadec-Klee property, we obtain that

Note that

It follows from (2.5) and (2.17) that

Since J is uniformly norm-to-norm continuous on any bounded sets, we have

From the assumption r n ≥ a, we see that

In view of  , we see that
, we see that

It follows from the condition (A 2) that

By taking the limit as n → ∞ in the above inequality, we from conditions (A 4) and (2.19) obtain that

For 0 < t < 1 and y ∈ C, define y t = ty + (1 - t)p. It follows that y t ∈ C, which yields that f(y t , p) ≤ 0. It follows from conditions (A 1) and (A 4) that

That is,

Letting t ↓ 0, from condition (A 3), we obtain that f(p, y) ≥ 0 ∀y ∈ C: This implies that p ∈ EP(f). This shows that  .
.
Finally, we prove that  . From
. From  , we see that
, we see that

Since  for each n ≥ 1, we have
for each n ≥ 1, we have

Letting n → ∞ in (2.20), we see that

In view of Lemma 1.3, we can obtain that  . This completes the proof.
. This completes the proof.
Remark 2.2. Theorem 2.1 improves Theorem QCK in the following aspects:
-
(a)
From a uniformly smooth and uniformly convex space to a uniformly smooth and strictly convex Banach space which has the Kadec-Klee property;
-
(b)
From a quasi-ϕ-nonexpansive mapping to an asymptotically quasi-ϕ-non-expansive mapping.
From the definition of quasi-ϕ-nonexpansive mappings, we see that every quasi-ϕ-nonexpansive mapping is asymptotically quasi-ϕ-nonexpansive with the constant sequence {1}. From the proof of Theorem 2.1, we have the following results immediately.
Corollary 2.3. Let E be a uniformly smooth and strictly convex Banach space which has the Kadec-Klee property and C a nonempty closed convex subset of E. Let f be a bifunction from C × C to ℝ satisfying (A 1)-(A 4) and T : C → C a closed and quasi- ϕ -nonexpansive mapping. Assume that is nonempty.
is nonempty.
Let {x n } be a sequence generated in the following manner:

where {α
n
} is a real sequence in [0, 1] such that lim infn→∞α
n
(1 - α
n
) > 0, {r
n
} is a real sequence in [a, ∞), where a is some positive real number and J is the duality mapping on E. Then the sequence {x
n
} converges strongly to , where
, where is the generalized projection from E onto
is the generalized projection from E onto .
.
Remark 2.4. Corollary 2.3 improves Theorem TZ in the following aspects.
-
(a)
For the framework of spaces, we extend the space from a uniformly smooth and uniformly convex space to a uniformly smooth and strictly convex Banach space which has the Kadec-Klee property (note that every uniformly convex Banach space has the Kadec-Klee property).
-
(b)
For the mappings, we extend the mapping from a relatively nonexpansive mapping to a quasi-ϕ-nonexpansive mapping (we remove the restriction
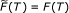 , where
, where 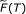 denotes the asymptotic fixed point set).
denotes the asymptotic fixed point set). -
(c)
For the algorithms, we remove the set "W n " in Theorem TZ.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Math Student 1994, 63: 123–145.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. J Nonlinear Convex Anal 2005, 6: 117–136.
Chadli O, Wong NC, Yao JC: Equilibrium problems with applications to eigenvalue problems. J Optim Theory Appl 2003, 117: 245–266. 10.1023/A:1023627606067
Chang SS, Lee HWJ, Chan CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Anal 2009, 70: 3307–3319. 10.1016/j.na.2008.04.035
Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings. Proc Am Math Soc 1972, 35: 171–174. 10.1090/S0002-9939-1972-0298500-3
Ceng LC, Yao JC: Hybrid viscosity approximation schemes for equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Appl Mathe Comput 2008, 198: 729–741. 10.1016/j.amc.2007.09.011
Colao V, Marino G, Xu HK: An iterative method for finding common solutions of equilibrium and fixed point problems. J Math Anal Appl 2008, 344: 340–352. 10.1016/j.jmaa.2008.02.041
Kim JK, Huang NJ: Approximation methods of solutions for equilibrium problem in Hilbert spaces. Dyn Syst Appl 2008, 17: 503–508.
Kim JK, Cho SY, Qin X: Some results on generalized equilibrium problems involving strictly pseudocontractive mappings. Acta Mathematica Scientia 2011,31B(5):1–17.
Kim JK, Cho SY, Qin X: Hybrid projection algorithms for generalized equilibrium problems and strictly pseudocontractive mappings. J Ineq Appl 2010,2010(312602):1–18.
Qin X, Shang M, Su Y: A general iterative method for equilibrium problems and fixed point problems in Hilbert spaces. Nonlinear Anal 2008, 69: 3897–3909. 10.1016/j.na.2007.10.025
Qin X, Cho SY, Kim JK: On the weak convergence of iterative sequences for generalized equilibrium problems and strictly pseudocontractive mappings. Optimization 2011, 1–17.
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J Math Anal Appl 2007, 331: 506–515. 10.1016/j.jmaa.2006.08.036
Wattanawitoon K, Kumam P: Strong convergence theorems by a new hybrid projection algorithm for fixed point problems and equilibrium problems of two relatively quasi-nonexpansive mappings. Nonlinear Anal 2009, 3: 11–20.
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems. Kluwer, Dordrecht; 1990.
Hudzik H, Kowalewski W, Lewicki G: Approximative compactness and full rotundity in Musielak-Orlicz spaces and Lorentz-Orlicz spaces. Zeitschrift fuer Analysis and ihre Anwendungen 2006, 25: 163–192.
Takahashi W: Nonlinear Functional Analysis. Yokohama-Publishers; 2000.
Alber YaI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Edited by: Kartsatos AG. Marcel Dekker, New York; 1996.
Alber YaI, Reich S: An iterative method for solving a class of nonlinear operator equations in Banach spaces. Panamer Math J 1994, 4: 39–54.
Reich S: A weak convergence theorem for the alternating method with Bregman distance. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Edited by: Kartsatos AG. Marcel Dekker, New York; 1996.
Butnariu D, Reich S, Zaslavski AJ: Asymptotic behavior of relatively nonexpansive operators in Banach spaces. J Appl Anal 2001, 7: 151–174. 10.1515/JAA.2001.151
Butnariu D, Reich S, Zaslavski AJ: Weak convergence of orbits of nonlinear operators in reflexive Banach spaces. Numer Funct Anal Optim 2003, 24: 489–508. 10.1081/NFA-120023869
Censor Y, Reich S: Iterations of paracontractions and firmly nonexpansive operatorswith applications to feasibility and optimization. Optimzation 1996, 37: 323–339. 10.1080/02331939608844225
Agarwal RP, Cho YJ, Qin X: Generalized projection algorithms for nonlinear operators. Numer Funct Anal Optim 2007, 28: 1197–1215. 10.1080/01630560701766627
Qin X, Cho YJ, Kang SM: Convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces. J Comput Appl Math 2009, 225: 20–30. 10.1016/j.cam.2008.06.011
Qin X, Cho YJ, Kang SM, Zhou H: Convergence of a modified Halpern-type iteration algorithm for quasi- ϕ -nonexpansive mappings. Appl Math Lett 2009, 22: 1051–1055. 10.1016/j.aml.2009.01.015
Zhou H, Gao G, Tan B: Convergence theorems of a modified hybrid algorithm for a family of quasi- ϕ -asymptotically nonexpansive mappings. J Appl Math Comput
Cho YJ, Qin X, Kang SM: Strong convergence of the modified Halpern-type iterative algorithms in Banach spaces. An St Univ Ovidius Constanta, Ser Math 2009, 17: 51–68.
Kim JK, Sahu D, Nam YM: Convergence theorem for fixed points of nearly uniformly L-Lipschitzian asymptotically generalized phi-hemicontractive mappings. Nonlinear Anal TMA 2009,71(12):2833–2838. 10.1016/j.na.2009.06.091
Kim JK, Nam YM, Sim JY: Convergence theorem of implicit iterative sequences for a finite family of asymptotically quasi-nonexpansive type mappings. Nonlinear Anal TMA 2009,71(12):2839–2848. 10.1016/j.na.2009.06.090
Saewan S, Kumam P: Modified hybrid block iterative algorithm for convex feasibility problems and generalized equilibrium problems for uniformly quasi-asymptotically nonexpansive mappings. Abst Appl Anal 2010, 2010: 22. (Article ID 357120)
Saewan S, Kumam P: A hybrid iterative scheme for a maximal monotone operator and two countable families of relatively quasi-nonexpansive mappings for generalized mixed equilibrium and variational inequality problems. Abst Appl Anal 2010, 2010: 31. (Article ID 123027)
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Anal 2009, 70: 45–57. 10.1016/j.na.2007.11.031
Takahashi W, Takeuchi Y, Kubota R: Strong convergence theorems by hybrid methods for families of nonexpansive mappings in Hilbert spaces. J Math Anal Appl 2008, 341: 276–286. 10.1016/j.jmaa.2007.09.062
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Anal 1991, 16: 1127–1138. 10.1016/0362-546X(91)90200-K
Zǎlinescu C: On uniformly convex functions. J Math Anal Appl 1983, 95: 344–374. 10.1016/0022-247X(83)90112-9
Acknowledgements
This work was supported by the Kyungnam University Foundation Grant 2010.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, J.K. Strong convergence theorems by hybrid projection methods for equilibrium problems and fixed point problems of the asymptotically quasi-ϕ-nonexpansive mappings. Fixed Point Theory Appl 2011, 10 (2011). https://doi.org/10.1186/1687-1812-2011-10
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-10



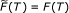 , where
, where