1 Introduction

In this paper, we consider the Variational Inequalities (VIs) of Fichera [17] and Stampacchia [40] in a unified framework. The VI is defined as finding a point \(x^{\dagger}\in C\) such that

$$ \bigl\langle Ax^{\dagger}, y - x^{\dagger}\bigr\rangle \geq0, \quad \forall y \in C, $$
(1.1)

where \(C \subseteq E\) is a nonempty, closed and convex set in a real Banach space E with dual \(E^{*}\), \(\langle\cdot,\cdot\rangle\) denotes the duality paring on E, and \(A:E \to E^{*}\) is a given operator. We denote the set of solutions of the VI by \(\mathit{VI}(C,A)\). The VI is a fundamental problem in optimization theory and captures various applications such as partial differential equations, optimal control, and mathematical programming (see, for instance, [19, 29]). A vast literature which deals on iterative methods for solving VIs can be found, for instance, in [1, 12, 14–16, 24–28, 41].

A classical method for solving the VI is the projection method given by

$$ x_{n+1} = P_{C}(x_{n} - \alpha_{n} Ax_{n}), $$
(1.2)

where \(P_{C}\) is the metric projection onto \(C \subset\mathbb{R}^{N}\). The projection method is a natural extension of the projected gradient method for solving optimization problems, originally proposed by Goldstein [20], and Levitin and Polyak [31]. Under the assumption that A is η-strongly monotone and L-Lipschitz continuous with \(\alpha_{n}\in (0,\frac{2}{L^{2}} )\), the projection method converges to a solution of the VI. But if these conditions are weakened, say for example, the strong monotonicity is reduced to monotonicity, the situation becomes complicated and yields a divergent sequence independent of the stepsize \(\alpha_{n}\) [13]. As a result of this set-back, Korpelevich [30] and Antipin [3] introduced the Extragradient Method (EM) which is a two-projection process and is defined as

$$ \textstyle\begin{cases} y_{n} = P_{C}(x_{n} - \alpha_{n} Ax_{n}), \\ x_{n+1} = P_{C} (x_{n} - \alpha_{n} Ay_{n}), \end{cases} $$
(1.3)

where \(\alpha_{n} \in(0,1/ L)\) and L is the Lipschitz constant of A in finite-dimensional settings. The EM has received great attention in recent days and many authors have introduced several improvements and modifications of the method. Observing that in the EM, there is need to calculate the projection onto the feasible set C twice per each iteration, and in a case where the set C is not simple to project onto, a minimal distance problem needs to be solved twice to obtain the next iterate (which can fact can affect the efficiency and applicability of the EM), Censor et al. [9] introduced the Subgradient Extragradient Method (SEM) in a real Hilbert space H, while the second projection onto C is replaced with a projection onto a half-space which can be calculated explicitly. In particular, the SEM is defined as

$$ \textstyle\begin{cases} y_{n} =P_{C}(x_{n} -\alpha_{n} Ax_{n}), \\ x_{n+1} = P_{T_{n}}(x_{n} - \alpha_{n} Ay_{n}),\\ \text{where}\\ T_{n} = \{w \in H: \langle x_{n} - \alpha_{n} Ax_{n} - y_{n}, w - y_{n} \rangle \leq0\}, \end{cases} $$
(1.4)

and \(\alpha_{n} \in(0,1 / L)\). Since the inception of the SEM, many authors have proposed various modifications of the SEM; see for instance [7, 8, 14, 41, 42, 44, 45].

Many of the results which deal with EM and SEM for solving the VI used the Euclidean norm distance and metric projections, which in certain cases do not allow for an application to the structure of generally feasible sets and efficient problem-solving. A possible way out is to use the Bregman divergence (or Bregman distance) introduced by Bregman [6] where he proposed a method of the type of cyclic projection for finding the common point of a convex set. His paper has initiated a new field in mathematical programming and nonlinear analysis. For solving the VI, one of the modern variants of the EM is the Nomirovski prox-method [34], which can be interpreted as a variant of the EM with projection understood in the sense of Bregman divergence. It sometimes allows for the consideration of the structure of a general feasible set of the problem. For example, for a simplex, it is possible to take the Kullback–Leibler divergence (Bregman divergence on negative entropy) as the distance and to obtain explicitly calculated operator of projection onto a simplex. See [37] for more details of the Bregman divergence.

Recently, Nomirovskii et al. [35] proposed the following two-stage method using the Bregman divergence with operator \(f:H \to \mathbb{R}\cup\{+\infty\}\) being continuously differentiable and σ-strongly convex.

Algorithm 1.1

Choose \(x_{0}, y_{0} \in C\) and positive number λ. Put \(n=1\).

Step 0::

Calculate \(x_{1} = P_{x_{0}}^{C}(-\lambda y_{0})\), \(y_{1} = P_{x_{1}}^{C}(-\lambda A y_{0})\).

Step 1::

Calculate \(x_{n+1} = P_{x_{n}}^{T_{n}}(-\lambda Ay_{n})\) and \(y_{n+1}=P_{x_{n+1}}^{C}(-\lambda Ay_{n})\) where

$$ T_{n} = \bigl\{ z\in H:\bigl\langle \nabla f(x_{n})- \lambda Ay_{n-1}-\nabla f(y_{n}),z-y_{n} \bigr\rangle \leq0\bigr\} . $$
Step 2::

If \(x_{n+1} = x_{n}\) and \(y_{n+1} = y_{n} = y_{n-1}\), then STOP and \(y_{n} \in \mathit{VI}(C,A)\). Otherwise put \(n:=n+1\) and go to Step 1,

where \(P_{x}^{C}\) is the projection defined by

$$P_{x}^{C}(a)=\mathop {\operatorname {argmin}}_{y\in C}\bigl\{ -\langle a, y-x\rangle+ D_{f}(y,x)\bigr\} ,\quad \forall a \in H, x \in \operatorname{int}(\operatorname{dom} f) $$

and \(D_{f}(y,x)\) is the Bregman divergence between x and y.

They proved a weak convergence result for the VI with a pseudo-monotone and L-Lipschitz continuous operator in a finite-dimensional linear normed space provided the stepsize λ satisfies

$$\lambda\in \biggl(0, (\sqrt{2}-1)\frac{\sigma}{L} \biggr). $$

Also, Gibali [18] introduced the following Bregman subgradient extragradient method for solving the VI with monotone and Lipschitz continuous operator in a real Hilbert space.

Algorithm 1.2

Choose \(x_{0},y_{0} \in H\), \(\lambda>0\). Given the current iterates \(x_{n}\) and \(y_{n}\), and also \(y_{n-1}\), if \(\nabla f(x_{n})-\lambda Ay_{n-1} \neq \nabla f(y_{n})\), construct the half-space

$$ T_{n}=\bigl\{ w\in H:\bigl\langle \nabla f(x_{n}) - \lambda Ay_{n-1}-\nabla f(y_{n}), w- y_{n}\bigr\rangle \leq0\bigr\} $$

and if \(\nabla f(x_{n}) - \lambda Ay_{n-1} = \nabla f(y_{n})\), take \(T_{n} = H\). Now compute the next iterates via

$$ \textstyle\begin{cases} x_{n+1} = \varPi_{T_{n}}((\nabla f)^{-1}(\nabla f(x_{n})-\lambda Ay_{n})),\\ y_{n+1} = \varPi_{C}((\nabla f)^{-1}(\nabla f(x_{n+1})-\lambda Ay_{n})), \end{cases} $$

where \(\varPi_{C}\) denotes the Bregman projection onto C (see Definition 2.2).

Gibali [18] proved a weak convergence result for the sequence generated by Algorithm 1.2 provided the stepsize satisfies the condition \(\lambda\in (0, \frac{\sqrt{2}-1}{L} )\), where L is the Lipschitz constant of A.

It is obvious that the stepsize used in the EM and SEM has an essential role in the convergence of the two methods. An obvious disadvantage of Algorithms 1.1 and 1.2, which impedes their wide usage, is the assumption that the Lipschitz constant of the operator is known or admits a simple estimate. Moreover, in many problems, operators may not satisfy the Lipschitz condition and the operator may not even be monotone as our Example 4.2 shows in Sect. 4.

Motivated by the above results, in this paper, we present modified Bregman subgradient extragradient algorithms with line search technique for solving VI with a pseudo-monotone operator without necessarily satisfying the Lipschitz condition. The stepsize of the algorithm is determined via an Armijo line search technique which helps us to avoid finding a prior estimate of the Lipschitz constant as well as improve the convergence of the algorithm by finding optimum stepsize for each iteration. We proved weak and strong convergence results for approximating solutions of VI in real reflexive Banach spaces and provide numerical examples to illustrate the performance of our algorithms. Our results improve and extend the corresponding results of [7, 12, 18, 34, 35] in the literature.

2 Preliminaries

In this section, we give some definitions and basic results which will be used in our subsequent analysis. Let E be a real Banach space with dual \(E^{*}\) and C be a nonempty, closed and convex subset of E. We denote the strong and the weak convergences of a sequence \(\{x_{n}\} \subseteq H\) to a point \(p \in E\) by \(x_{n} \rightarrow p\) and \(x_{n} \rightharpoonup p\), respectively.

We now introduce some necessary structure to formulate our algorithm. Let \(f:E \to\mathbb{R}\cup\{+\infty\}\) be a function satisfying the following:

  1. (i)

    \(\operatorname{int}(\operatorname{dom}f)\subseteq E\) is a nonempty convex set;

  2. (ii)

    f is continuously differentiable on \(\operatorname{int}(\operatorname{dom}f)\);

  3. (iii)

    f is strongly convex with strong convexity constant \(\sigma>0\), i.e.,

    $$ f(x) \geq f(y) - \bigl\langle \nabla f(y), x-y \bigr\rangle + \frac{\sigma}{2} \Vert x-y \Vert ^{2}, \quad\forall x \in \operatorname{dom}f \text{ and } y \in\operatorname {int}(\operatorname{dom}f). $$
    (2.1)

The subdifferential set of f at a point x denoted by ∂f is defined by

$$ \partial f(x) = \bigl\{ \xi\in E^{*}: f(y) - f(x) \geq\langle\xi,y-x\rangle, \forall y \in E\bigr\} . $$
(2.2)

Each element \(\xi\in\partial f(x)\) is called a subgradient of f at x. Since f is continuously differentiable, \(\partial f(x) = \{ \nabla f(x)\}\), which is the gradient of f at x. The Fenchel conjugate of f is the convex functional \(f^{*}:E^{*} \to\mathbb{R}\cup\{ +\infty\}\) defined by \(f^{*}(\xi) = \sup\{\langle\xi, x \rangle- f(x): x\in E\}\). Let E be a reflexive Banach space, the function f is said to be Legendre if and only if it satisfies the following two conditions:

  1. (L1)

    \(\operatorname{int}(\operatorname{dom}f)\neq\emptyset\) and ∂f is single-valued on its domain;

  2. (L2)

    \(\operatorname{int}(\operatorname{dom}f^{*}) \neq\emptyset\) and \(\partial f^{*}\) is single-valued on its domain.

The Bregman divergence (or Bregman distance) corresponding to the function f is defined by (see [6])

$$ D_{f}(x,y) = f(x) - f(y) - \bigl\langle \nabla f(y), x-y \bigr\rangle ,\quad \forall x \in \operatorname{dom}f \text{ and } y \in \operatorname{int}(\operatorname{dom}f). $$
(2.3)

Remark 2.1

Example of practically important Bregman divergence can be found in [5]. We consider the following two: for \(f(\cdot) = \frac{1}{2}\| \cdot\|^{2}\), we have \(D_{f}(x,y) = \frac{1}{2}\|x-y\|^{2}\) which is the Euclidean norm distance. Also, if \(f(x) = -\sum_{i=1}^{m} x_{i}\log(x_{i})\) which is the Shannon entropy for the non-negative orthant \(\mathbb {R}^{m}_{++}:= \{x\in\mathbb{R}^{m}:x_{i}>0\}\), we obtain the Kullback–Leibler cross entropy defined by

$$D_{f}(x,y) = \sum_{i=1}^{m} \biggl(x_{i}\log \biggl(\frac{x_{i}}{y_{i}} \biggr)-1 \biggr)+\sum _{i=1}^{m} y_{i}. $$

It is well known that the Bregman distance is not a metric, however, it satisfies the following three point identity:

$$ D_{f}(x,z) = D_{f}(x,y) + D_{f}(y,z) + \bigl\langle \nabla f(y)- \nabla f(z), x-y \bigr\rangle . $$
(2.4)

Also from the strong convexity of f, we have

$$ D_{f}(x,y) \geq\frac{1}{2} \Vert x-y \Vert ^{2}. $$
(2.5)

Definition 2.2

The Bregman projection (see e.g. [38]) with respect to f of \(x \in \operatorname{int}(\operatorname{dom}f)\) onto a nonempty closed convex set \(C \subset \operatorname{int}(\operatorname{dom}f)\) is the unique vector \(\varPi_{C}(x) \in C\) satisfying

$$ \varPi_{C}(x) := \inf\bigl\{ D_{f}(x,y):x \in C\bigr\} . $$

The Bregman projection is characterized by the inequality

$$ z = \varPi_{C}(x) \quad\iff\quad\bigl\langle \nabla f(x)-\nabla f(z), y-z \bigr\rangle \leq 0, \quad\forall y \in C. $$
(2.6)

Also

$$ D_{f}\bigl(y, \varPi_{C}(x)\bigr) + D_{f} \bigl(\varPi_{C}(x),x\bigr) \leq D_{f}(y,x), \quad\forall y \in C, x \in\operatorname{int}(\operatorname{dom}f). $$
(2.7)

Following [2, 10], we define the function \(V_{f}:E \times E \to[0, \infty)\) associated with f by

$$ V_{f}(x,y) = f(x) - \langle x,y \rangle+ f^{*}(y), \quad\forall x, y \in E. $$
(2.8)

\(V_{f}\) is non-negative and \(V_{f}(x,y) = D_{f}( x, \nabla f(y))\) for all \(x,y \in E\). Moreover, by the subdifferential inequality, it is easy to see that

$$ V_{f}(x,y) + \bigl\langle z, \nabla f^{*}(y) -x \bigr\rangle \leq V_{f}(x, z+y) $$
(2.9)

for all \(x,y,z \in E\). In addition, if \(f:E \to\mathbb{R}\cup\{+\infty \}\) is proper lower semicontinuous, then \(f^{*}:E \to\mathbb{R}\cup\{ +\infty\}\) is proper weak lower semicontinuous and convex. Hence, \(V_{f}\) is convex in second variable, i.e.,

$$ D_{f} \Biggl(z, \nabla f^{*}\Biggl(\sum_{i=1}^{N} t_{i} \nabla f(x_{i})\Biggr) \Biggr) \leq\sum _{i=1}^{N} t_{i} D_{f}(z,x_{i}), $$
(2.10)

where \(\{x_{i}\} \subset E\) and \(\{t_{i}\}\subset(0,1)\) with \(\sum_{i=1}^{N}t_{i}=1\).

Definition 2.3

(see [32, 33])

The Minty Variational Inequality Problem (MVI) is defined as finding a point \(\bar{x} \in C\) such that

$$\begin{aligned} \langle Ay, y - \bar{x} \rangle\geq0, \quad\forall y \in C. \end{aligned}$$
(2.11)

We denote by \(M(C,A)\) the set of solutions of (2.11). Some existence results for the MVI have been presented in [32]. Also, the assumption that \(M(C,A) \neq\emptyset\) has already been used for solving \(\mathit{VI}(C,A)\) in finite-dimensional spaces (see e.g. [39]). It is not difficult to prove that pseudo-monotonicity implies property \(M(C,A) \neq\emptyset\), but the converse is not true.

Lemma 2.4

(see [33])

Consider the VI (1.1). If the mapping\(h:[0,1] \rightarrow E^{*}\)defined as\(h(t) = A(tx + (1-t)y)\)is continuous for all\(x,y \in C\) (i.e., his hemicontinuous), then\(M(C,A) \subset \mathit{VI}(C,A)\). Moreover, ifAis pseudo-monotone, then\(\mathit{VI}(C,A)\)is closed, convex and\(\mathit{VI}(C,A) = M(C,A)\).

The following lemma was proved for the case of metric projection in [11] and can also be extended to Bregman projection.

Lemma 2.5

For every\(x \in E\)and\(\alpha\geq\beta>0\), the following inequalities hold:

$$\begin{aligned} \frac{ \Vert x - P_{C}(x-\alpha Ax) \Vert }{\alpha}\leq\frac{ \Vert x - P_{C}(x-\beta Ax) \Vert }{\beta} \end{aligned}$$
(2.12)

and

$$ \bigl\Vert x - P_{C}(x -\beta Ax) \bigr\Vert \leq \bigl\Vert x - P_{C}(x - \alpha Ax) \bigr\Vert . $$

One powerful tool for deriving weak or strong convergence of iterative sequence is due to Opial [36]. A Banach space E is said to satisfy Opial property [36] if for any weakly convergent sequence \(\{x_{n}\}\) in E with weak limit x, we have

$$\limsup_{n \rightarrow\infty} \Vert x_{n}-x \Vert < \limsup _{n \rightarrow\infty } \Vert x_{n}-y \Vert $$

for all y in E with \(y \neq x\). Note that all Hilbert space, all finite-dimensional Banach space and the Banach space \(l^{p}\) (\(1 \leq p < \infty\)) satisfy the Opial property. However, not every Banach space satisfies the Opial property; see for example [21]. But, the following Bregman Opial-like inequality for every Banach space E has been proved in [23].

Lemma 2.6

([23])

LetEbe a Banach space and let\(f: E \rightarrow(-\infty,\infty]\)be a proper strictly convex function so that it is Gâteaux differentiable and\(\{x_{n}\}\)is a sequence inEsuch that\(x_{n} \rightharpoonup u\)for some\(u \in E\). Then

$$\limsup_{n \rightarrow\infty}D_{f}(u,x_{n}) < \limsup_{n \rightarrow\infty }D_{f}(v, x_{n}) $$

for allvin the interior of domfwith\(u \neq v\).

Lemma 2.7

([46])

Let\(\{a_{n}\}\)be a non-negative real sequence satisfying\(a_{n+1} \leq (1-\alpha_{n})a_{n} + \alpha_{n} b_{n}\), where\(\{\alpha_{n}\}\subset(0,1)\), \(\sum_{n=0}^{\infty}\alpha_{n} =\infty\)and\(\{b_{n}\}\)is a sequence such that\(\limsup_{n\to\infty}b_{n} \leq0\). Then\(\lim_{n\to\infty}a_{n} = 0\).

3 Main results

In this section, we present our algorithms and discuss the convergence analysis. The main advantages of our algorithms are that the stepsize is determined by an Armijo line search technique and does not require the prior knowledge of any Lipschitz constant. We assume that the following conditions are satisfied:

  1. (A1)

    C is nonempty, closed and convex subset of a reflexive Banach space E;

  2. (A2)

    the operator \(A:E \to E^{*}\) is pseudo-monotone, i.e., for all \(x,y \in E\), \(\langle Ax, y-x \rangle\geq0\) implies \(\langle Ay,y-x \rangle\geq0\);

  3. (A3)

    the operator A is weakly sequentially continuous, i.e., if for any sequence \(\{x_{n}\}\subset E\), we have \(x_{n} \rightharpoonup x\) implies \(Ax_{n} \rightharpoonup Ax\);

  4. (A4)

    the set \(\mathit{VI}(C,A)\) is nonempty;

  5. (A5)

    the function \(f:E \to\mathbb{R}\cup\{+\infty\}\) is Legendre, uniformly Gâteaux differentiable, strongly convex, bounded on bounded subsets of E and its gradient ∇f is weak-weak continuous, i.e., \(x_{n}\rightharpoonup x\) implies that \(\nabla f(x_{n}) \rightharpoonup\nabla f(x)\).

First, we introduce a weak convergence Bregman subgradient extragradient method for approximating solutions of the VI in real Banach spaces.

Algorithm 3.1

Step 0: :

Given \(\gamma>0\), \(l \in(0,1)\), \(\mu\in (0,1)\). Let \(x_{1} \in E\) and set \(n=1\).

Step 1: :

Compute

$$ y_{n} =\varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n}) - \alpha_{n} Ax_{n}\bigr)\bigr), $$
(3.1)

where \(\alpha_{n}=\gamma l^{k_{n}}\), with \(k_{n}\) being the smallest non-negative integer k satisfying

$$ \gamma l ^{k} \Vert Ax_{n} -Ay_{n} \Vert \leq\mu \Vert x_{n} -y_{n} \Vert . $$
(3.2)

If \(x_{n} =y_{n}\) or \(Ay_{n} = 0\), stop, \(y_{n}\) is a solution of the VI. Else, do Step 2.

Step 2: :

Compute

$$ x_{n+1} = \varPi_{T_{n}}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n})-\alpha_{n} Ay_{n}\bigr)\bigr), $$
(3.3)

where \(T_{n}\) is the half-space defined by

$$ T_{n}=\bigl\{ w\in E: \bigl\langle \nabla f(x_{n}) - \alpha_{n} x_{n} - \nabla f(y_{n}), w-y_{n}\bigr\rangle \leq0\bigr\} . $$
(3.4)

Set \(n:=n+1\) and return to Step 1.

Remark 3.2

We note that our Algorithm 3.1 is proposed in real Banach spaces while that of Nomirovski et al. [34] and Denisov et al. [12] were proposed in finite-dimensional spaces. Furthermore, our method is more general than that of [12, 18, 34, 35] which used a fixed stepsize for all iterates. We will see in the following result that the stepsize rule defined by (3.2) is well defined.

Lemma 3.3

There exists a non-negative integerksatisfying (3.2). In addition\(0 < \alpha_{n} \leq\gamma\).

Proof

If \(x_{n} \in \mathit{VI}(C,A)\), then \(x_{n} = \varPi_{C}(\nabla f^{*}(\nabla f(x_{n})-\alpha_{n} A x_{n}))\) and \(k_{n} = 0\). Hence, we consider the case where \(x_{n} \notin \mathit{VI}(C,A)\) and assume the contrary, i.e. for \(k>0\),

$$ \gamma l^{k} \bigl\Vert Ax_{n} - A \varPi_{C}\bigl(\nabla f^{*}\bigl( \nabla f(x_{n})- \gamma l^{k} Ax_{n}\bigr)\bigr) \bigr\Vert > \mu \bigl\Vert x_{n} - \varPi_{C}\bigl(\nabla f^{*} \bigl(\nabla f(x_{n})- \gamma l^{k} Ax_{n}\bigr)\bigr) \bigr\Vert . $$

This implies that

$$ \bigl\Vert Ax_{n} - A \varPi_{C}\bigl(\nabla f^{*} \bigl(\nabla f(x_{n})- \gamma l^{k} Ax_{n} \bigr)\bigr) \bigr\Vert > \frac{ \Vert x_{n} - \varPi_{C}(\nabla f^{*} (\nabla f(x_{n})- \gamma l^{k} Ax_{n})) \Vert }{\gamma l^{k}}. $$
(3.5)

Next, we consider two possibilities, namely, when \(x_{n} \in C\) and when \(x_{n} \notin C\).

First, if \(x_{n} \in C\), then \(x_{n} = \varPi_{C}(x_{n})\). Since \(\varPi_{C}\) and A are continuous,

$$ \lim_{k\to\infty} \bigl\Vert x_{n} - \varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n})-\gamma l^{k} Ax_{n}\bigr)\bigr) \bigr\Vert = 0. $$

Consequently, by the continuity of A on bounded sets, we get

$$ \lim_{k\to\infty} \bigl\Vert Ax_{n} - A \varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n})-\gamma l^{k} Ax_{n}\bigr)\bigr) \bigr\Vert = 0. $$
(3.6)

Combining (3.5) and (3.6), we have

$$ \lim_{k\to\infty}\frac{ \Vert x_{n} - \varPi_{C}(\nabla f^{*} (\nabla f(x_{n})- \gamma l^{k} Ax_{n})) \Vert }{\gamma l^{k}} = 0. $$
(3.7)

Moreover, from the uniform continuity of ∇f on bounded subsets, we have

$$ \lim_{k\to\infty}\frac{ \Vert \nabla f(x_{n}) - \nabla f(\varPi_{C}(\nabla f^{*}((x_{n})-\gamma l^{k} Ax_{n}))) \Vert }{\gamma l^{k}} = 0. $$
(3.8)

Now let \(z_{n} = \varPi_{C}(\nabla f^{*}(\nabla f(x_{n})-\gamma l^{k} Ax_{n}))\), then, by (2.6), we obtain

$$ \bigl\langle \nabla f(z_{k}) - \nabla f(x_{n}) + \gamma l^{k} Ax_{n}, x - z_{n} \bigr\rangle \geq0, \quad\forall x \in C. $$

This means that

$$ \langle Ax_{n}, x - z_{n} \rangle\geq \biggl\langle \frac{\nabla f(x_{n})-\nabla f(z_{n})}{\gamma l^{k}}, x - z_{n} \biggr\rangle ,\quad\forall x \in C. $$

Hence by taking the limit as \(n \to\infty\) and from (3.8), we get

$$ \langle Ax_{n}, x - x_{n} \rangle\geq0, \quad\forall x \in C. $$

Therefore, \(x_{n} \in \mathit{VI}(C,A)\). This is a contradiction.

On the other hand, if \(x_{n} \notin C\), then

$$ \lim_{k\to\infty} \bigl\Vert x_{n} - \varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n})-\gamma l^{k} Ax_{n}\bigr)\bigr) \bigr\Vert = \bigl\Vert x_{n} - \varPi_{C}(x_{n}) \bigr\Vert >0 $$
(3.9)

and

$$ \lim_{k\to\infty}\gamma l^{k} \bigl\Vert Ax_{n} - A\varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n})-\gamma l^{k} Ax_{n}\bigr)\bigr) \bigr\Vert = 0. $$
(3.10)

Combining (3.5), (3.9) and (3.10), we get a contradiction. □

We now present the convergence analysis of Algorithm 3.1. The following lemma will be used in the sequel.

Lemma 3.4

Assume Conditions (A1)–(A5) hold. Let\(\{x_{n}\}\)and\(\{y_{n}\}\)be the sequences generated by Algorithm3.1. Then

$$ D_{f}(p, x_{n+1}) \leq D_{f}(p,x_{n}) - (1-\mu) D_{f}(y_{n}, x_{n}) - (1-\mu )D_{f}(x_{n+1},y_{n}) $$

for any\(p \in \mathit{VI}(C,A)\).

Proof

Since \(x_{n+1} \in T_{n}\), it follows from (2.7) that

$$\begin{aligned} D_{f}(p,x_{n+1}) =& D_{f} \bigl(p, \varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n})-\alpha _{n} Ay_{n}\bigr)\bigr) \bigr) \\ \leq& D_{f} \bigl(p, \nabla f^{*}\bigl(\nabla f(x_{n})- \alpha_{n} Ay_{n}\bigr) \bigr) - D_{f} \bigl(x_{n+1}, \nabla f^{*}\bigl(\nabla f(x_{n})- \alpha_{n} Ay_{n}\bigr) \bigr) \\ =& V_{f} \bigl(p, \nabla f(x_{n})- \alpha_{n} Ay_{n} \bigr) - V_{f} \bigl(x_{n+1}, \nabla f(x_{n}) - \alpha_{n} Ay_{n} \bigr) \\ =& f(p) - \bigl\langle p, \nabla f(x_{n}) - \alpha_{n} Ay_{n} \bigr\rangle + f^{*}\bigl( \nabla f(x_{n})- \alpha_{n} Ay_{n}\bigr) \\ & {}- f(x_{n+1}) + \bigl\langle x_{n+1}, \nabla f(x_{n}) - \alpha_{n} Ay_{n} \bigr\rangle - f^{*}\bigl(\nabla f(x_{n}) - \alpha_{n} Ay_{n} \bigr) \\ =& f(p) - \bigl\langle p, \nabla f(x_{n}) \bigr\rangle +f^{*}(x_{n}) - f(x_{n+1}) + \bigl\langle x_{n+1}, \nabla f(x_{n}) \bigr\rangle - f^{*}(x_{n}) \\ &{} + \alpha_{n} \langle p, Ay_{n} \rangle- \alpha_{n} \langle x_{n+1}, Ay_{n} \rangle \\ =& D_{f}(p,x_{n}) - D_{f}(x_{n+1},x_{n}) + \alpha_{n} \langle p -x_{n+1}, Ay_{n} \rangle. \end{aligned}$$
(3.11)

Since A is pseudo-monotone and \(p \in \mathit{VI}(C,A)\),

$$ \langle Ay_{n}, y_{n} -p \rangle\geq0. $$
(3.12)

Hence, using (3.12) and (2.4) in (3.11), we get

$$\begin{aligned} D_{f}(p,x_{n+1}) \leq& D_{f}(p,x_{n}) - D_{f}(x_{n+1},x_{n}) + \alpha_{n} \langle p-y_{n}, Ay_{n} \rangle+ \alpha_{n} \langle y_{n} - x_{n+1}, Ay_{n} \rangle \\ \leq& D_{f}(p,x_{n}) - D_{f}(x_{n+1},x_{n}) + \alpha_{n} \langle y_{n} - x_{n+1}, Ay_{n} \rangle \\ =& D_{f}(p,x_{n}) - D_{f}(x_{n+1}, y_{n}) - D_{f}(y_{n},x_{n}) + \bigl\langle \nabla f(x_{n}) - \nabla f(y_{n}), x_{n+1} - y_{n} \bigr\rangle \\ &{} + \alpha_{n} \langle y_{n} - x_{n+1}, Ay_{n} \rangle \\ =& D_{f}(p,x_{n}) - D_{f}(x_{n+1}, y_{n}) - D_{f}(y_{n},x_{n}) \\ &{}+ \bigl\langle \nabla f(x_{n}) - \alpha_{n} Ay_{n} - \nabla f(y_{n}), x_{n+1} - y_{n} \bigr\rangle . \end{aligned}$$
(3.13)

Now, we estimate the last variable in (3.13) as follows:

$$\begin{aligned}[b] \bigl\langle \nabla f(x_{n}) - \alpha_{n} Ay_{n} - \nabla f(y_{n}), x_{n+1} - y_{n} \bigr\rangle &= \bigl\langle \nabla f(x_{n}) - \alpha_{n} Ax_{n} - \nabla f(y_{n}), x_{n+1} - y_{n} \bigr\rangle \\ &\quad + \alpha_{n} \langle Ax_{n} - Ay_{n}, x_{n+1} - y_{n} \rangle \\ &\leq \alpha_{n} \langle Ax_{n} - Ay_{n}, x_{n+1} - y_{n} \rangle. \end{aligned} $$
(3.14)

Using the Cauchy–Schwartz inequality and (3.2), we have

$$\begin{aligned} \bigl\langle \nabla f(x_{n}) - \alpha_{n} Ay_{n} - \nabla f(y_{n}), x_{n+1} - y_{n} \bigr\rangle \leq& \alpha_{n} \Vert Ax_{n} - Ay_{n} \Vert \Vert x_{n+1}-y_{n} \Vert \\ \leq& \mu \Vert x_{n} - y_{n} \Vert \Vert x_{n+1}-y_{n} \Vert \\ \leq& \frac{\mu}{2}\bigl( \Vert y_{n} - x_{n} \Vert ^{2} + \Vert x_{n+1}-y_{n} \Vert ^{2}\bigr) \\ \leq& \mu\bigl(D_{f}(y_{n},x_{n})+D_{f}(x_{n+1},y_{n}) \bigr). \end{aligned}$$
(3.15)

Substituting (3.15) into (3.13), we get

$$ D_{f}(p,x_{n+1}) \leq D_{f}(p,x_{n}) - (1-\mu)D_{f}(y_{n},x_{n}) - (1-\mu )D_{f}(x_{n+1},y_{n}). $$

 □

Theorem 3.5

Assume that Conditions (A1)–(A5) holds and\(\liminf_{n\to\infty}\alpha _{n} >0\). Then any sequence\(\{x_{n}\}\)generated by Algorithm3.1converges weakly to an element of\(\mathit{VI}(C,A)\).

Proof

Claim 1: \(\{x_{n}\}\) is bounded. Indeed, let \(p \in \mathit{VI}(C,A)\), we have from Lemma 3.4

$$ D_{f}(p,x_{n+1}) \leq D_{f}(p,x_{n}). $$

This implies that \(\{D_{f}(p,x_{n})\}\) is bounded and nonincreasing, thus, \(\lim_{n \rightarrow\infty}D_{f}(p,x_{n})\) exists. Hence

$$ \lim_{n \rightarrow\infty}\bigl(D_{f}(p,x_{n})-D_{f}(p,x_{n+1}) \bigr) = 0. $$
(3.16)

Moreover, due to (2.5), we see that \(\{x_{n}\}\) is bounded. Consequently \(\{y_{n}\}\) is bounded.

Claim 2: \(\lim_{n\to\infty}\|x_{n} - y_{n}\| = \lim_{n\to\infty}\| x_{n+1}-y_{n}\|=\lim_{n\to\infty}\|x_{n+1}-x_{n}\|= 0\). Indeed, from Lemma 3.4, we get

$$ (1-\mu)D_{f}(y_{n},x_{n}) + (1- \mu)D_{f}(x_{n+1},y_{n}) \leq D_{f}(p, x_{n}) - D_{f}(p,x_{n+1}). $$

Since \(\mu\in(0,1)\), it follows from (3.16) that

$$ \lim_{n \rightarrow\infty}D_{f}(y_{n},x_{n}) = \lim_{n \rightarrow\infty }D_{f}(x_{n+1},y_{n})=0. $$
(3.17)

Hence from (2.5), we get

$$ \lim_{n \rightarrow\infty} \Vert x_{n} - y_{n} \Vert = \lim_{n \rightarrow\infty } \Vert x_{n+1}-y_{n} \Vert = 0, $$
(3.18)

and

$$ \lim_{n \rightarrow\infty} \Vert x_{n+1}-x_{n} \Vert = 0. $$

Claim 3: \(\{x_{n}\}\) weakly converges to an element of \(\mathit{VI}(C,A)\). Indeed, since \(\{x_{n}\}\) is a bounded sequence, there exists a subsequence \(\{x_{n_{k}}\}\) of \(\{x_{n}\}\) such that \(x_{n_{k}} \rightharpoonup z \in E\). From the fact that \(\lim_{n \rightarrow\infty }\|x_{n} -y_{n}\|= 0\), we obtain \(y_{n_{k}}\rightharpoonup z\), where \(\{ y_{n_{k}}\}\) is a subsequence of \(\{y_{n}\}\). Since

$$ y_{n_{k}}= \varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n_{k}})-\alpha_{n_{k}}Ax_{n_{k}}\bigr)\bigr), $$

it follows from (2.6) that

$$ \bigl\langle \nabla f(x_{n_{k}}) - \alpha_{n_{k}}Ax_{n_{k}} - \nabla f(y_{n_{k}}), y - y_{n_{k}} \bigr\rangle \leq0 ,\quad \forall y \in C. $$
(3.19)

This means that

$$ \frac{1}{\alpha_{n_{k}}}\bigl\langle \nabla f(x_{n_{k}}) - \nabla f(y_{n_{k}}), y - y_{n_{k}} \bigr\rangle \geq\langle Ax_{n_{k}}, y -y_{n_{k}} \rangle,\quad \forall y \in C. $$

Hence

$$ \frac{1}{\alpha_{n_{k}}}\bigl\langle \nabla f(x_{n_{k}}) - \nabla f(y_{n_{k}}), y - y_{n_{k}} \bigr\rangle + \langle Ax_{n_{k}}, y_{n_{k}} - x_{n_{k}} \rangle\leq \langle Ax_{n_{k}}, y - x_{n_{k}} \rangle,\quad\forall y \in C. $$

Now we show that

$$ \liminf_{k\to\infty}\langle Ax_{n_{k}}, y - x_{n_{k}} \rangle\geq0. $$
(3.20)

We consider two possible cases. First suppose that \(\liminf_{k\to\infty }\alpha_{n_{k}}>0\), since \(\|x_{n_{k}}-y_{n_{k}}\|\to0\) as \(k \to\infty\), by the weak-weak continuity of ∇f, we have \(\|\nabla f(x_{n_{k}}) - \nabla f(y_{n_{k}})\|\to0\) as \(k\to\infty\). Taking the limit of the above inequality as \(k\to\infty\) we get

$$ \liminf_{k\to\infty}\langle Ax_{n_{k}}, y - x_{n_{k}}\rangle\geq0 ,\quad \forall y \in C. $$
(3.21)

On the other hand, suppose \(\liminf_{k\to\infty}\alpha_{n_{k}} = 0\). Let \(z_{n_{k}} = \varPi_{C}(\nabla f^{*}(\nabla f(x_{n}) - \alpha _{n_{k}}l^{-1}Ax_{n_{k}}))\), we have \(\alpha_{n_{k}}l^{-1}> \alpha_{n_{k}}\) and by using Lemma 2.5, we obtain

$$ \Vert x_{n_{k}}-z_{n_{k}} \Vert \leq\frac{1}{l} \Vert x_{n_{k}}-y_{n_{k}} \Vert \to0 \quad \text{as } k \to\infty. $$

Furthermore, \(z_{n_{k}} \rightharpoonup z \in C\), which implies that \(\{ z_{n_{k}}\}\) is a bounded sequence. By the uniform continuity of A, we have

$$ \Vert Ax_{n_{k}} - Az_{n_{k}} \Vert \to0 \quad\text{as } k \to\infty. $$
(3.22)

Using the Armijo line search rule, we get

$$ \frac{1}{\mu} \Vert Ax_{n_{k}}-Az_{n_{k}} \Vert > \frac{ \Vert x_{n_{k}} - z_{n_{k}} \Vert }{\alpha_{n_{k}}l^{-1}}. $$
(3.23)

Combining (3.22) and (3.23), we get

$$ \lim_{k\to\infty}\frac{ \Vert x_{n_{k}}-z_{n_{k}} \Vert }{\alpha_{n_{k}}l^{-1}} = 0. $$

Moreover,

$$ \bigl\langle \nabla f(x_{n_{k}}) - \alpha_{n_{k}}l^{-1}Ax_{n_{k}} - \nabla f(z_{n_{k}}), x - z_{n_{k}} \bigr\rangle \leq0, \quad \forall x \in C. $$

Hence

$$ \frac{1}{\alpha_{n_{k}}l^{-1}}\bigl\langle \nabla f(x_{n_{k}}) - \nabla f(z_{n_{k}}), x - z_{n_{k}} \bigr\rangle + \langle Ax_{n_{k}}, z_{n_{k}} - x_{n_{k}} \rangle\leq\langle Ax_{n_{k}}, x - x_{n_{k}} \rangle,\quad\forall x \in C. $$

Taking the limit of the above inequality as \(k \to\infty\), we get

$$\liminf_{k\to\infty}\langle Ax_{n_{k}}, x - x_{n_{k}} \rangle \geq0. $$

Thus, the inequality is proven.

Now choose a sequence \(\{\epsilon_{k}\} \subset(0,1)\) such that \(\epsilon_{k} \to0\) as \(k \to\infty\). For each \(k\geq1\), there exists a smallest number \(N \in\mathbb{N}\) satisfying

$$ \langle Ax_{n_{k}}, y -x_{n_{k}}\rangle+ \epsilon_{k} \geq0, \quad\forall k \geq N. $$

This implies that

$$ \langle Ax_{n_{k}}, y+\epsilon_{k}t_{n_{k}} - x_{n_{k}} \rangle\geq0, \quad \forall k \geq N $$

for some \(t_{n_{k}} \in E\) satisfying \(1 = \langle Ax_{n_{k}}, t_{n_{k}}\rangle\) (since \(Ax_{n_{k}} \neq0\)). Since A is pseudo-monotone, we have

$$ \bigl\langle A(y+\epsilon_{k}t_{n_{k}}), y+ \epsilon_{k}t_{n_{k}} - x_{n_{k}} \bigr\rangle \geq0, \quad\forall k \geq N. $$

This implies that

$$ \langle Ay, y- x_{n_{k}} \rangle\geq\bigl\langle Ay - A(y+\epsilon _{k}t_{n_{k}}), y+ \epsilon_{k}t_{n_{k}}-x_{n_{k}} \bigr\rangle - \epsilon_{k}\langle Ay, t_{n_{k}} \rangle,\quad \forall k \geq N. $$
(3.24)

Since \(\epsilon_{k} \to0\) and A is continuous, then the right hand side of (3.24) tends to zero. Thus, we obtain

$$ \liminf_{k\to\infty}\langle Ay, y -x_{n_{k}}\rangle\geq0, \quad\forall y \in C. $$

Hence

$$ \langle Ay, y-z \rangle= \lim_{k\to\infty}\langle Ay, y - x_{n_{k}}\rangle\geq0 ,\quad\forall y \in C. $$

Therefore, from Lemma 2.4, we obtain \(z \in \mathit{VI}(C,A)\).

Finally, we show that z is unique. Assume the contrary, i.e., there exists a subsequence \(\{x_{n_{j}}\}\) of \(\{x_{n}\}\) such that \(x_{n_{j}}\rightharpoonup\hat{z}\) with \(\hat{z}\neq z\). Following a similar argument to the one above, we get \(\hat{z} \in \mathit{VI}(C,A)\). It follows from the Bregman Opial-like property of H (more precisely, Lemma 2.6) that

$$\begin{aligned} \lim_{n \rightarrow\infty}D_{f}(z,x_{n}) &= \lim _{k\to\infty}D_{f}(z, x_{n_{k}}) < \lim _{k\to\infty}D_{f}(\hat{z}, x_{n_{k}}) \\ &= \lim_{n \rightarrow\infty}D_{f}(\hat{z}, x_{n}) = \lim_{j\to\infty }D_{f}(\hat{z},x_{n_{j}}) \\ &< \lim_{j\to\infty}D_{f}(z, x_{n_{j}}) = \lim_{n \rightarrow\infty }D_{f}(z, x_{n}),\end{aligned} $$

which is a contradiction. Thus, we have \(z = \hat{z}\) and the desired result follows. This completes the proof. □

Next, we propose a strong convergence Bregman subgradient extragradient algorithm with Halpern iterative method [22] for solving the VI (1.1) in real Banach spaces. This is important for supporting the infinite-dimensional setting of our work.

Algorithm 3.6

Step 0: :

Given \(\gamma>0\), \(l \in(0,1)\), \(\mu\in (0,1)\), \(\{\delta_{n}\}\subset(0,1)\). Let \(x_{1},u \in E\) and set \(n=1\).

Step 1: :

Compute

$$ y_{n} =\varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n}) - \alpha_{n} Ax_{n}\bigr)\bigr), $$
(3.25)

where \(\alpha_{n}=\gamma l^{k_{n}}\), with \(k_{n}\) being the smallest non-negative integer k satisfying

$$ \gamma l ^{k} \Vert Ax_{n} -Ay_{n} \Vert \leq\mu \Vert x_{n} -y_{n} \Vert . $$
(3.26)

If \(x_{n} =y_{n}\) or \(Ay_{n} = 0\), stop, \(y_{n}\) is a solution of the VI. Else, do Step 2.

Step 2: :

Compute

$$ z_{n} = \varPi_{T_{n}}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n})-\alpha_{n} Ay_{n}\bigr)\bigr), $$
(3.27)

where \(T_{n}\) is the half-space defined by

$$ T_{n}=\bigl\{ w\in E: \bigl\langle \nabla f(x_{n}) - \alpha_{n} x_{n} - \nabla f(y_{n}), w-y_{n}\bigr\rangle \leq0\bigr\} . $$
(3.28)
Step 3: :

Compute

$$ x_{n+1} = \nabla f^{*}\bigl(\delta_{n}\nabla f(u) +(1- \delta_{n}) \nabla f(z_{n})\bigr). $$
(3.29)

Set \(n:=n+1\) and return to Step 1.

For proving the convergence of Algorithm 3.6, we assume that the following condition is satisfied.

  1. (C1)

    \(\lim_{n \rightarrow\infty}\delta_{n} = 0\) and \(\sum_{n=0}^{\infty}\delta_{n} = +\infty\).

We first prove the following lemmas which are crucial for our main theorem.

Lemma 3.7

The sequence\(\{x_{n}\}\)generated by Algorithm3.6is bounded.

Proof

Let \(p \in \mathit{VI}(C,A)\), then

$$\begin{aligned} D_{f}(p,z_{n}) =& D_{f} \bigl(p, \varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n})- \alpha_{n} Ay_{n}\bigr)\bigr) \bigr) \\ \leq& D_{f} \bigl(p, \nabla f^{*}\bigl(\nabla f(x_{n})- \alpha_{n} Ay_{n}\bigr) \bigr) - D_{f} \bigl(z_{n}, \nabla f^{*}\bigl(\nabla f(x_{n})- \alpha_{n} Ay_{n}\bigr) \bigr) \\ =& V_{f} \bigl(p, \nabla f(x_{n})- \alpha_{n} Ay_{n} \bigr) - V_{f} \bigl(z_{n}, \nabla f(x_{n}) - \alpha_{n} Ay_{n} \bigr) \\ =& f(p) - \bigl\langle p, \nabla f(x_{n}) - \alpha_{n} Ay_{n} \bigr\rangle + f^{*}\bigl( \nabla f(x_{n})- \alpha_{n} Ay_{n}\bigr) \\ &{} - f(z_{n}) + \bigl\langle z_{n}, \nabla f(x_{n}) - \alpha_{n} Ay_{n} \bigr\rangle - f^{*}\bigl(\nabla f(x_{n}) - \alpha_{n} Ay_{n} \bigr) \\ =& f(p) - \bigl\langle p, \nabla f(x_{n}) \bigr\rangle +f^{*}(x_{n}) - f(z_{n}) + \bigl\langle z_{n}, \nabla f(x_{n}) \bigr\rangle - f^{*}(x_{n}) \\ &{} + \alpha_{n} \langle p, Ay_{n} \rangle- \alpha_{n} \langle z_{n}, Ay_{n} \rangle \\ =& D_{f}(p,x_{n}) - D_{f}(z_{n},x_{n}) + \alpha_{n} \langle p -z_{n}, Ay_{n} \rangle. \end{aligned}$$
(3.30)

Since p is a solution of VI (1.1), we have \(\langle Ap, x-p\rangle\geq0\) for all \(x \in C\). By the pseudo-monotonicity of A on H, we get \(\langle Ax,x - p\rangle\geq0\) for all \(x \in C\). Hence \(\langle Ay_{n}, p - y_{n} \rangle\geq0\). Thus, we have

$$ \langle Ay_{n}, p -z_{n} \rangle= \langle Ay_{n}, p- y_{n}\rangle+ \langle Ay_{n}, y_{n} -z_{n} \rangle\leq\langle Ay_{n}, y_{n} -z_{n}\rangle. $$
(3.31)

From (3.30) and (3.31), we have

$$\begin{aligned} D_{f}(p,z_{n}) \leq& D_{f}(p,x_{n}) - D_{f}(z_{n}, x_{n}) + \langle Ay_{n}, y_{n} - z_{n}\rangle \\ =& D_{f}(p,x_{n}) - D_{f}(z_{n}, y_{n}) - D_{f}(y_{n},x_{n}) + \bigl\langle \nabla f(x_{n}) - \nabla f(y_{n}), z_{n} - y_{n} \bigr\rangle \\ &{} + \alpha_{n} \langle y_{n} - z_{n}, Ay_{n} \rangle \\ =& D_{f}(p,x_{n}) - D_{f}(z_{n}, y_{n}) - D_{f}(y_{n},x_{n}) \\ &{}+ \bigl\langle \nabla f(x_{n}) - \alpha_{n} Ay_{n} - \nabla f(y_{n}), z_{n} - y_{n} \bigr\rangle . \end{aligned}$$
(3.32)

Note that

$$\begin{aligned} \bigl\langle \nabla f(x_{n}) - \alpha_{n} Ay_{n} - \nabla f(y_{n}), z_{n} - y_{n} \bigr\rangle =& \bigl\langle \nabla f(x_{n}) - \alpha_{n} Ax_{n} - \nabla f(y_{n}), z_{n} - y_{n} \bigr\rangle \\ &{}+ \alpha_{n} \langle Ax_{n} - Ay_{n}, z_{n} - y_{n} \rangle \\ \leq& \alpha_{n} \langle Ax_{n} - Ay_{n}, z_{n} - y_{n} \rangle \\ \leq& \alpha_{n} \Vert Ax_{n} - Ay_{n} \Vert \Vert z_{n} -y_{n} \Vert \\ \leq& \mu \Vert x_{n} - y_{n} \Vert \Vert z_{n} -y_{n} \Vert \\ \leq& \frac{\mu}{2}\bigl( \Vert y_{n} -x_{n} \Vert ^{2}+ \Vert z_{n} -y_{n} \Vert ^{2}\bigr) \\ \leq& \mu\bigl(D_{f}(y_{n},x_{n})+D_{f}(z_{n},y_{n}) \bigr). \end{aligned}$$
(3.33)

Hence from (3.32) and (3.33), we get

$$\begin{aligned}[b] D_{f}(p,z_{n}) &\leq D_{f}(p,x_{n}) - (1-\mu)D_{f}(y_{n},x_{n}) - (1-\mu )D_{f}(z_{n},y_{n}) \\ &\leq D_{f}(p,x_{n}).\end{aligned} $$
(3.34)

Furthermore, from (3.29), we have

$$\begin{aligned} D_{f}(p,x_{n+1}) =& D_{f}\bigl(p,\nabla f^{*}\bigl(\delta_{n} \nabla f(u)+(1-\delta _{n})\nabla f(z_{n})\bigr)\bigr) \\ \leq& \delta_{n} D_{f}(p, u) + (1- \delta_{n}) D_{f}(p, z_{n}) \\ \leq& \delta_{n}D_{f}(p,u) + (1-\delta_{n})D_{f}(p,x_{n}) \\ \leq& \max\bigl\{ D_{f}(p,u), D_{f}(p, x_{n})\bigr\} \\ \vdots& \\ \leq& \max\bigl\{ D_{f}(p,u), D_{f}(p, x_{1})\bigr\} . \end{aligned}$$

This implies that \(\{D_{f}(p,x_{n})\}\) is bounded. Hence, \(\{x_{n}\}\) is bounded. Consequently, we see that \(\{\nabla f(x_{n})\}\), \(\{y_{n}\}\), \(\{ z_{n}\}\) are bounded. □

Lemma 3.8

The sequence\(\{x_{n}\}\)generated by Algorithm3.6satisfies the following estimates:

  1. (i)

    \(s_{n+1} \leq(1-\delta)s_{n} + \delta_{n} b_{n}\),

  2. (ii)

    \(-1 \leq\limsup_{n\to\infty}b_{n} < +\infty\),

where\(s_{n} = D_{f}(p,x_{n})\), \(b_{n} = \langle\nabla f(u) - \nabla f(p), x_{n+1} - p \rangle\)for all\(p \in \mathit{VI}(C,A)\).

Proof

From (2.9) we have

$$\begin{aligned} D_{f}(p, x_{n+1}) \leq& D_{f} \bigl(p, \nabla f^{*}\bigl(\delta_{n} \nabla f(u)+(1-\delta_{n}) \nabla f(z_{n})\bigr) \bigr) \\ =& V_{f} \bigl(p, \delta_{n} \nabla f(u)+(1- \delta_{n}) \nabla f(z_{n}) \bigr) \\ \leq& V_{f} \bigl(p, \delta_{n} \nabla f(u)+(1- \delta_{n}) \nabla f(z_{n})-\delta_{n}\bigl( \nabla f(u)-\nabla f(p)\bigr) \bigr) \\ &{}- \bigl\langle -\delta _{n}\bigl( \nabla f(u) - \nabla f(p)\bigr), x_{n+1}-p \bigr\rangle \\ =& V_{f} \bigl(p, \delta_{n} \nabla f(p) + (1- \delta_{n})\nabla f(z_{n}) \bigr) + \delta_{n} \bigl\langle \nabla f(u) - \nabla f(p), x_{n+1}-p \bigr\rangle \\ \leq& \delta_{n} V_{f}(p,p) + (1-\delta_{n})V_{f} \bigl(p, \nabla f(z_{n})\bigr) + \delta _{n} \bigl\langle \nabla f(u) - \nabla f(p), x_{n+1}-p \bigr\rangle \\ =& (1-\delta_{n})D_{f}(p,z_{n}) + \delta_{n} \bigl\langle \nabla f(u) - \nabla f(p), x_{n+1}-p \bigr\rangle \\ \leq& (1-\delta_{n}) D_{f}(p,x_{n}) + \delta_{n} \bigl\langle \nabla f(u) - \nabla f(p), x_{n+1}-p \bigr\rangle . \end{aligned}$$
(3.35)

This established (i). Next, we show (ii). Since \(\{x_{n}\}\) is bounded and \(\delta_{n} \in(0,1)\), we have

$$ \sup_{n\geq0}b_{n} \leq\sup_{n\geq0} \bigl\Vert \nabla f(u) - \nabla f(p) \bigr\Vert \Vert x_{n+1} - p \Vert < \infty. $$

We now show that \(\limsup_{n\to\infty}b_{n} \geq-1\). Assume the contrary, i.e., there exists \(n_{0} \in\mathbb{N}\) such that \(b_{n} \geq -1\) for all \(n \geq n_{0}\). Hence it follows that

$$\begin{aligned} s_{n+1} \leq& (1-\delta_{n})s_{n} + \delta_{n} b_{n} \\ < & (1-\delta_{n})s_{n} - \delta_{n} \\ =& s_{n} - \delta_{n}(s_{n} +1) \\ \leq& s_{n} - \delta_{n}. \end{aligned}$$

By induction, we obtain

$$ s_{n+1} \leq s_{n_{0}} - \sum_{i=1}^{n} \delta_{i}, \quad\forall n \geq n_{0}. $$

Taking the lim sup of the above inequality, we have

$$ \limsup_{n\to\infty}s_{n} \leq s_{n_{0}} - \lim_{n \rightarrow\infty}\sum_{i=1}^{n} \delta_{i} = -\infty. $$

This contradicts the fact that \(\{s_{n}\}\) is a non-negative real sequence. Thus \(\limsup_{n\to\infty}b_{n} \geq-1\). □

Next, we present our strong convergence theorem.

Theorem 3.9

Assume Conditions (A1)–(A5) and (C1) hold. Then the sequence\(\{x_{n}\} \)generated by Algorithm3.6converges strongly to an element in\(\mathit{VI}(C,A)\).

Proof

Let \(p \in \mathit{VI}(C,A)\) and \(\varGamma_{n} = D_{f}(p,x_{n})\). We divide the proof into two cases.

Case I: Suppose that there exists \(n_{0} \in\mathbb{R}\) such that \(\{\varGamma_{n}\}\) is monotonically non-increasing for \(n \geq n_{0}\). Since \(\{\varGamma_{n}\}\) is bounded (see Lemma 3.7), \(\{ \varGamma_{n}\}\) converges and therefore

$$ \varGamma_{n} - \varGamma_{n+1} \to0 \quad \text{as }n \to \infty. $$

From (3.34), we have

$$\begin{aligned} D_{f}(p,x_{n+1}) \leq& \delta_{n}D_{f}(p,u) + (1-\delta_{n})D_{f}(p, z_{n}) \\ \leq& \delta_{n} D_{f}(p,u) + (1-\delta_{n}) \bigl[ D_{f}(p,x_{n}) - (1-\mu )D_{f}(z_{n},y_{n}) - (1-\mu)D_{f}(y_{n},x_{n}) \bigr]. \end{aligned}$$

This implies that

$$ (1-\delta_{n}) (1-\mu) \bigl[D_{f}(z_{n},y_{n}) + D_{f}(y_{n},x_{n})\bigr] \leq\delta _{n}\bigl(D_{f}(p,u)-D_{f}(p,x_{n}) \bigr) + D_{f}(p,x_{n}) - D_{f}(p,x_{n+1}) . $$

Since \(\delta_{n} \to0\), we have

$$ \lim_{n \rightarrow\infty} (1-\mu) \bigl[D_{f}(z_{n},y_{n}) + D_{f}(y_{n},x_{n})\bigr] = 0. $$

Hence

$$ \lim_{n \rightarrow\infty}D_{f}(z_{n},y_{n}) = \lim_{n \rightarrow\infty }D_{f}(y_{n},x_{n}) = 0. $$

Using (2.5), we obtain

$$ \lim_{n \rightarrow\infty} \Vert z_{n} -y_{n} \Vert = \lim_{n \rightarrow\infty} \Vert y_{n} -x_{n} \Vert = 0. $$

This implies that

$$ \lim_{n \rightarrow\infty} \Vert z_{n} - x_{n} \Vert = 0 . $$
(3.36)

Furthermore

$$\begin{aligned} D_{f}(z_{n}, x_{n+1}) =& D_{f} \bigl(z_{n}, \nabla f^{*}\bigl(\delta_{n} \nabla f(u) + (1- \delta_{n})\nabla f(z_{n})\bigr)\bigr) \\ \leq& \delta_{n} D_{f}(z_{n}, u) + (1- \delta_{n}) D_{f}(z_{n}, z_{n}) \to0. \end{aligned}$$

Thus

$$ \lim_{n \rightarrow\infty} \Vert z_{n} - x_{n+1} \Vert = 0. $$
(3.37)

Therefore from (3.36) and (3.37), we get

$$ \lim_{n \rightarrow\infty} \Vert x_{n+1}-x_{n} \Vert = 0. $$

Since \(\{x_{n}\}\) is bounded, there exists a subsequence \(\{x_{n_{k}}\}\) of \(\{x_{n}\}\) such that \(x_{n_{k}} \rightharpoonup\bar{x}\). We now show that \(\bar{x} \in \mathit{VI}(C,A)\). From

$$ y_{n_{k}}= \varPi_{C}\bigl(\nabla f^{*}\bigl(\nabla f(x_{n_{k}})-\alpha_{n_{k}}Ax_{n_{k}}\bigr)\bigr), $$

we have

$$ \bigl\langle \nabla f(x_{n_{k}}) - \alpha_{n_{k}}Ax_{n_{k}} - \nabla f(y_{n_{k}}), x - y_{n_{k}} \bigr\rangle \leq0, \quad \forall x \in C. $$
(3.38)

This implies that

$$ \frac{1}{\alpha_{n_{k}}}\bigl\langle \nabla f(x_{n_{k}}) - \nabla f(y_{n_{k}}), x - y_{n_{k}} \bigr\rangle \geq\langle Ax_{n_{k}}, x -y_{n_{k}} \rangle,\quad \forall x \in C. $$

Hence

$$ \frac{1}{\alpha_{n_{k}}}\bigl\langle \nabla f(x_{n_{k}}) - \nabla f(y_{n_{k}}), x - y_{n_{k}} \bigr\rangle + \langle Ax_{n_{k}}, y_{n_{k}} - x_{n_{k}} \rangle\leq \langle Ax_{n_{k}}, x - x_{n_{k}} \rangle,\quad\forall x \in C. $$

Following a similar approach to Theorem 3.5, we can show that

$$ \liminf_{k\to\infty}\langle Ax_{n_{k}}, x - x_{n_{k}}\rangle\geq0, \quad \forall x \in C. $$
(3.39)

Let \(\{\epsilon_{k}\}\) be a sequence in \((0,1)\) such that \(\epsilon_{k} \to 0\) as \(k \to\infty\). For each \(k\geq1\), there exists a smallest number \(N \in\mathbb{N}\) satisfying

$$ \langle Ax_{n_{k}}, x -x_{n_{k}}\rangle+ \epsilon_{k} \geq0 ,\quad\forall k \geq N. $$

This implies that

$$ \langle Ax_{n_{k}}, x+\epsilon_{k}t_{n_{k}} - x_{n_{k}} \rangle\geq0 ,\quad \forall k \geq N $$

for some \(t_{n_{k}} \in E\) satisfying \(1 = \langle Ax_{n_{k}}, t_{n_{k}}\rangle\) (since \(Ax_{n_{k}} \neq0\)). Since A is pseudo-monotone, we have

$$ \bigl\langle A(x+\epsilon_{k}t_{n_{k}}), x+ \epsilon_{k}t_{n_{k}} - x_{n_{k}} \bigr\rangle \geq0, \quad\forall k \geq N. $$

Thus

$$ \langle Ax, x- x_{n_{k}} \rangle\geq\bigl\langle Ax - A(x+\epsilon _{k}t_{n_{k}}), x+ \epsilon_{k}t_{n_{k}}-x_{n_{k}} \bigr\rangle - \epsilon_{k}\langle Ax, t_{n_{k}} \rangle,\quad \forall k \geq N. $$
(3.40)

Since \(\epsilon_{k} \to0\) and A is continuous, the right hand side of (3.40) tends to zero. Thus, we obtain

$$ \liminf_{k\to\infty}\langle Ax, x -x_{n_{k}}\rangle\geq0, \quad\forall x \in C. $$

Hence

$$ \langle Ax, x-\bar{x} \rangle= \lim_{k\to\infty}\langle Ax, x - x_{n_{k}}\rangle\geq0, \quad\forall x \in C. $$

Therefore, from Lemma 2.4, we obtain \(\bar{x} \in \mathit{VI}(C,A)\). We now show that \(\{x_{n}\}\) converges strongly to p. It suffices to show that \(\limsup_{n\to\infty}\langle\nabla f(u) - \nabla f(p), x_{n+1} - p \rangle\leq0\). To do this, choose a subsequence \(\{ x_{n_{k}}\}\) of \(\{x_{n}\}\) such that

$$ \limsup_{n\to\infty} \bigl\langle \nabla f(u) - \nabla f(p), x_{n+1} - p \bigr\rangle = \lim_{k\to\infty}\bigl\langle \nabla f(u) - \nabla f(p), x_{n_{k}+1} - p \bigr\rangle . $$
(3.41)

Since \(\|x_{n_{k}+1}- x_{n_{k}}\| \to0\) and \(x_{n_{k}} \rightharpoonup\bar {x}\) as \(k \to\infty\), we have from (2.6) and (3.41)

$$\begin{aligned} \limsup_{n\to\infty} \bigl\langle \nabla f(u) - \nabla f(p), x_{n+1} - p \bigr\rangle =& \lim_{k\to\infty}\bigl\langle \nabla f(u) - \nabla f(p), x_{n_{k}+1} - p \bigr\rangle \\ =& \bigl\langle \nabla f(u) - \nabla f(p), \bar{x} - p \bigr\rangle \\ \leq& 0. \end{aligned}$$
(3.42)

Using Lemma 2.7, Lemma 3.8(i) and (3.42), we obtain \(\lim_{n \rightarrow\infty}D_{f}(p,x_{n}) = 0\). This implies that \(\|x_{n} -p\| \to0\), hence, \(\{x_{n}\}\) converges strongly to p. Consequently, \(\{y_{n}\}\) and \(\{z_{n}\}\) converges strongly to p.

Case II: Suppose \(\{D_{f}(p,x_{n})\}\) is not monotonically decreasing. Let \(\tau: \mathbb{N} \rightarrow\mathbb{N}\) for all \(n \geq n_{0}\) (for some \(n_{0}\) large enough) be defined by

$$\tau_{n} = \max\{k \in\mathbb{N}: \tau_{k} \leq \tau_{k+1}\}. $$

Clearly, τ is nondecreasing, \(\tau(n) \rightarrow\infty\) as \(n \rightarrow\infty\) and

$$0 \leq D_{f}(p, x_{\tau(n)}) \leq D_{f}(p, x_{\tau(n)+1}), \quad\forall n \geq n_{0}. $$

Following a similar argument to Case I, we obtain

$$\Vert x_{\tau(n)} - y_{\tau(n)} \Vert \rightarrow0, \qquad \Vert v_{\tau(n)} - Tv_{\tau(n)} \Vert \rightarrow0, \qquad \Vert x_{\tau(n)+1} - x_{\tau(n)} \Vert \rightarrow0 $$

as \(n \rightarrow\infty\) and \(\varOmega_{w}(x_{\tau(n)}) \subset \mathit{VI}(C,A)\), where \(\varOmega_{w}(x_{\tau(n)})\) is the weak subsequential limit of \(\{x_{\tau(n)}\}\). Also,

$$\begin{aligned} \limsup_{n \rightarrow\infty}\bigl\langle \nabla f(u) - \nabla f(p), x_{\tau(n)+1} - p \bigr\rangle \leq0. \end{aligned}$$
(3.43)

From Lemma 3.8(i), we have

$$D_{f}(p, x_{\tau(n)+1}) \leq(1-\delta_{\tau(n)})D_{f}(p, x_{\tau(n)}) + \delta_{\tau(n)}\bigl\langle \nabla f(u) - \nabla f(p), x_{\tau(n)+1} - p \bigr\rangle . $$

Since \(D_{f}(p, x_{\tau(n)}) \leq D_{f}(p, x_{\tau(n)+1})\),

$$\begin{aligned} 0 \leq& D_{f}(p, x_{\tau(n)+1}) - D_{f}(p, x_{\tau(n)}) \\ \leq& (1-\delta_{\tau(n)})D_{f}(p,x_{\tau(n)}) + \delta_{\tau (n)}\bigl\langle \nabla f(u) - \nabla f(p), x_{\tau(n)+1} -p \bigr\rangle -D_{f}(p, x_{\tau(n)}). \end{aligned}$$

Hence, from (3.42), we get

$$ D_{f}(p, x_{\tau(n)}) \leq\bigl\langle \nabla f(u) - \nabla f(p), x_{\tau (n)+1} - p \bigr\rangle \rightarrow0\quad \text{as }n \rightarrow\infty. $$

As a consequence, we obtain, for all \(n \geq n_{0}\),

$$0 \leq D_{f}(p, x_{n}) \leq\max\bigl\{ D_{f}(p, x_{\tau(n)}), D_{f}(p, x_{\tau (n)+1})\bigr\} = D_{f}(p, x_{\tau(n)+1}). $$

Thus

$$D_{f}(p, x_{n}) \rightarrow0\quad\text{as } n \rightarrow\infty. $$

Therefore, from (2.5)

$$\lim_{n \rightarrow\infty} \Vert x_{n} - p \Vert = 0. $$

This implies that \(\{x_{n}\}\) converges strongly to p. This completes the proof. □

Remark 3.10

  1. (i)

    We note that our results extend the results of [12, 35] from finite-dimensional spaces to real Banach spaces.

  2. (ii)

    We also extend the result of Gibali [18] to solving pseudo-monotone variational inequalities and real Banach spaces.

  3. (iii)

    Moreover, our algorithms does not require any prior estimate of the Lipschitz constant for their convergence. This improves the corresponding results of [7, 8, 12, 18, 35] in the literature.

  4. (iv)

    The strong convergence theorem proved in this paper is more desirable for solving optimization problems.

Remark 3.11

The operator A is said to be monotone if \(\langle Ax - Ay,x-y \rangle\geq0\) for all \(x,y \in E\). It is easy to see that every monotone operator is pseudo-monotone but the converse is not true (see Example 4.2). Moreover, we give the following example of a variational inequality problem satisfying assumptions (A2)–(A4), but not Lipschitz continuous (see also [43]).

Example 3.12

Let \(E = \ell_{2}(\mathbb{R})\), \(C = \{x = (x_{1},x_{2},\dots,x_{i},\dots)\in E: |x_{i}| \leq\frac{1}{i}, \forall i =1,2,\dots\}\) and

$$Ax = \biggl( \Vert x \Vert +\frac{1}{ \Vert x \Vert +1} \biggr)x. $$

It is easy to see that \(\mathit{VI}(C,A) \neq\emptyset\) since \(0 \in \mathit{VI}(C,A)\), A is pseudo-monotone, sequentially weakly continuous but not Lipschitz continuous on E. Indeed, let \(u,v \in C\) be such that \(\langle Ax, y-x \rangle\geq0\). This means that \(\langle x, y-x \rangle\geq0\). Consequently,

$$\begin{aligned} \langle Ay, y -x \rangle =& \biggl( \Vert y \Vert +\frac{1}{ \Vert y \Vert +1} \biggr)\langle y, y-x\rangle \\ >& \biggl( \Vert y \Vert +\frac{1}{ \Vert y \Vert +1} \biggr) \bigl(\langle y, y - x\rangle- \langle x, y -x \rangle\bigr) \\ =& \biggl( \Vert y \Vert +\frac{1}{ \Vert y \Vert +1} \biggr) \Vert y-x \Vert ^{2} >0. \end{aligned}$$

Hence, A is pseudo-monotone. Also, since A is compact, it is uniformly continuous and thus sequentially weakly continuous on E. To see that A is not L-Lipschitz continuous, let \(x = (L, 0 ,\dots, 0,\dots)\) and \(y = (0,0,\dots,0,\dots)\), then

$$ \Vert Ax - Ay \Vert = \Vert Ax \Vert = \biggl( \Vert x \Vert + \frac{1}{ \Vert x \Vert +1} \biggr) \Vert x \Vert = \biggl(L+\frac{1}{L+1} \biggr)L. $$

Moreover, \(\|Ax- Ay\| \leq L\|x-y\|\) is equivalent to

$$ \biggl(L + \frac{1}{L+1} \biggr)L \leq L^{2}. $$

This implies that

$$ \frac{1}{L+1}\leq0. $$

This is a contradiction, and thus A is not Lipschitz continuous on E.

4 Numerical illustrations

In this section, we present some numerical examples to illustrate the convergence and efficiency of the proposed algorithms. The projection onto C is computed effectively by using the function quadprog in Matlab optimization toolbox, while the projection onto the half-space is calculated explicitly. All program computation are performed on a Lenovo PC Intel(R) Core i7, 4.00 GB RAM. The stopping criterion used for the examples is \(\frac{\|x_{n+1}-x_{n}\|^{2}}{\|x_{2} -x_{1}\|^{2}}<\varepsilon\), where ε is stated in each example.

Example 4.1

Consider an operator \(A:\mathbb{R}^{m} \to\mathbb{R}^{m}\) defined by \(Ax = Mx+q\) with q being a vector in \(\mathbb{R}^{m}\) and

$$M= NN^{T} +S+D, $$

where N is a \(m\times m\) matrix, S is a \(m\times m\) skew-symmetric matrix and D is a \(m \times m\) diagonal matrix with its diagonal entries being non-negative (so that M is positive semidefinite). The feasible set C in this case is defined by

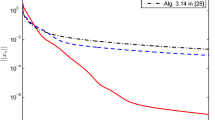
$$ C:=\bigl\{ x = (x_{1},x_{2},\dots,x_{m})\in \mathbb{R}^{m}:-5\leq x_{i}\leq5, i=1,2,\dots,m\bigr\} . $$

Clearly A is monotone (hence, pseudo-monotone). We set \(q=0 \in \mathbb{R}^{m}\) and choose the entries of N and S to be randomly generated in \((-2,2)\) while that of D are randomly generated in \((0,1)\). It is easy to see that \(\mathit{VI}(C,A) =\{0\in\mathbb{R}^{m}\}\). For the sake of simplicity, we define \(f(x) = \frac{1}{2}\|x\|^{2}_{2}\), we take \(\sigma=0.57\), \(\gamma=0.3\), \(l =5\), \(\mu= 0.02\) and test our algorithm for \(m=50,100,200\) and 500. We compare the performance of our algorithms with the algorithms of Nomirovski [35] and Gibali [18], taking \(\varepsilon= 10^{-4}\). The numerical result can be found in Table 1 and Fig. 1.

Figure 1
figure 1

Example 4.1, top left: \(m=50\); top right: \(m=100\), bottom left: \(m=200\); bottom right: \(m=500\)

Full size image
Table 1 Computation result for Example 4.1
Full size table

Next, we give an example in infinite-dimensional space to support the strong convergence of our algorithm. We take \(f(x) = \frac{1}{2}\|x\|^{2}\).

Example 4.2

Let \(E = L^{2}([0,1])\) with norm \(\|x\| = (\int_{0}^{1}|x(t)|^{2}\,dt)^{\frac {1}{2}}\) and inner product \(\langle x,y \rangle= \int _{0}^{1}x(t)y(t)\,dt\), \(x,y \in E\). Let C be the unit ball in E defined by \(C = \{x \in E:\|x\|\leq1\}\). Let \(B:C \rightarrow\mathbb {R}\) be an operator defined by \(B(u) = \frac{1}{1+\|u\|^{2}}\) and \(F: L^{2}([0,1]) \rightarrow L^{2}([0,1])\) be the Volterra integral operator defined by \(F(u)(t) = \int_{0}^{t} u (s)\,ds\) for all \(u \in L^{2}([0,1])\) and \(t\in[0,1]\). F is bounded, linear and monotone (cf. Exercise 20.12 in [4]). Now define \(A: C \rightarrow L^{2}([0,1])\) by \(A(u)(t) = (B(u)F(u))(t)\). Suppose \(\langle Au, v-u \rangle\geq0\) for all \(u,v \in C\), then \(\langle Fu, v-u \rangle\geq0\). Hence

$$\begin{aligned} \langle Av,v-u \rangle =& \langle BvFv, v-u \rangle \\ =& Bv \langle Fv, v-u \rangle \\ \geq& Bv\bigl(\langle Fv, v-u \rangle- \langle Fu, v-u \rangle\bigr) \\ =& Bv\langle Fv - Fu, v-u \rangle\geq0. \end{aligned}$$
(4.1)

Thus, A is pseudo-monotone. To see that A is not monotone, choose \(v =1\) and \(u =2\), then

$$\langle Av - Au,v- u \rangle= -\frac{1}{10} < 0. $$

Now consider the VI in which the underlying operator A is as defined above. Clearly, the unique solution of the VI is \(0 \in L^{2}([0,1])\). Choosing \(\sigma= 0.15\), \(\gamma= 0.7\), \(l = 7\), \(\mu=0.34\) and \(\varepsilon< 10^{-4}\). We plot the graph of \(\| x_{n+1} -x_{n}\|^{2}\) against number of iteration for Algorithm 3.6 and Algorithm 1.2 of [18]. We choose the same \(x_{1}\) for both algorithms and take u in Algorithm 3.6 to be \(y_{1}\) in Algorithm 1.2 as follows:

  1. Case I:

    \(x_{1} = \sin(t)\), \(u = t^{2} + t/5\),

  2. Case II:

    \(x_{1} = \exp(2t)/40\), \(u = \exp(3t)/7\).

The numerical result is reported in Fig. 2 and Table 2.

Figure 2
figure 2

Example 4.2, left: Case I; right: Case II

Full size image
Table 2 Computation result for Example 4.2
Full size table

Example 4.3

Finally, we consider \(E= \mathbb{R}^{N}\) with \(C=\{x \in\mathbb{R}^{N}: x_{i}\geq0, \sum_{i=1}^{N} x_{i} =1\}\) and \(f(x) = -\sum_{i=1}^{N} x_{i} \log (x_{i})\), \(x \in\mathbb{R}^{N}_{++}\). The projection onto C in this case is given by (see [5, 12])

$$ \varPi_{C}(x) = \biggl[\frac{x_{1}e_{1}}{\sum_{j=1}^{N}x_{j}e_{j}},\frac {x_{2}e_{2}}{\sum_{j=1}^{N}x_{j}e_{j}}, \dots,\frac{x_{m}e_{m}}{\sum_{j=1}^{N}x_{j}e_{j}} \biggr], $$

where \(e=(e_{1},e_{2},\dots,e_{N})\) is the standard basis of \(\mathbb{R}^{N}\). We define the operator A as

$$A(x) = \max\{x,0\}. $$

It is not difficult to see that A is monotone (hence pseudo-monotone) and \(\mathit{VI}(C,A) = \{0\}\). Taken \(\sigma= 0.02\), \(\gamma= 0.5\), \(l = 5\), \(\mu=0.9\) and \(\varepsilon< 10^{-5}\). We apply Algorithm 3.1 and 3.6 for solving the variational inequality with respect to the above operator A using different randomly generated initial point \(x_{1}\) for \(N =50\), \(N= 100\), \(N=200\) and \(N=500\). The numerical results can be found in Table 3 and Fig. 3.

Figure 3
figure 3

Example 4.2, top left: \(N=50\); top right: \(N=100\); bottom left: \(N=200\); bottom right: \(N=500\)

Full size image
Table 3 Computation result for Example 4.3
Full size table

5 Conclusion

The aim of the research is to study new subgradient extragradient methods for solving variational inequalities using Bregman distance approach in real reflexive Banach spaces. One of the advantages of the new methods is the use of an Armijo-like line search technique which prevents finding a prior estimate of the Lipschitz constant of the pseudo-monotone operator involved in the variational inequalities. Weak and strong convergence theorems were proved under mild conditions and some numerical experiments were performed to show the computational advantages of the new methods. The results in this paper improve and extend many recent results in the literature.