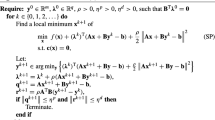A regularized alternating direction method of multipliers for a class of nonconvex problems

Abstract

In this paper, we propose a regularized alternating direction method of multipliers (RADMM) for a class of nonconvex optimization problems. The algorithm does not require the regular term to be strictly convex. Firstly, we prove the global convergence of the algorithm. Secondly, under the condition that the augmented Lagrangian function satisfies the Kurdyka–Łojasiewicz property, the strong convergence of the algorithm is established. Finally, some preliminary numerical results are reported to support the efficiency of the proposed algorithm.

1 Introduction

In this paper, we consider the following nonconvex optimization problem

$$ \min\quad f(x)+g(Ax), $$

(1)

where $f:R^{n}\rightarrow R\cup \{+\infty \}$ is a proper lower semicontinuous function, $g:R^{m}\rightarrow R$ is a continuous differentiable function with ∇g Lipschitz continuous and modulus $L>0$, while $A\in R^{m\times n}$ is a given matrix. When the functions f and g are convex, the problem (1) can be transformed into the split feasibility problem [1, 2]. Problem (1) is equivalent to the following constraint optimization problem:

$$\begin{aligned} &\min\quad f(x)+g(y) , \\ &\quad \mbox{s.t. } Ax-y=0. \end{aligned}$$

(2)

The augmented Lagrangian function of (2) is defined as follows:

$$\begin{aligned} \mathcal{L}_{\beta }(x,y,\lambda ) = f(x)+g(y)-\langle \lambda ,Ax-y \rangle +\frac{\beta }{2} \Vert Ax-y \Vert ^{2}, \end{aligned}$$

(3)

where $\lambda \in R^{m}$ is the Lagrangian parameter and $\beta >0$ is the penalty parameter.

The alternating direction method of multipliers (ADMM) was first proposed by Gabay and Mercier in 1970s, which is an effective algorithm for solving the two-block convex problems [3]. The iterative scheme of the classic ADMM for problem (2) is as follows:

$$ \textstyle\begin{cases} x^{k+1}\in \arg \min \{\mathcal{L}_{\beta }(x,y^{k},\lambda ^{k})\}, \\ y^{k+1}\in \arg \min \{\mathcal{L}_{\beta }(x^{k+1},y,\lambda ^{k})\}, \\ \lambda ^{k+1}=\lambda ^{k}-\beta (Ax^{k+1}-y^{k+1}). \end{cases} $$

(4)

If f, g are convex functions, then the convergence of ADMM is well-understood and there are some recent convergence rate analysis results [4,5,6,7,8]. However, when the objective function is nonconvex, ADMM does not necessarily converge. Recently, some scholars have proposed various improved ADMM for nonconvex problems, and analyzed their convergence [9,10,11,12,13,14,15]. In particular, Guo et al. [16, 17] analyzed the strong convergence of classical ADMM for the nonconvex optimization problem of (2). Wang et al. [12, 14] studied the convergence of the Bregman ADMM for the nonconvex optimization problems, where they need the augmented Lagrangian function with respect to x or the Bregman distance in the x-subproblem to be strongly convex.

The first formula of (4) has the following structure:

$$\begin{aligned} \min \biggl\{ f(x)+g\bigl(y^{k}\bigr)-\bigl\langle \lambda ^{k},Ax-y^{k}\bigr\rangle +\frac{ \beta }{2} \bigl\Vert Ax-y^{k} \bigr\Vert ^{2}\biggr\} . \end{aligned}$$

(5)

When A is not the identity matrix, the above problem may not be easy. Regularization is a popular technique to simplify the optimization problems [12, 14, 18]. For example, the regular term $\frac{1}{2}\|x-x^{k}\|^{2}_{G}$ could be added to the above problem (5), where G is a symmetric semidefinite matrix. Specifically, when $G=\alpha I-\beta A^{\top }A$, problem (5) is converted into the following form:

$$\begin{aligned} \min \biggl\{ f(x)+\frac{\alpha }{2} \bigl\Vert x-b^{k} \bigr\Vert ^{2}\biggr\} , \end{aligned}$$

(6)

with a certain known $b^{k}\in R^{n}$. Since the first formula of (4) has the form of (6) with $\alpha =1$, this paper considers the following regularized ADMM (in short, RADMM) for problem (2):

$$ \textstyle\begin{cases} x^{k+1}\in \arg \min \{\mathcal{L}_{\beta }(x,y^{k},\lambda ^{k})+ \frac{1}{2} \Vert x-x^{k} \Vert ^{2}_{G}\}, \\ y^{k+1}\in \arg \min \{\mathcal{L}_{\beta }(x^{k+1},y,\lambda ^{k})\}, \\ \lambda ^{k+1}=\lambda ^{k}-\beta (Ax^{k+1}-y^{k+1}), \end{cases} $$

(7)

where G is a symmetric semidefinite matrix, $\|x\|^{2}_{G}:=x^{ \top }Gx$.

The framework of this paper is as follows. In Sect. 2, we present some preliminary materials that will be used in this paper. In Sect. 3, we prove the convergence of algorithm (7). In Sect. 4, we report some numerical results. In Sect. 5, we draw some conclusions.

2 Preliminaries

For a vector $x=(x_{1},x_{2},\dots ,x_{n})^{\top }\in R^{n}$, we let $\|x\|=(\sum_{i=1}^{n} x_{i}^{2})^{\frac{1}{2}}$, $\|x\|_{1}= \sum_{i=1}^{n} |x_{i}|$, and $\|x\|_{\frac{1}{2}}=(\sum_{i=1}^{n} |x_{i}|^{\frac{1}{2}})^{2}$. Also $G\succeq 0$ $(\succ 0)$ denotes that G is a positive semidefinite (positive definite) matrix. For a subset $S\subseteq R^{n}$ and a point $x\in R^{n}$, if S is nonempty, let $d(x,S)=\inf_{y\in S}\|y-x \|$. When $S=\emptyset$, we set $d(x,S) = +\infty$ for all x. A function $f:R^{n}\rightarrow (-\infty ,+\infty ]$ is said to be proper, if there exists at least one $x\in R^{n}$ such that $f(x)< +\infty$. The effective domain of f is defined through $\operatorname{dom}f=\{x\in R ^{n}|f(x)< +\infty \}$.

Definition 2.1

([19])

The function $f:R^{n}\rightarrow R\cup \{+\infty \}$ is lower semicontinuous at x̄, if $f(\bar{x})\leq \liminf_{x\rightarrow \bar{x}}f(x)$. If f is lower semicontinuous at every point $x\in R^{n}$, then f is called a lower semicontinuous function.

Definition 2.2

([19])

Let $f:R^{n}\rightarrow R \cup \{+\infty \}$ be a proper lower semicontinuous function.

• (i) The Fréchet subdifferential, or regular subdifferential, of f at $x\in \operatorname{dom} f$, denoted by $\hat{\partial }{f(x)}$, is the set of all elements $u\in R^{n}$ which satisfy

  $$\hat{\partial } {f(x)}=\biggl\{ u\in R^{n}\Bigm| \lim _{y\neq x}\inf_{y\rightarrow x}\frac{f(y)-f(x)-\langle u, y-x\rangle }{ \Vert y-x \Vert }\geq 0\biggr\} , $$

  when $x \notin \operatorname{dom} f$, let $\hat{\partial } f(x)=\emptyset$;

• (ii) The limiting-subdifferential, or simply the subdifferential, of f at $x\in \operatorname{dom} f$, denoted by $\partial f(x)$, is defined as

  $$\partial f(x)=\bigl\{ u\in R^{n}\mid \exists x^{k} \rightarrow x, f\bigl(x^{k}\bigr) \rightarrow f(x), u^{k} \in \hat{\partial }f\bigl(x^{k}\bigr)\rightarrow u, k \rightarrow \infty \bigr\} . $$

Proposition 2.1

([20])

Let $f:R^{n}\rightarrow R \cup \{+\infty \}$ be a proper lower semicontinuous function, then

• (i) $\hat{\partial }f(x)\subseteq \partial f(x)$ for each $x\in R^{n}$, where the first set is closed and convex while the second one is only closed;

• (ii) Let $u^{k}\in \partial f(x^{k})$ and $\lim_{k\rightarrow \infty }(x^{k},u^{k})=(x,u)$, then $u\in \partial f(x)$;

• (iii) A necessary condition for $x\in R^{n}$ to be a minimizer of f is

  $$\begin{aligned} 0\in \partial f(x); \end{aligned}$$

  (8)

• (iv) If $g:R^{n}\rightarrow R$ is continuously differentiable, then $\partial (f+g)(x)=\partial f(x)+\nabla g(x)$ for any $x\in \operatorname{dom} f$.

A point that satisfies (8) is called a critical point or a stationary point. The set of critical points of f is denoted by crit f.

Lemma 2.1

([21])

Suppose that $H(x,y)=f(x)+g(y)$, where $f:R^{n}\rightarrow R\cup \{+\infty \}$ and $g:R^{m}\rightarrow R$ are proper lower semicontinuous functions, then

$$ \begin{aligned} &\partial H(x,y)=\partial _{x} H(x,y) \times \partial _{y} H(x,y)=\partial f(x)\times \partial g(y), \\ &\quad \textit{for all }(x,y)\in \operatorname{dom} H =\operatorname{dom}f\times \operatorname{dom}g. \end{aligned} $$

The following lemma is very important for the convergence analysis.

Lemma 2.2

([22])

Let function $h:R^{n}\rightarrow R$ be continuously differentiable and its gradient ∇h be Lipschitz continuous with modulus $L>0$, then

$$\bigl\vert h(y)-h(x)-\bigl\langle \nabla h(x),y-x\bigr\rangle \bigr\vert \leq \frac{L}{2} \Vert y-x \Vert ^{2},\quad \textit{for all }x, y\in R^{n}. $$

Definition 2.3

We say that $(x^{*},y^{*},\lambda ^{*})$ is a critical point of the augmented Lagrangian function $\mathcal{L_{\beta }(\cdot )}$ of (2) if it satisfies

$$ \textstyle\begin{cases} A^{\top }\lambda ^{*}\in \partial f(x^{*}), \\ \nabla g(y^{*})=\lambda ^{*}, \\ Ax^{*}-y^{*}=0. \end{cases} $$

(9)

Obviously, (2) is equivalent to $0\in \partial \mathcal{L _{\beta }}(x^{*},y^{*},\lambda ^{*})$.

Definition 2.4

([21] (Kurdyka–Łojasiewicz property))

Let $f:{R}^{n}\rightarrow {R}\cup \{+\infty \}$ be a proper lower semicontinuous function. If there exist $\eta \in (0,+\infty ]$, a neighborhood U of x̂, and a concave function $\varphi :[0, \eta )\rightarrow R_{+}$ satisfying the following conditions:

• (i) $\varphi (0)=0$;

• (ii) φ is continuously differentiable on $(0,\eta )$ and continuous at 0;

• (iii) $\varphi '(s)>0$ for all $s\in (0,\eta )$;

• (iv) $\varphi '(f(x)-f(\hat{x}))d(0,\partial f(x))\geq 1$, for all $x \in U\cap [f(\hat{x})< f(x)< f(\hat{x})+\eta ]$,

then f is said to have the Kurdyka–Łojasiewicz (KL) property at x̂.

Lemma 2.3

([23] (Uniform KL property))

Let $\varPhi _{\eta }$ be the set of concave functions which satisfy (i), (ii) and (iii) in Definition 2.4. Suppose that $f:R^{n}\rightarrow {R}\cup \{+\infty \}$ is a proper lower semicontinuous function and Ω is a compact set. If $f(x)\equiv a$ for all $x\in \varOmega$ and f satisfies the KL property at each point of Ω, then there exist $\varepsilon >0$, $\eta >0$, and $\varphi \in \varPhi _{\eta }$ such that

$$\varphi '\bigl(f(x)-a\bigr)d\bigl(0,\partial f(x)\bigr)\ge 1, $$

for all $x\in \{x\in {R}^{n}|d(x,\varOmega )<\varepsilon \}\cap [x:a<f(x)<a+ \eta ]$.

3 Convergence analysis

In this section, we prove the convergence of algorithm (7). Throughout this section, we assume that the sequence $\{z^{k}:=(x^{k},y ^{k},\lambda ^{k})\}$ is generated by RADMM (7). Firstly, the global convergence of the algorithm is established by the monotonically nonincreasing sequence $\{\mathcal{L}_{\beta }(z^{k})\}$. Secondly, the strong convergence of the algorithm is proved under the condition that $\mathcal{L}_{\beta }(\cdot )$ satisfies the KL property. From optimality conditions of each subproblem in (7), we have

$$ \textstyle\begin{cases} 0\in \partial f(x^{k+1})-A^{\top }\lambda ^{k}+\beta A^{\top }(Ax^{k+1}-y ^{k})+G(x^{k+1}-x^{k}), \\ 0=\nabla g(y^{k+1})+\lambda ^{k}-\beta (Ax^{k+1}-y^{k+1}), \\ \lambda ^{k+1}=\lambda ^{k}-\beta (Ax^{k+1}-y^{k+1}). \end{cases} $$

(10)

That is,

$$ \textstyle\begin{cases} A^{\top }\lambda ^{k+1}-\beta A^{\top }(y^{k+1}-y^{k})-G(x^{k+1}-x^{k}) \in \partial f(x^{k+1}), \\ -\lambda ^{k+1}=\nabla g(y^{k+1}), \\ \lambda ^{k+1}=\lambda ^{k}-\beta (Ax^{k+1}-y^{k+1}). \end{cases} $$

(11)

We need the following basic assumptions on problem (2).

Assumption 3.1

• (i) $f: R^{n}\rightarrow R\cup \{+\infty \}$ is proper lower semicontinuous;

• (ii) $g:R^{m}\rightarrow R$ is continuously differentiable, with $\|\nabla g(u)-\nabla g(v)\|\leq L\|u-v\|$, $\forall u,v\in R^{n}$;

• (iii) $\beta >2L$ and $\delta :=\frac{\beta -L}{2}-\frac{L^{2}}{ \beta }>0$;

• (iv) $G\succeq 0$ and $G+A^{\top }A \succ 0$.

The following lemma implies that sequence $\{\mathcal{L_{\beta }}(z ^{k})\}$ is monotonically nonincreasing.

Lemma 3.1

$$\begin{aligned} \mathcal{L}_{\beta }\bigl(z^{k+1}\bigr)\leq \mathcal{L}_{\beta }\bigl(z^{k}\bigr)- \delta \bigl\Vert y^{k}-y^{k+1}\bigr\Vert ^{2}-\frac{1}{2} \bigl\Vert x^{k+1}-x^{k}\bigr\Vert ^{2}_{G}. \end{aligned}$$

(12)

Proof

From the definition of the augmented Lagrangian function $\mathcal{L_{\beta }(\cdot )}$ and the third formula of (11), we have

$$ \begin{aligned}[b] \mathcal{L}_{\beta } \bigl(x^{k+1},y^{k+1},\lambda ^{k+1}\bigr) &= \mathcal{L}_{ \beta }\bigl(x^{k+1},y^{k+1},\lambda ^{k}\bigr) +\bigl\langle \lambda ^{k}-\lambda ^{k+1}, Ax^{k+1}-y^{k+1}\bigr\rangle \\ &=\mathcal{L}_{\beta }\bigl(x^{k+1},y^{k+1},\lambda ^{k}\bigr)+\frac{1}{\beta } \bigl\Vert \lambda ^{k}-\lambda ^{k+1} \bigr\Vert ^{2} \end{aligned} $$

(13)

and

$$ \begin{aligned}[b] &\mathcal{L}_{\beta } \bigl(x^{k+1},y^{k+1},\lambda ^{k}\bigr)- \mathcal{L}_{\beta }\bigl(x^{k+1},y^{k},\lambda ^{k}\bigr) \\ &\quad =g\bigl(y^{k+1}\bigr)-g\bigl(y^{k}\bigr)-\bigl\langle \lambda ^{k},y^{k}-y^{k+1}\bigr\rangle - \frac{ \beta }{2} \bigl\Vert Ax^{k+1}-y^{k}\bigr\Vert ^{2} \\ &\qquad {} +\frac{\beta }{2} \bigl\Vert Ax^{k+1}-y^{k+1}\bigr\Vert ^{2}. \end{aligned} $$

(14)

From Assumption 3.1(ii), Lemma 2.2 and (11), we have

$$\begin{aligned} g\bigl(y^{k+1}\bigr)-g\bigl(y^{k}\bigr) \leq \bigl\langle -\lambda ^{k+1},y^{k+1}-y^{k} \bigr\rangle + \frac{L}{2} \bigl\Vert y^{k}-y^{k+1} \bigr\Vert ^{2}. \end{aligned}$$

(15)

Inserting (15) into (14) yields

$$ \begin{aligned}[b] &\mathcal{L}_{\beta } \bigl(x^{k+1},y^{k+1},\lambda ^{k}\bigr)- \mathcal{L}_{\beta }\bigl(x^{k+1},y^{k},\lambda ^{k}\bigr) \\ &\quad \leq \bigl\langle \lambda ^{k}-\lambda ^{k+1},y^{k+1}-y^{k} \bigr\rangle -\frac{ \beta }{2} \bigl\Vert Ax^{k+1}-y^{k}\bigr\Vert ^{2} \\ &\qquad {} +\frac{\beta }{2} \bigl\Vert Ax^{k+1}-y^{k+1}\bigr\Vert ^{2}+ \frac{L}{2} \bigl\Vert y^{k}-y^{k+1} \bigr\Vert ^{2}. \end{aligned} $$

(16)

Since $\lambda ^{k+1}=\lambda ^{k}-\beta (Ax^{k+1}-y^{k+1})$, we have

$$\begin{aligned} Ax^{k+1}-y^{k+1}=\frac{1}{\beta } \bigl(\lambda ^{k}-\lambda ^{k+1}\bigr) \end{aligned}$$

(17)

and

$$Ax^{k+1}-y^{k}=\frac{1}{\beta }\bigl(\lambda ^{k}-\lambda ^{k+1}\bigr)-\bigl(y^{k}-y ^{k+1}\bigr). $$

It follows that

$$ \begin{aligned} \bigl\langle \lambda ^{k}- \lambda ^{k+1},y^{k+1}-y^{k}\bigr\rangle - \frac{\beta }{2}\bigl\Vert Ax^{k+1}-y^{k} \bigr\Vert ^{2} \\ =-\frac{\beta }{2} \bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2}-\frac{1}{2\beta } \bigl\Vert \lambda ^{k}-\lambda ^{k+1} \bigr\Vert ^{2}. \end{aligned} $$

(18)

Combining (16), (17) and (18), we have

$$ \begin{aligned} \mathcal{L}_{\beta } \bigl(x^{k+1},y^{k+1},\lambda ^{k}\bigr)- \mathcal{L}_{\beta }\bigl(x^{k+1},y^{k},\lambda ^{k}\bigr) \leq -\frac{\beta -L}{2} \bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2}. \end{aligned} $$

(19)

From $-\lambda ^{k+1}=\nabla g(y^{k+1})$ and Assumption 3.1(ii), we have

$$\begin{aligned} \frac{1}{\beta } \bigl\Vert \lambda ^{k}- \lambda ^{k+1} \bigr\Vert ^{2}\leq \frac{L^{2}}{ \beta } \bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2}. \end{aligned}$$

(20)

Adding (13), (19) and (20), one has

$$\mathcal{L}_{\beta }\bigl(x^{k+1},y^{k+1},\lambda ^{k+1}\bigr) \leq \mathcal{L} _{\beta }\bigl(x^{k+1},y^{k}, \lambda ^{k}\bigr)-\biggl(\frac{\beta -L}{2}-\frac{L^{2}}{ \beta } \biggr)\bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2}. $$

Since $x^{x+1}$ is the optimal solution of the first subproblem of (7), one has

$$\mathcal{L}_{\beta }\bigl(x^{k+1},y^{k},\lambda ^{k}\bigr) \leq \mathcal{L}_{ \beta }\bigl(x^{k},y^{k}, \lambda ^{k}\bigr)-\frac{1}{2}\bigl\Vert x^{k+1}-x^{k} \bigr\Vert ^{2}_{G}. $$

Thus

$$ \begin{aligned} &\mathcal{L}_{\beta }\bigl(x^{k+1},y^{k+1}, \lambda ^{k+1}\bigr) \\ &\quad \leq \mathcal{L}_{\beta }\bigl(x^{k},y^{k}, \lambda ^{k}\bigr)- \biggl( \frac{\beta -L}{2}- \frac{L^{2}}{\beta }\biggr) \bigl\Vert y^{k}-y^{k+1}\bigr\Vert ^{2}- \frac{1}{2} \bigl\Vert x^{k+1}-x^{k}\bigr\Vert ^{2}_{G}. \end{aligned} $$

 □

Lemma 3.2

If the sequence $\{z^{k}\}$ is bounded, then

$$\begin{aligned} \sum_{k=0}^{+\infty } \bigl\Vert z^{k}-z^{k+1} \bigr\Vert ^{2} < +\infty . \end{aligned}$$

Proof

Since $\{z^{k}\}$ is bounded, $\{z^{k}\}$ has at least one cluster point. Let $z^{*}=(x^{*},y^{*},\lambda ^{*})$ be a cluster point of $\{z^{k}\}$ and let a subsequence $\{z^{k_{j}}\}$ converge to $z^{*}$. Since f is lower semicontinuous and g is continuously differentiable, then $\mathcal{L}_{\beta }(\cdot )$ is lower semicontinuous, and hence

$$ \mathcal{L}_{\beta }\bigl(z^{*}\bigr)\leq \liminf_{k_{j}\rightarrow +\infty } \mathcal{L}_{\beta } \bigl(z^{k_{j}}\bigr). $$

(21)

Thus $\{\mathcal{L}_{\beta }(z^{k_{j}})\}$ is bounded from below. Furthermore, by Lemma 3.1, sequence $\{\mathcal{L}_{ \beta }(z^{k})\}$ is nonincreasing, and so $\{\mathcal{L}_{\beta }(z ^{k})\}$ is convergent. Moreover, $\mathcal{L}_{\beta }(z^{*})\leq \mathcal{L}_{\beta }(z^{k})$, for all k.

On the other hand, summing up of (12) for $k=0,1,2,\dots ,p$, it follows that

$$ \begin{aligned} &\frac{1}{2}\sum _{k=0}^{p} \bigl\Vert x^{k+1}-x^{k} \bigr\Vert ^{2}_{G} + \delta \sum _{k=0}^{p} \bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2} \leq \mathcal{L}_{\beta }\bigl(z ^{0}\bigr)-\mathcal{L}_{\beta }\bigl(z^{p+1} \bigr) \\ &\quad \leq \mathcal{L}_{\beta }\bigl(z^{0}\bigr)- \mathcal{L}_{\beta }\bigl(z^{*}\bigr) \\ &\quad < +\infty . \end{aligned} $$

Since $\delta >0$, $G\succeq 0$, and p is chosen arbitrarily,

$$\begin{aligned} \sum_{k=0}^{+\infty } \bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2}< +\infty , \qquad \sum_{k=0}^{+\infty } \bigl\Vert x^{k+1}-x^{k} \bigr\Vert ^{2}_{G}< +\infty . \end{aligned}$$

(22)

From (20) we have

$$\sum_{k=0}^{+\infty } \bigl\Vert \lambda ^{k+1}-\lambda ^{k} \bigr\Vert ^{2}< +\infty . $$

Next we prove $\sum_{k=0}^{+\infty }\|x^{k+1}-x^{k}\|^{2}< + \infty$. From $\lambda ^{k+1}=\lambda ^{k}-\beta (Ax^{k+1}-y^{k+1})$, we have

$$\lambda ^{k+1}-\lambda ^{k}=\lambda ^{k}- \lambda ^{k-1}+\beta \bigl(Ax^{k}-Ax ^{k+1} \bigr)+\beta \bigl(y^{k+1}-y^{k}\bigr). $$

Then

$$ \begin{aligned}[b] & \bigl\Vert \beta \bigl(Ax^{k}-Ax^{k+1}\bigr) \bigr\Vert ^{2} \\ &\quad = \bigl\Vert \bigl(\lambda ^{k+1}-\lambda ^{k} \bigr)-\bigl(\lambda ^{k}-\lambda ^{k-1}\bigr)-\beta \bigl(y ^{k+1}-y^{k}\bigr) \bigr\Vert ^{2} \\ &\quad \leq 3\bigl( \bigl\Vert \lambda ^{k+1}-\lambda ^{k} \bigr\Vert ^{2}+ \bigl\Vert \lambda ^{k}-\lambda ^{k-1} \bigr\Vert ^{2}+\beta ^{2} \bigl\Vert y^{k}-y^{k+1} \bigr\Vert ^{2} \bigr). \end{aligned} $$

(23)

Therefore, we have $\sum_{k=0}^{+\infty }\|x^{k+1}-x^{k}\|^{2} _{A^{\top }A}< +\infty$. Taking into account (22), we have

$$\sum_{k=0}^{+\infty } \bigl\Vert x^{k+1}-x^{k} \bigr\Vert ^{2}_{(A^{\top }A+G)}< + \infty . $$

Since $A^{\top }A+G\succ 0$ (see Assumption 3.1(iv)), one has $\sum_{k=0}^{+\infty }\|x^{k+1}-x^{k}\|^{2}< +\infty$.

Therefore, $\sum_{k=0}^{+\infty }\|z^{k+1}-z^{k}\|^{2}< + \infty$. □

Lemma 3.3

Define

$$ \textstyle\begin{cases} \varepsilon ^{k+1}_{x}=\beta A^{\top }(y^{k}-y^{k+1})+A^{\top }(\lambda ^{k}-\lambda ^{k+1})-G(x^{k+1}-x^{k}), \\ \varepsilon ^{k+1}_{y}=\lambda ^{k+1}-\lambda ^{k}, \\ \varepsilon ^{k+1}_{\lambda }=\frac{1}{\beta }(\lambda ^{k+1}-\lambda ^{k}). \end{cases} $$

Then $(\varepsilon ^{k+1}_{x}, \varepsilon ^{k+1}_{y}, \varepsilon ^{k+1}_{\lambda })^{\top }\in \partial \mathcal{L_{\beta }}(z^{k+1})$. Furthermore, if $A^{\top }A\succ 0$, then there exists $\tau >0$ such that

$$d\bigl(0,\partial \mathcal{L_{\beta }}\bigl(z^{k+1}\bigr) \bigr)\leq \tau \bigl( \bigl\Vert y^{k+1}-y^{k} \bigr\Vert + \bigl\Vert y^{k}-y^{k-1} \bigr\Vert \bigr),\quad k\geq 1. $$

Proof

By the definition of $\mathcal{L}_{\beta }(\cdot )$, one has

$$ \textstyle\begin{cases} \partial _{x}\mathcal{L}_{\beta }(z^{k+1})=\partial f(x^{k+1})-A^{ \top }\lambda ^{k+1}+\beta A^{\top }(Ax^{k+1}-y^{k+1}), \\ \partial _{y}\mathcal{L}_{\beta }(z^{k+1})=\nabla g(y^{k+1})+\lambda ^{k+1}-\beta (Ax^{k+1}-y^{k+1}), \\ \partial _{\lambda }\mathcal{L}_{\beta }(z^{k+1})=-(Ax^{k+1}-y^{k+1}). \end{cases} $$

(24)

Combining (24) and (11), we get

$$ \textstyle\begin{cases} \beta A^{\top }(y^{k}-y^{k+1})+A^{\top }(\lambda ^{k}-\lambda ^{k+1})-G(x ^{k+1}-x^{k}) \in \partial _{x}\mathcal{L}_{\beta }(z^{k+1}), \\ \lambda ^{k+1}-\lambda ^{k}\in \partial _{y}\mathcal{L}_{\beta }(z^{k+1}), \\ \frac{1}{\beta }(\lambda ^{k+1}-\lambda ^{k})\in \partial _{\lambda } \mathcal{L}_{\beta }(z^{k+1}). \end{cases} $$

(25)

From Lemma 2.1, one has $(\varepsilon ^{k+1}_{x}, \varepsilon ^{k+1}_{y}, \varepsilon ^{k+1}_{\lambda })^{\top }\in \partial \mathcal{L_{\beta }}(z^{k+1})$.

On the other hand, it is easy to see that there exists $\tau _{1}>0$ such that

$$\begin{aligned} \bigl\Vert \bigl(\varepsilon ^{k+1}_{x}, \varepsilon ^{k+1}_{y}, \varepsilon ^{k+1} _{\lambda }\bigr)^{\top } \bigr\Vert \leq \tau _{1} \bigl( \bigl\Vert y^{k+1}-y^{k} \bigr\Vert + \bigl\Vert \lambda ^{k+1}- \lambda ^{k} \bigr\Vert + \bigl\Vert x^{k+1}-x^{k} \bigr\Vert \bigr). \end{aligned}$$

(26)

Due to $A^{\top }A\succ 0$ and (23), there exists $\tau _{2}>0$ such that

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{k} \bigr\Vert \leq \tau _{2}\bigl( \bigl\Vert y^{k+1}-y^{k} \bigr\Vert + \bigl\Vert \lambda ^{k+1}- \lambda ^{k} \bigr\Vert + \bigl\Vert \lambda ^{k}-\lambda ^{k-1} \bigr\Vert \bigr),\quad k\geq 1. \end{aligned}$$

(27)

Since $(\varepsilon ^{k+1}_{x}, \varepsilon ^{k+1}_{y}, \varepsilon ^{k+1} _{\lambda })^{\top }\in \partial \mathcal{L_{\beta }}(z^{k+1})$, from (26), (20) and (27), there exists $\tau >0$ such that

$$ \begin{aligned} &d\bigl(0,\partial \mathcal{L}_{\beta } \bigl(z^{k+1}\bigr)\bigr) \leq \bigl\Vert \bigl(\varepsilon ^{k+1} _{x},\varepsilon ^{k+1}_{y}, \varepsilon ^{k+1}_{\lambda }\bigr)^{\top } \bigr\Vert \leq \tau \bigl( \bigl\Vert y^{k+1}-y^{k} \bigr\Vert + \bigl\Vert y^{k}-y^{k-1} \bigr\Vert \bigr), \\ &\quad k\geq 1. \end{aligned} $$

 □

Theorem 3.1

(Global convergence)

Let Ω denote the cluster point set of the sequence $\{z^{k}\}$. If $\{z^{k}\}$ is bounded, then

• (i) Ω is a nonempty compact set, and $d(z^{k},\varOmega ) \rightarrow 0$, as $k\rightarrow +\infty$,

• (ii) $\varOmega \subseteq \operatorname{crit}\mathcal{L_{\beta }}$,

• (iii) $\mathcal{L_{\beta }}(\cdot )$ is constant on Ω, and $\lim_{k\rightarrow +\infty }\mathcal{L_{\beta }}(z^{k})=\mathcal{L _{\beta }}(z^{*})$ for all $z^{*}\in \varOmega$.

Proof

(i) From the definitions of Ω and $d(z^{k}, \varOmega )$, the claim follows trivially.

(ii) Let $z^{*}=(x^{*},y^{*},\lambda ^{*})\in \varOmega$, then there is a subsequence $\{z^{k_{j}}\}$ of $\{z^{k}\}$, such that $\lim_{k_{j}\rightarrow +\infty }z^{k_{j}}=z^{*}$. Since $x^{k+1}$ is a minimizer of function $\mathcal{L}_{\beta }(x,y^{k},\lambda ^{k})+ \frac{1}{2}\|x-x^{k}\|^{2}_{G}$ for the variable x, one has

$$\mathcal{L}_{\beta }\bigl(x^{k+1},y^{k},\lambda ^{k}\bigr)+\frac{1}{2} \bigl\Vert x^{k+1}-x ^{k} \bigr\Vert ^{2}_{G} \leq \mathcal{L}_{\beta }\bigl(x^{*},y^{k},\lambda ^{k}\bigr)+ \frac{1}{2} \bigl\Vert x^{*}-x^{k} \bigr\Vert ^{2}_{G}, $$

that is,

$$\begin{aligned} \mathcal{L}_{\beta }\bigl(x^{k+1},y^{k}, \lambda ^{k}\bigr)\leq \mathcal{L}_{ \beta } \bigl(x^{*},y^{k},\lambda ^{k}\bigr) + \frac{1}{2} \bigl\Vert x^{*}-x^{k}\bigr\Vert ^{2}_{G}- \frac{1}{2} \bigl\Vert x^{k+1}-x^{k}\bigr\Vert ^{2}_{G}. \end{aligned}$$

(28)

Lemma 3.1 implies that $\lim_{k\rightarrow \infty }\|x^{k+1}-x^{k}\|^{2}_{G}=0$. Since $\mathcal{L}_{\beta }(\cdot )$ is continuous with respect to y and λ, we have

$$ \begin{aligned}[b] \limsup_{k_{j}\rightarrow +\infty } \mathcal{L}_{\beta }\bigl(z^{k _{j}+1}\bigr) &=\limsup _{k_{j}\rightarrow +\infty }\mathcal{L}_{\beta }\bigl(x ^{k_{j}+1},y^{k_{j}}, \lambda ^{k_{j}}\bigr) \\ &\leq \limsup_{k_{j}\rightarrow +\infty }\mathcal{L}_{\beta }\bigl(x ^{*},y^{k},\lambda ^{k}\bigr) \\ &=\mathcal{L}_{\beta }\bigl(z^{*}\bigr). \end{aligned} $$

(29)

On the other hand, since $\mathcal{L}(\cdot )$ is lower semicontinuous,

$$ \liminf_{k_{j}\rightarrow +\infty }\mathcal{L}_{\beta } \bigl(z^{k_{j}+1}\bigr) \geq \mathcal{L}_{\beta } \bigl(z^{*}\bigr). $$

(30)

Combining (29) and (30), we get $\lim_{k_{j}\rightarrow +\infty }\mathcal{L}_{\beta }(z^{k_{j}})= \mathcal{L}_{\beta }(z^{*})$. Then $\lim_{k_{j}\rightarrow +\infty }f(x^{k_{j}})=f(x^{*})$. By taking the limit $k_{j}\rightarrow +\infty$ in (11), we have

$$ \textstyle\begin{cases} A^{\top }\lambda ^{*}\in \partial f(x^{*}), \\ \nabla g(y^{*})=-\lambda ^{*}, \\ Ax^{*}-y^{*}=0. \end{cases} $$

that is, $z^{*}\in \rm {crit}\mathcal{L}_{\beta }$.

(iii) Let $z^{*}\in \varOmega$. There exists $\{z^{k_{j}}\}$ such that $\lim_{k_{j}\rightarrow +\infty }z^{k_{j}}= z^{*}$. Combining $\lim_{k_{j}\rightarrow +\infty }\mathcal{L}_{\beta }(z^{k_{j}})= \mathcal{L}_{\beta }(z^{*})$ and the fact that $\{\mathcal{L}_{\beta }(z^{k})\}$ is monotonically nonincreasing, for all $z^{*}\in \varOmega$, we have

$$\lim_{k\rightarrow +\infty }\mathcal{L}_{\beta }\bigl(z^{k} \bigr)= \mathcal{L}_{\beta }\bigl(z^{*}\bigr), $$

and so $\mathcal{L}_{\beta }(\cdot )$ is constant on Ω. □

Theorem 3.2

(Strong convergence)

If $\{z^{k}\}$ is bounded, $A^{\top }A\succ 0$, and $\mathcal{L}_{\beta }(z)$ satisfies the KL property at each point of Ω, then

• (i) $\sum_{k=0}^{+\infty }\|z^{k+1}-z^{k}\|< +\infty$,

• (ii) The sequence $\{z^{k}\}$ converges to a stationary point of $\mathcal{L}_{\beta }(\cdot )$.

Proof

(i) Let $z^{*}\in \varOmega$. From Theorem 3.1, we have $\lim_{k\rightarrow +\infty }\mathcal{L}_{\beta }(z ^{k}) =\mathcal{L}_{\beta }(z^{*})$. We consider two cases:

(a) There exists an integer $k_{0}$, such that $\mathcal{L}_{\beta }(z ^{k_{0}})=\mathcal{L}_{\beta }(z^{*})$. From Lemma 3.1, we have

$$ \begin{aligned} &\frac{1}{2} \bigl\Vert x^{k+1}-x^{k} \bigr\Vert ^{2}_{G}+ \delta \bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2} \\ &\quad \leq \mathcal{L}_{\beta }\bigl(z^{k}\bigr)- \mathcal{L}_{\beta }\bigl(z^{k+1}\bigr)\leq \mathcal{L}_{\beta }\bigl(z^{k_{0}}\bigr)-\mathcal{L}_{\beta } \bigl(z^{*}\bigr)=0,\quad k \geq k_{0}. \end{aligned} $$

Then, one has $\|x^{k+1}-x^{k}\|^{2}_{G}=0$, $y^{k+1}=y^{k}$, $k\geq k_{0}$. From (20), one has $\lambda ^{k+1}=\lambda ^{k}$, $k>k_{0}$. Furthermore, from (23) and $A^{\top }A\succ 0$, we have $x^{k+1}=x^{k}$, $k>k_{0}+1$. Thus $z^{k+1}=z^{k}$, $k>k_{0}+1$. Therefore, the conclusions hold.

(b) Suppose that $\mathcal{L}_{\beta }(z^{k})>\mathcal{L}_{\beta }(z ^{*})$, $k\geq 1$. From Theorem 3.1(i), it follows that for $\varepsilon >0$, there exists $k_{1}>0$, such that $d(z^{k},\varOmega )< \varepsilon$, for all $k>k_{1}$. Since $\lim_{k\rightarrow +\infty }\mathcal{L}_{\beta }(z^{k})= \mathcal{L}_{\beta }(z^{*})$, for given $\eta >0$, there exists $k_{2}>0$, such that $\mathcal{L}_{\beta }(z^{k})<\mathcal{L}_{\beta }(z^{*})+\eta$, for all $k>k_{2}$. Consequently, one has

$$ d\bigl(z^{k},\varOmega \bigr)< \varepsilon , \mathcal{L}_{\beta }\bigl(z^{*}\bigr)< \mathcal{L}_{\beta } \bigl(z^{k}\bigr)< \mathcal{L}_{\beta }\bigl(z ^{*}\bigr)+\eta ,\quad \mbox{for all }k> \tilde{k}=\max \{k_{1},k_{2}\}. $$

It follows from the KL property, that

$$\begin{aligned} \varphi '\bigl(\mathcal{L}_{\beta } \bigl(z^{k}\bigr)-\mathcal{L}_{\beta }\bigl(z^{*} \bigr)\bigr)d\bigl(0, \partial \mathcal{L}_{\beta }\bigl(z^{k} \bigr)\bigr)\geq 1,\quad \mbox{for all }k> \tilde{k}. \end{aligned}$$

(31)

By the concavity of φ and since $\mathcal{L}_{\beta }(z^{k})- \mathcal{L}_{\beta }(z^{k+1})=(\mathcal{L}_{\beta }(z^{k})- \mathcal{L}_{\beta }(z^{*})) -(\mathcal{L}_{\beta }(z^{k+1})- \mathcal{L}_{\beta }(z^{*}))$, we have

$$ \begin{aligned} &\varphi \bigl(\mathcal{L}_{\beta } \bigl(z^{k}\bigr)-\mathcal{L}_{\beta }\bigl(z^{*} \bigr)\bigr)- \varphi \bigl(\mathcal{L}_{\beta }\bigl(z^{k+1} \bigr) -\mathcal{L}_{\beta }\bigl(z^{*}\bigr)\bigr) \\ &\quad \geq \varphi '\bigl(\mathcal{L}_{\beta } \bigl(z^{k}\bigr)-\mathcal{L}_{\beta }\bigl(z^{*} \bigr)\bigr) \bigl(\mathcal{L}_{\beta }\bigl(z^{k}\bigr)- \mathcal{L}_{\beta }\bigl(z^{k+1}\bigr)\bigr). \end{aligned} $$

(32)

Let $\bigtriangleup _{p,q}=\varphi (\mathcal{L}_{\beta }(z^{p})- \mathcal{L}_{\beta }(z^{*}))- \varphi (\mathcal{L}_{\beta }(z^{q})- \mathcal{L}_{\beta }(z^{*}))$. Combining $\varphi '(\mathcal{L}_{ \beta }(z^{k})-\mathcal{L}_{\beta }(z^{*}))>0$, (31) and (32), we have

$$\begin{aligned} \mathcal{L}_{\beta }\bigl(z^{k}\bigr)-\mathcal{L}_{\beta } \bigl(z^{k+1}\bigr) \leq \frac{ \bigtriangleup _{k,k+1}}{\varphi '(\mathcal{L}_{\beta }(z^{k})- \mathcal{L}_{\beta }(z^{*}))}\leq d\bigl(0,\partial \mathcal{L}_{\beta }\bigl(z ^{k}\bigr)\bigr)\bigtriangleup _{k,k+1}. \end{aligned}$$

From Lemma 3.3, we obtain

$$\begin{aligned} \mathcal{L}_{\beta }\bigl(z^{k}\bigr)-\mathcal{L}_{\beta } \bigl(z^{k+1}\bigr) \leq \tau \bigl( \bigl\Vert y^{k}-y^{k-1} \bigr\Vert + \bigl\Vert y^{k-1}-y^{k-2} \bigr\Vert \bigr)\bigtriangleup _{k,k+1}. \end{aligned}$$

From Lemma 3.1 and the above inequality, we have

$$ \begin{aligned} &\frac{1}{2} \bigl\Vert x^{k+1}-x^{k} \bigr\Vert _{G}^{2}+ \delta \bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2} \\ &\quad \leq \tau \bigl( \bigl\Vert y^{k}-y^{k-1} \bigr\Vert + \bigl\Vert y^{k-1}-y^{k-2} \bigr\Vert \bigr) \triangle _{k,k+1},\quad \mbox{for all }k>\tilde{k}. \end{aligned} $$

Thus

$$\bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2} \leq \frac{\tau }{\delta }\bigl( \bigl\Vert y^{k}-y^{k-1} \bigr\Vert + \bigl\Vert y ^{k-1}-y^{k-2} \bigr\Vert \bigr)\triangle _{k,k+1},\quad \mbox{for all } k>\tilde{k}. $$

Furthermore,

$$ \begin{aligned} &3 \bigl\Vert y^{k+1}-y^{k} \bigr\Vert \\ &\quad \leq 2\bigl( \bigl\Vert y^{k}-y^{k-1} \bigr\Vert + \bigl\Vert y^{k-1}-y^{k-2} \bigr\Vert \bigr)^{\frac{1}{2}} \biggl( \frac{3}{2}\sqrt{\frac{\tau }{\delta }} \triangle _{k,k+1}^{ \frac{1}{2}}\biggr),\quad \mbox{for all } k> \tilde{k}. \end{aligned} $$

Using the fact that $2ab\leq a^{2}+b^{2}$, we obtain

$$ \begin{aligned}[b] &3 \bigl\Vert y^{k+1}-y^{k} \bigr\Vert \\ &\quad \leq \bigl( \bigl\Vert y^{k}-y^{k-1} \bigr\Vert + \bigl\Vert y^{k-1}-y^{k-2} \bigr\Vert \bigr)+ \frac{9\tau }{4\delta } \triangle _{k,k+1},\quad \mbox{for all } k> \tilde{k}. \end{aligned} $$

(33)

Summing up the above inequality for $k=\tilde{k}+1,\dots ,s$, yields

$$3\sum_{k=\tilde{k}+1}^{s} \bigl\Vert y^{k+1}-y^{k} \bigr\Vert \leq \sum _{k=\tilde{k}+1} ^{s}\bigl( \bigl\Vert y^{k}-y^{k-1} \bigr\Vert + \bigl\Vert y^{k-1}-y^{k-2} \bigr\Vert \bigr)+\frac{9\tau }{4\delta } \triangle _{\tilde{k}+1,s+1}. $$

Thus

$$\sum_{k=\tilde{k}+1}^{s} \bigl\Vert y^{k+1}-y^{k} \bigr\Vert \leq \bigl(2 \bigl\Vert y^{ \tilde{k}+1}-y^{\tilde{k}} \bigr\Vert + \bigl\Vert y^{\tilde{k}}-y^{\tilde{k}-1} \bigr\Vert \bigr) +\frac{9 \tau }{4\delta } \triangle _{\tilde{k}+1,s+1}. $$

Notice that $\varphi (\mathcal{L}_{\beta }(z^{s+1})-\mathcal{L}_{ \beta }(z^{*}))>0$, so taking the limit $s\rightarrow +\infty$, we have

$$ \begin{aligned}[b] &\sum _{k=\tilde{k}+1}^{+\infty } \bigl\Vert y^{k+1}-y^{k} \bigr\Vert \\ &\quad \leq \bigl(2 \bigl\Vert y^{\tilde{k}+1}-y^{\tilde{k}} \bigr\Vert + \bigl\Vert y^{\tilde{k}}-y^{\tilde{k}-1} \bigr\Vert \bigr) + \frac{9\tau }{4\delta }\varphi \bigl(\mathcal{L}_{\beta } \bigl(z^{ \tilde{k}+1}\bigr)-\mathcal{L}\bigl(z^{*}\bigr)\bigr). \end{aligned} $$

(34)

Thus

$$\sum_{k=\tilde{k}+1}^{+\infty } \bigl\Vert y^{k+1}-y^{k} \bigr\Vert < +\infty . $$

It follows from (20) that

$$\sum_{k=\tilde{k}+1}^{+\infty } \bigl\Vert \lambda ^{k+1}-\lambda ^{k} \bigr\Vert < +\infty . $$

From $A^{\top }A\succ 0$, (23) and the above two formulas, we obtain

$$\sum_{k=\tilde{k}+1}^{+\infty } \bigl\Vert x^{k+1}-x^{k} \bigr\Vert < +\infty . $$

Since

$$\begin{aligned} \bigl\Vert z^{k+1}-z^{k} \bigr\Vert &=\bigl( \bigl\Vert x^{k+1}-x^{k} \bigr\Vert ^{2}+ \bigl\Vert y^{k+1}-y^{k} \bigr\Vert ^{2}+ \bigl\Vert \lambda ^{k+1}-\lambda ^{k} \bigr\Vert ^{2}\bigr)^{\frac{1}{2}} \\ &\leq \bigl\Vert x^{k+1}-x^{k} \bigr\Vert + \bigl\Vert y^{k+1}-y^{k} \bigr\Vert + \bigl\Vert \lambda ^{k+1}-\lambda ^{k} \bigr\Vert , \end{aligned}$$

we know

$$\sum_{k=\tilde{k}+1}^{m} \bigl\Vert z^{k+1}-z^{k} \bigr\Vert < +\infty . $$

(ii) From (i), we known that $\{z^{k}\}$ is a Cauchy sequence and so is convergent. Theorem 3.2(ii) follows immediately from Theorem 3.1(ii). □

In the above results, we have assumed the boundedness of the sequence $\{z^{k}\}$. Next, we present two sufficient conditions ensuring this requirement.

Lemma 3.4

Suppose that $A^{\top }A\succ 0$ and

$$\begin{aligned} \varGamma :=\inf_{y\in R^{m}}\biggl\{ g(y)-\frac{1}{2L} \bigl\Vert \nabla g(y) \bigr\Vert ^{2}\biggr\} >- \infty . \end{aligned}$$

If one of the following statements is true:

• (i) f is coercive, i.e., $\lim_{\|x\|\rightarrow + \infty }f(x)=+\infty$,

• (ii) f is bounded from below and g is coercive, i.e., $\inf_{x\in R^{n}}f(x)>-\infty$ and $\lim_{\|x\|\rightarrow +\infty }g(x)=+\infty$,

then $\{z^{k}\}$ is bounded.

Proof

(i) Suppose that f is coercive. From Lemma 3.1, we know that $\mathcal{L}_{\beta }(z^{k})\leq \mathcal{L}_{\beta }(z^{1})<+\infty$, for all $k\geq 1$. Combining with $\nabla g(x^{k})=-\lambda ^{k}$, one has

$$ \begin{aligned}[b]\mathcal{L}_{\beta } \bigl(z^{1}\bigr)\geq{}& f\bigl(x^{k}\bigr)+g \bigl(y^{k}\bigr)-\bigl\langle \lambda ^{k},Ax^{k}-y^{k} \bigr\rangle +\frac{\beta }{2} \bigl\Vert Ax^{k}-y^{k} \bigr\Vert ^{2} \\ ={}&f\bigl(x^{k}\bigr)+g\bigl(y^{k}\bigr)- \frac{1}{2\beta } \bigl\Vert \lambda ^{k} \bigr\Vert ^{2}+ \frac{\beta }{2} \biggl\Vert Ax^{k}-y^{k}- \frac{1}{\beta }\lambda ^{k} \biggr\Vert ^{2} \\ ={}&f\bigl(x^{k}\bigr)+\biggl(g\bigl(y^{k}\bigr)- \frac{1}{2L} \bigl\Vert \nabla g\bigl(y^{k}\bigr) \bigr\Vert ^{2}\biggr)+\biggl( \frac{1}{2L}- \frac{1}{2\beta }\biggr) \bigl\Vert \lambda ^{k} \bigr\Vert ^{2} \\ &{} +\frac{\beta }{2} \biggl\Vert Ax^{k}-y^{k}- \frac{1}{\beta }\lambda ^{k} \biggr\Vert ^{2} \\ \geq{}& f\bigl(x^{k}\bigr)+\varGamma +\biggl(\frac{1}{2L}- \frac{1}{2\beta }\biggr) \bigl\Vert \lambda ^{k} \bigr\Vert ^{2}+\frac{\beta }{2} \biggl\Vert Ax^{k}-y^{k}- \frac{1}{\beta }\lambda ^{k} \biggr\Vert ^{2}. \end{aligned} $$

(35)

Since $\beta >2L$ and f is coercive, it is easy to see that $\{x^{k}\}$, $\{\lambda ^{k}\}$, and $\{\frac{\beta }{2}\|Ax^{k}-y^{k}-\frac{1}{ \beta }\lambda ^{k}\|^{2}\}$ are bounded. Furthermore, $\{y^{k}\}$ is bounded. Thus $\{z^{k}\}$ is bounded.

(ii) Similar as with (i), we have

$$ \begin{aligned} \mathcal{L}_{\beta }\bigl(z^{1} \bigr) \geq {}&f\bigl(x^{k}\bigr)+g\bigl(y^{k}\bigr)- \frac{1}{2\beta } \bigl\Vert \lambda ^{k} \bigr\Vert ^{2}+\frac{\beta }{2} \biggl\Vert Ax^{k}-y^{k}- \frac{1}{\beta } \lambda ^{k} \biggr\Vert ^{2} \\ \geq{}& f\bigl(x^{k}\bigr)+\frac{1}{2}g \bigl(y^{k}\bigr)+\frac{1}{2}\varGamma +\frac{1}{4L} \bigl\Vert \nabla g\bigl(y^{k}\bigr) \bigr\Vert ^{2}- \frac{1}{2\beta } \bigl\Vert \lambda ^{k} \bigr\Vert ^{2} \\ &{}+\frac{\beta }{2} \biggl\Vert Ax^{k}-y^{k}- \frac{1}{\beta }\lambda ^{k} \biggr\Vert ^{2} \\ \geq{}& f\bigl(x^{k}\bigr)+\frac{1}{2}g \bigl(y^{k}\bigr)+\frac{1}{2}\varGamma +\biggl( \frac{1}{4L}-\frac{1}{2 \beta }\biggr) \bigl\Vert \lambda ^{k} \bigr\Vert ^{2} +\frac{\beta }{2} \biggl\Vert Ax^{k}-y^{k}-\frac{1}{ \beta }\lambda ^{k} \biggr\Vert ^{2}. \end{aligned} $$

Notice that $\beta >2L$, function f is bounded from below, g is coercive and Assumption 3.1(ii) holds, thus $\{y^{k}\}$, $\{\lambda ^{k}\}$, and $\{\frac{\beta }{2}\|Ax^{k}-y^{k}-\frac{1}{ \beta }\lambda ^{k}\|^{2}\}$ are bounded. Since $A^{\top }A\succ 0$, $\{x^{k}\}$ is bounded. Thus $\{z^{k}\}$ is bounded. □

4 Numerical examples

In compressed sensing, one needs to find the sparsest solution of a linear system, which can be modeled as

$$\begin{aligned} &\min\quad \Vert x \Vert _{0}, \\ &\quad \mbox{s.t. } Dx=b, \end{aligned}$$

(36)

where $D\in R^{m\times n}$ is the measuring matrix, $b\in R^{m}$ is observed data, $\|x\|_{0}$ denotes the number of nonzero elements of x, which is called the $l_{0}$ norm.

Problem (36) is NP-hard. In practical applications, one may relax the $l_{0}$ norm to the $l_{1}$ norm or $l_{\frac{1}{2}}$ norm, and consider their regularized versions, which lead to the following convex problem (37) and nonconvex problem (38):

$$\begin{aligned} &\min \quad \gamma \Vert x \Vert _{1}+ \Vert y \Vert ^{2}, \\ &\quad \mbox{s.t. } Dx-y=b, \end{aligned}$$

(37)

and

$$\begin{aligned} & \min\quad \gamma \Vert x \Vert ^{\frac{1}{2}}_{\frac{1}{2}}+ \Vert y \Vert ^{2}, \\ &\quad \mbox{s.t. }Dx-y=b. \end{aligned}$$

(38)

In this section, we will apply RADMM (7) to solve the above two problems. For simplicity, we set $b=0$ throughout this section. Applying RADMM (7) to problem (37) with $G=\alpha I-\beta D^{ \top }D$ yields

$$ \textstyle\begin{cases} x^{k+1}\in S(x^{k}-\frac{\beta }{\alpha }D^{\top }Dx^{k}+\frac{1}{ \alpha }D^{\top }(\beta y^{k}+\lambda ^{k}));\frac{\gamma }{2\alpha }), \\ y^{k+1}=\frac{1}{2+\beta }(\beta D x^{k+1}-\lambda ^{k}), \\ \lambda ^{k+1}=\lambda ^{k}-\beta (Dx^{k+1}-y^{k+1}), \end{cases} $$

(39)

where $S(\cdot ;\mu )=\{s_{\mu }(x_{1}),s_{\mu }(x_{2}),\dots ,s_{ \mu }(x_{n})\}^{\top }$ is the soft shrinkage operator [24] defined as follows:

$$ s_{\mu }(x_{i})=\textstyle\begin{cases} x_{i}+\frac{\mu }{2},&\mbox{if }x_{i} \leq -\frac{\mu }{2}, \\ 0,&\mbox{if } |x| < \frac{\mu }{2}, \\ x_{i}-\frac{\mu }{2},&\mbox{if }x_{i} \geq \frac{\mu }{2}. \end{cases} $$

Applying RADMM (7) to problem (38) with $G=\alpha I- \beta D^{\top }D$ yields

$$ \textstyle\begin{cases} x^{k+1}\in H(x^{k}-\frac{\beta }{\alpha }D^{\top }Dx^{k}+\frac{1}{ \alpha }D^{\top }(\beta y^{k}+\lambda ^{k}));\frac{\gamma }{\alpha }), \\ y^{k+1}=\frac{1}{2+\beta }(\beta D x^{k+1}-\lambda ^{k}), \\ \lambda ^{k+1}=\lambda ^{k}-\beta (Dx^{k+1}-y^{k+1}), \end{cases} $$

(40)

where $H(\cdot ;\mu )=\{h_{\mu }(x_{1}),h_{\mu }(x_{2}),\dots ,h_{ \mu }(x_{n})\}^{\top }$ is the half-shrinkage operator [25] defined as follows:

$$ h_{\mu }(x_{i})=\textstyle\begin{cases} \frac{2x_{i}}{3}(1+\cos \frac{2}{3}(\pi -\varphi ( \vert x_{i} \vert ))),& \vert x_{i} \vert >\frac{ \sqrt[3]{54}}{4}\mu ^{\frac{2}{3}}, \\ 0,&\text{otherwise}, \end{cases} $$

with $\varphi (x)=\arccos (\frac{\mu }{8}(\frac{x_{i}}{3})^{- \frac{3}{2}})$.

For simplicity, we denote algorithms (39) and (40) by SRADMM and HRADMM, respectively. The selection of relevant parameters in numerical experiments is given below. We now conduct an experiment to verify convergence of the nonconvex RADMM, and reveal its advantages in sparsity-inducing and efficiency through comparing the performance of HRADMM and SRADMM. In the experiment, $m=511$, $n=512$, the matrix $D\in R^{511\times 512}$ is obtained by unitizing the matrix with randomly generated entries obeying the normal distribution $\mathcal{N}(0,1)$, the noise vector $\varepsilon \sim \mathcal{N}(0,1)$, the recovery vector $r=Dx^{0}+\varepsilon$, and the regularization parameters are $\gamma =0.0015$, $\beta =0.8$, $\alpha =2.5$.

The experimental results are shown in Fig. 1, where the restoration accuracy is measured by means of the mean squared error:

$$\begin{aligned} &\operatorname{MSE}\bigl( \bigl\Vert x^{*}-x^{k} \bigr\Vert \bigr)=\frac{1}{n} \bigl\Vert x^{*}-x^{k} \bigr\Vert , \\ &\operatorname{MSE}\bigl( \bigl\Vert y^{*}-y^{k} \bigr\Vert \bigr)=\frac{1}{n} \bigl\Vert y^{*}-y^{k} \bigr\Vert , \end{aligned}$$

where $(x^{*},y^{*})=(0,0)$ is the optimal solution for the problems (37) and (38), respectively.

Figure 1

Comparison the performance of HRADMM and SRADMM

Programming is performed on Matlab R2014a, a computer running the program is configured as follows: Windows 7 system, Inter(R) Core(TM) i7-4790 CPU 3.60 GHz, 4 GB memory. Numerical results show that algorithm (7) is efficient and stable. As shown in Fig. 1, both sequences $x^{k}$ and $y^{k}$ were fairly near the true solution. i.e., the convergence is justified. It is readily seen that HRADMM converges faster than SRADMM.

5 Conclusion and outlook

In this paper, a regularized alternating direction method of multipliers is proposed for a class of nonconvex problems. Firstly, the global convergence of the algorithm is analyzed. Secondly, under the condition that the augmented Lagrangian function $\mathcal{L}_{\beta }(\cdot )$ satisfies the Kurdyka–Łojasiewicz property, the strong convergence of the algorithm is analyzed. Finally, the effectiveness of the algorithm is verified by numerical experiments.