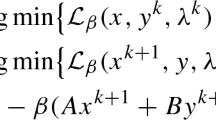Abstract
This work investigates the theoretical performance of the alternating-direction method of multipliers (ADMM) as it applies to nonconvex optimization problems, and in particular, problems with nonconvex constraint sets. The alternating direction method of multipliers is an optimization method that has largely been analyzed for convex problems. The ultimate goal is to assess what kind of theoretical convergence properties the method has in the nonconvex case, and to this end, theoretical contributions are twofold. First, this work analyzes the method with local optimal solution of the ADMM subproblems, which contrasts with much analysis that requires global solutions of the subproblems. Such a consideration is important to practical implementations. Second, it is established that the method still satisfies a local convergence result. The work concludes with some more detailed discussion of how the analysis relates to previous work.
Similar content being viewed by others
Notes
Let zy≠0 and consider z = (0,zy). The only way that the positive definiteness condition can hold is if Bzy≠0. This implies that B must have full column rank.
The gradient of the augmented Lagrangian is given by:
$$ \begin{array}{@{}rcl@{}} &&\nabla_{x} {L}_{\rho,\mathbf{r},\mathbf{q}}(\mathbf{x},\mathbf{y}) = \nabla f(\mathbf{x}) - \mathbf{r} + \nabla \mathbf{c}(\mathbf{x}) \hat{\boldsymbol{\mu}}(\mathbf{r},\mathbf{q}) + \rho \nabla \mathbf{c}(\mathbf{x}) \mathbf{c}(\mathbf{x}) + \mathbf{A}^{\mathrm{T}} \hat{\boldsymbol{\lambda}}(\mathbf{r},\mathbf{q}) + \rho \mathbf{A}^{\mathrm{T}} (\mathbf{A}\mathbf{x} + \mathbf{B}\mathbf{y} - \mathbf{b} -\mathbf{q}), \\ &&\nabla_{y} {L}_{\rho,\mathbf{r},\mathbf{q}}(\mathbf{x},\mathbf{y}) = \mathbf{B}^{\mathrm{T}} \hat{\boldsymbol{\lambda}}(\mathbf{r},\mathbf{q}) + \rho \mathbf{B}^{\mathrm{T}} (\mathbf{A}\mathbf{x} + \mathbf{B}\mathbf{y} - \mathbf{b} -\mathbf{q}). \end{array} $$The radius of this neighborhood depends on the minimum eigenvalue of \(\nabla ^{2} L_{\rho } (\mathbf {x}^{*},\mathbf {y}^{*})\). In particular, the radius is non-decreasing as this minimum eigenvalue increases. While \(\nabla ^{2} L_{\rho } (\mathbf {x}^{*},\mathbf {y}^{*})\) does depend on the value of ρ, the minimum eigenvalue can only increase with increasing ρ; compare with the expression for Hρ in the proof of Lemma 3.1, part 2. Thus, the radius of the neighborhood on which x∗ is a minimizer is independent of ρ, as long as ρ is above the critical value.
References
Introduction to IPOPT: a tutorial for downloading, installing, and using IPOPT. https://coin-or.github.io/Ipopt/. Accessed: 2017-7-21
Bai X, Scheinberg K (2015) Alternating direction methods for non convex optimization with applications to second-order least-squares and risk parity portfolio selection. http://www.optimization-online.org/DB_FILE/2015/02/4776.pdf. Accessed: 2019-1-22
Bertsekas DP (1979) Convexification procedures and decomposition methods for nonconvex optimization problems. J Optim Theory Appl 29(2):169–197
Bertsekas DP (1996) Constrained optimization and lagrange multiplier methods. Athena Scientific, Belmont
Bertsekas DP (1999) Nonlinear programming, 2nd edn. Athena Scientific, Belmont
Boyd S, Parikh N, Chu E, Peleato B, Eckstein J (2011) Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn 3(1):1–122
Chatzipanagiotis N, Dentcheva D, Zavlanos MM (2015) An augmented Lagrangian method for distributed optimization. Math Program 152 (1-2):405–434
Chatzipanagiotis N, Zavlanos MM (2017) On the convergence of a distributed augmented Lagrangian method for nonconvex optimization. IEEE Trans Autom Control 62(9):4405–4420
Chiang N, Petra CG, Zavala VM (2014) Structured nonconvex optimization of large-scale energy systems using PIPS-NLP. In: Power Systems Computation Conference (PSCC), 2014, pp 1–7
Curtis FE, Raghunathan AU (2017) Solving nearly-separable quadratic optimization problems as nonsmooth equations. Comput Optim Appl 67(2):317–360
Dinh QT, Necoara I, Diehl M (2013) A dual decomposition algorithm for separable nonconvex optimization using the penalty function framework. In: Decision and Control (CDC), 2013 IEEE 52nd annual conference on, pp 2372–2377
Eckstein J, Yao W (2015) Understanding the convergence of the alternating direction method of multipliers: theoretical and computational perspectives. http://www.optimization-online.org/DB_FILE/2015/06/4954.pdf. Accessed: 2019-1-22
Feng X, Mukai H, Brown RH (1990) New decomposition and convexification algorithm for nonconvex large-scale primal-dual optimization. J Optim Theory Appl 67(2):279–296
Fiacco AV (1976) Sensitivity analysis for nonlinear programming using penalty methods. Math Program 10(1):287–311
Fiacco AV, Ishizuka Y (1990) Sensitivity and stability analysis for nonlinear programming. Ann Oper Res 27(1):215–235
Hong M, Luo Z-Q, Razaviyayn M (2016) Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. SIAM J Optim 26(1):337–364
Hours J-H, Jones CN (2014) An augmented Lagrangian coordination-decomposition algorithm for solving distributed non-convex programs. In: American control conference (ACC), vol 2014, pp 4312–4317
Houska B, Frasch J, Diehl M (2016) An augmented Lagrangian based algorithm for distributed nonconvex optimization. SIAM J Optim 26 (2):1101–1127
Kang J, Cao Y, Word DP, Laird C (2014) An interior-point method for efficient solution of block-structured NLP problems using an implicit Schur-complement decomposition. Comput Chem Eng 71:563–573
Li G, Pong TK (2016) Douglas–Rachford splitting for nonconvex optimization with application to nonconvex feasibility problems. Math Program 159 (1-2):371–401
Magnusson S, Chathuranga P, Rabbat M, Fischione C (2015) On the convergence of alternating direction Lagrangian methods for nonconvex structured optimization problems. IEEE Trans Control Netw Syst PP(99):1–1
Nocedal J, Wright SJ (2006) Numerical optimization, 2nd edn. Springer, New York
Rodriguez JS, Nicholson B, Laird C, Zavala VM (2018) Benchmarking ADMM in nonconvex NLPs. Comput Chem Eng 119:315–325
Shapiro A, Sun J (2004) Some properties of the augmented Lagrangian in cone constrained optimization. Math Oper Res 29(3):479–491
Stephanopoulos G, Westerberg AW (1975) The use of Hestenes’ method of multipliers to resolve dual gaps in engineering system optimization. J Optim Theory Appl 15(3):285–309
Strang G (2006) Linear algebra and its applications, 4th edn. Thomson Brooks/Cole, Boston
Tanikawa A, Mukai H (1985) A new technique for nonconvex primal-dual decomposition of a large-scale separable optimization problem. IEEE Trans Autom Control 30(2):133–143
Wächter A, Biegler LT (2006) On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program 106(1):25–57
Wang Y, Yin W, Zeng J (2019) Global convergence of ADMM in nonconvex nonsmooth optimization. J Sci Comput 78(1):29–63
Zhang X, Byrd RH, Schnabel RB (1992) Parallel methods for solving nonlinear block bordered systems of equations. SIAM J Sci Stat Comput 13(4):841–859
Acknowledgments
The author would like to thank his colleagues Shivakumar Kameswaran, Thomas Badgwell, and Francisco Trespalacios for fruitful discussions in developing this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The author declares that he has no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
An earlier version of this article is present on a university repository website and can be accessed on http://export.arxiv.org/abs/1902.07815. This article is not published nor is under publication elsewhere.
Appendices
Appendix: A Regularity of overall problem and subproblems
This section establishes the claim that Assumption 2 implies Assumption 4; that is, that a solution of the main problem (P) which satisfies conditions including the second-order sufficient conditions implies that the subproblems also have solutions satisfying similar conditions. This is established through the following lemmata. This next result is a modification of [5, Lemma 3.2.1].
Lemma A.1
Let \(\mathbf {H} \in \mathbb {R}^{n \times n}\) be a symmetric matrix and let \(\mathbf {C} \in \mathbb {R}^{p \times n}\) and \(\mathbf {D} \in \mathbb {R}^{p^{\prime } \times n}\). Assume that H is positive definite on the nullspace of \(\begin {bmatrix} \mathbf {C} \\ \mathbf {D} \end {bmatrix}\): zTHz > 0 for all z≠0 with Cz = 0 and Dz = 0. Then there exists ρ∗ such that for all ρ > ρ∗,
for all z≠0 with Cz = 0.
Proof
Assume the contrary. Then for all \(k \in \mathbb {N}\), there exists zk≠0 such that (zk)T(H + kDTD)zk ≤ 0 and Czk = 0. Assume without loss of generality that \(\left \| \mathbf {z}^{k} \right \| = 1\) (we can scale zk as necessary). Since \(\left (\mathbf {z}^{k} \right )_{k}\) is in a compact set, we have a subsequence converging to some point \(\bar {\mathbf {z}}\) with \(\left \| {\bar {\mathbf {z}}} \right \| = 1\) and \(\mathbf {C}\bar {\mathbf {z}} = \mathbf {0}\). Taking the limit superior of (zk)T(H + kDTD)zk ≤ 0 over this subsequence, we get:
Since (zk)TDTDzk ≥ 0 for all k, we must have (the subsequence) {(zk)TDTDzk} converging to zero, or else the limsup would be infinite. Thus, \((\mathbf {D}\bar {\mathbf {z}})^{\mathrm {T}} \mathbf {D} \bar {\mathbf {z}} = 0\), which implies \(\mathbf {D}\bar {\mathbf {z}} = \mathbf {0}\). But by hypothesis, this means \(\bar {\mathbf {z}}^{\mathrm {T}} \mathbf {H}\bar {\mathbf {z}} > 0\). Combined with the fact that \(\limsup _{k} k (\mathbf {z}^{k})^{\mathrm {T}} \mathbf {D}^{\mathrm {T}} \mathbf {D} \mathbf {z}^{k}\) must be nonnegative (since each term is nonnegative), this contradicts Inequality (18). □
Lemma A.2
Let Assumption 2 hold. Then for all sufficiently large ρ, Assumption 4 holds.
Proof
If (x∗,y∗,μ∗,λ∗) is a KKT point of the overall problem (P), then we have:
Since we have Ax∗ + By∗ = b, we can add AT(ρ(Ax∗ + By∗−b)) to the first equation to get:
which we recognize as the KKT conditions of the subproblem when yk = y∗ and λk = λ∗. (see Eq. ??).
Differentiability of f and c and the linear independence constraint qualification for the subproblems follow directly from the conditions of Assumption 2. It remains to show that the second-order sufficient conditions hold. Let H∗ equal the Hessian of the Lagrangian of Problem (P) at the given KKT point; that is, let:
(where Hxx is defined in Assumption 2). By Assumption 2, for any z satisfying z≠0, Cz = 0, we must have zTH∗z > 0 (where, again, C is defined in Assumption 2). Noting the form of C, by Lemma 3.1 this means that there exists ρ∗ such that for all ρ > ρ∗,
for all z with z≠0 and \(\left [\nabla \mathbf {c}(\mathbf {x}^{*})^{\mathrm {T}} \mathbf {0} \right ] \mathbf {z} = \mathbf {0}\). In particular, this means that for any \(\mathbf {z}_{x} \in \mathbb {R}^{n}\) satisfying zx≠0 and \(\nabla \mathbf {c}(\mathbf {x}^{*})^{\mathrm {T}} \mathbf {z}_{x} = \mathbf {0}\), we have z = (zx,0) satisfies:
Finally, we note that \(\mathbf {H}_{xx}(\mathbf {x}^{*},\boldsymbol {\mu }^{*}) + \rho \mathbf {A}^{\mathrm {T}} \mathbf {A}\) is the Hessian of the Lagrangian of the subproblem (SP) evaluated at (x∗,μ∗). □
Appendix: B A result in parametric optimization
Required by the proof of Lemma 3.1, the following is a technical result, although it relies on standard and straightforward results. It is a modification of a classic sufficiency result for local optimality in the parametric setting, stating that there is a minimum size neighborhood on which local optimality holds, for all problems in a perturbed family.
Lemma B.1
Let h : (z,p)↦h(z,p) be a real-valued mapping (on \(\mathbb {R}^{n_{z}} \times \mathbb {R}^{n_{p}}\)) such that h is twice-continuously differentiable with respect to z on some open set Dz, for all p in some open set Dp. In addition, assume that \(\nabla _{zz}^{2} h\) is continuous on Dz × Dp. Assume that for all p ∈ Dp, there exists z∗(p) ∈ Dz such that \(\nabla _{z} h(\mathbf {z}^{*}(\mathbf {p}),\mathbf {p}) = \mathbf {0}\) and \(\nabla _{zz}^{2} h(\mathbf {z}^{*}(\mathbf {p}),\mathbf {p})\) is positive definite. Then for any \(\bar {\mathbf {p}} \in D_{p}\), there exist positive constants 𝜖 and δ such that for all \(\mathbf {p} \in N_{\delta }(\bar {\mathbf {p}})\), if \(\left \| {\mathbf {z}^{*}(\mathbf {p}) - \mathbf {z}^{*}(\bar {\mathbf {p}})} \right \| \le \epsilon \), then z∗(p) minimizes h(⋅,p) on the neighborhood \(N_{\epsilon }(\mathbf {z}^{*}(\mathbf {p}))\).
Proof
That z∗(p) minimizes h(⋅,p), for all p, follows from the standard second-order sufficient conditions for unconstrained minimization; see, for instance [5, Prop. 1.1.3]. The challenge is to show that the radius of the neighborhood on which it is a minimizer is constant with respect to p. Choose \(\bar {\mathbf {p}} \in D_{p}\). Since \(\nabla _{zz}^{2} h(\mathbf {z}^{*}(\bar {\mathbf {p}}),\bar {\mathbf {p}})\) is positive definite and \(\nabla _{zz}^{2} h\) is continuous, for all (z,p) sufficiently close to \((\mathbf {z}^{*}(\bar {\mathbf {p}}),\bar {\mathbf {p}})\), \(\nabla _{zz}^{2} h(\mathbf {z},\mathbf {p})\) is positive definite. In particular, we can choose \(\epsilon ^{\prime }\), δ so that:
and \(\nabla _{zz}^{2} h(\mathbf {z},\mathbf {p})\) is positive definite for all (z,p) ∈ K. Since the eigenvalues of a matrix depend continuously on the elements of a matrix ([5, Proposition A.14]), we have that the eigenvalues of \(\nabla _{zz}^{2} h(\mathbf {z},\mathbf {p})\) (and in particular the minimum eigenvalue) are continuous and positive for all (z,p) ∈ K, and since K is compact, we can choose a constant λ > 0 which is a lower bound on the minimum eigenvalue for all (z,p) ∈ K.
Now choose any \(\mathbf {p} \in N_{\delta }(\bar {\mathbf {p}})\) and assume \(\left \| \mathbf {z}^{*}(\mathbf {p}) - \mathbf {z}^{*}(\bar {\mathbf {p}}) \right \| \le \frac {\epsilon ^{\prime }}{2}\). Consider a Taylor expansion of h(⋅,p) at z∗(p): for any s such that \(\left \| \mathbf {s} \right \| \le \frac {\epsilon ^{\prime }}{2}\), there exists αs,p ∈ (0, 1) such that:
where the linear term may be ignored because \(\nabla _{z} h(\mathbf {z}^{*}(\mathbf {p}),\mathbf {p}) = \mathbf {0}\). Note that (z∗(p) + αs,ps,p) ∈ K, no matter what the specific value of αs,p is. Consequently, we can use the lower bound λ on the minimum eigenvalue of the Hessian to see that:
(see for instance [5, Prop. A.18]). Define \(\epsilon \equiv \frac {\epsilon ^{\prime }}{2}\). The right-hand side of the above inequality is nonnegative, showing that z∗(p) is a minimizer of h(⋅,p) on the neighborhood \(N_{\epsilon }(\mathbf {z}^{*}(\mathbf {p}))\). □
Rights and permissions
About this article
Cite this article
Harwood, S.M. Analysis of the Alternating Direction Method of Multipliers for Nonconvex Problems. SN Oper. Res. Forum 2, 9 (2021). https://doi.org/10.1007/s43069-020-00043-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43069-020-00043-y