Finite element formulation for the free vibration analysis of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory

Abstract

The present paper is concerned with the free vibration analysis of double-walled carbon nanotubes embedded in an elastic medium and based on Eringen's nonlocal elasticity theory. The effects of the transverse shear deformation and rotary inertia are included according to the Timoshenko beam theory. The governing equations of motion which are coupled with each other via the van der Waals interlayer forces have been derived using Hamilton's principle. The thermal effect is also incorporated into the formulation. Using the statically exact beam element with displacement fields based on the first order shear deformation theory, the finite element method is employed to discretize the coupled governing equations which are then solved to find the natural frequencies. The effects of the small scale parameter, boundary conditions, thermal effect, changes in material constant of the surrounding elastic medium, and geometric parameters on the vibration characteristics are investigated. Furthermore, our analysis includes nonlocal double-walled carbon nanotubes with different boundary conditions between inner and outer tubes which seem to be scarcely considered in the literature, and the corresponding given results for this case can be considered as a benchmark for further studies. Comparison of the present numerical results with those from the open literature shows an excellent agreement.

Introduction

Carbon nanotubes (CNTs) have occupied the chief topic of research in nanotechnology since they were first discovered by Iijima [1] in 1991. During the past two decades, research on CNTs increased as reflected by extensive number of publications devoted to synthesis, fundamentals, and applications of these nanostructured materials. Their unique physical (mechanical, electrical, and thermal) as well as chemical properties enable them for a large variety of new applications in nanoelectronics, nanodevices, nanocomposites, and so on [2–7]. They possess extraordinary strength which is measured up to 100 times that of steel at one-sixth of the weight [8], as well as superior electrical and thermal conductivities.

Until now, a wide range of studies have been conducted on the mechanical behavior of CNTs such as buckling and bending problems using experimental methods and molecular-dynamics (MD) simulations, but performing experiments at the scale of nanometers is very difficult and needs high expenses. Also, the atomistic methods such as MD simulations are dependent to the small-scale modeling. Therefore, developing continuum models which may overcome these restrictions are expected to be the dominant tool for modeling structures at the scale of nanometers and performing analytical analysis of CNTs of larger scales.

Recently, many elastic continuum models have been successfully used for studying the bending, buckling, and vibrational behaviors of CNTs including cylindrical shell models [9–12] and beam models [13–21]. The beam models implemented are often developed on the basis of the Euler-Bernoulli theory [13–17] and the Timoshenko beam theory [18–21] which takes the effects of shear deformation and rotary inertia into the consideration. Fu et al. [22] studied the nonlinear vibrations of embedded multiwalled nanotubes, with the inclusion of intertube radial displacements and the internal van der Waals (vdW) forces, using the incremental harmonic balanced method. They only considered CNTs with simply supported end conditions. Xu et al. [23] studied free linear vibrations of double-walled nanotubes (DWNTs) modeled as elastic beams due to different boundary conditions between inner and outer tubes. Related to the work done by Fu et al. [22], Ansari et al. [24] and Ansari and Hemmatnezhad [25] investigated the nonlinear vibrations of single-, double- and triple-walled CNTs on the basis of a multiple-beam model and found the nonlinear frequencies using the homotopy perturbation method and the variational iteration method Recently, they proposed a general finite element formulation for investigating the nonlinear oscillations of DWNTs with different boundary conditions [26]. They also extended the work done by Xu et al. [23] to the large-amplitude vibrations of DWNTs with different boundary conditions between inner and outer tubes.

However, the continuum models proposed in all of these works, so-called the classical continuum models, are scale-independent and their application in small-scale nanomaterials are of some concern. In fact, the size effects are becoming more pronounced as the dimensions of the nanostructures become very small. Hence, continuum models more appropriate than the classical elastic continuum models are expected to accommodate the size dependence of nanomaterials in studies of these materials at very small scales. Nonlocal elasticity theory was formally initiated by Eringen [27, 28] to account for the scale effect in elasticity by assuming that the stress state at a given point is considered as a function of the strain state of all points in the body. The application of nonlocal continuum mechanics allowing for the small scale effects to the vibrational analysis of CNTs has been suggested by many research workers including both beam and shell theories [29–35]. Ansari and Ramezannezhad in one of their recent publications studied the nonlinear vibrations of embedded multiwalled carbon nanotubes in thermal environments based upon the nonlocal Timoshenko beam model [36]. They implemented the harmonic balance approach in order to analytically solve the set of coupled nonlinear differential equations. The free vibration response of single-walled carbon nanotubes (SWNTs) using various nonlocal beam theories was also investigated Ansari and Sahmani [37]. In that work, the generalized differential quadrature method (DQM) was employed to discretize the governing differential equations and obtain the fundamental frequencies of SWNTs with different boundary conditions. They also implemented MD simulations in order to validate the obtained results. Based on the nonlocal Euler-Bernoulli and Timoshenko beam theories, the Ansari et al. also studied the dynamic stability of embedded SWNTs under axial compression in a thermal environment [38].

A literature survey shows that the number of publications conducted on the free vibrations of CNTs using the finite element method and based on the nonlocal elasticity theory is scarce. Based upon a nonlocal Timoshenko beam model, this paper studies the free vibration analysis of embedded DWNTs with different boundary conditions between inner and outer tubes in thermal environments. The Hamilton's principle is employed to derive the governing differential equations of motion which are then solved using the finite element method (FEM). The influences of nonlocal parameter, some commonly used boundary conditions, stiffness of the elastic medium, temperature change, and variations of the nanotube's geometrical parameters on the vibration frequencies are examined.

Nonlocal beam model for double-walled carbon nanotubes

Unlike the conventional local elasticity, in the nonlocal elasticity theory, it is assumed that the stress at a point is a function of strains at all points in the continuum. The nonlocal constitutive equation given by Eringen is [27, 28] as follows:

$$\left(1-\mu {\nabla }^2\right)\sigma =t,$$

(1)

where t is the macroscopic stress tensor at a point, and σ is the Hookean stress tensor. μ = e_0a/l is the small scale factor, where e_0a is a constant appropriate to each material, α and l are the internal and external characteristic lengths, respectively. When the nonlocal parameter goes to zero, nonlocal elasticity theory reduces to classical (local) elasticity theory. Hooke's law relates the stress tensor to strain as the equation below:

$$t=S:\epsilon ,$$

(2)

wherein S is the fourth order elasticity tensor, and ‘:’ stands for the double dot product. Since each of the tubes is modeled as a single beam, the nonlocal constitutive relations can be approximated to the following relations for the beams with transverse motion in the x-z plane [34]:

$${\sigma }_{\mathit{xx}}-{\left(e_{0a}\right)}^2\frac{{\mathrm{d}}^2{\sigma }_{\mathit{xx}}}{\mathrm{d}{x}^2}=E{\epsilon }_{\mathit{xx}},{\sigma }_{\mathit{xz}}-{\left(e_{0a}\right)}^2\frac{{\mathrm{d}}^2{\sigma }_{\mathit{xz}}}{\mathrm{d}{x}^2}=G{\gamma }_{\mathit{xz}}.$$

(3)

In the above equation, E and G are the Young's and shear modulus, respectively. ε _xx is the axial strain and γ _xz stands for the shear strain. As can be seen from Equation (3), setting the nonlocal parameter e_0a equal to zero, we arrive at the constitutive relations of the local theories.

Thermal vibration of nonlocal DWNTs

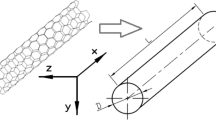
In the case of DWNTs, each of the tubes is considered as a beam model. The main point in the analysis is the consideration of vdW forces between the inner and outer tubes, that is, the pressure at any point between any two adjacent tubes depends on the difference of their deflections at that point. Figure 1 shows the model of a DWNT with length l, inner diameter d₁, and outer diameter d₂ embedded in an elastic medium with material constant k as described in the Winkler model [39, 40].

Figure 1

Model of an embedded double-walled carbon nanotube.

According to the Timoshenko beam theory, the axial and transverse displacement components can be written as below:

$$U\left(x,t\right)=u\left(x,t\right)-\mathit{z\theta }\left(x,t\right),W\left(x,t\right)=w\left(x,t\right)$$

(4)

in which u(x, t) and w(x, t) are the axial and transverse displacements of the mid-plane in the x and z directions, respectively; θ (x, t) is the cross-sectional rotation. At a distance z from the mid-plane, the strain–displacement relations can be written as follows:

$${\epsilon }_{\mathit{xx}}=\frac{\partial u}{\partial x}-z\frac{\partial \theta }{\partial x},{\gamma }_{\mathit{xz}}=-\theta +\frac{\partial w}{\partial x}.$$

(5)

The strain energy of the DWNT embedded in an elastic medium can be defined as

$$\begin{array}{l}V=\frac{1}{2}{\displaystyle {\int }_0^L{\displaystyle {\int }_{A_1}\left({\sigma }_{\mathit{xx}1}{\epsilon }_{\mathit{xx}1}+{\sigma }_{\mathit{xz}1}{\gamma }_{\mathit{xz}1}\right)\mathrm{d}{A}_1\mathrm{d}x}}\\ +\frac{1}{2}{\displaystyle {\int }_0^L{\displaystyle {\int }_{A_2}\left({\sigma }_{\mathit{xx}2}{\epsilon }_{\mathit{xx}2}+{\sigma }_{\mathit{xz}2}{\gamma }_{\mathit{xz}2}\right)\mathrm{d}{A}_2\mathrm{d}x}}+\frac{1}{2}k{\displaystyle {\int }_0^L{w}_2{2}^{}\mathrm{d}x}\\ -\frac{1}{2}{N}_{T1}{\displaystyle {\int }_0^L{w}_1{{\prime }^{}}^2\mathrm{d}x}-\frac{1}{2}{N}_{T2}{\displaystyle {\int }_0^L{w}_2{{\prime }^{}}^2\mathrm{d}x},\end{array}$$

(6)

where, A₁ and A₂ are the cross-sectional areas of the inner and outer tubes, respectively. The two last integrals in Equation (6) is the energy induced due to the compressive loads N _Ti (i = 1, 2) corresponding to a temperature rise ΔT. The thermal loads can be defined as

$$N_{\mathit{Ti}}=-\mathit{E\alpha }{A}_i\mathit{\Delta T},$$

(7)

in which α is the thermal expansion coefficient. The resultant force, moment, and the shear force are defined as

$$N_{\mathit{xi}}=\underset{A_i}{{\displaystyle \int }}{\sigma }_{\mathit{xxi}}\mathrm{d}{A}_i,M_{\mathit{xi}}=\underset{A_i}{{\displaystyle \int }}{\sigma }_{\mathit{xxi}}z\mathrm{d}{A}_i,Q_{\mathit{xi}}=\underset{A_i}{{\displaystyle \int }}{\sigma }_{\mathit{xzi}}\mathrm{d}{A}_i.$$

(8)

Substituting Equation (5) into Equation (6) and using Equation (8) gives

$$\begin{array}{l}V=\frac{1}{2}{\displaystyle {\int }_0^L\left\{N_{x1}\frac{\partial u_1}{\partial x}-M_{x1}\frac{\partial {\theta }_1}{\partial x}+Q_{x1}\left(-{\theta }_1+\frac{\partial w_1}{\partial x}\right)\right\}\mathrm{d}x}\\ +\frac{1}{2}{\displaystyle {\int }_0^L\left\{N_{x2}\frac{\partial u_2}{\partial x}-M_{x2}\frac{\partial {\theta }_2}{\partial x}+Q_{x2}\left(-{\theta }_2+\frac{\partial w_2}{\partial x}\right)\right\}\mathrm{d}x}\\ +\frac{1}{2}k{\displaystyle {\int }_0^L{w}_2{2}^{}\mathrm{d}x}-\frac{1}{2}{N}_{T1}{\displaystyle {\int }_0^L{w}_1{{\prime }^{}}^2\mathrm{d}x}-\frac{1}{2}{N}_{T2}{\displaystyle {\int }_0^L{w}_2{{\prime }^{}}^2\mathrm{d}x}.\end{array}$$

(9)

The work done by the vdW interaction forces can be written as

$${\Gamma }_c=\frac{1}{2}\underset{0}{\overset{L}{{\displaystyle \int }}}{f}_1{w}_1\mathrm{d}x+\frac{1}{2}\underset{0}{\overset{L}{{\displaystyle \int }}}{f}_2{w}_2\mathrm{d}x,$$

(10)

where

$$f_1=c_1\left(w_2-w_1\right),f_2=-c_1\left(w_2-w_1\right),$$

(11)

in which c₁ is the coefficient of the vdW force between inner and outer tubes defined as in [33]

$$c_1=\frac{320\times \left(2R_1\right)\mathrm{erg}/{\mathrm{cm}}^2}{0.16{△}^2},△=0.142\mathrm{nm}.$$

(12)

The kinetic energy of the DWNT is given by

$$\begin{array}{l}T=\frac{1}{2}{\displaystyle {\int }_0^L\left(\rho A_1{\left(\frac{\partial u_1}{\partial t}\right)}^2+\rho A_1{\left(\frac{\partial w_1}{\partial t}\right)}^2+\rho I_1{\left(\frac{\partial {\theta }_1}{\partial t}\right)}^2\right)\mathrm{d}x}\\ +\frac{1}{2}{\displaystyle {\int }_0^L\left(\rho A_2{\left(\frac{\partial u_2}{\partial t}\right)}^2+\rho A_2{\left(\frac{\partial w_2}{\partial t}\right)}^2+\rho I_2{\left(\frac{\partial {\theta }_2}{\partial t}\right)}^2\right)\mathrm{d}x},\end{array}$$

(13)

where I₁ and I₂ denote the second moment of area of the inner and outer tubes, respectively, and ρ is the mass density of the nanotubes. The governing equations of motion for the nonlocal DWNTs can be derived by applying Hamilton's principle as

$$\underset{0}{\overset{t}{{\displaystyle \int }}}\left(\mathit{\delta T}-\mathit{\delta V}+\delta {\Gamma }_c\right)\mathrm{d}t=0.$$

(14)

Substituting Equations (9), (10), and (13) into the above equation, using variation technique and setting the coefficients of δu _i , δw _i , and δθ _i equal to zero results into the following differential equations of motion for a DWNT

$$\frac{\partial N_{\mathit{xi}}}{\partial x}=\rho A_i\frac{{\partial }^2{u}_i}{\partial t^2},$$

(15a)

$$\frac{\partial Q_{\mathit{xi}}}{\partial x}-\mathit{mk}{w}_2-N_{\mathit{Ti}}\frac{{\partial }^2{w}_i}{\partial x^2}+f_i=\rho A_i\frac{{\partial }^2{w}_i}{\partial t^2},$$

(15b)

$$\frac{\partial M_{\mathit{xi}}}{\partial x}-Q_{\mathit{xi}}=\rho I_i\frac{{\partial }^2{\theta }_i}{\partial t^2},$$

(15c)

where m = 0 stands for i = 1, and m = 1 for i = 2. Using Equations (3), (5), (8), and (15), the resultant force, moment, and shear force of the nonlocal Timoshenko beam theory can be written as

$$N_{\mathit{xi}}-{\left(e_{0a}\right)}^2\frac{{\partial }^2{N}_{\mathit{xi}}}{\partial x^2}=E{A}_i\frac{\partial u_i}{\partial x},$$

(16a)

$$M_{\mathit{xi}}-{\left(e_{0a}\right)}^2\frac{{\partial }^2{M}_{\mathit{xi}}}{\partial x^2}=-E{I}_i\frac{\partial {\theta }_i}{\partial x},$$

(16b)

$$Q_{\mathit{xi}}-{\left(e_{0a}\right)}^2\frac{{\partial }^2{Q}_{\mathit{xi}}}{\partial x^2}=k_{\mathit{si}}G{A}_i\left(-{\theta }_i+\frac{\partial w_i}{\partial x}\right),$$

(16c)

where k _si (i = 1, 2) is the shear correction factor of the tubes. Substituting Equation (16) into Equation (15) gives the expressions for the nonlocal resultant force, moment, and shear force as follows

$$N_{\mathit{xi}}=E{A}_i\frac{\partial u_i}{\partial x}+\rho A_i{\left(e_{0a}\right)}^2\frac{{\partial }^3{u}_i}{\partial x\partial t^2},$$

(17a)

$$\begin{array}{l}{M}_{\mathit{xi}}=-E{I}_i\frac{\partial {\theta }_i}{\partial x}\\ +{\left(e_{0a}\right)}^2\left(\rho I_i\frac{{\partial }^3{\theta }_i}{\partial x\partial t^2}+\rho A_i\frac{{\partial }^2{w}_i}{\partial t^2}+\mathit{mk}{w}_2+N_{\mathit{Ti}}\frac{{\partial }^2{w}_i}{\partial x^2}-f_i\right)\end{array}$$

(17b)

$$\begin{array}{l}{Q}_{\mathit{xi}}=k_{\mathit{si}}G{A}_i\left(-{\theta }_i+\frac{\partial w_i}{\partial x}\right)\\ +{\left(e_{0a}\right)}^2\left(\rho A_i\frac{{\partial }^3{w}_i}{\partial x\partial t^2}+\mathit{mk}\frac{\partial w_2}{\partial x}+N_{\mathit{Ti}}\frac{{\partial }^3{w}_i}{\partial x^3}-\frac{\partial f_i}{\partial x}\right),\end{array}$$

(17c)

with f _i = (−1)^{i + 1}c₁(w₂ − w₁). Finally, by substituting Equation (17) into the differential equations of motion of (15), we arrive at the following set of coupled differential equations of motion for nonlocal DWNTs

$$E{A}_i\frac{{\partial }^2{u}_i}{\partial x^2}=\rho A_i\frac{{\partial }^2}{\partial t^2}\left[u_i-{\left(e_{0a}\right)}^2\frac{{\partial }^2{u}_i}{\partial x^2}\right],$$

(18a)

$$\begin{array}{l}{k}_{\mathit{si}}G{A}_i\left(\frac{{\partial }^2{w}_i}{\partial x^2}-\frac{\partial {\theta }_i}{\partial x}\right)-\mathit{mk}\left(w_2-{\left(e_{0a}\right)}^2\frac{{\partial }^2{w}_2}{\partial x^2}\right)\\ -N_{\mathit{Ti}}\left(\frac{{\partial }^2{w}_i}{\partial x^2}-{\left(e_{0a}\right)}^2\frac{{\partial }^4{w}_i}{\partial x^4}\right)+{\left(-1\right)}^{i+1}{c}_1\\ \times \left[\left(w_2-w_1\right)-{\left(e_{0a}\right)}^2\left(\frac{{\partial }^2{w}_2}{\partial x^2}-\frac{{\partial }^2{w}_1}{\partial x^2}\right)\right]\\ =\rho A_i\frac{{\partial }^2}{\partial t^2}\left[w_i-{\left(e_{0a}\right)}^2\frac{{\partial }^2{w}_i}{\partial x^2}\right],\end{array}$$

(18b)

$$\begin{array}{l}-E{I}_i\frac{{\partial }^2{\theta }_i}{\partial x^2}-k_{\mathit{si}}G{A}_i\left(\frac{\partial w_i}{\partial x}-{\theta }_i\right)\\ =\rho I_i\frac{{\partial }^2}{\partial t^2}\left[{\theta }_i-{\left(e_{0a}\right)}^2\frac{{\partial }^2{\theta }_i}{\partial x^2}\right].\end{array}$$

(18c)

Finite element formulation for the vibrations of DWNTs

Assume that each layer has a periodic motion. Therefore, the displacement fields of the i th layer can be expressed in the following form

$$\begin{array}{l}{u}_{\left(i\right)}(x,t)=u_{\left(i\right)}\left(x\right)e^{j\omega t},\\ w_{\left(i\right)}(x,t)=w_{\left(i\right)}\left(x\right)e^{j\omega t},i=1,2\\ {\theta }_{\left(i\right)}(x,t)={\theta }_{\left(i\right)}\left(x\right)e^{j\omega t}\end{array}$$

(19)

in which w denotes the natural frequencies of DWNT and

$$\begin{array}{l}{u}_{\left(i\right)}\left(x\right)=N_1{u}_{1\left(i\right)}+N_2{u}_{2\left(i\right)},\\ w_{\left(i\right)}\left(x\right)=N_3{w}_{1\left(i\right)}+N_4{\theta }_{1\left(i\right)}+N_5{w}_{2\left(i\right)}+N_6{\theta }_{2\left(i\right)},\\ {\theta }_{\left(i\right)}\left(x\right)=N_7{w}_{1\left(i\right)}+N_8{\theta }_{1\left(i\right)}+N_9{w}_{2\left(i\right)}+N_{10}{\theta }_{2\left(i\right)}\end{array}$$

(20)

here N _k (k = 1,⋯,10) are the statically exact shape functions for axial, transverse, and rotational degrees of freedom, respectively, and are given as [41]

$$\begin{array}{l}{N}_1=1-\frac{x}{L},\\ N_2=\frac{x}{L},\\ N_3=1-\frac{12x}{L\left(12+\eta L^2\right)}-\frac{3\eta x^2}{\left(12+\eta L^2\right)}+\frac{2\eta x^3}{L\left(12+\eta L^2\right)},\\ N_4=\frac{\left(\eta L^2+6\right)x}{\left(12+\eta L^2\right)}-\frac{\left(6+2\eta L^2\right)x^2}{L\left(12+\eta L^2\right)}+\frac{\eta }{6}\left(1-\frac{\left(\eta L^3+6L\right)}{L\left(12+\eta L^2\right)}\right)x^3,\\ N_5=\frac{12x}{L\left(12+\eta L^2\right)}+\frac{3\eta x^2}{\left(12+\eta L^2\right)}-\frac{2\eta x^3}{L\left(12+\eta L^2\right)},\\ N_6=-\frac{6x}{\left(12+\eta L^2\right)}-\frac{\left(\eta L^2-6\right)x^2}{L\left(12+\eta L^2\right)}+\frac{\eta x^3}{\left(12+\eta L^2\right)},\\ N_7=-\frac{6\eta x}{\left(12+\eta L^2\right)}+\frac{6\eta x^2}{L\left(12+\eta L^2\right)},\\ N_8=1-\frac{2\left(2\eta L^2+6\right)x}{L\left(12+\eta L^2\right)}+\frac{\eta }{2}\left(1-\frac{\left(\eta L^3+6L\right)}{L\left(12+\eta L^2\right)}\right)x^2,\\ N_9=\frac{6\eta x}{\left(12+\eta L^2\right)}-\frac{6\eta x^2}{L\left(12+\eta L^2\right)},\\ N_{10}=-\frac{2\left(\eta L^2-6\right)x}{L\left(12+\eta L^2\right)}+\frac{3\eta x^2}{\left(12+\eta L^2\right)}\end{array}$$

(21)

wherein η = GA/EI, where G is the shear modulus. Substituting Equation (19) into Equation (18) and applying the Galerkin method, one would have a set of discretized equations which can be written in the matrix form as

$$\left({\left[\mathbf{K}\right]}^e-{\omega }^2{\left[\mathbf{M}\right]}^e\right){\left\{\delta \right\}}^e=0,$$

(22)

where superscript e stands for an element. Assembling the element matrices into the global matrix yields

$$\left(\left[\mathbf{K}\right]-{\omega }^2\left[\mathbf{M}\right]\right)\left\{\delta \right\}=0,$$

(23)

where K and M are the global stiffness and mass matrices, and ω is the natural frequency to be defined.

Results and discussion

Consider a DWNT with an inner diameter d₁ = 2R₁ = 0.7 nm and an outer diameter d₂ = 2R₂ = 1.4 nm, where R₁ and R₂ denote the radius of the inner and outer tube centerline, respectively. Both tubes have Young's modulus of E = 1TPa, Poisson's ratio υ = 0.25, effective thickness h = 0.35 nm, mass density ρ = 2,300 kg/m³, and the shear correction factors for tubes are k_{s 1} = 0.75 and k_{s 2} = 0.64. For the present DWNT with R₁ = 0.35 nm, Equation (12) gives the vdW coefficient as c 1 = 0.06943TPa. Table 1 lists the dimensionless frequencies $\Omega =\sqrt[4]{{\omega }^2\mathit{\rho A}{L}^4/\left(\mathit{EI}\right)}$ of DWNTs in which A = A₁ + A₂ and I = I₁ + I₂. The boundary conditions considered in the present analysis include combinations of simply supported (S) and clamped (C) end conditions. A number of 30 elements for each tube are used in the following numerical evaluations. As can be seen from Table 1, the present results match very well with those obtained by Wang et al. [31]. Table 2 illustrates a comparison of the dimensionless frequencies of local and nonlocal DWNTs for different boundary conditions (L/d₂ = 10, k = 10⁷ N/m²). It is found that the difference between the local and nonlocal theories tends to increase as μ increases. As would be observed, an excellent agreement is achieved with those via DQM [34]. Table 3 shows the influence of spring constant k on the fundamental frequencies of nonlocal DWNTs with various boundary conditions (L/d₂ = 10, μ = 0.1). The significant dependency of this oscillation to the surrounding elastic medium is observed. The vibration frequencies of nanotubes rise rapidly with an increment in the stiffness of the medium. Once again, a good agreement has been achieved with those evaluated via DQM [34]. Figure 2 illustrates the variation of the nonlocal to the local frequency ratio over the nonlocal parameter of a SS DWNT for different length to the outer diameter ratios. It is shown clearly that the influence of small-scale effect is more significant for higher length to the outer diameter ratios. Figure 3 is a similar figure for DWNT with CC end conditions. Figure 4 examines the effect of the nonlocal parameter on the first four modes of SS nonlocal DWNT which shows the obvious dependency of higher modes to the nonlocal effect.

Table 1 Frequency parameters of DWNTs with different end conditions ( k = 0, e _{0 a} = 0)

Table 2 Dimensionless fundamental frequencies for different nonlocal parameters ( L / d ₂ = 10, k = 10 ⁷ N/m ² )

Table 3 Dimensionless linear fundamental frequencies for different nonlocal parameters ( L / d ₂ = 10, μ = 0.1)

Figure 2

Effect of the nonlocal parameter on the fundamental frequencies of SS nonlocal DWNT.

Figure 3

Effect of the nonlocal parameter on the fundamental frequencies of CC nonlocal DWNT.

Figure 4

Effect of the nonlocal parameter on the first four modes of SS nonlocal DWNT ( L / d ₂ = 10).

Since no literature results readily available to the authors' knowledge, we now investigate the problem of free vibrations of a nonlocal DWNT with different boundary conditions of inner and outer tubes. The material and geometrical parameters are taken from [23], the coefficient of vdW force c₁ is taken as 0.711 × 10¹² N/m²_, and the other parameters are the same as used before. The first three frequencies of a DWNT with SS inner tube and CC outer tube for various lengths to the outer diameter ratios are listed in Table 4. This table presents new results of the nonlocal effect on the vibration frequencies of DWNT with different boundary conditions between the tubes which can be used as a benchmark for further studies. The obtained results are compared with those presented based upon the Euler-Bernoulli beam theory in [23] and admit a remarkable accuracy. As can be seen, the results given by [23] overestimate the frequencies. Also, with the increment of the length to the diameter of the nanotubes, the linear vibration frequencies decrease.

Table 4 Benchmark for the resonant frequencies (THz) of a DWNT with a simple inner tube and clamped outer tube with various length to the outer diameter ratios ( k = 0)

The influence of temperature change on the vibration characteristics of nonlocal DWNTs is discussed. For the case of high temperature, we set α = 1.1 × 10⁻⁶ K⁻¹, while for the case of low or room temperature, this value reads as α = −1.6 × 10⁻⁶ K⁻¹[42]. Figure 5 clarifies the effect of temperature changes on the fundamental frequencies of a DWNT with SS inner tube and CC outer tube against the small scale factor for the case of high temperature (L/d₂ = 50). Figure 6 is a similar plot for the case of low or room temperature. It can be concluded that at low or room temperature, the vibration frequencies for the nanotube including the thermal effect are larger than those excluding the thermal effect and increase with the increase of temperature, while at high temperatures, the trend becomes reverse and the vibration frequencies decrease with increasing temperature.

Figure 5

Effect of temperature changes on the fundamental frequencies of a DWNT for high temperatures ( L / d ₂ = 50).

Figure 6

Effect of temperature changes on the fundamental frequencies of a DWNT for low temperatures ( L / d ₂ = 50).

Conclusions

On the basis of Eringen's nonlocal elasticity theory and Timoshenko beam theory, the free vibration characteristics of embedded double-walled carbon nanotubes with arbitrary end conditions are investigated in thermal environments. Theoretical formulations include the small scale effect and take the effects of transverse shear deformation and rotary inertia into account. A multiple-elastic beam model is used, in which equations of motion are coupled with the aid of the van der Waals interlayer interactions between neighbor layers. The finite element method is employed to obtain the vibration frequencies of DWNT with arbitrary end conditions. The results obtained have been compared with those available in the open literature, and excellent correlation has been achieved. The significant dependency of this oscillation to the surrounding elastic medium, length to the outer diameter ratio, and the small-scale effect is observed. The vibration frequencies of nanotubes rise rapidly with increasing medium stiffness. Results obtained show that an increase in the nonlocal parameter results into smaller frequencies. The ratio of the nonlocal frequency to the local frequency increases with an increase in the length, and decreases with an increment in the vibrational mode number of the DWNTs.

The finite element formulation applied here is general and can be readily extended to DWNTs with different boundary conditions between inner and outer tubes. In this regard, the effect of the nonlocal parameter on the vibration frequencies of a DWNT with different boundary conditions of each tube has been examined in our analysis, and some novel numerical results are presented perhaps for the first time. These results can be used as a benchmark for future works in this field of study.

Furthermore, the influence of temperature change on the vibrational behavior of DWNTs is discussed. As a result, the thermal effect on the natural frequency is related to the temperature changes. It has been shown that at low or room temperature, the presence of temperature change increases the natural frequencies, while at high temperatures, the natural frequencies decrease with increasing temperature.