A study of nonlocal problems of impulsive integrodifferential equations with measure of noncompactness

Abstract

In this paper, we show the existence of mild solutions to a nonlocal problem of impulsive integrodifferential equations via a measure of noncompactness in a Banach space. Our work is based on a new fixed point theorem and it generalizes some existing results on the topic in the sense that we do not require the semigroup and nonlinearity involved in the problem to be compact.

1 Introduction

In this paper, we discuss the existence of solutions for the following nonlocal problem of integrodifferential equations:

$$\begin{array}{l}\frac{du(t)}{dt}=Au(t)+f(t,u(t),Gu(t)),t\in [0,K],t\ne t_i,\\ u(0)=u_0+g(u),\\ \mathrm{\Delta }u(t_i)=I_i(u(t_i)),i=1,2,3,\dots ,p,\end{array}$$

(1.1)

where A generates a $C_0$-semigroup $T(t)$, $t\ge 0$, in a Banach space X, $f:[0,K]\times X\times X\to X$, $Gu(t)={\int }_0^{t}H(t,s)u(s)ds$, $H\in C[D,R^{+}]$, $D=\{(t,s)\in R^2:0\le s\le t\le K\}$, $0<t_1<t_2<t_3<\cdots <t_p<K$ with $t_{p+1}=K$, $g:X\to X$, $u_0\in X$, and $\mathrm{\Delta }u(t_i)=u(t_i^{+})-u(t_i^{-})$ with $u(t_i^{+})$, $u(t_i^{-})$ representing the right and left limit of u at $t_i$, respectively. Here $PC([0,K];X)$ = {$u:[0,K]\to X$ is continuous at $t\ne t_i$, left continuous at $t=t_i$, and the right-hand limit $u(t_i^{+})$ exists for $i=1,2,\dots ,p$}. Notice that the set $PC([0,K];X)$ equipped with the norm $\parallel u\parallel =sup\{\parallel u(t)\parallel :t\in [0,K]\}$ is a Banach space.

Integrodifferential equations arise in the mathematical modeling of several natural phenomena and various investigations led to the exploration of their different aspects. The theory of semigroups of bounded linear operators is closely related to the solution of differential and integrodifferential equations in Banach spaces. In recent years, this theory has been applied to a large class of nonlinear differential equations in Banach spaces. Based on the method of semigroups, the existence and uniqueness of mild, strong and classical solutions of semilinear evolution equations were discussed by Pazy [1]. For further details, see [2–5] and the references cited therein.

The theory of impulsive differential equations is an important branch of differential equations and has an extensive physical background. Impulsive differential equations help modeling many physical systems whose states are subject to abrupt changes at certain moments. Examples include population biology, the diffusion of chemicals, the spread of heat, the radiation of electromagnetic waves, etc. [6–9]. Dynamical systems with impulsive effects have been an object of intensive investigations [10–12]. The study of semilinear nonlocal initial problem was initiated by Byszewski [13, 14] and the importance of the problem lies in the fact that it is more general and yields better effect than the classical initial conditions. Therefore, it has been extensively studied under various conditions on the operator A and the nonlinearity f by several authors [15–17].

Byszewski and Lakshmikantham [18] showed the existence and uniqueness of mild solutions and classical solutions when f and g in (1.1) satisfy Lipschitz type conditions. Ntouyas and Tsamotas [19, 20] studied the case of compact-valued f and T. Zhu et al. [21] discussed the existence of mild solutions for abstract semilinear evolution equations in Banach spaces. In [11], the author discussed the existence and uniqueness of mild and classical solutions for the impulsive semilinear differential evolution equation. In [22], Agarwal et al. studied the existence and dimension of the set of mild solutions to semilinear fractional differential inclusions. Lizama and Pozo [23] investigated the existence of mild solutions for semilinear integrodifferential equation with nonlocal initial conditions by using Hausdorff measure of noncompactness via a fixed-point. In a recent paper [24], the authors studied the existence of mild solutions to an impulsive differential equation with nonlocal conditions by applying Darbo-Sadovskii’s fixed point theorem. For some more recent results and details, see [25–37].

Motivated by [23], in this paper we aim to establish some existence results for mild solutions of (1.1) without demanding the compactness condition on T and f. In this scenario, our work extends and improves some results obtained in [38, 39]. In Section 2, we recall some definitions and facts about $C_0$ semigroup T and the measure of noncompactness, while Section 3 deals with the existence of mild solutions for (1.1).

2 Preliminary result

Let $L^1([0,K];X)$ denote the space of X-valued Bochner functions on $[0,K]$ with the norm defined by $\parallel u\parallel ={\int }_0^K\parallel u(s)\parallel ds$. A $C_0$-semigroup $T(t)$ is said to be compact if $T(t)$ is compact for any $t>0$. If the semigroup $T(t)$ is compact, then $t\to T(t)u$ are equicontinuous at all $t>0$ with respect to u in all bounded subset of X, that is, the semigroup $T(t)$ is equicontinuous.

In this paper, α denotes the Hausdorff measure of noncompactness on both X and $PC([0,K];X)$. The following lemma describes some properties of the Hausdorff measure of noncompactness.

Lemma 2.1 [40]

Let ${\beta }_{\mathbb{Y}}$ and ${\beta }_{\mathbb{Z}}$ denote Hausdorff measures of noncompactness on the real Banach spaces 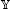and ℤ, respectively, and $B,C\subseteq \mathbb{Y}$ be bounded. Then

• 1. B is pre-compact if and only if ${\beta }_{\mathbb{X}}(B)=0$;

• 2. ${\beta }_{\mathbb{Y}}(B)={\beta }_{\mathbb{Y}}(\overline{B})={\beta }_{\mathbb{Y}}(convB)$, where $\overline{B}$ and convB mean the closure and convex hull of B, respectively;

• 3. ${\beta }_{\mathbb{Y}}(B)\le {\beta }_{\mathbb{Y}}(C)$, where $B\subseteq C$;

• 4. ${\beta }_{\mathbb{Y}}(B+C)\le {\beta }_{\mathbb{Y}}(B)+{\beta }_{\mathbb{Y}}(C)$, where $B+C=\{x+y:x\in B,y\in C\}$;

• 5. ${\beta }_{\mathbb{Y}}(B\cup C)\le max\{{\beta }_{\mathbb{Y}}(B),{\beta }_{\mathbb{Y}}(C)\}$;

• 6. ${\beta }_{\mathbb{Y}}(\lambda B)\le |\lambda |{\beta }_{\mathbb{Y}}(B)$ for any $\lambda \in \mathbb{R}$;

• 7. If the map $Q:D(Q)\subseteq \mathbb{Y}\to \mathbb{Z}$ is Lipschitz continuous with constant k, then ${\beta }_{\mathbb{Z}}(QB)\le k{\beta }_{\mathbb{Y}}(B)$ for any bounded subset $B\subseteq D(Q)$;

• 8. ${\beta }_{\mathbb{Y}}(B)=inf\{d_{\mathbb{Y}}(B,C);C\subseteq \mathbb{Y}\mathit{\text{is precompact}}\}=inf\{d_{\mathbb{Y}}(B,C);C\subseteq \mathbb{Y}\mathit{\text{is finite valued}}\}$, where $d_{\mathbb{Y}}(B,C)$ means the nonsymmetric (or symmetric) Hausdorff distance between B and C in ;

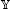• 9. If ${\{W_n\}}_{n=1}^{+\mathrm{\infty }}$ is a decreasing sequence of bounded closed nonempty subsets of 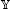and ${lim}_{n\to \mathrm{\infty }}{\beta }_{\mathbb{Y}}(W_n)=0$, then ${\bigcap }_{n=1}^{+\mathrm{\infty }}{W}_n$ is nonempty and compact in .

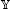The map $Q:W\subseteq \mathbb{Y}\to \mathbb{Y}$ is said to be a ${\beta }_{\mathbb{Y}}$-contraction if there exists a constant $0<k<1$ such that ${\beta }_{\mathbb{Y}}(Q(B))\le k{\beta }_{\mathbb{Y}}(B)$ for any bounded closed subset $B\subs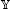eteq W$, where is a Banach space.

In the sequel, we need the following known results.

Lemma 2.2 [40]

If $W\subseteq PC([0,K];X)$ is bounded, then $\alpha (W(t))\le \alpha (W)$ for all $t\in [0,K]$, where $W(t)=\{u(t):u\in W\}\subseteq X$. Furthermore, if W is equicontinuous on $[0,K]$, then $\alpha (W(t))$ is continuous on $[0,K]$, and $\alpha (W)=sup\{\alpha (W(t)):t\in [0,K]\}$.

Lemma 2.3 [41]

If ${\{u_n\}}_{n=1}^{\mathrm{\infty }}\subset L^1(0,K;X)$ is uniformly integrable, then $\alpha ({\{u_n(t)\}}_{n=1}^{\mathrm{\infty }})$ is measurable and

$$\alpha \left({\{{\int }_0^t{u}_n(s)ds\}}_{n=1}^{\mathrm{\infty }}\right)\le 2{\int }_0^t\alpha {\{u_n(s)\}}_{n=1}^{\mathrm{\infty }}ds.$$

Lemma 2.4 [39]

If the semigroup $T(t)$ is equicontinuous and there exists $\eta \in L^1(0,K;R^{+})$, then the set

$$\{t\to {\int }_0^{t}T(t-s)u(s)ds;u\in L^1(0,K;R^{+}),\parallel u(s)\parallel \le \eta (s),\mathit{\text{for a.e}}s\in [0,K]\}$$

is equicontinuous on $[0,K]$.

Lemma 2.5 [42]

If W is bounded, then for each $\epsilon >0$, there is a sequence ${\{u_n\}}_{n=1}^{\mathrm{\infty }}\subseteq W$ such that $\alpha (W)\le 2\alpha ({\{u_n\}}_{n=1}^{\mathrm{\infty }})+\epsilon$.

Lemma 2.6 [43]

Suppose that $0<\epsilon <1$, $h>0$ and let

$$S={\epsilon }^n+C_n^1{\epsilon }^{n-1}h+C_n^2{\epsilon }^{n-2}\frac{h^2}{2!}+\cdots +\frac{h^n}{n!},n\in N.$$

Then $S=o(1/n^s)$ ($n\to +\mathrm{\infty }$), where $s>1$ is an arbitrary real number and $C_n^1,C_n^2,\dots$ are binomial coefficients [44].

Lemma 2.7 ([45] Fixed point theorem)

Let Q be a closed and convex subset of a real Banach space X, let $A:Q\to Q$ be a continuous operator and $A(Q)$ be bounded. For each bounded subset $B\subset Q$, set

$$A^1(B)=A(B),A^n(B)=A\left(\overline{co}(A^{n-1}(B))\right),n=2,3,\dots .$$

If there exist a constant $0\le k\le 1$ and a positive integer $n_0$ such that for each bounded subset $B\subset Q$, $\alpha (A^{n_0}(B))\le k\alpha (B)$, then A has a fixed point in Q.

Definition 2.8 A function $u:[0,K]\to X$ is called a mild solution of system (1.1) if $u\in PC([0,K]:X)$ and satisfies the following equation:

$$u(t)=\{\begin{array}{c}T(t)[u_0-g(u)]+{\int }_0^{t}T(t-s)f(s,u(s),Gu(s))ds,t\in [0,t_1];\hfill \\ T(t-t_1)(u(t_1^{-})+I_1(u(t_1^{-})))+{\int }_{t_1}^{t}T(t-s)f(s,u(s),Gu(s))ds,t\in (t_1,t_2];\hfill \\ ⋮\hfill \\ T(t-t_p)(u(t_p^{-})+I_p(u(t_p^{-})))+{\int }_{t_p}^{t}T(t-s)f(s,u(s),Gu(s))ds,t\in (t_p,K].\hfill \end{array}$$

3 Existence result

In this section, we show the existence of solutions for problem (1.1) by applying Lemma 2.7.

For some real constants r and w, we define

$$W=\{u\in PC([0,K];X),\parallel u(t)\parallel \le r,\parallel Gu(t)\parallel \le w,\mathrm{\forall }t\in [0,K]\}.$$

(3.1)

For the forthcoming analysis, we need the following assumptions:

(${\mathrm{A}}_1$) The $c_0$ semigroup $T(t)$ generated by A is equicontinuous and $N=sup\{\parallel T(t)\parallel ;t\in [0,K]\}$;

(${\mathrm{A}}_2$) $g:X\to X$ is such that there exist positive constants c and d such that $\parallel g(u)\parallel \le c\parallel u\parallel +d$, for all $u\in PC([0,K];X)$;

(${\mathrm{A}}_3$) $f:[0,K]\times X\times X\to X$ is of Caratheódory type, that is, $f(\cdot ,u,Gu)$ is measurable for all $u\in X$, and $f(t,\cdot ,\cdot )$ is continuous for a.e. $t\in [0,K]$;

(${\mathrm{A}}_4$) there exist a function $m\in L^1(0,K;R^{+})$ and a nondecreasing continuous function $\mathrm{\Omega }:R^{+}\to R^{+}$ such that $\parallel f(t,u,(Gu))\parallel \le m(t)\mathrm{\Omega }(\parallel u\parallel ,\parallel Gu\parallel )$ for all $u\in X$ a.e. $t\in [0,K]$;

(${\mathrm{A}}_5$) there exist $L,L_1\in L^1(0,K;R^{+})$ such that for any bounded sets $D_1,D_2\subset X$,

$$\alpha (f(t,D_1,D_2))\le L(t)\alpha (D_1)+L_1(t)\alpha (D_2)$$

for a.e. $t\in [0,K]$;

(${\mathrm{A}}_6$) The functions $I_k:X\to X$, $k=1,2,\dots ,p$, are completely continuous and uniformly bounded, and ${max}_{1\le k\le p,u\in W}\parallel I_k(u)\parallel =\mathrm{\Lambda }$;

(${\mathrm{A}}_7$) there exists a positive constant γ such that

$$N[\parallel u_0\parallel +(cr+d)+\mathrm{\Lambda }]+N\mathrm{\Omega }(r,w){\int }_0^{K}m(s)ds\le \gamma ,$$

where N, c, d, Ω, Λ are given by assumptions (${\mathrm{A}}_1$), (${\mathrm{A}}_2$), (${\mathrm{A}}_4$), (${\mathrm{A}}_6$).

In passing, we remark that

• (i) If A is the generator of an analytic semigroup $T(t)$ or a differentiable semigroup $T(t)$, then $T(t)$ is an equicontinuous $c_0$-semigroup [1].

• (ii) If $\parallel f(t,u_1,u_2)-f(t,v_1,v_2)\parallel \le L\parallel u_1-v_1\parallel +L_1\parallel u_2-v_2\parallel$, $t\in [0,K]$, $u_1,u_2,v_1,v_2\in X$, then $\alpha (f(t,D_1,D_2))\le L(t)\alpha (D_1)+L_1(t)\alpha (D_2)$ for any bounded sets $D_1,D_2\subset X$ and a.e. $t\in [0,K]$.

Theorem 3.1 Assume that conditions (${\mathrm{A}}_1$)-(${\mathrm{A}}_7$) hold. Then there exists at least one mild solution for problem (1.1).

Proof Let us define an operator $Q:PC([0,K];X)\to PC([0,K];X)$ by

$$Qu(t)=\{\begin{array}{c}T(t)[u_0-g(u)]+{\int }_0^{t}T(t-s)f(s,u(s),Gu(s))ds,t\in [0,t_1];\hfill \\ T(t-t_1)(u(t_1^{-})+I_1(u(t_1^{-})))\hfill \\ +{\int }_{t_1}^{t}T(t-s)f(s,u(s),Gu(s))ds,t\in (t_1,t_2];\hfill \\ ⋮\hfill \\ T(t-t_p)(u(t_p^{-})+I_p(u(t_p^{-})))\hfill \\ +{\int }_{t_p}^{t}T(t-s)f(s,u(s),Gu(s))ds,t\in (t_p,K]\hfill \end{array}$$

(3.2)

for all $u\in PC([0,K];X)$ and show that the operator Q satisfies the hypothesis of Lemma 2.7. The proof consists of several steps.

• (i) Q is continuous. Let $(u_n)$be a sequence in $PC([0,K];X)$ such that $u_n\to u$ in $PC([0,K];X)$. Then, in view of (${\mathrm{A}}_3$), it follows that $f(s,u_n(s),G{u}_n(s))\to f(s,u(s),Gu(s))$ as $n\to \mathrm{\infty }$. Now, for small $\epsilon >0$ and $n\to \mathrm{\infty }$, we have

  $$\begin{array}{l}\parallel Q{u}_n(t)-Qu(t)\parallel \le N{\int }_0^{t_1}\parallel f(s,u_n(s),G{u}_n(s))\parallel -\parallel f(s,u(s),Gu(s))\parallel ds\\ \phantom{\parallel Q{u}_n(t)-Qu(t)\parallel }\le \epsilon N,\mathrm{\forall }t\in [0,t_1],\end{array}$$

  (3.3)

$$\begin{array}{l}\parallel Q{u}_n(t)-Qu(t)\parallel \le N[\parallel u_n\left(t_i^{-}\right)-u\left(t_i^{-}\right)\parallel \\ \phantom{\parallel Q{u}_n(t)-Qu(t)\parallel \le }+\parallel I_i\left(u_n\left(t_i^{-}\right)\right)-I_i\left(u\left(t_i^{-}\right)\right)\parallel ]+\epsilon N,\mathrm{\forall }t\in (t_i,t_{i+1}],\end{array}$$

(3.4)

for $i=1,2,\dots ,p$. By assumption (${\mathrm{A}}_6$) together with (3.3)-(3.4), we obtain

$$\underset{n\to \mathrm{\infty }}{lim}{\parallel Q{u}_n-Qu\parallel }_{PC}=0.$$

Thus, $W\subseteq PC([0,K];X)$ is bounded and convex (W is defined by (3.1)).

For any $u\in W$, $t\in [0,t_1]$, we have

$$\begin{array}{rcl}\parallel (Qu)(t)\parallel & \le & \parallel T(t)[u_0-g(u)]\parallel +{\int }_0^{t_1}\parallel T(t-s)f(s,u(s),Gu(s))\parallel ds\\ \le & N[\parallel u_0\parallel +(c\parallel u\parallel +d)]+N\mathrm{\Omega }(r,w){\int }_0^{t_1}m(s)ds\\ \le & N[\parallel u_0\parallel +(cr+d)]+N\mathrm{\Omega }(r,w){\int }_0^{t_1}m(s)ds.\end{array}$$

(3.5)

Similarly, for any $u\in W$ and $i=1,2,\dots ,p$, we get

$$\parallel (Qu)(t)\parallel \le N[\parallel u_0\parallel +(cr+d)+\mathrm{\Lambda }]+N\mathrm{\Omega }(r,w){\int }_0^{K}m(s)ds,t\in (t_i,t_{i+1}].$$

(3.6)

Using (3.5)-(3.6) and (${\mathrm{A}}_6$)-(${\mathrm{A}}_7$), we obtain

$$\parallel (Qu)(t)\parallel \le N[\parallel u_0\parallel +(cr+d)+\mathrm{\Lambda }]+N\mathrm{\Omega }(r,w){\int }_0^{K}m(s)ds\le \gamma ,t\in [0,K],$$

which implies that $Q:W\to W$ is a bounded operator.

• (ii) $Q(W)$ is equicontinuous, where W is defined by (3.1). For all $s_1,s_2\in [0,t_1]$ and for each $Q\in W(u)$, we have by Lemma 2.4 that

  $$\begin{array}{l}\parallel (Qu)(s_2)-(Qu)(s_1)\parallel \\ \le \parallel T(s_2)-T(s_1)\parallel \parallel u_0-g(u)\parallel +\parallel {\int }_0^{s_2}T(s_2-s)f(s,u(s),Gu(s))ds\\ -{\int }_0^{s_1}T(s_1-s)f(s,u(s),Gu(s))ds\parallel \\ \le \parallel T(s_2)-T(s_1)\parallel \parallel u_0-g(u)\parallel +{\int }_0^{s_1}\parallel T(s_2-s)-T(s_1-s)\parallel m(s)\mathrm{\Omega }(r,w)ds\\ +{\int }_{s_1}^{s_2}\parallel T(s_2-s)\parallel m(s)\mathrm{\Omega }(r,w)ds\\ \le \parallel T(s_2)-T(s_1)\parallel [\parallel u_0\parallel +(cr+d)]\\ +{\int }_0^{s_1}\parallel T(s_2-s)-T(s_1-s)\parallel m(s)\mathrm{\Omega }(r,w)ds\\ +{\int }_{s_1}^{s_2}\parallel T(s_2-s)\parallel m(s)\mathrm{\Omega }(r,w)ds.\end{array}$$

  (3.7)

Similarly, for all $s_1,s_2\in (t_i,t_{i+1}]$, with $s_1<s_2$, $i=1,2,\dots ,p$, we get

$$\begin{array}{l}\parallel (Qu)(s_2)-(Qu)(s_1)\parallel \\ \le \parallel T(s_2)-T(s_1)\parallel [\parallel u_0\parallel +(cr+d)+\mathrm{\Lambda }]\\ +{\int }_0^{s_1}\parallel T(s_2-s)-T(s_1-s)\parallel m(s)\mathrm{\Omega }(r,w)ds\\ +{\int }_{s_1}^{s_2}\parallel T(s_2-s)\parallel m(s)\mathrm{\Omega }(r,w)ds.\end{array}$$

(3.8)

Thus, from inequalities (3.7) and (3.8), we obtain

$$\underset{s_1\to s_2}{lim}\parallel (Qu)(s_2)-(Qu)(s_1)\parallel =0.$$

So, $Q(W)$ is equicontinuous.

Let $B_0=\overline{co}(Q(W))$. For any $B\subset B_0$ and $\epsilon >0$, we know from Lemma 2.5 that there is a sequence ${\{u_n\}}_{n=1}^{\mathrm{\infty }}\subset B$ such that

$$\begin{array}{rcl}\alpha (Q^{1}B(t))& =& \alpha (QB(t))\\ \le & 2\alpha ({\int }_0^{t}T(t-s)f(s,{\{u_n(s)\}}_{n=1}^{\mathrm{\infty }},\left(G{\{u_n(s)\}}_{n=1}^{\mathrm{\infty }}\right)))ds+\epsilon \\ \le & 4{\int }_0^t\alpha (T(t-s)f(s,{\{u_n(s)\}}_{n=1}^{\mathrm{\infty }},\left(G{\{u_n(s)\}}_{n=1}^{\mathrm{\infty }}\right)))ds+\epsilon \\ \le & 4N{\int }_0^t(L(s)\alpha {\{u_n(s)\}}_{n=1}^{\mathrm{\infty }}+k{L}_1(s)\alpha {\{u_n(s)\}}_{n=1}^{\mathrm{\infty }})ds+\epsilon \\ \le & 4N(\alpha {\{u_n(s)\}}_{n=1}^{\mathrm{\infty }}{\int }_0^{t}L(s)ds+k\alpha {\{u_n(s)\}}_{n=1}^{\mathrm{\infty }}{\int }_0^t{L}_1(s)ds)+\epsilon \\ \le & 4N({\alpha }_{PC}(B){\int }_0^{t}L(s)ds+k{\alpha }_{PC}(B){\int }_0^t{L}_1(s)ds)+\epsilon \\ \le & 4N{\alpha }_{PC}(B){\int }_0^t(L(s)+k{L}_1(s))ds+\epsilon ,t\in [0,t_1],\end{array}$$

where we have used Lemma 2.3. Similarly, we have

$$\alpha (Q^{1}B(t))\le 4N{\alpha }_{PC}(B){\int }_0^t(L(s)+k{L}_1(s))ds+{\mathrm{\Lambda }}_1{\alpha }_{PC}+\epsilon ,t\in (t_i,t_{i+1}],i=1,2,\dots ,p.$$

Using the fact that there is a continuous function $\varphi :[0,K]\to R^{+}$ with $max\{|\varphi (t)|:t\in [0,K]\}=M$ satisfying the relation ${\int }_0^K|L(s)+k{L}_1(s)-\varphi (s)|ds<\delta$ for any $\delta >0$ ($\delta <\frac{1}{N}$), the above inequality takes the form

$$\begin{array}{rcl}\alpha (Q^{1}B(t))l& \le & 4N({\int }_0^t|L(s)+k{L}_1(s)-\varphi (s)|ds+{\int }_0^t|\varphi (s)|ds){\alpha }_{PC}(B)+{\mathrm{\Lambda }}_1{\alpha }_{PC}+\epsilon \\ \le & (a+bt){\alpha }_{PC}(B)+{\mathrm{\Lambda }}_1{\alpha }_{PC}+\epsilon ,\end{array}$$

where $a=4N\delta$, $b=4NM$ and ${\mathrm{\Lambda }}_1=2N{\sum }_{i=1}^p{\beta }_i$. Again, by Lemma 2.5, for any $\epsilon >0$, there is a sequence ${\{v_n\}}_{n=1}^{\mathrm{\infty }}\subset \overline{co}(Q^{1}B)$ such that

$$\begin{array}{rcl}\alpha (Q^{2}B(t))& =& \alpha \left(Q\left(\overline{co}(Q^{1}B(t))\right)\right)\\ \le & 2\alpha ({\int }_0^{t}T(t-s)f(s,{\{v_n(s)\}}_{n=1}^{\mathrm{\infty }},\left(G{\{v_n(s)\}}_{n=1}^{\mathrm{\infty }}\right)))ds+\epsilon \\ \le & 4{\int }_0^t\alpha (T(t-s)f(s,{\{v_n(s)\}}_{n=1}^{\mathrm{\infty }},\left(G{\{v_n(s)\}}_{n=1}^{\mathrm{\infty }}\right)))ds+\epsilon \\ \le & 4N{\int }_0^t(L(s)\alpha {\{v_n(s)\}}_{n=1}^{\mathrm{\infty }}+k{L}_1(s)\alpha {\{v_n(s)\}}_{n=1}^{\mathrm{\infty }})ds+\epsilon \\ \le & 4N{\int }_0^t(L(s)+k{L}_1(s))(Q^{1}B(s))ds+\epsilon \\ \le & 4N{\int }_0^t\{|L(s)+k{L}_1(s)-\varphi (s)|+|\varphi (s)|\}[(a+bs)+{\mathrm{\Lambda }}_1]{\alpha }_{PC}(B)ds+\epsilon .\end{array}$$

Similarly, for $t\in (t_i,t_{i+1}]$, $i=1,2,\dots ,p$, we can obtain

$$\begin{array}{rcl}\alpha (Q^{2}B(t))& \le & 4N{\int }_0^t\{|L(s)+k{L}_1(s)-\varphi (s)|+|\varphi (s)|\}[(a+bs)+{\mathrm{\Lambda }}_1]{\alpha }_{PC}(B)ds\\ +{\mathrm{\Lambda }}_2{\alpha }_{PC}(B)+\epsilon \\ \le & 4N{\int }_0^t|L(s)+k{L}_1(s)-\varphi (s)|ds[(a+bt)+{\mathrm{\Lambda }}_1]{\alpha }_{PC}(B)\\ +4N{\int }_0^t\left[M[(a+bs)+{\mathrm{\Lambda }}_1]ds\right]{\alpha }_{PC}(B)+{\mathrm{\Lambda }}_2{\alpha }_{PC}(B)+\epsilon \\ \le & (a^2+2abt+\frac{{(bt)}^2}{2!}){\alpha }_{PC}(B)+[(a+bt){\mathrm{\Lambda }}_1]{\alpha }_{PC}(B)+{\mathrm{\Lambda }}_2{\alpha }_{PC}(B)+\epsilon .\end{array}$$

Hence, by mathematical induction, for any positive integer n and $t\in [0,K]$, we obtain

$$\begin{array}{rcl}{\alpha }_{PC}(Q^{n}B(t))& \le & (a^n+C_n^1{a}^{n-1}(bt)+C_n^2{a}^{n-2}\frac{{(bt)}^2}{2!}+\cdots +\frac{{(bt)}^n}{n!}){\alpha }_{PC}(B)\\ +(a^{n-1}+C_{n-1}^1{a}^{n-2}(bt)+C_{n-1}^2{a}^{n-3}\frac{{(bt)}^2}{2!}+\cdots +\frac{{(bt)}^{n-1}}{(n-1)!}){\mathrm{\Lambda }}_{n-1}{\alpha }_{PC}(B)\\ +{\mathrm{\Lambda }}_n{\alpha }_{PC}(B).\end{array}$$

By Lemma 2.2, we have

$$\begin{array}{rcl}\alpha \left(Q^{n}B\right)& \le & (a^n+C_n^1{a}^{n-1}b+C_n^2{a}^{n-2}\frac{{(b)}^2}{2!}+\cdots +\frac{{(b)}^n}{n!}){\alpha }_{PC}(B)\\ +(a^{n-1}+C_{n-1}^1{a}^{n-2}(b)+C_{n-1}^2{a}^{n-3}\frac{{(b)}^2}{2!}+\cdots +\frac{{(b)}^{n-1}}{(n-1)!}){\mathrm{\Lambda }}_{n-1}{\alpha }_{PC}(B)\\ +{\mathrm{\Lambda }}_n{\alpha }_{PC}(B).\end{array}$$

From Lemma 2.6, there exists a positive integer $n_0$ such that

$$\begin{array}{c}{a}^{n_0}+C_{n_0}^1{a}^{n_0-1}b+C_{n_0}^2{a}^{n_0-2}\frac{{(b)}^2}{2!}+\cdots +\frac{{(b)}^{n_0}}{n_0!}=R<1,\hfill \\ a^{n_0-1}+C_{n_0-1}^1{a}^{n_0-2}(b)+C_{n_0-1}^2{a}^{n_0-3}\frac{{(b)}^2}{2!}+\cdots +\frac{{(b)}^{n_0-1}}{(n_0-1)!}=T<1,\hfill \\ {\mathrm{\Lambda }}_{n_0-1}=l\text{and}{\mathrm{\Lambda }}_{n_0}=q.\hfill \end{array}$$

Then

$$\begin{array}{rcl}{\alpha }_{PC}\left(Q^{n_0}B\right)& \le & R{\alpha }_{PC}(B)+Tl{\alpha }_{PC}+q{\alpha }_{PC}\\ \le & (R+Tl+q){\alpha }_{PC}.\end{array}$$

Thus, it follows by Lemma 2.7 that Q has at least one fixed point in $B_0$, that is, the nonlocal integrodifferential equation (1.1) has at least one mild solution in $B_0$. This completes the proof. □

Remark 3.2 In [38], the author discussed the nonlocal initial value problem by taking f to be compact in (1.1). From the above theorem, we notice that the key condition in [38] is no more required. So, Theorem 3.1 generalizes the related results in [38]. Furthermore, we extend the problem addressed in [23] to the impulse case with the nonlinearity of a more general form $f(t,u(t),Gu(t))$.

Theorem 3.3 If assumptions (${\mathrm{A}}_1$)-(${\mathrm{A}}_6$) are satisfied, then there is at least one mild solution for (1.1) provided that

$${\int }_0^{K}m(s)ds<\underset{T\to \mathrm{\infty }}{lim}\frac{T-N[\parallel u_0\parallel +(cT+d)+\mathrm{\Lambda }]}{N\mathrm{\Omega }(T,w)}.$$

Proof We do not provide the proof of this theorem as it is similar to that of Theorem 3.1. □

For our final result, we introduce the following condition:

(${\mathrm{A}}_2^{\prime }$) Let $g:PC([0,K];X)\to X$ be continuous and compact. Then there exists a positive constant $M>0$ such that $\parallel g(u)\parallel \le M$ for every $u\in PC([0,K];X)$.

Theorem 3.4 Suppose that conditions (${\mathrm{A}}_1$)-(${\mathrm{A}}_2^{\prime }$) and (${\mathrm{A}}_3$)-(${\mathrm{A}}_6$) hold. Then there exists at least one mild solution for (1.1) if there exists a constant r such that

$$N[\parallel u_0\parallel +M+\mathrm{\Lambda }]+N\mathrm{\Omega }(r,w){\int }_0^{K}m(s)ds\le \gamma .$$

Proof We omit the proof as it is similar to that of Theorem 3.1. This completes the proof. □

Example Consider a nonlocal problem of integrodifferential equations given by

$$\begin{array}{r}\begin{array}{rl}\frac{\partial u(t,w)}{\partial t}=& \frac{{\partial }^{2}u(t,w)}{\partial w^2}u(t,w)\\ +{sin}^{2}u(t,w)+{\int }_0^K\frac{u(s,w)}{\sqrt{(1+t){(2+s)}^3}}ds,t\in [0,K],\end{array}\\ u(0)=u_0+{\int }_0^K\sqrt{3+s^2}log(2+|u(s,w)|)ds,\\ \mathrm{\Delta }u(t)={\int }_0^K\frac{(1+|{cos}^{2}u(s)|)}{\sqrt[i]{t^2+s^2+7}}ds,i\ge 1,\end{array}$$

(3.9)

with $0<t_1<t_2<\cdots <t_p<K$, $0<s_1<s_2<\cdots <s_q<K$. Let us take $X=L^2([0,K],R)$ and define the operator A by $A(t)y=y^{″}$ with the domain $D(A)$ = {$y\in X$: y, $y^{\prime }$ are absolutely continuous, $y^{″}\in X$, $y(0)=0$, $y(K)=0$}. The assumptions of Theorem 3.1 clearly hold for a large positive constant γ. Hence the conclusion of Theorem 3.1 applies to problem (3.9).