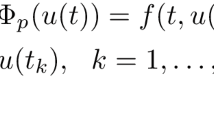Applications of variational methods to the impulsive equation with non-separated periodic boundary conditions

Abstract

In this paper, we study the existence of classical solutions for a second-order impulsive differential equation with non-separated periodic boundary conditions. By using the variational method and critical point theory, we give some new criteria to guarantee that the impulsive problem has at least one solution under some different conditions. Our results extend and improve some recent results.

1 Introduction

Many dynamical systems have an impulsive dynamical behavior due to abrupt changes at certain instants during the evolution process. The mathematical description of these phenomena leads to the impulsive differential equations. Recent developments in this field have been motivated by many applied problems, such as control theory [1, 2], population dynamic [3], medicine [4–6], and some physics or mechanics problems [7]. In the last few years, a great deal of work has been done in the study of the existence of solutions for impulsive boundary value problems. Some classical tools or techniques have been used to study such problems in the literature, such as coincidence degree theory of Mawhin [8], the method of upper and lower solutions with the monotone iterative technique [9–12], and some fixed point theorems in cones [13–15]. For some general and recent work on the theory of impulsive differential equation, we refer the interested reader to [16–18].

In this paper, we are concerned with the existence of solutions for the following boundary value problem (BVP) with impulses:

$$\begin{aligned}& - \bigl(p(t)u'(t) \bigr)'= f \bigl(t,u(t) \bigr),\quad t \neq t_{k}, t\in J, \end{aligned}$$

(1.1a)

$$\begin{aligned}& \Delta \bigl(u^{[1]}(t_{k}) \bigr)=I_{k} \bigl(u(t_{k}) \bigr), \quad k=1,2,\ldots, m, \end{aligned}$$

(1.1b)

$$\begin{aligned}& u(0)=u(T), \qquad u^{[1]}(0)=u^{[1]}(T). \end{aligned}$$

(1.1c)

Here T be a fixed positive number, $u^{[1]}(t)=p(t)u'(t)$ denotes the quasi-derivative of $u(t)$. Condition (1.1c) is called a non-separated periodic boundary value condition for (1.1a).

We assume throughout, and without further mention, that the following conditions hold.

(H) Let $J=[0,T]$, and $0=t_{0}< t_{1}< t_{2}<\cdots<t_{m}<t_{m+1}=T$, $f\in C(J\times\mathbb{R}^{+}, \mathbb{R}^{+})$, $I_{k}\in C(\mathbb{R}, \mathbb{R})$, $\mathbb{R}^{+}=[0, +\infty)$. $\Delta(u^{[1]}(t_{k}))=u^{[1]}(t_{k}^{+})-u^{[1]}(t_{k}^{-})$, where $u^{[1]}(t_{k}^{+})$ (respectively, $u^{[1]}(t_{k}^{-})$) denotes the right limit (respectively left limit) of $u^{[1]}(t)$ at $t=t_{k}$.

(H1) The function $f(t,u)$ is measurable in $t\in[0,T]$ for each $u\in\mathbb{R}$, continuous in $u\in\mathbb{R}$ for a.e. $t\in[0,T]$ (Caratheodory function), and there exist $a(t)\in C(\mathbb{R}^{+},\mathbb{R}^{+})$ and a Lebesgue measurable function $b(t)\geq0$ such that $b(t)\in L^{1}(0,T;\mathbb{R}^{+})$ and $|f(t,u)|\leq a(|u|)b(t)$, for all $u\in\mathbb{R}$ and a.e. $t\in [0,T]$. We have

$$\int_{0}^{T}\frac{1}{p(t)}\,dt< \infty,\quad p(t)>0 \mbox{ on } [0,T]. $$

A function $u(t)$ defined on $J^{-}=J\backslash\{t_{1},t_{2},\ldots,t_{m}\}$ is called a classical solution of BVP (1.1a)-(1.1c) if its first derivative $u'(t)$ exists for each $t\in J^{-}$, $p(t)u'(t)$ is absolutely continuous on each closed subinterval of $J^{-}$, there exist finite values $u^{[1]}(t_{k}^{\pm})$, the impulse conditions (1.1b), and the boundary conditions (1.1c) are satisfied, and equation (1.1a) is satisfied almost everywhere on $J^{-}$.

For the case of $I_{k}=0$ ($k=1,2,\ldots,m$), problem (1.1a)-(1.1c) is related to a non-separated periodic boundary value problem of ODE. More precisely, Atici and Guseinov [19] considered the following non-separated periodic boundary value problem:

$$ \left \{ \textstyle\begin{array}{@{}l} -[p(x)y']'+q(x)y=f(x,y), \quad 0\leq x\leq\omega,\\ y(0)=y(\omega), \qquad y^{[1]}(0)=y^{[1]}(\omega). \end{array}\displaystyle \right . $$

(1.2)

The authors proved the existence of a positive and twin positive solutions to BVP (1.2) by applying a fixed point theorem for the completely continuous operators in cones.

Based upon the properties of the Green’s function obtained in [19], Graef and Kong [20] extended and improved the work of [19] by using topological degree theory. They derived new criteria for the existence of non-trivial solutions, positive solutions, and negative solutions of problem (1.2) when f is a sign-changing function and not necessarily bounded from below even over $[0,\omega]\times \mathbb{R}^{+}$.

Very recently, by introducing a variational framework for a class of second-order nonlinear differential equations with non-separated periodic boundary value conditions, Han [21] obtained some results on the existence of non-trivial, positive, and negative solutions of problem (1.2), where the nonlinearities are unbounded and satisfy Ahmad-Lazer-Paul type conditions. The problem (1.2) in the case of $p\equiv1$, the usual periodic boundary value problem, has been extensively investigated; see [22, 23] for some results.

For the impulsive case of (1.2), Huseynov [24, 25] considered the following problem:

$$ \left \{ \textstyle\begin{array}{@{}l} -[p(x)y'(x)]'+q(x)y(x)=h(x), \quad x\in[a,c)\cup(c, b],\\ y(c^{-})=d_{1}y(c^{+}),\qquad y^{[1]}(c^{-})=d_{2}y^{[1]}(c^{+}),\\ y(a)=y(b), \qquad y^{[1]}(a)=y^{[1]}(b). \end{array}\displaystyle \right . $$

(1.3)

In [24], Huseynov investigated the Green’s function of the boundary value problem (1.3), sufficient conditions that ensure the positiveness of the Green’s function are established. The author also investigated nonlinear second-order differential equations subject to linear impulse conditions and non-separated periodic boundary conditions in [25].

Motivated by the above facts, in this paper, our aim is to study the existence of solutions for the impulsive boundary value problem (1.1a)-(1.1c). To the best of our knowledge, there has so far been no paper concerning the non-separated boundary value problem with impulses via variational methods. In addition, this paper is a generalization of [21], in which impulsive effects are not involved. For some general and recent work on the critical point theory and variational methods, we refer the reader to [26–36]. It is a novel approach to apply variational methods to the impulsive boundary value problem.

Throughout this paper, we will use the following notations: $L^{q}(0,T)$ is the usual Banach space with norm $\|u\|_{q}=(\int_{0}^{T}|u|^{q}\,dt)^{1/q}$, $\|u\|_{\infty}=\max_{t\in[0,T]}|u(t)|$, and $\|u\|_{p,2}=(\int_{0}^{T}pu^{2}\,dt)^{1/2}$. $C,C_{1},C_{2},\ldots$ denote the positive (possibly different) constants.

2 Preliminaries

In this sections, we recall some basic facts which will be used in the proofs of our main results. In order to apply the critical point theory, we construct a variational structure. With this variational structure, we can reduce the problem of finding solutions of (1.1a)-(1.1c) to that of seeking the critical points of a corresponding functional.

Let $W_{p,T}^{1,2}$ be the Sobolev space

$$W_{p,T}^{1,2}= \bigl\{ u\in AC[0,T]|u(0)=u(T), \sqrt{p}u'\in L^{2}(0,T) \bigr\} $$

with the norm

$$\|u\|= \biggl( \int_{0}^{T} p(t) \bigl|u'(t) \bigr|^{2}\,dt+ \int_{0}^{T} u^{2}(t)\,dt \biggr)^{1/2}. $$

Certainly, $W_{p,T}^{1,2}$ is also a Hilbert space with the inner product induced by its norm. For more details, see [21].

In the meantime, according to Proposition 2.5 in [21], the problem

$$\left \{ \textstyle\begin{array}{@{}l} -(p(t)u'(t))'=\mu u,\\ u(0)=u(T), \qquad u^{[1]}(0)=u^{[1]}(T) \end{array}\displaystyle \right . $$

has a sequence of eigenvalues, $0=\mu_{0}<\mu_{1}<\cdots<\mu_{n}<\cdots$, and corresponding eigenfunctions, $\psi_{n}$ ($n=0,1,2,\ldots$), where we can choose $\psi _{0}(t)\equiv1$ in $[0,T]$. It is obvious that $\psi_{n}$ ($n=0,1,\ldots$) are mutually orthogonal in $L^{2}(0,T)$. Set $\overline{W}=\operatorname{span}\{1\}\subset W_{p,T}^{1,2}$ and $\widetilde{W}=\overline{\operatorname{span}}\{\psi_{1},\psi_{2},\ldots\}\subset W_{p,T}^{1,2}$, then $W_{p,T}^{1,2}=\overline{W}\oplus\widetilde{W}$. Accordingly, for every $u\in W_{p;T}^{1,2}$, $u=\overline{u}+\widetilde{u}$. As in the proof of Proposition 2.5 in [21], we have

$$\mu_{1} \int_{0}^{T}u^{2}\,dt\leq \int_{0}^{T} p\bigl|u'\bigr|^{2}\,dt, \quad\forall u\in \widetilde{W}. $$

From Theorem 4.1 in [21], we have the inequality

$$\|\widetilde{u}\|_{\infty}\leq C \biggl( \int_{0}^{T}p\widetilde{u}^{\prime2} \,dt \biggr)^{1/2}, \quad \forall u\in W_{p,T}^{1,2}. $$

The above two important inequalities can be simply rewritten as follows:

$$\begin{aligned}& \|\widetilde{u}\|_{\infty}\leq C \bigl\| \widetilde{u}' \bigr\| _{p,2}, \quad \forall u\in W_{p,T}^{1,2}, \end{aligned}$$

(2.1)

$$\begin{aligned}& \|\widetilde{u}\|_{ 2}^{2}\leq \frac{1}{\mu_{1}}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{2}, \quad \forall u\in \widetilde{W}. \end{aligned}$$

(2.2)

Proposition 2.1

([21], Proposition 2.1)

Suppose that the condition (H1) holds, then $W_{p,T}^{1,2}$ is compactly imbedded in $C[0,T]$.

For $u\in W_{p,T}^{1,2}$, we set

$$J(u)=\frac{1}{2} \int_{0}^{T}pu^{\prime2}\,dt- \int_{0}^{T} F(t,u)\,dt+\sum _{k=1}^{m} \int_{0}^{u(t_{k})}I_{k}(s)\,ds, $$

where

$$F(t,u)= \int_{0}^{u}f(t,s)\,ds. $$

In view of the condition (H1), we can prove that $J(u)$ is well defined and is $C^{1}$ on $W_{p,T}^{1,2}$. Furthermore, we have

$$\bigl(J'(u), v \bigr)= \int_{0}^{T} pu'v'\,dt- \int_{0}^{T}f(t,u)v\,dt+\sum _{k=1}^{m} I_{k} \bigl(u(t_{k}) \bigr)v(t_{k}), $$

for all $u,v\in W_{p,T}^{1,2}$. The proofs can be given as in the corresponding results in [32, 33].

Definition 2.1

$u\in W_{p,T}^{1,2}$ is a weak solution of problem (1.1a)-(1.1c), if

$$\int_{0}^{T} pu'v'\,dt- \int_{0}^{T}f(t,u)v\,dt+\sum _{k=1}^{m} I_{k} \bigl(u(t_{k}) \bigr)v(t_{k})=0, $$

for all $v\in W_{p,T}^{1,2}$.

By Definition 2.1, the weak solutions of problems (1.1a)-(1.1c) correspond to the critical points of J.

Theorem 2.1

If $u\in W_{p,T}^{1,2}$ is a critical point of the functional J, then u is a classical solution of (1.1a)-(1.1c).

Proof

Let $u\in W_{p,T}^{1,2}$ be a critical point of the functional J. It shows that

$$\int_{0}^{T} pu'v'\,dt- \int_{0}^{T}f(t,u)\,dt+\sum _{k=1}^{m}I_{k} \bigl(u(t_{k}) \bigr)v(t_{k})=0 $$

holds for any $v\in W_{p,T}^{1,2}$. By integrating by parts, we have

$$\begin{aligned} 0 =& \sum_{k=0}^{m} \int _{t_{k}}^{t_{k+1}}pu'v'\,dt- \int_{0}^{T}f(t,u)v\,dt+\sum _{k=1}^{m}I_{k}\bigl(u(t_{k}) \bigr)v(t_{k}) \\ =& \sum_{k=0}^{m}\bigl[pu'v|_{t_{k}^{+}}^{t_{k+1}} \bigr]- \int _{0}^{T}\bigl(pu' \bigr)'v\,dt- \int_{0}^{T}f(t,u)v\,dt+\sum _{k=1}^{m}I_{k}\bigl(u(t_{k}) \bigr)v(t_{k}) \\ =&p(t_{1})u'(t_{1})v(t_{1})-p(0)u'(0)v(0) \\ &{}+p(t_{2})u'(t_{2})v(t_{2})-p \bigl(t_{1}^{+}\bigr)u'\bigl(t_{1}^{+}\bigr)v \bigl(t_{1}^{+}\bigr)+\cdots \\ &{}+p(T)u'(T)v(T)-p\bigl(t_{m}^{+}\bigr)u' \bigl(t_{m}^{+}\bigr)v\bigl(t_{m}^{+}\bigr)- \int _{0}^{T}\bigl(pu' \bigr)'v\,dt \\ &{}- \int_{0}^{T}f(t,u)v\,dt+ \sum _{k=1}^{m}I_{k}\bigl(u_{(}t_{k}) \bigr)v(t_{k}). \end{aligned}$$

(2.3)

In view of $v\in W_{p,T}^{1,2}$ and Proposition 2.1, it follows that $v(t_{k})=v(t_{k}^{+})$. Equation (2.3) implies

$$\begin{aligned} &{-}\sum_{k=1}^{m}\Delta \bigl(p(t_{k})u'(t_{k}) \bigr)v(t_{k})+p(T)u'(T)v(T)-p(0)u'(0)v(0) \\ &\quad{}- \int_{0}^{T} \bigl(pu' \bigr)'v\,dt- \int_{0}^{T} f(t,u)v\,dt+\sum _{k=1}^{m} I_{k} \bigl(u(t_{k}) \bigr)v(t_{k})=0 \end{aligned}$$

(2.4)

holds for all $v\in W_{p,T}^{1,2}$. Without loss of generality, we assume that $v\in C_{0}^{\infty}(t_{k},t_{k+1})$ satisfying $v(t)\equiv0$, $t\in[0, t_{k}]\cup[t_{k+1},T]$, then substituting v into (2.4) we get

$$\int_{t_{k}}^{t_{k+1}} \bigl[- \bigl(pu' \bigr)'-f(t,u) \bigr]v\,dt=0, $$

which means

$$- \bigl(p(t)u'(t) \bigr)'-f \bigl(t,u(t) \bigr)=0, \quad t\in (t_{k},t_{k+1}). $$

Thus u satisfies equation (1.1a). So (2.4) becomes

$$ \sum_{k=1}^{m} \bigl[I_{k} \bigl(u(t_{k}) \bigr)-\Delta \bigl(p(t_{k})u'(t_{k}) \bigr) \bigr]v(t_{k})+p(T)u'(T)v(T)-p(0)u'(0)v(0)=0. $$

(2.5)

Now we will show that u satisfies the impulsive condition (1.1b). If not, without loss of generality, we assume that there exists $k\in\{1,2,\ldots, m\}$ such that

$$ I_{k} \bigl(u(t_{k}) \bigr)-\Delta \bigl(p(t_{k})u'(t_{k}) \bigr)\neq0. $$

(2.6)

Set $v(t)=\prod_{j=0, j\neq k}^{m+1}(t-t_{j})=t(t-t_{1})\cdots(t-t_{k-1})(t-t_{k+1})\cdots(t-T)$, combining (2.6) we get

$$\begin{aligned} &\sum_{k=1}^{m} \bigl[I_{k} \bigl(u(t_{k}) \bigr)-\Delta \bigl(p(t_{k})u'(t_{k}) \bigr) \bigr]v(t_{k})+p(T)u'(T)v(T)-p(0)u'(0)v(0) \\ &\quad= \bigl[I_{k} \bigl(u(t_{k}) \bigr)-\Delta \bigl(p(t_{k})u'(t_{k}) \bigr) \bigr]v(t_{k})\neq0, \end{aligned}$$

which contradicts (2.5). So u satisfies the impulsive condition (1.1b). From the above, we can obtain

$$p(T)u'(T)v(T)-p(0)u'(0)v(0)=0. $$

Notice that $v\in W_{p,T}^{1,2}$ and $v(0)=v(T)$, so

$$p(T)u'(T)=p(0)u'(0). $$

Hence u satisfies the non-separated periodic boundary condition (1.1c). Therefore, u is a classical solution of problem (1.1a)-(1.1c). □

Definition 2.2

([32], $P_{81}$)

Let X be a real Banach space and $I\in C^{1}(X,R)$. I is said to satisfy the P.S. condition on X if any sequence $\{x_{n}\}\subseteq X$ for which $I(x_{n})$ is bounded and $I'(x_{n})\rightarrow0$ as $n\rightarrow \infty$ possesses a convergent subsequence in X.

Theorem 2.2

([32], Theorem 4.7)

Let X be a Banach space and let $\Phi\in C^{1}(X,\mathbb{R})$. Assume that X splits into a direct sum of closed subspaces $X=X^{-}\oplus X^{+}$ with

$$\operatorname{dim}X^{-}< \infty $$

and

$$\sup_{S_{R}^{-}}\Phi< \inf_{X^{+}}\Phi, $$

where $S_{R}^{-}=\{u\in X^{-}:\|u\|=R\}$. Let

$$\begin{aligned}& B_{R}^{-}= \bigl\{ u\in X^{-}:\|u\|=R \bigr\} , \qquad M= \bigl\{ h\in C \bigl(B_{R}^{-}, X \bigr):h(s)=s \textit{ if } s\in S_{R}^{-} \bigr\} , \end{aligned}$$

and

$$c=\inf_{h\in M}\max_{s\in B_{R}^{-}}\Phi \bigl(h(s) \bigr). $$

Then, if Φ satisfies the P.S. condition, c is a critical value of Φ.

3 Main results

Theorem 3.1

Assume the following conditions are satisfied:

• (H2) There exist $g, h\in L^{1}[0,T]$ and constant $\alpha\in[0,1)$ such that

  $$\bigl|f(t,u) \bigr|\leq g(t)|u|^{\alpha}+h(t) $$

  for all $u\in\mathbb{R}$, and a.e. $t\in[0,T]$.

• (H3) $|u|^{-2\alpha} \int_{0}^{T} F(t,u)\,dt\rightarrow-\infty$, as $|u|\rightarrow\infty$.

• (H4) For any $k\in\{1,2,\ldots, m\}$, $I_{k}(u)u\geq0$, $\forall u\in \mathbb{R}$.

Then problem (1.1a)-(1.1c) has at least one weak solution that minimizes the function J.

Proof

It follows from (H2) and (2.1) that

$$\begin{aligned} \biggl| \int_{0}^{T}\bigl(F(t,u)-F(t,\overline{u})\bigr) \,dt\biggr| =&\biggl| \int_{0}^{T}\biggl( \int _{0}^{1}f(t,\overline{u}+s\widetilde{u}) \widetilde{u}\,ds\biggr)\,dt\biggr| \\ \leq& \int_{0}^{T}\,dt \int_{0}^{1} \bigl|f(t,\overline{u}+s\widetilde{u})\bigr|| \widetilde{u}|\,ds \\ \leq& \int_{0}^{T}\,dt \int_{0}^{1} \bigl[g(t)|\overline{u}+s \widetilde{u}|^{\alpha}+h(t)\bigr]|\widetilde{u}|\,ds \\ \leq& \int_{0}^{T}\bigl[g(t)2^{\alpha}\bigl(| \overline{u}|^{\alpha}+|\widetilde {u}|^{\alpha}\bigr)+h(t)\bigr]| \widetilde{u}|\,dt \\ \leq& \int_{0}^{T}\bigl(g(t)2^{\alpha}| \overline{u}|^{\alpha}|\widetilde {u}|+g(t)2^{\alpha}| \widetilde{u}|^{\alpha+1}+h(t)|\widetilde{u}|\bigr)\,dt \\ \leq& 2^{\alpha}|\overline{u}|^{\alpha}\|\widetilde{u} \|_{\infty}\|g\|_{1}+2^{\alpha}\| \widetilde{u} \|_{\infty}^{\alpha+1}\|g\|_{1}+\|\widetilde{u} \|_{\infty}\|h\| _{1} \\ \leq&\|g\|_{1}2^{\alpha}|\overline{u}|^{\alpha}C\bigl\| \widetilde{u}'\bigr\| _{p,2}+2^{\alpha}\|g\|_{1}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{\alpha+1}+\|h\|_{1}C \bigl\| \widetilde{u}'\bigr\| _{p,2} \\ \leq& \frac{1}{4}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{2}+C_{3}| \overline{u}|^{2\alpha}+C_{1}\bigl\| \widetilde{u}' \bigr\| _{p,2}^{\alpha+1}+C_{2}\bigl\| \widetilde{u}' \bigr\| _{p,2}. \end{aligned}$$

By (H4), we have

$$\phi(u)=\sum_{k=1}^{m} \int_{0}^{u(t_{k})}I_{k}(s)\,ds\geq0 $$

for all $u\in W_{p,T}^{1,2}$.

Therefore, we obtain

$$\begin{aligned} J(u)&= \frac{1}{2} \int_{0}^{T}pu^{\prime2}\,dt- \int_{0}^{T} F(t,u)\,dt+\sum _{k=1}^{m} \int_{0}^{u(t_{k})}I_{k}(s)\,ds \\ &\geq \frac{1}{2} \int_{0}^{T}pu^{\prime2}\,dt- \int _{0}^{T}\bigl(F(t,u)-F(t,\overline{u})\bigr) \,dt- \int_{0}^{T}F(t,\overline{u})\,dt \\ &\geq \frac{1}{2}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{2}- \frac{1}{4}\bigl\| \widetilde {u}'\bigr\| _{p,2}^{2}-C_{3}| \overline{u}|^{2\alpha} -C_{1}\bigl\| \widetilde{u}' \bigr\| _{p,2}^{\alpha+1}-C_{2}\bigl\| \widetilde{u}'\bigr\| _{p,2}- \int_{0}^{T}F(t,\overline{u})\,dt \\ &\geq \frac{1}{4}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{2}-| \overline{u}|^{2\alpha }\biggl(|\overline{u}|^{-2\alpha} \int_{0}^{T}F(t,\overline{u})\,dt+C_{3} \biggr) -C_{1}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{\alpha+1}-C_{2} \bigl\| \widetilde{u}'\bigr\| _{p,2} \end{aligned}$$

(3.1)

for all $u\in W_{p,T}^{1,2}$. As $\|u\|\rightarrow\infty$ if and only if $(\|\widetilde{u}'\|_{p,2}^{2}+|\overline{u}|^{2})^{1/2}\rightarrow\infty$, (3.1) and condition (H3) imply that

$$J(u)\rightarrow+\infty \quad\mbox{as } \|u\|\rightarrow\infty. $$

Similar to the Lemma 3.1 in [34], it is easy to prove that J is weakly lower semi-continues. By Theorem 1.1 in [32], J has a minimum point on $W_{p,T}^{1,2}$, which is a critical point of J. Hence problem (1.1a)-(1.1c) has at least one weak solution. □

Theorem 3.2

Assume (H2), (H3), and the following condition (H5) holds:

• (H5) $\liminf_{|x|\rightarrow\infty}|x|^{\beta}\int_{0}^{x}I_{k}(s)\,ds>-m_{0}$ for some $\beta\in(0, 2\alpha)$ and constant $m_{0}>0$, $k\in \{1,2,\ldots,m\}$.

Then problem (1.1a)-(1.1c) has at least one weak solution.

Proof

Obviously, (H5) implies that there exists M such that $\forall x\in\mathbb{R}$

$$ \int_{0}^{x}I_{k}(s)\,ds \geq-m_{0}|x|^{\beta}-M. $$

(3.2)

From Theorem 3.1, we obtain

$$ \biggl| \int_{0}^{T} \biggl( \int_{0}^{1}f(t,\overline{u}+s\widetilde{u}) \widetilde {u}\,ds \biggr)\,dt\biggr|\leq \frac{1}{4}\bigl\| \widetilde{u}' \bigr\| _{p,2}^{2}+C_{3}|\overline{u}|^{2\alpha}+C_{1} \bigl\| \widetilde{u}'\bigr\| _{p,2}^{\alpha+1}+C_{2}\bigl\| \widetilde{u}'\bigr\| _{p,2}. $$

(3.3)

By (2.1) we have

$$\begin{aligned} \sum_{k=1}^{m} \bigl|u(t_{k})\bigr|^{\beta}& \leq m\|u\|_{\infty}^{\beta}=m\|\overline{u}+\widetilde{u} \|_{\infty}^{\beta}\leq 2^{\beta}m\bigl(| \overline{u}|^{\beta}+|\widetilde{u}|^{\beta}\bigr) \\ &\leq2^{\beta}m|\overline{u}|^{\beta}+2^{\beta}mC\bigl\| \widetilde{u}'\bigr\| _{p,2}^{\beta}. \end{aligned}$$

Also

$$\begin{aligned} J(u)&= \frac{1}{2} \int_{0}^{T}p\bigl(u' \bigr)^{2}\,dt- \int_{0}^{T}F(t,u)\,dt +\sum _{k=1}^{m} \int_{0}^{u(t_{k})}I_{k}(s)\,ds \\ &= \frac{1}{2} \int_{0}^{T}p\bigl(u' \bigr)^{2}\,dt- \int _{0}^{T}\bigl(F(t,u)-F(t,\overline{u})\bigr) \,dt- \int_{0}^{T}F(t,\overline{u})\,dt +\sum _{k=1}^{m} \int_{0}^{u(t_{k})}I_{k}(s)\,ds. \end{aligned}$$

Substituting (3.2) and (3.3) into the above equation, we have

$$\begin{aligned} J(u)\geq{}& \frac{1}{2}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{2}- \frac{1}{4}\bigl\| \widetilde {u}'\bigr\| _{p,2}^{2}-C_{3}| \overline{u}|^{2\alpha}-C_{1}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{\alpha+1}-C_{2}\bigl\| \widetilde{u}' \bigr\| _{p,2} \\ &{}- \sum_{k=1}^{m} m_{0}\bigl|u(t_{k})\bigr|^{\beta}-mM- \int_{0}^{T}F(t,\overline{u})\,dt \\ ={}& \frac{1}{4}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{2}-C_{3}| \overline {u}|^{2\alpha}-C_{1}\bigl\| \widetilde{u}' \bigr\| _{p,2}^{\alpha+1}-C_{2}\bigl\| \widetilde {u}' \bigr\| _{p,2}-C_{6}|\overline{u}|^{\beta}-\bigl\| \widetilde{u}'\bigr\| _{p,2}^{\beta}\\ &{}- \int_{0}^{T} F(t,\overline{u})\,dt+C_{7} \\ \geq{}& \frac{1}{4}\bigl\| \widetilde{u}'\bigr\| _{p,2}^{2}-| \overline{u}|^{2\alpha }\biggl[|\overline{u}|^{-2\alpha} \int_{0}^{T}F(t,\overline{u})\,dt + \frac{C_{6}|\overline{u}|^{\beta}}{|\overline{u}|^{2\alpha}} +C_{3}\biggr]\\ &{}-C_{1}\bigl\| \widetilde{u}' \bigr\| _{p,2}^{\alpha+1}-C_{2}\bigl\| \widetilde{u}' \bigr\| _{p,2}+C_{7}. \end{aligned}$$

Since $\beta\in(0,2\alpha)$, the above inequality and (H3) imply that

$$J(u)\rightarrow+\infty, \quad\mbox{as } \|u\|\rightarrow\infty. $$

So J has a minimum point on $W_{p,T}^{1,2}$, which is a critical point of J. Hence problem (1.1a)-(1.1c) has at least one solution. □

Theorem 3.3

Suppose that the condition (H2) of Theorem  3.1 hold. Assume the following:

• (H6) There exist $a_{k}, b_{k}>0$, and $\gamma\in(0,\alpha)$ such that

  $$\bigl|I_{k}(s)\bigr|\leq a_{k}+b_{k}|s|^{\gamma}, $$

  for every $s\in\mathbb{R}$, $k\in \{1,2,\ldots,m\}$.

• (H7) For any $k\in\{1,2,\ldots,m\}$, $I_{k}(s)s\leq0$, $\forall s\in \mathbb{R}$.

• (H8) $|u|^{-2\alpha} \int_{0}^{T}F(t,u)\,dt\rightarrow+ \infty$, as $|u|\rightarrow+\infty$.

Then problem (1.1a)-(1.1c) has at least one weak solution.

First of all, we prove the following lemma.

Lemma 3.1

Suppose that the conditions of Theorem  3.3 hold, then J satisfies the P.S. condition.

Proof

Let $\{u_{n}\}\subset W_{p,T}^{1,2}$ be a P.S. sequence for J, that is, $\{J(u_{n})\}$ is bounded, $J'(u_{n})\rightarrow 0$ as $n\rightarrow\infty$. It follows from (H2) and (2.1) that

$$\begin{aligned} \biggl| \int_{0}^{T} f(t,u_{n}) \widetilde{u}_{n}\,dt\biggr|&\leq \int_{0}^{T} \bigl|f(t, u_{n})\bigr|| \widetilde{u}_{n}|\,dt \\ &\leq \int_{0}^{T}\bigl(g(t)|u_{n}|^{\alpha}+h(t) \bigr)|\widetilde{u}_{n}|\,dt \\ &\leq \int_{0}^{T}g(t)|u_{n}|^{\alpha}| \widetilde{u}_{n}|\,dt+ \int _{0}^{T}h(t)|\widetilde{u}_{n}|\,dt \\ &\leq \|u_{n}\|_{\infty}^{\alpha}\|\widetilde{u}_{n} \|_{\infty}\|g\|_{1}+\|\widetilde {u}_{n} \|_{\infty}\|h\|_{1} \\ &\leq \|\overline{u}_{n}+\widetilde{u}_{n} \|_{\infty}^{\alpha}\|\widetilde{u}_{n}\| _{\infty}\|g\|_{1}+\|\widetilde{u}_{n}\|_{\infty}\|h \|_{1} \\ &\leq 2^{\alpha}\bigl(|\overline{u}|^{\alpha}+\| \widetilde{u}_{n}\|_{\infty}^{\alpha}\bigr)\| \widetilde{u}_{n}\|_{\infty}\|g\|_{1}+\| \widetilde{u}_{n}\|_{\infty}\|h\|_{1} \\ &\leq 2^{\alpha}|\overline{u}|^{\alpha}\|\widetilde{u}_{n} \|_{\infty}\|g\|_{1}+2^{\alpha}\|\widetilde{u}_{n} \|_{\infty}^{\alpha+1}\|g\|_{1}+\|\widetilde{u}_{n} \|_{\infty}\|h\|_{1} \\ &\leq 2^{\alpha}|\overline{u}_{n}|^{\alpha}\|g \|_{1}C\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}+2^{\alpha}\|g\|_{1}C^{\alpha+1}\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha +1}+C_{2}C \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2} \\ &\leq \frac{1}{4}\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}+C_{4}|\overline {u}_{n}|^{2\alpha}+C_{5} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}+C_{6} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}. \end{aligned}$$

Therefore

$$\begin{aligned} \bigl\langle J'(u_{n}),\widetilde{u}_{n} \bigr\rangle ={}& \int_{0}^{T} pu_{n}' \widetilde{u}_{n}'\,dt- \int_{0}^{T} f(t,u_{n}) \widetilde{u}_{n}\,dt+\sum_{k=1}^{m} I_{k}\bigl(u_{n}(t_{k})\bigr) \widetilde{u}_{n}(t_{k}) \\ \geq{}& \frac{3}{4}\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}-C_{4}|\overline {u}_{n}|^{2\alpha}- C_{5}\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}-C_{6} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}+ \sum _{k=1}^{m} I_{k}\bigl(u_{n}(t_{k}) \bigr)\widetilde{u}_{n}(t_{k}) \\ \geq{}& \frac{3}{4}\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}-C_{4}|\overline {u}_{n}|^{2\alpha}- C_{5}\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}-C_{6} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}\\ &{}- \sum _{k=1}^{m}\bigl(a_{k}+b_{k}\bigl|u_{n}(t_{k})\bigr|^{\gamma}\bigr)\bigl|\widetilde {u}_{n}(t_{k})\bigr|. \end{aligned}$$

Let $a=\max\{a_{i}\}$, $b=\max\{b_{i}\}$, one has

$$\begin{aligned} \bigl\langle J'(u_{n}),\widetilde{u}_{n} \bigr\rangle \geq{}& \frac{3}{4}\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}-C_{4}|\overline {u}_{n}|^{2\alpha}- C_{5}\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}-C_{6} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2} \\ &{}-am\|\widetilde{u}_{n}\|_{\infty}-b \sum _{k=1}^{m}2\bigl(|\overline {u}_{n}|^{\gamma}+\|\widetilde{u}_{n}\|_{\infty}^{\gamma}\bigr)\| \widetilde{u}_{n}\|_{\infty}\\ \geq{}& \frac{3}{4}\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}-C_{4}|\overline {u}_{n}|^{2\alpha}-C_{5} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}-C_{6} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}-amC\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2} \\ &{} -2mb|\overline{u}_{n}|^{\gamma}\|\widetilde{u}_{n} \|_{\infty}-2bmC\bigl\| \widetilde {u}_{n}' \bigr\| _{p,2}^{\gamma+1}. \end{aligned}$$

By Yang inequality and (2.1), the following inequality holds:

$$|\overline{u}_{n}|^{\gamma}\|\widetilde{u}_{n} \|_{\infty}\leq \frac{(|\overline{u}_{n}|^{\gamma})^{2\alpha/\gamma}}{2\alpha/\gamma}+\frac {\|\widetilde{u}_{n}\|_{\infty}^{\frac{2\gamma}{2\alpha-\gamma}}}{\frac {2\alpha}{2\alpha-\gamma}}. $$

From the above, we have

$$\begin{aligned} \|\widetilde{u}_{n}\|\geq{}&\bigl\langle J'(u_{n}), \widetilde{u}_{n}\bigr\rangle \geq \frac{3}{4} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{2}-C_{4}| \overline{u}_{n}|^{2\alpha}-C_{5}\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}-C_{6} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2} \\ &{}-amC\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}-2bm\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\gamma +1}-C_{7}| \overline{u}_{n}|^{2\alpha}-C_{8}\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\frac {2\alpha}{2\alpha-\gamma}}. \end{aligned}$$

On the other hand, in view of (2.2), we have

$$\begin{aligned} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{2}& \leq \|\widetilde{u}_{n}\|^{2}= \int_{0}^{T}p \bigl(\widetilde{u}_{n}' \bigr)^{2}\,dt+ \int _{0}^{T}(\widetilde{u}_{n})^{2} \,dt \\ &\leq \int_{0}^{T}p \bigl(\widetilde{u}_{n}' \bigr)^{2}\,dt+\frac{1}{\mu_{1}} \int_{0}^{T}p \bigl(\widetilde {u}_{n}' \bigr)^{2}\,dt= \biggl(1+\frac{1}{\mu_{1}} \biggr)\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}. \end{aligned}$$

(3.4)

So,

$$C\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}\geq \frac{3}{4}\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{2}-(C_{4}+C_{7})| \overline{u}_{n}|^{2\alpha }-C_{5}\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}-amC\bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}, $$

which means

$$ C_{9}|\overline{u}_{n}|^{\alpha}\geq \| \widetilde{u}_{n}'\|_{p,2}-C_{10}. $$

(3.5)

Like in the proof of Theorem 3.1, we have

$$ \biggl| \int_{0}^{T} \bigl[F(t,u_{n})-F(t, \overline{u}_{n}) \bigr]\,dt\biggr|\leq \frac{1}{4}\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}+C_{4}| \overline{u}_{n}|^{2\alpha}+C_{5} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}+C_{6} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}. $$

(3.6)

By the boundedness of $\{J(u_{n})\}$, (H7), (3.5), and (3.6), there exists a constant C such that

$$\begin{aligned} C&\leq J(u_{n})= \frac{1}{2} \int_{0}^{T}p\bigl(u_{n}' \bigr)^{2}\,dt- \int_{0}^{T}F(t,u_{n})\,dt +\sum _{k=0}^{m} \int_{0}^{u_{n}(t_{k})}I_{k}(s)\,ds \\ &\leq \frac{1}{2}\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}- \int _{0}^{T}\bigl[F(t,u_{n})-F(t, \overline{u}_{n})\bigr]\,dt- \int_{0}^{T}F(t,\overline{u}_{n})\,dt \\ &\leq \frac{3}{4}\bigl\| \widetilde{u}_{n}' \bigr\| _{p,2}^{2}+C_{4}|\overline {u}_{n}|^{2\alpha}+C_{5} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}^{\alpha+1}+C_{6} \bigl\| \widetilde{u}_{n}'\bigr\| _{p,2}- \int_{0}^{T} F(t,\overline{u})\,dt \\ &\leq |\overline{u}_{n}|^{2\alpha}\biggl(-|\overline{u}_{n}|^{2\alpha} \int_{0}^{T} F(t,\overline{u}_{n}) \,dt+C_{11}\biggr). \end{aligned}$$

(3.7)

It follows from (3.7) and (H8) that $\{|\overline{u}_{n}|\}$ is bounded. Hence $\{u_{n}\}$ is bounded in $W_{p,T}^{1,2}$ by (3.5). Therefore, there exists a subsequence of ${u_{n}}$ (for simplicity denoted again by $\{u_{n}\}$) such that

$$ u_{n}\rightharpoonup u \quad \mbox{in } W_{p,T}^{1,2}. $$

(3.8)

By Proposition 2.1, one has

$$ u_{n}\rightarrow u \quad\mbox{in } C[0, T]. $$

(3.9)

On the other hand, we have

$$\begin{aligned} \bigl\langle J'(u_{n})-J'(u), u_{n}-u \bigr\rangle ={}& \int_{0}^{T}p \bigl(u_{n}'-u' \bigr)^{2}\,dt - \int_{0}^{T} \bigl(f(t,u_{n})-f(t,u) \bigr) (u_{n}-u)\,dt \\ &{}+\sum_{k=1}^{m} \bigl(I_{k} \bigl(u_{n}(t_{k}) \bigr)-I_{k} \bigl(u(t_{k}) \bigr) \bigr) \bigl(u_{n}(t_{k})-u(t_{k}) \bigr). \end{aligned}$$

(3.10)

From (3.8)-(3.10), (H), and the continuity of $I_{k}$, it follows that $u_{n}\rightarrow u$ in $W_{p,T}^{1,2}$. Thus, J satisfies the P.S. condition. □

Now, we prove Theorem 3.3.

Proof

From Section 2, we know $W_{p,T}^{1,2}=\overline{W}\oplus \widetilde{W}$. We show that

$$ J(u)\rightarrow+\infty \quad\mbox{as } u\in\widetilde{W}, \|u\|\rightarrow \infty. $$

(3.11)

If $u\in\widetilde{W}$, then $\overline{u}=0$. Like in the proof of Theorem 3.1, we have

$$ \biggl| \int_{0}^{T} \bigl[F(t,u)-F(t,0) \bigr]\,dt\biggr|\leq \frac{1}{4}\bigl\| {u}'\bigr\| _{p,2}^{2}+C_{5} \bigl\| {u}'\bigr\| _{p,2}^{\alpha+1}+C_{6} \bigl\| u'\bigr\| _{p,2}. $$

(3.12)

By (H6) and (2.1) we find

$$\begin{aligned} \psi(u)&:=\sum_{k=1}^{m} \int_{0}^{u(t_{k})}I_{k}(s)\,ds\leq \sum _{k=1}^{m} \int_{0}^{u(t_{k})} \bigl(a_{k}+b_{k}|s|^{\gamma} \bigr)\,ds \\ &\leq am\|u\|_{\infty}+b\sum_{k=1}^{m} \|u\|_{\infty}^{\gamma+1} \\ &\leq amC\bigl\| u'\bigr\| _{p,2}+b\sum_{k=1}^{m} \bigl\| u'\bigr\| _{p,2}^{\gamma+1}, \end{aligned}$$

(3.13)

for all $u\in\widetilde{W}$. It follows from (3.12) and (3.13) that

$$\begin{aligned} J(u)&= \frac{1}{2} \int_{0}^{T} pu^{\prime2}\,dt- \int_{0}^{T}\bigl[F(t,u)-F(t,0)\bigr]\,dt- \int_{0}^{T} F(t,0)\,dt+\psi(u) \\ &\geq \frac{1}{4}\bigl\| u'\bigr\| _{p,2}^{2}-C_{5} \bigl\| u'\bigr\| _{p,2}^{\alpha+1}-C_{6} \bigl\| u'\bigr\| _{p,2}-C_{7}\bigl\| u' \bigr\| _{p,2}-C_{8} \sum_{k=1}^{m} \bigl\| u'\bigr\| _{p,2}^{\gamma+1} \end{aligned}$$

(3.14)

for all $u\in\widetilde{W}$. Hence, (3.11) follows from (3.4) and (3.14).

On the other hand, by (H7), we obtain

$$ \psi(u)\leq0 $$

(3.15)

for all $u\in W_{p,T}^{1,2}$. Hence, by (3.15) and (H8), one has

$$\begin{aligned} J(u)&=- \int_{0}^{T}F(t,u)\,dt+\psi(u) \\ &\leq|u|^{2\alpha}\biggl[-|u|^{-2\alpha} \int_{0}^{T} F(t,u)\,dt\biggr]\rightarrow-\infty \end{aligned}$$

as $|u|\rightarrow\infty$ in $\mathbb{R}$. By Theorem 2.2 and Lemma 3.1, problem (1.1a)-(1.1c) has at least one weak solution. □