Abstract
We study the strong convergence of two kinds of viscosity iteration processes for approximating common fixed points of the pseudocontractive semigroup in uniformly convex Banach spaces with uniformly Gâteaux differential norms. As special cases, we get the strong convergence of the implicit viscosity iteration process for approximating common fixed points of the nonexpansive semigroup in Banach spaces satisfying some conditions. The results presented in this paper extend and generalize some results concerned with the nonexpansive semigroup in (Chen and He, 2007) and the pseudocontractive mapping in (Zegeye et al., 2007) to the pseudocontractive semigroup in Banach spaces under different conditions.
Similar content being viewed by others
1. Introduction
Let  be a real Banach space with the dual space
be a real Banach space with the dual space  and
and  be a normalized duality mapping defined by
be a normalized duality mapping defined by

where  denotes the generalized duality pairing. It is well known that (see, e.g., [1, pages 107–113])
denotes the generalized duality pairing. It is well known that (see, e.g., [1, pages 107–113])
(i) is single-valued if
is single-valued if  is strictly convex;
is strictly convex;
(ii) is uniformly smooth if and only if
is uniformly smooth if and only if  is single-valued and uniformly continuous on any bounded subset of
is single-valued and uniformly continuous on any bounded subset of  .
.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . A mapping
. A mapping  is said to be
is said to be
-
(i)
nonexpansive if
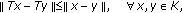 (1.2)
(1.2)
(ii) -Lipschitzian if there exists a constant
-Lipschitzian if there exists a constant  such that
such that

(iii) -strongly pseudocontractive if there exist a constant
-strongly pseudocontractive if there exist a constant  and
and  such that
such that

(iv)pseudocontractive if there exists  such that
such that

It is easy to see that the pseudocontractive mapping is more general than the nonexpansive mapping.
A pseudocontractive semigroup is a family,

of self-mappings on  such that
such that
(1) for all
for all  ;
;
(2) for all
for all  and
and  ;
;
(3) is pseudocontractive for each
is pseudocontractive for each  ;
;
(4)for each  , the mapping
, the mapping  from
from  into
into  is continuous.
is continuous.
If the mapping  in condition (3) is replaced by
in condition (3) is replaced by
 is nonexpansive for each
is nonexpansive for each  ;
;
then  is said to be a nonexpansive semigroup on
is said to be a nonexpansive semigroup on  .
.
We denote by  the common fixed points set of pseudocontractive semigroup
the common fixed points set of pseudocontractive semigroup  , that is,
, that is,

In the sequel, we always assume that  .
.
In recent decades, many authors studied the convergence of iterative algorithms for nonexpansive mappings, nonexpansive semigroup, and pseudocontractive mapping in Banach spaces (see, e.g., [2–14]). Let  be a nonexpansive semigroup from
be a nonexpansive semigroup from  into itself and
into itself and  be a contractive mapping. It follows from Banach's fixed theorem that the following implicit viscosity iteration process is well defined:
be a contractive mapping. It follows from Banach's fixed theorem that the following implicit viscosity iteration process is well defined:

where  and
and  . Some authors studied the convergence of iteration process (1.8) for nonexpansive mappings in certain Banach spaces (see [5, 10]). Recently, Xu [11] studied the following implicit iteration process: for any
. Some authors studied the convergence of iteration process (1.8) for nonexpansive mappings in certain Banach spaces (see [5, 10]). Recently, Xu [11] studied the following implicit iteration process: for any  ,
,

where  ,
,  , and obtained the convergence theorem as follows.
, and obtained the convergence theorem as follows.
Theorem 1 (see [11]).
Let  be a uniformly convex Banach space having a weakly continuous duality map
be a uniformly convex Banach space having a weakly continuous duality map  with gauge
with gauge  ,
,  a nonempty closed convex subset of
a nonempty closed convex subset of  and
and

a nonexpansive semigroup on  such that
such that  . If
. If

then  generated by (1.9) converges strongly to a member of
generated by (1.9) converges strongly to a member of  .
.
Xu [11] also proposed the following problem.
Problem 1 (see [11]).
We do not know if Theorem X holds in a uniformly convex and uniformly smooth Banach (e.g.,  for
for ).
).
This problem has been solved by Li and Huang [15] and Suzuki [8], respectively.
Moudafi's viscosity approximation method has been recently studied by many authors (see, e.g., [2, 3, 5, 10, 13, 15–17] and the references therein). Chen and He [3] studied the convergence of (1.8) constructed from a nonexpansive semigroup and a contractive mapping in a reflective Banach space with a weakly sequentially continuous duality mapping. Zegeye et al. [13] studied the convergence of (1.8) constructed from a pseudocontractive mapping and a contractive mapping.
On the other hand, many authors (see [2, 3, 5, 13]) studied the following explicit viscosity iteration process: for any given  ,
,

where  ,
,  and
and  . Chen and He [3] studied the convergence of (1.12) constructed from a nonexpansive semigroup and obtained some convergence results.
. Chen and He [3] studied the convergence of (1.12) constructed from a nonexpansive semigroup and obtained some convergence results.
An interesting work is to extend some results involving nonexpansive mapping, nonexpansive semigroup, and pseudocontractive mapping to the semigroup of pseudocontractive mappings. Li and Huang [15] generalized some corresponding results to pseudocontractive semigroup in Banach spaces. Some further study concerned with approximating common fixed points of the semigroup of pseudocontractive mappings in Banach spaces, we refer to Li and Huang [16].
Motivated by the works mentioned above, in this paper, we study the convergence of implicit viscosity iteration process (1.8) constructed from the pseudocontractive semigroup  and
and  -strongly pseudocontractive mapping in uniformly convex Banach spaces with uniformly Gâteaux differential norms. As special cases, we obtain the convergence of the implicit iteration process for approximating the common fixed point of the nonexpansive semigroup in certain Banach spaces. We also study the convergence of the explicit viscosity iteration process (1.12) constructed from the pseudocontractive semigroup
-strongly pseudocontractive mapping in uniformly convex Banach spaces with uniformly Gâteaux differential norms. As special cases, we obtain the convergence of the implicit iteration process for approximating the common fixed point of the nonexpansive semigroup in certain Banach spaces. We also study the convergence of the explicit viscosity iteration process (1.12) constructed from the pseudocontractive semigroup  and
and  -strongly pseudocontractive mapping in uniformly convex Banach spaces with uniformly Gâteaux differential norms. The results presented in this paper extend and generalize some results concerned with the nonexpansive semigroup in [3] and the pseudocontractive mapping in [13] to the pseudocontractive semigroup in Banach spaces under different conditions.
-strongly pseudocontractive mapping in uniformly convex Banach spaces with uniformly Gâteaux differential norms. The results presented in this paper extend and generalize some results concerned with the nonexpansive semigroup in [3] and the pseudocontractive mapping in [13] to the pseudocontractive semigroup in Banach spaces under different conditions.
2. Preliminaries
A real Banach space  is said to have a weakly continuous duality mapping if
is said to have a weakly continuous duality mapping if  is single-valued and weak-to-
is single-valued and weak-to- sequentially continuous (i.e., if each
sequentially continuous (i.e., if each  is a sequence in
is a sequence in  weakly convergent to
weakly convergent to  , then
, then  converges
converges  to
to  ). Obviously, if
). Obviously, if  has a weakly continuous duality mapping, then
has a weakly continuous duality mapping, then  is norm-to-
is norm-to- sequentially continuous. It is well known that
sequentially continuous. It is well known that  posses duality mapping which is weakly continuous (see, e.g., [11]).
posses duality mapping which is weakly continuous (see, e.g., [11]).
Let  be the Banach space of all bounded real-valued sequences. A Banach limit
be the Banach space of all bounded real-valued sequences. A Banach limit  (see [1]) is a linear continuous functional on
(see [1]) is a linear continuous functional on  such that
such that

for each  . If
. If  is a Banach limit, then it follows from [1, Theorem 1.4.4] that
is a Banach limit, then it follows from [1, Theorem 1.4.4] that

for each  .
.
A mapping  with domain
with domain  and range
and range  in
in  is said to be demiclosed at a point
is said to be demiclosed at a point  if whenever
if whenever  is a sequence in
is a sequence in  which converges weakly to
which converges weakly to  and
and  converges strongly to
converges strongly to  , then
, then  .
.
For the sake of convenience, we restate the following lemmas that will be used.
Lemma 2.1 (see [18]).
Let  be a Banach space,
be a Banach space,  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and
, and  be a strongly pseudocontractive and continuous mapping. Then
be a strongly pseudocontractive and continuous mapping. Then  has a unique fixed point in
has a unique fixed point in  .
.
Lemma 2.2 (see [19]).
Let  be a Banach space and
be a Banach space and  be the normalized duality mapping. Then for any
be the normalized duality mapping. Then for any  and
and  ,
,

Lemma 2.3 (see [12]).
Let  . Then a real Banach space
. Then a real Banach space  is uniformly convex if and only if there exists a continuous and strictly increasing convex function
is uniformly convex if and only if there exists a continuous and strictly increasing convex function  with
with  such that
such that

for all  ,
,  , where
, where  .
.
Lemma 2.4 (see [9]).
Let  be a sequence of nonnegative real numbers such that
be a sequence of nonnegative real numbers such that

where  ,
,  ,
,  is fixed,
is fixed,  , and
, and  . Then
. Then  .
.
3. Main Results
We first discuss the convergence of implicit viscosity iteration process (1.8) constructed from a pseudocontractive semigroup  .
.
Theorem 3.1.
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . Let
. Let  be an
be an  -Lipschitzian semigroup of pseudocontractive mappings and
-Lipschitzian semigroup of pseudocontractive mappings and  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that for any bounded subset
-strongly pseudocontractive mapping. Suppose that for any bounded subset  ,
,

Then the sequence  generated by (1.8) is well defined. Moreover, if
generated by (1.8) is well defined. Moreover, if

then  for any
for any  .
.
Proof.
Let

Since

we know that  is strongly pseudocontractive and strongly continuous. It follows from Lemma 2.1 that
is strongly pseudocontractive and strongly continuous. It follows from Lemma 2.1 that  has a unique fixed point (say)
has a unique fixed point (say)  , that is,
, that is,  generated by (1.8) is well defined.
generated by (1.8) is well defined.
Taking  , we have
, we have

and so  . This means
. This means  is bounded. By the Lipschitzian conditions of
is bounded. By the Lipschitzian conditions of  and
and  , it follows that
, it follows that  and
and  are bounded. Therefore,
are bounded. Therefore,

For any given  ,
,

where  is the integral part of
is the integral part of  . Since
. Since  and
and  is continuous for any
is continuous for any  , it follows from (3.1) that
, it follows from (3.1) that

This completes the proof.
Theorem 3.2.
Let  be a uniformly convex Banach space with the uniformly Gâteaux differential norm and
be a uniformly convex Banach space with the uniformly Gâteaux differential norm and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be an
be an  -Lipschitzian semigroup of pseudocontractive mappings satisfying (3.1) and let
-Lipschitzian semigroup of pseudocontractive mappings satisfying (3.1) and let  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that
-strongly pseudocontractive mapping. Suppose that  is a sequence generated by (1.8) and
is a sequence generated by (1.8) and
(1) ;
;
(2) , where
, where  with
with  for all
for all  .
.
Then  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  that is the unique solution in
that is the unique solution in  to the following variational inequality:
to the following variational inequality:

Proof.
From Theorem 3.1, we know that  is bounded and
is bounded and  . It is easy to see that
. It is easy to see that  is a nonempty bounded closed convex subset of
is a nonempty bounded closed convex subset of  (see, e.g., [10]).
(see, e.g., [10]).
Now, we show that there exists a common fixed point of  in
in  . For any
. For any  and
and  , it follows from
, it follows from  that
that

and so

Next, we prove that  is a singleton. In fact, since
is a singleton. In fact, since  is uniformly convex, by Lemma 2.3 that there exists a continuous and strictly increasing convex function
is uniformly convex, by Lemma 2.3 that there exists a continuous and strictly increasing convex function  with
with  such that, for any
such that, for any  and
and  ,
,

Taking Banach limit  on the above inequality, it follows that
on the above inequality, it follows that

This implies  and so
and so  is a singleton. Therefore, (3.11) implies that there exists
is a singleton. Therefore, (3.11) implies that there exists  such that
such that  .
.
For any  , from (1.8), we have
, from (1.8), we have

Since  , it follows from (3.14) that
, it follows from (3.14) that

Furthermore, for any  , by Lemma 2.2, we have
, by Lemma 2.2, we have

For any  , since
, since  has a uniformly Gâteaux differential norm, we know that
has a uniformly Gâteaux differential norm, we know that  is norm-to-
is norm-to- uniformly continuous on any bounded subset of
uniformly continuous on any bounded subset of  (see, e.g., [1, pages 107–113]) and so there exists sufficient small
(see, e.g., [1, pages 107–113]) and so there exists sufficient small  such that
such that

This implies that

By the arbitrariness of  , it follows that
, it follows that

Adding inequalities (3.15) and (3.19), we have

This implies that there exists subsequence  which converges strongly to
which converges strongly to  . From the proof of (3.20), we know that
. From the proof of (3.20), we know that  for any subsequence
for any subsequence  and so there exists subsequence of
and so there exists subsequence of  which converges strongly to
which converges strongly to  . If there exists another subsequence
. If there exists another subsequence  which converges strongly to
which converges strongly to  , then it follows from Theorem 3.1 that
, then it follows from Theorem 3.1 that  . From (3.14), we have
. From (3.14), we have

Thus

This implies that  and so
and so  . Therefore,
. Therefore,  converges strongly to
converges strongly to  . From (3.14) and the deduction above, we know that
. From (3.14) and the deduction above, we know that  is also the unique solution to the variational inequlity
is also the unique solution to the variational inequlity

This completes the proof.
Remark 3.3.
-
(1)
Theorem 3.2 extends and generalizes Theorem 3.1 of [3] from nonexpansive semigroup to Lipschitzian pseudocontractive semigroup in Banach spaces with different conditions; (2) If
 is a pseudocontractive mapping, then condition (3.1) is trivial.
is a pseudocontractive mapping, then condition (3.1) is trivial.
If  is a nonexpansive semigroup, then
is a nonexpansive semigroup, then  is an
is an  -Lipschitzian semigroup of pseudocontractive mappings, condition
-Lipschitzian semigroup of pseudocontractive mappings, condition  of Theorem 3.2 holds trivially. From Theorem 3.2, we have the following result.
of Theorem 3.2 holds trivially. From Theorem 3.2, we have the following result.
Corollary 3.4.
Let  be a uniformly convex Banach space with the uniformly Gâteaux differential norm and
be a uniformly convex Banach space with the uniformly Gâteaux differential norm and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a nonexpansive semigroup satisfying (3.1) and let
be a nonexpansive semigroup satisfying (3.1) and let  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that
-strongly pseudocontractive mapping. Suppose that  is a sequence generated by (1.8). If
is a sequence generated by (1.8). If

then  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  that is the unique solution in
that is the unique solution in  to VI (3.9).
to VI (3.9).
Theorem 3.5.
Let  be a uniformly smooth Banach space and
be a uniformly smooth Banach space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a nonexpansive semigroup satisfying (3.1) and let
be a nonexpansive semigroup satisfying (3.1) and let  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that
-strongly pseudocontractive mapping. Suppose that  is a sequence generated by (1.8). If
is a sequence generated by (1.8). If

then  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  that is the unique solution in
that is the unique solution in  to VI (3.9).
to VI (3.9).
Proof.
For the nonexpansive semigroup  , condition
, condition  of Theorem 3.2 is trivial and so formula (3.11) holds. Since uniformly smooth Banach space
of Theorem 3.2 is trivial and so formula (3.11) holds. Since uniformly smooth Banach space  has the fixed point property for nonexpansive mapping
has the fixed point property for nonexpansive mapping  (see, e.g., [10]),
(see, e.g., [10]),  has a fixed point
has a fixed point  . The rest proof is similar to the proof of Theorem 3.2 and so we omit it. This completes the proof.
. The rest proof is similar to the proof of Theorem 3.2 and so we omit it. This completes the proof.
Theorem 3.6.
Let  be a real Hilbert space and
be a real Hilbert space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be an
be an  -Lipschitzian semigroup of pseudocontractive mappings satisfying (3.1) and let
-Lipschitzian semigroup of pseudocontractive mappings satisfying (3.1) and let  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that
-strongly pseudocontractive mapping. Suppose that  is a sequence generated by (1.8). If
is a sequence generated by (1.8). If

then  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  that is the unique solution in
that is the unique solution in  to the following variational inequality:
to the following variational inequality:

Proof.
From the proof of Theorem 3.1, we know that  is bounded and so there exists subsequence
is bounded and so there exists subsequence  which converges weakly to some point
which converges weakly to some point  . By Theorem 3.1, we have
. By Theorem 3.1, we have

It follows from [20, Theorem 3.18b] that  is demiclosed at zero for each
is demiclosed at zero for each  , where
, where  is an identity mapping. This implies that
is an identity mapping. This implies that  .
.
In addition, from (1.8), we have

and so

This implies that  converges strongly to
converges strongly to  . Similar to the proof of Theorem 3.2, it is easy to show that
. Similar to the proof of Theorem 3.2, it is easy to show that  converges strongly to
converges strongly to  that is also the unique solution to VI (3.27). This completes the proof.
that is also the unique solution to VI (3.27). This completes the proof.
Now we turn to discuss the convergence of explicit viscosity iteration process (1.12) for approximating the common fixed point of the pseudocontractive semigroup  .
.
Theorem 3.7.
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . Let
. Let  be an
be an  -Lipschitzian semigroup of pseudocontractive mappings with
-Lipschitzian semigroup of pseudocontractive mappings with  such that (3.1) holds. Let
such that (3.1) holds. Let  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that the sequence
-strongly pseudocontractive mapping. Suppose that the sequence  is generated by (1.12) and the following conditions hold:
is generated by (1.12) and the following conditions hold:
(i) ,
,  , for all
, for all  ;
;
(ii) ,
,  ,
, 
 ;
;
-
(iii)
there exists some constant
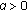 such that
such that  (3.31)
(3.31)
(iv)The following equation holds:

Then  for any
for any  .
.
Proof.
Let  denote the sequence defined as in (1.8) with
denote the sequence defined as in (1.8) with  . By virtue of condition (ii) and Theorem 3.1, we know that
. By virtue of condition (ii) and Theorem 3.1, we know that  is well defined and
is well defined and  for any
for any  . From (1.8), we have
. From (1.8), we have


To obtain the assertion of Theorem 3.7, we first give a serial of estimations: using (3.33), we get

which implies that

where  . From the proof of Theorem 3.1, we know that
. From the proof of Theorem 3.1, we know that  is bounded. Therefore, there exists a constant
is bounded. Therefore, there exists a constant  such that
such that

By using (1.12) and (3.33), we have

It follows from (1.12) and (3.34) that

By virtue of (1.12), (3.34), and Lemma 2.2, we have

Since  , then
, then  by condition (iii). Thus for sufficient large
by condition (iii). Thus for sufficient large  , we know
, we know

Consequently, by condition (iv) we can have

Squaring on both sides of (3.42) and using (3.37), we get

Setting  and
and  , then it follows from conditions (i)–(iv) that
, then it follows from conditions (i)–(iv) that

By Lemma 2.4, we know that  , which implies that
, which implies that

Consequently, since  by (3.37), we have
by (3.37), we have

Now we prove that  for any
for any  . Since
. Since

by Theorem 3.1 and (3.46) we know that for any  ,
,

This completes the proof.
Remark 3.8.
An example for the conditions (i)–(iii) of Theorem 3.7 is given by

for all  , where
, where  is an any given positive real number. It is easy to see that the conditions with regard to
is an any given positive real number. It is easy to see that the conditions with regard to  and
and  in Theorem 3.7 hold. If the mapping
in Theorem 3.7 hold. If the mapping  is Lipschitz continuous for any
is Lipschitz continuous for any  , then condition (iv) in Theorem 3.7 also holds.
, then condition (iv) in Theorem 3.7 also holds.
Theorem 3.9.
Let  be a uniformly convex Banach space with the uniformly Gâteaux differential norm and
be a uniformly convex Banach space with the uniformly Gâteaux differential norm and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be an
be an  -Lipschitzian semigroup of pseudocontractive mappings with
-Lipschitzian semigroup of pseudocontractive mappings with  such that (3.1) holds. Let
such that (3.1) holds. Let  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that the sequence
-strongly pseudocontractive mapping. Suppose that the sequence  is generated by (1.12) and conditions (i)–(iv) of Theorem 3.7 hold. Assume further that condition (2) of Theorem 3.2 holds, where
is generated by (1.12) and conditions (i)–(iv) of Theorem 3.7 hold. Assume further that condition (2) of Theorem 3.2 holds, where  is generated by (1.8) with
is generated by (1.8) with  . Then
. Then  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  that is the unique solution in
that is the unique solution in  to VI (3.9).
to VI (3.9).
Proof.
By Theorem3.2, we know that  converges strongly to a fixed point
converges strongly to a fixed point  of
of  that is the unique solution in
that is the unique solution in  to VI (3.9), where
to VI (3.9), where  is generated by (1.8) with
is generated by (1.8) with  . It follows from (3.46) that
. It follows from (3.46) that  . This completes the proof.
. This completes the proof.
Remark 3.10.
-
(1)
Theorem 3.9 extends Theorem 4.1 of [13] from Lipschitzian pseudocontractive mapping to Lipschitzian pseudocontractive semigroup in Banach spaces under different conditions; (2) Theorem 3.9 also extends Theorem 3.2 of [3] from nonexpansive semigroup to Lipschitzian pseudocontractive semigroup in Banach spaces under different conditions.
If  is a nonexpansive semigroup, then
is a nonexpansive semigroup, then  is an
is an  -Lipschitzian semigroup of pseudocontractive mappings, condition
-Lipschitzian semigroup of pseudocontractive mappings, condition  of Theorem 3.2 holds trivially. Therefore, Theorem 3.9 gives the following result.
of Theorem 3.2 holds trivially. Therefore, Theorem 3.9 gives the following result.
Corollary 3.11.
Let  be a uniformly convex Banach space with the uniformly Gâteaux differential norm and
be a uniformly convex Banach space with the uniformly Gâteaux differential norm and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a nonexpansive semigroup satisfying (3.1) and
be a nonexpansive semigroup satisfying (3.1) and  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that the sequence
-strongly pseudocontractive mapping. Suppose that the sequence  is generated by (1.12) and conditions (i)–(iv) of Theorem 3.7 hold. Then
is generated by (1.12) and conditions (i)–(iv) of Theorem 3.7 hold. Then  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  that is the unique solution in F(T) to VI (3.9).
that is the unique solution in F(T) to VI (3.9).
Theorem 3.12.
Let  be a uniformly smooth Banach space and
be a uniformly smooth Banach space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a nonexpansive semigroup satisfying (3.1) and let
be a nonexpansive semigroup satisfying (3.1) and let  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that the sequence
-strongly pseudocontractive mapping. Suppose that the sequence  is generated by (1.12) and conditions (i)–(iv) of Theorem 3.7 hold. Then
is generated by (1.12) and conditions (i)–(iv) of Theorem 3.7 hold. Then  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  that is the unique solution in
that is the unique solution in  to VI (3.9).
to VI (3.9).
Proof.
Let  denote the sequence defined as in (1.8) with
denote the sequence defined as in (1.8) with  . By Theorem 3.5, we know that
. By Theorem 3.5, we know that  converges strongly to a fixed point
converges strongly to a fixed point  of
of  that is the unique solution in
that is the unique solution in  to VI (3.9). It follows from (3.46) that
to VI (3.9). It follows from (3.46) that  . This completes the proof.
. This completes the proof.
Theorem 3.13.
Let  be a real Hilbert space and
be a real Hilbert space and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be an
be an  -Lipschitzian semigroup of pseudocontractive mappings with
-Lipschitzian semigroup of pseudocontractive mappings with  such that (3.1) holds. Let
such that (3.1) holds. Let  be an
be an  -Lipschitzian
-Lipschitzian  -strongly pseudocontractive mapping. Suppose that the sequence
-strongly pseudocontractive mapping. Suppose that the sequence  is generated by (1.12) and conditions (i)–(iv) of Theorem 3.7 hold. Then
is generated by (1.12) and conditions (i)–(iv) of Theorem 3.7 hold. Then  converges strongly to a common fixed point
converges strongly to a common fixed point  of
of  that is the unique solution in
that is the unique solution in  to VI (3.27).
to VI (3.27).
Proof.
Let  denote the sequence defined as in (1.8) with
denote the sequence defined as in (1.8) with  . By Theorem 3.6, we know that
. By Theorem 3.6, we know that  converges strongly to a fixed point
converges strongly to a fixed point  of
of  that is the unique solution in
that is the unique solution in  to VI (3.27). It follows from (3.46) that
to VI (3.27). It follows from (3.46) that  . This completes the proof.
. This completes the proof.
References
Takahashi W: Nonlinear Functional Analysis. Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Chang S-S: Viscosity approximation methods for a finite family of nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 2006,323(2):1402–1416. 10.1016/j.jmaa.2005.11.057
Chen R, He H: Viscosity approximation of common fixed points of nonexpansive semigroups in Banach space. Applied Mathematics Letters 2007,20(7):751–757. 10.1016/j.aml.2006.09.003
Huang N-j, Bai M-R: A perturbed iterative procedure for multivalued pseudo-contractive mappings and multivalued accretive mappings in Banach spaces. Computers & Mathematics with Applications 1999,37(6):7–15. 10.1016/S0898-1221(99)00072-3
Jung JS: Viscosity approximation methods for a family of finite nonexpansive mappings in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications. Series A 2006,64(11):2536–2552. 10.1016/j.na.2005.08.032
Reich S: Strong convergence theorems for resolvents of accretive operators in Banach spaces. Journal of Mathematical Analysis and Applications 1980,75(1):287–292. 10.1016/0022-247X(80)90323-6
Suzuki T: On strong convergence to common fixed points of nonexpansive semigroups in Hilbert spaces. Proceedings of the American Mathematical Society 2003,131(7):2133–2136. 10.1090/S0002-9939-02-06844-2
Suzuki T: Browder's type convergence theorems for one-parameter semigroups of nonexpansive mappings in Banach spaces. Israel Journal of Mathematics 2007,157(1):239–257. 10.1007/s11856-006-0010-6
Weng X: Fixed point iteration for local strictly pseudo-contractive mapping. Proceedings of the American Mathematical Society 1991,113(3):727–731. 10.1090/S0002-9939-1991-1086345-8
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Xu H-K: A strong convergence theorem for contraction semigroups in Banach spaces. Bulletin of the Australian Mathematical Society 2005,72(3):371–379. 10.1017/S000497270003519X
Xu H-K, Ori RG: An implicit iteration process for nonexpansive mappings. Numerical Functional Analysis and Optimization 2001,22(5–6):767–773. 10.1081/NFA-100105317
Zegeye H, Shahzad N, Mekonen T: Viscosity approximation methods for pseudocontractive mappings in Banach spaces. Applied Mathematics and Computation 2007,185(1):538–546. 10.1016/j.amc.2006.07.063
Zeng W-Y, Huang N-j, Zhao C-W: Viscosity approximation methods for generalized mixed equilibrium problems and fixed points of a sequence of nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-15.
Li X-s, Huang N-j: Strong convergence theorems for fixed points of pseudo-contractive semigroup. Bulletin of the Australian Mathematical Society 2007,76(3):441–452.
Li X-s, Huang N-j: Viscosity approximation methods for pseudo-contractive semigroup in Banach spaces. In Research Report. Sichuan University, Chengdu, China; 2007.
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Deimling K: Zeros of accretive operators. Manuscripta Mathematica 1974,13(4):365–374. 10.1007/BF01171148
Petryshyn WV: A characterization of strict convexity of Banach spaces and other uses of duality mappings. Journal of Functional Analysis 1970, 6: 282–291. 10.1016/0022-1236(70)90061-3
Browder FE: Nonlinear mappings of nonexpansive and accretive type in Banach spaces. Bulletin of the American Mathematical Society 1967, 73: 875–882. 10.1090/S0002-9904-1967-11823-8
Acknowledgments
This work was supported by the National Science Foundation of China (10671135, 70831005), the Specialized Research Fund for the Doctoral Program of Higher Education (20060610005) and the Open Fund (PLN0703) of State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, Xs., Kim, J.K. & Huang, Nj. Viscosity Approximation of Common Fixed Points for  -Lipschitzian Semigroup of Pseudocontractive Mappings in Banach Spaces.
J Inequal Appl 2009, 936121 (2009). https://doi.org/10.1155/2009/936121
-Lipschitzian Semigroup of Pseudocontractive Mappings in Banach Spaces.
J Inequal Appl 2009, 936121 (2009). https://doi.org/10.1155/2009/936121
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/936121



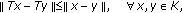
 is a pseudocontractive mapping, then condition (3.1) is trivial.
is a pseudocontractive mapping, then condition (3.1) is trivial.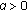 such that
such that 