1 Introduction

      Waveguides that are filled with plasma [1,2,3,4,5,6,7,8,9] have been received more attention from engineers, mathematicians, and physical researchers because of their applications in communications, astronomy, technological, and technical industries. TM and TE modes are allowed inside these waveguides where the components of electromagnetic fields are found when \(H_{z}\ne 0\) or \(E_{z}\ne 0\) and \(E_{z}=0\) or \(H_{z}=0\). The behavior of the EM wave is based on the propagating medium, so plasma is an excited background for propagation. Fractional dimensional space is of great interest for physical applications, such as optical systems, high-power millimeter generation, radar imaging, high-density information transmission, and wave amplifiers by exciting plasma electromagnetic (EM) waves. Common waveguides are broadly classified as either rectangular waveguides or cylindrical waveguides. Solving the Helmholtz equation is very important in the fractional space to generalize the solution from non-integer to the usual integer space. Fractional calculus and solving fractional differential equations are discussed in [10,11,12,13,14,15,16,17,18,19,20,21].

The new part of this work is to solve the wave equation in fractional space and use other techniques such as local fractional derivative \(\left( \text { LFD}\right) \). These generalized solutions are useful to check the validity of classical results. This paper is to extend the works of [6, 22] in rectangular waveguide and optics. This paper is organized as follows: Sect. 1 represents an introduction; Sect. 2 focuses on the mathematical formulation of the problem including Cherenkov resonance condition, governing equations, TM mode; Sect. 3 includes the Exact solution of the wave equation in fractional D-dimensional space with discussion, Sect. 4, is devoted to classical results with discussion; Sect. 5 aims to find the Exact solution of the wave equation using local fractional derivative \(\left( \text {LFD}\right) \), and Sect. 6 is devoted to the conclusion.

2 Problem formulation

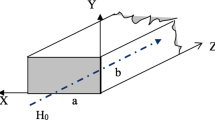
      For surveillance, the attenuation and the field stability in the rectangular waveguide of dimensions \(\left( a\ \times b\right) \) cm\(^{2},\) the Cherenkov free electron laser beam can be injected into the rectangular waveguide filled with warm plasma. The TM mode that propagates through this waveguide has a finite z-component electrical field. In order to transform an electron beam into EM energy, it should be passed through an FEL traveling-wave tube (FELTWT). Figure 1 shows a schematic of the C-FEL beam when the source of the beam is ready to emit electrons into the rectangular waveguide. Here, the aim is to investigate the C-FEL beam’s interaction with the plasma’s electrons to produce the EM wave and then see how this wave’s amplitude can be excited in fractional dimensional space. This procedure is similar to two-stream instability. In this analysis, electron electrohydrodynamics (E-EHD) has been considered for the warm plasma model, in which its basic equations are the continuity equation, motion equation, and Maxwell equations. E-EHD may be extended to include the effects of density perturbation of the interaction between C-FEL and warm plasma inside the rectangular waveguide.

Fig. 1
figure 1

Reaction of C-FEL with plasma-filled rectangular waveguide

Full size image

2.1 Cherenkov free electron laser (C-FEL)

      The C-FEL is a device that produces a wave that travels slower than an EM wave. The prospect of creating EM waves using a FEL beam from a Cherenkov device to adjust the field of the plasma-filled rectangular waveguide attenuation was studied using an analytical technique.

Cherenkov resonance condition: when an electron releases a photon from a wave with a frequency \(\omega \) and wave vector \({\textbf{K}}\), there is energy and momentum conservation; therefore, the following condition must be met:

$$\begin{aligned} \omega -{\textbf{V}}_{\alpha }\cdot {\textbf{K}}=0 \end{aligned}$$
(1)

where \({\textbf{V}}_{\alpha }\) denotes the velocity of the beam, FEL beam is supposed to be bundled and transfer the net energy/power to the EM wave at slow retardation times.

2.2 Governing equations and wave equation

Continuity equation

$$\begin{aligned} \frac{\partial N_{\alpha }}{\partial t}+\mathbf {\nabla \cdot }\left( N_{\alpha }{\textbf{V}}_{\alpha }\right) = 0 \end{aligned}$$
(2)

Momentum equation

$$\begin{aligned} \frac{d{\textbf{P}}}{dt}= & {} -e_{\alpha }\mathbf {E-}e_{\alpha }{\textbf{V}} _{\alpha }\times \mathbf {B-}\nu _{\alpha }{\textbf{V}}_{\alpha } \nonumber \\{} & {} -\frac{1}{N_{\alpha }m_{\alpha }}\mathbf {\nabla }p \end{aligned}$$
(3)

In order to calculate the fields of the mode, we use the following Maxwell’s equations, which obey harmonic time dependence \(e^{-i\omega t}\)            

$$\begin{aligned} \mathbf {\nabla \times E}&\mathbf {=}&i\omega \mu _{0}{\textbf{H}} \end{aligned}$$
(4)
$$\begin{aligned} \mathbf {\nabla \times H}&\mathbf {=}&N_{\alpha }e_{\alpha }{\textbf{V}} _{\alpha }\mathbf {-}i\omega \epsilon _{0}{\textbf{E}} \end{aligned}$$
(5)

Here the velocity \({\textbf{V}}_{\alpha }\) is calculated using the electron equation of motion as \({\textbf{V}}_{\alpha }\mathbf {=}\frac{e_{\alpha } {\textbf{E}}}{m_{\alpha }i\omega }\). Using this expression in Eq. (5), we get

$$\begin{aligned} \mathbf {\nabla \times H=-}\frac{N_{\alpha }e_{\alpha }^{2}{\textbf{E}}}{ m_{\alpha }i\omega }\mathbf {-}i\omega \epsilon _{0}\mathbf {E=-}i\omega \epsilon _{0}\epsilon _{r}{\textbf{E}} \end{aligned}$$
(6)

where \(N_{\alpha }\) is the plasma and beam electron density, \(m_{\alpha }\) is the rest mass, and \(\nu _{\alpha }\ \)is the collision frequency between \( e_{\alpha }\) and \(e_{\alpha }\), \(\epsilon _{r}\ \)stands for dielectric constant or relative permittivity, \(\epsilon _{0}\ \)for free space permittivity, \({\textbf{E}}\) for electric field intensity, \({\textbf{H}}\) for magnetic field intensity, \(\mathbf {\nabla }p\) for pressure gradient due to thermal effect, \(\omega \) is the C-FEL wave’s operating frequency, and \( {\textbf{P}}\) is the momentum where

$$\begin{aligned} {\textbf{P}}=m_{\alpha }\frac{{\textbf{V}}_{\alpha }}{\sqrt{1-\frac{ V_{\alpha }^{2}}{c^{2}}}} \end{aligned}$$

The wave equation can now be calculated using Maxwell’s equations (4) and (6) when the dielectric is loaded into the rectangular waveguide. After taking a curl of Eq. (4) and substituting from Eq. (6), we get

$$\begin{aligned} \nabla ^{2}\mathbf {E+}\varpi ^{2}{\textbf{E}}{\small =}{\textbf{0}} \end{aligned}$$
(7)

where \(\varpi ^{2}{\small =}\varpi _{x}^{2}+\varpi _{y}^{2}+\varpi _{z}^{2}=\mu _{0}\epsilon _{0}\epsilon _{r}\omega ^{2}.\) The wave constants in the x-direction, y-direction, and z-directionare \(\varpi _{x},\ \varpi _{y},\) and \(\varpi _{z}\) respectively.

2.3 TM mode

      There are two types of modes in the waveguides: transverse magnetic waves (TM-mode) with \(\mathbf {E=}\left( E_{x},E_{y},E_{z}\right) \) and \( \mathbf {H=}\left( H_{x},H_{y},0\right) \) and transverse electric modes (TE-mode) with \(\mathbf {E=}\left( E_{x},E_{y},0\right) \) and \(\textbf{H} = \left( H_{x},H_{y},H_{z}\right) \). Both modes need to satisfy Maxwell’s equations. We focus on the transverse magnetic (TM) mode where the magnetic field is transverse to the direction of propagation while the electric field is normal to the direction of propagation. So, the z-component of the wave equation is derived, and Eq. (7) becomes       

$$\begin{aligned} \nabla ^{2}E_{z}\left( x,y,z\right) {+}\varpi ^{2}E_{z}\left( x,y,z\right) { =}0 \end{aligned}$$
(8)

3 Exact solution of the wave equation in fractional D-dimensional space

      This research looks into propagation in the z-direction, so the electric and magnetic components are perpendicular to the propagation. The Laplacian operator in D-dimensional fractional space [19] can be written as

$$\begin{aligned} \nabla ^{2}= & {} \frac{\partial ^{2}}{\partial x^{2}}+\frac{\gamma _{1}-1}{x} \frac{\partial }{\partial x}+\frac{\partial ^{2}}{\partial y^{2}}+\frac{ \gamma _{2}-1}{y}\frac{\partial }{\partial y} \nonumber \\{} & {} +\frac{\partial ^{2}}{\partial z^{2}}+\frac{\gamma _{3}-1}{z}\frac{ \partial }{\partial z}. \end{aligned}$$
(9)

The solution was achieved in fractional D-dimensional space by inserting ( 9) into (8) as

$$\begin{aligned}{} & {} \frac{\partial ^{2}E_{z}\left( x,y,z\right) }{\partial x^{2}}+\frac{\gamma _{1}-1}{x}\frac{\partial E_{z}\left( x,y,z\right) }{\partial x} \nonumber \\{} & {} +\frac{\partial ^{2}E_{z}\left( x,y,z\right) }{\partial y^{2}}+\frac{ \gamma _{2}-1}{y}\frac{\partial E_{z}\left( x,y,z\right) }{\partial y} \nonumber \\{} & {} +\frac{\partial ^{2}E_{z}\left( x,y,z\right) }{\partial z^{2}}+\frac{ \gamma _{3}-1}{z}\frac{\partial E_{z}\left( x,y,z\right) }{\partial z} \nonumber \\{} & {} +\varpi ^{2}E_{z}\left( x,y,z\right) =0 \end{aligned}$$
(10)

where \(D=\gamma _{1}+\gamma _{2}+\gamma _{3}\) is the fractional parameter.

3.1 Method of solution

      Using the separation of variables method, Eq. (10) can be solved by assuming

$$\begin{aligned} E_{z}\left( x,y,z\right) =F\left( x\right) G\left( y\right) I\left( z\right) . \end{aligned}$$
(11)

As a result, the following ordinary differential equations emerge:

$$\begin{aligned}{} & {} \left( x^{2}\frac{\partial ^{2}}{\partial x^{2}}+x\left( \gamma _{1}-1\right) \frac{\partial }{\partial x}+\varpi _{x}^{2}x^{2}\right) {\small F}\left( x\right) \nonumber \\&{\small =}\,{\small 0} \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \left( y^{2}\frac{\partial ^{2}}{\partial y^{2}}+y\left( \gamma _{2}-1\right) \frac{\partial }{\partial y}+\varpi _{y}^{2}y^{2}\right) {\small G}\left( y\right) \nonumber \\&{\small =}\,{\small 0} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \left( z^{2}\frac{\partial ^{2}}{\partial z^{2}}+z\left( \gamma _{3}-1\right) \frac{\partial }{\partial z}+\varpi _{z}^{2}z^{2}\right) {\small I}\left( z\right) \nonumber \\&{\small =}\,{\small 0} \end{aligned}$$
(14)

where \(\varpi ^{2}{ =}\varpi _{x}^{2}+\varpi _{y}^{2}+\varpi _{z}^{2}\) is the total frequency of the wave.

Next, we solve the above equations to find the x-dependent part, y-dependent part, and z-dependent part. Equations (12–14) are a form of Bessel’s equation with the solution [6, 10]

$$\begin{aligned} F\left( x\right)= & {} x^{k_{1}}\left( C_{1}J_{k_{1}}\left( \varpi _{x}x\right) +C_{2}Y_{k_{1}}\left( \varpi _{x}x\right) \right) \nonumber \\{} & {} \end{aligned}$$
(15)
$$\begin{aligned} G\left( y\right)= & {} y^{k_{2}}\left( C_{3}J_{k_{2}}\left( \varpi _{y}y\right) +C_{4}Y_{k_{2}}\left( \varpi _{y}y\right) \right) \nonumber \\{} & {} \end{aligned}$$
(16)
$$\begin{aligned} I\left( z\right)= & {} z^{k_{3}}\left( C_{5}J_{k_{3}}\left( \varpi _{z}z\right) +C_{6}Y_{k_{3}}\left( \varpi _{z}z\right) \right) \end{aligned}$$
(17)

where

$$\begin{aligned} k_{1}= & {} 1-\frac{\gamma _{1}}{2},\ k_{2}=1-\frac{\gamma _{2}}{2}\ \text {, } \nonumber \\ \text {and \ \ }k_{3}= & {} 1-\frac{\gamma _{3}}{2} \end{aligned}$$
(18)

Then the complete solution \(E_{z}\left( x,y,z\right) \) denotes TM-mode propagation in a plasma-filled rectangular waveguide in fractional D-dimensional space takes the form

$$\begin{aligned}{} & {} E_{z}\left( x,y,z\right) =x^{k_{1}}y^{k_{2}}z^{k_{3}}\left[ C_{1}J_{k_{1}}\left( \varpi _{x}x\right) \right. \nonumber \\{} & {} \left. +C_{2}Y_{k_{1}}\left( \varpi _{x}x\right) \right] \nonumber \\{} & {} \times \left[ C_{3}J_{k_{2}}\left( \varpi _{y}y\right) +C_{4}Y_{k_{2}}\left( \varpi _{y}y\right) \right] \nonumber \\ \times{} & {} \left[ C_{5}J_{k_{3}}\left( \varpi _{z}z\right) +C_{6}Y_{k_{3}}\left( \varpi _{z}z\right) \right] \end{aligned}$$
(19)

where \(C_{1}-C_{6}\ \)are constants.

3.2 Results and discussion in fractional space

      Figures 2, 3, 4, 5, and 6 indicate the wave propagation within the fractional space at different values of the fractional parameters \(\gamma _{1},\ \gamma _{2},\ \)and \(\gamma _{3}.\) The total dimension of fractional space is denoted by D,  where \(D=\gamma _{1}+\gamma _{2}+\gamma _{3}\) at a specific frequency \(\varpi ^{2}=3\) for plasma and a certain length of propagation \( z=0\longrightarrow 50.\) The amplitude of the waves depends on the fractional distribution parameter D. Figure 2 shows the propagation at \(\gamma _{1}=\gamma _{2}=\gamma _{3}=\frac{1}{4}\) i.e., \(D=\frac{3}{4};\ \)the amplitude is gradually increasing toward of increasing this means that the signals entire the rectangular waveguide is very high comparing to the waveguide beginning. By increasing the fractional parameters in Fig. 3 compared to Fig. 2, we notice the vertical scale remains the same, unlike the other figures. Figure 4 displays the plasma distribution inside the wave guide at \(D=1.25\). It is noticed that the wave’s amplitude increases when the fractional distribution parameter approaches an integer value ( as a classical value). By continually increasing the wavelength of the electromagnetic spectrum, we may observe more than one type, such as gamma rays, X-rays, ultraviolet, visible infrared, microwaves, and radio waves. However, the rectangular waveguide is wideband and often microwave frequencies. The rectangular waveguide can transmit the signals power in communication such as telephone cables. TM-mode allows the cutoff frequency to be at the lowest frequency within the propagation. The open-ended waveguide has a flow/defect due to the presence of wave leakage rather than a cavity resonator. Figures 5 and 6 at various fractional parameters. It is necessary to report that the amplitude in Figs. 5 and 6 is higher than the amplitude in Figs. 2, 3 and 4. This is because of un-unique values for \(\gamma _{1},\ \gamma _{2},\ \)and \(\gamma _{3}.\) Therefore, by taking different values of fractional parameters, i.e., \(\gamma _{1}\ne \) \( \gamma _{2}\) or \(\gamma _{1}\ne \) \(\gamma _{3}\) or \(\gamma _{2}\ne \) \( \gamma _{3},\) we get a higher amplitude. This is important for designing and controlling the power of signals.

Fig. 2
figure 2

\(E_{z}\left( x,y,z\right) \ \text {in fractional space} \text {at }\gamma _{1}=\gamma _{2}=\gamma _{3}=\frac{1}{4}\ \text {of dimension} \text { }D=\frac{3}{4},\ \varpi ^{2}=3,\ \text {and }z=0\longrightarrow 50\)

Full size image
Fig. 3
figure 3

\(E_{z}\left( x,y,z\right) \ \text {in fractional space} \text {at }\gamma _{1}=\gamma _{2}=\ \gamma _{3}=\frac{1}{2}\text { of dimension} \,\, D=\frac{3}{2},\ \varpi ^{2}=3,\ \text {and }z=0\longrightarrow 50\)

Full size image
Fig. 4
figure 4

\(E_{z}\left( x,y,z\right) \ \text {in fractional space} \text {at }\gamma _{1}=\gamma _{2}=\frac{1}{2},\ \gamma _{3}=\frac{1}{4}\text { of dimension} \,\, D=\frac{5}{4},\ \varpi ^{2}=3,\ andz=0\longrightarrow 50\)

Full size image
Fig. 5
figure 5

\(E_{z}\left( x,y,z\right) \ \text {in fractional space} \text {at }\gamma _{1}=\frac{1}{3},\ \gamma _{2}=\ \gamma _{3}=\frac{2}{3} \text { of dimension} \text { }D=\frac{5}{3},\ \varpi ^{2}=3,\ \text {and }z=0\longrightarrow 50\)

Full size image
Fig. 6
figure 6

\(E_{z}\left( x,y,z\right) \ \text {in fractional space} \text {at }\gamma _{1}=\ \gamma _{2}=\frac{1}{4},\ \ \gamma _{3}=\frac{2}{3} \text { of dimension} \text { }D=\frac{7}{6},\ \varpi ^{2}=3,\ \text {and }z=0\longrightarrow 50\)

Full size image

4 Conversion the fractional D-dimension to usual integer dimension

4.1 Exact solution

      In order to find the exact solution in the usual three-dimensional integer space, we take \(\gamma _{1}\), \(\gamma _{2}\), and \(\gamma _{3}\) as follow if \(\gamma _{1}=1\)

$$\begin{aligned} F\left( x\right) =\sqrt{x}\left( C_{1}J_{\frac{1}{2}}\left( \varpi _{x}x\right) +C_{2}Y_{\frac{1}{2}}\left( \varpi _{x}x\right) \right) , \end{aligned}$$
(20)

if \(\gamma _{2}=1\)

$$\begin{aligned} G\left( y\right) =\sqrt{y}\left( C_{3}J_{\frac{1}{2}}\left( \varpi _{y}y\right) +C_{4}Y_{\frac{1}{2}}\left( \varpi _{y}y\right) \right) , \end{aligned}$$
(21)

if \(\gamma _{3}=1\)

$$\begin{aligned} I\left( z\right) =\sqrt{z}\left( C_{5}J_{\frac{1}{2}}\left( \varpi _{z}z\right) +C_{6}Y_{\frac{1}{2}}\left( \varpi _{z}z\right) \right) , \end{aligned}$$
(22)

where Bessel functions of order \(\frac{1}{2}\) is given by

$$\begin{aligned} J_{\frac{1}{2}}\left( x\right)= & {} \sqrt{\frac{2}{\pi x}}\sin \left( x\right) , \end{aligned}$$
(23)
$$\begin{aligned} Y_{\frac{1}{2}}\left( x\right)= & {} -\sqrt{\frac{2}{\pi x}}\cos \left( x\right) , \end{aligned}$$
(24)

as shown [6].

Using the expression of Eqs. (23, 24), then Eqs. (20–22) take the form:

$$\begin{aligned} F\left( x\right)= &\, C_{1}^{^{\prime }}\sin \left( \varpi _{x}x\right) -C_{2}^{^{\prime }}\cos \left( \varpi _{x}x\right) , \nonumber \\ \ C_{i}^{^{\prime }}= & {} C_{i}\ \sqrt{\frac{2}{\pi \varpi _{x}}}, \quad i=1,2 \end{aligned}$$
(25)
$$\begin{aligned} G\left( y\right)= & {} C_{3}^{^{\prime }}\sin \left( \varpi _{y}y\right) -C_{4}^{^{\prime }}\cos \left( \varpi _{y}y\right) ,\ \nonumber \\ C_{j}^{^{\prime }}= & {} C_{j}\ \sqrt{\frac{2}{\pi \varpi _{y}}},j=3,4 \end{aligned}$$
(26)
$$\begin{aligned} I\left( z\right)= & {} C_{5}^{^{\prime }}\sin \left( \varpi _{z}z\right) -C_{6}^{^{\prime }}\cos \left( \varpi _{z}z\right) ,\ \nonumber \\ C_{l}^{^{\prime }}= & {} C_{l}\ \sqrt{\frac{2}{\pi \varpi _{z}}},l=5,6. \end{aligned}$$
(27)

substituting from Eqs. ( 25–27) into Eq. ( 11), the exact solution \(E_{z}\left( x,y,z\right) \) in three-dimensional space \((D=3)\) is obtained as follows

$$\begin{aligned}{} & {} E_{z}\left( x,y,z\right) =\left[ C_{1}^{^{\prime }}\sin \left( \varpi _{x}x\right) -C_{2}^{^{\prime }}\cos \left( \varpi _{x}x\right) \right] \nonumber \\{} & {} \times \left[ C_{3}^{^{\prime }}\sin \left( \varpi _{y}y\right) -C_{4}^{^{\prime }}\cos \left( \varpi _{y}y\right) \right] \nonumber \\{} & {} \times \left[ C_{5}^{^{\prime }}\sin \left( \varpi _{z}z\right) -C_{6}^{^{\prime }}\cos \left( \varpi _{z}z\right) \right] \end{aligned}$$
(28)

4.2 Results and discussion in integer space

Classical results are shown in Fig. 7 when we select the usual integer values, i.e., \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1.\) This was unable to get us the Bessel functions of order 0.5. \(J_{\frac{1}{2}}\left( x\right) \) and \(Y_{ \frac{1}{2}}\left( x\right) \) are represented by sine and cosine waves and this in turn to classical waves. The usual waves appear at \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\) which means that the fractional parameters obeys to 3-D integer space. It is observed that the amplitude is unique and constant through the propagation.

Fig. 7
figure 7

\(E_{z}\left( x,y,z\right) \ \text {in fractional space} \text {at }\gamma _{1}=\gamma _{2}=\gamma _{3}=1\text { of dimension} \text { }D=3,\ \varpi ^{2}=3,\ \text {and }z=0\longrightarrow 50\)

Full size image

5 Exact solution using local fractional derivative (LFD)

5.1 Exact solution

      The local fractional derivative (LFD) of the function \( f\left( x\right) \) of order \(\beta \ \)at \(x=x_{0}\) is defined as [15]

$$\begin{aligned} f^{\beta }\left( x_{0}\right) \,= \,& {} \frac{\text {d}^{\beta }}{\textrm{d}x^{\beta }} f\left( x\right) |_{x=x_{0}} \nonumber \\= & {} \lim \limits _{x\longrightarrow x_{0}}\frac{\Delta ^{\beta }\left( f\left( x\right) -f\left( x_{0}\right) \right) }{\left( x-x_{0}\right) ^{\beta }} \end{aligned}$$
(29)

with

$$\begin{aligned}{} & {} \Delta ^{\beta }\left( f\left( x\right) -f\left( x_{0}\right) \right) \cong \nonumber \\{} & {} \Gamma \left( 1+\beta \right) \Delta \left( f\left( x\right) -f\left( x_{0}\right) \right) \end{aligned}$$
(30)

Now, the Laplacian operator for the three-dimensional coordinate system can be written as

$$\begin{aligned} \nabla ^{2\beta }=\frac{\partial ^{2\beta }}{\partial x^{2\beta }}+\frac{ \partial ^{2\beta }}{\partial y^{2\beta }}+\frac{\partial ^{2\beta }}{ \partial z^{2\beta }} \end{aligned}$$
(31)

Then, by inserting (31) into (8), the local fractional wave equation is given by

$$\begin{aligned}{} & {} \frac{\partial ^{2\beta }E_{z}\left( x,y,z\right) }{\partial x^{2\beta }}+ \frac{\partial ^{2\beta }E_{z}\left( x,y,z\right) }{\partial y^{2\beta }} \nonumber \\{} & {} +\frac{\partial ^{2\beta }E_{z}\left( x,y,z\right) }{\partial z^{2\beta }} +\varpi ^{2}E_{z}\left( x,y,z\right) =0 \end{aligned}$$
(32)

Using separation of variable method as in ( 11), we obtain

$$\begin{aligned}{} & {} \frac{1}{F\left( x\right) }\frac{\textrm{d}^{2\beta }F\left( x\right) }{\textrm{d}x^{2\beta } }+\frac{1}{G\left( y\right) }\frac{\textrm{d}^{2\beta }G\left( y\right) }{\textrm{d}y^{2\beta } } \nonumber \\{} & {} +\frac{1}{I\left( z\right) }\frac{\partial ^{2\beta }I\left( z\right) }{ \partial z^{2\beta }}=-\varpi _{x}^{2}-\varpi _{y}^{2}-\varpi _{z}^{2}. \end{aligned}$$
(33)

The x-dependent part, y-dependent part, and z-dependent part can be written as

$$\begin{aligned} \frac{\textrm{d}^{2\beta }F\left( x\right) }{\textrm{d}x^{2\beta }}+\varpi _{x}^{2}F\left( x\right)= & {} 0, \end{aligned}$$
(34)
$$\begin{aligned} \frac{\textrm{d}^{2\beta }G\left( y\right) }{\textrm{d}y^{2\beta }}+\varpi _{y}^{2}G\left( y\right)= & {} 0, \end{aligned}$$
(35)

and

$$\begin{aligned} \frac{\textrm{d}^{2\beta }I\left( z\right) }{\textrm{d}z^{2\beta }}+\varpi _{z}^{2}I\left( z\right) =0 \end{aligned}$$
(36)

The solutions of Eqs. (34–36) [23] is:

$$\begin{aligned} F\left( x\right)= & {} E_{2\beta }\left( -\varpi _{x}^{2}x^{2\beta }\right) \end{aligned}$$
(37)
$$\begin{aligned} G\left( y\right)= & {} E_{2\beta }\left( -\varpi _{y}^{2}y^{2\beta }\right) \end{aligned}$$
(38)
$$\begin{aligned} I\left( z\right)= & {} E_{2\beta }\left( -\varpi _{z}^{2}z^{2\beta }\right) \end{aligned}$$
(39)

where

$$\begin{aligned} E_{\beta }\left( q\right) =\sum \limits _{j=0}^{\infty }\frac{q^{j}}{\Gamma (1+\beta j)} \end{aligned}$$
(40)

is Mittage–Leffler function [24, 25].

Finally, the exact solution of the wave equation using local fractional derivative can be obtain as

$$\begin{aligned}{} & {} E_{z}\left( x,y,z\right) =E_{2\beta }\left( -\varpi _{x}^{2}x^{2\beta }\right) \nonumber \\{} & {} \times E_{2\beta }\left( -\varpi _{y}^{2}y^{2\beta }\right) \times E_{2\beta }\left( -\varpi _{z}^{2}z^{2\beta }\right) \end{aligned}$$
(41)

In the first case, \(\beta =\frac{1}{2},\) we have

$$\begin{aligned} E_{z}\left( x,y,z\right)= & {} E_{1}\left( -\varpi _{x}^{2}x\right) \times E_{1}\left( -\varpi _{y}^{2}y\right) \nonumber \\ \times E_{1}\left( -\varpi _{z}^{2}z\right)= & {} e^{-\left( \varpi _{x}^{2}x+\varpi _{y}^{2}y+\varpi _{z}^{2}z\right) } \end{aligned}$$
(42)

In the second case, \(\beta =1,\) the Mittage–Leffler function transforms into hyperbolic cosines. Then

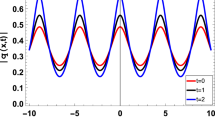
$$\begin{aligned} E_{z}\left( x,y,z\right)= & {} E_{2}\left( -\varpi _{x}^{2}x^{2}\right) \times E_{2}\left( -\varpi _{y}^{2}y^{2}\right) \nonumber \\{} & {} \times E_{2}\left( -\varpi _{z}^{2}z^{2}\right) \nonumber \\= & {} \cosh \left( i\varpi _{x}x\right) \times \cosh \left( i\varpi _{y}y\right) \nonumber \\{} & {} \times \cosh \left( i\varpi _{z}z\right) \nonumber \\= & {} \cos \left( \varpi _{x}x\right) \times \cos \left( \varpi _{y}y\right) \nonumber \\{} & {} \times \cos \left( \varpi _{z}z\right) \end{aligned}$$
(43)

5.2 Results and discussion of LFD in usual integer space at \({\beta =1}\)

      Figure 8 simulates a discussion of the local fractional derivative in usual integer space with a fractional parameter \(\beta =1\). Good agreement has been achieved between both methods that are used in this paper, where in the integer space, the behavior of the wave is similar in FS or LFD. The EM wave propagation in Fig. 8 has a constant amplitude. This is important in communication if we need a uniform distribution of signals. The standard validity of solutions is the usual integer space because most experiments occur in the usual conditions.

Fig. 8
figure 8

\(E_{z}\left( x,y,z\right) \ \text {using LFD derivative} \text {at }\beta =1,\ \varpi ^{2}=3,\ \text {and }z=0\longrightarrow 50\)

Full size image

6 Conclusion

This paper sheds light on electromagnetic wave propagation inside the rectangular waveguide filled with plasma. The source of the electromagnetic waves is the reaction between an injected Cherenkov free electron laser beam and plasma electrons. The goal of this study is to find the exact solution using both paths, either fractional space (FS) or local fractional derivative (LFD). The salient conclusions can be summarized as:

  1. 1.

    Bessel and Neumann functions influence the behavior of EM wave propagation in fractional space.

  2. 2.

    Mittage–Leffler functions influence the behavior of EM wave propagation using local fractional derivatives.

  3. 3.

    The exact solution in both fractional space and LFD is directly proportional to the fractional parameters \(D=\gamma _{1}+\gamma _{2}+\gamma _{3}\) or \(\beta \).

  4. 4.

    The usual solution that produces the classical results is obtained at \( D=1,\ 2,\ 3\) or \(\beta =1.\)

  5. 5.

    The fractionality of the rectangular waveguide is the most important factor in power redistribution, where the power of signals is proportional to their amplitudes.

  6. 6.

    It has been observed that the electromagnetic wave propagates with constant amplitude only in integer space.

  7. 7.

    In the core of the waveguide, the EM’s power increases whenever the fractional parameters increase.

  8. 8.

    By taking the C-FEL’s power or/and plasma density, the efficiency can be controlled.

  9. 9.

    C-FEL enhances the excitation of plasma electrons depending on the waveguide dimensions and the fractional parameters.

  10. 10.

    Bessel modes and Mittage–Leffler functions are used in fractional space to describe traveling and standing waves.