1 Introduction

In nonlinear sciences, the study of exact and analytic solutions to NLFPDEs is important because physical processes in the real world may be efficiently described by using the model of fractional order integrals and derivatives. Fractional calculus has had a noteworthy impact on applied science and engineering over the last two decades (Du et al. 2013; Caputo and Fabrizio 2015). It is a version of calculus that is an evolution of ordinary calculus which was established in 1695 as a result of a conversation between Leibniz and L’Hospital that lasted a few months and the discussion of fractional derivatives probably would not end with their absence (David et al. 2011). Experiments in physics and engineering have lately demonstrated that fractional calculus may be applied to define an extensive range of phenomena (Ali et al. 2019; Alquran et al. 2022, 2012). Fractional partial differential equations (FPDEs) are global forms of NLFPDEs and they play a significant role in detecting nonlinear singularities in practical sciences (Ekici et al. 2016; Akbulut and Kaplan 2018). Fluid mechanics, hydrodynamics, electromagnetic, plasma, optics, electro-chemistry, and aerodynamics are just a few of the domains where these equations are applied as well as a wide range of applied sciences. Correspondingly, these NLFPDEs have been used to describe a variety of nonlinear events such as assessing digital circuit creation, legged robots, controller tuning, and a variety of other applications. The importance of NLFPDEs in this field has made developing efficient solutions an interesting research issue (Arefin et al. 2022; Cevikel 2022). According to a detailed review of the literature, NLFPDEs and fractional calculus are applicable to simulate a large sector of physical science phenomena (Yang et al. 2018; Rahman et al. 2019). Many scholars have demonstrated the value of fractional calculus in modeling and control theory (Calderón et al. 2006). Many effective and powerful methods for determining exact answers, such as the residual power series approach (Alquran et al. 2017), the fractional Maclaurin series (Alquran 2023a), the modified simple equation technique (Chen 2019), the Kudryashov expansion method (Alquran 2023b), the direct algebraic approach (Chun-Ping et al. 2004), the modified Jacobi elliptic expansion method (Hosseini et al. 2023), new generalized \(({G}{\prime}{\prime}/G)\)-expansion approach (Zaman et al. 2022 Jun), the extended tanh-function method (Sadiya et al. 2022), the double \(({{G}{\prime}}{\prime}{\prime}/G,1/G)\)-expansion approach (Uddin et al. 2018), the homotopy perturbation approach (Alquran 2023c), the modified Kudryashov method (Hosseini et al. 2022; Çevikel and Aksoy 2021), exp-function technique (Uddin et al. 2019), and other methods. Among these, the extended tanh-function technique is the utmost widely used method. Malfliet (1996) implemented the efficient and successful tanh technique for such a dependable technique for the non-linear equations of waves in his seminal work. Afterward, Wazwaz (2007a) invented the extended tanh method, which is an algebraic approach that is both direct and efficient for dealing with nonlinear equations (Yusufoglu and Bekir 2007). Solvable equations applied to the extended tanh method often have a unique category of solutions known as solitons. Traveling waves are known as solitons that maintain their shape even though they collide with other solitons. The importance of waves (solitary) is rather frequent in electrical circuits, plasmas, physics of solid states, shallow water, and wave propagation, mechanics of fluids, chemical kinematics, optical fibers, heat transfer phenomenon, and other fields (Wazwaz 2005).

The space–time fractional Duffing model is a well-known NLFPDEs that appears in many engineering, physical, and biological situations. Chaos, relativistic energy–momentum correlations, local and global bifurcations, and resonances, electromagnetic interactions, and quantum relativistic one-particle theory could all benefit from the above equation. Sheu et al. (2007) examine the fractionally Duffing model by applying the chaotic dynamics method. Borowiec et al. (2007) used the Melnikov criteria to investigate the Duffing system, a global homoclinic divergence, and shift into the chaos that occurred by means of non-linear fractional damping behavior. Ge and Ou (2007) studied the disordered behaviors of nonlinear fractional Duffing model in the sense of phase portraits, poincare maps, and bifurcation in a fractional order. Cao et al. (2010) applied the 4th-order Runge–Kutta approach and the tenth-order CFE–Euler approach to derive the non-linear dynamic forces of the Duffing system by fractional curbing. The fractional sub-equation approach was investigated by Jafari et al. (2013) to extract the exact results of the fractional order Duffing system, in addition, non-linear fractional order Sharma-Tasso-Olver equation. Scientists Guner and Bekir (2015) utilize the Exp-function approach to investigate the exact results of various fractional diffusion–reaction equations that arise duffing model.

The space–time fractional modified Benjamin-Bona-Mahony (mBBM) is an estimate for long surface waves in non-linear diffusing media that was first developed to describe a space–time fractional approximation. This equation is identified to the water-magnetized waves of cold plasma, audio waves through discordant crystals, and waves of acoustic gravity incompressible fluids are all described. By means of the sub-equation method, Alzaidy (2013) derived to build analytical solution in mathematical physics namely the mBBM equation. With the modified Kudryashov approach, Misirli and Ege (2014) have found numerous precise analytical results for this equation. Bekir et al. (2015) utilize the first integral approach to achieve new exact solutions in this equation. Numerous studies have taken the possibility of solutions to this equation into consideration. (Yusufoğlu 2008; Abbasbandy and Shirzadi 2010).

It is comprehended to observe that, the space–time fractional mBBM equation and duffing model are yet to be examined using an extended tanh-function approach. This investigation determines the development of the mentioned equations with the extended tanh-function method to obtain some new closed from traveling wave solutions to the suggested models. This method has the benefit, that yielding us to acquire additional arbitrary constants and more kinds of solutions than other methods.

The following is how the rest of the article is structured: We drive through several definitions of conformable derivatives in segment 2. Then, in Sect. 3, the Methodology for finding accurate traveling wave solutions for NLFPDEs. In segment 4, the space–time fractional mBBM equation and Duffing model now have a novel closed-form travelling wave solution. In segment 5, Graphical representation and physical interpretation of the solution are represented. In segment 6, comparison between our obtained results and others obtain results are shown graphically, after which there will be a conversation about the conclusions.

2 Meaning and preamble

Consider, \(f:\left[0,\infty \right)\to {\mathbb{R}}\), is a function. The \(\alpha\)-order “conformable derivative’’ of \(f\) is defined as Khalil et al. (2014):

$$K_{\alpha } \left( f \right)\left( t \right) = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{{f\left( {t + \varepsilon t^{1 - \alpha } } \right) - f\left( t \right)}}{\varepsilon }$$
(2.1)

meant for each \(t>0,\alpha \in \left(\mathrm{0,1}\right)\). If \(f\) be \(\alpha\)-differentiable in approximately \(\left(0,a\right)\),\(a>0\) and \(\underset{t\to {0}^{+}}{{\text{lim}}}{f}^{\left(\alpha \right)}\left(t\right)\) be real, then express \({f}^{\left(\alpha \right)}\left(0\right)=\underset{t\to {0}^{+}}{{\text{lim}}}{f}^{\left(\alpha \right)}\left(t\right)\). Formulae that survey a limiting axiom and are satisfied to this derivative.

Theorem 1

Assume \(\alpha \in \left(\mathrm{0,1}\right]\) and as well supposed \(f,g\) be \(\alpha\)- differentiable at a point \(t>0\). Then,

  • \({K}_{\alpha }\left(xf+yg\right)=x{K}_{\alpha }\left(f\right)+y{K}_{\alpha }\left(g\right)\), for all \(x,y\in {\mathbb{R}}\).

  • \({K}_{\alpha }\left({t}^{z}\right)=h{t}^{K-\alpha }\), for all \(z\in {\mathbb{R}}\).

  • \({K}_{\alpha }\left(u\right)=0\), for all constant function \(f\left(t\right)=u\).

  • \({K}_{\alpha }\left(fg\right)=f{K}_{\alpha }\left(g\right)+g{K}_{\alpha }\left(f\right)\).

  • \({K}_{\alpha }\left(\frac{f}{g}\right)=\frac{g{K}_{\alpha }\left(f\right)-f{K}_{\alpha }\left(g\right)}{{g}^{2}}\).

  • Additionally, if \(f\) is differentiable, and then \({KT}_{\alpha }\left(f\right)\left(t\right)={t}^{1-\alpha }\frac{df}{dt}\).

Some various properties like the integration procedures, Tailor series expansion, chain law, the Laplace transform, the exponential function, and Gronwall’s inequality in terms of it (Khalil et al. 2014).

Theorem 2

Consider \(f\) is an \(\alpha\)- differentiable function in conformable differentiable in addition assume that \(g\) is also demarcated and differentiable in range of \(f\), so that.

$$M_{\alpha } \left( {f \circ g} \right)\left( t \right) = t^{1 - \alpha } g^{\prime } \left( t \right)f_{g} \left( t \right)$$
(2.2)

3 Methodology

By using exhaustive Wazwaz (2007b), the extended tanh-function strategy is characterized for finding several exact solutions of non-linear evolution equations (NLEEs). The key concept of this technique is to describe the solution like a polynomial in the hyperbolic roles and then resolve the variable coefficient of PDE by first-order ODEs and iterative procedures. We capture an NLEE of function \(u=u\left(x,t\right)\) as follows:

$$G\left( {u,D_{t}^{\alpha } u,D_{x}^{\beta } u,D_{t}^{\alpha } D_{t}^{\alpha } u,D_{t}^{\alpha } D_{x}^{\beta } u,D_{x}^{\beta } D_{x}^{\beta } , \ldots \ldots \ldots } \right) = 0 ,\,\,0 < \alpha ,\beta \le 1,$$
(3.1)

where the unnamed function \(u\), with temporal and spatial derivatives \(t\) and \(x\), and \(G\) provide a polynomial of \(u\left(x,t\right)\) also its linear derivatives for which highest order besides non-linear terms of highest order are connected. Taking the transformation of waves.

$$\xi = k\frac{{x^{\beta } }}{\beta } + c\frac{{t^{\alpha } }}{\alpha },\,u\left( {x,t} \right) = u\left( \xi \right),$$
(3.2)

Here the random nonzero constants are \(c\) as well as \(k\).

It is redrafted as shadows after put on the wave transformation in (3.1):

$$R\left( {u,u^{\prime } ,u^{\prime\prime},u^{\prime\prime\prime}, \ldots \ldots \ldots } \right) = 0,$$
(3.3)

where \(u\) represented the ordinary derivative (OD).

Stage 1: Let’s a recognized solution of ODE in the resulting construction

$$u\left( \xi \right) = \mathop \sum \limits_{i = 0}^{n} a_{i} Y^{i} + \mathop \sum \limits_{i = 1}^{n} b_{i} Y^{ - i} ,$$
(3.4)

as for

$$Y = \tanh \left( {\mu \xi } \right),$$
(3.5)

here \(\mu\) presented some random value.

Stage 2: Describe the non-negative constant \(n\) by provide balance to the maximum order linear and non-linear terms called homogeneous balance in Eq. (3.3).

Stage 3: By replacing solution (3.4) and (3.5) to Eq. (3.3) by the rate of \(n\) acquired in Stage 2, polynomials in \(Y\) are found. When every coefficient for the resultant polynomials is set to null, \({a}_{i}{\prime}s\) along with \({b}_{i}{\prime}s\) are obtained. Resolve these equations \({a}_{i}{\prime}s\) along with \({b}_{i}{\prime}s\) by dint of representational computation gears like Maple.

Stage 4: Then, we generate closed form travelling wave results of the non-linear evolution Eq. (3.4) by implanting ideals from Stage 3 to Eq. (3.4) with the Eq. (3.5) and (3.1).

3.1 Advantage

The advantages of the suggested method over other methods are substantial. The proposed method is effective for creating multiple traveling wave solutions for nonlinear partial differential equations and a powerful tool for dealing with nonlinear problems. It is a straightforward and simple technique, making it accessible for a wide range of applications in solving nonlinear phenomena. In conclusion, the extended tanh-function method is a strong and approachable tool for solving nonlinear partial differential equations, providing efficiency, simplicity, and diversity in its applications.

4 Investigation of the solutions

In this area, we like to find the solutions of fractional type mBBM equation and Duffing model using the extended tanh-function technique via conformable derivative.

4.1 The nonlinear fractional mBBM equation

This subsection uses extended tanh-method to examine novel and further general closed-form wave solutions to the mentioned equation. The mentioned equation is:

$$D_{t}^{\alpha } u\left( {x,t} \right) + D_{x}^{\alpha } u\left( {x,t} \right) - \upsilon u^{2} \left( {x,t} \right)D_{x}^{\alpha } u\left( {x,t} \right) + D_{x}^{3\alpha } u\left( {x,t} \right) = 0,$$
(4.1.1)

where nonzero constant is \(\upsilon\), \({D}_{x}^{\alpha }u\) and \({D}_{t}^{\alpha }u\) represent conformable derivative with respect to \(x\) and \(t\). The coefficient associated with the nonlinear fractional mBBM equation is a critical parameter that influences the behavior, stability, and characteristics of solutions in the system described by the equation. It allows for the fine-tuning and control of various aspects of the system's dynamics and wave propagation. Surface long waves in a nonlinear disseminative medium were first approximated using this equation. This equation also describes acoustic gravity waves, cold plasma for hydro-magnetic waves, and audio waves in inharmonic crystals. The transformation for mBBM Eq. (4.1.1), we represent:

$$\xi = k\frac{{x^{\alpha } }}{\alpha } + c\frac{{t^{\alpha } }}{\alpha },\,u\left( {x,t} \right) = u\left( \xi \right),$$
(4.1.2)

where \(c\) denoted the speed traveling wave. Through the transformation (4.1.2), (4.1.1) is reduced to the resulting non-fractional order ODE:

$$\left( {c + k} \right)u^{\prime} - \upsilon ku^{2} u^{\prime} + k^{3} u^{\prime\prime\prime} = 0$$
(4.1.3)

Using zero as the constant in the integration of Eq. (4.1.3), we arrive

$$\left( {c + k} \right)u - \frac{{\upsilon ku^{3} }}{3} + k^{3} u^{\prime\prime} = 0$$
(4.1.4)

The balancing number is 1 where the maximum order linear and non-linear term is calculated called homogeneous balance. The equation of (3.4) is determined as

$$u\left( \xi \right) = a_{0} + a_{1} Y + b_{1} Y^{ - 1} .$$
(4.1.5)

Taking the place of Eq. (4.1.4) to the Eq. (4.1.5) with the Eq. (3.5), in \(Y\), and the left-hand side translates to a polynomial. A series of algebraic equations appears when all of the coefficients of the polynomial are set to zero (intended to be utilized for simplicity, we attempt to get around them for explanation) for \({a}_{0}\), \({a}_{1}\),\({a}_{2}, {b}_{1},{b}_{2},k\) and \(c\). When a set of equations is solved using a computational program like Maple, the following conclusions are reached:

Assortment 1

\(k= \frac{1}{6}\frac{\sqrt{6\nu }{b}_{1}}{\mu }, c=\frac{\left(-3+\nu {{b}_{1}}^{2}\right)}{18}\frac{\sqrt{6\nu }{b}_{1}}{\mu }, {a}_{0}=0,{a}_{1}=0 and {b}_{1}={b}_{1}.\)

The values of the assortment 1 produce an explicit coth function result.

$${u}_{1}\left(x,t\right)={\left[{\text{tanh}}\left( \frac{\sqrt{2x}}{\sqrt{3}}-\frac{2\sqrt{2t}}{3\sqrt{3}}\right)\right]}^{-1}$$
(4.1.6)

This equation can be rewritten as follows:

$${u}_{2}\left(x,t\right)=\sqrt{1+{{\text{cosech}}\left(\frac{\sqrt{2x}}{\sqrt{3}}-\frac{2\sqrt{2t}}{3\sqrt{3}}\right)}^{2}}$$
(4.1.7)

Assortment 2

\(k= \frac{1}{6}\frac{\sqrt{6\nu }{a}_{1}}{\mu }, c=\frac{\left(-3+\nu {a}_{1}^{2}\right)}{18}\frac{\sqrt{6\nu }{a}_{1}}{\mu },{a}_{0}=0,{a}_{1}={a}_{1} and {b}_{1}=0.\)

Using those values assortment 2 create an explicit solution provide tanh functions.

$${u}_{3}\left(x,t\right)={\text{tanh}}\left(\frac{\sqrt{2x}}{\sqrt{3}}-\frac{2\sqrt{2t}}{3\sqrt{3}} \right).$$
(4.1.8)

This solution can be reproduced by the formulation below:

$${u}_{4}\left(x,t\right)=\sqrt{1-{{\text{Sech}}\left(\frac{\sqrt{2x}}{\sqrt{3}}-\frac{2\sqrt{2t}}{3\sqrt{3}}\right)}^{2}}.$$
(4.1.9)

Assortment 3

$$k= \frac{1}{6}\frac{\sqrt{6\nu }{b}_{1}}{\mu }, c=\frac{\left(-3+4\nu {b}_{1}^{2}\right)}{18}\frac{\sqrt{6\nu }{b}_{1}}{\mu }, {a}_{0}=0,{a}_{1}={b}_{1}and {b}_{1}={b}_{1}.$$

The values of parameters in Step 3 produce a solution for the coth and tanh functions.

$${u}_{5}\left(x,t\right)={\text{tanh}}\left(\frac{2\sqrt{x}}{\sqrt{6}}+\frac{2\sqrt{t}}{3\sqrt{6}}\right)+{\text{coth}}\left(\frac{2\sqrt{x}}{\sqrt{6}}+\frac{2\sqrt{t}}{3\sqrt{6}}\right).$$
(4.1.10)

This solution can be reproduced by the formulation below.

$${u}_{6}\left(x,t\right)=\sqrt{1-{{\text{sech}}\left(\frac{2\sqrt{x}}{\sqrt{6}}+\frac{2\sqrt{t}}{3\sqrt{6}}\right)}^{2}}+\sqrt{1+{{\text{cosech}}\left(\frac{2\sqrt{x}}{\sqrt{6}}+\frac{2\sqrt{t}}{3\sqrt{6}}\right)}^{2}}.$$
(4.1.11)

Assortment 4

$$k= \frac{1}{6}\frac{\sqrt{6\nu }{b}_{1}}{\mu }, c=\frac{\left(-3+4\nu {b}_{1}^{2}\right)}{18}\frac{\sqrt{6\nu }{b}_{1}}{\mu }, {a}_{0}=0,{a}_{1}={-b}_{1} and {b}_{1}={b}_{1}.$$

The values of assortment 4 are an explicit result in functions of coth and tanh.

$${u}_{7}\left(x,t\right)=-{\text{tanh}}\left(\frac{\sqrt{x}}{\sqrt{3}}+\frac{5\sqrt{2t}}{3\sqrt{3}}\right)+{\left[{\text{tanh}}\left(\frac{5\sqrt{6x}}{9}+\frac{\sqrt{6t}}{3}\right)\right]}^{-1}.$$
(4.1.12)

This result can be reproduced to the formula below.

$${u}_{8}\left(x,t\right)=-\frac{{\text{sinh}}\left[\frac{\sqrt{x}}{\sqrt{3}}+\frac{5\sqrt{2t}}{3\sqrt{3}}\right]}{{\text{cosh}}\left[\frac{\sqrt{x}}{\sqrt{3}}+\frac{5\sqrt{2t}}{3\sqrt{3}}\right]}+\sqrt{1+{{\text{cosech}}\left(\frac{\sqrt{x}}{\sqrt{3}}+\frac{5\sqrt{2t}}{3\sqrt{3}}\right)}^{2}.}$$
(4.1.13)

It is striking to note that the solutions of traveling wave \({u}_{1}-{u}_{8}\) of space–time fractional mBBM equation are novel also more general than those studied previously. inharmonic crystals in Acoustic waves, cold plasma for hydromagnetic waves, and waves in acoustic-gravity for incompressible fluids can all be described using these solutions forces.

4.2 The space–time fractional Duffing model

The fundamental nonlinear space–time fractional Duffing model forces on the damping, which is proportional to the first-order derivative of the displacement. Because fractional order damping may clarify certain frequency links materials for dampening, increasing the non-fractional order for damping to the non-integer order for damping has been used to explain several practical applications in mechanical engineering. Both theoretically and experimentally, the presence of fission and fusion processes for solitons has been confirmed. Using the extended tanh-function technique, we investigate abundant solutions of soliton for the nonlinear fractional Duffing model in this article. In this part, we utilize the method outlined above to create correct solitary wave results and the solitons for the nonlinear fractional Duffing model. Think about the equation below.

$$\frac{{\partial }^{2\alpha }u\left(x,t\right)}{{\partial t}^{2\alpha }}+au\left(x,t\right)+b{u}^{3}\left(x,t\right)=0; t>0, 0<\alpha <1,$$
(4.2.1)

where \(b\) are real parameters and \(\alpha\) be fractional constant. These coefficients indicate the nature and strength of nonlinearity, affect the amplitude of oscillations, and crucial in analyzing the stability of solutions. Taking the travelling wave transformation

$$\xi =x+\omega \frac{{t}^{\alpha }}{\alpha }, u\left(x,t\right)=u\left(\xi \right).$$
(4.2.2)

where \(\omega\) is a travelling wave variable. The Eq. (4.2.1) renovates into ordinary equation as follow:

$${\omega }^{2}{u}^{{\prime}{\prime}}+au+b{u}^{3}=0.$$
(4.2.3)

When the maximum order derivative part is balanced with the maximum order non-linear part, and one is the balancing number. Formerly the solution of the Eq. (3.4) converts.

$$u\left(\xi \right)={a}_{0}+{a}_{1}Y+{b}_{1}{Y}^{-1}.$$
(4.2.4)

Using (4.2.3) to (4.2.4) along (3.5), in\(Y\), then, the left-hand side converts to a polynomial. Each of the coefficients of polynomial is use to zero, and a set of arithmetical equations develops (used for clarity, and we omit them from the display in order to be clear) meant for\({a}_{0}\),\({a}_{1}\),\({b}_{1}, \delta\) and \(\upsilon\). The results are attained by using a computer program like, Maple to calculated this across a set of equations:

Assembly 1

$$\omega =\frac{\sqrt{2a}}{2\mu }, {a}_{0}=0,{a}_{1}=0 and {b}_{1}={b}_{1}.$$

The terms functions of coth, the parameters values specified in Assembly 1 produce an explicit solution.

$${u}_{9}\left(x,t\right)={\text{coth}}\left(x+\sqrt{2t}\right).$$
(4.2.5)

This equation can be rewritten like this:

$${u}_{10}\left(x,t\right)=\sqrt{1+{{\text{cosech}}\left(x+\sqrt{2t}\right)}^{2}}.$$
(4.2.6)

Assembly 2

\(\omega =\frac{\sqrt{2a}}{2\mu }, {a}_{0}=0,{a}_{1}={a}_{1}\mathrm{ and }{b}_{1}=0.\)

The parameters values provided in assembly 2 constitute a result by tanh-functions.

$${u}_{11}\left(x,t\right)={\text{tanh}}\left(x+\sqrt{2t} \right).$$
(4.2.7)

The equation can be used to reproduce this following formula:

$${u}_{12}\left(x,t\right)=\sqrt{1-{{\text{sech}}\left(x+\sqrt{2t}\right)}^{2}}.$$
(4.2.8)

Assembly 3

\(\omega =\frac{\sqrt{-a}}{2\mu }, {a}_{0}=0,{a}_{1}={a}_{1}\mathrm{ and }{b}_{1}={b}_{1}.\)

The functions of coth and tanh, the range of parameters specified for assembly 3 produce a traveling wave explicit solution.

$${u}_{13}\left(x,t\right)={\text{tanh}}\left(x+\sqrt{-1t}\right)+{\text{coth}}\left(x+\sqrt{-1t}\right).$$
(4.2.9)

This equation could be reproduced by the formula below.

$${u}_{14}\left(x,t\right)=\sqrt{1-{{\text{sech}}\left(x+\sqrt{-1t}\right)}^{2}}+\sqrt{1+{{\text{cosech}}\left(x+\sqrt{-1t}\right)}^{2}}.$$
(4.2.10)

Likewise

$${u}_{15}\left(x,t\right)={\text{tanh}}\left(x+\sqrt{-1t}\right)+\sqrt{1+{{\text{cosech}}\left(x+\sqrt{-1t}\right)}^{2}}.$$
(4.2.11)

Besides

$${u}_{16}\left(x,t\right)=\sqrt{1-{{\text{sech}}\left(x+\sqrt{-1t}\right)}^{2}}+{\text{coth}}\left(x+\sqrt{-1t}\right).$$
(4.2.12)

Assembly 4

\(\omega =\frac{\sqrt{2a}}{4\mu }, {a}_{0}=0,{a}_{1}={a}_{1}\mathrm{ and }{b}_{1}={b}_{1}.\)

The rate of the assembly 4 represent an explicit result of coth and tanh functions.

$${u}_{17}\left(x,t\right)={\text{tanh}}\left(\frac{\left(x+\sqrt{2t}\right)}{2}\right)+{\text{coth}}\left(\frac{\left(x+\sqrt{2t}\right)}{2}\right).$$
(4.2.13)

This equation could be reproduced by the formula below.

$${u}_{18}\left(x,t\right)=\sqrt{1-{{\text{sech}}\left(\frac{\left(x+\sqrt{2t}\right)}{2}\right)}^{2}}+\sqrt{1+{{\text{cosech}}\left(\frac{\left(x+\sqrt{2t}\right)}{2}\right)}^{2}}.$$
(4.2.14)

Correspondingly,

$${u}_{19}\left(x,t\right)={\text{tanh}}\left(\frac{\left(x+\sqrt{2t}\right)}{2}\right)+\sqrt{1+{{\text{cosech}}\left(\frac{\left(x+\sqrt{2t}\right)}{2}\right)}^{2}}.$$
(4.2.15)

Similarly

$${u}_{20}\left(x,t\right)=\sqrt{1-{{\text{sech}}\left(\frac{\left(x+\sqrt{2t}\right)}{2}\right)}^{2}}+{\text{coth}}\left(\frac{\left(x+\sqrt{2t}\right)}{2}\right).$$
(4.2.16)

The achieved solutions could be used to analyze chaotic vibrations, relativistic energy–momentum connections, global and local bifurcations, interactions of electromagnetic, and one-particle theory of quantum relativistic.

5 Graphical representation and physical interpretation

5.1 Graphic delegation of the solution

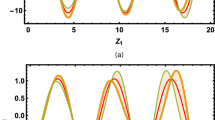
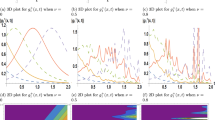
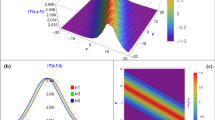
This section discovers graphic delegation for specified resolutions for the equation in this portion for dissimilar standards of the constraint. This solution creates an extensive range of exceedingly stable solutions that can be envisaged for several values \(\omega =1, \mu =1,\upsilon =1,\alpha =\frac{1}{2}\). 3D, contour, listpoint, and 2D plots of the solution are bounded by diverse intermissions for \(t\) and\(x\).

5.2 Physical clarification of the resolution

The physical abbreviation of the achieved solution of the deduced NLFPDEs, which are the time fractional mBBM equation and Duffing model are recapitulated in this segment visual delegation. Solution \({u}_{1}\left(x,t\right)\) for space–time fractional mBBM equation proves anti-kink travelling wave solutions shows in Fig. 1 for the range \(\mu =1,\beta =1,\alpha =\frac{1}{2}\) and \(0\le x\le 10, 0\le t\le 10\). Solution \({u}_{2}\left(x,t\right)\) for space–time fractional mBBM equation demonstrate anti-bell type travelling wave solution which is shown in Fig. 2 for the range \(\mu =1,\beta =1,\alpha =\frac{1}{2}\) and \(0\le x\le 90, 0\le t\le 90\). Also, for demonstrates kink type travelling wave solutions displays Figs. 3, 5, 6, 8, which was solution of \({u}_{3}\left(x,t\right)\), \({u}_{5}\left(x,t\right)\), \({u}_{6}\left(x,t\right)\) and \({u}_{9}\left(x,t\right)\), using the range \(0<x<10\,and\,0<t<34,\) \(0<x<10\,and\,0<t<35,\) \(0<x<10\,and\,0<t<34\), and \(0<x<0.7\,and\,0<t<0.10\) respectively for the values \(\mu =1,\beta =1,\alpha =\frac{1}{2}\). Kink type soliton is a soliton that changes from one asymptotic state to the next. Infinity is where the kink soliton approaches the constant. The Fig. 4, the nature of compaction solitary wave resolution for space–time fractional mBBM equation is described by \({u}_{4}\left(x,t\right)\) for the range \(\mu =1,\beta =1,\alpha =\frac{1}{2}\) and \(0\le x\le 15\,, 0\le t\le 35\). The solution \({u}_{8}\left(x,t\right)\) for the range \(\mu =1,\beta =1,\alpha =\frac{1}{2}\) and \(0\le x\le 900\,, 0\le t\le 1350\) and \({u}_{14}\left(x,t\right)\) for the range \(\mu =1,\beta =1,\alpha =\frac{1}{2}\) and \(0\le x\le 60\,, 0.5\le t\le 710\) are depicts in Figs. 7 and 11 for space–time fractional mBBM equation and Duffing model respectively.

Fig. 1
figure 1

Illustration of the anti-kink shape wave solution (4.1.6), showing the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{1}\)(x, t) with the interval \(0<x<10\) and \(0<t<10\)

Full size image
Fig. 2
figure 2

The figure presented the anti-bell form wave solution (4.1.7) and display the 3-D structure in (a), contour plot in (b), 3-D listpoint plotline in (c) and 2D plot in (d) of \({{\text{u}}}_{2}\)(x, t) with the interval \(0<x<90\) and \(0<t<90\)

Full size image
Fig. 3
figure 3

The illustration gives kink form wave solution (4.1.8), presenting the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{3}\)(x, t) with the interval \(0<x<10\) and \(0<t<34\)

Full size image
Fig. 4
figure 4

The diagram shows compaction solitary wave solution (4.1.9), displaying the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{4}\)(x, t) with the interval \(0<x<15\) and \(0<t<35\)

Full size image
Fig. 5
figure 5

Illustration of the kink form wave solution (4.1.10), showing the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{5}\)(x, t) with the interval \(0<x<10\) and \(0<t<35\)

Full size image
Fig. 6
figure 6

Figure of the kink form wave solution (4.1.11), displaying the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{6}\)(x, t) with the interval \(0<x<.7\) and \(0<t<5\)

Full size image
Fig. 7
figure 7

Illustration of the multiple-solitons form wave solution (4.1.13), presenting the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{8}\)(x, t) with the interval 0 < x < 900 and 0 < t < 1350

Full size image
Fig. 8
figure 8

Illustration of the kink form wave solution (4.2.5), presenting the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{9}\)(x, t) with the interval 0 < x < 0.7 and 0 < t < 0.10

Full size image
Fig. 9
figure 9

Sketch of the bell form wave solution (4.2.8), presenting the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{12}\)(x, t) with the interval \(-8<x<1.50\) and \(0<t<10\)

Full size image
Fig. 10
figure 10

Illustration of the imaginary-shape wave solution (4.2.9), displaying the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{13}\)(x, t) with the interval \(0<x<10\) and \(0<t<10\)

Full size image
Fig. 11
figure 11

Figure of the multiple soliton form wave solution (4.2.10), presenting the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{14}\)(x, t) with the interval \(0<x<60\) and \(0<t<710\)

Full size image

Also, Figs. 9 is represented the bell form wave solution \({u}_{12}\left(x,t\right)\), for \(\mu =1,\beta =1,\alpha =\frac{1}{2}\) and \(-8\le x\le 1.50, 0\le t\le 100\) of space–time fractional Duffing model. Furthermore, for Fig. 12 gained in this learning is travelling wave results of \({u}_{17}\left(x,t\right)\) for \(\mu =1,\beta =1,\alpha =\frac{1}{2}\) and \(0\le x\le 100, 0\le t\le 100\) performs single soliton wave solution of space–time fractional Duffing model. A single soliton is a different kind of solitary waveform that displays a singularity, traditionally an infinite interruption. Solitary solitons frequently have a connection to solitary waves when the initial concept is imaginary. Finally, the result of \({u}_{13}\left(x,t\right)\) for the range of \(\mu =1,\beta =1,\alpha =\frac{1}{2}\) and \(0\le x\le 10, 0\le t\le 10\) acquired in this study was an imaginary-shape travelling wave results of space–time fractional Duffing model display in Fig. 10. Representative calculation software for example MATHEMATICA was used to trace out the accompanying Figs. 1–12 and we avoid repeating that because the rest of the solution paints a similar picture.

Fig. 12
figure 12

Illustration of the single soliton form wave results (4.2.13), presenting the 3-D structure (a), contour plot (b), 3-D listpoint plotline (c) and 2D plot (d) of \({{\text{u}}}_{17}\)(x, t) with the interval \(0<x<100\) and \(0<t<100\)

Full size image

6 Comparison of results

This subsection represents some of the obtained solutions which are strong similarities to the solutions that were previously established. The previous researchers are using different types of methods to solve these mentioned equations. We apply the extended tanh-function method via confirmable derivative through above mentioned equations and get many tremendous results which are more general and fresher also great comparable to the previous researchers.

The novelty of the space–time fractional mBBM equation is first discussed. Guner and Bekir (2016) also worked on this equation, and we compared their established solutions to our obtained solutions, which are provided in the table below (Table 1):

Table 1 Comparison of the obtained solutions to the space–time fractional mBBM equation with the solutions found by Guner and Bekir (2016)
Full size table

The above table provided that the solutions (4.1.6), (4.1.8) and (4.1.9) are similar to solutions (38) and (25) of Guner and Bekir (2016). Furthermore, we can say that the other solutions are completely new and innovative solutions, which represent the novelty of our work.

Besides, we describe the originality of the space–time fractional duffing model. We compared the existing solutions of Kadkhoda and Jafari (2019) to our obtained solutions, which are shown in the table below:

Kadkhoda and Jafari (2019)

Obtained solutions

If b = c \(=1\) and \(\alpha =\) fractal dimension of derivative, then the solution (37) converts:

\({\varphi }_{1}\left(x,t\right)=\frac{3b}{2c}(1\pm {\text{tanh}}\left(k(\frac{{x}^{\alpha }}{\alpha }-2r\frac{{t}^{\alpha }}{\alpha })\right))\)

If \(\alpha =\) fractal dimensions of derivative then the solution (4.2.7) becomes:

\({u}_{11}\left(x,t\right)={\text{tanh}}\left(x+\sqrt{2t}\right)\)

If b = c \(=1\) and \(\alpha =\) fractal dimension of derivative, then the solution (38) converts:

\({\varphi }_{1}\left(x,t\right)=\frac{3b}{2c}(-1\pm \sqrt{2}{\text{sech}}\left(k(\frac{{x}^{\alpha }}{\alpha }-2r\frac{{t}^{\alpha }}{\alpha })\right))\)

If \(\alpha =\) fractal dimensions of derivative then the solution (4.2.8) develops:

\({u}_{12}\left(x,t\right)=\sqrt{1-{{\text{sech}}\left(x+\sqrt{2t}\right)}^{2}}\)

According to the above table, the solutions (4.2.7) and (4.2.8) were comparable to solutions (37) and (38) of Kadkhoda and Jafari (2019). We can also claim to have some wholly original solutions, which reflect the novelty of this study.

7 Conclusion

In this study, the well-known method namely the extended tanh-function method was used to extract diverse categories of wave resolutions, such as singular soliton, multiple solitons, kink type, compaction solitary wave, anti-kink type, anti-bell type, bell type and imaginary type traveling wave solutions, and many more types of solutions of the NLFPDEs with a variety of free parameters. These free parameters have significant consequences, such as the ability to find specific solutions by changing the free parameter values of an individual solution, and the solutions are delineated in 3D, contour, listpoint, and 2D outlines of two NLFPDEs, specifically the space time fractional Duffing model and also for the time fractional mBBM equation. The value of the unknown coefficients can be calculated with the use of symbolic computational tools like Maple or Mathematica. It is important to note that all derived solutions are directly replaced with the original equations to ensure their accuracy. The amplitude of vibration in the nontrivial system builds on the damping exponent in the domain of character. As a result, one of the most significant submissions of the Duffing model remains to reduce harmful vibration. The proposed method is more dependable and simpler to use than the other approaches for determining the specific answers derived in this investigation. The technique might be essential meant for extra investigation of dissimilar NLFPDEs in plasma physics, theoretic and mathematical physics, also extra divisions of non-linear disciplines. To our understanding, the type of innovative findings obtained in this learning has never been achieved previously. Our achieve solutions are competent to describes acoustic gravity waves, cold plasma for hydro-magnetic waves, and audio waves in inharmonic crystals. The recognized results of the two mentioned equations raised above are ideal for investigating the fusion and fission phenomena. Similar phenomena can be found in solitons, plasma physics, optimal control theory, electromagnetic interactions, one-particle theory of quantum relativistic, acoustic waves in inharmonic crystals, the relativistic energy–momentum connection, cold plasma, acoustic-gravity waves, and other fields.