1 Introduction

The nonlinear Schrödinger equation (NLSE) introduced by Erwin Schrödinger in 1927 has great importance for soliton dynamics in optical fibers. So, numerous models based on NLSE that explain various physical phenomena have been improved and examined in the literature. So, miscellaneous optical soliton solutions of NLSE have been derived by combining varied analytical and numerical techniques, such as Radhakrishnan–Kundu–Lakshmanan having various nonlinearity [1,2,3,4,5,6,7], Chen–Lee–Liu [8,9,10,11], Lakshmanan–Porsezian–Daniel model [12, 13], the Fokas–Lenells model [14,15,16], the Schrödinger–Hirota (SH) equation [17,18,19,20,21,22,23], Biswas–Milovic [24,25,26,27,28], various forms of Maxwell–Bloch model [29, 30]. Especially, the SH model, which was derived from the NLSE with the help of the Lie transform [31], forms a substantial class of the NLSE and has been intensely developed in the last decades utilizing different computational methods. The SH equation also governs the propagation of optical pulses in dispersive optical fibers. Moreover, deriving diverse kinds of optical soliton solutions to NLSEs helps both interpret their physical properties and update or develop the mathematical model or helps to collect the knowledge of the mechanism of this application in the medium it expresses. So, a number of effective analytical and numerical procedures were developed to generate various optical soliton solutions. Some of such methods are the extended Jacobi’s elliptic expansion function approach [32], the enhanced Kudryashov’s scheme [33], the Sardar sub-equation procedure [34], the improved Bernoulli sub-equation function method [35], the improved tanh approach [36], the extended Fan sub-equation tool [37], the generalized Riccati equation mapping scheme [38], F-expansion technique [39], the unified Riccati equation expansion approach [40], the Melnikov scheme [41], the generalized \(G^{\prime }/G\)-expansion approach [42], the extended trial function method [43], Painleve approach [44], the simplest equation technique [45], Sine-Gordon equation technique [46], the Riemann–Hilbert technique [47, 48] and more.

The last quarter century has witnessed tremendous developments in terms of both communication and internet technologies. Fiber optics is an integral part and an outstanding building block for these technologies. Soliton transmission emerges as a substantial concept, especially when it comes to the transmission of very large volume data packets over very long distances. Although the Schrödinger equation is a model used in modeling many physical phenomena, the Schrödinger–Hirota equation is particular from ordinary Schrödinger’s equations and is one of the important models that include soliton propagation in optical fibers. The Schrödinger–Hirota equation was created from the Schrödinger equation with the help of Lie transform [49]. One of the main elements underlying several other models that model soliton transmission in fiber optics, such as the Schrödinger–Hirota equation, is the investigation of the delicate balance between chromatic dispersion and self-phase modulation. In this context, different forms related to the term self-phase modulation (Kerr, power, parabolic, dual-power, triple power, anti-cubic, polynomial, generalized anti-cubic, cubic-quintic-sextic-nonic, log-law, etc.) exist, and each form has a different physical behavior in soliton conduction in optical fibers. In recent years, the concept of refractive has been added to such nonlinearity forms. This study scrutinizes the situation of cubic–quintic–-septic law nonlinearity form for the Schrödinger–Hirota equation.

The perturbed Schrödinger–Hirota equation [8] with cubic–quintic–septic law in the presence of spatiotemporal dispersion is presented as:

$$\begin{aligned}& i U_t+\alpha \, U_{xx}+ \beta \, U_{xt}+\left( \lambda _1 \, |U|^{2}+\lambda _2 \, |U|^{4}+\lambda _3 \, |U|^{6} \right)U +i \left( \eta U_{xxx}+\mu |U|^2 U_{x}\right) \nonumber \\&\quad =i \left( \gamma U_{x}+ a \left( |U|^2 U\right) _x + b \left( |U|^2 \right) _x U\right) . \end{aligned}$$
(1)

Herein, \(U=U(x,t)\) is the complex soliton profile. \(\alpha \) and \(\beta \) state the group velocity dispersion (GVD) and spatiotemporal dispersion (STD) terms. Furthermore, \(\lambda _1,\lambda _2,\lambda _3\) are the coefficients of the cubic, quintic, and septic nonlinear terms from self-phase modulation. The coefficients of \(\gamma \) and a express the inter-modal dispersion, and self-steepening, respectively. Besides b and \(\mu \) state also for nonlinear dispersions. Various SH equations have been introduced, and a vast research area has been created. Some of these can be listed as Kudryashov scrutinized the fourth-order SH equation [17]. SH equation having Kerr law nonlinearity was scrutinized in [18, 19]. Cakicioglu et al. considered the dispersive SH equation having parabolic law linearity [20]. [50] contains the perturbed SH equation with the spatiotemporal dispersion. Kaur and Wazwaz gained bright and dark solitons to the SH equation with variable coefficients in the presence of power law nonlinearity [51]. Koprulu surveyed conformable fractional SH equation [52]. In [53], Houwe et al. explored diverse soliton structures of the perturbed SH equation. Inc et al. analyzed the modulational instability of the SH equation with STD having Kerr law nonlinearity [54]. Anjan et al. examined the SH equation with power law nonlinearity [55]. The coupled nonlinear SH equation was analyzed in detail by Tang [56]. Anwar et al. acquired various solutions for the perturbed nonlinear SH equation with STD via various schemes [57]. [58] recovers dispersive optical solitons to the SH equation with differential group delay and white noise, and [59,60,61,62] include various structures of the SH equation have been examined in other studies.

The remainder of the paper is planned as: The nonlinear ordinary differential equation (NLODE) structure is acquired utilizing a complex transformation in Sect. 2. The simple version of the new extended auxiliary equation method (SAEM26) is summarized, and its applications are presented in Sect. 3. The derived results are expressed in Sect. 4. The conclusion part is offered in Sect. 5.

2 Extracting the NLODE of eq. (1)

To get the NLODE of eq. (1), we benefit from the following complex transformation:

$$\begin{aligned} U(x,t)=U(\xi )\, e^{i\left( -\kappa x+ \omega t + \varphi _0\right) }, \,\,\, \xi =x- \nu t, \end{aligned}$$
(2)

in which \(U(\xi )\) is the soliton pulse profile, \(\varphi _0\) is phase constant, and \( \omega , \kappa ,\nu \) are frequency, wave number and velocity. Inserting eq. (2) to eq. (1), the imaginary and real components of the acquired equation are presented in the following structure, respectively:

$$\begin{aligned} \eta U^{\prime \prime \prime }-\left( \left( 3 a +2 b-\mu \right) U^{2}+\left( 2 \alpha -\beta \nu \right) \kappa +3 \kappa ^2 \eta -\beta \omega +\nu +\gamma \right) U^\prime =0, \end{aligned}$$
(3)
$$\begin{aligned} \left( \alpha -\beta \nu +3\eta \kappa \right) U^{\prime \prime }+\lambda _{3} U^{7} +\lambda _{2} U^{5} -\left( \left( a -\mu \right) \kappa -\lambda _{1}\right) U^{3}-\left( \eta \kappa ^3+\alpha \,\kappa ^{2}+\left( \gamma -\beta \omega \right) \kappa +\omega \right) U =0. \end{aligned}$$
(4)

If eq. (3) is integrated and the integration constant is assumed as zero, then we attain,

$$\begin{aligned} \eta U^{\prime \prime } +\left( \mu -3a -2b\right) U^{3}+3\left( \beta \kappa \nu -3 \eta \kappa ^2 -2 \alpha \kappa +\beta \omega -\gamma -\nu \right) U =0. \end{aligned}$$
(5)

Equation (5) gives the following constraints:

$$\begin{aligned} \mu =3a + 2b, \,\, \nu =\frac{3 \kappa ^2 \eta +2 \alpha \kappa -\beta \omega +\gamma }{\beta \kappa -1},\,\, \eta =0. \end{aligned}$$
(6)

Obtaining as \(\eta =0\) in eq. (6) demonstrates that the model presented eq. (1) does not accept the third-order dispersion term. Carrying out a proper arrangement on the perturbation term, an examination of a model containing this term can be contemplated as the subject of another study.

In eq. (4), balancing the terms \(U^{\prime \prime }\) and \(U^{7}\), the balance constant is achieved as \(\frac{1}{3}\). Since the balance constant is defined as a positive integer, we need to perform the following transformation:

$$\begin{aligned} U(\xi )= H^{1/3}(\xi ). \end{aligned}$$
(7)

If eq. (4) is rearranged considering eqs. (6),(7), it gives the following expression:

$$\begin{aligned} 9 \left( 2\left( a +b \right) \kappa +\lambda _{1}\right) H^{\frac{8}{3}}+9 \lambda _{2} \varrho H^{\frac{10}{3}}-3 H \left( \alpha \beta \kappa -\beta ^{2} \omega +\beta \gamma +\alpha \right) H^{\prime \prime } \nonumber \\ +2\Phi \left( H^{\prime }\right) ^{2}+9 \varrho H^{2} \left( H^{2} \lambda _{3}-\alpha \,\kappa ^{2}+\left( \beta \omega -\gamma \right) \kappa -\omega \right) =0, \end{aligned}$$
(8)

in which \(\varrho =\left( \beta \kappa -1\right) \) and \(\Phi =\alpha \beta \kappa -\beta ^{2} \omega + \beta \gamma + \alpha \). For integrability of eq. (8), we must set,

$$\begin{aligned} \lambda _1=-2\kappa (a+b),\lambda _2=0. \end{aligned}$$
(9)

As a result, the NODE form in eq. (8) is formed as follows:

$$\begin{aligned} -3 \Phi H H^{\prime \prime }+2 \Phi (H^{\prime })^{2} +9 \varrho \left( H^{2} \lambda _{3}-\alpha \,\kappa ^{2}+\left( \beta \omega -\gamma \right) \kappa -\omega \right) H^{2}=0. \end{aligned}$$
(10)

From eqs. (10), (11), and (12), the homogeneous balance constant J is figured out as 2.

3 Application

3.1 SAEM26

The SAEM26 [63] offers that eq. (10) has a solution as the following truncated series form:

$$\begin{aligned} H(\xi )=\sum _{j=0}^{J}\Lambda _{j}\Upsilon ^{j}(\xi ), \,\, \Lambda _{J}\ne 0, \end{aligned}$$
(11)

in which \(\Lambda _j\) are real constants, J is the positive integer balance constant which was computed as 2. The function \(\Upsilon (\xi )\) states the solution of the following equation:

$$\begin{aligned} (\Upsilon ^{\prime }(\xi ))^2=\sigma ^2\Upsilon ^2(\xi )\left[ 1-\chi \Upsilon ^4(\xi )\right] , \,\, \end{aligned}$$
(12)

in which \(\chi \), and \(\sigma \) are nonzero real values. We express one of the solutions for eq. (12) with the following structures:

$$\begin{aligned} \Upsilon (\xi )=\sqrt{\frac{2}{\sqrt{\chi } \left( e^{2 \sigma \xi } + e^{-2\sigma \,\xi }\right) }} \,\,\,\,\,\,\, or \,\,\,\, \,\,\,\, \Upsilon (\xi )= \sqrt{\frac{2}{ e^{2 \sigma \xi } + \chi e^{-2\sigma \xi }}}, \end{aligned}$$
(13)

or in the hyperbolic form:

$$\begin{aligned} \Upsilon (\xi )= \sqrt{\frac{{{\,\textrm{sech}\,}}(2\sigma \xi )}{\sqrt{\chi } }}, \end{aligned}$$
(14)

which serves the bright soliton. Since \(J=2\), eq. (11) turns into the following form:

$$\begin{aligned} H(\xi )=\Lambda _{0}+\Lambda _{1}\Upsilon (\xi )+\Lambda _{2}\Upsilon ^{2}(\xi ), \,\, \Lambda _2\ne 0. \end{aligned}$$
(15)

When we insert eqs. (15), (12) into eq. 10, then gather all coefficients of \(\Upsilon ^{j}\) and equalize them to zero, we produce:

$$\begin{aligned}&\Upsilon ^0(\xi ): \Xi _1 \Lambda _{0}^{2} =0, \nonumber \\&\Upsilon ^1(\xi ): \left( \Xi _2 \sigma ^{2}+6 \Xi _1\right) \Lambda _{0} \Lambda _{1} -6 \lambda _3 \Lambda _{0}^{3} \Lambda _{1} =0, \nonumber \\&\Upsilon ^2(\xi ): \Xi _2 \sigma ^{2} (12\Lambda _{0} \Lambda _{2} + \Lambda _{1}^{2} )+9 (\Xi _1-\lambda _3 \Lambda _{0}^{2}) \left( 2 \Lambda _{2} \Lambda _{0}+\Lambda _{1}^{2}\right) -36 \lambda _3\Lambda _{0}^{2} \Lambda _{1}^{2} =0, \nonumber \\&\Upsilon ^3(\xi ):7 \Xi _2 \sigma ^{2} \Lambda _{1} \Lambda _{2} -18 \Lambda _{0}^{2} \Lambda _{1} \Lambda _{2} \lambda _3 -36 \Lambda _{0} \Lambda _{1} \left( 2 \Lambda _{2} \Lambda _{0}+\Lambda _{1}^{2}\right) \lambda _3 +18 \Lambda _{1} \Lambda _{2} \Xi _1=0, \nonumber \\&\Upsilon ^4(\xi ): 4 \Xi _2 \sigma ^2 \Lambda _{2}^{2} -9 \Lambda _{0}^{2} \Lambda _{2}^{2} \lambda _3 -72 \Lambda _{0} \Lambda _{1}^{2} \Lambda _{2} \lambda _3 -9 \left( 2 \Lambda _{2} \Lambda _{0}+\Lambda _{1}^{2}\right) ^{2} \lambda _3 +9 \Lambda _{2}^{2} \Xi _1=0, \\&\Upsilon ^5(\xi ): \Xi _2 \sigma ^{2} \chi \Lambda _{0} \Lambda _{1} +4 \lambda _3 \Lambda _{0} \Lambda _{1} \Lambda _{2}^{2}+4 \left( 2\Lambda _{2} \Lambda _{0}+\Lambda _{1}^{2}\right) \Lambda _{1} \Lambda _{2} \lambda _3=0, \nonumber \\&\Upsilon ^6(\xi ): (24 \Xi _2\sigma ^{2} \chi +36 \lambda _3 \Lambda _2^2) \Lambda _{0} \Lambda _{2} + (7 \Xi _2 \sigma ^{2} \chi +54 \Lambda _{2}^{2} \lambda _3 )\Lambda _{1}^{2} =0 , \nonumber \\&\Upsilon ^7(\xi ): \left( 25 \Xi _2 \sigma ^{2} \chi +36 \lambda _3 \Lambda _{2}^{2} \right) \Lambda _{1} \Lambda _{2}=0, \nonumber \\&\Upsilon ^8(\xi ): \left( 16 \Xi _2 \sigma ^{2} \chi +9 \lambda _3 \Lambda _{2}^{2}\right) \Lambda _{2}^{2} =0,\nonumber \end{aligned}$$
(16)

where \(\Xi _1=\left( \kappa ^{2} \alpha -\kappa \beta \omega -\lambda _3 \Lambda _{0}^{2}+\kappa \gamma +\omega \right) \) and \(\Xi _2=\left( \frac{\beta \left( 2 \alpha \kappa -\beta \omega +\gamma \right) }{\beta \kappa -1}-\alpha \right) \). The solution of the system in eq. (16) gives the following set:

Set-1.

$$\begin{aligned} \left\{ \begin{aligned} \sigma =- \frac{ \sqrt{-9 \Phi \left( \alpha \left( \beta ^2 \kappa ^2-1 \right) -\beta \omega \left( \beta -1\right) ^2 \right) }}{2 \left( \alpha \left( \beta \kappa +1\right) -\beta \omega \left( \beta -1\right) \right) }, \Lambda _{0} = 0, \Lambda _{1} = 0, \Lambda _{2} =\mp \frac{2 \sqrt{\lambda _3 \chi \Phi }}{\lambda _3} \end{aligned} \right\} , \end{aligned}$$
(17)

in which \(\Phi =\left( \alpha \kappa ^2+\gamma \kappa -\beta \kappa \omega +\omega \right) \). Unifying eq. (15) with eqs. (2), (7), and (13), we derive the following solution:

$$\begin{aligned} U_1\left( x,t\right) =\left( \frac{2 \Lambda _{2}}{\sqrt{\chi }\, \left( {\mathrm e}^{2 \sigma \left( x -\nu t\right) }+{\mathrm e}^{-2 \sigma \left( x -\nu t\right) }\right) }\right) ^{\frac{1}{3}} {\mathrm e}^{\textrm{i} \left( -\kappa x +\omega t +{\psi _0} \right) }. \end{aligned}$$
(18)

Herein, \(\sigma , \Lambda _2, \nu \) are found in eqs. (6), (17).

4 Modulation instability analysis

We intend to scrutinize the modulation instability of eq. (1) utilizing the standard linear stability analysis [64,65,66,67,68]. In order to carry out this aim, assume eq. (1) has the following structure of steady-state (SS) solution:

$$\begin{aligned} U(x,t)=\left( \sqrt{K}+\Psi (x,t)\right) e^{i\Theta }, \end{aligned}$$
(19)

in which \(\Theta = \tau _1 K+ (\tau _2 -\epsilon )K^2\), \(\epsilon \) is a real constant, and K represents the normalized optical power. \(\Psi (x,t)\) is also a small perturbation which satisfies the condition \(\Psi (x,t)\ll \sqrt{K}\). Combining eq. (19) with eq. (1) and collecting linear terms, we get

$$\begin{aligned} \beta \Psi _{xt}+\alpha \Psi _{xx}+\textrm{i}\left( \beta \left( \tau _2 -\epsilon \right) K^{2}+\left( \beta \tau _1 -2 \, a - b + \mu \right) K - \gamma \right) \Psi _{x} -\textrm{i} \left( a +b \right) K \Psi ^*_{x}+\textrm{i} \Psi _{t} \nonumber \\ +K\left( 4 K^{2} \lambda _3 +\left( \epsilon -\tau _2 +3 \lambda _2 \right) K+\left( 2 \lambda _1 -\tau _1 \right) \right) \Psi +K\left( 3 K^{2} \lambda _3 +2 K \lambda _2 + \lambda _1 \right) \Psi ^*=0, \end{aligned}$$
(20)

in which (\(^*\)) is the complex conjugate of \(\Psi (x, t)\). Presume that the solution of eq. (20) is stated as:

$$\begin{aligned}&\Psi (x,t)=\alpha _1 e^{i \left( \Omega x -{\mathcal {F}} t\right) }+\alpha _2 e^{-i \left( \Omega x -{\mathcal {F}} t\right) },\nonumber \\&\Psi ^*(x,t)=\alpha _1 e^{-i \left( \Omega x -{\mathcal {F}} t\right) }+\alpha _2 e^{i \left( \Omega x -{\mathcal {F}} t\right) }, \end{aligned}$$
(21)

where \(\alpha _1, \alpha _2\) are real-valued coefficients, \({\mathcal {F}}\) and \(\Omega \) state the frequency of perturbation and normalized wave number. Unifying eq. (21) with eq. (20), considering separately the coefficients of \(e^{i \left( \Omega x -{\mathcal {F}} t\right) }\) and \(e^{-i \left( \Omega x -{\mathcal {F}} t\right) }\), the following system is acquired,

$$\begin{aligned} T_1 \alpha _1+ T_2 \alpha _2=0, \nonumber \\ T_3 \alpha _1+ T_4 \alpha _2=0, \end{aligned}$$
(22)

in which

$$\begin{aligned} T_1&=4 K^{3} \lambda _3 +\left( \beta \left( \epsilon -\tau _2 \right) \Omega +\epsilon +3 \lambda _2 -\tau _2 \right) K^{2}-\Omega ^{2} \alpha +\left( {\mathcal {F}} \beta +\gamma \right) \Omega +{\mathcal {F}} \nonumber \\ &\quad +\left( \left( 2 a +b -\mu -\beta \tau _1 \right) \Omega +2 \lambda _1 -\tau _1 \right) K, \end{aligned}$$
(23)
$$\begin{aligned} T_2=3 K^{3} \lambda _3 +2 K^{2} \lambda _2 +\left( \left( a +b \right) \Omega +\lambda _1 \right) K, \end{aligned}$$
(24)
$$\begin{aligned} T_3=3 K^{3} \lambda _3 +2 K^{2} \lambda _2 -\left( \left( a +b \right) \Omega +\lambda _1 \right) K, \end{aligned}$$
(25)
$$\begin{aligned} T_4&=2 4 K^{3} \lambda _3 +\left( -\beta \left( \epsilon -\tau _2 \right) \Omega +\epsilon +3 \lambda _2 -\tau _2 \right) K^{2} -\Omega ^{2} \alpha +\left( \Upsilon \beta -\gamma \right) \Omega -{\mathcal {F}} \nonumber \\ &\quad \left( \left( \beta \tau _1 -2 a -b +\mu \right) \Omega +2 \lambda _1 -\tau 1 \right) K. \end{aligned}$$
(26)

The system can be written in the matrix form:

$$\begin{aligned} \begin{pmatrix} T_1 &{} T_2 \\ T_3 &{} T_4 \end{pmatrix} \times \begin{pmatrix} \alpha _1 \\ \alpha _2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}. \end{aligned}$$
(27)

Figuring out the determinant of the matrix in eq. (27) taking into account eqs. (23)–(26) for \({\mathcal {F}}\), the following relation is gained:

$$\begin{aligned} {\mathcal {F}}=\frac{\sqrt{G_1 K^{6}+G_2 K^5+G_3 K^4+G_4 K^3+G_5 K^{2}+G_6}+G_7}{\Omega ^{2} \beta ^{2}-1} \end{aligned}$$
(28)

where \(\Omega ^{2} \beta ^{2}-1 \ne 0\), and

$$\begin{aligned} G_1&=9 \Omega ^{2} \beta ^{2} \lambda _3^{2}+7 \lambda _3^{2},\\ G_2&=-4 \left( \beta ^{2} \left( 2\epsilon -3 \lambda _2-2\tau _2 \right) \Omega ^{2}-2\epsilon -3 \lambda _2+2\tau _2 \right) \lambda _3 ,\\ G_3&=-2 \beta \left( \left( \epsilon ^{2}+\left( 3 \lambda _2 -2 \tau _2 \right) \epsilon -3 \lambda _1 \lambda _3 -2 \lambda _2^{2}-3 \lambda _2 \tau _2 -4 \lambda _3 \tau _1 +\rho 2^{2}\right) +4 \left( 2a +b-\mu \right) \lambda _3 \right) \Omega ^{2}\nonumber \\&\quad +\beta ^{4} \left( \epsilon -\tau _2 \right) ^{2} \Omega ^{4}+\epsilon ^{2}+\left( 6 \lambda _2 -2 \tau _2 \right) \epsilon +10 \lambda _1 \lambda _3 +5 \lambda _2^{2}-6 \lambda _2 \tau _2 -8 \lambda _3 \tau _1 +\tau _2^{2},\\ G_4&=2 \beta ^{3} \left( -\beta \tau _1+a +b-\mu \right) \left( \epsilon -\tau _2 \right) \Omega ^{4}+ \left( \left( -4 \lambda _1 +4 \tau _1 \right) \epsilon +\left( 6 \lambda _2 -4 \tau _2 \right) \tau _1 +4 \lambda _1 \left( \lambda _2 +\tau _2 \right) \right) \Omega ^{2}\beta ^{2} \nonumber \\&\quad +\left( \left( \left( -4 a -2 b +2 \mu \right) \epsilon +\left( 4 a +2 b -2 \mu \right) \tau _2 +\left( -12 a -6 b +6 \mu \right) \lambda _2 -8 \lambda _3 \gamma \right) \beta -8 \alpha \lambda _3 \right) \Omega ^{2}\nonumber \\&\quad+\left( 4 \lambda _1 -2 \tau _1 \right) \epsilon +\left( -6 \lambda _2 +2 \tau _2 \right) \tau _1 +4 \left( 2\lambda _2 -\tau _2\right) \lambda _1 , \nonumber \\ G_5&=\beta ^{2} \left( \beta ^{2} \tau _1^{2}+2\left( \epsilon \gamma +\left( -2 a -b +\mu \right) \tau _1 -\gamma \tau _2 \right) \beta +2\alpha \epsilon -2\alpha \tau _2 + \left( a -\mu \right) \left( 3a +2b-\mu \right) \right) \Omega ^{4}\nonumber \\&\quad+\left( \left( \lambda _1^{2}+4 \lambda _1 \tau _1 -2 \tau _1^{2}\right) \beta ^{2}+\left( -2 \epsilon (\alpha + \gamma ) +\left( 4 a +2 b -2 \mu \right) (\tau _1-2\lambda _1) +2 \gamma \tau _2 -6 \lambda _2 \gamma \right) \beta \right) \Omega ^{2} \nonumber \\&\quad+( 2 \alpha \tau _2 -6 \alpha \lambda _2 +\left( a +b \right) ^{2})\Omega ^{2}+3 \lambda _1^{2}-4 \lambda _1 \tau _1 +\tau _1^{2}, \nonumber \\ G_6&=2\left( \beta \left( -\beta \tau _1+2a +b-\mu \right) \Omega ^{2}+2\lambda _1 -\tau _1\right) \Omega ^{2} \left( \beta \gamma +\alpha \right) K +\Omega ^{4} \left( \beta \gamma +\alpha \right) ^{2},\nonumber \\ G_7&=\Omega ^{3} \alpha \beta +\left( -4 \lambda _3 \beta \,K^{3}-3 \lambda _2 \beta \,K^{2}+\left( -2 \beta \lambda _1 +2 a +b -\mu \right) K +\gamma \right) \Omega . \end{aligned}$$

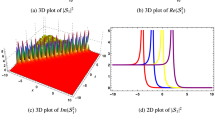
The SS stability is examined by applying the achieved dispersion term. If there is an imaginary component of \({\mathcal {F}}\), then the SS solution changes unstable as the perturbation exponentially enlarges. Thus, it is observed that the modulation instability arises if \(G_1 K^{6}+G_2 K^5+G_3 K^4+G_4 K^3+G_5 K^{2}+G_6<0\) in eq. (28). On the contrary, if \({\mathcal {F}}\) is real for each real value, that is, \(G_1 K^{6}+G_2 K^5+G_3 K^4+G_4 K^3+G_5 K^{2}+G_6>0\), the SS is stable against small perturbations (Fig. 1).

The gain spectrum of eq. (28) is indicated as:

$$\begin{aligned} G(\Omega )=2Im\left( {\mathcal {F}}\right) . \end{aligned}$$
(29)
Fig. 1
figure 1

Gain spectrum for eq. (29) for \( \lambda _1 = -0.4, \lambda _2 = 0.12, \lambda _3 = 0.2, b = 2, \beta = 2, \mu = 1, \gamma = 0.5, a = -2, \alpha = 1, \tau _1 = 0.5, \epsilon =0.7, \tau _2 = 1\)

Full size image

5 Results and discussion

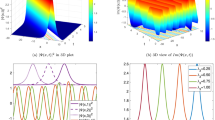
This part consists of some views of the acquired soliton solution. We intend to indicate some sketches of the \(|U_1(x,t)|^2\) in Fig. 2. Figure 2 expresses the bright soliton for the values \(\alpha = -1.5, \beta = -1, \lambda _3=\gamma = 1,\omega = 0.25, \kappa =\chi = 0.5, \psi _0 =10\). Yellow, red, and blue waves in Fig. 2d indicate the structure of the soliton for \(t=1,3,5\). Thus, the wave moves to the left preserving the bright soliton view.

Fig. 2
figure 2

Some depictions of \(U_{1}(x,t)\) when \( \alpha = 0.2, \beta =\lambda _3=\chi =\gamma = 1, \kappa = -0.75,\omega = 0.5, \psi _0 = 10 \)

Full size image

Figure 3 comprises various 2D views of \(U_1(x,t)\). The figures depict the influences of varied coefficients on the soliton form. Figure 3a represents the impacts of \(\alpha \) on the soliton structure. According to Fig. 3a, when \(\alpha \) is positive and increases, the height of bright soliton positively shifts, whereas the amplitude of bright soliton decreases. But, when \(\alpha \) is negative and enlarges, the amplitude of bright soliton positively shifts, but the height of bright soliton decreases. The effect of \(\beta \) indicates that as \(\beta \) increases, the height of the bright soliton changes positively, whereas the width of the soliton narrows. According to Fig. 3c, the parameter \(\lambda _3\) has a negative effect on the height of bright soliton for increasing \(\lambda _3\) values. Furthermore, increasing the value of \(\gamma \) has a positive influence on the dynamics of the soliton in terms of expanding the amplitude of the derived soliton in Fig. 3d, while it has a negative effect on the elevation of the soliton. Consequently, the charts in Fig. 3 highlight the significance of diverse parameter values in forming the bright soliton structure of eq.(1).

Fig. 3
figure 3

2D depictions of \(U_{1}(x,t)\) when \( \chi = 1, \kappa = -0.75,\omega = 0.5, \psi _0 = 10 \)

Full size image

6 Conclusion

In this paper, the new extended auxiliary equation technique, an effective and powerful technique, has been utilized to produce novel soliton solutions of the perturbed Schrödinger–Hirota equation with cubic–quintic–septic law having spatiotemporal dispersion. The model was constructed to include the spatiotemporal dispersion term. But, it was observed that the model did not accept the third-order nonlinear dispersion term while obtaining the NLODE of the model. Necessary arrangements were made in this direction, and within the framework of the obtained constraint relations, the coefficient of the quintic law nonlinearity term was acquired as zero. Thus, the bright solution was generated. Diverse depictions of the derived soliton solution were indicated, and the impacts of the parameters in the model were analyzed and added physical interprets with 2D graphics as well. The paper will provide to the literature in terms of both degenerating the model to the cubic–septic law nonlinearity form by not accepting the term quintic law nonlinearity for the examined form and showing the parameter effects on the bright soliton formed in this case. In the future, the creation of stochastic, fractional, multi-soliton, and bifurcation analysis forms and the inclusion of other methods in terms of their ability to produce other soliton types can be counted among some of the goals and may be the focus of attention of those who do research in this field. Eventually, it is able to extremely observe that the soliton solutions will present sights to a number of researchers investigating the branch of fiber optics.