1 Introduction

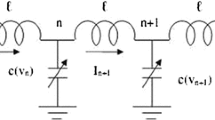
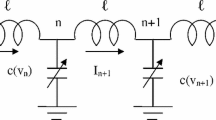
Transmission lines were the first electromagnetic waveguides ever invented. Examples of transmission lines are shown in Fig. 1. The symbol for a transmission line is usually represented by two pieces of parallel wires, but in practice, these wires need not be parallel. The nonlinear dynamics of the electrical transmission line equation come out in a large variety of scientific and engineering fields as distributing cable television signals, connecting radio transmitters and receivers with their antennas, computer network connections and high-speed computer data buses, trunklines routing calls between telephone switching centers [1,2,3,4,5,6,7,8,9,10]. In the electrical system, the nonlinearity balancing the dispersion (related to the ladder nature of the line) is introduced by a capacitor, whose capacitance is controlled by the imposed bias voltage, thus acting like a capacitive diode (“varicap” diode or varactor). The nonlinear signal generated in this nonlinear transmission line (NLTL) is a localized electrical signal with a bell shape, propagating with features of pulse soliton (i.e., translate at constant speed keeping a permanent bell shape) due to the effect of varactors periodically loaded throughout the line [14]. The nonlinear electrical transmission line models (NETLEs) are convenient tools to study the propagation of electrical solitons which can propagate in the form of voltage waves in nonlinear dispersive media. Afshari and Hajimiri [1], Zayed and Alurrfi [2, 3] solved the electrical transmission lines equation using first-order linear approximation, and Malwe et al. [4] and El-Borai et al. [5] used the second-order curve fitting for the diode characteristics [11].

In this article, we introduce optical soliton solutions of the nonlinear transmission lines equation using two simple methods, first one presented by Kudryashov [17]; it was applied in [18, 19], and the second presented by Ali [16]. The nonlinear electrical transmission line (NETL) is described as a model for long transmission lines. Our model is the voltage wave propagation of an electrical transmission line which has been presented by Tala-Tebue [12, 13] as:

$$\begin{aligned} u_{tt}-\sigma (u^{2})_{tt}+\beta (u^{3})_{tt}-u_{0}^{2}\delta _{1}^{2}u_{xx}-u_{0}^{2}\frac{\delta _{1}^{4}}{12}u_{xxxx}-w_{0}^{2}\delta _{2}^{2}u_{yy}-w_{0}^{2}\frac{\delta _{2}^{4}}{12}u_{yyyy}=0, \end{aligned}$$
(1)

where \(\alpha ,\beta ,u_{0},w_{0},\delta _{1},\delta _{2}\) are real nonzero constants, and \(u=u(x,y,t)\) is the voltage in the transmission lines. (1) is the differential equation governing the wave propagation in the network. The variables x and y are the propagation distances, and t is the time. \(\delta _{1}\) is the space between two adjacent sections in the longitudinal direction, while \(\delta _{2}\) is the space between two adjacent sections in the transverse direction. This nonlinear electrical transmission line model (NETLM) explains the wave distributions on the network lines [12, 13].

This manuscript is composed of the following sections: In Sect. 2, a mathematical description of the model is presented. In Sect. 3, we give an overview of the used methods. In Sect. 4, the implementation of the proposed methods for finding the new exact solutions describing nonlinear transmission lines is given. In Sect. 5, we illustrate our solutions by some graphs. Physical explanations for some solutions are presented in Sect. 6. Finally, we briefly make a conclusion in Sect. 7.

2 Mathematical description of the model

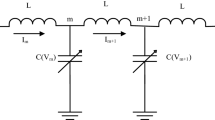
Consider the NLTLs as depicted in Fig. 2. \( u_{n,m}(t)\) is the voltage through the capacitor, \(C(u_{n,m}) \) is the capacitance in the shunt branch, and \(L_{1}\) is the constant inductor in the series branch. Many identical dispersive lines are connected with each node by the inductance \(L_{2}\) as shown in Fig. 2. The nodes have two distinct coordinates m and n, where m labels in the transverse direction and n specifies the nodes in the propagation direction of the wave.

Fig. 1
figure 1

Schematic representation of the NETL

Full size image

The capacitance varied with the applied voltage which admits by the nonlinear capacitance of this network or varicap diode. The voltage dependence relation is assumed to have a polynomial form given by

$$\begin{aligned} C(u_{n,m})=(3\beta u_{n,m}^{2}-2\sigma u_{n,m}+1)C_{0}, \end{aligned}$$
(2)

where \( C_{0},\sigma \) and \( \beta \) are constants. The electric charge stored in the capacitors is determined by this coefficients. Using the Kirchhoff voltage law and Kirchhoff current law leads to the following set of propagation equations:

$$\begin{aligned} \begin{aligned}&\frac{d^{2}}{dt^{2}}(\beta u_{n,m}^{3}-\sigma u_{n,m}^{2}+u_{n,m})=(u_{n,m-1}+u_{n,m+1}-2u_{n,m})w_{0}^{2}+\\&(u_{n-1,m}+u_{n+1,m}-2u_{n,m})u_{0}^{2}, \end{aligned} \end{aligned}$$
(3)

with \(u_{0}^{2}=\frac{1}{L_{1}C_{0}}\) and \(w_{0}^{2}=\frac{1}{L_{2}C_{0}}\). (3) is the differential equation governing the wave propagation in the network under consideration. All of the lines have the same characteristic frequency. This is due to the fact that all of the lines are identical. The continuum approximation is used by assuming \(u_{n,m}\longrightarrow u(x,y,t)\) for a weak nonlinearity and by setting that the wavelength is sufficiently large relative to the length of a segment. Assuming that \(\delta _{2}\) and \(\delta _{1}\) are the spacings between two adjacent portions in the m and n directions, respectively, we can use the continuum approximation to expand \(u_{n,m\pm 1}\) and \(u_{n\pm 1,m}\)as:

$$\begin{aligned} \begin{aligned}&u_{n,m\pm 1}=u\pm \delta _{2}\frac{\partial u}{\partial y}+\frac{\delta _{2}^{2}}{2!}\frac{\partial ^{2} u}{\partial y^{2}}\pm \frac{\delta _{2}^{3}}{3!}\frac{\partial ^{3} u}{\partial y^{3}}+\frac{\delta _{2}^{4}}{4!}\frac{\partial ^{4} u}{\partial y^{4}}+...\\&u_{n,m+1}+u_{n,m-1}-2u_{n,m}=\delta _{2}^{2}\frac{\partial ^{2} u}{\partial y^{2}}+ \frac{\delta _{2}^{4}}{12}\frac{\partial ^{4} u}{\partial y^{4}}+...\\&u_{n\pm 1,m}=u\pm \delta _{1}\frac{\partial u}{\partial x}+\frac{\delta _{1}^{2}}{2!}\frac{\partial ^{2} u}{\partial x^{2}}\pm \frac{\delta _{1}^{3}}{3!}\frac{\partial ^{3} u}{\partial x^{3}}+\frac{\delta _{1}^{4}}{4!}\frac{\partial ^{4} u}{\partial x^{4}}+...\\&u_{n+1,m}+u_{n-1,m}-2u_{n,m}=\delta _{1}^{2}\frac{\partial ^{2} u}{\partial x^{2}}+ \frac{\delta _{1}^{4}}{12}\frac{\partial ^{4} u}{\partial x^{4}}+... \end{aligned} \end{aligned}$$
(4)
Fig. 2
figure 2

Graph of (22) using the first simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.2,\Omega =0.1,u_{0}=0.1,w_{0}=0.3,\) \(a_{1}=0.3,c=0.8,\delta _{1}=2,\delta _{2}=1\)

Full size image

From the previous equations and for the perturbed voltage u, we acquire the following nonlinear partial differential equation:

$$\begin{aligned} \frac{\partial ^{2}}{\partial t^{2}}(u-\sigma u^{2}+\beta u^{3})-u_{0}^{2}(\delta _{2}^{2}\frac{\partial ^{2} u}{\partial y^{2}}+ \frac{\delta _{2}^{4}}{12}\frac{\partial ^{4} u}{\partial y^{4}})-w_{0}^{2}(\delta _{1}^{2}\frac{\partial ^{2} u}{\partial x^{2}}+ \frac{\delta _{1}^{4}}{12}\frac{\partial ^{4} u}{\partial x^{4}})=0. \end{aligned}$$
(5)

Equation (5) models the wave propagation in an NETL [15].

3 Overview of the methods

3.1 First simple method presented by Kudryashov [17]

Consider the following nonlinear partial differential equation

$$\begin{aligned} F(u,u_{t},u_{x},u_{y},u_{tt},u_{xx},u_{yy},...)=0, \end{aligned}$$
(6)

where \(u=u(x,y,t)\) is the unknown function, and F is a polynomial in u and its partial derivatives.

  1. Step 1:

    Use the wave transformation:

    $$\begin{aligned} u(x,y,t)=U(\xi ),\,\ \xi =ax+by-ct, \end{aligned}$$
    (7)

    where a, b are constants and c is the velocity of the traveling wave; (6) is reduced to a nonlinear ordinary differential equation as:

    $$\begin{aligned} P(U',U'',U''',...)=0, U'=\frac{dU}{d\xi } \end{aligned}$$
    (8)
  2. Step 2:

    Assume the solution of (8) takes the form of a finite series

    $$\begin{aligned} U(\xi )=\sum _{i=0}^N A_{i} (Q(\xi ))^{i}, \end{aligned}$$
    (9)

    where \(A_{i}(i=0,1,2,...,N),A_N\ne 0\), are unknowns with \((A_{i}\ne 0\) to be calculated. The positive integer N will be calculated by homogeneous balance technique.

  3. Step 3:

    The function \(Q(\xi )\) satisfies the auxiliary differential equation:

    $$\begin{aligned} (Q^{\prime }(\xi ))^{2}=\alpha ^{2}Q(\xi )^{2}(1-\Omega Q(\xi )^{2}); \end{aligned}$$
    (10)

    (10) gives the following solution:

    $$\begin{aligned} Q(\xi )=\frac{4a_{1}\exp (-\alpha \xi )}{4a_{1}^{2}+\Omega \exp (-2\alpha \xi )}. \end{aligned}$$
    (11)
  4. Step 4:

    By substituting (9) and (10) into (8) and collecting all terms with the same power of \(Q(\xi )\)together, (8) converted into a polynomial, taking each coefficient equal to zero, we obtain a system of algebraic equations.

  5. Step 5:

    By using the Mathematica program, we can solve the system of algebraic equations to get the exact solution of (8).

3.2 Second simple method presented by Ali [16]

We illustrate the modified Kudryashov method in this section as follows:

  1. Step 1:

    Suppose a solution of (8) given in a series form:

    $$\begin{aligned} U(\xi )=\sum _{i=0}^N A_{i}(Q(\xi ))^{i}, \end{aligned}$$
    (12)

    where \(A_{i}(i=0,1,2,...,N),A_N\ne 0\), are unknowns with \((A_{i}\ne 0\) to be calculated.

  2. Step 2:

    The function \(Q(\xi )\) fulfills the differential equation:

    $$\begin{aligned} (Q^{\prime }(\xi ))^{2}=\alpha ^{2} (\log (m))^{2} Q(\xi )^{2}(1-\Omega Q(\xi )^{2}); \end{aligned}$$
    (13)

    the solution of (13) is introduced by:

    $$\begin{aligned} Q(\xi )=\frac{4a_{1}m^{(-\alpha \xi )}}{4a_{1}^{2}+\Omega m^{(-2\alpha \xi )}}. \end{aligned}$$
    (14)
  3. Step 3:

    By substituting (12) and (13) into (8), we acquire a polynomial of \(Q(\xi )\). Setting all the coefficients of the like powers of \(Q(\xi )\) to zero, we obtain a system of equations.

  4. Step 4:

    We use the Mathematica program to solve the system of equations. Consequently, we can get the exact solution of (8).

4 Implementations of the methods

Using the transformation (7) into (1), it can be reduced to a nonlinear ordinary differential equation as below:

$$\begin{aligned}&-2c^{2}(\sigma -3\beta U(\xi ))U^{\prime }(\xi )^{2}+(a^{2}u_{0}^{2}\delta _{1}^{2}-b^{2}w_{0}^{2}\delta _{2}^{2}+c^{2}(1-2\sigma U(\xi )+3\beta U(\xi )^{2}))U^{\prime \prime }(\xi )\nonumber \\&\qquad +\frac{1}{12}(a^{4}u_{0}^{2}\delta _{1}^{4}-b^{4}w_{0}^{2}\delta _{2}^{4})U^{(4)}(\xi )=0. \end{aligned}$$
(15)

Integrating twice and considering the zero for both constants, we get:

$$\begin{aligned} (c^{2}+a^{2}u_{0}^{2}\delta _{1}^{2}-b^{2}w_{0}^{2}\delta _{2}^{2})U(\xi )-c^{2}\sigma U(\xi )^{2}+c^{2}\beta U(\xi )^{3}+\frac{1}{12}(a^{4}u_{0}^{2}\delta _{1}^{4}-b^{4}w_{0}^{2}\delta _{2}^{4})U^{\prime \prime }(\xi )=0. \end{aligned}$$
(16)

Balancing \(U^{3}\) with \(U^{\prime \prime }\) in (16), we have the following relation:

$$\begin{aligned} 3N=N+2\Rightarrow N=1. \end{aligned}$$
(17)

4.1 First simple method

From (9), the solution of (16) can be given in the form:

$$\begin{aligned} U(\xi )=A_{0}+A_{1}Q(\xi ), \end{aligned}$$
(18)

By substituting (18) in Eq. (16) with (10) and equating factors of each power of \(Q(\xi )\) in the resulting equation to zero, we reach a nonlinear algebraic system as follows:

$$\begin{aligned}&c^{2}A_{0}-c^{2}\sigma A_{0}^{2}+c^{2}\beta A_{0}^{3}+a^{2}A_{0}u_{0}^{2}\delta _{1}^{2}-b^{2}A_{0}w_{0}^{2}\delta _{2}^{2}=0,\\&\quad c^{2}A_{1}-2c^{2}\sigma A_{0}A_{1}+3c^{2}\beta A_{0}^{2}A_{1}+a^{2}A_{1}u_{0}^{2}\delta _{1}^{2}+\frac{1}{12}a^{4}\alpha ^{2}A_{1}u_{0}^{2}\delta _{1}^{4}-b^{2}A_{1}w_{0}^{2}\delta _{2}^{2}\\&\quad -\frac{1}{12}b^{4}\alpha ^{2}A_{1}w_{0}^{2}\delta _{2}^{4}=0,\\&\quad -c^{2}\sigma A_{1}^{2}+3c^{2}\beta A_{0}A_{1}^{2}=0,\\&\quad c^{2}\beta A_{1}^{3}-\frac{1}{6}a^{4}\alpha ^{2}\Omega A_{1}u_{0}^{2}\delta _{1}^{4}+\frac{1}{6}b^{4}\alpha ^{2}\Omega A_{1}w_{0}^{2}\delta _{2}^{4}=0. \end{aligned}$$

Solving the previous system, we can get the following sets of solutions:

Set 1:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=-\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}(-9\beta +2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{-1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta ^{2}w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(19)

Substituting (19) in (18) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{1,2}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}\exp (-\alpha (ax+by-ct)))}{4a_{1}^{2}+\Omega \exp (-2\alpha (ax+by-ct))))}. \end{aligned} \end{aligned}$$
(20)

Set 2:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}(-9\beta +2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{-1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta ^{2}w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(21)

Substituting (21) in (18) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{3,4}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}\exp (-\alpha (ax+by-ct)))}{4a_{1}^{2}+\Omega \exp (-2\alpha (ax+by-ct))))}. \end{aligned} \end{aligned}$$
(22)

Set 3:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=-\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}(-9\beta +2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta ^{2}w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(23)

Substituting (23) in (18) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{5,6}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}\exp (-\alpha (ax+by-ct)))}{4a_{1}^{2}+\Omega \exp (-2\alpha (ax+by-ct))))}. \end{aligned} \end{aligned}$$
(24)

Set 4:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}(-9\beta +2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta ^{2}w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(25)

Substituting (25) in (18) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{7,8}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}\exp (-\alpha (ax+by-ct)))}{4a_{1}^{2}+\Omega \exp (-2\alpha (ax+by-ct))))}. \end{aligned} \end{aligned}$$
(26)

Set 5:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=-\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}(-9\beta +2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{-1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta ^{2}w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(27)

Substituting (27) in (18) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{9,10}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}\exp (-\alpha (ax+by-ct)))}{4a_{1}^{2}+\Omega \exp (-2\alpha (ax+by-ct))))}. \end{aligned} \end{aligned}$$
(28)

Set 6:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}(-9\beta +2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{-1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta ^{2}w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(29)

Substituting (29) in (18) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{11,12}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}\exp (-\alpha (ax+by-ct)))}{4a_{1}^{2}+\Omega \exp (-2\alpha (ax+by-ct))))}. \end{aligned} \end{aligned}$$
(30)

Set 7:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=-\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}(-9\beta +2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta ^{2}w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(31)

Substituting (31) in (18) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{13,14}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}\exp (-\alpha (ax+by-ct)))}{4a_{1}^{2}+\Omega \exp (-2\alpha (ax+by-ct))))}. \end{aligned} \end{aligned}$$
(32)

Set 8:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}(-9\beta +2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta ^{2}w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(33)

Substituting (33) in (18) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{15,16}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}\exp (-\alpha (ax+by-ct)))}{4a_{1}^{2}+\Omega \exp (-2\alpha (ax+by-ct))))}. \end{aligned} \end{aligned}$$
(34)

4.2 Second simple method

From (12), the solution of (16) is taken in the form:

$$\begin{aligned} U(\xi )=A_{0}+A_{1}Q(\xi ), \end{aligned}$$
(35)

By setting above solution (35) in (16) with (13) and equating the coefficients of the like powers of \(Q(\xi )\), we will arrive at a set of nonlinear algebraic equations:

$$\begin{aligned}&c^{2}A_{0}-c^{2}\sigma A_{0}^{2}+c^{2}\beta A_{0}^{3}+a^{2}A_{0}u_{0}^{2}\delta _{1}^{2}-b^{2}A_{0}w_{0}^{2}\delta _{2}^{2}=0, \\&\quad c^{2}A_{1}-2c^{2}\sigma A_{0}A_{1}+3c^{2}\beta A_{0}^{2}A_{1}+a^{2}A_{1}u_{0}^{2}\delta _{1}^{2}+\frac{1}{12}a^{4}\alpha ^{2}\log ^{2}(m) A_{1}u_{0}^{2}\delta _{1}^{4}-b^{2}A_{1}w_{0}^{2}\delta _{2}^{2} \\&\quad -\frac{1}{12}b^{4}\alpha ^{2}\log ^{2}(m) A_{1}w_{0}^{2}\delta _{2}^{4}=0, \\&\quad -c^{2}\sigma A_{1}^{2}+3c^{2}\beta A_{0}A_{1}^{2}=0, \\&\quad c^{2}\beta A_{1}^{3}-\frac{1}{6}a^{4}\alpha ^{2}\Omega \log ^{2}(m) A_{1}u_{0}^{2}\delta _{1}^{4}+\frac{1}{6}b^{4}\alpha ^{2}\Omega \log ^{2}(m) A_{1}w_{0}^{2}\delta _{2}^{4}=0. \end{aligned}$$

Now, the following new exact solutions for (1) will be produced:

Set 1:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=-\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}\log ^{2}(m)(-9\beta +2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}\log ^{2}(m)(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{-1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta \log ^{2}(m) w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta ^{2}\log ^{2}(m) w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}\log ^{2}(m) u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}\log ^{2}(m)+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(36)

Substituting (36) in (35) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{1,2}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}m^{-\alpha (ax+by-ct)})}{(4a_{1}^{2}+\Omega m^{-2\alpha (ax+by-ct)})}. \end{aligned} \end{aligned}$$
(37)

Set 2:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}\log ^{2}(m)(-9\beta +2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}\log ^{2}(m)(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{-1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta \log ^{2}(m) w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta ^{2}\log ^{2}(m) w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}\log ^{2}(m) u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}\log ^{2}(m)+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(38)

Substituting (38) in (35) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{3,4}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}m^{-\alpha (ax+by-ct)})}{(4a_{1}^{2}+\Omega m^{-2\alpha (ax+by-ct)})}. \end{aligned} \end{aligned}$$
(39)

Set 3:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=-\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}\log ^{2}(m)(-9\beta +2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}\log ^{2}(m)(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta \log ^{2}(m) w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta ^{2}\log ^{2}(m) w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}\log ^{2}(m) u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}\log ^{2}(m)+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(40)

Substituting (40) in (35) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{5,6}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}m^{-\alpha (ax+by-ct)})}{(4a_{1}^{2}+\Omega m^{-2\alpha (ax+by-ct)})}. \end{aligned} \end{aligned}$$
(41)

Set 4:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}\log ^{2}(m)(-9\beta +2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}\log ^{2}(m)(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta \log ^{2}(m) w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta ^{2}\log ^{2}(m) w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}\log ^{2}(m) u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}\log ^{2}(m)+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(42)

Substituting (42) in (35) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{7,8}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}m^{-\alpha (ax+by-ct)})}{(4a_{1}^{2}+\Omega m^{-2\alpha (ax+by-ct)})}. \end{aligned} \end{aligned}$$
(43)

Set 5:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=-\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}\log ^{2}(m)(-9\beta +2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}\log ^{2}(m)(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{-1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta \log ^{2}(m) w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta ^{2}\log ^{2}(m) w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}\log ^{2}(m) u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}\log ^{2}(m)+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(44)

Substituting (44) in (35) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{9,10}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}m^{-\alpha (ax+by-ct)})}{(4a_{1}^{2}+\Omega m^{-2\alpha (ax+by-ct)})}. \end{aligned} \end{aligned}$$
(45)

Set 6:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}\log ^{2}(m)(-9\beta +2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}\log ^{2}(m)(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{-1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta \log ^{2}(m) w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta ^{2}\log ^{2}(m) w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}\log ^{2}(m) u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}\log ^{2}(m)+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(46)

Substituting (46) in (35) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{11,12}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}m^{-\alpha (ax+by-ct)})}{(4a_{1}^{2}+\Omega m^{-2\alpha (ax+by-ct)})}. \end{aligned} \end{aligned}$$
(47)

Set 7:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=-\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}\log ^{2}(m)(-9\beta +2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}\log ^{2}(m)(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta \log ^{2}(m) w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta ^{2}\log ^{2}(m) w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}\log ^{2}(m) u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}\log ^{2}(m)+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(48)

Substituting (48) in (35) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{13,14}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}m^{-\alpha (ax+by-ct)})}{(4a_{1}^{2}+\Omega m^{-2\alpha (ax+by-ct)})}. \end{aligned} \end{aligned}$$
(49)

Set 8:

$$\begin{aligned} \begin{aligned}&A_{0}=\frac{\sigma }{3\beta }, A_{1}=\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta },a=\frac{\sqrt{\frac{c^{2}\alpha ^{2}\beta u_{0}^{2}\delta _{2}^{2}\log ^{2}(m)(-9\beta +2\sigma ^{2})+P_{1}}{\alpha ^{2}\beta \delta _{2}^{2}\log ^{2}(m)(u_{0}^{2}-w_{0}^{2})}}}{3\sqrt{\beta }u_{0}\delta _{1}},\\&b=\frac{1}{3}\sqrt{\frac{c^{2}\alpha ^{2}\beta \log ^{2}(m) w_{0}^{2}\delta _{2}^{2}(9\beta -2\sigma ^{2})-P_{1}}{\alpha ^{2}\beta ^{2}\log ^{2}(m) w_{0}^{2}\delta _{2}^{4}(-u_{0}^{2}+w_{0}^{2})}},\\&P_{1}=\sqrt{c^{2}\alpha ^{2}\beta ^{2}\log ^{2}(m) u_{0}^{2}w_{0}^{2}(c^{2}\alpha ^{2}(9\beta -2\sigma ^{2})^{2}\log ^{2}(m)+108\beta \sigma ^{2}(-u_{0}^{2}+w_{0}^{2}))\delta _{2}^{4}}. \end{aligned} \end{aligned}$$
(50)

Substituting (50) in (35) with (11) and (7), we get the following solutions of (1):

$$\begin{aligned} \begin{aligned}&u_{15,16}(x,y,t)=\frac{\sigma }{3\beta }\pm \frac{\sqrt{2}\sigma \sqrt{\Omega }}{3\beta }\frac{(4a_{1}m^{-\alpha (ax+by-ct)})}{(4a_{1}^{2}+\Omega m^{-2\alpha (ax+by-ct)})}. \end{aligned} \end{aligned}$$
(51)

5 Graphical illustrations

In this manuscript, we have presented only a few results to avoid the overload of the document. One could obtain more general results by more general choices of the parameters. For example, the graph of (22) using the first simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.2,\Omega =0.1,u_{0}=0.1,w_{0}=0.3,\) \(a_{1}=0.3,c=0.8,\delta _{1}=2,\delta _{2}=1\) is introduced in Fig. 2. In Fig. 3, the graph of (28) using the first simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.2,\Omega =0.1,u_{0}=0.1,w_{0}=0.3,\) \(a_{1}=0.8,c=0.8,\delta _{1}=0.6,\delta _{2}=1\) is presented. In Fig. 4, the graph of (34) using the first simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.2,\Omega =0.1,u_{0}=0.1,w_{0}=0.3,\) \(a_{1}=0.8,c=0.8,\delta _{1}=0.6,\delta _{2}=1\) is presented. The graph of (37) using the second simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.1,\Omega =0.15,u_{0}=0.1,w_{0}=0.3,\) \(m=0.1,a_{1}=0.1,c=0.8,\delta _{1}=1.5,\delta _{2}=1\) is presented in Fig. 5. In Fig. 6, the graph of (41) using the second simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.1,\Omega =0.2,u_{0}=0.1,w_{0}=0.3,\) \(m=0.1,a_{1}=0.2,c=0.8,\delta _{1}=2,\delta _{2}=1\) is presented. Finally, we showed the graph of (51) using the second simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.2,\Omega =0.1,u_{0}=0.1,w_{0}=0.3,\) \(m=0.1,a_{1}=0.8,c=0.8,\delta _{1}=0.6,\delta _{2}=1\) in Fig. 7.

Fig. 3
figure 3

Graph of (28) using the first simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.2,\Omega =0.1,u_{0}=0.1,w_{0}=0.3,\) \(a_{1}=0.8,c=0.8,\delta _{1}=0.6,\delta _{2}=1\)

Full size image
Fig. 4
figure 4

Graph of (34) using the first simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.2,\Omega =0.1,u_{0}=0.1,w_{0}=0.3,\) \(a_{1}=0.8,c=0.8,\delta _{1}=0.6,\delta _{2}=1\)

Full size image
Fig. 5
figure 5

Graph of (37) using the second simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.1,\Omega =0.15,u_{0}=0.1,w_{0}=0.3,\) \(m=0.1,a_{1}=0.1,c=0.8,\delta _{1}=1.5,\delta _{2}=1\)

Full size image
Fig. 6
figure 6

Graph of (41) using the second simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.1,\Omega =0.2,u_{0}=0.1,w_{0}=0.3,\) \(m=0.1,a_{1}=0.2,c=0.8,\delta _{1}=2,\delta _{2}=1\)

Full size image
Fig. 7
figure 7

Graph of (51) using the second simple method at \(\alpha =0.01,\beta =0.1,\sigma =0.2,\Omega =0.1,u_{0}=0.1,w_{0}=0.3,\) \(m=0.1,a_{1}=0.8,c=0.8,\delta _{1}=0.6,\delta _{2}=1\)

Full size image
Fig. 8
figure 8

Graph of (34) using the first simple method

Full size image
Fig. 9
figure 9

Graph of (51) using the second simple method

Full size image

6 Physical explanations for some solutions

In this section, we illustrate the application of the results established above. These solutions are solitons and are obtained by using two methods. The solutions that were found have application in telecommunications for the transport of information because solitons have the capability to propagate at long distances without attenuation and without changing their shapes. The solutions have shown that these solitons are more resistant to perturbations than others. Therefore, using the solutions in the network under consideration, we conclude that the system might be more robust to weak external perturbations. Also, in Fig. 8, we see at \(\sigma =0.3,0.35,0.4\) the amplitude of the wave is growing as \(\sigma \) increases and as \(\beta \) varies: \(\beta =0.2,0.25,0.3\), the amplitude of the wave wanes as \(\beta \) increases. In Fig. 9, when m increases: \(m=0.2,0.3,0.45\), also the amplitude of the wave increases and when \(a_{1}\) varies: \(a_{1}=1,1.5,2\), the amplitude of the wave decreases as \(a_{1}\) is raised.

7 Conclusion

At the end of this work, we studied the \((2+1)\)-dimensional nonlinear electrical transmission line equation and it has important applications in many fields such as physics and telecommunications engineering. We acquired the soliton solutions by using two simple methods. We obtained various analytical solutions for this model using two newly well-established methods. The solutions that we obtained show that the two methods are effective methods that produce different types of solutions. We have shown the accuracy of the obtained results by introducing illustrative proper figures.