Permanent shear localization in dense disordered materials due to microscopic inertia

Abstract

In this work using computer simulations of 3D model of dense disordered solids we show, for the first time, the appearance of shear localization in the stationary flow under homogeneous driving conditions. To rationalize our simulation results we develop a continuum model, that couples the dynamics of the local flow to the evolution of a kinetic temperature field related to the local inertial dynamics. Our model predicts that the coupling of the flow field to this additional destabilizing field appears only as a necessary condition for shear localization, a minimum system size is necessary to accommodate the flow instability. Moreover we show that this size criterion resulting from our continuum description is in quantitative agreement with our particle-based simulation results.

Graphic abstract

Appendix

1.1 Simulation details

The model disordered system is characterised by an interaction potential defined by $U(r) = 4\epsilon \left[ (a_{ij}/r_{ij})^{12} - (a_{ij}/r_{ij})^{6} \right] + \epsilon$, for $r_{ij} \le 2^{1/6} a_{ij}$, else $U(r_{ij})=0$. Here $a_{ij} = (a_i+a_j)/2$ defines the distance between the center of particles i (with diameter $a_i$) and j (with diameter $a_j$) at contact and the unit energy $\epsilon =1$ for all particles. The diameters of the particles are drawn from a Gaussian distribution with a variance of 10%. The initial configurations are prepared by quenching a equilibrated liquid configuration at a volume fraction $\phi =0.70$, with a chosen set of simulation box dimensions ($L_x$, $L_y$ and $L_z$). The quench rate used here is $\Gamma =5 \cdot 10^{-3} \epsilon /(k_B \tau _0)$ and we find that the steady state flow features do not depend on preparation protocol. Before subjecting the sample to shear, we take the system to the zero temperature limit using conjugate gradient energy minimisation technique. Samples so prepared is subjected to shear deformation at a finite shear rate using Lees-Edwards boundary condition and evolving the system by solving the Dissipative Particle Dynamics (DPD) equation of motion given by

$$\begin{aligned} m \frac{d^2\textbf{r}_i}{dt^2} = - \zeta \sum _{j(\ne i)} \omega (r_{ij}) (\hat{r}_{ij}\cdot \textbf{v}_{ij})\hat{r}_{ij} - \nabla _{\textbf{r}_i} U \end{aligned}$$

(14)

where the first term in the right hand side (RHS) is the damping force which depends on the damping coefficient $\zeta$ and m is the mass of the particle. The relative velocity $\textbf{v}_{ij} = \textbf{v}_j - \textbf{v}_i$ is computed over a cut-off distance $r_{ij} \le 2.5 a_{ij}$, with the weight factor $\omega (r_{ij})=1$. The second term in the RHS is the force due to interactions between particles. As a measure of the extent of over damping, we define an inertial quality factor $Q=\tau _\textrm{damp}/\tau _\textrm{vib}$, where $\tau _\textrm{damp}=m/\zeta$ is the viscous timescale and $\tau _\textrm{vib}=\sqrt{m a^2 / \epsilon }$ defines an elastic timescale. The inertial quality factor measures the number of inertial oscillation within the damping time. The shear rate in our simulations is defined in the units $\tau _\textrm{vib}^{-1}$.

1.2 Steady state flow

We make sure that a sample has indeed reached a steady state flow, by monitoring the macroscopic load curve as well as the microscopic flow profiles ($V_x$ vs. Y) and stress profiles. Reaching steady state, the macroscopic shear stress fluctuates around a mean stress value. Similarly the flow profiles as well as the distribution of local stresses do not evolve any longer with time (strain) (Fig. 7).

Fig. 6

a Flow curve data (open circle) obtained from overdamped simulations with HB fits (lines). b Measured stress against the measured kinetic temperature from underdamped simulations at different shear rates (annotated values)

Fig. 7

a Derivative of HB equation with fit values obtained in Fig. 6(a). b Numerical derivative of the data in Fig. 6(b)

1.3 Minimum length to accommodate an instability in molecular simulations

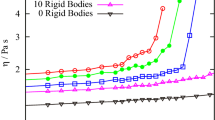
In order to obtain the minimum length scale to accommodate the flow instability, using the Eq. (6), one needs to compute the thermal conductivity $\lambda _T$, heat capacity $c_V$, the time associated with the relaxation of kinetic energy $\tau$, along with the derivative of stress with respect to temperature $\partial _T \sigma$ and to shear rate $\partial _{\dot{\gamma }}\sigma$. We compute $\lambda _T$, for a system size of $N=10^5$, using the reverse non-equilibrium molecular dynamics method introduced by Muller-Plathe (JCP 106, 6082 (1997)) and its value is $\lambda _T=30$ (LJ units). We have performed a slow quenching run to prepare the initial sample. From this data we compute the heat capacity as the slope of total energy vs. temperature. To compute $\ell _c$, we use $c_V=3.0$ (LJ units). To compute the relaxation time associated with the kinetic energy, we monitor the dissipation of kinetic energy with time at a fixed dissipation constant corresponding to $Q=10^4$ and we find $\tau _\textrm{KE} \equiv \tau \approx 350 \tau _\textrm{vib}$. The partial derivative of stress w.r.t. temperature ($\partial _{T}\sigma$) should be obtained by measuring, at a given shear rate, the stress in the finite temperature simulations in overdamped conditions ($Q=1$). However it turns out that for the data quality we are able to reach at this stage the error bars within this method are too large to come to a conclusive result for the critical length. This is especially true in the low shear rate limit. This is why we opted for a different method to approximate this term through another measurement. We measure for a given shear rate in an underdamped simulation ($Q=10^4$), the associated stress and the kinetic temperature and obtain a numerical derivative of this curve (see Fig. 6) The $\partial _{\dot{\gamma }} \sigma$ is obtained using Herschel-Bulkley fits with fitting parameters obtained from the flow curve for $Q=1$ using the data presented in Fig. 1.

1.4 Herschel-Bulkley fitting parameters

To obtain the Herschel-Bulkley (HB) fitting parameters for a finite temperature, over-damped system ($Q=1$), we have performed molecular simulations, over shear rates ranging between $\dot{\gamma }=10^{-5}\tau _\textrm{vib}^{-1}$ to $\dot{\gamma }=10^{-1}$, of a system of $10^4$ particles keeping all other parameters the same as the under-damped simulations. In order to extract over-damped HB parameters ($\sigma _Y$, A and n) at finite temperature we make sure that at each temperature (ranging between $T=0 \epsilon /k_B$ to $T=7.5 \epsilon /k_B$), the system has reached a steady state.

1.5 Flow curve for the continuum description

The assumed local constitutive relation used in the continuum description with the chosen model parameters is displayed in Fig. 8.

Fig. 8

Assumed constitutive relation for the analytical model obtained from solving Eqs. (3) and (10), using the implicit expression: $\sigma = \sigma _y + A\dot{\gamma }^n - B(\frac{\tau }{c_V} \sigma \dot{\gamma })^\alpha$ with the following parameters (in LJ units): $c_V = 3$, $\rho = 1.337$, $\tau = 350$, $\sigma _y = 2.7$, $A = 12$, $B = 2.3$, $n = 0.5$, and $\alpha = 0.3$ Since there is no general form of the temperature dependence of the flow-curve we implement the most simple form that reproduces the minimum in the flow-curve, $\dot{\gamma }_\textrm{min}\simeq 5. 10^{-2}$ and $\sigma _\textrm{min}\simeq 1.21$. The red line indicates $\sigma ^*\simeq 1.2374$

1.6 A remark on shear-concentration coupling effects

To be sure that in our case it is really the local heating effect that plays the role for the instability to occur we also provide additional measurements to disentangle potential mass migration effects from local kinetic temperature effects. To do so we measure alongside the local shear-rate profile also the steady state density profiles in the unstable region, shown in Fig. 9a and b. The question is whether these variations in the local volume fraction could as well explain the instability. To answer this question we also measured the yield stress dependence on density. We estimate the yield stress values for the range of different packing fractions that we observed in the density profiles of the simulations. And indeed we find that these are all above the actual homogeneous stress value, as shown in Fig. 9. This means that the change of local volume fraction cannot induce an instability in our dynamics. However, the change of the local yield stress due to a finite kinetic temperature is much more drastic within the temperature range that we measure in the profiles. Therefore temperature is indeed inducing an instability to make the system flow in the high kinetic temperature regions where the temperature dependent yield stress is smaller than the homogeneous stress value. This is for us is a proof that the observed migration is not the source of the instability but rather a consequence of another type of instability induced by the heating effect.

Fig. 9

Steady state measurement of a Local shear rate, b Local volume fraction and c Local stress and yield stress for a underdamped system (Q=$10^4$) with a system size $L_y=360a$, sheared at $\dot{\gamma }=10^{-2}\tau _vib^{-1}$