1 Introduction

The classical electromagnetic fields in vacuum are described by the linear Maxwell’s equations. Several theories assert that a nonlinear correction arises from virtual electron–positron pairs, but these have yet to be observed in experiments. The nonlinear correction is considered to affect such as the radiation from pulsars [1, 2] or neutron stars [3], the Wichmann–Kroll correction [4] on the Lamb shift, and the interaction between a nucleus and electrons through the Uehling potential [5,6,7]. The most widely considered theories are the Heisenberg–Euler model [8, 9] and the Born–Infeld model [10], which is sometimes applied to calculate a hydrogen atom [11,12,13,14].

In experiments, a cavity system is often used, such as the PVLAS (Polarizzazione del Vuoto con LASer) [15, 16], BMV (Biréfringence Magnétique du Vide) [17], and OVAL (Observing VAcuum with Laser) experiments [18]. These instruments explore the changes in the refractive index, or birefringence, when light passes through an external magnetic field. The calculation of the refractive index is, for example, concisely summarized in Refs. [19,20,21]. In these calculations, a stationary plane wave with non-classical dispersion relation is assumed to derive the refractive index. In a mathematical viewpoint, assuming a stationary solution and solving an eigenvalue problem would require an infinitely long time. On the other hand, there are few studies which treat the nonlinear correction in a shorter timescale. For example, it has been considered partially in Refs. [22, 23]. A resonant phenomenon has been reported recently in Ref. [23] showing that the nonlinear corrective term to the classical field can increase resonantly with time. Such an increasing behavior may make it easy to detect the vacuum nonlinearity. Therefore, studying the resonant behavior in more detail may prove valuable in developing more effective experiment.

In this study, we consider the nonlinear correction in a one-dimensional cavity system. We solve the initial and boundary problem and derive the minimum nonlinear correction for a general classical electromagnetic field. Based on the solution, we discuss its property and in particular, the resonant behavior of the nonlinear correction such as its dependency on external static electromagnetic fields and a polarization change. In addition, we show that the present study does not contradict the calculation of the well-known birefringence.

2 Notations

We normalize electromagnetic fields by using the electric constant \(\varepsilon _0\) and magnetic constant \(\mu _0\). The electric field \(\varvec{E}\) is multiplied by \(\varepsilon _0^{1/2}\), and the magnetic flux density \(\varvec{B}\) is divided by \(\mu _0^{1/2}\). Two Lorentz invariants are defined as \(F=E^2-B^2\) and \(G=\varvec{E}\cdot \varvec{B}\), and the nonlinear electromagnetic Lagrangian we consider in this study is given by

$$\begin{aligned} L=\frac{1}{2}F+C_{2,0}F^2+C_{0,2}G^2, \end{aligned}$$
(1)

where \(C_{2,0}\) and \(C_{0,2}\) are the nonlinear parameters and we suppose them to be sufficiently small. For the analysis, their values are not necessary and the results can be applied not only for the Heisenberg–Euler model but also for the Born–Infeld model provided that the Lagrangian in Eq. (1) is a good approximation. We use the ratio of the Heisenberg–Euler model, i.e., \(C_{0,2}/C_{2,0}=7\) only in Fig. 1.

This Lagrangian leads to nonlinear Maxwell’s equations. A part of the electromagnetic fields can be described by the linear classical Maxwell’s equations. We refer to this part as “classical term” and express it by a subscript c. The classical term does not always satisfy the nonlinear Maxwell’s equations. The difference from the classical term is referred to as “nonlinear corrective term” and expressed by a subscript n. By these notations, we express both the electric field and magnetic flux density as \(\varvec{E}=\varvec{E}_c+\varvec{E}_n, \varvec{B}=\varvec{B}_c+\varvec{B}_n\), respectively. For a given classical term, if it is overwhelmingly larger than the nonlinear corrective term, by using \(F_c=E_c^2-B_c^2\) and \(G_c=\varvec{E}_c\cdot \varvec{B}_c\), the polarization and magnetization of vacuum can be approximated as

$$\begin{aligned} \begin{aligned}&\varvec{P}^{(0)}= 4C_{2,0}F_c\varvec{E}_c +2C_{0,2}G_c\varvec{B}_c,\\&\varvec{M}^{(0)}= -4C_{2,0}F_c\varvec{B}_c +2C_{0,2}G_c\varvec{E}_c.\\ \end{aligned} \end{aligned}$$
(2)

As in Ref. [23], we call the corresponding corrective term as the “minimum corrective term” and express the components by \(\varvec{E}_n^{(0)}, \varvec{B}_n^{(0)}\), respectively. These satisfy the following linearized equations:

$$\begin{aligned} \begin{aligned}&\nabla \cdot \varvec{B}_n^{(0)}=0,\\&\nabla \times \varvec{E}_n^{(0)}+ c^{-1}\partial _t\varvec{B}_n^{(0)}= \varvec{0},\\&\nabla \cdot \varvec{E}_n^{(0)}= -\nabla \cdot \varvec{P}^{(0)},\\&\nabla \times \varvec{B}_n^{(0)}- c^{-1}\partial _t\varvec{E}_n^{(0)}= c^{-1}\partial _t\varvec{P}^{(0)} +\nabla \times \varvec{M}^{(0)},\\ \end{aligned} \end{aligned}$$
(3)

where c is the speed of light and \(\partial _t\) expresses the partial derivative with respect to time t. These equations may be good approximations, while the minimum corrective term is much smaller than the classical term. If the electromagnetic fields are of class \(C^2\), by eliminating the magnetic flux density and using

$$\begin{aligned} \varvec{S}^{(0)}= \nabla \left( \nabla \cdot \varvec{P}^{(0)}\right) -c^{-2}\partial _t^2\varvec{P}^{(0)} -c^{-1}\partial _t\nabla \times \varvec{M}^{(0)}, \end{aligned}$$
(4)

we obtain a wave equation for the minimum corrective electric field as

$$\begin{aligned} \left( \triangle -c^{-2}\partial _t^2\right) \varvec{E}_n^{(0)}=-\varvec{S}^{(0)}. \end{aligned}$$
(5)

The “resonant condition” shown in Ref. [23] is

$$\begin{aligned} \varvec{S}^{(0)}\ne \varvec{0}, \ \ \left( \triangle -c^{-2}\partial ^2_t\right) \varvec{S}^{(0)}=\varvec{0}. \end{aligned}$$
(6)

More precisely, if a part of \(\varvec{S}^{(0)}\) satisfies this condition, the corresponding minimum corrective term increases resonantly, in proportion to time or distance.

3 One-dimensional cavity system and classical term

We consider a one-dimensional cavity system. Two mirrors of perfect conductor are located at \(x=0,l\), and we calculate in the inside region of \(0\le x\le l\). All functions depend only on x and t. We introduce new variables as

$$\begin{aligned} \alpha =t-c^{-1}x, \ \ \beta =t+c^{-1}x. \end{aligned}$$
(7)

We first describe the classical term. Its input begins at a certain negative time, and at \(t\ge 0\), we assume that the classical term can be expressed by the sum of a stationary wave part (with a subscript r) and a static part (with a subscript s) as

$$\begin{aligned} \varvec{E}_c=\varvec{E}_r+\varvec{E}_s, \ \ \varvec{B}_c=\varvec{B}_r+\varvec{B}_s. \end{aligned}$$
(8)

The static part depends only on x in the case of one dimension and therefore must be a constant. As for the stationary wave part, the boundary conditions are given such that the y, z components of the electric field and the x component of the magnetic flux density are always zero at \(x=0,l\). The boundary conditions are related only to the wave part. Let \(\tau =c^{-1}l\), and by using arbitrary functions p and q to have a period of \(2\tau \) and being of class \(C^3\), a general stationary wave part at \(t\ge 0\) can be expressed as

$$\begin{aligned} \varvec{E}_r= \begin{pmatrix} 0\\ p(\alpha )-p(\beta )\\ q(\alpha )-q(\beta )\\ \end{pmatrix} , \ \ \varvec{B}_r= \begin{pmatrix} 0\\ -q(\alpha )-q(\beta )\\ p(\alpha )+p(\beta )\\ \end{pmatrix}. \end{aligned}$$
(9)

The period \(2\tau \) of p and q is necessary to satisfy the boundary conditions at \(x=l\). We can assume as

$$\begin{aligned} \int _0^{2\tau } p(\xi )\text {d}\xi =0, \ \ \int _0^{2\tau } q(\xi )\text {d}\xi =0, \end{aligned}$$
(10)

without loss of generality because adding a constant to p and q is the same as changing the static magnetic flux density. For the following calculations, we extend the domains of p and q to all real numbers by the periodicity.

Both p and q can have shorter periods. For example, let \(kl=n\pi , n\in \mathbb {N}\) and \(\omega =ck\), a standing wave of a single mode is given by \(p(\xi )=(A_p/2)\cos \omega \xi , q=0\). This yields \(\varvec{E}_r=A_p\sin kx \sin \omega t \varvec{e}_y\) and \(\varvec{B}_r=A_p\cos kx \cos \omega t \varvec{e}_z\), where \(\varvec{e}_{y,z}\) are the unit vectors along the y, z directions, respectively. The fundamental period of p is \(2\pi /\omega =2\tau /n\). Then, we define the fundamental period as \(2\tau _p\) if p is not identically zero. \(\tau /\tau _p\) is a natural number. \(\tau _q\) is defined in a similar manner. We also introduce a symbol \(\tau _M\). If both p and q are not identically zero, \(\tau _M\) expresses the larger one of \(\tau _p\) and \(\tau _q\). If only one of \(\tau _p\) or \(\tau _q\) is defined, \(\tau _M\) expresses the defined one.

The amplitude A of the wave part is defined by

$$\begin{aligned} A=2\max \left( \max _{\xi }|p(\xi )|,\max _{\xi } |q(\xi )|\right) . \end{aligned}$$
(11)

Hence, we obtain \(A=A_p\) in the above example. From the form of the wave part, \(A_p\) is obviously the amplitude in the conventional sense, and thus, the present definition is consistent. Another indicator to express the magnitude of the wave part is introduced by

$$\begin{aligned} A'=\frac{2\tau _M}{\pi } \max \left( \max _{\xi }|p'(\xi )|,\max _{\xi } |q'(\xi )| \right) . \end{aligned}$$
(12)

In the example, \(A'=A_p\) and is equal to the amplitude. In general, \(A'\) and A are different values.

Lastly, we give a limitation to the magnitudes of the classical term. The considered Lagrangian in Eq. (1) is limited to the quadratic with respect to F and G. In addition, we only consider the minimum corrective term. For these treatments, we assume the following inequality:

$$\begin{aligned} (C_{2,0}+C_{0,2})(E_s+B_s+A)^2 \ll 1. \end{aligned}$$
(13)

Note that this inequality does not contain \(A'\). It is uncertain how \(A'\) can differ from A, and thus excluded in this evaluation.

4 Solution of the minimum corrective term

We calculate the minimum corrective term for the classical term described in the preceding section. The nonlinear correction exists from the very beginning of the input, and the minimum corrective term depends on the classical term at \(t<0\). However, investigation of the variety of inputs is beyond the focus of our present study. Rather, the response of the minimum corrective term for the classical term at \(t\ge 0\) expressed in Eq. (8) is more important as it implies possibility of resonant behavior. Then, we consider a general initial distribution of the minimum corrective term at \(t=0\) to absorb the effect of the classical term at \(t<0\).

4.1 x component

In the one-dimensional system, the x component of the minimum corrective term can be calculated alone. The corresponding \(\nabla \times \) terms in Eq. (3) do not have the x component. Then, using a constant a, the following expression is necessary:

$$\begin{aligned} E_{nx}^{(0)}(x,t)=-P_x^{(0)}(x,t)+a. \end{aligned}$$
(14)

If the initial distribution can be expressed by \(-P_x^{(0)}(x,0)+a\), it is the unique solution. Otherwise, the solution does not exist. The solution is that of a longitudinal standing wave. The magnetic flux density is always zero because it is independent of x and the boundary condition requires \(B_{nx}^{(0)}(0,t)=0\).

4.2 y and z components

Both \(E_{sx}\) and \(B_{sx}\) do not contribute to the y, z components of the minimum corrective term and are omitted hereinafter. We define the following two-dimensional vectors as

$$\begin{aligned} \begin{aligned}&\tilde{\varvec{E}}_n= \begin{pmatrix} E_{ny}^{(0)}\\ E_{nz}^{(0)}\\ \end{pmatrix}, \ \ \tilde{\varvec{B}}_n= \begin{pmatrix} B_{nz}^{(0)}\\ -B_{ny}^{(0)}\\ \end{pmatrix}, \\&\varvec{j}= \begin{pmatrix} j_y\\ j_z\\ \end{pmatrix} = \begin{pmatrix} \partial _tP_y^{(0)}-c\partial _xM_z^{(0)}\\ \partial _tP_z^{(0)}+c\partial _xM_y^{(0)}\\ \end{pmatrix}.\\ \end{aligned} \end{aligned}$$
(15)

We made an special definition for \(\tilde{\varvec{B}}_n\) to simplify the expressions in the following calculation. The boundary conditions are expressed as \(\tilde{\varvec{E}}_n(0,t)=\varvec{0}\) and \(\tilde{\varvec{E}}_n(l,t)=\varvec{0}\) and the initial distribution as \(\tilde{\varvec{E}}_0(x)=\tilde{\varvec{E}}_n(x,0)\) and \(\tilde{\varvec{B}}_0(x)=\tilde{\varvec{B}}_n(x,0)\). Each component is supposed to be of class \(C^2[0,l]\) and to be much smaller than A. From the boundary conditions, the following are necessary:

$$\begin{aligned} \tilde{\varvec{E}}_0(0)=\varvec{0}, \ \ \tilde{\varvec{E}}_0(l)=\varvec{0}. \end{aligned}$$
(16)

For the arguments of \(\varvec{j}\), we use \((\alpha ,\beta )\), not (x, t). We can uniquely divide \(\varvec{j}\) into an even part \(\varvec{j}^{\text {(e)}}\) and odd part \(\varvec{j}^{\text {(o)}}\) such that

$$\begin{aligned} \varvec{j}(\alpha ,\beta )= \varvec{j}^{\text {(e)}}(\alpha ,\beta ) +\varvec{j}^{\text {(o)}}(\alpha ,\beta ), \end{aligned}$$
(17)

where \(\varvec{j}^{\text {(e)}}(\alpha ,\beta ) =\varvec{j}^{\text {(e)}}(\beta ,\alpha )\) and \(\varvec{j}^{\text {(o)}}(\alpha ,\beta ) =-\varvec{j}^{\text {(o)}}(\beta ,\alpha )\). Their detailed forms are shown in Appendix A. Because p and q are periodic, both \(\varvec{j}^{\text {(e)}}\) and \(\varvec{j}^{\text {(o)}}\) have a period of \(2\tau \) in both \(\alpha \) and \(\beta \).

The minimum corrective term which satisfies the boundary conditions at \(x=0,l\) is given by

$$\begin{aligned} \begin{aligned} \tilde{\varvec{E}}_n(x,t)=&-\frac{1}{4} \int _{\alpha }^{\beta } \varvec{j}^{\text {(e)}}(\alpha ,\xi ) -\varvec{j}^{\text {(e)}}(\xi ,\beta )\text {d}\xi \\&-\frac{1}{4} \left( \int _{-\alpha }^{\beta } \varvec{j}^{\text {(o)}}(\alpha ,\xi )\text {d}\xi + \int _{-\beta }^{\alpha } \varvec{j}^{\text {(o)}}(\xi ,\beta )\text {d}\xi \right) \\&+\varvec{K}(\alpha )-\varvec{K}(\beta ),\\ \tilde{\varvec{B}}_n(x,t)=&-\frac{1}{4} \int _{\alpha }^{\beta } \varvec{j}^{\text {(e)}}(\alpha ,\xi ) +\varvec{j}^{\text {(e)}}(\xi ,\beta )\text {d}\xi \\&-\frac{1}{4} \left( \int _{-\alpha }^{\beta } \varvec{j}^{\text {(o)}}(\alpha ,\xi )\text {d}\xi - \int _{-\beta }^{\alpha } \varvec{j}^{\text {(o)}}(\xi ,\beta )\text {d}\xi \right) \\&+\varvec{K}(\alpha )+\varvec{K}(\beta ),\\ \end{aligned} \end{aligned}$$
(18)

where the function \(\varvec{K}(Z)\) is defined at \(Z\ge -\tau \) and has a period of \(2\tau \) because of the boundary conditions at \(x=l\). The values of the function at \(-\tau \le Z \le \tau \) are determined by the initial distribution as follows:

$$\begin{aligned} \varvec{K}(Z)= {\left\{ \begin{array}{ll} \begin{aligned} &{}-\frac{1}{4}\int _{-Z}^Z\varvec{j}^{\text {(e)}}(\xi ,Z)\text {d}\xi \\ &{}+\frac{1}{2} \left[ \tilde{\varvec{B}}_0(-cZ)+\tilde{\varvec{E}}_0(-cZ) \right] \\ \end{aligned} &{} (-\tau \le Z \le 0)\\ \begin{aligned} &{}\frac{1}{4}\int _{-Z}^Z\varvec{j}^{\text {(e)}}(\xi ,Z)\text {d}\xi \\ &{}+\frac{1}{2} \left[ \tilde{\varvec{B}}_0(cZ)-\tilde{\varvec{E}}_0(cZ) \right] \\ \end{aligned} &{} (0 \le Z \le \tau ).\\ \end{array}\right. } \end{aligned}$$
(19)

For \(Z \ge \tau \), the function is periodically connected as \(\varvec{K}(Z)=\varvec{K}(Z-2\tau )\). This function \(\varvec{K}(Z)\) is of class \(C^2[-\tau ,\infty )\) if and only if

$$\begin{aligned} \begin{aligned}&\tilde{\varvec{B}}_0'(0) =-c^{-1}\varvec{j}^{\text {(e)}}(0,0), \ \ \tilde{\varvec{B}}_0'(l) =-c^{-1}\varvec{j}^{\text {(e)}}(\tau ,\tau ),\\&\tilde{\varvec{E}}_0''(0) =c^{-2}\partial _t\varvec{j}^{\text {(e)}}(0,0), \ \ \tilde{\varvec{E}}_0''(l) =c^{-2}\partial _t\varvec{j}^{\text {(e)}}(\tau ,\tau ).\\ \end{aligned} \end{aligned}$$
(20)

Inversely, if the initial distribution satisfies the conditions in Eqs. (16,20), the function \(\varvec{K}\) can be defined as in Eq. (19) and extended as \(\varvec{K}(Z)=\varvec{K}(Z-2\tau )\) for \(Z\ge \tau \). (The extended function is expressed by the same symbol.) Then, the minimum corrective term which satisfies the initial and boundary conditions is uniquely given by Eq. (18). Each component is of class \(C^2\) in \((x,t) \in [0,l]\times [0,\infty )\).

4.3 Explicit resonant behavior

One remarkable and interesting behavior of the minimum corrective term is the resonant increase with time. For this purpose, we fix x and regard Eq. (18) as functions of t. First, \(\varvec{K}\) has a period of \(2\tau \) and it never contributes to the resonance. This indicates that the initial distribution is irrelevant to the resonance. Second, the integrals of \(\varvec{j}^{\text {(e)}}\) from \(\alpha \) to \(\beta \) also have a period of \(2\tau \) and they do not contribute to the resonance. This fact leads to the result that although \(\varvec{S}^{(0)}\) satisfies the resonant condition in Eq. (6), the corresponding minimum corrective term does not always increase resonantly. An example will be provided in the subsequent Sect. 5.1.

The situation slightly differs for \(\varvec{j}^{\text {(o)}}\). Let

$$\begin{aligned} \varvec{\varGamma }(\alpha )= \frac{1}{2\tau }\int _0^{2\tau } \varvec{j}^{\text {(o)}}(\alpha ,\xi )\text {d}\xi , \end{aligned}$$
(21)

we obtain

$$\begin{aligned} \int _{-\alpha }^{\beta }\varvec{j}^{\text {(o)}}(\alpha ,\xi )\text {d}\xi =2t\varvec{\varGamma }(\alpha )+\int _{-\alpha }^{\beta } \varvec{j}^{\text {(o)}}(\alpha ,\xi ) -\varvec{\varGamma }(\alpha )\text {d}\xi , \end{aligned}$$
(22)

where the second term of the right-hand side has a period of \(2\tau \). Obviously, the resonant behavior is determined by \(\varvec{\varGamma }\). The functions \(p^2,pq\) and \(q^2\) have a period of \(2\tau \) and let their mean values be \(\varLambda _{2p},\varLambda _{pq}\) and \(\varLambda _{2q}\). Defining \(Q_{1,2,3}\) as

$$\begin{aligned} \begin{aligned} Q_1&= 4C_{2,0}\left( 4\varLambda _{2p}+E_{sy}^2+B_{sz}^2\right) \\&\quad +C_{0,2}\left( 4\varLambda _{2q}+E_{sz}^2+B_{sy}^2\right) ,\\ Q_2&= 4C_{2,0}\left( 4\varLambda _{2q}+E_{sz}^2+B_{sy}^2\right) \\&\quad +C_{0,2}\left( 4\varLambda _{2p}+E_{sy}^2+B_{sz}^2\right) ,\\ Q_3&= (4C_{2,0}-C_{0,2}) \left( 4\varLambda _{pq}+E_{sy}E_{sz}-B_{sy}B_{sz}\right) ,\\ \end{aligned} \end{aligned}$$
(23)

then \(\varvec{\varGamma }\) is given by

$$\begin{aligned} \begin{aligned}&\varGamma _y(\xi )=2\left[ Q_1p'(\xi )+Q_3q'(\xi )\right] ,\\&\varGamma _z(\xi )=2\left[ Q_3p'(\xi )+Q_2q'(\xi )\right] .\\ \end{aligned} \end{aligned}$$
(24)

Rewriting the minimum corrective term, we obtain

$$\begin{aligned} \begin{aligned}&\begin{pmatrix} E_{ny}^{(0)} \\ E_{nz}^{(0)} \\ \end{pmatrix} =- \begin{pmatrix} Q_1 &{} Q_3 \\ Q_3 &{} Q_2 \\ \end{pmatrix} t\frac{\partial }{\partial t} \begin{pmatrix} E_{ry} \\ E_{rz} \\ \end{pmatrix} +\dots , \\&\begin{pmatrix} B_{ny}^{(0)} \\ B_{nz}^{(0)} \\ \end{pmatrix} = \begin{pmatrix} -Q_2 &{} Q_3 \\ Q_3 &{} -Q_1 \\ \end{pmatrix} t\frac{\partial }{\partial t} \begin{pmatrix} B_{ry} \\ B_{rz} \\ \end{pmatrix} +\dots ,\\ \end{aligned} \end{aligned}$$
(25)

where the dots on the right-hand sides of both expressions have a period of \(2\tau \) and do not increase resonantly, while the exhibited parts express the resonant increase. These expressions explicitly show the relation between the classical term and the resonant part of the minimum corrective term. For example, possible sum and difference of frequencies do not increase resonantly. They can only appear in the omitted part shown by dots.

4.4 Limits on applicable time

The linearization shown in Eq. (3) is acceptable only when the minimum corrective term is much smaller than the classical wave part. In the case that the minimum corrective term can increase resonantly, there must be an upper limit to the applicable time.

However, it is not clear whether the upper limit can be determined by using only the resonant part shown in Eq. (25). Hence, an evaluation of the omitted parts becomes necessary as shown in the next two sections. As we show later, if \(E_s=0\) and \(q=0\), the omitted parts are much smaller than the classical wave part. In this case, the applicable time can be evaluated only by the resonant part.

Let us calculate for a standing wave of a single mode of \(p(\xi )=(A/2)\cos \omega \xi \) and \(q=0\), where \(\omega =ck, kl=n\pi , n \in \mathbb {N}\). The classical term is given by

$$\begin{aligned} \varvec{E}_c=AS_XS_T\varvec{e}_y, \ \ \varvec{B}_c=B_{sy}\varvec{e}_y+ (AC_XC_T+B_{sz})\varvec{e}_z. \end{aligned}$$
(26)

In here and later examples, we define \(X=kx,T=\omega t\) and the trigonometric functions \(\sin ,\cos \) are expressed by the capital letters S, C with a subscript. For example, \(\sin kx\) is abbreviated as \(S_X\).

In this example, \(\varLambda _{2p}=A^2/8\) and \(\varvec{j}^{\text {(e)}}=\varvec{0}\). It can be seen that the zero initial distribution is compatible with the boundary conditions in Eq. (20) and is adopted here. The corresponding electric field is given as

$$\begin{aligned} \begin{aligned} E_{ny}^{(0)}(x,t)=&-AQ_1S_XTC_T\\&+\frac{1}{4}C_{2,0}A^3\\&\times \left[ 3S_X(S_{3T}-3S_T)+S_{3X}(S_T-3S_{3T})\right] \\&-4C_{2,0}A^2B_{sz}S_{2X}S_{2T}\\&-(4C_{2,0}B_{sz}^2+C_{0,2}B_{sy}^2)AS_XS_T,\\ E_{nz}^{(0)}(x,t)=&-AQ_3S_XTC_T\\&+(4C_{2,0}-C_{0,2})AB_{sy}\\&\times \left( \frac{1}{2}AS_{2X}S_{2T}+B_{sz}S_XS_T\right) .\\ \end{aligned} \end{aligned}$$
(27)

For each component, the first line on the right-hand side is the resonant part and the remaining terms are the non-resonant part. Worth noting is that the z component of the electric field can increase resonantly. This wave component never exists in the classical wave.

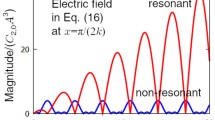
Figure 1 demonstrates the resonant increase of the minimum corrective electric field for \(B_{sy}/A=2,B_{sz}/A=0.5\) at \(X=\pi /2\). The absolute values of the resonant and non-resonant parts are shown, respectively. Contrary to the phase difference of both parts, they are not correlated. The superficial correlation is caused by the choice of X. At this point, the non-resonant parts of y and z components are \((3/2)C_{2,0}A^3(S_{3T}-21S_T) \approx -(63/2)C_{2,0}A^3S_T\) and \(-3C_{2,0}A^3S_T\), respectively, and they show the \(\pi /2\) phase offset to the resonant parts. At other points, the terms of \(S_{2T}\) and \(S_{3T}\) can stand out. Note that both parts are derived by the classical term and their interaction is discarded within the range of the linearization. Therefore, they cannot interact within the range of this study.

We would like also to mention the difference in magnitudes of both the resonant parts of y and z components in Fig. 1. Quantitatively, the values of \(Q_1=31C_{2,0}A^3\) and \(Q_3=3C_{2,0}A^3\) are the reason. Qualitatively, the origin of the resonant behavior of y and z components is slightly different. For the classical term in Eq. (26), \(q=0\) and \(\varvec{E}_s=\varvec{0}\) and the classical electric field has only the y component. The resonant part of the y component of the minimum corrective electric field is generated by the classical electromagnetic wave regardless of the static magnetic flux density. On the other hand, for the generation of the resonant part of the z component, the classical electromagnetic wave needs to be converted to the orthogonal component through \(\varvec{P}^{(0)}\) or \(\varvec{M}^{(0)}\). It is accomplished by the existence of both \(B_{sy}\) and \(B_{sz}\). This feature is represented in \(Q_3\) which is proportional to \(B_{sy}B_{sz}\).

Fig. 1
figure 1

Magnitudes of the resonant and non-resonant parts of the minimum corrective electric field of the a y and b z components, normalized by \(C_{2,0}A^3\). The static magnetic flux density is given by \(B_{sy}/A=2,B_{sz}/A=0.5\), and the results at \(X=\pi /2\) are shown

Full size image

We then evaluate the applicable time. If the linearization is possible, while the resonant part is sufficiently smaller than A, an upper bound can be evaluated as

$$\begin{aligned} \omega t \ll \frac{1}{|Q_1|}, \frac{1}{|Q_3|}. \end{aligned}$$
(28)

In particular, if \(B_{sy}=0\), then \(Q_3=0\) and we obtain the last inequality in Ref. [23].

5 Evaluation of the omitted terms of \(\varvec{j}^{\text {(e)}}\)

In this section, we evaluate the magnitudes of the integrals of \(\varvec{j}^{\text {(e)}}\), i.e.,

$$\begin{aligned} \int _{\alpha }^{\beta } \varvec{j}^{\text {(e)}}(\alpha ,\xi )\text {d}\xi . \end{aligned}$$
(29)

The other integrals can be evaluated similarly.

We calculate for the terms appearing in Eq. (A.1) in Appendix A. Similar discussion can be done for the other expressions. The integral becomes

$$\begin{aligned} \begin{aligned}&-2E_{sy}\left( 2p'(\alpha )\int _{\alpha }^{\beta } p(\xi )\text {d}\xi +q'(\alpha )\int _{\alpha }^{\beta } q(\xi )\text {d}\xi \right) \\&-2E_{sz}q'(\alpha )\int _{\alpha }^{\beta } p(\xi )\text {d}\xi \\&+2c^{-1}x(E_{sy}B_{sy}-E_{sz}B_{sz})q'(\alpha )\\&-4c^{-1}xE_{sy}B_{sz}p'(\alpha )+o_A, \\ \end{aligned} \end{aligned}$$
(30)

where several terms which will be of the order of \((C_{2,0}+C_{0,2})(E_s+B_s+A)^2A\) when multiplied by the nonlinear parameters; for example, \(E_{sy}p(\alpha )p(\beta )\) are gathered by the symbol \(o_A\). Recalling that p and q have periods of \(2\tau _p\) and \(2\tau _q\), respectively, the three integrals in the first and second lines are of the order of \(C_{2,0}E_sAA'\). If \(A'\) and A are comparable, these terms are much smaller than A.

On the other hand, the terms containing \(c^{-1}x\) will be of the order of \((\tau /\tau _M)C_{2,0}E_sB_sA'\) and \(\tau /\tau _M\) can be much larger than unity. This suggests that the linearization can collapse at the initial time \(t=0\). In another viewpoint, the evaluation that \((\tau /\tau _M)C_{2,0}E_sB_sA' \ll A\) may indicate an upper bound of the applicable frequency. It can be easily shown that the \(c^{-1}x\) containing term remains in the entire minimum corrective term. Therefore, we have to investigate the magnitude of this term and check the validity of the linearization for each individual case.

Another natural question may arise about the symmetry with respect to x. If both p and q are symmetric for x and \(l-x\), the minimum corrective electric field should have the same symmetry. Although the form of \(c^{-1}x\) is not apparently consistent with the symmetry, it is solved by calculating \(\varvec{K}\).

5.1 Example of non-resonant property

Let us consider as an example

$$\begin{aligned} \varvec{E}_c=(AS_XS_T+E_s)\varvec{e}_y, \ \ \varvec{B}_c=B_s\varvec{e}_y+AC_XC_T\varvec{e}_z, \end{aligned}$$
(31)

where \(E_s\ne 0, B_s\ne 0,\omega =ck, kl=n\pi \) and \(n \in \mathbb {N}\). We show the following three properties: (1) Even though \(\varvec{S}^{(0)}\) satisfies the resonant condition, the corresponding minimum corrective term does not increase resonantly. (2) The spatial symmetry about x and \(l-x\) holds. (3) The term containing \(c^{-1}x\) is not necessarily much smaller than A.

For our purpose above, we only consider \(S_z^{(0)}\) and corresponding \(E_{nz}^{(0)}\) and \(B_{ny}^{(0)}\). It can be seen that \(\partial _tj_z^{\text {(o)}}=0\), and we obtain

$$\begin{aligned} S_z^{(0)}=-c^{-2}\partial _tj_z^{\text {(e)}} =2k^2(4C_{2,0}-C_{0,2})AE_sB_sC_XC_T. \end{aligned}$$
(32)

Clearly, this satisfies the resonant condition in Eq. (5). Nevertheless, from the above discussion, the corresponding minimum corrective components \(E_{nz}^{(0)},B_{ny}^{(0)}\) do not increase resonantly. In fact, letting \(c_1=-(4C_{2,0}-C_{0,2})AE_sB_s\) and \(c_2=(4C_{2,0}-C_{0,2})A^2B_s/2\) yields

$$\begin{aligned} \begin{aligned} E_{nz}^{(0)}&= c_1XS_XC_T +c_2S_{2X}S_{2T} +K_z(\alpha )-K_z(\beta ),\\ B_{ny}^{(0)}&= c_1(XC_X+S_X)S_T +c_2C_{2X}(1-C_{2T})\\&\quad -K_z(\alpha )-K_z(\beta ),\\ \end{aligned} \end{aligned}$$
(33)

and no resonant increase with time.

We next consider the second property, i.e., the symmetry about x and \(l-x\). In \(E_{nz}^{(0)}\), the term including \(c^{-1}x\) is proportional to \(c_1\) and a part of \(K_z\) is also proportional to \(c_1\) through the integral of \(j_z^{\text {(e)}}\). We discard the influence of the initial distribution because it is somewhat arbitrary.

Let us fix a position \(0<x<l/2\). It is sufficient to calculate the time from zero to \(2\tau \). Let \(\varPsi =\omega \tau =n\pi \). Finally, the whole part proportional to \(c_1\) in \(E_{nz}^{(0)}\) at x is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} -C_XT S_T &{} (0\le T<X) \\ -XC_XS_T-S_X(T-X) C_T &{} (X\le T< \varPsi -X) \\ C_X(T-\varPsi )S_T +(2X-\varPsi )S_XC_T &{} (\varPsi -X\le T< \varPsi +X) \\ XC_XS_T+S_X(T+X-2\varPsi )C_T &{} (\varPsi +X\le T< 2\varPsi -X) \\ -C_X(T-2\varPsi )S_T &{} (2\varPsi -X\le T < 2\varPsi ). \\ \end{array}\right. } \end{aligned}$$
(34)

A similar calculation at \(l-x\) shows that the corresponding value is always multiplied by \(C_{\varPsi }=(-1)^n\), and the magnitudes at x and \(l-x\) are equal. As for the magnetic flux density, the whole part proportional to \(c_1\) at \(l-x\) can be obtained by multiplying \(-C_{\varPsi }\) to the corresponding part at x. Including \(K_z\), the natural symmetry is confirmed to hold. Noting that the second derivative of Eq. (34) with respect to time is not continuous, this discontinuity is compensated by the part of the initial distribution proportional to \(c_1\) and the whole minimum corrective term is confirmed to be of class \(C^2\).

We turn to the third property by evaluating the magnitude of Eq. (34). It has yet to be shown that this term is much smaller than the classical amplitude A. Because \(c_1\ll A\), it would be desirable that this term is at most in the order of unity. The values in Eq. (34) take the form of \(aS_T+bC_T\). As a more readable form, we introduce the envelope given by \((a^2+b^2)^{1/2}\). Then, we randomly select \(0<X<\varPsi /2\), as \(X=(\sqrt{2}/10)\varPsi , 0.2\varPsi +\text {Sin}^{-1}0.1, (\pi /10)\varPsi \), and calculate for \(0\le T<2\varPsi \). The envelopes for \(n=100,1000\) are shown in Fig. 2. The vertical axis is of the order of n and not unity.

Fig. 2
figure 2

The envelopes of Eq. (34) at \(X=(\sqrt{2}/10)\varPsi , 0.2\varPsi +\text {Sin}^{-1}0.1, (\pi /10)\varPsi \) for a \(n=100\) and b \(n=1000\). Note that the maximum values are of the order of n

Full size image

6 Evaluation of the omitted terms of \(\varvec{j}^{\text {(o)}}\)

We next evaluate the integral of the second term on the right-hand side of Eq. (22). For terms appearing in Eq. (A.5) in Appendix A, we obtain

$$\begin{aligned} \begin{aligned}&4p'(\alpha )\int _{-\alpha }^{\beta }p^2(\xi )-\varLambda _{2p}\text {d}\xi +4q'(\alpha )\int _{-\alpha }^{\beta } p(\xi )q(\xi )-\varLambda _{pq}\text {d}\xi \\&\quad -2B_{sy}q'(\alpha )\int _{-\alpha }^{\beta }p(\xi )\text {d}\xi \\&\quad +2B_{sz} \left[ 2p'(\alpha )\int _{-\alpha }^{\beta }p(\xi )\text {d}\xi +q'(\alpha )\int _{-\alpha }^{\beta }q(\xi )\text {d}\xi \right] +o_A. \end{aligned} \end{aligned}$$
(35)

Except for the second term, after multiplying \(8C_{2,0}\) the integrals are shown to be of the order of \((C_{2,0}+C_{0,2})(A+B_s)AA'\), which will be much smaller than A. The second term will be of the order of \((\tau /\tau _M)(C_{2,0}+C_{0,2})A^2A'\). It is not necessarily smaller than A because the ratio \(\tau /\tau _M\) can be very large. Similar evaluations hold for the other terms.

6.1 Example for integral of pq

We evaluate the magnitude of the second term because it is also not proven to be much smaller than A. We consider an example given by \(p(\xi )=(A_p/2)\cos \omega _p\xi \) and \(q(\xi )=(A_q/2)\cos \omega _q\xi \), where \(A_p\) and \(A_q\) are the respective amplitudes and \(\omega _p=cn_p\pi /l, \omega _q=cn_q\pi /l\) and \(n_p,n_q\in \mathbb {N}\). If the difference between \(n_p\) and \(n_q\) is unity, the second term is of the order of \(n_pC_{2,0}A_pA_q^2\), and the term can exceed A for a large \(n_p\). Mathematically, it has been confirmed that we can enlarge the term including the integral of pq by considering large \(n_p\) and \(n_q\). However, a physical picture of the nonlinear Lagrangian will impose an upper bound for these integers, i.e., there will be a shortest applicable wavelength. Within this limitation, a careful evaluation is necessary to confirm the premise of the linearization.

7 Relation to birefringence

The birefringence may be the most widely studied nonlinear optical effect when light passes through a static electromagnetic field. Here, we clarify the relationship between the birefringence and the present calculation.

In the calculation of birefringence, a plane wave passing through static electromagnetic fields is assumed to have a general dispersion relation, which is determined by solving an eigenvalue problem. Then, the refractive index is determined. In this process, a direct time evolution of the nonlinear correction is not treated. Instead, a possible stationary behavior is only assumed. The stationary plane wave has an amplitude which is compatible to the classical wave. So in the viewpoint of time evolution, such a large non-classical plane wave cannot emerge suddenly. Such a plane wave can only be achieved after a very long, or infinite, time as the classical light eventually varies with a somewhat small nonlinear effect. In other words, considering a stationary nonlinear correction and an eigenvalue problem corresponds to considering a very long timescale.

On the other hand, the present calculation is done in a relatively short timescale, as can be seen by the inequality of an upper bound of the applicable time. Therefore, the timescales of the birefringence and present study are completely different and under these conditions, it is expected that both results may be independent.

8 Example of resonant behavior in three-dimensional system

We also consider a three-dimensional example to prove that the resonant behavior is not a characteristic of one-dimensional systems only. The details of the calculation are stated in Appendix B, and the result includes both solutions for two- and one-dimensional systems. We show an example here. The classical term is given by Eq. (B.2), and the corresponding minimum corrective electric field is given by Eq. (B.10). Figure 3 shows the magnitudes of the resonant and the remaining parts of the minimum corrective electric field in Eq. (B.10) for \(\hat{\varvec{k}}=(\sqrt{2}/4,\sqrt{2}/4,\sqrt{3}/2)\) and \(\mathscr {E}=(\sqrt{6}/4,\sqrt{6}/4,-1/2)\), at \(k_1x=\pi /2,k_2y=\pi /4,k_3z=\pi /4\). Compared to Fig. 1(a), the value of the vertical axis is only about 1/150. There are two reasons for this difference. One is the existence of the static magnetic flux density in the calculation in Fig. 1. The values of \(B_{sy}=2A\) and \(B_{sz}=A/2\) yield \(Q_1=31C_{2,0}A^3\). If the static field does not exist, it drops to \(Q_1=2C_{2,0}A^3\). The other stems from the conditions of divergence free of the transverse component of the electric field and magnetic flux density. In the one-dimensional system, both \(\varvec{E}_n^{(0)}\) and \(\varvec{B}_n^{(0)}\) have only y and z components and spatially depend only on x. Therefore, the conditions of divergence free hold automatically. On the contrary, these conditions do not clearly hold in the three-dimensional system. All components are connected through the conditions, and the resonant increase will be restricted. The magnitude of the resonant part is given in Eq. (B.13). Its maximum value is shown in Eq. (B.14) and is about \(0.32C_{2,0}A^3\) for the present parameters. At the selected point, the magnitude is smaller and about \(0.21C_{2,0}A^3\). The ratio of 31 : 0.21 is about 600 : 4, and we can understand the difference of the vertical axes of Figs. 1, 3. Note that the magnitude of the resonant part of the three-dimensional system depends not only on the position but also on the directions of wavenumber and polarization.

Fig. 3
figure 3

Example of resonant behavior in a three-dimensional system. In the minimum corrective electric field in Eq. (B.10) (see “Appendix B”), the magnitudes of the resonant part in Eq. (B.12) and the remaining part are shown. The classical parameters are \(\hat{\varvec{k}}=(\sqrt{2}/4,\sqrt{2}/4,\sqrt{3}/2)\) and \(\mathscr {E}=(\sqrt{6}/4,\sqrt{6}/4,-1/2)\). The calculation is performed at \(k_1x=\pi /2,k_2y=\pi /4,k_3z=\pi /4\)

Full size image

9 Final remarks

We have investigated in extensive details the minimum corrective term of nonlinear electromagnetism in the one-dimensional cavity system. In Eq. (18), we have shown both the y and z components of the minimum corrective term for a general classical term given in Eq. (8). In particular, the resonant increase is explicitly shown in the form of Eq. (25) and the effect of external static electromagnetic fields is elucidated through the parameters \(Q_{1,2,3}\) in Eq. (23). An upper bound for the applicable time of the linearization in Eq. (28) is also evaluated. For future experiments, these equations may prove valuable in determining an effective magnitude of the external fields. A desirable experimental apparatus may be capable of a precise measurement and a strong external magnetic field, for example, systems for the PVLAS experiment or an optical lattice clock [24].

The most remarkable effect of the external fields that is revealed in the present study is that a light component perpendicular to the incident classical component can also increase resonantly, as shown in Fig. 1 and \(E_{nz}^{(0)}\) in Eq. (27). This result can likewise benefit present and future experimental systems to distinguish the generated nonlinear correction from the incident light. Moreover, the results obtained here also do not contradict the well-known change in refractive index because both calculations are performed in completely different timescales.

According to the analysis of \(\varvec{j}^{\text {(e)}}\) and the example in Sect. 5.1, it has been shown that the resonance does not occur just by satisfying the resonant condition in Eq. (6). A physical reason is attributed to the boundary conditions. For example, the first term of \(E_{nz}^{(0)}\) in Eq. (33) is proportional to \(XS_XC_T\), which is a special solution of the wave equation. Ignoring the boundary condition, a temporally resonant special solution is possible, in the form of \(C_XTS_T\). Therefore, for the resonant increase of the minimum corrective term, the compatibility of \(\varvec{S}^{(0)}\) satisfying the resonant condition and the boundary conditions is of importance. By extension, this compatibility is also important in two- and three-dimensional systems.

To precisely evaluate the resonant behavior, an analysis beyond the linearization is essential. Probably, the increase of the nonlinear correction will be restrained at the applicable upper bound or comparable timescale. The analysis without linearization can conserve the total energy and, therefore, will allow us to fully grasp the essence of the resonant increase. Concrete analysis and evaluation of these effects in an actual experiment will be the subject of future studies.