1 Introduction

General relativity (GR) is the most celebrated theory of gravity, which beautifully summarizes the relation between the geometry of space-time and the distribution of matter through some simple partial differential equations known as Einstein’s field equations (EFE). Since its inception in 1915, GR has successfully explained many physical phenomena like mercury perihelion, bending of light, gravitation redshift, etc., which Newtonian mechanics could not understand. New observational evidence [1,2,3,4,5,6] suggests that Universe is accelerating and dark matter does exist which poses a substantial theoretical hurdle for theories of gravity to explain these phenomena. The composition of matter in the Universe, including ordinary baryonic matter, dark matter, and dark energy, is proposed to be approximately 4, 20, and \(76\%\), respectively. This conclusion stems from analyses of cosmic microwave background radiation (CMBR) and surveys of supernovae (see Refs.: [7,8,9,10]). An interpretation of these observations suggests that the Einstein gravity model of GR may fail at large scales, and a more comprehensive action better describes the gravitational field.

Hence, several modified gravity theories have surfaced to expand and generalize GR. Traditionally, when deviating from conventional gravitational models, the primary strategy has been to enhance the geometric aspect within the gravitational action. The f(R) theory of gravity is one of the earliest theories falling under this category, whose action adopts the structure of an arbitrary function of the Ricci scalar R, producing an expression [11,12,13,14]

$$\begin{aligned} S = \frac{1}{(16\pi )} \int \sqrt{-g} f(R) d^4x + \int \sqrt{-g} L_{m} d^{4}x \end{aligned}$$
(1)

Nonetheless, several modifications, such as the previously mentioned f(R) gravity, primarily focus on altering the geometry part in the action with the assumption that the Lagrangian of matter performs a secondary (non-active) role [15]. This assumption naturally arises from the minimal coupling of matter with geometry. However, a foundational theoretical principle restricting a general coupling between matter and geometry has yet to be articulated and does not inherently exist. If such couplings between matter and geometry are allowed, one can formulate numerous theoretical gravitational models with exceptionally intriguing properties. One of these models is f(R, T) [16], which has recently gained considerable attention. The f(R, T) gravity model offers a fascinating perspective, expanding Einstein’s equations of motion to incorporate terms linked to the Ricci scalar and energy-momentum tensor trace. This theoretical framework has recently garnered significant interest due to its capacity to explain diverse cosmological phenomena. Furthermore, it can be an alternate gravity theory that accommodates dark matter and dark energy [7,8,9]. In recent times, multiple studies in the context of f(R, T) gravity have been noticed in literature [17,18,19,20,21].

As predicted by GR, black holes exhibit gravitational forces of such intensity that nothing, not even light, can elude their gravitational pull. It is a compelling notion that the impact of f(R, T) gravity might be more pronounced for compact entities like black holes. Consequently, delving into the study of black holes within the f(R, T) gravity framework becomes intriguing. Recognizing this perspective, Santos et al. [22] formulated a black hole solution reminiscent of Kiselev [23] within the f(R, T) gravity framework. Subsequently, the rotating counterpart of the black hole solution presented in Ref. [22] has been expounded upon in [24].

The strongly believed assumption about black holes that they are not only gravitational entities but possess rich thermodynamic properties made them a center of attraction in the physics fraternity. It was first shown by Wheeler [25, 26] that a system consists a black hole does not follow the second law of classical thermodynamics (non-decreasing entropy law); a black hole must have some temperature and entropy. Later, Bardeen et al. [27] gave four laws that govern the thermodynamics of black holes. Black holes display diverse phase transitions, offering intriguing insights from multiple perspectives. Notably, the correlation between the dynamical cosmological constant and the pressure term has been identified [28, 29], giving rise to extended thermodynamics. This, in turn, has paved the way for the emergence of the field known as black hole chemistry [30,31,32]. This exploration has been expanded to encompass other black holes and gravity theories [30, 33, 34, 34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57]

Therefore, it is natural to establish a connection between the phase structure and photon orbits of a black hole and investigate if the properties of photon orbits can serve as indicators of black hole phase transitions. Interestingly, photon orbits have been found to indicate a potential York–Hawking–Page phase transition [58, 59]. Subsequently, it shows a more distinct relationship between photon orbits and the phase transitions of Reissner–Nordstrom-AdS black holes [60], extending later to rotating Kerr-AdS black holes [61]. Specifically, the radius of the photon orbits (\(r_{ps}\)) as well as the critical impact parameter (\(u_{ps}\)) does not exhibit monotonic behaviours with Hawking temperature when pressure is lower than critical pressure, indicating the existence of phase transitions. Furthermore, drastic changes occur in both \(r_{ps}\) and \(u_{ps}\) along with the phase transition. These changes diminish as the system reaches a critical point, indicating that these entities (\(r_{ps}\) and \(u_{ps}\)) serve as order parameters for van der Walls (vdW)-like first-order phase transition. Changes \(\Delta r_{ps}\) and \(\Delta u_{ps}\) exhibit a universal exponent of \(\frac{1}{2}\) near the critical point. This investigation has been expanded to encompass other black holes [62] and gravity theories [63,64,65,66]. A comprehensive proof of these relationships between photon orbits and phase transitions is provided in reference [63, 67, 68]. Therefore, examining how photon orbit radius is related to the phase transition is particularly interesting for Kiselev-AdS black holes in f(R, T).

We organised the paper as follows. The next section reviews the Kiselev-AdS black hole solution in f(R, T) gravity and discusses the horizon structure. Section 3 is dedicated to analysing various thermodynamic properties of the concerned solution. We obtain the photon orbit radius and find its relationship with the phase structure of Kiselev-AdS black holes in f(R, T) gravity in Sect. 4. Then, we summarise our paper in Sect. 5.

2 Field equations and the black hole solution

Here, we are interested in obtaining a static spherically symmetric AdS black hole solution given by Kiselev in the context of f(R, T) gravity. To do so we begin with Einstein-Hilbert action for f(R, T) gravity in (\(3+1\)) dimensions [16]

$$\begin{aligned} S =\frac{1}{16\pi }\int [f(R,T)-2\Lambda ]\! \sqrt{-g}\,d^{4}x \!+\! \int \sqrt{-g}\,d^{4}x {\mathcal {L}}_m,\nonumber \\ \end{aligned}$$
(2)

a function of the Ricci scalar R, and trace T of the energy-momentum tensor, g is the determinant of the metric tensor \(g_{\mu \nu }\), \({\mathcal {L}}_{m}\) gives the Lagrangian density of an anisotropic fluid [69] effectively connected to Kiselev black holes

$$\begin{aligned} {\mathcal {L}}_{m} = -\frac{1}{3}\,(p_{r}+2p_{t}), \end{aligned}$$
(3)

and \(\Lambda =-3/l^2\) is the negative cosmological constant with l being the AdS length scale. Now, the variation of the action (2) with respect to metric tensor (\(g_{\mu \nu }\)) leads us to equations of motion [22, 70]

$$\begin{aligned}{} & {} f_{r} (R,T) R_{\mu \nu }-\frac{g_{\mu \nu }}{2}f(R,T)+(g_{\mu \nu } \Box - \nabla _{\mu }\nabla _{\nu })f_{R}(R,T)\nonumber \\{} & {} \quad -\frac{1}{2}g_{\mu \nu }\Lambda = 8\pi T_{\mu \nu }-f_{T}(R,T)T_{\mu \nu }-f_{T}(R,T)\Theta _{\mu \nu },\nonumber \\ \end{aligned}$$
(4)

where \(f_R(R,T)\) and \(f_T(R,T)\) represents the derivative of f(R, T) with respect to R and T, respectively. And

$$\begin{aligned} \Theta _{\mu \nu }=g^{\eta \xi }\frac{\partial T_{\eta \xi }}{\partial g_{\mu \nu }}\equiv -2T_{\mu \nu }+g_{\mu \nu }{\mathcal {L}}_{m}-2g^{\eta \xi }\frac{\partial ^{2} {\mathcal {L}}_{m}}{\partial g^{\mu \nu }g^{\eta \xi }}. \end{aligned}$$
(5)

For our study we consider the following special form of f(R, T) [16]

$$\begin{aligned} f(R,T)=R+2f(T) \end{aligned}$$
(6)

which leads to

$$\begin{aligned} R_{\mu \nu }-\frac{g_{\mu \nu }}{2}R -\Lambda g_{\mu \nu }= & {} 8\pi T_{\mu \nu }-2\frac{df(T)}{dT}[\Theta _{\mu \nu }+T_{\mu \nu }]\nonumber \\{} & {} +f(T)g_{\mu \nu }. \end{aligned}$$
(7)

We are assuming here a static geometry in spherically symmetric space-time, which can be described by the following line element

$$\begin{aligned} ds^{2}=B(r)dt^{2}-A(r)dr^{2}-r^{2}(d\theta ^{2}+sin^{2}\theta d\phi ^{2}). \end{aligned}$$
(8)

Next, we need to determine the form of the unknown function B(r) and A(r). For Kiselev black hole holes, the components of the energy-momentum tensor are given as [23]

$$\begin{aligned} T^{t}_{t}= & {} T^{r}_{r}=\rho (r),\end{aligned}$$
(9)
$$\begin{aligned} T^{\theta }_{\theta }= & {} T^{\phi }_{\phi }=-\frac{1}{2}\rho (3 \omega +1), \end{aligned}$$
(10)

where \(\omega \) is representing the equation of state parameter. Interestingly, the components of the energy-momentum tensor of Kishlev black holes [23] can be effectively connected to an anisotropic fluid whose energy-momentum reads

$$\begin{aligned} T^{\mu }_{\nu } = \text{ diag } \left( -\rho ,p_{r},p_{\theta },p_{\phi }\right) , \end{aligned}$$
(11)

where \(p_{r}=-\rho \) and \(p_{t}=1/2\rho (3\omega +1)\). One can extract the energy-momentum tensor given in Eq. (11) from the following general form of the energy-momentum tensor of anisotropic fluid [71]

$$\begin{aligned} T_{\mu \nu } = -p_{t}g_{\mu \nu }+(p_{t}+\rho )U_{\nu }U_{\mu }+(p_{r}-p_{t})N_{\mu }N_{\nu } \end{aligned}$$
(12)

where \(\rho \), \(p_{t}(r)\), and \(p_{r}(r)\) are the notation of energy density and tangential and radial pressure of the fluid, respectively. The objects, \(U^{\mu }=\left( B(r),0,0,0\right) \) and \(N^{\mu }=\left( 0,1/A(r),0,0\right) \) are four velocity and radial unit vector, respectively, which obeys the conditions \(U_{\nu }U^{\nu }=1\), \(N_{\nu }N^{\nu }=-1\), and \(U_{\nu }N^{\nu }=0\). Using Eq. (3) in Eq. (5), we get the

$$\begin{aligned} \Theta _{\mu \nu }=-2T_{\mu \nu }-\frac{1}{3}(p_{r}+2p_{t})g_{\mu \nu }. \end{aligned}$$
(13)

Now, by using Eqs. (7), (8) and (13), and using the form \(f(T)=\gamma T\), we obtain the unknown functions as

$$\begin{aligned} B(r)=\frac{1}{A(r)}\equiv 1-\frac{2M}{r}+\frac{k }{r^{{\frac{8\left( 3\pi \omega +\omega \gamma +\pi \right) }{3\gamma +8\pi -\omega \gamma }}}}+\frac{r^2}{l^2}, \end{aligned}$$
(14)

where \(\gamma \) is the f(R, T) gravity parameter, M is the mass of black hole and k is constant of integration. By taking \(\gamma \rightarrow 0\), we can get the well-known Kiselev-AdS black hole solution in GR [72]

$$\begin{aligned} B(r)|_{\gamma \rightarrow 0}= 1-\frac{2M}{r}+\frac{k }{r^{(3\omega +1)}}+\frac{r^2}{l^2} \end{aligned}$$
(15)

2.1 Horizon structure

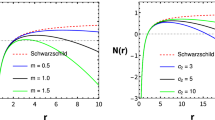
Now, we want to consider the horizon structure of the black hole solution. It is very well known that one can get the location of the horizons of the black hole by solving \(B(r)=0\). In our case, we could not find the analytic solution for the horizon; hence we take the numerical route to find the horizons by plotting B(r) vs radial coordinate r in Fig. 1 for different values of the equation of state parameter \(\omega \) and f(R, T) gravity parameter \(\gamma \) to find out that the possible number of horizons depend upon the parameter \(\gamma \) for given \(\omega \). We consider some specific cases, e.i. \(\omega =0\) (dust field), \(\omega =1/3\) (radiation field), \(\omega =-2/3\) (quintessence field) and \(\omega =-4/3\) (phantom field). For dust, radiation, and quintessence field, we have two horizons (Cauchy and event) when \(\gamma _{0}<\gamma <\gamma _{01}\), where \(\gamma _0\) is a specific value of f(R, T) parameter at which the black hole has degenerate horizon and for \(\gamma <\gamma _{0}\) there exists no black hole solution. For \(\gamma \ge \gamma _{01}\), only an event horizon exists. Interestingly, for phantom field \(\gamma >\gamma _0\) represents no black hole solution whereas \(\gamma _{0}<\gamma <\gamma _{01}\) signifies a black hole solution with Cauchy and the event horizons. When \(\gamma \ge \gamma _{01}\), black holes with only event horizon exist.

Fig. 1
figure 1

Horizon structure of Kiselev-AdS black holes in f(R, T) gravity for different values of f(R, T) parameter \(\gamma \) and equation of state parameter \(\omega \). Black holes with a single event horizon exist for \(\gamma \ge \gamma _{01}\). We keep \(k=1\), and \(l=1\)

Full size image

3 Thermodynamics of Kiselev-AdS bh in f(R, T) gravity

Black hole thermodynamics offers valuable insights into the quantum characteristics of gravitational fields, with a particular focus on the thermodynamic aspects of AdS black holes, capturing astrophysicists’ attention. This interest was sparked by the groundbreaking research conducted by Hawking and Page [73], which proposed the presence of a phase transition within AdS black holes and radiation. In this section, we shall derive various thermodynamic quantities of the solution in consideration and discuss their behaviour to analyse the thermodynamic aspects of the black hole. The black hole mass can be obtained by solving \(B(r_{+})=0\) as

$$\begin{aligned} M_+ = \frac{1}{2}r_+\left( 1 + \frac{r_+^2}{l^2} + k r_+^{-{\frac{8(3\pi \omega +\omega \gamma +\pi )}{3\gamma +8\pi -\omega \gamma }}}\right) , \end{aligned}$$
(16)

where \(r_+\) is the event horizon. The metric (8) possesses symmetry about t coordinate e.i. have a timelike Killing vector \(\xi ^{\mu }_{(t)}\) and hence, there exists a conserved quantity connected to the Killing vector. The conserved quantity can be obtained in the following manner:

$$\begin{aligned} \nabla ^{\nu }[\xi ^{\mu }\xi _{\mu }]=-2\kappa \xi ^{\nu }, \end{aligned}$$
(17)

\(\nabla _{\nu }\) denotes covariant derivative and \(\kappa \) is constant along the orbits defined by the Killing vector \(\xi ^{\mu }_{(t)}\) with constant quantity \(\kappa \) termed surface gravity remains constant across the horizon. Hawking’s groundbreaking research, as detailed in Reference [74], unveiled the phenomenon of radiation emission by black holes. This radiation is believed to be related to the Hawking temperature that is defined by \(T = \kappa /2 \pi \) [75,76,77,78]. In our specific case, it can be expressed in the following manner

$$\begin{aligned}{} & {} T_+ = \frac{1}{4\pi }\nonumber \\{} & {} \,\,\left[ \frac{1}{r_+}\!+\!\frac{3r_+}{l^2}\!+\!\frac{3k\left( -8\pi \omega \!+\!\gamma \!-\!3\omega \right) r_+^{\frac{8\pi (2+3\omega )+(3+7\omega )\gamma }{-8\pi + (-3+\omega ) \gamma }}}{8\pi -(-3+\omega )\gamma }\right] .\nonumber \\ \end{aligned}$$
(18)
Fig. 2
figure 2

The plot of Hawking temperature \(T_+\) vs horizon \(r_+\) for quintessence (\(\omega =-2/3\)) (left) and phantom field (\(\omega =-4/3\)) (right). The black curve represents the Kiselev-AdS black holes in GR, which exhibit only local minima, which is indicative of the Haking-Page phase transition

Full size image
Fig. 3
figure 3

The plot of specific heat \(C_{P}\) vs horizon \(r_{+}\) for quintessence (\(\omega =-2/3\)) and phantom field (\(\omega =-4/3\)). The black curve represents the Kiselev-AdS black holes in GR which shows divergence at the local minimum of Hawking temperature i.e these solutions have only two phases unstable SBH with negative specific heat and stable LBH with positive specific heat

Full size image

The behaviour of Hawking temperature has been illustrated in Fig. 2. While inspecting the Hawking temperature behaviour we found that for a fixed value of k and AdS radius l, there exists a critical value of f(R, T) parameter \(\gamma =\gamma _c\) such that when we take \(\gamma >\gamma _c\) for the quintessential field (\(\omega =-2/3\)), the Hawking temperature for the system in consideration exhibits local maxima and minima at \(r_{max}\) and \(r_{min}\) respectively. For the phantom field (\(\omega =-4/3\)), one gets maxima and minima for \(\gamma <\gamma _c\). This behaviour confirms the vdW-like first-order phase transition between small black holes (SBH) and large black holes (LBH) depicted by the red curve in Fig. 2. At \(\gamma =\gamma _c\), both extrema merge (blue curve), whereas for \(\gamma <\gamma _c\) (\(\gamma >\gamma _c\)), Hawking temperature increases monotonically for \(\omega =-2/3\) (\(\omega =-4/3\)), and hence no phase transition exists. We fixed \(k=1=l\) to find that \(\gamma _c\) for the quintessence field (\(\gamma _c=-5.63265\)) is greater than that for the phantom field (\(\gamma _c=-6.6772\)). But, for Kiselev-AdS black holes in GR (black curve in Fig. 2), there exists only local minima which means that there are only two phases i.e. unstable SBH (negative slope of temperature curve) and stable LBH (positive slope of temperature curve). This kind of behaviour confirms that Kiselev-AdS black holes in the framework of GR exhibit Hawking–Page (HP)-like phase transition [73] instead of vdW phase transition shown by these black holes in f(R, T) gravity. We use the well-known Hawking–Bekenstein area law [79] to write the entropy \(S_+\) in terms of event horizon radius \(r_+\) for our solution as

$$\begin{aligned} S_+=\pi r_+^2. \end{aligned}$$
(19)

Next, we want to check the local thermodynamic stability of the black hole to the thermal fluctuations that can be done by analyzing the behaviour of specific heat. A black hole exhibiting a positive heat capacity (\(C_+ > 0\)) indicates its local thermodynamic stability. In contrast, when the heat capacity is negative (\(C_+ < 0\)), it points to that the black hole is thermodynamically unstable in response to thermal fluctuations [80, 81]. We use \(C_{P} = T \left( dS/dT\right) \) [82, 83] to get the specific heat as given

$$\begin{aligned}{} & {} C_{P_+}\nonumber \\{} & {} \,\,=\!\frac{2\pi r \left[ \frac{1}{r}\!+\!\frac{3r}{l^2}\!+\!\frac{3kr^\frac{8\pi (2+3\omega )+(3+7\omega )\gamma }{-8\pi +(-3+\omega )\gamma }(-8\pi \omega +(1-3\omega )\gamma )}{8\pi -(-3+\omega )\gamma }\right] }{\frac{3}{l^2}\!-\!\frac{1}{r^2}\!+\!\frac{3kr^{\frac{6(1+\omega )(4\pi +\gamma )}{-8\pi +(-3+\omega )\gamma }}(8\pi \omega +(-1+3\omega )\gamma )(8\pi (2+3\omega )+(3+7\omega )\gamma )}{{(-8\pi +(-3+\omega )\gamma })^2}},\nonumber \\ \end{aligned}$$
(20)
Fig. 4
figure 4

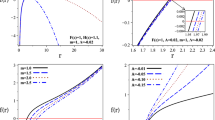
The plot of Gibbs free energy \(G_+\) vs temperature \(T_+\) showing a swallowtail for \(P<P_{c}\) depicting a first order phase transition. The curve attains a cusp at \(P=P_{c}\), which is also a point of second-order phase transition and becomes monotonically increasing for \(P>P_{c}\). The value of \(P_c\) for quintessence and phantom field is 0.00312914 and 0.0115975, respectively

Full size image

whose numerical behaviour is depicted in Fig. 3. When we take \(\gamma >\gamma _c\) for \(\omega =-2/3\) or \(\gamma <\gamma _c\) for \(\omega =-4/3\), the Hawking temperature exhibits local maxima and minima at \(r_{\text {max}}\) and \(r_{\text {min}}\) and hence specific heat shows divergence at those points such that the regions where \(r_+<r_{\text {max}}\) (SBH) and \(r_+>r_{\text {min}}\) (LBH) have positive specific heat which means these thermodynamic states are locally stable. For a region with \(r_{\text {max}}<r_{+}<r_{\text {min}}\) (intermediate BH) we got a locally unstable state with negative specific heat (Fig. 3). Hence, we can conclude that when \(\gamma >\gamma _c\) for the quintessential field and \(\gamma <\gamma _c\) for the phantom field, there exists a phase transition whose order can be determined through behavioural analysis of Gibbs free energy. For \(\gamma <\gamma _c\) (\(\gamma >\gamma _c\)), the specific heat is always positive for the quintessential field (phantom field), and thus, we get only one locally thermodynamic stable phase. The Kiselev-AdS black holes in GR (black curve) have only two regions: SBH with negative specific heat and LBH with positive specific heat.

3.1 Critical point and phase transition

This subsection is dedicated to discussing the phase transition and critical behaviour of the Kiselev-AdS black holes in f(R, T) gravity that can be done through behavioural analysis of Gibbs free energy (\(G_+\)) and pressure (P). First, we need to obtain the equation of state; to do so, we use the very well-known relation between the pressure P of the black hole and the cosmological constant \(\Lambda \), \(P=-\Lambda /8\pi \), in Eq. (18) and get the expression for P in terms of Hawking temperature and event horizon as

$$\begin{aligned} P_+= & {} \frac{T_+}{2r_+}-\frac{1}{8\pi r_+^2}\nonumber \\{} & {} +\frac{3k\left( -8\pi \omega +\gamma -3\omega \right) r_+^{\frac{8\pi (2+3\omega )+(3+7\omega )\gamma }{-8\pi + (-3+\omega ) \gamma }}}{8\pi r_+^2\left( 8\pi -(-3+\omega )\gamma \right) }, \end{aligned}$$
(21)

where \(r_+\) is a function of black hole volume given as

$$\begin{aligned} V_+=\frac{4}{3}\pi r_+^3. \end{aligned}$$
(22)

The critical points of the considered system can be obtained by solving the following system of equations

$$\begin{aligned} \left( \frac{\partial P}{\partial r_+}\right) _T=0, \ \text{ and } \ \left( \frac{\partial ^2P}{\partial r_+^2}\right) _T=0. \end{aligned}$$
(23)

We numerically solve the above system of equations to find the critical values of pressure, temperature, and horizon radius, which depend upon the values of different parameters of the black hole system we are considering. These critical values can help us to analyze the transition between different phases of the thermodynamic system. For this, firstly we derived the expression of Gibbs free energy, which read

$$\begin{aligned} G_+= & {} \frac{r_+}{4}-\frac{2}{3}\pi Pr_+^3\nonumber \\{} & {} +\frac{r_+^{3\frac{-8\pi \omega +\gamma -3\omega \gamma }{8\pi -(-3+\omega )\gamma }}(8\pi (2+3\omega )+(3+7\omega )\gamma )}{4(8\pi -(-3+\omega )\gamma )}. \end{aligned}$$
(24)
Fig. 5
figure 5

The plot of Gibbs free energy \(G_+\) vs temperature \(T_+\) for Kiselev-AdS black holes in GR

Full size image
Fig. 6
figure 6

The Pressure \(P_+\) vs volume \(V_+\) plot for quintessence (\(\omega =-2/3\)) and phantom field (\(\omega =-4/3\)). The red curve shows oscillatory behaviour for \(T<T_c\), which indicates vdW-like first-order phase transition. At \(T=T_c\),there exist inflection point which signifies second-order phase transition. For \(T>T_c\), pressure decreases monotonically with volume (no phase transition). The value of \(T_c\) for quintessence and phantom field is 0.042386 and 0.08571, respectively

Full size image

We plotted the isobars on the \(G_+-T_+\) plane in Fig. 4 to find out that depending on the pressure value, our system can undergo different types of phase transition. When \(P<P_c\), we can see a swallowtail made up of three different phases of a black hole, namely SBH (stable), intermediate BH (unstable), and LBH (stable). It is very well known that the minima of Gibbs free energy represent the thermodynamic stable phase; hence, the system will go directly from a stable SBH to a stable LBH instead of following the swallowtail structure, which is similar to the first-order phase transition between liquid–gas of vdW fluid. As we increase the pressure to \(P_+=P_c\), we see a cusp where SBH and LBH phases meet, which signifies that SBH undergoes a second-order phase transition to LBH. For \(P_+>P_c\), the curve becomes smooth, and we can conclude that the black hole system remains in the same phase throughout (Fig. 4). The \(G_+-T_+\) isobars for Kiselev-AdS black holes in GR are given in Fig. 5, in which it can clearly be seen that there exists HP-like phase transition instead of vdW-like first-order phase transition. Next, we look into the phase structure and transition of the Kiselev AdS black holes in f(R, T) gravity in the reduced parameter space where the dimensionless reduced quantities are

Fig. 7
figure 7

Phase structure of Kiselev spacetime in f(R, T) gravity in AdS spaces in \({\tilde{P}}-{\tilde{T}}\) (left) and \({\tilde{T}}-{\tilde{V}}\) (right) diagrams. The coexistence curves are shown in the solid line, and the spinodal curves in the dashed blue line. The coexistence line shows the points of coexistence of SBH and LBH which ends at critical point

Full size image
$$\begin{aligned} {\tilde{P}}=\frac{P_+}{P_{c}}, \quad {\tilde{V}}=\frac{V_+}{V_{c}}, \quad {\tilde{T}}=\frac{T_+}{T_{c}}, \quad {\tilde{G}}=\frac{G_+}{G_{c}}. \end{aligned}$$
(25)

The point of intersection shown by the red solid curve in Fig. 4 is the coexistence point of two phases namely liquid and gas. The points taken from Fig. 4 (left panel) are fitted to give the coexistence curve whose fitting equation is as follows

$$\begin{aligned} {\tilde{P}}= & {} -0.00455604 \!+\! 0.144792 {\tilde{T}} \!-\! 1.2357 {\tilde{T}}^{2} \!+\!14.0561 {\tilde{T}}^{3} \nonumber \\{} & {} - 61.4954 {\tilde{T}}^{4}+ 175.587 {\tilde{T}}^{5} -327.824{\tilde{T}}^{6} \nonumber \\{} & {} + 398.365 {\tilde{T}}^{7} - 303.1 {\tilde{T}}^{8} + 131.06 {\tilde{T}}^{9} - 24.5533 {\tilde{T}}^{10}\nonumber \\ \end{aligned}$$
(26)

corresponding to \(\omega =-2/3\) (quintessence) for \(\gamma =-6\) (Fig. 6). In turn we also obtain the spinodal curve for \(\omega =-2/3\) (quintessence) through the equation

$$\begin{aligned} (\partial _{{\tilde{V}}}{\tilde{P}})_{{\tilde{T}}}=0. \end{aligned}$$
(27)

We did not write the explicit form of the spinodal curve but we plotted it with the coexistence curve in Fig. 7. The blue lines in the graph represent spinodal curves, appearing on both sides of the coexistence curve (red line) and converging with it at the critical point. The region bounded by the coexistence curve and the spinodal curves indicates the presence of metastable phases. Specifically, the zone below the coexistence curve and above the spinodal curve corresponds to the supercooled LBH phase. In contrast, the area above the coexistence curve and between the spinodal curves corresponds to the superheated SBH phase. Beyond the critical point, the phase transition becomes second-order, making SBH and LBH indistinguishable; this phase is known as the supercritical black hole phase.

Fig. 8
figure 8

Behaviour of effective potential of Kiselev black hole for quintessence and phantom field in f(R, T) gravity with \(\gamma =-6\)

Full size image

4 Photon orbits and their relation with phase transition

In this section, we discuss the motion of photons around the considered black hole and try to establish the relation between photon orbits and phase transition. In further calculations, we have kept ourselves to only one case with \(\omega =-2/3\). The motion of a free photon orbiting a black hole can be derived from the Lagrangian

$$\begin{aligned} 2 {\mathcal {L}}=-{\textbf {B(r)}}{\dot{t}}^2+\frac{{\dot{r}}^2}{{\textbf {B(r)}}}+r^2{\dot{\phi }}^2. \end{aligned}$$
(28)

Equation (28) exhibits two killing vectors [84] \(\partial _{t}\) and \(\partial _{\phi }\) in the equatorial hyperplane (\(\theta =\pi /2\)) such that

$$\begin{aligned} -{\textbf {B(r)}}{\dot{t}}\equiv E, \quad \quad r^2{\dot{\phi }} \equiv L. \end{aligned}$$
(29)

Here, the dot represents the derivative with respect to the affine parameter. Eq. (29) signifies the conserved quantities associated with these Killing vectors: energy (E) and orbital angular momentum (L). We use these constants of motion to write t and \(\phi \) equations of motion as

$$\begin{aligned} {\dot{t}}=\frac{E}{f(r)},\;\; {\dot{\phi }}=\frac{L}{r^2 \sin ^2\theta }. \end{aligned}$$
(30)

The motion of photons around the black hole is analysed by solving \({\mathcal {H}}=0\), where the Hamiltonian \({\mathcal {H}}\) for the Kiselev black holes in \({\textbf {f(R,T)}}\) gravity is given as follows

$$\begin{aligned} 2{\mathcal {H}}=-E{\dot{t}}+L{\dot{\phi }}+{\dot{r}}^2/f(r). \end{aligned}$$
(31)

The effective potential of our solution is calculated only in the radial motion of the photon which is obtained from the t and \(\phi \) equations of motion from Eq. (31),

$$\begin{aligned} {\dot{r}}^2+V_{eff}=0. \end{aligned}$$
(32)

Here, \(V_{eff}\) denotes the effective potential that in dimensionless form, \({\tilde{V}}_{eff}=V_{eff}/E^2\), can be written as given below

$$\begin{aligned} {\tilde{V}}_{eff}=\frac{u^2}{r^2}f(r)-1, \end{aligned}$$
(33)

where \(u=L/E\) denotes the impact parameter. The nature of trajectories of photons around the black hole is dictated by the behaviour of effective potential. The photons can possess the orbital trajectories only if \(V_{eff}<0\); this condition arises from the requirement that \({\dot{r}}^2>0\). In Fig. 8, we plotted the effective potential along the radial coordinate r for different impact parameter values u. The behaviour of the effective potential can be categorized broadly for the three different cases which are (a) \(u>u_{ps}\), (b) \(u<u_{ps}\), (c) \(u=u_{ps}\), where \(u_{ps}\) is a specific value of angular momentum for which photon orbits around the black hole in unstable circular orbital known as photon sphere orbits.

The photons exhibit an unbounded motion when \(u>u_{ps}\) and are scattered away from the black hole (blue curve), whereas for \(u<u_{ps}\), the photons fall straight into the black hole (red and green curves in Fig. 8). The black curve in Fig. 8 shows the critically bounded photon that circles the black hole and is observed to make the photon sphere in a phenomenon called strong gravitational lensing of black holes [60, 85]. When \({\tilde{V}}_{eff}=0\), the quantity u attains a critical value, and hence photon radial velocity vanishes. The radial coordinate value corresponding to which radial velocity vanishes is called photon orbit radius \(r_{ps}\). The unstable circular orbits can be obtained by using the following conditions,

$$\begin{aligned} V_{eff}=0\quad , \quad V'_{eff}=0 \quad , \quad V''_{eff}<0, \end{aligned}$$
(34)
Fig. 9
figure 9

Pressure vs the photon orbit radius \(r_{ps}\) (left) and the minimum impact parameter \(u_{ps}\) (right)

Full size image
Fig. 10
figure 10

Hawking temperature \(T_+\) vs the photon orbit radius \(r_{ps}\)(left) and the minimum impact parameter \(u_{ps}\)(right) with \(\omega =-2/3\) and \(\gamma =-6\)

Full size image
Fig. 11
figure 11

Variation in reduced photon sphere radius (\({\tilde{r}}_{ps}\)) vs reduced Hawking temperature \({\tilde{T}}\) (left) and the reduced minimum impact parameter (\({\tilde{u}}_{ps}\)) vs \({\tilde{T}}\) (right) for \(\omega =-2/3\) and \(\gamma =-6\)

Full size image

where the prime represents the differentiation to r.Now, by using \(V'_{eff}=0\), we find the \(r_{ps}\) satisfies

$$\begin{aligned} 2f(r_{ps})-r_{ps}\partial _r f(r_{ps})=0. \end{aligned}$$
(35)

The value of photon orbit radius and minimum impact factor for \(\gamma =-6\) and \(\omega =-2/3\) (quintessence field) at critical pressure \(P_c\) and temperature \(T_c\) are \(r_{ps}=4.69533\) and \(u_{ps}=4.95517\).

Wei and Liu [60] were the first to show that the phase transition of black holes can be explained through the behaviour of photon orbit parameters i.e. photon orbits (\(r_{ps}\)) and critical impact parameter (\(u_{ps}\)) of the black holes. We followed their method to explore the relationship between the phase structure and photon orbits of Kiselev-AdS black holes in the framework of f(R, T) gravity. While exploring the behaviour of Hawking temperature with \(r_{ps}\) and \(u_{ps}\), we found that for \(\gamma >\gamma _c = - 5.63265\) the temperature exhibits non-monotonic behaviour (shows local maximum and minimum), which is similar to the behaviour of temperature vs horizon radius \(r_+\) which can be confirmed from Figs. 2 and 10. Hence, we can conclude that the phase structure of Kiselev-AdS black holes in f(R, T) gravity can be explained in terms of \(r_{ps}\) and \(u_{ps}\). We also plotted the isotherms on \(P_+-r_{ps}\) and \(P_+-u_{ps}\) planes in Fig. 9, which shows an oscillatory behaviour for temperature less than the critical temperature. This behaviour of pressure vs \(r_{ps}\) and \(u_{ps}\) shows the same behaviour as \(P_+-V_+\) plots that can be confirmed from Fig. 6. The resemblance observed between \(T_+-r_+\) and \(T_+-r_{ps}\) (\(T_+-u_{ps}\)), and \(P_+-V_+\) and \(P_+-r_{ps}\) (\(P_+-u_{ps}\)) validates a robust correlation between the phase transition and the photon orbit radius (critical impact parameter) of the black hole.

4.1 Photon orbits in the neighbourhood of critical points of Kiselev black holes in f(R, T) gravity

Fig. 12
figure 12

Behaviours of difference of the photon orbit radius \(\text {ln}({\tilde{r}}_{ps})\) vs temperature \(\text {ln}(1-{\tilde{T}})\) (right) and minimum impact parameter \(\text {ln}({\tilde{u}}_{ps})\) vs temperature \(\text {ln}(1-{\tilde{T}})\) (right) near the critical point for \(\omega =-2/3\), and \(\gamma =-6\). The solid red dots are the numerical results and the solid blue lines are fitting results

Full size image

We can see that the Kiselev black holes in f(R, T) gravity undergo a first-order phase transition from SBH to LBH below the critical points. Estimating photon orbit parameters enabled an explanation of the thermodynamic phase transitions of the black hole solution in terms of the \(r_{ps}\) and \(u_{ps}\). Having observed the resemblance between \(T_+-r_+\), \(T_+-r_{ps}\), and \(T_+-u_{ps}\), we used the Maxwell equal area law to discern the shifts in behaviour of \(r_{ps}\) and \(u_{ps}\) along the coexistence curve illustrated in Fig. 11. It is evident from the figure that the photon orbit radius and critical impact parameter show similar behaviours. Figure 11 depicts an increasing \(r_{ps}\) and \(u_{ps}\) curve for the SBH phase as the temperature increases in contrast to the LBH phase, where the curve decreases for increasing temperature. Further, the curves take a sharp turn at \({\tilde{T}}=1\), which is a coexistence phase for SBH/LBH, much like liquid/ gas (c.f. Fig. 11). The quantities \(\Delta r_{ps}\) and \(\Delta u_{ps}\) play the role of parameters that characterize the phase transition phenomenon of a black hole. The critical exponent \(\delta \) is evaluated using the equal area law, which replaces an oscillating part of an isotherm with an isobar in the \(P-V\) plane [62]. We use the expression for the pressure \({\tilde{P}}\) (Eq. (26)), obtained from the coexistence points of SBH-LBH phases from Fig. 4. For getting the numerical value of \(\delta \), we use the following function [60] to fit the numerical data

$$\begin{aligned} \Delta r_{ps},\Delta u_{ps} \approx a (1-{\tilde{T}})^{\delta }, \end{aligned}$$
(36)

which leads to

$$\begin{aligned} \Delta {\tilde{r}}_{ps}= & {} 3.29096\, (1-{\tilde{T}})^{0.499107}, \nonumber \\ \Delta {\tilde{u}}_{ps}= & {} 1.2038 \, (1-{\tilde{T}})^{0.513914}. \end{aligned}$$
(37)

Taking the logarithm of Eq. (36), we have

$$\begin{aligned} \ln \Delta {\tilde{r}}_{ps}, \quad \ln \Delta {\tilde{u}}_{ps} \sim \delta \ln (1-{\tilde{T}})+\ln a, \end{aligned}$$
(38)

from which it is clear that \(\ln \Delta {\tilde{r}}_{ps}\) and \(\ln \Delta {\tilde{u}}_{ps}\) vary linearly with \(\ln ({\tilde{T}}-1)\). We obtained the numerical results of \(\ln \Delta {\tilde{r}}_{ps}\) and \(\ln \Delta {\tilde{u}}_{ps}\) by running \({\tilde{T}}\) from 0.9873 to 0.99999. These results are depicted in Fig. 12 (blue dashed lines). We also find the fitting results for the numerical data points shown by the solid red line in Fig. 12.

5 Conclusion

This study focuses on the intriguing dynamics of photon orbits and phase transitions within Kiselev-AdS black holes governed by f(R, T) gravity. Building upon Santos et al.’s foundational work on the Kiselev black hole solution in f(R, T) gravity [22], we expanded our analysis to encompass AdS spacetime focusing on the thermodynamic properties and geometric aspects of the resulting Kiselev-AdS black hole solution. Our investigation provided intriguing insights into black hole behaviour influenced by f(R, T) gravity parameters, especially \(\gamma \) and the equation of state parameter \(\omega \). The geometrical analysis leads us to uncover horizon structures dependent on the interplay between \(\gamma \) and \(\omega \), with distinct cases such as \(\omega =0, 1/3, -2/3\) exhibiting varying numbers of horizons based on the critical values \(\gamma _0\) and \(\gamma _{01}\). Notably, the case \(\omega =-4/3\) (phantom field) showcased an opposite horizon behaviour, underscoring the sensitivity of black hole solutions to the choice of parameters. For analysing the thermodynamic aspect, we studied the interplay between photon orbits and phase transitions in Kiselev-AdS black holes, emphasizing the impact of the f(R, T) gravity parameter \(\gamma \). Incorporating \(\gamma \) into our analysis revealed profound effects on these black holes’ thermodynamic properties and phase behaviour, showcasing their sensitivity to this gravitational parameter through distinct horizon structures and critical phenomena.

We adopted a black hole chemistry perspective, relating the cosmological constant \(\Lambda \) to pressure via \(P=-\Lambda \). Through this lens, we examined key thermodynamic variables like Hawking temperature, specific heat, and entropy, culminating in a comprehensive understanding of the phase transition phenomena within our black hole system. Our exploration using Gibbs free energy and the equation of state revealed first-order phase transitions from small to large black holes below critical points, highlighting the system’s dynamic nature. While doing the comparisons of our results with that of Kiselev-AdS black holes in GR, we found that the Kiselev-AdS black holes in f(R, T) gravity show vdW-like phase transition between stable SBH and LBH, whereas on the other hand, in the context of GR Kiselev-AdS black holes exhibit HP-like phase transition.

Furthermore, our study of photon dynamics around these black holes unveiled a profound relationship between phase transitions and key parameters such as the photon orbit radius (\(r_{ps}\)) or minimum impact parameter (\(u_{ps}\)). We observed the similarity between \(T_+-r_+\) and \(T_+-r_{ps}\) or \(T_+-u_{ps}\) i.e. for \(\gamma <\gamma _c\), the behaiour of temperature \(T_+\) is non-monotonic with \(r_+\), \(r_{ps}\) and \(u_{ps}\) which is indicative of vdW-like first order phase transition. In other words, we can say that the phase transition behaviour of the system is imprinted in the circular orbits of surrounding photons. The similarity between \(P_+-V_+\) and \(P_+-r_{ps}\) or \(P_+-u_{ps}\) also support the above statement. In the vicinity of critical points \(r_{ps}\) (\(u_{ps}\)) showed drastic changes suggesting their potential as order parameters, characterized by a critical exponent of 1/2 similar to conventional thermal systems.

Our findings underscore the intricate interplay between gravity theories, thermodynamics, and geometric properties within the context of f(R, T) gravity, paving the way for further exploration and deeper understanding of fundamental gravitational phenomena. In conclusion, investigating the correlation between the photon sphere radius and thermodynamic phase transitions has provided a valuable means of distinguishing between general relativity and f(R, T) gravity theory models. This exploration enhances our understanding of gravitational phenomena and provides insights into the nature of dark energy.