1 Introduction

General relativity (GR) has undoubtedly been successful in accounting for observational results in the solar system and beyond [1, 2]. GR theory predicts with great accuracy the precession of the perihelion of planet Mercury [1, 3] and bending of light due to gravitational field [4] in the local as well as distant observations. GR has predicted the existence of black holes and gravitational waves (GWs) which has been recently experimentally verified by the LIGO-Virgo collaboration [5,6,7,8,9]. The recent direct images of the black hole shadows published by the Event Horizon Telescope (EHT) group [10,11,12,13,14,15] also back GR in terms of experimental verification of the theory. In spite of these successes, GR fails to address recent observations like the accelerated expansion of the Universe [16,17,18]. Indeed, it does not provide any insights regarding the dark components of the Universe [19, 20]. Thus, to overcome these issues, physicists worked on modified theories of gravity, the most common among them includes the \(\Lambda \)CDM [21] model, f(R) gravity theory [22,23,24], f(R, T) gravity theory [25], f(Q) gravity theory [26,27,28,29] and so on (see [30]). These theories can compensate for the effects of dark components [31], explain galactic rotation curves [32], accelerated expansion of the Universe [33, 34] and are well constrained by modern observations. Rastall gravity proposed in 1972 is arguably a unique modified theory of gravity which does not follow from an established Lagrangian formalism [35]. It advocates the violation of conservation of energy–momentum tensor \(T_{\mu \nu }\) and equates it to the derivative of the Ricci scalar R. In recent times, a number of f(R) gravity models have been proposed, some of them include Starobinsky [36], Hu–Sawicki [37], Sujikawa [39] and other two models mentioned in Refs. [38, 40] to name a few. These models have been extensively studied in the literature regarding various aspects like their cosmological and astrophysical implications [32, 41,42,43], dynamical system analysis [44, 45], early Universe mysteries [46] and so on. Similarly, f(Q) gravity has also attracted a lot of attention in the recent times and many cosmological studies have been carried out in this theory, for instance see Refs. [45, 47,48,49] and references therein.

The first vacuum solution of the Einstein field equations leading to a black hole was given by Schwarzschild in 1916 [50]. Since then, a number of black hole solutions have been proposed from time to time in various frameworks of gravity. Black holes are often studied with an engulfing field around them. These fields may include quintessence fluid [51,52,53,54], matter in the form of dust, radiation [55], plasma [56], dark matter halo [57] and so on. These surrounding fields have impacts on various thermodynamic properties, quasinormal modes (QNMs), shadow radius etc. of black holes and have been extensively studied in the literature. In a recent paper [52], GUP-improved Schwarzschild-type solution, its thermodynamic properties and quasinormal modes have been studied. In another work [58], a Schwarzschild-type black hole in Bumblebee gravity has been considered and its thermodynamics and shadow have been studied.

Black hole solutions have been derived in the framework of f(R) gravity in many recent papers. In Ref. [38], Saffari and Rahvar derived novel black hole solutions in the f(R) framework and also proposed a novel f(R) form that is feasible in both local and galactic scales. In Ref. [59], the authors derived black hole solutions in various f(R) models. In a recent work [60], novel black hole solutions were derived in various f(R) models and the authors studied topological and thermodynamic properties of the solutions obtained. Motivated by these ongoing researches, we derive novel black hole solutions in Hu–Sawicki gravity. Here, we intend to study various properties relating to the black hole solutions obtained. Our solution is unique in the sense that the black hole solution for the Hu–Sawicki model of f(R) gravity has not been worked out before to the best of our knowledge and thus we are motivated to study its properties including QNMs, thermodynamics as well as shadow radius and greybody factors.

Further, the black hole’s shadow also has gained a fair amount of attention, credits to the recently released data and images of the black holes at the center of M87 galaxy and Sgr A. This has opened up a new window to constrain various theories of gravity and parameter values as well. Recently in Ref. [61], different parameters of modified theories of gravity have been constrained using modern shadow radius data. Another work [62] constraints regular black hole parameters with shadow data of the EHT. Recent works regarding black hole shadows have gained momentum as shadow provides interesting new insights and data to constrain black hole physics [63,64,65,66,67,68,69,70,71].

QNMs of oscillations of a perturbed black hole hold promise of constraining physics at the extreme regimes of black holes. The QNMs are basically complex frequencies linked to GWs produced when a black hole is perturbed by some external means. There has been an upsurge of research regarding various aspects of QNMs, new techniques of computing QNMs, their relationships with shadow data and so on. The WKB method of computing QNMs is the most widely used technique, though many spectral and analytical techniques are often used in combination. There has been a wide range of applications of QNMs in understanding various phenomena such as testing the No-Hair theorem [72] and constraining theories of modified gravity [73]. QNMs can also be used to study the stability of background spacetime when it is acted upon by a minute perturbation [74]. The relation between shadow radius and QNMs has been dealt with in Ref. [71]. QNMs and Hawking radiation sparsity for GUP-corrected black holes with topological defects have been studied in Ref. [75]. A brief account of various methods employed in recent times to compute the QNMs can be found in the Refs. [75,76,77,78,79].

Black hole thermodynamics has gained momentum and attracted a lot of attention following the path-breaking work of Bekenstein and Hawking [80,81,82]. Their idea led to the development of four laws of black hole thermodynamics. Recently a number of research works have been carried out in this field. Schwarzschild black holes with quantum corrections have been investigated for scattering and absorption cross-section [83]. In Ref. [84], the authors studied absorption and scattering by a black hole with a global monopole in f(R) gravity. Recently, thermodynamic properties of extended GUP-corrected black holes has been carried out in Ref. [85]. Thermodynamics of static dilaton black holes have been studied in Ref. [86].

In this work, we derive black hole solutions in the Hu–Sawicki model of f(R) gravity and study its thermodynamic properties along with its QNMs using the 6th-order WKB method. We compute the shadow radius and present the plots of its variation with respect to different model parameters. The primary motivation for choosing the Hu–Sawicki model is that black hole solutions have not been worked out in this model, and thus it is really intriguing to study the properties of such a solution. The Hu–Sawicki model is a viable choice as it is observationally consistent in cosmological scales [87, 88]. It is consistent with the solar system tests and thus shows viability in the local scales as well [89]. Another reason for choosing this model is that the model parameters of Hu–Sawicki gravity have not been constrained using the available shadow radius data of black holes, although it should be noted that data from cosmological observations have been utilised to constrain this model’s parameters. The choice of this model is thus motivated by the gap in the literature and the viability of the model. Some recent articles that utilise the Hu–Sawicki model to study various aspects of astrophysics and cosmology can be found in Refs. [37, 90, 91].

The plan of the paper is as follows. In the second section, we introduce the field equations in the f(R) gravity framework and briefly discuss the method of solving the equations. After attaining the black hole solution, we move to the third section where we compute QNMs of the black hole. Then in the fourth section, we discuss the thermodynamic properties including temperature, entropy and heat capacity along with greybody factors. Then in the fifth section, we compute the shadow radius and plot it for variations in parameters. Finally, we conclude the work with a brief summary and future scopes.

2 Field equations in \(\varvec{f(R)}\) gravity theory

The field equations for the f(R) gravity theory will be presented here in the spherically symmetric spacetime by adopting the metric formalism of the theory, in which the variation of action is done with respect to the metric only. The f(R) gravity field equation can be obtained from an action in which the Ricci scalar R in the Einstein–Hilbert action is replaced by some function f(R) of R. Thus the generic action of the f(R) gravity theory can be written as [59]:

$$\begin{aligned} S=\frac{1}{2\kappa }\int d^4 x\, \sqrt{-g} f(R) + S_m, \end{aligned}$$
(1)

where \(\kappa = 8\pi G c^{-4}\) and \(S_m\) is the matter part of the action. As mentioned already, taking the variation of the above action (1) with respect to the metric \(g_{\mu \nu }\), one can obtain the field equations of f(R) gravity as

$$\begin{aligned} F R_{\mu \nu }-\frac{1}{2}f(R) g_{\mu \nu }-\left( \nabla _{\mu }\nabla _{\nu }-g_{\mu \nu }\square \right) F=\kappa \, T_{\mu \nu }, \end{aligned}$$
(2)

where \(F=df(R)/dR\) and \(\square =\nabla _{\alpha }\nabla ^{\alpha }\). Taking the trace of this (2), we can write the function f(R) as

$$\begin{aligned} f(R) = \frac{1}{2}\left( 3\,\square F + FR - \kappa T\right) . \end{aligned}$$
(3)

The derivative of this Eq. (3) with respect to the radial coordinate r leads to an equation in terms of F and R as given by

$$\begin{aligned} F' R-F R'+3(\square F)'=\kappa T', \end{aligned}$$
(4)

where the prime denotes the derivative with respect to the radial coordinate r. This equation will serve as a consistency relation for the function F that any solution for F must satisfy this relation in order to be a solution of the field equations, Eq. (2). Further, using Eq. (3) in Eq. (2), the field equations can be expressed in terms F instead of f(R) as

$$\begin{aligned} R_{\mu \nu }-\frac{1}{4}\,g_{\mu \nu }R= & \frac{\kappa }{F}\Big (T_{\mu \nu }-\frac{1}{4}\,g_{\mu \nu }T\Big )\nonumber \\ & +\frac{1}{F}\Big (\nabla _{\mu }\nabla _{\nu } F-\frac{1}{4}\,g_{\mu \nu }\square F\Big ). \end{aligned}$$
(5)

Considering the case of the vacuum where the energy-momentum tensor and its trace vanish, we can rewrite the above equation as

$$\begin{aligned} F R_{\mu \nu }-\nabla _{\mu }\nabla _{\nu } F=\frac{1}{4}\,g_{\mu \nu }\Big (F R-\square F\Big ). \end{aligned}$$
(6)

Since we are interested in the solution of this time-independent spherically symmetric vacuum field equations following the procedure adopted in Ref. [59], we consider a generic spherically symmetric metric in the form:

$$\begin{aligned} g_{\mu \nu }=\begin{pmatrix} -N(r) & 0 & 0 & 0 \\ 0 & M(r) & 0 & 0 \\ 0 & 0 & r^2 & 0\\ 0 & 0 & 0 & r^2 \sin ^2 \theta \\ \end{pmatrix}, \end{aligned}$$
(7)

where N(r) and M(r) are metric coefficients to be determined, associated with the time and space components of the metric respectively which are indeed functions of r. For this spherically symmetric metric, both sides of Eq. (6) become diagonal and accordingly, we can define an index independent parameter from this equation as

$$\begin{aligned} P_{\mu }\equiv \frac{F R_{\mu \mu }-\nabla _{\mu }\nabla _{\mu } F}{g_{\mu \mu }}. \end{aligned}$$
(8)

As this quantity \(P_{\mu }\) is independent of indices, we can have \(P_{\mu }-P_{\nu }=0\) for all \(\mu \) and \(\nu \) values and hence from this property one can obtain the following expressions:

$$\begin{aligned}&2F \frac{X'}{X}+r F' \frac{X'}{X}-2\, r F'' = 0, \end{aligned}$$
(9)
$$\begin{aligned}&N''+\left( \frac{F'}{F}-\frac{X'}{2X}\right) N'-\frac{2}{r}\left( \frac{F'}{F}-\frac{X'}{2X}\right) \nonumber \\&N-\frac{2}{r^2}N + \frac{2}{r^2} = 0. \end{aligned}$$
(10)

Here \(X=MN\). In this work, our solution is considered to have constant curvature for the sake of simplicity. Hence the terms \(F'\) and \(F''\) vanish and the field Eqs. (9) and (10) take the forms:

$$\begin{aligned}&N M'+N' M = 0, \end{aligned}$$
(11)
$$\begin{aligned}&1-M+\frac{r}{2}\left( \frac{N'}{N}+\frac{M'}{M}\right) \left( \frac{r}{2} \frac{N'}{N}-1\right) -\frac{r^2 N''}{2N} = 0. \end{aligned}$$
(12)

Solving these two Eqs. (11) and (12), one can obtain:

$$\begin{aligned} M(r)=\frac{s_1}{N(r)},\;\;\; \text {and}\;\;\; N(r)=s_1 + \frac{s_2}{r}+s_3\, r^2, \end{aligned}$$
(13)

where \(s_1\), \(s_2\) and \(s_3\) are constants of integration. In order to get these coefficients, we follow the procedure in Refs. [59, 60] and compare the second solution with the standard Schwarzschild–de Sitter solution. The standard Schwarzschild-de Sitter black hole metric coefficient is [59]

$$\begin{aligned} C(r)=1-\frac{2M}{r}-\frac{\Lambda r^2}{3}. \end{aligned}$$
(14)

Again, the relationship between the scalar curvature and cosmological constant is [59]

$$\begin{aligned} R=-\,4\Lambda . \end{aligned}$$
(15)

Now, comparing the second solution in Eq. (13) with Eq. (14), we have

$$\begin{aligned} s_1 = 1, s_2 = -\,2M, s_3 = -\,\frac{\Lambda }{3} = \frac{R}{12}. \end{aligned}$$

From (3), considering the vacuum case and constant curvature \(R_0\), we have

$$\begin{aligned} R_0=\frac{2f(R_0)}{F(R_0)}. \end{aligned}$$
(16)

As mentioned earlier, the f(R) gravity model we employed in our work is the Hu–Sawicki model [37], which is given by

$$\begin{aligned} f(R)=-\,m^2\frac{c_1(\frac{R}{m^2})^n}{c_2 (\frac{R}{m^2})^n +1}, \end{aligned}$$
(17)

where m, \(n\, (>0)\), \(c_1\) and \(c_2\) are the model parameters. Here \(c_1\) and \(c_2\) are dimensionless and m represents the mass (energy) scale [31]. For this model, we solve Eq. (16) to get the constant curvature

$$\begin{aligned} R_0=12 s_3=m^2 \bigg (\frac{n-2}{2\,c_2}\bigg )^\frac{1}{n}\!\!\!. \end{aligned}$$
(18)

Thus, we arrive at our black hole solution for the Hu–Sawicki model as

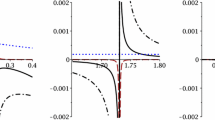
$$\begin{aligned} N(r)=1-\frac{2M}{r}+ \frac{m^2}{12} \bigg (\frac{n-2}{2c_2}\bigg )^\frac{1}{n}r^2. \end{aligned}$$
(19)

It is clear that our black hole solution is independent of the Hu–Sawicki model parameter \(c_1\). Figure 1 shows the metric function versus radial distance for the other two Hu–Sawicki model parameters m and \(c_2\), while taking the parameter \(n=1\) for simplicity (this is considered for the whole study if we do not mention otherwise). In the plots, it is seen that the black hole solution (19) has two horizons for a range of parameter values. The first plot shows that with increasing m, the outer horizon moves closer to the inner horizon, while the second plot shows that for higher values of \(c_2\), the outer horizon increases. After a certain higher value of the parameter m and the lower value of the parameter \(c_2\), the black hole appears to be a horizonless singularity for the given values of the other parameters.

Fig. 1
figure 1

Black hole metric function versus radial distance r for different values of parameters. In the left plot, we use \(c_2 = 3\) and \(n = 1\) while in the right plot, we use \(m = 0.5\) and \(n = 1\). The red dashed line shows the ideal Schwarzschild case

Full size image

3 Quasinormal modes of the black hole

In this section, we compute the QNMs of the black hole (19) using the most common method, the 6th-order WKB approximation method. To this end, we apply a perturbation to the black hole in the form of a probe coupled minimally to a scalar field \(\Phi \) and having the equation of motion [53]:

$$\begin{aligned} \frac{1}{\sqrt{-g}}\,\partial _{\alpha }\Big (\sqrt{-g}g^{\alpha \beta }\partial _{\beta }\Big )\Phi =\mu ^2 \Phi , \end{aligned}$$
(20)

where \(\mu \) is the mass of the scalar field, which for our convenience will be taken as a massless scalar field with \(\mu =0\). We can express the scalar field \(\Phi \) in terms of spherical harmonics of the form [53]:

$$\begin{aligned} \Phi (t,r,\theta ,\phi )=e^{-i \omega t}\frac{\Psi (r)}{r}\,Y_l^p(\theta ,\phi ). \end{aligned}$$
(21)

Here \(\Psi (r)\) represents the radial part of the wave and \(Y_l^p\) represents the spherical harmonic part. Employing Eq. (21) in Eq. (20), we get a Schrödinger-type equation, as given below:

$$\begin{aligned} \frac{d^2\Psi }{dx^2}+\left[ \omega ^2-V(x)\right] \Psi =0, \end{aligned}$$
(22)

with the new variable, the tortoise coordinate, which is defined as

$$\begin{aligned} x=\int \frac{dr}{N(r)}. \end{aligned}$$
(23)

The effective potential in Eq. (22) can be expressed as

$$\begin{aligned} V(r)=N(r)\bigg (\frac{N'(r)}{r}+\frac{l(l+1)}{r^2}\bigg ). \end{aligned}$$
(24)

It is necessary to apply the appropriate boundary conditions to Eq. (22) for the physical consistency both at the black hole horizon and at infinity. For spacetime which is flat asymptotically the following quasinormal criteria have to be satisfied:

$$\begin{aligned} \Psi (x) \rightarrow {\left\{ \begin{array}{ll} A e^{+i \omega x} \;\;\; \text {if} \;\; x \rightarrow -\infty ,\\ B e^{-i \omega x} \;\;\; \text {if} \;\; x \rightarrow +\infty \end{array}\right. }. \end{aligned}$$
(25)

Here, the coefficients A and B represent the amplitudes of the waves. These ingoing and outgoing waves are in accordance with the physical requirements that nothing can escape from the black hole horizon and no radiation comes from the infinity respectively. Further, these make sure of the existence of an infinite set of discrete complex numbers, usually known as the QNMs.

To study the behaviour of the potential (24) before calculating the QNMs of the black hole (19), we plot the potential versus r for different variations of model parameters in Fig. 2. As seen from the left plot of Fig. 2, the peak of the potential decreases for higher m values. From the middle plot, one can see that increasing values of parameter \(c_2\) enhances the peak of the potential. A similar trend is seen with mutipole l values, where peaks are found to increase for higher l values.

Fig. 2
figure 2

Behaviours of black hole potential with respect to radial distance r for different model parameters. The left plot uses values of \(c_{2} = 2\), \(n = 1\) and multipole \(l = 1\). The middle plot uses \(m = 0.5\), \(n = 1\) and multipole \(l = 1\). The right plot uses \(m = 0.1\), \(n = 1\) and \(c_{2}= 2\)

Full size image

The QNMs have been calculated utilising the 6th-order WKB method in the form of their amplitude and damping varying with the model parameters. As seen from Fig. 3, the general trend of amplitude and damping of QNMs is that both decrease with the parameter m for all values of multiple l. On the other hand, Fig. 4 shows that both amplitude and damping increase slightly with the parameter \(c_2\) for all l values. In both cases, the effect of l is more dominating on the amplitude than that on the damping. Moreover, in both cases of m and \(c_2\) variations, the amplitude increases, while the damping decreases with the increasing value of l.

Fig. 3
figure 3

Variation of amplitude and damping of QNMs with respect to parameter m for three values of multipole l. Here we use \(n=1\), \(M=1\) and \(c_2=4\) to represent the features of QNMs

Full size image
Fig. 4
figure 4

Variation of amplitude and damping of QNMs with respect to parameter \(c_2\) for three values of multipole l. Here parameters \(n=1\), \(M=1\) and \(m=1\) have been used

Full size image

We compute the error associated with the WKB QNMs with a prescribed formula that has been used extensively in the literature. This error estimating formula for the WKB method is as follows [53, 75, 76]:

$$\begin{aligned} \Delta _6=\frac{\big |W\!K\!B_7-W\!K\!B_5\big |}{2}, \end{aligned}$$
(26)

where \(W\!K\!B_5\) and \(W\!K\!B_7\) are respectively the QNMs obtained from the 5th and 7th order WKB method. In Table 1, we present the 6th-order WKB QNMs along with the associated errors for various values of the model parameters along with the multipole number l. It is clear that the errors are reduced for higher multipole numbers l. Similar trends in variations of QNMs with respect to different parameters as seen in Figs. 3 and 4 are displayed in the tabulated data. The estimated errors in most of the cases lie around \(10^{-4}-10^{-5}\).

Table 1 6th-order WKB QNMs of the black hole specified by the metric function (19) for the multipoles \(l=1,2,3\) with \(n=0\) and for different values of the model parameters. The estimated errors associated with the WKB results have also been shown. The QNMs with \(m=c_2=0\) represent the Schwarzschild case, which are listed for the comparison purpose only
Full size table

4 Thermodynamic characteristics of the black hole

As mentioned earlier, a black hole as a thermodynamic system was first conceptualised in the ground-breaking work of Hawking and Bekenstein in the early 1970s. In this paper, we analyse the black hole temperature and the grey body factors which are important properties that give useful insights in this regard. The temperature of a black hole is an important property that is associated with the quantum particles created near its horizon. It is inversely related to the size or mass of the black hole, that is a larger black hole will have a lower temperature. Hawking conceptualised the temperature of black hole in the form of radiation, which is today referred to as Hawking radiation. It remains a challenge to detect such radiation experimentally. We can theoretically compute the black hole temperature from the metric solution (19), by employing the simple relation:

$$\begin{aligned} T_{BH}=\frac{N'(r)}{4\pi } =\frac{1}{4\pi r_H^2}\bigg [2M+\frac{m^2}{12}\Big (\frac{n-2}{c_2}\Big )^{\frac{1}{n}}r_H^3\bigg ]. \end{aligned}$$
(27)

It can also be calculated using the First law of black hole thermodynamics as follows:

$$\begin{aligned} T_{BH}=\frac{dM}{dS}=\frac{dM'}{dS'} = \frac{1}{4\pi r_H^2}\bigg [2M+\frac{m^2}{12}\Big (\frac{n-2}{c_2}\Big )^{\frac{1}{n}}r_H^3\bigg ].\nonumber \\ \end{aligned}$$
(28)

This confirms our computation of the black hole temperature from the first law. We plot the thermodynamic temperature (27) with respect to the horizon radius \(r_H\) in Fig. 5. Here, we see clearly that with horizon radius \(r_H\), the temperature of the black hole is always in the decreasing trend. The left plot shows the temperature variations with respect to \(r_H\) for three different values of parameter m. It is seen that higher values of m lead to negative temperatures. While for the parameter \(c_2\), lower values lead to negative temperatures as can be seen from the right panel of Fig. 5. Though the negative temperature seems unphysical, this has been encountered in the literature and explained as a possible state of formation of ultra-cold black holes [53, 79]. Negative temperatures may also suggest that the black hole is thermodynamically unstable [92].

Fig. 5
figure 5

Variation of temperature versus \(r_H\) for three different values of m on the left plot and for three different values of \(c_{2}\) on the right plot. For the left plot, we use \(n = M = 1\) and \(c_{2} = 2\), while for the right plot, we use \(M = n = 1\) and \(m = 0.5\)

Full size image

To study the thermodynamic stability of the black hole solution, we have computed the heat capacity of the solution. Following the first law of black hole thermodynamics, the formula for calculating the heat capacity of the black hole can be found as:

$$\begin{aligned} C_{BH}=\frac{dM}{dT}=3 \pi r^2 \left( \frac{4 (6 M+r)}{m^2 r^3 \left( \frac{\frac{n}{2}-1}{\text {c}_2}\right) ^{1/n}-24 M}+1\right) .\nonumber \\ \end{aligned}$$
(29)

The plots of the heat capacity of the black hole for different values of the model’s parameters are shown in Fig. 6. Here we have considered the constraint values of the model’s parameters that are obtained from the shadow analysis as can be seen from Fig. 9. In the left hand plot of Fig. 6, we have used \(m=0.5\) and \(c_2 =2\), which are the extreme bounds obtained from shadow radius. It is seen that when \(r_H\ge 8\), the heat capacity takes positive values, otherwise it remains negative. In the right hand plot of the same figure, we have used intermediate values of the parameters in the viable range suggested by shadow analysis. It is seen from this plot that the heat capacity always remains negative, which indicates thermodynamic instability. Thus we may comment that the black hole is mostly thermodynamically unstable.

Fig. 6
figure 6

Heat capacity of the black hole versus horizon radius is shown. The left plot shows that for \(r_H\ge 8\), the heat capacity takes positive values, otherwise the heat capacity remains negative. It indicates the black hole is thermodynamically unstable in most of the parameter space

Full size image

The greybody factor or the transmission coefficient is a measure of the probability that a particle created by quantum processes near the event horizon of a black hole will escape to infinity or get absorbed inside the black hole. Greybody factor (\(T^2\)) equal to 1 means that all the particles that are created are able to escape the black hole while lower values of it mean that some of them end up inside it. If \(T^2=0\), it means that the black hole is completely dark and absorbs every single particle. The greybody factor has been extensively studied in the literature in various scenarios. We can express the reflection and transmission of the particles hitting the black hole barrier potential in the following form [93]:

$$\begin{aligned} \psi (x)&= T(\omega ) \exp (-i \omega x), \;\; x \rightarrow -\infty , \end{aligned}$$
(30)
$$\begin{aligned} \psi (x)&= \exp (-i \omega x) + R(\omega ) \exp (i \omega x),\;\; x \rightarrow +\infty , \end{aligned}$$
(31)

where \(R(\omega )\) and \(T(\omega )\) are respectively reflection and transmission coefficients and are functions of frequency \(\omega \). WKB approximation formula is used to get to the computational form of these two coefficients which are presented below [93]:

$$\begin{aligned} |R(\omega )|^2&=\frac{1}{1+\exp (-2\pi i \tau )}, \end{aligned}$$
(32)
$$\begin{aligned} |T(\omega )|^2&= \frac{1}{1+\exp (2\pi i \tau )}, \end{aligned}$$
(33)

where the parameter \(\tau \) is defined in the WKB method as the following [93]:

$$\begin{aligned} \tau =\frac{i (\omega ^2 -V_0)}{\sqrt{-2V_0^{''}}}-\Lambda _j. \end{aligned}$$
(34)

Here double primes represent the double derivative of the maximum of the effective potential \(V_0\) with respect to x and \(\Lambda _j\) can be obtained from the WKB formula found in Ref. [78]. In Fig. 7, we plot the greybody factors with respect to frequency \(\omega \) for three values of the model parameters m considering \(n=1\), \(c_2=1\) and \(M=1\) with multipole \(l=1\) (left plot) and \(l=2\) (right plot). It is seen that for higher m values the greybody factor increases faster with respect to \(\omega \) than that for smaller m values. Also, for a smaller l value (\(l=1\)), the greybody factor increase is more rapid and begins from a smaller \(\omega \) value as compared to a higher l value (\(l=2\)). It needs to be mentioned that the values of the parameter \(c_2\) are found to be insensitive in the variation of the greybody factors with respect to \(\omega \) as shown in Fig. 7.

Fig. 7
figure 7

Greybody factors versus frequency \(\omega \) for different values of m with \(l=1\) (left plot) and \(l=2\) (right plot). We have used \(M=n=1\) and \(c_{2}=1\) in the first two plots and \(m=0.1\) for the third plot. The third plot shows that greybody factor is independent of parameter \(c_2\)

Full size image

5 Shadow of the black hole

Black hole shadow has been extensively studied in the literature as it provides good scope to test various theories of gravity and black hole physics in extreme gravity regimes. The recent observational data of black hole shadow radius has provided the scientific community an opportunity to constrain model parameters using these data. In this section, we compute the photon sphere and the shadow radius expression and plot the same for analysing its dependence on various model parameters. We also try to constrain the parameter space with observational data of the EHT group.

The simple condition to determine the photon sphere radius of a black hole in spherical symmetry consideration is given by the following relation [70, 71]:

$$\begin{aligned} 2-\frac{r N'(r)}{N(r)}=0. \end{aligned}$$
(35)

Using the form of N(r) from Eq. (19), we solve the Eq. (30) for r to get the photon sphere radius as

$$\begin{aligned} r_{ph}=3M. \end{aligned}$$
(36)

From the photon radius, we can derive the shadow radius as follows:

$$\begin{aligned} r_{sh}=\frac{r_{ph}}{\sqrt{N(r)}|_{r\rightarrow r_{ph}}}=\frac{3 M}{\sqrt{\frac{3}{4} m^2 M^2 \left( \frac{n-2}{\text {2\,c2}}\right) ^{1/n}+\frac{1}{3}}}. \end{aligned}$$
(37)

Obviously, the shadow radius depends on all three model parameters associated with N(r). It is also evident that when model parameters \(m=n=c_2=0\), we recover the standard \(r_{sh}=3\sqrt{3}M\) which is the shadow radius for the Schwarzschild black hole. Now, for the 2-D stereoscopic projection of shadow radius, we define celestial coordinates X and Y as given by [70, 71]

$$\begin{aligned} X&=\lim _{r_{0}\rightarrow \infty }\left( -\,r_{0}^{2}\sin \theta _{0}\left. \frac{d\phi }{dr}\right| _{r_{0}}\right) , \end{aligned}$$
(38)
$$\begin{aligned} Y&=\lim _{r_{0}\rightarrow \infty }\left( r_{0}^{2}\left. \frac{d\theta }{dr}\right| _{(r_{0},\theta _{0})}\right) . \end{aligned}$$
(39)

Here \(\theta _0\) is the observer’s angular position with regards to the plane of the black hole. In Fig. 8, we show the variation of the shadow radius with parameters m and \(c_2\). It is seen from the left plot that with an increase in m, the shadow radius increases. In the right plot, it is evident that the shadow radius decreases with increasing \(c_2\) values. Thus, the parameters m and \(c_2\) have opposite influences on the shadow radius.

Fig. 8
figure 8

Stereoscopic projection of shadow radius in terms of celestial coordinates. The left plot is for the variation of m with parameters \(c_{2}=M=n=1\) and the right plot is for the variation of \(c_2\) with \(M=n=1\) and \(m=0.1\)

Full size image

In order to constrain the parameters of the model, we shall employ the technique mentioned in Ref. [70]. We briefly present some important steps in this direction. The main point of the methodology is that we compare the observed angular radius of the Sgr A* black hole as captured by the EHT group recently with the theoretically calculated shadow radius from the expression (32) by constraining the model parameters. This requires the prior value of the mas-to-distance ratio for Sgr A*. Another feature that is required for this method is the calibration factor that correlates the observed to the calculated shadow radius. This method has been used to constrain model parameters in the literature [94,95,96] and we shall follow the same route.

A new parameter \(\delta \) defined by the EHT group to refer to the fractional deviation between the observed shadow radius \(r_{s}\) and shadow radius of a Schwarzschild black hole \(r_{sch}\) is [70]

$$\begin{aligned} \delta =\frac{r_{s}}{r_{sch}}-1=\frac{r_{s}}{3\sqrt{3}M}-1. \end{aligned}$$
(40)

This parameter was estimated by the Keck and VLTI measurements as [70]

$$\begin{aligned} \text {Keck}: \delta =- \,0.04^{+0.09}_{-0.10}\\ \text {VLTI}: \delta =-\, 0.08^{+0.09}_{-0.09} \end{aligned}$$

For simplification, we shall adopt the mean of the two observations as considered in Ref. [70] in the rest of the work, which is

$$\begin{aligned} \delta =-\,0.060 \pm 0.065. \end{aligned}$$
(41)

This leads to \(\delta \) parameter’s 1\(\sigma \) and \(2\sigma \) intervals as

$$\begin{aligned} -\,0.125&\lesssim \,\delta \lesssim 0.005\, (1\sigma ), \end{aligned}$$
(42)
$$\begin{aligned} -\,0.190&\lesssim \,\delta \lesssim 0.070\,(2\sigma ). \end{aligned}$$
(43)

It is found that the bounds (42) and (43) when imposed upon Eq. (34) give the bounds on \(r_{sh}\) as follows [70]:

$$\begin{aligned} 4.55&\lesssim \, r_{sh}/M \lesssim 5.22\, (1\sigma ), \end{aligned}$$
(44)
$$\begin{aligned} 4.21&\lesssim \, r_{sh}/M \lesssim 5.56\, (2\sigma ). \end{aligned}$$
(45)

We plot the shadow radius with the bounds imposed by the observations of Keck and VLTI in Fig. 9. The left plot shows that the shadow radius increases with increasing m values as found in Fig. 8. It shows that for smaller values of \(c_{2}\), the shadow radius quickly moves to the forbidden region. With increasing \(c_{2}\) values, the shadow radius within the allowed region increases. In the right plot, the shadow radius is plotted versus \(c_{2}\) which shows that the shadow radius decreases with increasing \(c_{2}\) values as observed earlier. The plots are within the 2\(\sigma \) allowed region in this case with the exception of larger m and smaller \(c_{2}\) values as clearly visible from the plot. It is quite evident that the constraints imposed are not rigid but depend on the range of values of the parameters of the model.

This method of constraining parameters of a theory has been adopted in the literature [94, 95] and by the EHT group themselves [96] and provides a robust way of constraining parameters. But in cases of model parameters exceeding one, we need some supporting constraining methods so that one parameter can be cornered and rigorous constraints can be obtained. However, we leave this as a future extension of the work.

Fig. 9
figure 9

Shadow radius versus parameter m and \(c_{2}\) have been plotted in the background of Keck and VLTI constrains [70] from observations of Sgr A*. We have chosen \(M=1\) and \(n=1\) for these plots. The red portion represents the zone forbidden by Keck-VLTI observation

Full size image

6 Conclusion

In this work, we derive novel black hole solutions in the framework of Hu–Sawicki gravity. We plot the metric function versus r for various values of model parameters and encountered two horizons of the black hole. It is seen that higher m values cause the horizon radius to shrink while opposite trend is observed for parameter \(c_2\). We then analyse the QNMs of the novel black hole solution with 6th order WKB approximation. The amplitude increases with increase in \(c_2\) while it decreases with m. The damping decreases with increasing m while it increases slightly with \(c_2\). This trend can be realised from the tabulated QNM data in Table 1. It is evident that the QNM frequencies are affected by the model parameters. The associated error is found to be around \(10^{-4}\) to \(10^{-5}\) in some cases.

Thermodynamic temperature associated with the black hole is investigated and it is found to decrease with \(r_H\) in all cases. The temperature can also become negative, suggesting the possibility of formation of ultra-cold black hole. The heat capacity of the black hole has been computed and plotted the same with respect to the horizon radius. It is seen that the heat capacity takes negative values for most of the parameter space, indicating thermodynamic instability of the obtained black hole solution. The greybody factors are also computed, specially the transmission coefficients with respect to frequency \(\omega \) and the dependence of the model parameter m is studied. Higher m results in swifter increase in the greybody factors towards saturation value of 1. It is noteworthy that increasing the multipole l lowers the rate of increase of greybody factors and saturation is achieved at higher \(\omega \).

The photon radius and the shadow radius associated with the spherically symmetric black hole spacetime are then studied. We presented the stereographic projection of the shadow in celestrial coordinate system and using contour-type feature, showed the variation of the shadow radius with increasing model parameters m and \(c_{2}\). Using the already established constraints on \(r_{sh}\) by Keck and VLTI observations, we constrain our model parameters using a well proven scheme. The parameter m is roughly constrained to be less that \(\sim \)0.5 while parameter \(c_{2}\) is constrained to be greater than \(\sim \)2, as can be seen from Fig. 9.

The recent technical advancements made in the fields of astrophysics and observational astronomy has made the present era very suitable for theoretical physicists to constrain and test fundamental theories and models, which was not possible until a decade back. With ground-breaking leaps in the form of LIGO-Virgo team’s observation of Gravitational Waves in 2015 along with the first-ever image of the black hole M87* and later that of Sgr A*, scientists plan to further enhance sensitivity of the present detectors as well as new ambitious projects like the space-based LISA project and the Einstein Telescope are already in the planning stages. As a future scope of this work, we can analyse other viable models of gravity like f(R, T) and f(Q) and work on new black hole solutions as well as rotating Kerr-type solutions can also be explored. The study of black hole shadows surely holds a lot of potential in constraining fundamental physics and it certainly deserves further investigation.

Funding We did not have any funding for this work.