1 Introduction

Black holes are some of the most fascinating and mind-bending objects in the cosmos. They can help our knowledge from the points of theoretical and experimental theories of physics. Among them, one of the most interesting black holes is related to the accelerating black hole, which is described by the C-metric [1,2,3,4,5]. The accelerating black hole includes a conical singularity which can be imagined as a cosmic string with a tension providing the force driving the acceleration. This black hole attracted much attention due to the existence of a string-like singularity along one polar axis attached to it [6,7,8,9,10,11,12,13,14,15]. In addition, there has been a significant amount of research conducted on various aspects related to the accelerating black holes. These include the examination of their global causal structure [16], black hole shadows [17], quantum thermal properties [18], holographic heat engines and complexity [19,20,21,22], and more. One specific area of focus has been the study of the thermodynamics of accelerating black holes, which the first time was explored in Ref. [6] and further addressed in subsequent references [7, 9, 23,24,25]. These studies have successfully extended the first law of thermodynamics, the Bekentein-Smarr and Christodoulou-Ruffini-type mass formula, to encompass (un)charged rotating accelerating black holes.

Studying the effects of modified theories of gravity on the accelerating black hole’s properties is an interesting subject. For example, three and four-dimensional accelerating black holes in F(R) gravity have been evaluated [26] and [27], respectively. In addition, a three-dimensional accelerating black hole in gravity’s rainbow is obtained in Ref. [28]. However, there are no four-dimensional accelerating black hole solutions in gravity’s rainbow yet. So, we first focus on extracting the accelerating black hole solutions in this theory of gravity.

Gravity’s rainbow, initially proposed by Magueijo and Smolin and investigated within the framework of double special relativity [29], introduces a geometry dependent on the energy of moving particles. In this formalism, varying particle energies lead to distinct distortions in spacetime. When investigating the quantum gravity effects of moving probes on the geometry, the notion of a singular spacetime background is replaced by a family of line elements, referred to as the “rainbow functions” which are parameterized by the energy of these moving probes. Gravity’s rainbow theory admitted the invariant energy scale connected to the Planck energy and the invariant velocity of light at low energies [30,31,32,33,34,35,36]. The modified energy-momentum dispersion relation in this formalism can be expressed as follows [33, 34, 37, 38]

$$\begin{aligned} E^{2}F^{2}\left( {\varepsilon }\right) -p^{2}c^{2}H^{2}\left( {\varepsilon } \right) =m^{2}c^{4} \end{aligned}$$
(1)

where \(F\left( {\varepsilon }\right) \) and \(H\left( {\varepsilon }\right) \) stand for rainbow functions that are characterized by the ratio \( \varepsilon =\)\(\frac{E}{E_{p}}\). Here, \(E_{p}\) denotes the energy on the Planck scale, while E represents the energy of the system. To investigate the impact of the gravity’s rainbow model on the thermodynamics and geodesic equations for this black hole – which we will subsequently utilize – the following rainbow functions are taken into account [39,40,41]

$$ \begin{aligned} F\left( {\varepsilon }\right) =1,{~~} \& ~~\ H\left( {\varepsilon }\right) = \sqrt{1-\gamma {\varepsilon }^{2}}, \end{aligned}$$
(2)

here, \(\gamma \) denotes a dimensionless free parameter in the model.

In light of gravity’s rainbow theory and its applications in the literature, people have explored theories of cosmology, astrophysics, modified gravity, as well as deformed structure of the spacetime around the black hole region and wormhole geometries [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62]. Following the release of the EHT images [63], scientists became interested in comparing the data from EHT with theoretical models to determine the black hole’s characteristics, including mass and spin [64,65,66,67,68,69]. A clear picture of how the acceleration of the black hole impacts the photon trajectory around the AdS black hole in energy-dependent C-metric is still a mystery, and in this paper, we focus on one such case. Therefore, we are interested in investigating the trajectories of light rays in the vicinity of such an accelerating black hole, as well as determine the radius of the photon sphere and the corresponding critical impact parameter, to gain insight into AdS black hole physics by adding the gravity’s rainbow to C-metric.

2 Exact solutions

To obtain the accelerating black hole, we have to construct a kind of energy-dependent C-metric. For this purpose we use the mentioned method in Ref. [70] as

$$\begin{aligned} h\left( \varepsilon \right) =\eta ^{\mu \nu }e_{\mu }\left( \varepsilon \right) \otimes e_{\nu }\left( \varepsilon \right) , \end{aligned}$$
(3)

where \(e_{0}\left( \varepsilon \right) =\frac{1}{F\left( \varepsilon \right) }\widetilde{e_{0}}\), and \(e_{i}\left( \varepsilon \right) =\frac{1}{H\left( \varepsilon \right) }\widetilde{e_{i}}\). Notably, the tilde quantities refer to the energy-independent frame fields. Using the above conditions, we can create a suitable energy-dependent C-metric to obtain an accelerating black hole in gravity’s rainbow. Considering the introduced C-metric in Ref. [6] and by applying \(e_{0}\left( \varepsilon \right) \) and \( e_{i}\left( \varepsilon \right) \), we can get energy-dependent C-metric as

$$\begin{aligned} ds^{2}= & {} \frac{1}{\mathcal {K}^{2}\left( r,\theta \right) }\left[ -\frac{f(r)}{ F^{2}\left( \varepsilon \right) }dt^{2}+\frac{dr^{2}}{f(r)H^{2}\left( \varepsilon \right) }\right. \nonumber \\{} & {} \left. +\frac{r^{2}}{H^{2}\left( \varepsilon \right) }\left( \frac{d\theta ^{2}}{g\left( \theta \right) }+\frac{g\left( \theta \right) \sin ^{2}\theta d\varphi ^{2}}{K^{2}}\right) \right] , \end{aligned}$$
(4)

where \(\mathcal {K}\left( r,\theta \right) =1+Ar\cos \theta \), which is called the conformal factor.

Now, we are in a position to find suitable metric functions f(r) and \( g\left( \theta \right) \) by using all components of equations of motion \( G_{\mu \nu }+\Lambda \textrm{g}_{\mu \nu }=0\) (where \(\textrm{g}_{\mu \nu }\) is metric tensor). Considering the metric (4) and equations of motion, one can find that

$$\begin{aligned} Eq_{tt}= & {} Eq_{rr}=\sin \theta g^{\theta \theta }\mathcal {K} ^{2}\left( r,\theta \right) +3\left( Ar\cos ^{2}\theta \right. \nonumber \\{} & {} \left. +\frac{4Ar\sin ^{2}\theta }{3}+\cos \theta \right) g^{\theta }\mathcal {K}\left( r,\theta \right) \nonumber \\{} & {} +2r^{2}\sin \theta \left[ 3gA^{2}\cos ^{2}\theta +\frac{\left( f-g\right) \left( 1-2Ar\cos \theta \right) }{r^{2}}\right. \nonumber \\{} & {} \left. +\frac{\mathcal {K}\left( r,\theta \right) f^{\prime }}{r}+\frac{\Lambda }{H^{2}\left( \varepsilon \right) } \right] , \end{aligned}$$
(5)
$$\begin{aligned} Eq_{\theta \theta }= & {} Eq_{\varphi \varphi }=r^{2}\mathcal {K}^{2}\left( r,\theta \right) f^{\prime \prime }+2\left( 1-A^{2}r^{2}\cos ^{2}\theta \right) rf^{\prime }\nonumber \\{} & {} +2Ar\sin \theta \mathcal {K}\left( r,\theta \right) g^{\theta } \nonumber \\{} & {} +6gA^{2}r^{2}\sin ^{2}\theta +\frac{2\Lambda r^{2}}{H^{2}\left( \varepsilon \right) }+2Ar\cos \theta \left[ 2\left( g-f\right) \right. \nonumber \\{} & {} \left. +Ar\cos \theta \left( f+2g\right) \right] , \end{aligned}$$
(6)

where \(f=f\left( r\right) \), \(g=g\left( \theta \right) \), \(f^{\prime }=\frac{ df(r)}{dr}\), \(f^{\prime \prime }=\frac{d^{2}f(r)}{dr^{2}}\), \(g^{\mathcal { \theta }}=\frac{dg(\theta )}{d\theta }\), and \(g^{\theta \theta }= \frac{d^{2}g(\theta )}{d\theta ^{2}}\). It is notable that \(Eq_{tt}\), \( Eq_{rr} \), \(Eq_{\theta \theta }\) and \(Eq_{\varphi \varphi }\) are related to components of tt, rr, \(\theta \theta \) and \(\varphi \varphi \) of the equations of motion.

After some calculations, we find the exact solutions of Eqs. (5) and (6) for the functions f(r) and \(g\left( \theta \right) \) in the following forms

$$\begin{aligned} f\left( r\right)= & {} \left( 1-A^{2}r^{2}\right) \left( 1-\frac{2m}{r}\right) - \frac{\Lambda r^{2}}{3H^{2}\left( \varepsilon \right) }, \nonumber \\ g\left( \theta \right)= & {} 1+2mA\cos \theta , \end{aligned}$$
(7)

where \(\Lambda \), and m, are the cosmological constant, and a constant that is related to the total mass of the black hole, respectively. It is worthwhile to mention that we consider \(G=c=1\).

Notably, we can define K as introduced in Refs. [6, 9], which is related to the presence of cosmic string. In other words, by looking at the angular part of the metric and the behavior of \(g\left( \theta \right) \) at both poles \(\theta _{+}=0\) (north pole), and \(\theta _{-}=\pi \) (south pole), we can find the presence of cosmic string. The regularity of the metric at a pole requires \(K_{\pm }=g\left( \theta _{\pm }\right) =1\pm 2mA\), where \(K_{\pm }\) is chosen to regularize one pole and another pole is left with either a conical deficit or a conical excess along the other pole. Here we would make the black hole regular on the north pole, i.e., \(\theta =0 \), by fixing \(K=K_{+}=1+2mA\).

Also, in the absence of the accelerating parameter (\(A=0\)), the solution (7) reduces to the black hole solutions in gravity’s rainbow in the form

$$\begin{aligned} f\left( r\right) =1-\frac{2m}{r}-\frac{\Lambda r^{2}}{3H^{2}\left( \varepsilon \right) }, \end{aligned}$$
(8)

and by considering \(H^{2}\left( \varepsilon \right) =1\), the above solution turns to the well-known Schwartzshield black hole solutions in the present of the cosmological constant as \(f\left( r\right) =1-\frac{2\,m}{r}-\frac{ \Lambda r^{2}}{3}\).

To find the curvature singularity(ies) of the spacetime, we calculate the Ricci and Kretschmann scalars. Using the metric (4) and after some algebraic manipulation, one can find the Ricci scalar (\(\mathcal {R}\)) and Kretschmann scalar (\(\mathcal {R}_{\alpha \beta \gamma \delta }\mathcal {R} ^{\alpha \beta \gamma \delta }\)) in the following forms

$$\begin{aligned} \mathcal {R}= & {} 4\Lambda , \end{aligned}$$
(9)
$$\begin{aligned} \mathcal {R}_{\alpha \beta \gamma \delta }\mathcal {R}^{\alpha \beta \gamma \delta }= & {} \frac{48\mathcal {A}_{0}}{r^{6}}+\frac{288\mathcal {A}_{1}}{r^{5}}+ \frac{720\mathcal {A}_{2}}{r^{4}}+\frac{960\mathcal {A}_{3}}{r^{3}}\nonumber \\{} & {} +\frac{720 \mathcal {A}_{4}}{r^{2}}+\frac{288\mathcal {A}_{5}}{r} +48\mathcal {A}_{6}+\frac{8\Lambda ^{2}}{3}, \end{aligned}$$
(10)

where \(\mathcal {A}_{n}=H^{4}\left( \varepsilon \right) m^{2}A^{n}\cos ^{n}\theta \). The above equation indicates that the Kretschmann scalar diverges at \(r=0\), i.e.,

$$\begin{aligned} \underset{r\longrightarrow 0}{\lim }\mathcal {R}_{\alpha \beta \gamma \delta } \mathcal {R}^{\alpha \beta \gamma \delta }\longrightarrow \infty , \end{aligned}$$
(11)

so we encounter with a curvature singularity at \(r=0\). Also, the asymptotical behavior is dependent on the parameters of this theory. Indeed, the rainbow function \(H\left( \varepsilon \right) \) and the parameter of accelerating black holes affect the asymptotical behavior of spacetime, i.e.,

$$\begin{aligned} \underset{r\longrightarrow \infty }{\lim }\mathcal {R}_{\alpha \beta \gamma \delta }\mathcal {R}^{\alpha \beta \gamma \delta }\longrightarrow 48\mathcal {A }_{6}+\frac{8\Lambda ^{2}}{3}. \end{aligned}$$
(12)

We study the effects of various parameters on horizons. Our findings indicate that; (i) by increasing the accelerating parameter, these black holes may encounter with two horizons (inner and outer horizons), see the up left panel in Fig. 1. (ii) by increasing the rainbow function \( H\left( \varepsilon \right) \), the event horizon increases (see the up right panel in Fig. 1). (iii) massive black holes have large radii, as we expected (see the down left panel in Fig. 1). (iv) by increasing \( \left| \Lambda \right| \), we encounter with small black holes (see the down right panel in Fig. 1).

Fig. 1
figure 1

f(r) versus r for different values of parameters

Full size image

3 Thermodynamics

Considering the black hole as a thermodynamic system, we are going to obtain some of the conserved and thermodynamic quantities of the accelerating black holes in the content of gravity’s rainbow such as the Hawking temperature, entropy and then study the local stability by evaluating the heat capacity.

3.1 Hawking temperature

By equating \(g_{tt}=f(r)=0\), we get the geometrical mass (m) in the following form

$$\begin{aligned} m=\frac{(\Lambda +3A^{2}H^{2}(\varepsilon ))r_{+}^{3}-3H^{2}(\varepsilon )r_{+}}{6(A^{2}r_{+}^{2}-1)H^{2}(\varepsilon )}. \end{aligned}$$
(13)

To get the Hawking temperature, we employ the definition of surface gravity

$$\begin{aligned} \kappa =\sqrt{\frac{-1}{2}\left( \nabla _{\mu }\chi _{\nu }\right) \left( \nabla ^{\mu }\chi ^{\nu }\right) }, \end{aligned}$$
(14)

where \(\chi =\partial _{t}\) is the Killing vector. By using the metric (4) and Eq. (14), we get the surface gravity as

$$\begin{aligned} \kappa =\frac{\left. \left( \frac{df\left( r\right) }{dr}\right) \right| _{r=r_{+}}H(\varepsilon )}{2F(\varepsilon )}, \end{aligned}$$
(15)

and by considering the obtained metric function (7), Eq. (13) and the surface gravity (15) within the Hawking temperature relation ( \(T_{H}=\frac{\kappa }{2\pi }\)), we get it

$$\begin{aligned} T_{H}=\frac{H(\varepsilon )\mathcal {B}_{3}A^{2}r_{+}^{4}+3H(\varepsilon )\left( 1-\mathcal {B}_{2}r_{+}^{2}\right) }{12\pi r_{+}\left( A^{2}r_{+}^{2}-1\right) F\left( \varepsilon \right) }, \end{aligned}$$
(16)

where \(\mathcal {B}_{n}=\) \(\frac{\Lambda }{H^{2}(\varepsilon )}+nA^{2}\). Also, \(r_{+}\) is related to the event horizon of the black hole. The obtained Hawking temperature depends on all the parameters of these black holes.

Fig. 2
figure 2

\(T_{H}\) versus \(r_{+}\) for different values of parameters

Full size image

The high-energy limit (where the limit \(r_{+}\rightarrow 0\) is known as the high-energy limit) of the temperature (16) is given by \(\underset{ r_{+}\rightarrow 0}{\lim }T_{H}\propto \frac{H(\varepsilon )}{4\pi F\left( \varepsilon \right) r_{+}}\), where indicates that the high-energy limit of the temperature only depends on rainbow functions \(F\left( \varepsilon \right) \) and \(H(\varepsilon )\). Also, in this limit, the temperature is always positive. As a result, the temperature of small accelerating black holes in gravity’s rainbow is positive.

The asymptotic behavior of the temperature (16) is obtained \( \underset{r_{+}\rightarrow \infty }{\lim }T_{H}\propto \frac{-H(\varepsilon ) \mathcal {B}_{3}r_{+}}{12\pi F\left( \varepsilon \right) }\), where reveals the asymptotic behavior of the temperature is dependent on the cosmological constant, acceleration parameter and rainbow functions \(F\left( \varepsilon \right) \) and \(H(\varepsilon )\). To have the positive temperature, we must respect to \(\mathcal {B}_{3}=\frac{\Lambda }{H^{2}(\varepsilon )}+3A^{2}<0\), which leads to \(\Lambda <-3A^{2}H^{2}(\varepsilon )\). In other words, the asymptotic behavior of the temperature can be positive when the cosmological constant is negative.

We plot the Hawking temperature versus \(r_{+}\) to study of the behavior of temperature. The results reveal that:

  1. (i)

    there is a singularity for the temperature at \(r_{div}=\frac{1}{A}\). This singularity only depends on the accelerating parameter. Such behavior exists for entropy (see Eq. (18), in the next subsection). We have to omit this point to have the physical behavior of the temperature and the entropy.

  2. (ii)

    there is a zero point for the temperature (\(r_{+_{T=0}}\)) which depends on the parameters of the system.

  3. (iii)

    the temperature is positive for \(r_{+}<r_{div}\) (small black holes), and \(r_{+}>r_{+_{T=0}}\) (large black holes).

  4. (iv)

    Figure 2a reveals that the roof of \(T_{H}\) decreases by increasing \(\left| A\right| \).

  5. (v)

    Figure 2b indicates that by increasing A, the divergence point decreases (as we expected), and the root of the temperature decreases.

  6. (vi)

    by increasing \(H(\varepsilon )\), the root of temperature increases (see Figure 2c).

  7. (vii)

    the root of temperature is independent of \(F\left( \varepsilon \right) \), see Fig. 2d.

3.2 Entropy

To obtain the entropy of black holes, one can use the area law in the form \( S=\frac{\mathcal {A}}{4}\), where \(\mathcal {A}\) is the horizon area and is defined as

$$\begin{aligned} \mathcal {A}= & {} \left. \int _{0}^{2\pi }\int _{0}^{\pi }\sqrt{g_{\theta \theta }g_{\varphi \varphi }}\right| _{r=r_{+}}\nonumber \\= & {} \left. \frac{4\pi r^{2}}{ H^{2}\left( \varepsilon \right) \left( 1-A^{2}r^{2}\right) K}\right| _{r=r_{+}}=\frac{4\pi r_{+}^{2}}{H^{2}\left( \varepsilon \right) \left( 1-A^{2}r_{+}^{2}\right) K}, \nonumber \\ \end{aligned}$$
(17)

by replacing the horizon area (17) within \(S=\frac{\mathcal {A}}{4}\), the entropy of accelerating black holes in gravity’s rainbow is given

$$\begin{aligned} S=\frac{\pi r_{+}^{2}}{H^{2}\left( \varepsilon \right) \left( 1-A^{2}r_{+}^{2}\right) K}, \end{aligned}$$
(18)

where in the absence of acceleration parameter and rainbow function it turns to \(S=\pi r_{+}^{2}\), as we expected. Indeed, in the absence of the accelerating parameter, A is zero, and \(K=1\).

In addition, there is a singularity for the entropy (18) at \(r_{+}= \frac{1}{A}\). This singularity depends on the acceleration parameter. There is such behavior for the mass (13) and the obtained temperature (16). Also, the existence of such singularity is reported for charged accelerating BTZ black holes [71]. To remove this singularity, we have to consider \(r_{+}\ne \frac{1}{A}\). In other words, we do not permit to consider \(r_{+}=\frac{1}{A}\), because this radius leads to a singularity in the geometrical mass (13), temperature (16) and entropy (18).

Now, we series the entropy (18) versus the event horizon (\(r_{+}\)) in the limit \(r_{+}\rightarrow 0\) and \(r_{+}\rightarrow \infty \), to study the high-energy and asymptotic behavior of the entropy.

The high-energy limit of the entropy (18) is obtained

$$\begin{aligned} \underset{r_{+}\rightarrow 0}{\lim }S\propto \frac{\pi r_{+}^{2}}{ H^{2}\left( \varepsilon \right) K}, \end{aligned}$$
(19)

the high-energy limit of the entropy depends on \(H(\varepsilon )\), and K. It is notable that in the high-energy limit, the entropy is positive because K and \(H^{2}\left( \varepsilon \right) \) are positive. So, the entropy of small accelerating black holes in gravity’s rainbow is always positive.

The asymptotic behavior of the entropy (18) is given by

$$\begin{aligned} \underset{r_{+}\rightarrow \infty }{\lim }S\propto \frac{-\Lambda }{ A^{2}H^{2}\left( \varepsilon \right) K}, \end{aligned}$$
(20)

where reveals the asymptotic behavior of the entropy can be positive, provided \(\Lambda <0\).

3.3 Heat capacity

In the canonical ensemble context, a thermodynamic system’s local stability can be studied by heat capacity. So we study the heat capacity to find the local stability for such black holes. In other words, we evaluate the effects of rainbow functions (\(F\left( \varepsilon \right) \), and \(H\left( \varepsilon \right) \)), and the acceleration parameter A on the local stability of accelerating black holes.

The heat capacity is defined as

$$\begin{aligned} C=\frac{T}{\left( \frac{\partial T}{\partial S}\right) }=\frac{T}{\left( \frac{\partial T}{\partial r_{+}}\right) /\left( \frac{\partial S}{\partial r_{+}}\right) }, \end{aligned}$$
(21)

by considering the obtained temperature (16) and the entropy (18), and some calculations, we can get the heat capacity in the following form

$$\begin{aligned} C=\frac{2\pi \left( A^{2}\mathcal {B}_{3}r_{+}^{4}+3\left( 1-\mathcal {B} _{2}r_{+}^{2}\right) \right) }{H^{2}(\varepsilon )\left( A^{6}\mathcal {B} _{3}r_{+}^{6}-A^{4}\mathcal {B}_{6}r_{+}^{4}+3\left( \frac{A^{2}\Lambda r_{+}^{2}}{H^{2}(\varepsilon )}-\mathcal {B}_{-2}-\frac{1}{r_{+}^{2}}\right) \right) K}. \nonumber \\ \end{aligned}$$
(22)

To obtain the high-energy limit of the heat capacity (22), we evaluate it in the limit \(r_{+}\rightarrow 0\) and get

$$\begin{aligned} \underset{r_{+}\rightarrow 0}{\lim }C\propto \frac{-2\pi r_{+}^{2}}{ H^{2}\left( \varepsilon \right) K}, \end{aligned}$$
(23)

where indicates that in the high-energy limit, the heat capacity is negative. As a result, the heat capacity of small accelerating black holes in gravity’s rainbow is always negative. In other words, the accelerating black holes with small radius cannot satisfy the local stability condition.

We obtain the asymptotic behavior of the heat capacity (22) in the limit \(r_{+}\rightarrow \infty \), which is given by

$$\begin{aligned} \underset{r_{+}\rightarrow \infty }{\lim }C\propto \frac{2\pi }{H^{2}\left( \varepsilon \right) KA^{4}r_{+}^{2}}, \end{aligned}$$
(24)

where reveals the asymptotic behavior of the heat capacity is always positive. Indeed, the accelerating black holes with large radii satisfy the local stability.

Fig. 3
figure 3

C versus \(r_{+}\) for different values of parameters

Full size image

Our analysis reveals two important points, which are; (i) the temperature and entropy of small accelerating black holes are always positive, but the heat capacity is negative. (ii) The large accelerating black holes can have positive values for the temperature and entropy when the cosmological constant is negative. In other words, large AdS accelerating black holes are physical objects. However, the heat capacity is always positive in this range (Table 1).

Fig. 4
figure 4

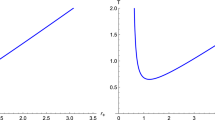
Photon behavior for various values of \(A=0.001, 0.1\). A selection of related photon trajectories is displayed in the right panel, taking \((r, \varphi )\) as Euclidean polar coordinates, while the fractional number of orbits, \(n = \frac{\varphi }{2\pi }\), is displayed in the left panel. \(\varphi \) represents the total change in (orbit plane) azimuthal angle outside the horizon

Full size image
Table 1 Regions of direct rays, lensing rings, and photon rings for two different values of the acceleration parameter A
Full size table

According to the behavior of the temperature, entropy, and heat capacity, accelerating black holes with large radii in gravity’s rainbow can be physical objects and satisfy the local stability when the cosmological constant is negative.

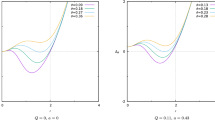
We plot the heat capacity versus \(r_{+}\) for further investigation. The results show that:

  1. (i)

    there are two divergence points for the heat capacity, which we denote by \(r_{{div}_{1}}\), and \(r_{{div}_{2}}\). \(r_{{div}_{1}}\) refers to the first divergence point and \(r_{{div}_{2}}\) refers to the second divergence point. There is also a zero point (\(r_{C=0}\)). Further details can be found in Fig. 3.

  2. (ii)

    the heat capacity at \(r_{{div}_{1}}<r_{+}<r_{{div}_{2}}\), and \(r_{+}>r_{C=0}\), is positive.

  3. (iii)

    by increasing \(\left| \Lambda \right| \), \(r_{{div}_{1}}\) decreases but \(r_{{div}_{2}}\) does not change (see Fig. 3a, b). By comparing the temperature (Fig. 2a) and the heat capacity (Fig. 3a, b), we find that the local stability area increases by increasing \(\left| \Lambda \right| \).

  4. (iv)

    Figure 3c, d, indicate that \(r_{{div}_{1}}\), \(r_{{div}_{2}}\) and \(r_{C=0}\) decrease by increasing the accelerating parameter. In addition, the local stability area increases by increasing A (compare Fig. 2a with Fig. 3c, d).

  5. (v)

    by increasing \(H(\varepsilon )\), the first divergence point (\(r_{{div}_{1}}\)), and the root of the heat capacity (\(r_{C=0}\)) increase. However, the second divergence point (\(r_{{div}_{2}}\)) of the heat capacity does not change (see Fig. 3e, f). By comparing the temperature (Fig. 2c) and the heat capacity (Fig. 3e, f), the local stability area decreases by increasing \(H(\varepsilon )\).

  6. (vi)

    the heat capacity is independent of the change of \(F(\varepsilon )\), see Fig. 3g, h. So, the local stability area does not change by varying \(F(\varepsilon )\).

4 Geodesic equations

First, we need to determine the geodesic motion of photons in a rotationally symmetric and static spacetime metric in the presence of gravity’s rainbow. The modified C-metric, which depends on four parameters: the mass parameter m with length dimension, the acceleration parameter A with inverse length dimension [4, 5], the cosmological constant \( \Lambda \) and rainbow functions, is used to describe this scenario. The rainbow functions, which are introduced in the model, further influence the motion of photons in this spacetime. To analyze this motion, we formulate the Lagrangian \(\mathcal {L}(x,\dot{x})=\frac{1}{2}\textrm{g}_{\mu \nu }\dot{x }^{\mu }\dot{x}^{\nu }\) for the geodesics. The Lagrangian allows us to analyze how photons move around an accelerating black hole under the effects of Gravity’s rainbow can be written as

$$\begin{aligned} \mathcal {L}= & {} \frac{1}{2\,\mathcal {K}^{2}\left( r,\theta \right) }\left( - \frac{f(r)}{F^{2}\left( \varepsilon \right) }\dot{t}^{2}+\frac{1}{ f(r)H^{2}\left( \varepsilon \right) }\dot{r}^{2}\right. \nonumber \\{} & {} \left. +\frac{r^{2}}{g\left( \theta \right) H^{2}\left( \varepsilon \right) }\dot{\theta }^{2}+\frac{g\left( \theta \right) r^{2}\sin ^{2}\theta }{H^{2}\left( \varepsilon \right) {K^{2}} }\dot{\varphi }^{2}\right) , \end{aligned}$$
(25)

with the dot notation that represents differentiation with respect to an affine parameter denoted as \(\lambda \), which is defined along the geodesic. To examine the trajectories of light rays in the vicinity of an accelerating black hole, as well as determine the radius of the photon sphere and the corresponding critical impact parameter, it is permissible to confine the motion of the photon to the equatorial plane of the accelerating black hole, that is, \(\theta =\pi /2\) and \(\dot{\theta }=0\). Since the metric coefficient function cannot be determined by the t and \(\theta \) coordinates, there exist two conserved quantities, E, and L [64, 65], which correspond to energy and angular momentum, respectively. The given expressions are

$$ \begin{aligned} E=-\frac{\partial \mathcal {L}}{\partial \dot{t}}=\frac{f(r)}{F^{2}\left( \varepsilon \right) }\dot{t},~~ \& ~~L=\frac{\partial \mathcal {L}}{\partial \dot{\varphi }}=\frac{r^{2}\dot{\varphi }}{H^{2}\left( \varepsilon \right) }. \end{aligned}$$
(26)

The orbit equation for the null geodesic \(\mathcal {L}=0\) can thus be found as follows

$$\begin{aligned} \left( \frac{dr}{d\varphi }\right) ^{2}=r^{2}f(r)\left( \frac{ r^{2}F^{2}(\varepsilon )}{b^{2}f(r)H^{2}(\varepsilon )}-1\right) . \end{aligned}$$
(27)

We can observe that the term on the right-hand side of the equation serves as an effective potential for particles moving in the r direction. Thus, it is evident that the orbit equation for a particular metric relies solely on one constant of motion, such as the impact parameter \(b=L/E\). In cases where the light ray approaches the center and then exits after reaching a minimum radius R, it is more convenient to express the orbit Eq. (27) in terms of R rather than b. Since R represents the turning point of the trajectory, the condition \(dr/d\varphi |_{R=0}\) must be satisfied [66]. By using the orbit Eq. (27), we can derive the relationship between R and the impact parameter b as

$$\begin{aligned} \frac{1}{b^{2}}=\frac{f(R)H^{2}(\varepsilon )}{R^{2}F^{2}(\varepsilon )}. \end{aligned}$$
(28)

We shall now introduce the following function

$$\begin{aligned} U(r)=\sqrt{\frac{r^{2}F^{2}(\varepsilon )}{f(r)H^{2}(\varepsilon )K^{2}}}. \end{aligned}$$
(29)

It is useful to define the impact parameter b with respect to the function U(r) as \(b\equiv U(R)\). When the acceleration parameter and gravity’s rainbow are absent as well as \(\Lambda =0\), the function U(r) can be considered equivalent to the “effective potential” found in the Schwarzschild case. This effective potential pertains to the motion of photons in Schwarzschild’s gravity. By substituting Eqs. (28) and (29) in Eq. (27), we can re-express Eq. (27) in the following form

$$\begin{aligned} \left( \frac{dr}{d\varphi }\right) ^{2}=\frac{r^{2}f(r)}{K^{2}}\left( \frac{ U^{2}(r)}{U^{2}(R)}-1\right) . \end{aligned}$$
(30)

Likewise, we can safely consider the limit \(R \rightarrow r_{\text {ph}}\) from this point forward.

To proceed, it is necessary to determine the radius of the photon sphere, denoted as \(r_{\text {ph}}\). This can be accomplished by satisfying two conditions along a circular light orbit; \(V_{\text {eff}}|_{r=r_{\text {ph} }}=0 \) and \(\frac{dV_{\text {eff}}}{dr}|_{r=r_{\text {ph}}}=0\). By solving these two equations simultaneously, we obtain the equation for the radius of a circular light orbit, which takes the form

$$\begin{aligned} \frac{f^{\prime }(r_{\text {ph}})}{f(r_{\text {ph}})}-\frac{2}{r_{\text {ph}}} =0. \end{aligned}$$
(31)

Equations (29) and (31) allow us to obtain both the position of the photon sphere and the critical impact parameter, \(b_{\text {c} }\equiv U\left( r_{\text {ph}}\right) \), given by

$$\begin{aligned} r_{\text {ph}}=\frac{\sqrt{\eta _{3}}-1}{2A^{2}m},~~\,and\,\,~b_{\text {c}}= \frac{\sqrt{3\,\eta _{2}}F(\varepsilon )}{\sqrt{3A^{2}\eta _{1}-\eta _{2}\Lambda }}, \end{aligned}$$
(32)

where

$$\begin{aligned} \eta _{1}= & {} \sqrt{\eta _{3}}-1-8A^{4}m^{4}\left( 1+\frac{H^{2}(\varepsilon )\left( 5-2\sqrt{\eta _{3}}\right) }{4A^{2}m^{2}}\right) , \nonumber \\ \eta _{2}= & {} 1-\sqrt{\eta _{3}}+3A^{2}m^{2}\left( 3-\sqrt{\eta _{3}}\right) , \nonumber \\ \eta _{3}= & {} 1+12A^{2}m^{2}. \end{aligned}$$
(33)

We now aim to explore the trajectory of a light ray as it traverses the vicinity of a black hole. The transformation \(x=\frac{1}{r}\) is a convenient choice [67, 68]. This results in the transformation of the orbit equation as follows

$$\begin{aligned} \left( \frac{dx}{d\phi }\right) ^{2}=W(x), \end{aligned}$$
(34)

with

$$\begin{aligned} W\left( x\right) =\left( \frac{F^{2}\left( \varepsilon \right) }{ b^{2}H^{2}\left( \varepsilon \right) }-\left( x^{2}-A^{2}\right) \left( 1-2mx\right) +\frac{\Lambda }{3H^{2}\left( \varepsilon \right) }\right) . \end{aligned}$$
(35)

Regarding the interaction of light rays with a black hole: (i) In the case when the impact parameter \(b>b_{c}\), the light beam approaches one nearest point before retreating back to infinity from the black hole. (ii) The light ray infalls into the black hole in all cases when the impact parameter is \( b<b_{c}\). (iii) At a radius of \(r_{c}\), or the photon sphere radius, the light ray will circle the black hole when \(b=b_{c}\) [67, 68].

The smallest positive real root of \(W(x)=0\), which we indicate as \(x_{m} \), is the turning point for the \(b>b_{c}\) case. Using Eq. (34), one may compute

$$\begin{aligned} \varphi =2 \int _{0}^{x_{m}}\frac{dx}{\sqrt{W(x)}},\quad b>b_{c}, \end{aligned}$$
(36)

to find the whole variation in azimuthal angle \(\varphi \) for a given trajectory with impact parameter b. In the case where \(b<b_{c}\), our interest is directed towards the trajectory beyond the horizon \(r_{h}\). Consequently, the overall variation in the azimuthal angle \(\varphi \) may be determined using the integration

$$\begin{aligned} \varphi =\int _{0}^{x_{+}}\frac{dx}{\sqrt{W(x)}},\quad b<b_{c}, \end{aligned}$$
(37)

where \(x_{+}=\frac{1}{r_{+}}\).

The authors in [18] classified trajectories into three categories, direct, lensed, and photon rings to analyze the apparent characteristics of emission emanating from close proximity to a black hole. We provide a brief overview here. The total number of orbits n, given by \(n=\frac{\varphi }{2\pi }\), is dependent on the impact parameter b. We express the solution of \(n(b)= \frac{2\xi -1}{4}\), where \(\xi =1,2,3,\dots \) by \(b_{\xi }^{\pm }\) so that \( b_{\xi }^{-}<b_{c}\) and \(b_{\xi }^{+}>b_{c}\). Following this, all trajectories can be categorized in this way: (i) direct rays case corresponds to \(\frac{1}{4}<n<\frac{3}{4}\), with \(b\in \left( b_{1}^{-},b_{2}^{-}\right) \cup \left( b_{2}^{+},\infty \right) \). (ii) lensing rings case corresponds to \(\frac{3}{4}<n<\frac{5}{4}\), with \(b\in \left( b_{2}^{-},b_{3}^{-}\right) \cup \left( b_{3}^{+},b_{2}^{+}\right) \). (iii) photon rings case corresponds to \(n>\frac{5}{4}\), with \(b\in \left( b_{3}^{-},b_{3}^{+}\right) \) [67, 68].

In Fig. 4, one can observe the variations in the trajectory of light rays by changing both the acceleration parameter A and impact parameter b. As such, we show how the trajectory of light rays changes for associated black hole parameters, including the acceleration parameter, while keeping fixed values for the cosmological constant \(\Lambda \) and the rainbow functions \(F(\varepsilon )\) and \(H(\varepsilon )\). Figure 2 depicts the number of orbits n versus the impact parameter b. The blue color indicates direct emission rays, cyan denotes lensing rays, and red denotes photon ring rays. The photon orbit and the event horizon of the black hole are depicted by the dashed black circle and the black disk respectively in the ray tracing picture.

Moreover, if we set \(m=1\), \(\Lambda =-0.02\), \(F(\varepsilon )=1\), \( H(\varepsilon )=0.9\), we can see from the table and figures that the range of lensing rings grows with the increasing acceleration parameter A. In the \( (b,\varphi )\) plane, the photon orbit displays a narrow peak when the impact parameter is extremely close to the critical impact parameter \(b\pm b_{c}\) [69]. Afterward, as b grows, the photon trajectories are always direct rays in any scenario.

5 Discussion and conclusions

We extracted accelerating black hole solutions in gravity’s rainbow. Then, we studied the effects of various parameters on the horizons of these black holes in Fig. 1. We evaluated the Hawking temperature and entropy for these black holes to find the local stability area using heat capacity. Our findings indicated that the accelerating black holes with large radii satisfied the local stability. In addition, we found that there were two divergence points and one real root for the heat capacity. The local stability areas increased by increasing \(\left| \Lambda \right| \), and the accelerating parameter (A). However, the local stability decreased by increasing \(H(\varepsilon )\). It is worthwhile to mention that the local stability was independent of another rainbow function (\(F(\varepsilon )\)).

The near-horizon region of energy-dependent C-metric is influenced by both the acceleration parameter and rainbow functions of the AdS black hole, making it an interesting area to explore. Of particular interest is the strong gravitational lensing effect in this region. A critical curve with an impact parameter \(b_{c}\) which gives rise to a photon sphere with a radius \( r_{\text {ph}}\), provides a valuable opportunity to investigate the trajectories of light rays categorized as direct, lensed, and photon rings.

As a consequence, given the dependence of the event horizon and critical impact parameter on the rainbow functions (noting that, for the event horizon, this dependence is confined to \(H(\varepsilon )\)), one observes that an increase in the values of \(H(\varepsilon )\) results in an increase and decrease, respectively, in the event horizon and critical impact parameter. Meanwhile, the photon sphere radius remains unaffected by these functions.

Moreover, our findings indicate a dependency of the critical impact parameter, photon sphere radius, and event horizon on the acceleration parameter. In turn, both the photon sphere radius and event horizon exhibit a similar trend in response to changing acceleration parameter values, whereas the trend differs for the critical impact parameter. Specifically, an increase in the acceleration parameter leads to a decrease in both the photon sphere radius and event horizon, while causing an increase in the critical impact parameter.

Besides, we observed that the range of lensing rings increased with the rising acceleration parameter A. In the \((b, \varphi )\) plane, the photon orbit exhibited a narrow peak when the impact parameter was near the critical value. Subsequently, as b increased, the photon trajectories consistently presented as direct rays in all scenarios.