1 Introduction

The ultracompact objects, such as black holes, are of central importance in theoretical studies and have been considered in the context of thermodynamics, particle motion, and the accretion processes by different authors [1,2,3,4,5,6,7,8,9,10]. The recent observations of the black hole shadows of M87\(^{*}\) and Sgr\(A^*\) [11, 12] by the EHT collaboration, and the detection of the gravitational waves by the LIGO-VIRGO collaboration [13], have greatly influenced the field of black hole Physics. These observations of the black hole shadows and gravitational waves have confirmed the Einstein theory of gravity i.e. General Relativity (GR) in the strong field regime. Despite these observational facts the GR still have some limitations to fully address the unresolved issues related with dark energy [14], dark matter [15], quantization of gravity [16] and the accelerated expansion of our Universe [17]. Therefore, there exist a room for alternate theories of gravity to resolve such issues in their frameworks. To have in hand a well accepted theory of gravity, different modifications in the Einstein-Hilbert action of the GR have been proposed [18]. Recently the Starobinski–Bel–Robinson (SBR) modified theory of gravity has been proposed by adding quadratic terms, that involve the Bel–Robinson tensor and the Ricci scalar, in the Einstein-Hilbert action [19]. The SBR modified theory of gravity is linked to the low energy eleven-dimensional string theory or M-theory which is characterized by a new dimensionless coupling parameter, \(\beta >0\), and may be chosen by the compactification of the M-theory [20].

The timelike circular geodesics around black holes are of great importance astrophysically [21]. These circular geodesics are used to describe the accretion phenomenon around black holes. Therefore, the study of the motion of test particles in the closed vicinity of the event horizon of a black hole may provide with insight of the gravitational field around these ultracompact objects in the cosmos. Dynamics of particles in black hole spacetimes in the theory of GR and other modified theories of gravity have been intensively studied in the literature [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63]. These studies of test particles around black holes have been contributed in constraining the spacetime parameters in different theories of gravity [64,65,66]. The detection of the gravitational waves from a binary of black holes may be thought of an outcome of these studies of circular timelike geodesics in black hole spacetimes.

Another interesting aspect of the motion of test particles in black hole spacetimes is that it can be linked with the observed QPOs in radiation of some microquasars in their X-ray spectrum [67]. From the astrophysical point of view the studies of QPOs are considered to be interesting to provide a solid justification for the validity of the gravitational models in the strong field regime. Besides, QPOs are thought of as a useful tool for measuring the spin and other parameters of black holes [68, 69]. From the time of the discovery of QPOs, almost three decades ago, they have been widely used as potential tools in the astrophysical studies. Different theoretical models, namely (i) the disc-seismic models, (ii) the warped disk models, (iii) the hot-spot models and (iv) the resonance models have been put forwarded to fully comprehend the origin of the QPOs, [70]. However, the physical nature of the origin of the QPOs is still unambiguous. The QPOs have been remain an interesting topic of investigations in the GR and also in the modified theories of gravity [71,72,73,74,75,76,77,78]. For the physical origin and observational phenomenology of the QPOs, interested readers may study, for example a useful review given in the Ref. [79].

The Keplerian thin accretion disks around central ultra compact objects can be described by stable circular orbits (SCOs) [80, 81]. The oscillations in such SCOs are governed by the frequencies of QPOs, which are epicyclic in nature. This situation can be elaborated by epicyclic models or geodesic models of the QPOs in the vicinity of the event horizons of supermassive black holes at the centre of the galaxies [82]. The generalization of these geodesic models becomes possible when considering the electromagnetic interaction between charged hot spots and the large-scale magnetic field around black holes. Including this interaction in the analysis enhances our understanding of the frequencies of the epicyclic oscillations [83,84,85,86]. The QPOs detected in the X-ray spectrum are thought to be closely linked to the oscillations that occur in the regions where the accretion disk approaches the ISCO [87].

The particle dynamics and thermodynamics in the spacetime of the Schwarzschild-like black hole in the SBR theory of gravity have been studied in the literature [19, 88]. Recently the gravitational lensing and the shadow of the Schwarzschild-like black hole in the SBR theory of gravity have been carried out [89]. In this present work we are interested to examine the QPOs in the vicinity of the SCOs for the Schwarzschild-like black hole in the SBR theory of gravity for different astrophysical black hole candidates namely GRO J1655-40, GRS 1915+105, XTE J1859+226, and XTE J1550-564 to obtain constraints on the spacetime parameters by utilising the Markov Chain Monte Carlo (MCMC) analysis methodology. The details are given in the subsequent sections.

In this study, in the Sect. 2 we discus the radial dependence of the lapse function for different values of the parameter \(\beta \) for the Schwarzschild-like black hole solution in the SBR theory of gravity. We notice that the presence of the parameter \(\beta \) reduces the radius of the event horizon for the black hole. In the Sect. 3 the dynamics of test particles in the vicinity of the Schwarzschild-like black hole in the SBR theory of gravity are discussed. We observe that test particles can have both outermost stable circular orbit (OSCO) and ISCO for different values of the parameter \(\beta \), where they are compared to the Schwarzschild black hole scenario of GR. In the Sect. 4 the QPOs of test particles in the vicinity of the Schwarzschild-like black hole in the SBR theory of gravity are discussed. The Sect. 5 is devoted to to explain the observational data obtained for several black hole candidates including GRO J1655- 40, GRS 1915+105, XTE J1859+226, and XTE J1550-564 and get some constraints on their spacetime parameters by employing the MCMC analysis. In the Sect. 6 we give a conclusion of our analysis.

2 Spacetime around the Schwarzschild-like black hole in the Starobinsky–Bel–Robinson gravity

In this section we give a brief review of the static and spherically symmetric black hole solution within the framework of the SBR gravity. The SBR gravity is situated within the M-theory, which is considered to be operated in an eleven-dimensional spacetime, as exemplified in [90]. The M-theory is distinguished by a distinct bosonic sector that introduces a metric and a tensor 3-form CMND, coupled to the M2-brane and dully linked to the M5-brane, as discussed in [91]. Through a process of compactification, incorporating stringy fluxes essential for stabilization scenarios, one can derive corresponding four-dimensional gravity models [20, 90]. To be more specific, the action can be expressed in the following manner.

$$\begin{aligned} S_{SBR}{} & {} =\frac{M^2_{pl}}{2}\int d^4x\sqrt{-g}\nonumber \\{} & {} \times \left[ R+\frac{R^2}{6m^2}-\frac{\beta }{32M_{pl}^6}(\mathcal {P}^2-\mathcal {G}^2)\right] , \end{aligned}$$
(1)

In this context, g represents the determinant of the metric tensor, \(M_{pl}\) corresponds to the reduced Planck mass, defined as \(M_{pl} = 1/\sqrt{8\pi G}\) and approximately equal to \(2 \times 10^{18}\,\textrm{GeV}\). The symbol R signifies the Ricci scalar curvature. The free mass parameter m can be construed differently based on the specific theory under consideration. Furthermore, the quartic contributions \(\mathcal {P}^2\) and \(\mathcal {G}^2\) are linked to the Pontryagin and Euler topological densities, while the final term is associated with the Bel–Robinson tensor, as elaborated in [20, 90]

$$\begin{aligned} T^{\mu \nu \lambda \rho }T_{\mu \nu \lambda \rho }=\frac{1}{4}(\mathcal {P}^2-\mathcal {G}^2), \end{aligned}$$
(2)

where the new 4-rank tensor

$$\begin{aligned} T^{\mu \nu \lambda \sigma }=R^{\mu \rho \gamma \lambda }R^{\nu \sigma }_{\rho \gamma } +R^{\mu \rho \gamma \sigma }R^{\nu \lambda }_{\rho \gamma }-\frac{1}{2}g^{\mu \nu }R^{\rho \gamma \alpha \lambda }R^{\sigma }_{\rho \gamma \alpha } \end{aligned}$$
(3)

is introduced.

The SBR gravity action introduces two additional parameters, labeled as m and \(\beta \), in contrast to the Hilbert action in GR. Researchers have employed this expanded framework to formulate innovative physical models, including inflation, as extensively discussed in [92]. Moreover, the SBR modification of the GR is well-suited for empirically testable scenarios within the black hole Physics and the investigation of Hawking radiation during the early epoch of our Universe [19].

In the realm of the SBR gravity, solutions for static black holes resembling the Schwarzschild-type metrics have been established. The determination of the parameter m involved solving the equation of motion, revealing that the thermodynamic properties are influenced by the stringy gravity parameter \(\beta \). Consequently, the line element for this non-rotating solution can be articulated as follows [20]:

$$\begin{aligned} ds^2=-a(r)dt^2+\frac{1}{a(r)}dr^2+r^2d\Omega ^2, \end{aligned}$$
(4)

with lapse function a(r) to be

$$\begin{aligned} a(r)=1-\frac{r_s}{r}+\beta M^6 \left( \frac{4\sqrt{2}\pi r_s}{r^3}\right) ^3\left( \frac{108r-97r_s}{5r}\right) , \end{aligned}$$
(5)

where \(r_s = 2M\) with total mass parameter M.

We show the change in the lapse function for the radial coordinate in Fig. 1 for different values of the parameter \(\beta \). One can see from the graph that presence of parameter \(\beta \) changes the lapse function considerably in the near vicinity of the central black hole having its maximum at the point \(r=2M\). Since zero values of the lapse function give us the location of the event horizon of a black hole it can be easily noticed from the figure that the presence of the parameter \(\beta \) shifts the radius of the event horizon towards smaller distances.

Fig. 1
figure 1

Radial dependence of the lapse function for the different values of the parameter \(\beta \)

Full size image

3 Test particle motion around Schwarzschild-type black hole in Starobinskiy–Bel–Robinson gravity

3.1 Effective potential

In this section, we investigate the dynamics of test particles in the vicinity of a spherically symmetric Schwarzschild-type black hole.

The Hamiltonian of a particle moving around a black hole can be expressed as follows:

$$\begin{aligned} H =\frac{1}{2} g^{\mu \nu }p_{\mu }p_{\nu } +\frac{1}{2}m_0^2, \end{aligned}$$
(6)

where \(p^{\mu }=m_0\dot{x}^{\mu } = m_0\frac{dx^{\mu }}{d\tau }\) represents the derivative of the coordinate \(x^{\mu }\) with respect to the proper time \(\tau \). Our spacetime exhibits spherical symmetry, leading to the existence of two conserved quantities. One of these constants of motion is associated with the temporal direction, while the other is associated with the azimuthal (\(\varphi \)) direction.

We can write the Hamiltonian equations as follows:

$$\begin{aligned} \dot{x}^{\mu } = \frac{\partial H}{\partial p_{\mu }}, \quad \dot{p}_{\mu } = -\frac{\partial H}{\partial x^{\mu }}. \end{aligned}$$
(7)

Furthermore, as mentioned above, we have two conserved quantities:

$$\begin{aligned} E= & {} -p_t = m_0 a(r) \dot{t}, \nonumber \\ L= & {} p_{\varphi } =m_0 r^2 \sin ^2\theta \dot{\varphi }. \end{aligned}$$
(8)

We can write specific energy and angular momentum in the following way:

$$\begin{aligned} \mathcal {E}= \frac{E}{m_0}, \quad \mathcal {L}= \frac{L}{m_0}. \end{aligned}$$
(9)

If we plug Eq. (8) into Eq. (6) we will obtain the following equation

$$\begin{aligned} H= \frac{1}{2a(r)}(p^r)^2+ \frac{r^2}{2}(p^{\theta })^2 + \frac{m_0^2}{2a(r)}(V_{eff}^2-\mathcal {E}^2). \end{aligned}$$
(10)

The effective potential is:

$$\begin{aligned} V_{eff}(r,\theta )=\sqrt{a(r)\left( 1+\frac{\mathcal {L}^2}{r^2 \sin ^2{\theta }}\right) }. \end{aligned}$$
(11)

The effective potential of the test particle can be thoroughly investigated in a two-dimensional (2D) plot, as shown in Fig. 2. This particular figure corresponds to a specific set of parameters, namely \(\beta = 0.003\) and angular momentum \(\mathcal {L} = 3.2\). Two bottom panels in the figure represent the dependence of the effective potential from the radial distance x and vertical axis z to the equatorial plane. The top plot corresponds to the 3D view of the same dependence from these two coordinates simultaneously. The first bottom panel shows that given effective potential, it can have two extremums which allows one to suspect that in the given spacetime test particles can have OSCO in addition to the ISCO. This statement will be clarified later in detail. The right bottom plot demonstrates that the effective potential of the test particle at fixed radial distance goes up monotonically with the increase of z coordinate suggesting that effective potential becomes stronger at poles.

Due to the symmetric nature of the particle’s motion, we can focus our investigation on the equatorial plane (\(\theta = \pi /2\)), as indicated in Fig. 2. This allows us to specifically examine the motion of the particle in a simplified manner, providing valuable insights into its dynamics within this plane. An expression for the effective potential takes the following form:

$$\begin{aligned} V_{eff}(r)=\sqrt{a(r)\left( 1+\frac{\mathcal {L}^2}{r^2 }\right) }. \end{aligned}$$
(12)

By analyzing the expression of the effective potential, we can gain insight into the dynamics of a particle in the vicinity of a black hole. In particular, we can determine the particle’s angular momentum and specific energy in a circular orbit by considering the conditions that its radial velocity and radial acceleration vanish. This condition leads to the equations \(V_{\text {eff}} = \mathcal {E}\) and \(V'_{\text {eff}} = 0\), where \(\mathcal {E}\) represents the specific energy. Solving these equations yields the following expressions for the angular momentum and energy of the particle in a circular orbit:

$$\begin{aligned}{} & {} \mathcal {L}^2 = \frac{r^3 a'(r)}{2 a(r)-r a'(r)}, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \mathcal {E}=\sqrt{\text {a}(r) \left( 1-\frac{r \text {a}'(r)}{2 \text {a}(r)-r \text {a}'(r)}\right) }. \end{aligned}$$
(14)

These quantities provide essential information about the particle’s motion and characterize its behavior in the gravitational field of the black hole.

Let us analyze the one-dimensional effective potential, as given by Eq. (12), for the particle shown in Fig. 3. The limits of the effective potential adhere to the standard limit \(\lim _{r\rightarrow \infty } V_{\text {eff}} = 1\), representing its behavior at large distances.

Figure 3 consists of three panels, each providing valuable insights into the characteristics of the effective potential. The first panel (left panel) illustrates the radial dependence of the effective potential for various values of the particle’s angular momentum while keeping \(\beta = 0.003\) constant. This panel reveals an intriguing behavior of our spacetime, where the effective potential exhibits two circular regions. This phenomenon may be attributed to the presence of the spacetime parameter \(\beta \). Additionally, an increase in the particle’s angular momentum leads to a corresponding increase in the effective potential.

Fig. 2
figure 2

The radial dependence of the two-dimensional effective potential is investigated for a parameter value of \(\beta = 0.003\)

Full size image

The middle panel of Fig. 3 displays the radial dependence of the effective potential for different values of the spacetime parameter \(\beta \), with the angular momentum \(\mathcal {L}\) fixed at 3.4 (applies to the right panel as well). As \(\beta \) becomes more prominent and increases, we observe the appearance of a second region closer to the compact object. Consequently, an increase in the parameter \(\beta \) results in an expansion of the second region of the effective potential nearer to the compact object.

Fig. 3
figure 3

Radial dependence of the effective potential for the different values of \(\beta \) parameter

Full size image
Fig. 4
figure 4

Radial dependence of the specific energy and angular momentum of a particle in circular orbits

Full size image

The right panel of Fig. 3 showcases the behavior for larger values of the \(\beta \) parameter. From the figure, it is evident that such an increase in the \(\beta \) parameter leads to a significant escalation in the effective potential of the test particle. However, it is noteworthy that in the remainder of the article, we will focus on small values of \(\beta \), as indicated in the paper [20], which states that \(\beta \ll 1\).

In our study, we extensively discussed the behavior of the specific energy and angular momentum of a particle in a circular orbit, which is given by Eqs. (13)–(14). The results are depicted in Fig. 4, where the left panel illustrates the variation of the specific energy, and the right panel represents the changes in angular momentum for a particle in a circular orbit.

From the left panel, it is evident that an increase in the \(\beta \) parameter leads to a decrease in the energy of the particle, particularly in the region near the black hole. However, for regions farther away from the compact object, there is negligible effect of \(\beta \) on the particle’s energy. A similar trend can be observed in the case of the angular momentum of the particle, as depicted in the right panel of Fig. 4

3.2 Trajectories of a test particle

We present trajectories of test particles around a black hole in Cartesian coordinates in the following way:

$$\begin{aligned} x = r \cos {\varphi }\sin {\theta }, \quad y = r \sin {\varphi }\sin {\theta }, \quad z = r\cos {\theta }. \end{aligned}$$
(15)

We use Hamiltonian of a test particle as given by Eqs. (10) and (7) to graphically analyze trajectories of a test particle as given in Fig. 5. The first row is for the Schwarzschild solution (i.e. when \(\beta =0\)) while the rest corresponds to the black hole in the SBR gravity. In the first and second rows the test particle is shot from the point relatively far from the central black hole while in the last row, it is shot from a relatively close distance to see the effect of the SBR gravity parameter. One can see that in the SBR gravity, there are two regions shown with dashed black lines where particle (with chosen angular momentum, energy, and initial position) can stably orbit while in the traditional Schwarzschild case, we deal with only one region in the vicinity of the black hole. This suggests that when the accretion disk is formed around a black hole in the SBR gravity it should have a small inner accretion disk inside the ISCO. Since this small piece of accretion disk is closer to the central black hole, therefore, the energy of particles in this disk and thus the temperature of this disk should be much higher compared to the traditional outer part of the accretion disk. This suggests a detailed investigation of the energetic properties of such regions which may play a crucial role when it comes to e.g. power jets formed around black hole, Penrose and magnetic Penrose processes (when external magnetic field is considered) etc. But we are not going to investigate these phenomena since this is out of the topic of our present work and may be dealt separately.

Fig. 5
figure 5

The trajectories of the test particle are examined for the Schwarzschild-type case in the SBR gravity when \(\beta = 0.003\). The particle’s behavior is analyzed in the equatorial plane

Full size image

3.3 Innermost stable circular orbits

To investigate black holes, spacetime structure, and the accretion process, the analysis of stable circular orbits proves crucial. This section focuses on the ISCO within the framework of SBR gravity applied to a Schwarzschild-like black hole background. The identification of a stable circular orbit involves satisfying two conditions: radial velocity must be zero (\(dr/d\tau = 0\) or \({V}_{eff} = {{\mathcal {E}}}\)), and the particle should lack radial acceleration (\(d^2r/d\tau ^2=0\) or \(d{{\mathcal {V}}}_{eff}/dr=0\)). While these criteria aid in determining circular orbits, comprehending the inner edge or ISCO necessitates an additional criterion concerning the stability of this point. To evaluate stability, we analyze the second derivative of the effective potential. A negative second derivative at a certain point suggests that there is no other point in its vicinity with higher energy, indicating instability. Conversely, a positive second derivative at a certain point indicates that this point is the least energetic in its vicinity, thereby confirming its stability. Consequently, we necessitate the following additional condition:

$$\begin{aligned} \frac{d^2{V}_{eff}}{dr^2} \ge 0. \end{aligned}$$
(16)

To establish the ISCO region, solving a system of equations is imperative: \({V}_{eff}={{\mathcal {E}}}\), \(d {V}_{eff}/dr=0\), and \(d^2{V}_{eff}/dr^2=0\). Solving the second equation yields the radial function of angular momentum. Substituting this expression into the first equation provides the energy of the particle at the circular orbit. Similarly, substituting the angular momentum expression into the third equation yields the ISCO equation for the particle.

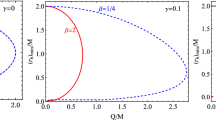
In the Fig. 6 we present the dependence of the ISCO and OSCO radius for the spacetime parameter \(\beta \). One can see that an increase of the parameter \(\beta \) decreases the ISCO radius and increases the OSCO one and at some specific value (\(\beta \simeq 0.008\)) these two coincide with each other.

Fig. 6
figure 6

Dependence of ISCO radius to the \(\beta \) spacetime parameter

Full size image

4 Quasi periodic oscillations of the particles

The QPOs serve as prominent observational quantities in the context of relativistic compact objects. In this study, our focus is on calculating the radial and vertical epicyclic frequencies of test particles. To accomplish this, we employ the standard approach [87] by expressing the effective potential as

$$\begin{aligned} g_{rr}\dot{r}^2 + g_{\theta \theta }\dot{\theta }^2 = V_{eff}. \end{aligned}$$
(17)

Within the linear weak perturbation regime, small perturbations around circular equatorial orbits can be separated into radial and vertical components. Specifically, by assuming \(\dot{\theta }=0\) for the radial direction, we can express \(\dot{r}=\dot{t}(dr/dt)\). This transformation leads us to a modified form of Eq. (17):

$$\begin{aligned} \left( \frac{dr}{dt}\right) ^2 = \frac{1}{g_{rr}\dot{t}^2} V_{eff}. \end{aligned}$$
(18)

Upon taking the derivative with respect to the coordinate t, the following expression emerges:

$$\begin{aligned} \frac{d^2r}{dt^2}= & {} \frac{1}{2} \frac{\partial }{\partial r} \left( \frac{1}{g_{rr} \dot{t}^2} V_{eff} \right) \nonumber \\= & {} \frac{V_{eff}}{2} \frac{\partial }{\partial r} \left( \frac{1}{g_{rr} \dot{t}^2} \right) +\frac{1}{2 g_{rr} \dot{t}^2} \frac{\partial V_{eff}}{\partial r}. \end{aligned}$$
(19)

Considering that \(\delta r\) represents a small displacement from the mean orbit (i.e., \(r=r_0+\delta _r\)), we find:

$$\begin{aligned} \frac{d^2r}{dt^2}= & {} \frac{d^2\delta _r}{dt^2}, \end{aligned}$$
(20)
$$\begin{aligned} V_{eff}(r_0+\delta _r)= & {} V_{eff}(r_0)+\left( \frac{\partial V_{eff}}{\partial r}\right) _{r=r_0}\delta _r \nonumber \\{} & {} +O(\delta _r^2)=V_{eff}(r_0)+O(\delta _r^2), \end{aligned}$$
(21)
$$\begin{aligned} \left( \frac{\partial V_{eff}}{\partial r}\right) _{r=r_0+\delta _r}= & {} \left( \frac{\partial V_{eff}}{\partial r}\right) _{r=r_0} \nonumber \\ {}{} & {} +\left( \frac{\partial ^2 V_{eff}}{\partial r^2}\right) _{r=r_0} \delta _r+O(\delta _r^2) \nonumber \\ {}= & {} \left( \frac{\partial ^2 V_{eff}}{\partial r^2}\right) _{r=r_0} \delta _r+O(\delta _r^2). \end{aligned}$$
(22)

Similarly, by introducing a small displacement from the mean orbit \(\delta _\theta \) as \(\theta =\pi /2+\delta _\theta \), we can derive the expression for the vertical epicyclic frequency with respect to the coordinate \(\theta \). Within the linear regime, neglecting quadratic terms \(O(\delta _r^2)\) and \(O(\delta _\theta ^2)\), we obtain the following differential equations:

$$\begin{aligned} \frac{d^2\delta _r}{dt^2}+\Omega _r^2 \delta _r=0, \end{aligned}$$
(23)
$$\begin{aligned} \frac{d^2\delta _\theta }{dt^2}+\Omega _r^2 \delta _\theta =0, \end{aligned}$$
(24)

where

$$\begin{aligned} \Omega _r^2=-\frac{1}{2g_{rr}\dot{t}^2} \frac{\partial ^2 V_{eff}}{\partial r^2}, \end{aligned}$$
(25)
$$\begin{aligned} \Omega _\theta ^2=-\frac{1}{2g_{\theta \theta }\dot{t}^2} \frac{\partial ^2 V_{eff}}{\partial \theta ^2}. \end{aligned}$$
(26)

Here, \(\nu _r=\frac{1}{2 \pi } \frac{c^3}{G M} \Omega _r\) represents the radial epicyclic frequency, \(\nu _\theta =\frac{1}{2 \pi } \frac{c^3}{G M} \Omega _\theta \) represents the vertical frequency, and \(\nu _\phi =\frac{1}{2 \pi } \frac{c^3}{G M} \Omega \) represents the Keplerian frequency.

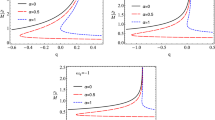
Change of the fundamental frequencies with the change of the radial coordinate is shown in Fig. 7. One can see a considerable deviation of the radial epicyclic frequency dependence in the SBR gravity from the GR in the close vicinity of the black hole. In the far distances, however, the lines are identical. It can be seen that lines have a maximum point for the radial component of the epicyclic frequencies which shifts towards bigger distances and bigger frequencies with the increase of the parameter \(\beta \). In the bottom panel, it is shown how the Kepplerian epicyclic frequency changes with the coordinate r for different values of the parameter \(\beta \). We again see a completely different behavior of the lines in the close environment of the central black hole as compared with the Schwarzschild case (black solid line). We see that the line takes some maximum value before going down to zero as one approaches the central black hole while in the Schwarzschild case, the lines go up exponentially. Again, the difference between the SBR gravity and GR is only considerable in the close environment of the central black hole while in the far distances the lines are identical with very high precision.

Fig. 7
figure 7

Change of the Kepplerian and radial fundamental frequencies of test particles moving around the central black hole in SBR gravity for various values of the \(\beta \) parameter

Full size image

The model of relativistic precision (RP), originally introduced by Stella and Vietri [93] to interpret the twin-peak QPOs observed in the frequency range of 0.2 to 1.25 kHz in low-mass X-ray binary systems (LMXRBs) with neutron stars, was subsequently found to apply to binary systems featuring both black hole candidates and neutron stars [94]. Ingram [95] later refined the RP model for precise measurements of the mass and spin of central black holes in microquasars, leveraging data from the power-density spectrum of the black hole accretion disk. According to the RP model, the upper and lower frequencies can be expressed in terms of the frequencies associated with radial, vertical, and orbital oscillations, given by \(\nu _U = \nu _{\phi }\) and \(\nu _L = \nu _{\phi }-\nu _r,\) respectively.

The relation between the upper and lower frequencies in the RP model is given in Fig. 8 for the stellar mass black hole with \(M=10 M_{\odot }\). The shaded region corresponds to the case when the lower frequency becomes greater than the upper frequency which is not acceptable. One can see that the black solid line that represents the Schwarzschild black hole in GR has a continuous and limited line. The case of the Schwarzschild-type black hole in the SBR theory of gravity however, shows that (\(\beta \ne 0\)), one can have both continuous lines (e.g. \(\beta =0.009\) case) and discontinuous ones (e.g. \(\beta =0.006\) and \(\beta =0.003\)). One can easily notice that for smaller values of the upper and lower frequencies, the difference between the Schwarzschild black hole and the Schwarzschild-type black hole in the SBR gravity is indistinguishable and becomes detectable starting from \(\nu \sim 100\) Hz. For frequencies less than \(\nu _U\sim 270\) Hz, in general, we see that an increase of the \(\beta \) parameter makes the upper frequency greater for fixed lower frequency while for \(\nu _U\gtrsim 270\) Hz for bigger \(\beta \) we have smaller values of upper frequency for the fixed \(\nu _L\).

Fig. 8
figure 8

The relation between the upper and lower frequencies of Schwarzschild-type black hole in SBR for RP model when \(M/M_\odot =10\)

Full size image

In the Fig. 8 we have seen that the lines for relatively smaller values of \(\beta \) can be discontinuous in the RP model. Let us now see this issue in detail. To do so, we need to keep in mind that in the RP model, the upper frequency is defined as \(\nu _u=\nu _K\) while \(\nu _L=\nu _K-\nu _r\). So, we just need to explore how these two frequencies behave for different values of \(\beta \). In Fig. 9 we show the radial dependence of these two frequencies for different \(\beta \). From the top-left plot we can see that in the Schwarzschild case, the upper and lower frequency lines intersect at ISCO radius and then (for smaller r) they do not intersect at all. For \(\beta =0.003\) case however, it is clearly shown that we have two distinct regions where the lower frequency becomes less than the upper one thus suggesting two discontinuous lines in Fig. 8. Finally, the plot in the bottom demonstrates that for relatively bigger values of the parameter \(\beta \) (\(\beta =0.009\)) the lower frequency again becomes less than the upper one and thus the lines in Fig. 8 again become continuous.

Fig. 9
figure 9

The radial dependence of upper and lower frequencies for different values of \(\beta \) parameter and \(M/M_\odot =10\). We restricted the lower frequency up to the values where it intersects the upper frequency

Full size image

5 Constraints on black hole parameters in the context of Starobinsky–Bel–Robinson gravity

In this section, we embark on an investigation of four X-ray binary systems to establish constraints on the parameters pertinent to our black hole model within the framework of SBR gravity theory. These constraints are to be ascertained through a meticulous analysis of data concerning QPOs. The celestial objects under consideration encompass GRO J1655-40 and GRS 1915+10.

Subsequently, we will present the optimal parameter values situated within the parameter space. These values have been derived through the employment of a MCMC analysis methodology.

5.1 Analysis using Markov chain Monte Carlo

The MCMC analysis was executed by employing the Python library emcee [96]. The primary objective of this analysis was to establish constraints on the parameters related to the ultra compact object under investigation. The analysis was conducted using the relativistic precision (RP) method.

The posterior probability \(\mathcal {P}(\Theta |\mathcal {D},\mathcal {M})\), as per the Ref. [97], is defined as:

$$\begin{aligned} \mathcal {P}(\Theta |\mathcal {D},\mathcal {M}) = \frac{P(\mathcal {D}|\Theta ,\mathcal {M})\pi (\Theta |\mathcal {M})}{P(\mathcal {D}|\mathcal {M})}. \end{aligned}$$
(27)

Here, \(\pi (\Theta )\) represents the prior distribution, and \(P(\mathcal {D}|\Theta ,\mathcal {M})\) is the likelihood function. The priors are specified as Gaussian distributions with boundaries:

$$\begin{aligned} \pi (\Theta _i) \sim \exp \left( \frac{1}{2}\left( \frac{\Theta _i - \Theta _{0,i}}{\sigma _i}\right) ^2\right) , \end{aligned}$$
(28)

where \(\Theta _{\text {low},i}< \Theta _i < \Theta _{\text {high},i}\) for the parameters \(\Theta _i = [M, \beta , r]\), and \(\sigma _i\) are the corresponding standard deviations. The prior values for the black hole parameters are detailed in Table 2.

In consideration of the upper and lower frequency data obtained in Sect. 4, our MCMC analysis is designed to incorporate two separate datasets. Central to this analysis is the likelihood function denoted as l, which can be formulated as follows:

$$\begin{aligned} \log l = \log l_{\text {up}} + \log l_{\text {low}} \end{aligned}$$
(29)

Here, \(\log l_{\text {up}}\) characterizes the likelihood associated with the upper-frequency data, expressed as:

$$\begin{aligned} \log l_{\text {up}} = - \frac{1}{2} \sum _{i} \frac{(\nu _{\text {up, obs}}^i - \nu _{\text {up, th}}^i)^2}{(\sigma _{\text {up, obs}}^i)^2} \end{aligned}$$
(30)

On the other hand, \(\log l_{\text {low}}\) represents the likelihood on the lower frequency data, defined as:

$$\begin{aligned} \log l_{\text {low}} = -\frac{1}{2} \sum _{i} \frac{(\nu _{\text {low, obs}}^i - \nu _{\text {low, th}}^i)^2}{(\sigma _{\text {low, obs}}^i)^2} \end{aligned}$$
(31)

Here, \(\nu ^i_{\text {up, obs}}\) and \(\nu ^i_{\text {low, obs}}\) denote the observed results for the upper and lower frequencies (\(\nu _{\text {up}}\) and \(\nu _{\text {low}}\), respectively), and \(\nu ^i_{\text {up, th}}\) and \(\nu ^i_{\text {low, th}}\) correspond to their respective theoretical predictions. Additionally, within these expressions, \(\sigma ^i_{x, \text {obs}^i}\) represents the statistical uncertainties associated with the given quantities.

Table 1 The mass, upper and lower frequencies of QPOs from the X-ray binaries selected for analysis
Full size table
Table 2 The Gaussian prior of the black hole parameters in SBR gravity from QPOs for the X-ray Binaries
Full size table

In the Fig. 10 we show the outcome based on the MCMC method for the observational data obtained for the sources GRO J1655-40, GRS 1915+105, XTE J1859+226, and XTE J1550-564. From the top left panel, one can see that the RP model suggests the following constraints on the black hole parameters of the source GRO J1655-40 at \(68\%\) confidence level (CL): The mass in the range \(M\simeq 6.33\pm 0.11 M_{\odot }\), \(\beta \simeq 0.012^{+0.00049}_{-0.00047}\), \(r=4.94^{+0.061}_{-0.059} M\). In the top-right panel, we show the result of MCMC method for the source GRS 1915+105 where the constraints on black hole parameters at \(68\%\) CL are: \(M\simeq 11.86^{+0.57}_{-0.52} M_{\odot }\), \(\beta \simeq 0.0083^{+0.0034}_{-0.0036}\), \(r\simeq 6.42^{+0.175}_{-0.19} M\). For the source XTE J1859+226, the results are shown in bottom-left panel and they are: \(M\simeq 7.39^{+0.26}_{-0.22} M_{\odot }\), \(\beta \simeq 0.013^{+0.0059}_{-0.0063}\), \(r\simeq 7.17^{+0.13}_{-0.15} M\) at \(68\%\) CL. Lastly, in the bottom-right panel, we have shown the results for XTE J1550-564 which are: \(M\simeq 9.22^{+0.23}_{-0.25} M_{\odot }\), \(\beta =0.0143\pm 0.00063\), \(r\simeq 5.37\pm 0.1 M\) at \(68\%\) CL.

Fig. 10
figure 10

Constraints on black hole mass, \(\beta \), and r parameters for the microquasars, GRO J1655-40 (black), GRS 1915+105(blue), XTE J1859+226 (magenta), and XTE J1550-564 (brown) using MCMC code

Full size image

6 Conclusion

Our study delved into the properties of the spacetime around the Schwarzschild-type black hole within the framework of the SBR gravity. We explored the effects of the additional spacetime parameter \(\beta \) on various aspects of particle motion, including the effective potential, energy, angular momentum, trajectories, and QPOs. Our analysis revealed distinct features in the behavior of these quantities compared to the Schwarzschild case in GR.

One notable result is the shift in the location of the event horizon, as indicated by the lapse function, which depends on the parameter \(\beta \). The effective potential exhibits intriguing behavior, revealing the influence of \(\beta \) on the radial and vertical motion of test particles. The analysis of circular orbits demonstrated how the specific energy and angular momentum vary with the spacetime parameter, providing insights into the stability of these orbits.

The trajectories of test particles illustrated the impact of \(\beta \) on the particle’s motion in both the equatorial and off-equatorial planes. Notably, the ISCO and OSCO depend on \(\beta \), showcasing the altered dynamics in the SBR gravity compared to GR.

We further investigated the QPOs of test particles, calculating radial and vertical epicyclic frequencies. The following key findings are derived from our calculations:

  • In the far distances from the central black hole both, the Schwarzschild black hole in GR and the Schwarzschild-like black hole in the SBR gravity give the same radial and epicyclic frequencies i.e. the effect of SBR gravity is indistinguishable from its GR counterpart.

  • In the close vicinity of the central black hole the behavior of radial and vertical frequencies is totally different in GR and in the SBR gravity. The radial fundamental frequency can take one more maximum before reaching zero and this maximum shifts toward bigger orbits for bigger values of \(\beta \) in the case of the SBR gravity. The vertical epicyclic frequency in the case of the Schwarzschild black hole in GR goes up exponentially. In contrast, in the SBR gravity the lines reach maximum near the central black hole and then monotonically goes down to zero.

Finally, we have applied our black hole model to the observational data of X-ray binary systems, seeking constraints on the spacetime parameters within the SBR gravity framework. This analysis offers an avenue for testing the viability of the modified gravity theory in explaining astrophysical observations. Our results based on MCMC analysis and RP model reveals that mass and the SBR gravity parameter for the observed QPOs data of the source GRO J1655-40 are: \(M\simeq 6.33\pm 0.11 M_{\odot }\), \(\beta \simeq 0.012^{+0.00049}_{-0.00047}\) (at \(68\%\) CL); for the source GRS 1915+105 they are: \(M\simeq 11.86^{+0.57}_{-0.52} M_{\odot }\), \(\beta \simeq 0.0083^{+0.0034}_{-0.0036}\) (at \(68\%\) CL); for the source XTE J1859+226 they are \(M\simeq 7.39^{+0.26}_{-0.22} M_{\odot }\), \(\beta \simeq 0.013^{+0.0059}_{-0.0063}\) (at \(68\%\) CL); and lastly, for XTE J1550-564 they read: \(M\simeq 9.22^{+0.23}_{-0.25} M_{\odot }\), \(\beta =0.0143\pm 0.00063\) (at \(68\%\) CL).

In conclusion, our investigation has provided a comprehensive understanding of the characteristics of black holes in the SBR gravity, shedding light on the interplay between modified gravity theories and astrophysical phenomena. Further observational studies and refinements in modeling can enhance our understanding of the nature of gravity in extreme environments and provide additional constraints on the parameters of alternative gravity theories.