1 Introduction

The existence of dark energy and dark matter in the Universe has been discovered using several independent experiments and the observations [2]. Despite the attempts to explain the phenomenons related to dark energy and dark matter, there is no complete theory describing the nature of these matters. The general theory of relativity is the classical theory of the gravity and unfortunately, it has some fundamental issues related to existence of the singular points and inconsistency with the quantum field theory. Thus, one needs to construct the modifications of the Einstein’s theory with the aim to further construction of the unified theory. Particularly, Moffat [8] has proposed a new approach based on modification of the gravity (MOG) which may be one of the promising models of gravity in the way of building the unified theory of gravity. This model contains the scalar and the massive vector field and can be referred as scalar-tensor-vector gravity (STVG). To avoid the break-down of the theory at a short distance within the MOG theory the massive vector field with the source charge \(Q=\sqrt{\alpha G}M\) has been introduced, where G is the gravitational constant, M is the mass of the central object and \(\alpha \) is the new coupling parameter. This term creates the additional repulsive force, which becomes significant at the quantum level.

In the literature, several solutions describing the compact gravitating object in MOG gravity have been obtained. Particularly in Ref. [9] the non-rotating and rotating black hole (BH) solutions have been obtained and refereed as Schwarzschild-MOG and Kerr-MOG BHs, respectively. Test particle motion and stability of their circular orbits around a compact object in MOG gravity have been explored in Ref. [4]. Applications and properties of the solutions of field equations in MOG gravity such as solar system tests [8], galaxy rotation curve [12, 14], test the gravity through X-ray observations [11], BH shadow [1, 9, 10], thermodynamic properties [15], supernovae [31], gravitational lensing [13], quasinormal modes [7] and electromagnetic fields around neutron stars[18] have been extensively studied in the literature. Other properties of the MOG gravity and corresponding solutions have been explored in Refs. [3, 5, 6, 16, 17, 19, 23, 24].

Particle motion is a useful tool to test the gravity models and the properties of the spacetime around a compact gravitating object. On the other hand, the particle dynamics may lead to another interesting phenomenon related to QPOs. The source of the QPOs detected in X-ray are the microquasars, which are the binary system including the black hole. The friction of the accreting matter near the ISCO is the main dynamo of the X-ray radiation and corresponding QPO frequencies. Different models have been proposed to explain the nature and mechanism of the QPOs around compact object by several authors [21, 22, 27,28,29] including disc-seismic models, hot-spot models, warped disk models and resonance models. In this paper, we plan to study the QPO around a compact object described by different solutions.

Here we plan to analyse the Schwarzschild and regular MOG BHs solutions. The spacetime around spherical symmetric BHs describes by the following standard form [9, 15]:

$$\begin{aligned} \mathrm{d}s^2=-f(r)\mathrm{d}t^2+\frac{1}{f(r)}\mathrm{d}r^2+r^2 (d\theta ^2 +\sin ^2\theta d\phi ^2)\ , \end{aligned}$$
(1)

where f(r) is radial lapse function. The lapse function for the regular MOG (RMOG) BH has the following form

$$\begin{aligned} f(r)=1-\frac{2M}{r}\frac{\alpha +1}{\left[ 1+\alpha (\alpha +1) \frac{M^2}{r^2} \right] ^{3/2}} +\frac{\alpha (\alpha +1) \frac{M^2}{r^2}}{\left[ 1+\alpha (\alpha +1) \frac{M^2}{r^2} \right] ^{2}}, \end{aligned}$$
(2)

and for Schwarzschild-MOG (SMOG) BH reads as

$$\begin{aligned} f(r)=1-\frac{2(1+\alpha ) M}{r}+\frac{\alpha (1+\alpha )M^2}{r^2}. \end{aligned}$$
(3)

The both solution reduce to the Schwarzschild BH solution in the absence of SVTG field, at \(\alpha =0\).

2 Effective potential

In this section, we investigate test particle motion in the spacetime of a spherical symmetric black hole in MOG gravity. Here we use the Hamilton–Jacobi formalism and corresponding Hamiltonian in the form

$$\begin{aligned} \mathcal{H}=g^{\alpha \beta } \frac{\partial S}{\partial x^\alpha } \frac{\partial S}{\partial x^\beta }=\frac{1}{2} \kappa , \end{aligned}$$

with \(\kappa =-m^2\), where m is the mass of the test particle. The action \(\mathcal{S}\) for the Hamilton–Jacobi reads as

$$\begin{aligned} \mathcal{S}=-\frac{1}{2}\kappa \tau -Et+L\varphi +\mathcal{S}_{r}(r)+\mathcal{S}_{\theta }(\theta ), \end{aligned}$$
(4)

where E and L are the conserved quantities associated with the time translations and spatial rotations and describe the energy E and angular momentum L of the particle, respectively. \(S_{r}\) and \(S_{\theta }\) in Eq. (4) are the functions of only r and \(\theta \), respectively. Now one can easily rewrite the Hamilton–Jacobi equation in the following form,

$$\begin{aligned} \kappa =-\frac{E^2}{f(r)}+f(r) \left( \frac{\partial \mathcal{S}_{r}}{\partial r}\right) ^2 +\frac{1}{r^2}\left( \frac{\partial \mathcal{S}_{\theta }}{\partial \theta }\right) ^2+ \frac{L^2}{r^2\sin ^2\theta }. \end{aligned}$$
(5)

In case of spherical symmetric spacetime one may consider the motion of the particles at constant plane. Using Eq. (5) and radial equation of motion \(\dot{r}^2=\mathcal{E}^2-V_\mathrm{eff}(r)\) one may get the effective potential of radial motion in the following form:

$$\begin{aligned} V_\mathrm{eff}(r;\theta ,\mathcal{L})=f(r)\left( 1+\frac{\mathcal{L}^2}{r^2\sin ^2\theta }\right) , \end{aligned}$$
(6)

where \(\mathcal{E}=E/m\) and \(\mathcal{L}=L/m\) are specific energy and angular momentum per unit mass, respectively.

Fig. 1
figure 1

Radial profiles of the effective potential for the radial motion of test particles with specific angular momentum \(\mathcal{L}=4.3M\), around SMOG and RMOG BHs for the fixed value of the MOG parameter \(\alpha =0.1\)

Full size image

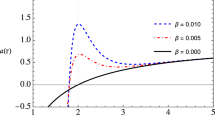
Radial dependence of effective potential for radial motion of test particles around regular and singular BHs in MOG is shown in Fig. 1 for the value of \(\alpha =0.1\). It is seen from the figure that the peak of the effective potential and its minimum are sufficiently decreased in the presence of MOG parameter \(\alpha =0.1\).

Now, we consider circular motion of test particles at the equatorial plane, defined by the conditions implying no radial motion (\(\dot{r}=0\)) and no forces (\(\ddot{r}=0\)) in the radial direction. In order to obtain the specific angular momentum and specific energy for circular motion of the particles at the equatorial plane around spherically symmetric BHs, one may use the standard conditions \(V_\mathrm{eff}(r,\mathcal{L})=\mathcal{E}, \quad \partial _r V_\mathrm{eff}(r,\mathcal{L})=0\) and get

$$\begin{aligned} \mathcal{L}^2= \frac{r^3 \partial _r\ln f(r)}{2-r \partial _r\ln f(r)} \ , \qquad \mathcal{E}^2=\frac{2 f(r)}{2-r \partial _r\ln f(r)}\ , \end{aligned}$$
(7)
Fig. 2
figure 2

Specific energy and angular momentum for the circular motion of test particles around SMOG and RMOG BHs as functions of the radial coordinate. In all plots, a fixed value of a parameter \(\alpha =0.1\) has been used

Full size image

Figure 2 shows the radial dependence of the specific energy (left panel) and angular momentum (right panel) of test particles around regular and Schwarzschild BHs in MOG. One can see from Fig. 2 that the minimum of the energy in MOG slightly decreases, while the angular momentum increases and shifts outward of the central BH. Note that in all plots we used \(\alpha =0.1\).

ISCO radius for the test particles around spherically symmetric BH is defines as the solution of the equation governed by the condition \(\partial _{rr}V \ge 0\):

$$\begin{aligned} \partial _r\ln f(r) f(r) (2 r \partial _r\ln f(r)-3)\ge r f''(r), \end{aligned}$$
(8)

where the prime \('\) stands for partial derivatives with respect to the radial coordinate. Numerical analysis has shown that ISCO radius increases with the increase of the MOG parameter for the both types of BH. However, it is increased faster in SMOG than RMOG model (see Fig. 4).

2.1 Keplerian frequency

The angular velocity for a distant observer, so-called the Keplerian frequency, is determined as

$$\begin{aligned} \varOmega _K=\frac{d\phi }{\mathrm{d}t}=\frac{\dot{\phi }}{\dot{t}}. \end{aligned}$$
(9)

One way of describing the Keplerian frequency in spacetime of a static BH is to rewrite the expression (9) in the following form

$$\begin{aligned} \varOmega _K=\sqrt{\frac{f'(r)}{2r}} . \end{aligned}$$
(10)

It is, respectively, for the SMOG and RMOG BHs takes the following forms,

$$\begin{aligned} \varOmega _K^S= & {} \frac{\sqrt{ (r-\alpha M)(\alpha +1) M}}{r^2}\\ \nonumber \varOmega _K^R= & {} \frac{\sqrt{\alpha +1} \sqrt{M}}{\left( \alpha (\alpha +1) M^2+r^2\right) ^{3/2}} \Bigg \{\alpha ^2 (\alpha +1) M^3-\alpha M r^2 \end{aligned}$$
(11)
$$\begin{aligned}&-\sqrt{1+\frac{\alpha (\alpha +1) M^2}{r^2}}r\left[ 2 \alpha (\alpha +1) M^2 -r^2\right] \Bigg \}^{\frac{1}{2}} . \end{aligned}$$
(12)

In order to have an idea abut the values of the fundamental frequencies, we express them in the units of Hz:

$$\begin{aligned} \nu = \frac{1}{2\pi }\frac{c^3}{GM} \varOmega . \end{aligned}$$
(13)

Converting from the geometrical unit to the unit of Hz, we use speed of light in vacuum and the gravitational constant as \(c=3\cdot 10^8 \mathrm{m/sec}\) and \(G=6.67\cdot 10^{-11}\mathrm{m}^3/(\mathrm{kg}^2\cdot \mathrm{sec})\), respectively.

2.2 Harmonic oscillations

Frequencies of radial and vertical oscillations of test particles orbiting can be obtained by equations for harmonic oscillator for displacements of the coordinates, \(\delta r\) and \(\delta \theta \) expanding the effective potential in terms of the coordinates,

$$\begin{aligned} \frac{d^2\delta r}{\mathrm{d}t^2}+\varOmega _r^2 \delta r=0\, \qquad \frac{d^2\delta \theta }{\mathrm{d}t^2}+\varOmega _\theta ^2 \delta \theta =0, \end{aligned}$$
(14)

where \(\varOmega _r\) and \(\varOmega _\theta \) are radial and angular frequencies measured by a distant observer, respectively. Using the following expressions,

$$\begin{aligned}&\varOmega _r^2=-\frac{1}{2g_{rr}(u^t)^2}\partial _r^2V_\mathrm{eff}(r,\theta )\Big |_{\theta =\pi /2}\ , \end{aligned}$$
(15)
$$\begin{aligned}&\varOmega _\theta ^2=-\frac{1}{2g_{\theta \theta }(u^t)^2}\partial _\theta ^2V_\mathrm{eff}(r,\theta )\Big |_{\theta =\pi /2}\ . \end{aligned}$$
(16)

One can easily calculate the radial and the vertical frequencies in the both solutions of MOG BHs using the above equations, and we will apply them to QPO models. Finally, radial and vertical frequencies (\(\varOmega _r\) and \(\varOmega _{\theta ,\phi }\)) around a static BH takes the following form,

$$\begin{aligned}&\varOmega _r =\varOmega _K \sqrt{\left( 3+\frac{r f''(r)}{f'(r)}\right) f(r)-2rf'(r)}\ , \end{aligned}$$
(17)
$$\begin{aligned}&\varOmega _\theta = \varOmega _K, \end{aligned}$$
(18)
$$\begin{aligned}&\varOmega _\phi =\varOmega _K. \end{aligned}$$
(19)

In the coming section we apply our calculations to QPO models.

3 QPO models in MOG

Investigation of twin peak QPOs around BHs is one of the interesting issues of relativistic astrophysics. Importance of this topic is connected with the effects of the models of gravity dominated around the BH and physical processes in which QPOs are generated. In other words, the effects of the parameters of regular and singular MOG BHs on QPOs can be compared with the effects due to the parameters of the Schwarzschild and Kerr BHs [26].

As mentioned above, it is hard to determine the type of the central BH of a twin-peaked QPO, analysing the X-ray data. On the other hand, different types of BH can play a role in the source of QPOs generating the same frequencies with the corresponding values of parameters of the solutions. Here, we aimed to show how to distinguish the types of BH through the analysis of twin peaked QPOs [20].

In this way, we suggest an approach to analyse QPOs constructing equations for the QPO’s upper and lower frequencies as functions of radial coordinate and including an additional BH parameter to its total mass within the framework of particular QPO model. For this, we will provide an exact value of the frequencies, keeping the BH parameter to be constant. Then, we plot all possible values of the lower and upper frequencies. As an example, the relativistic precession (RP) model proposed by Stella et al. [25] identifying upper and lower frequencies of twin peak QPOs by radial and orbital frequencies as \(\nu _U=\nu _\phi \) and \(\nu _L=\nu _\phi -\nu _r\), respectively, has been used. According to RP model, harmonic oscillations of test particles orbiting along circular geodesic orbits near the ISCO are used to explain the formation of QPOs.

Fig. 3
figure 3

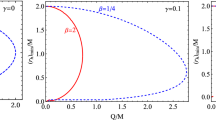
The figure shows the \(\nu _U-\nu _L\) diagram for twin peak QPOs in RP model. Large dashed line corresponds to extreme rotating Kerr BH model [30], red line corresponds to SMOG BHs and blue-dashed line stands for RMOG BH with the critical value of the parameter \(\alpha =\alpha _\mathrm{cr}=0.6727\). Inclined lines correspond to the QPOs with the ratio of upper and lower frequencies with the ratio 3:2. We imply that under the 1:1 line, any twin peak QPOs can be located. This means upper and lower peaks coincide with each other. Here, the value of the total mass of the BH is taken to be \(9M_\odot \) at the left panel and 12.5 \(M_\odot \) at the right one

Full size image

In Fig. 3, we demonstrate the relations between twin-peaked QPOs’ upper and lower frequencies generated around the Schwarzschild, Schwarzschild MOG, RMOG and extreme rotating Kerr BHs in RP model by test particles. For the central black hole mass, we used the value \(9M_{\odot }\) (left panel) and \(12.5M_\odot \) (right panel). One can see from inclined lines for the ratio of twin peak QPOs as 3:2 and the line with the ratio 1:1 being graveyard for the twin peak QPOs. It implies that if a QPO object lies on this line, the two peaks coincide with each other and becomes a single peak. Under the line, upper frequency becomes less than a lower one. For this reason, we can say under this line any twin peak QPOs can take place in their \(\nu _U-\nu _L\) space. Red and blue rectangles stand for the QPO objects called XTE 1150–564 (with mass 9\(M_\odot \), upper and lower frequencies: (179, 273) Hz) and GRS 1915+105 (with mass 12,5\(M_\odot \), and the peak frequencies: (113, 168) Hz), respectively. One can easily see that the data from the objects XTE 1150 – 564 and GRS 1915 + 105 are cannot be explained by both MOG BHs. However, one may numerically obtain that it can be modelled by a rotating Kerr BH at the centre of the objects with the parameter \(a \simeq 0.36M\) and \(a=0.16M_\odot \) with the total mass \(M=9M_\odot \) and \(M=12.5M_\odot \), respectively (see black-dotted line in Fig. 3). One can easily see that the central BH of these objects can be either a RMOG or SMOG BH with the negative MOG parameters. Our detailed numerical analyses have shown that the parameter can be for XTE 1150–564 \(\alpha =-0.33\) in RMOG BH model or \(\alpha =-0.48\) in SMOG BH one, while the object GRS 1915 + 105 can be powered by SMOG BH with \(\alpha =-0.17\) or RMOG BH with \(\alpha =-0.26\).

Now, we are interested in the distance from central BH to an orbit where particles generate the QPOs. We provide our analysis for twin peak QPOs with the ratio 3:2 by setting the equation

$$\begin{aligned} 3 \nu _L(r/M; \alpha ) =2 \nu _U(r/M; \alpha )\ . \end{aligned}$$
(20)

One can see that the equation has two unknown parameters: r/M and \(\alpha \) that makes it difficult to solve analytically. However, it is possible to get relations between the unknown quantities in graphics form for the models of RMOG and SMOG BHs.

Fig. 4
figure 4

The distance where QPO shine (solid lines) and ISCOs (dashed lines) around RMOG (blue lines) and SMOG (red lines) BHs

Full size image

Figure 4 shows the dependence of radius of orbits where the QPO with ratio 3:2 take place and ISCO position from MOG parameter. One can see from this figure that QPOs do not shine at ISCO, but at outer stable orbits. There is a correlation between ISCO and the orbits where QPOs are generated: as ISCO increase, the QPO goes outward from the central BH.

As an example, we study the distance where GRS J1915 + 105 and XTE 1550–564 QPOs shine from RMOG and SMOG BHs using their observational data.

Fig. 5
figure 5

The range of orbits of twin peak QPOs called GRS J1915 + 105 and XTE 1550–564 shine around SMOG (light-blue area) and RMOG (light-orange area) BHs

Full size image

The ranges of radii of orbits where the object GRS J1915 + 105 and XTE 1550–564 located around RMOG and SMOG BHs, are located in light-blue and light-orange areas, respectively. One can see from Fig. 5 that at small MOG parameters the possible orbits of GRS J1915 + 105 and XTE 1550 – 564 take place cross each other, and RMOG and SMOG BHs can not be distinguished. As the MOG parameter increase, the range of the orbits becomes larger and separable.

4 Conclusions

In this paper, we have investigated the possible way to distinguish RMOG and SMOG BHs using twin-peaked QPOs generated by test particles in stable orbits around the BHs. We have shown that the presence of MOG field causes sufficiently increase of the maximum of effective potential for the radial motion of test particles, and the effect of MOG field is stronger in SMOG BHs than RMOG. Similar results in the effect of MOG parameter on specific angular momentum and energy have been also obtained. We have focused on explorations of QPOs around the BHs in RP model and the relations of upper and lower frequencies of twin peak QPOs in SMOG and RMOG BH models together with extreme rotating Kerr and Schwarzschild BH. Moreover, possible parameters for the central BHs of the objects GRS J1915 + 105 and XTE 1550 – 564 have been also numerically studied. Finally, we have also provided comparisons ISCO and the orbits where twin peak QPOs with the ratio 3:2 are located and concluded that such QPOs can not be generated at/inside ISCO and there is a correlation between the radius of ISCO and QPO orbits.